1.3 Bases du langage R
R est un langage de programmation. Il vous permet de communiquer avec votre ordinateur pour lui donner des tâches à accomplir. Dans cette section, nous abordons les bases du langage. Ce type de section introductive à R est présente dans tous les manuels sur R; elle est donc incontournable. À la première lecture, elle vous semblera probablement aride, et ce, d’autant plus que nous ne réalisons pas d’analyse à proprement parler. Gardez en tête que l’analyse de données requiert au préalable une phase de structuration de ces dernières, opération qui nécessite la maîtrise des notions abordées dans cette section. Nous vous recommandons une première lecture de ce chapitre pour comprendre les manipulations que vous pouvez effectuer avec R, avant de poursuivre avec de la lecture des chapitres suivants dédiés aux analyses statistiques. Vous pourrez revenir consulter cette section au besoin. Notez aussi que la maîtrise des différents objets et des différentes opérations de base de R ne s’acquiert qu’en pratiquant. Vous gagnerez cette expertise au fil de vos prochains codes R, période durant laquelle vous pourrez consulter ce chapitre tel un guide de référence des objets et des notions fondamentales de R.
1.3.1 Hello World!
Une introduction à un langage de programmation se doit de commencer par le rite de passage Hello World. Il s’agit d’une forme de tradition consistant à montrer aux néophites comment afficher le message Hello World à l’écran avec le langage en question.
print("Hello World")## [1] "Hello World"Bravo! Vous venez officiellement de faire votre premier pas dans R!
1.3.2 Objets et expressions
Dans R, nous passons notre temps à manipuler des objets à l’aide d’expressions. Prenons un exemple concret : si vous tapez la syntaxe 4 + 3, vous manipulez deux objets (4 et 3) avec une expression indiquant que vous souhaitez obtenir la somme des deux objets.
4 + 3## [1] 7Cette expression est correcte, R comprend vos indications et effectue le calcul.
Il est possible d’enregistrer le résultat d’une expression et de le conserver dans un nouvel objet. On appelle cette opération : « déclarer une variable ».
ma_somme <- 4 + 3Concrètement, nous venons de demander à R d’enregistrer le résultat de 4 + 3 dans un espace spécifique de notre mémoire vive. Si vous regardez dans votre fenêtre Environment, vous verrez en effet qu’un objet appelé ma_somme est actuellement en mémoire et a pour valeur 7.
Notez ici que le nom des variables ne peut être composé que de lettres, de chiffres, de points (.) et de tirets bas (_) et doit commencer par une lettre. R est sensible à la casse; en d’autres termes, les variables Ma_somme, ma_sommE, ma_SOMME, et MA_SOMME renvoient toutes à un objet différent. Attention donc aux fautes de frappe. Si vous déclarez une variable en utilisant le nom d’une variable existante, la première est écrasée par la seconde :
age <- 35
age## [1] 35age <- 45
age## [1] 45Portez alors attention aux noms de variables que vous utilisez et réutilisez. Réutilisons notre objet ma_somme dans une nouvelle expression :
ma_somme2 <- ma_somme + ma_sommeAvec cette nouvelle expression, nous indiquons à R que nous souhaitons déclarer une nouvelle variable appelée ma_somme2, et que cette variable aura pour valeur ma_somme + ma_somme, soit 7 + 7. Sans surprise, ma_somme2 a pour valeur 14.
Notez que la mémoire vive (l’environnement) est vidée lorsque vous fermez R. Autrement dit, R perd complètement la mémoire lorsque vous le fermez. Vous pouvez bien sûr recréer vos objets en relançant les mêmes syntaxes. C’est pourquoi vous devez conserver vos feuilles de codes et ne pas seulement travailler dans la console. La console ne garde aucune trace de votre travail. Pensez donc à bien enregistrer votre code!
Nous verrons dans une prochaine section comment sauvegarder des objets et les recharger dans une session ultérieure de R (section 1.6). Ce type d’opération est pertinent quand le temps de calcul nécessaire à la production de certains objets est très long.
1.3.3 Fonctions et arguments
Dans R, nous manipulons le plus souvent nos objets avec des fonctions. Une fonction est elle-même un objet, mais qui a la particularité de pouvoir effectuer des opérations sur d’autres objets. Par exemple, déclarons l’objet taille avec une valeur de 175,897 :
taille <- 175.897Nous utilisons la fonction round, dont l’objectif est d’arrondir un nombre avec décimales pour obtenir un nombre entier.
round(taille)## [1] 176Pour effectuer leurs opérations, les fonctions ont généralement besoin d’arguments. Ici, taille est un argument passé à la fonction round. Si nous regardons la documentation de round avec help(round) (figure 1.11), nous constatons que cette fonction prend en réalité deux arguments : x et digits. Le premier est le nombre que nous souhaitons arrondir et le second est le nombre de décimales à conserver. Nous pouvons lire dans la documentation que la valeur par défaut de digits est 0, ce qui explique que round(taille) a produit le résultat de 176.

Figure 1.11: Arguments de la fonction round
Réutilisons maintenant la fonction round, mais en gardant une décimale :
round(taille, digits = 1)## [1] 175.9Il est aussi possible que certaines fonctions ne requièrent pas d’argument. Par exemple, la fonction now indique la date précise (avec l’heure) et n’a besoin d’aucun argument pour le faire :
now()## [1] "2023-02-24 22:07:46 EST"Par contre, si nous essayons de lancer la fonction round sans argument, nous obtenons une erreur :
round()
Le message est très clair, round a besoin d’au moins un argument pour fonctionner. Si, au lieu d’un nombre, nous avions donné du texte à la fonction round, nous aurions aussi obtenu une erreur :
round("Hello World")
À nouveau le message est très explicite : nous avons passé un argument non numérique à une fonction mathématique. Lisez toujours vos messages d’erreurs : ils permettent de repérer les coquilles et de corriger votre code!
Nous terminons cette section avec une fonction essentielle, print, qui permet d’afficher la valeur d’une variable.
print(ma_somme)## [1] 71.3.4 Principaux types de données
Depuis le début de ce chapitre, nous avons déclaré plusieurs variables et essentiellement des données numériques. Dans R, il existe trois principaux types de données de base :
- Les données numériques qui peuvent être des nombres entiers (appelés integers) ou des nombres décimaux (appelés floats ou doubles), par exemple
15et15.3. - Les données de type texte qui sont des chaînes de caractères (appelées strings) et déclarées entre guillemets
"abcdefg". - Les données booléennes (booleans) qui peuvent n’avoir que deux valeurs : vrai (
TRUE) ou faux (FALSE).
Déclarons une variable pour chacun de ces types :
age <- 35
taille <- 175.5
adresse <- '4225 rue de la gauchetiere'
proprietaire <- TRUESimples ou doubles quotes?
Pour déclarer des données de type texte, il est possible d’utiliser des quotes simples ' (apostrophe) ou des quotes doubles " (guillemets), cela ne fait aucune différence pour R. Cependant, si la chaîne de caractères que vous créez contient une apostrophe, il est nécessaire d’utiliser des quotes doubles et inversement si votre chaîne de caractère contient des guillemets.
phrase1 <- "J'adore le langage R!"
phrase2 <- 'Je cite : "il est le meilleur langage de statistique".'Si la chaîne de caractère contient des guillemets et des apostrophes, il est nécessaire d’utiliser la barre oblique inversée \ pour indiquer à R que ces apostrophes ou ces guillemets ne doivent pas être considérés comme la fin de la chaîne de caractère.
phrase3 <- "Je cite : \"j'en rêve la nuit\"."
cat(phrase3)## Je cite : "j'en rêve la nuit".Les barres obliques inversées ne font pas partie de la chaîne de caractère, ils sont là pour “échapper” les guillemets qui doivent rester dans la chaîne de caractère. Si une chaîne de caractère doit contenir une barre oblique inversée, alors il faut l’échapper également en utilisant une deuxième barre oblique inversée.
phrase4 <- "Une phrase avec une barre oblique inversée : \\"
cat(phrase4)## Une phrase avec une barre oblique inversée : \Faites attention à la coloration syntaxique de RStudio! Elle peut vous aider à repérer facilement une chaîne de caractère qui aurait été interrompue par un guillemet ou une apostrophe mal placés.
Si vous avez un doute sur le type de données stockées dans une variable, vous pouvez utiliser la fonction typeof. Par exemple, cela permet de repérer si des données qui sont censées être numériques sont en fait stockées sous forme de texte comme dans l’exemple ci-dessous.
typeof(age)## [1] "double"typeof(taille)## [1] "double"# Ici tailletxt est définie comme une chaîne de caractère car la valeur est
# définie entre des guillemets.
tailletxt <- "175.5"
typeof(tailletxt)## [1] "character"Notez également qu’il existe des types pour représenter l’absence de données :
- pour représenter un objet vide, nous utilisons l’objet
NULL, - pour représenter une donnée manquante, nous utilisons l’objet
NA, - pour représenter un texte vide, nous utilisons une chaîne de caractère de longueur 0, soit
"".
age2 <- NULL
taille2 <- NA
adresse2 <- ''1.3.5 Opérateurs
Nous avons vu que les fonctions permettent de manipuler des objets. Nous pouvons également effectuer un grand nombre d’opérations avec les opérateurs.
1.3.5.1 Opérateurs mathématiques
Les opérateurs mathématiques (tableau 1.1) permettent d’effectuer des calculs avec des données de type numérique.
| Opérateur | Description | Syntaxe | Résultat |
|---|---|---|---|
+
|
Addition |
4 + 4
|
8,0 |
-
|
Soustraction |
4 - 3
|
1,0 |
*
|
Multiplication |
4 * 3
|
12,0 |
/
|
Division |
12 / 4
|
3,0 |
^
|
Exponentiel |
4 ^ 3
|
64,0 |
**
|
Exponentiel |
4 ** 3
|
64,0 |
%%
|
Reste de division |
15,5 %% 2
|
1,5 |
%/%
|
Division entière |
15,5 %/% 2
|
7,0 |
1.3.5.2 Opérateurs relationnels
Les opérateurs relationnels (tableau 1.2) permettent de vérifier des conditions dans R. Ils renvoient un booléen, TRUE si la condition est vérifiée et FALSE si ce n’est pas le cas.
| Opérateur | Description | Syntaxe | Résultat |
|---|---|---|---|
==
|
Égalité |
4 == 4
|
TRUE |
!=
|
Différence |
4 != 4
|
FALSE |
>
|
Est supérieur |
5 > 4
|
TRUE |
<
|
Est inférieur |
5 < 4
|
FALSE |
>=
|
Est supérieur ou égal |
5 >= 4
|
TRUE |
<=
|
Est inférieur ou égal |
5 <= 4
|
FALSE |
1.3.5.3 Opérateurs logiques
Les opérateurs logiques (tableau 1.3) permettent de combiner plusieurs conditions :
L’opérateur ET (
&) permet de vérifier que deux conditions (l’une ET l’autre) sont TRUE. Si l’une des deux est FALSE, il renvoie FALSE.L’opérateur OU (
|) permet de vérifier que l’une des deux conditions est TRUE (l’une OU l’autre). Si les deux sont FALSE, alors il renvoie FALSE.L’opérateur NOT (
!) permet d’inverser une condition. Ainsi, NOT TRUE donne FALSE et NOT FALSE donne TRUE.
| Opérateur | Description | Syntaxe | Résultat |
|---|---|---|---|
&
|
ET |
TRUE & FALSE
|
FALSE |
|
|
OU |
TRUE | FALSE
|
TRUE |
!
|
NOT |
! TRUE
|
FALSE |
Prenons le temps pour un rapide exemple :
A <- 4
B <- 10
C <- -5
# Produit TRUE car A est bien plus petit que B et C est bien plus petit que A
A < B & C < A## [1] TRUE# Produit FALSE car si A est bien plus petit que B,
# B est en revanche plus grand que c
A < B & B < C## [1] FALSE# Produit TRUE car la seconde condition est inversée
A < B & ! B < C## [1] TRUE# Produit TRUE car au moins une des deux conditions est juste
A < B | B < C## [1] TRUENotez que l’opérateur ET est prioritaire sur l’opérateur OU et que les parenthèses sont prioritaires sur tous les opérateurs :
# Produit TRUE car nous commençons par tester A < B puis B < C ce qui donne FALSE
# On obtient ensuite
# FALSE | A > C
# Enfin, A est bien supérieur à C, donc l'une des deux conditions est vraie
A < B & B < C | A > C## [1] TRUENotez qu’en arrière-plan, les opérateurs sont en réalité des fonctions déguisées. Il est donc possible de définir de nouveaux comportements pour les opérateurs. Il est par exemple possible d’additionner ou de comparer des objets spéciaux comme des dates, des géométries, des graphes, etc.
1.3.6 Structures de données
Jusqu’à présent, nous avons utilisé des objets ne comprenant qu’une seule valeur. Or, des analyses statistiques nécessitent de travailler avec des volumes de données bien plus grands. Pour stocker des valeurs, nous travaillons avec différentes structures de données : les vecteurs, les matrices, les tableaux de données et les listes.
1.3.6.1 Vecteurs
Les vecteurs sont la brique élémentaire de R. Ils permettent de stocker une série de valeurs du même type dans une seule variable. Pour déclarer un vecteur, nous utilisons la fonction c() :
ages <- c(35,45,72,56,62)
tailles <- c(175.5,180.3,168.2,172.8,167.6)
adresses <- c('4225 rue de la gauchetiere',
'4223 rue de la gauchetiere',
'4221 rue de la gauchetiere',
'4219 rue de la gauchetiere',
'4217 rue de la gauchetiere')
proprietaires <- c(TRUE,TRUE,FALSE,TRUE,TRUE)Nous venons ainsi de déclarer quatre nouvelles variables étant chacune un vecteur de longueur cinq (comprenant chacun cinq valeurs). Ces vecteurs représentent, par exemple, les réponses de plusieurs personnes à un questionnaire.
Il existe dans R une subtilité à l’origine de nombreux malentendus : la distinction entre un vecteur de type texte et un vecteur de type facteur. Dans l’exemple précédent, le vecteur adresses est un vecteur de type texte. Chaque nouvelle valeur ajoutée dans le vecteur peut être n’importe quelle nouvelle adresse. Déclarons un nouveau vecteur qui contient cette fois-ci la couleur des yeux de personnes ayant répondu au questionnaire.
couleurs_yeux <- c('marron','marron','bleu','bleu','marron','vert')Contrairement aux adresses, il y a un nombre limité de couleurs que nous pouvons mettre dans ce vecteur. Il est donc intéressant de fixer les valeurs possibles du vecteur pour éviter d’en ajouter de nouvelles par erreur. Pour cela, nous devons convertir ce vecteur texte en vecteur de type facteur, ci-après nommé simplement facteur, avec la fonction as.factor.
couleurs_yeux_facteur <- as.factor(couleurs_yeux)Notez qu’à présent, nous pouvons ajouter une nouvelle couleur dans le premier vecteur, mais pas dans le second.
couleurs_yeux[7] <- "rouge"
couleurs_yeux_facteur[7] <- "rouge"## Warning in `[<-.factor`(`*tmp*`, 7, value = "rouge"): niveau de facteur incorrect, NAs générésLe message d’erreur nous informe que nous avons tenté d’introduire une valeur invalide dans le facteur.
Les facteurs peuvent sembler restrictifs et, très régulièrement, nous préférons travailler avec de simples vecteurs de type texte plutôt que des facteurs. Cependant, de nombreuses fonctions d’analyse nécessitent d’utiliser des facteurs, car ils assurent une certaine cohérence dans les données. Il est donc essentiel de savoir passer du texte au facteur avec la fonction as.factor. À l’inverse, il est parfois nécessaire de revenir à une variable de type texte avec la fonction as.character.
Notez que des vecteurs numériques peuvent aussi être convertis en facteurs :
tailles_facteur <- as.factor(tailles)Cependant, si vous souhaitez reconvertir ce facteur en format numérique, il faudra passer dans un premier temps par le format texte :
as.numeric(tailles_facteur)## [1] 4 5 2 3 1Comme vous pouvez le voir, convertir un facteur en valeur numérique renvoie des nombres entiers. Ceci est dû au fait que les valeurs dans un facteur sont recodées sous forme de nombres entiers, chaque nombre correspondant à une des valeurs originales (appelées niveaux). Si nous convertissons un facteur en valeurs numériques, nous obtenons donc ces nombres entiers.
as.numeric(as.character(tailles_facteur))## [1] 175.5 180.3 168.2 172.8 167.6Morale de l’histoire : ne confondez pas les données de type texte et de type facteur. Dans le doute, vous pouvez demander à R quel est le type d’un vecteur avec la fonction class.
class(tailles)## [1] "numeric"class(tailles_facteur)## [1] "factor"class(couleurs_yeux)## [1] "character"class(couleurs_yeux_facteur)## [1] "factor"Quasiment toutes les fonctions utilisent des vecteurs. Par exemple, nous pouvons calculer la moyenne du vecteur ages en utilisant la fonction mean présente de base dans R.
mean(ages)## [1] 54Cela démontre bien que le vecteur est la brique élémentaire de R! Toutes les variables que nous avons déclarées dans les sections précédentes sont aussi des vecteurs, mais de longueur 1.
1.3.6.2 Matrices
Il est possible de combiner des vecteurs pour former des matrices. Une matrice est un tableau en deux dimensions (colonnes et lignes) et est généralement utilisée pour représenter certaines structures de données comme des images (pixels), effectuer du calcul matriciel ou plus simplement présenter des matrices de corrélations. Vous aurez rarement à travailler directement avec des matrices, mais il est bon de savoir ce qu’elles sont. Créons deux matrices à partir de nos précédents vecteurs.
matrice1 <- cbind(ages,tailles)
# Afficher la matrice 1
print(matrice1)## ages tailles
## [1,] 35 175.5
## [2,] 45 180.3
## [3,] 72 168.2
## [4,] 56 172.8
## [5,] 62 167.6# Afficher les dimensions de la matrice 1 (1er chiffre : lignes; 2e chiffre : colonnes)
print(dim(matrice1))## [1] 5 2matrice2 <- rbind(ages, tailles)
# Afficher la matrice 2
print(matrice2)## [,1] [,2] [,3] [,4] [,5]
## ages 35.0 45.0 72.0 56.0 62.0
## tailles 175.5 180.3 168.2 172.8 167.6# Afficher les dimensions de la matrice 2
print(dim(matrice2))## [1] 2 5Comme vous pouvez le constater, la fonction cbind permet de concaténer des vecteurs comme s’ils étaient les colonnes d’une matrice, alors que rbind les combine comme s’ils étaient les lignes d’une matrice. La figure 1.12 présente graphiquement le passage du vecteur à la matrice.
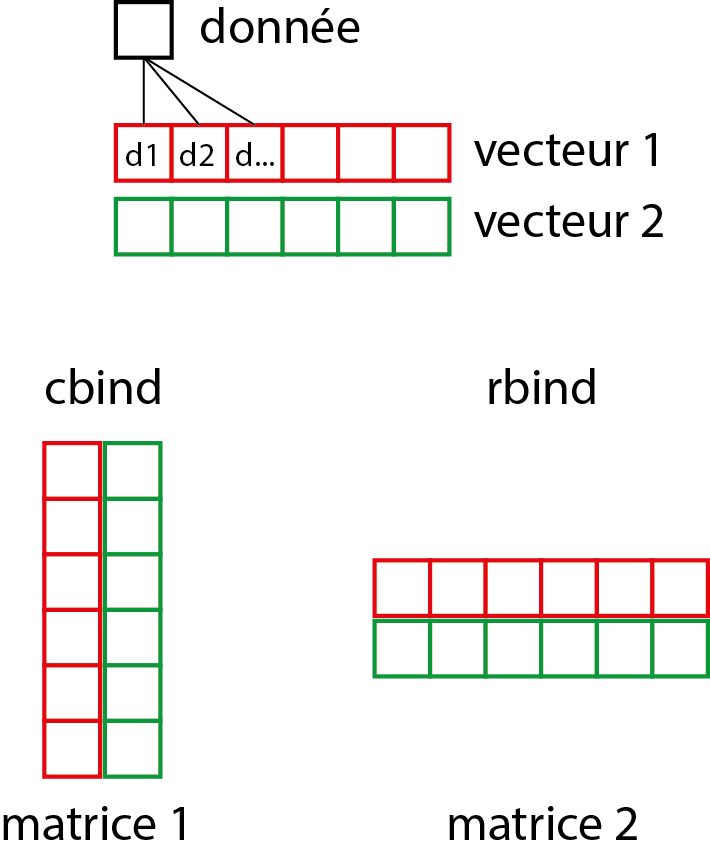
Figure 1.12: Du vecteur à la matrice
Notez que vous pouvez transposer une matrice avec la fonction t. Si nous essayons maintenant de comparer la matrice 1 à la matrice 2 nous allons avoir une erreur, car elles n’ont pas les mêmes dimensions.
matrice1 == matrice2
En revanche, nous pouvons transposer la matrice 1 et refaire cette comparaison :
t(matrice1) == matrice2## [,1] [,2] [,3] [,4] [,5]
## ages TRUE TRUE TRUE TRUE TRUE
## tailles TRUE TRUE TRUE TRUE TRUELe résultat souligne bien que nous avons les mêmes valeurs dans les deux matrices. Il est aussi possible de construire des matrices directement avec la fonction matrix, ce que nous montrons dans la prochaine section.
1.3.6.3 Arrays
S’il est rare de travailler avec des matrices, il est encore plus rare de manipuler des arrays. Un array est une matrice spéciale qui peut avoir plus que deux dimensions. Un cas simple serait un array en trois dimensions : lignes, colonnes, profondeur, que nous pourrions représenter comme un cube, ou une série de matrices de mêmes dimensions et empilées. Au-delà de trois dimensions, il devient difficile de les représenter mentalement. Cette structure de données peut être utilisée pour représenter les différentes bandes spectrales d’une image satellitaire. Les lignes et les colonnes délimiteraient les pixels de l’image et la profondeur délimiterait les différentes bandes composant l’image (figure 1.12).
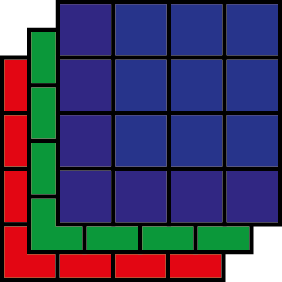
Figure 1.13: Un array avec trois dimensions
Créons un array en combinant trois matrices avec la fonction array. Chacune de ces matrices est composée respectivement de 1, de 2 et de 3 et a une dimension de 5 x 5. L’array final a donc une dimension de 5 x 5 x 3.
mat1 <- matrix(1, nrow = 5, ncol = 5)
mat2 <- matrix(2, nrow = 5, ncol = 5)
mat3 <- matrix(3, nrow = 5, ncol = 5)
mon_array <- array(c(mat1, mat2, mat3), dim = c(5,5,3))
print(mon_array)## , , 1
##
## [,1] [,2] [,3] [,4] [,5]
## [1,] 1 1 1 1 1
## [2,] 1 1 1 1 1
## [3,] 1 1 1 1 1
## [4,] 1 1 1 1 1
## [5,] 1 1 1 1 1
##
## , , 2
##
## [,1] [,2] [,3] [,4] [,5]
## [1,] 2 2 2 2 2
## [2,] 2 2 2 2 2
## [3,] 2 2 2 2 2
## [4,] 2 2 2 2 2
## [5,] 2 2 2 2 2
##
## , , 3
##
## [,1] [,2] [,3] [,4] [,5]
## [1,] 3 3 3 3 3
## [2,] 3 3 3 3 3
## [3,] 3 3 3 3 3
## [4,] 3 3 3 3 3
## [5,] 3 3 3 3 31.3.6.4 DataFrames
S’il est rare de manipuler des matrices et des arrays, le DataFrame (tableau de données en français) est la structure de données la plus souvent utilisée. Dans cette structure, chaque ligne du tableau représente un individu et chaque colonne représente une caractéristique de cet individu. Ces colonnes ont des noms qui permettent facilement d’accéder à leurs valeurs. Créons un DataFrame (tableau 1.4) à partir de nos quatre vecteurs et de la fonction data.frame.
df <- data.frame(
"age" = ages,
"taille" = tailles,
"adresse" = adresses,
"proprietaire" = proprietaires
)| age | taille | adresse | proprietaire |
|---|---|---|---|
| 35 | 175,5 | 4225 rue de la gauchetiere | TRUE |
| 45 | 180,3 | 4223 rue de la gauchetiere | TRUE |
| 72 | 168,2 | 4221 rue de la gauchetiere | FALSE |
| 56 | 172,8 | 4219 rue de la gauchetiere | TRUE |
| 62 | 167,6 | 4217 rue de la gauchetiere | TRUE |
Dans RStudio, vous pouvez visualiser votre tableau de données avec la fonction View(df). Comme vous pouvez le constater, chaque vecteur est devenu une colonne de votre tableau de données df. La figure 1.14 résume ce passage d’une simple donnée à un DataFrame en passant par un vecteur.
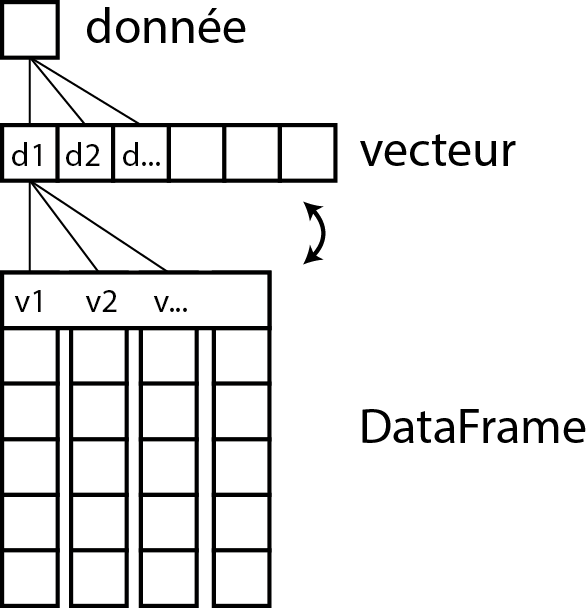
Figure 1.14: De la donnée au DataFrame
Plusieurs fonctions de base de R fournissent des informations importantes sur un DataFrame :
namesrenvoie les noms des colonnes du DataFrame;nrowrenvoie le nombre de lignes;ncolrenvoie le nombre de colonnes.
names(df)## [1] "age" "taille" "adresse" "proprietaire"nrow(df)## [1] 5ncol(df)## [1] 4Vous pouvez accéder à chaque colonne de df en utilisant le symbole $ ou [["nom_de_la_colonne"]]. Recalculons ainsi la moyenne des âges :
mean(df$age)## [1] 54mean(df[["age"]])## [1] 541.3.6.5 Listes
La dernière structure de données à connaître est la liste. Elle ressemble à un vecteur, au sens où elle permet de stocker un ensemble d’objets les uns à la suite des autres. Cependant, une liste peut contenir n’importe quel type d’objets. Vous pouvez ainsi construire des listes de matrices, des listes d’arrays, des listes mixant des vecteurs, des graphiques, des DataFrames, des listes de listes…
Créons ensemble une liste qui va contenir des vecteurs et des matrices à l’aide de la fonction list.
ma_liste <- list(c(1,2,3,4),
matrix(1, ncol = 3, nrow = 5),
matrix(5, ncol = 3, nrow = 7),
'A'
)Il est possible d’accéder aux éléments de la liste par leur position dans cette dernière en utilisant les doubles crochets [[ ]] :
print(ma_liste[[1]])## [1] 1 2 3 4print(ma_liste[[4]])## [1] "A"Il est aussi possible de donner des noms aux éléments de la liste et d’utiliser le symbole $ pour y accéder. Créons une nouvelle liste de vecteurs et donnons-leur des noms avec la fonction names.
liste2 <- list(c(35,45,72,56,62),
c(175.5,180.3,168.2,172.8,167.6),
c(TRUE,TRUE,FALSE,TRUE,TRUE)
)
names(liste2) <- c("age",'taille','proprietaire')
print(liste2$age)## [1] 35 45 72 56 62Si vous avez bien suivi, vous devriez avoir compris qu’un DataFrame n’est en fait rien d’autre qu’une liste de vecteurs avec des noms!
Bravo! Vous venez de faire le tour des bases du langage R. Vous allez apprendre désormais à manipuler des données dans des DataFrames!