8.1 Qu’est qu’un modèle GLM?
Nous avons vu qu’une régression linéaire multiple (LM) ne peut être appliquée que si la variable dépendante analysée est continue et si elle est normalement distribuée, une fois les variables indépendantes contrôlées. Il s’agit d’une limite très importante puisqu’elle ne peut être utilisée pour modéliser et prédire des variables binaires, multinomiales, de comptage, ordinales ou plus simplement des données anormalement distribuées. Une seconde limite importante des LM est que l’influence des variables indépendantes sur la variable dépendante ne peut être que linéaire. L’augmentation d’une unité de X conduit à une augmentation (ou diminution) de \(\beta\) (coefficient de régression) unités de Y, ce qui n’est pas toujours représentatif des phénomènes étudiés. Afin de dépasser ces contraintes, Nelder et Wedderburn (1972) ont proposé une extension des modèles LM, soit les modèles linéaires généralisés (GLM).
8.1.1 Formulation d’un GLM
Puisqu’un modèle GLM est une extension des modèles LM, il est possible de traduire un modèle LM sous forme d’un GLM. Nous utilisons ce point de départ pour détailler la morphologie d’un GLM. Nous avons vu dans la section précédente qu’un modèle LM est formulé de la façon suivante (notation matricielle) :
\[\begin{equation} Y = \beta_0 + X\beta + \epsilon \tag{8.1} \end{equation}\]
Avec \(\beta_0\) la constante (intercept en anglais) et \(\beta\) un vecteur de coefficients de régression pour les k variables indépendantes (X).
D’après cette formule, nous modélisons la variable Y avec une équation de régression linéaire et un terme d’erreur que nous estimons être normalement distribué. Nous pouvons reformuler ce simple LM sous forme d’un GLM avec l’écriture suivante :
\[\begin{equation} \begin{aligned} &Y \sim Normal(\mu,\sigma)\\ &g(\mu) = \beta_0 + \beta X\\ &g(x) = x \end{aligned} \tag{8.2} \end{equation}\]
Pas de panique! Cette écriture se lit comme suit : la variable Y est issue d’une distribution normale \((Y \sim Normal)\) avec deux paramètres : \(\mu\) (sa moyenne) et \(\sigma\) (son écart-type). \(\mu\) varie en fonction d’une équation de régression linéaire (\(\beta_0 + \beta X\)) transformée par une fonction de lien g (détaillée plus loin). Dans ce cas précis, la fonction de lien est appelée fonction identitaire puisqu’elle n’applique aucune transformation (\(g(x) = x\)). Notez ici que le second paramètre de la distribution normale \(\sigma\) (paramètre de dispersion) a une valeur fixe et ne dépend donc pas des variables indépendantes à la différence de \(\mu\). Dans ce modèle spécifiquement, les paramètres à estimer sont \(\sigma\), \(\beta_0\) et \(\beta\). Notez que dans la notation traditionnelle, la fonction de lien est appliquée au paramètre modélisé. Il est possible de renverser cette notation en utilisant la réciproque (\(g'\)) de la fonction de lien (\(g\)) :
\[\begin{equation} g(\mu) = \beta_0 + \beta X \Longleftrightarrow \mu = g'(\beta_0 + \beta X) \text{ si : }g'(g(x)) = x \tag{8.3} \end{equation}\]
Dans un modèle GLM, la distribution attendue de la variable Y est déclarée de façon explicite ainsi que la façon dont nos variables indépendantes conditionnent cette distribution. Ici, c’est la moyenne (\(\mu\)) de la distribution qui est modélisée, nous nous intéressons ainsi au changement moyen de Y provoqué par les variables X.
Avec cet exemple, nous voyons les deux composantes supplémentaires d’un modèle GLM :
- La distribution supposée de la variable Y conditionnée par les variables X (ici, la distribution normale).
- Une fonction de lien associant l’équation de régression formée par les variables indépendantes et un paramètre de la distribution retenue (ici, la fonction identitaire et le paramètre \(\mu\)).
Notez également que l’estimation des paramètres d’un modèle GLM (ici, \(\beta_0\), \(\beta X\) et \(\sigma\)) ne se fait plus avec la méthode des moindres carrés ordinaires utilisée pour les modèles LM. À la place, la méthode par maximum de vraisemblance (maximum likelihood) est la plus souvent utilisée, mais certains packages utilisent également la méthode des moments (method of moments). Ces deux méthodes nécessitent des échantillons plus grands que la méthode des moindres carrés. Dans le cas spécifique d’un modèle GLM utilisant une distribution normale, la méthode des moindres carrés et la méthode par maximum de vraisemblance produisent les mêmes résultats.
8.1.2 Autres distributions et rôle de la fonction de lien
À première vue, il est possible de se demander pourquoi ajouter ces deux éléments puisqu’ils ne font que complexifier le modèle. Pour mieux saisir la pertinence des GLM, prenons un exemple appliqué au cas d’une variable binaire. Admettons que nous souhaitons modéliser / prédire la probabilité qu’une personne à vélo décède lors d’une collision avec un véhicule motorisé. Notre variable dépendante est donc binaire (0 = survie, 1 = décès) et nous souhaitons la prédire avec trois variables continues que sont : la vitesse de déplacement du ou de la cycliste (\(x_1\)), la vitesse de déplacement du véhicule (\(x_2\)) et la masse du véhicule (\(x_3\)). Puisque la variable Y n’est pas continue, il serait absurde de supposer qu’elle est issue d’une distribution normale. Il serait plus logique de penser qu’elle provient d’une distribution de Bernoulli (pour rappel, une distribution de Bernoulli permet de modéliser un phénomène ayant deux issues possibles comme un lancer de pièce de monnaie, section 2.4). Plus spécifiquement, nous pourrions formuler l’hypothèse que nos trois variables \(x_1\), \(x_2\) et \(x_3\) influencent le paramètre p (la probabilité d’occurrence de l’évènement) d’une distribution de Bernoulli. À partir de ces premières hypothèses, nous pouvons écrire le modèle suivant :
\[\begin{equation} \begin{aligned} &Y \sim Bernoulli(p)\\ &g(p) = \beta_0 + \beta X\\ &g(x) = x \end{aligned} \tag{8.4} \end{equation}\]
Toutefois, le résultat n’est pas entièrement satisfaisant. En effet, p est une probabilité et, par nature, ce paramètre doit être compris entre 0 et 1 (entre 0 et 100 % de « chances de décès », ni plus ni moins). L’équation de régression que nous utilisons actuellement peut produire des résultats compris entre \(-\infty\) et \(+\infty\) pour p puisque rien ne contraint la somme \(\beta_0+ \beta_1x_1+\beta_2x_2+ \beta_3x_3\) à être comprise entre 0 et 1. Il est possible de visualiser le problème soulevé par cette situation avec les figures suivantes. Admettons que nous avons observé une variable Y binaire et que nous savons qu’elle est influencée par une variable X qui, plus elle augmente, plus les chances que Y soit 1 augmentent (figure 8.1).
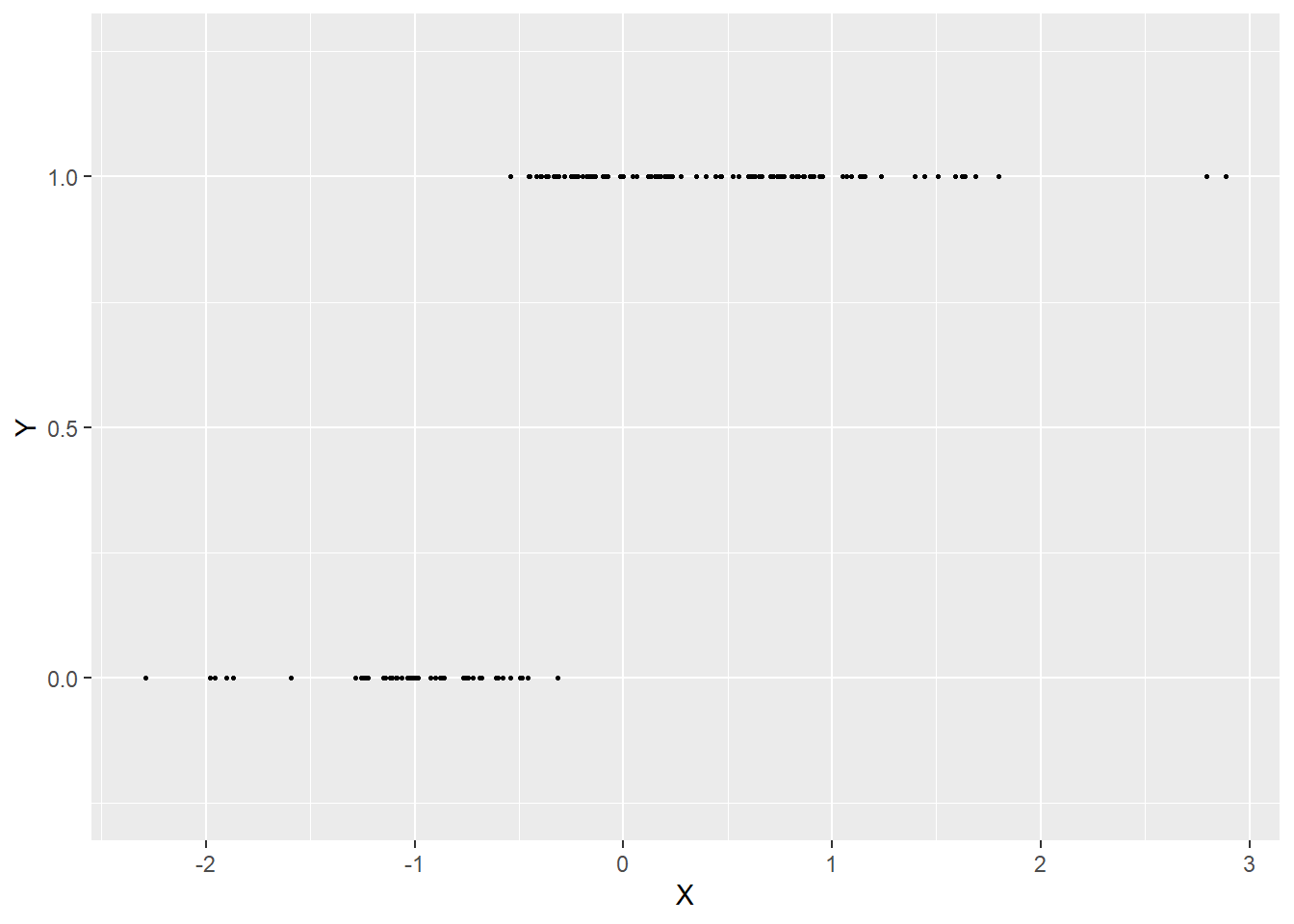
Figure 8.1: Exemple de données issues d’une distribution de Bernoulli
Si nous utilisons l’équation de régression actuelle, cela revient à trouver la droite la mieux ajustée passant dans ce nuage de points (figure 8.2).
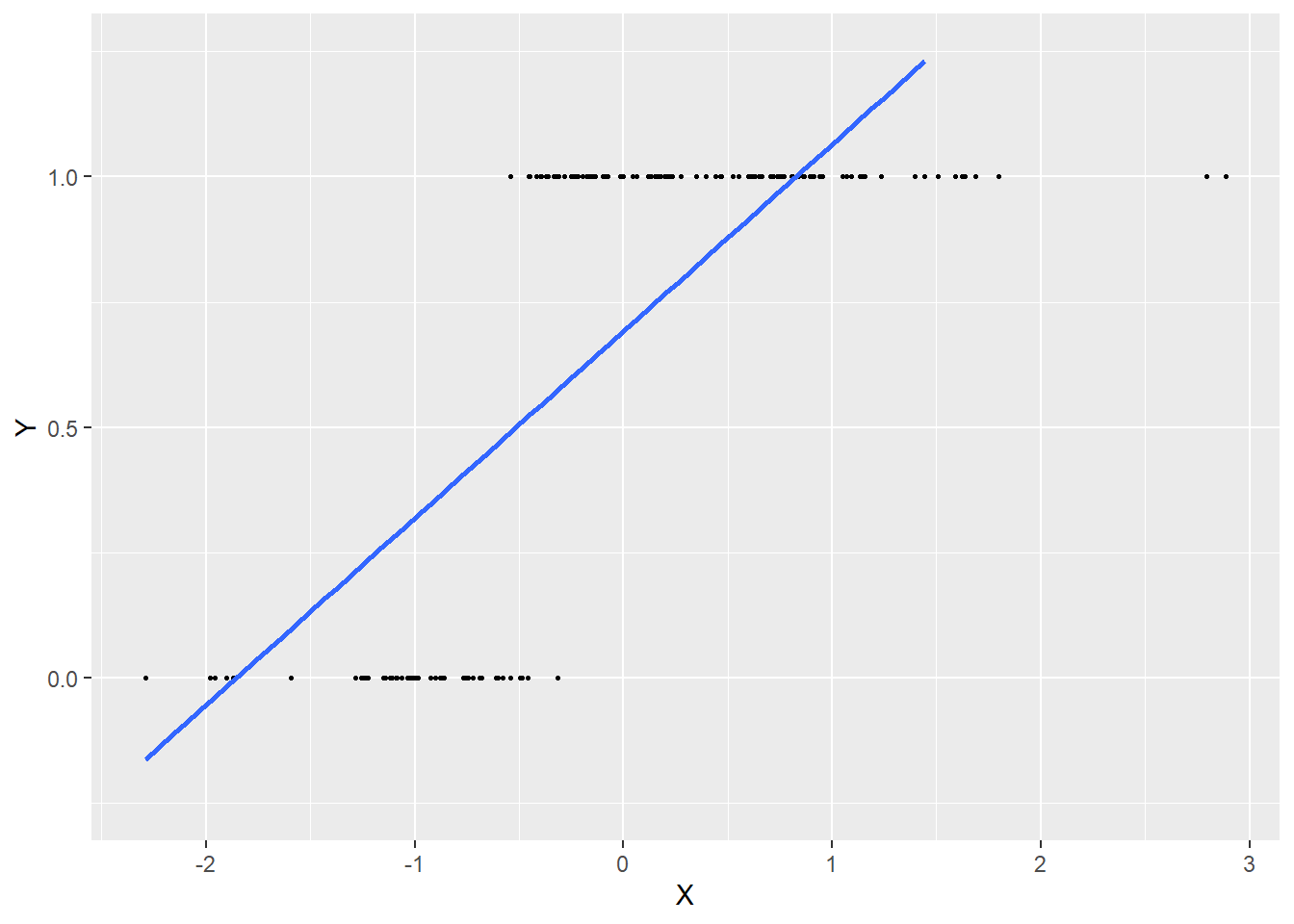
Figure 8.2: Ajustement d’une droite de régression aux données issues d’une distribution de Bernoulli
Ce modèle semble bien cerner l’influence positive de X sur Y, mais la droite est au final très éloignée de chaque point, indiquant un faible ajustement du modèle. De plus, la droite prédit des probabilités négatives lorsque X est inférieur à −2,5 et des probabilités supérieures à 1 quand X est supérieur à 1. Elle est donc loin de bien représenter les données.
C’est ici qu’intervient la fonction de lien. La fonction identitaire que nous avons utilisée jusqu’ici n’est pas satisfaisante, nous devons la remplacer par une fonction qui conditionnera la somme \(\beta_0+ \beta_1x_1+\beta_2x_2+ \beta_3x_3\) pour donner un résultat entre 0 et 1. Une candidate toute désignée est la fonction sigmoidale, plus souvent appelée la fonction logistique!
\[\begin{equation} \begin{aligned} &Y \sim Bernoulli(p)\\ &S(p) = \beta_0 + \beta X\\ &S(x) = \frac{e^{x}}{e^x+1} \end{aligned} \tag{8.5} \end{equation}\]
La fonction logistique prend la forme d’un S. Plus la valeur entrée dans la fonction est grande, plus le résultat produit par la fonction est proche de 1 et inversement. Si nous reprenons l’exemple précédent, nous obtenons le modèle illustré à la figure 8.3.

Figure 8.3: Utilisation de la fonction de lien logistique
Une fois cette fonction insérée dans le modèle, nous constatons qu’une augmentation de la somme \(\beta_0+ \beta_1x_1+\beta_2x_2+ \beta_3x_3\) conduit à une augmentation de la probabilité p et inversement, et que cet effet est non linéaire. Nous avons donc maintenant un GLM permettant de prédire la probabilité d’un décès lors d’un accident en combinant une distribution et une fonction de lien adéquates.
8.1.3 Conditions d’application
La famille des GLM englobe de (très) nombreux modèles du fait de la diversité de distributions existantes et des fonctions de liens utilisables. Cependant, certaines combinaisons sont plus souvent utilisées que d’autres. Nous présentons donc dans les prochaines sections les modèles GLM les plus communs. Les conditions d’application varient d’un modèle à l’autre, il existe cependant quelques conditions d’application communes à tous ces modèles :
- l’indépendance des observations (et donc des erreurs);
- l’absence de valeurs aberrantes / fortement influentes;
- l’absence de multicolinéarité excessive entre les variables indépendantes.
Ces trois conditions sont également valables pour les modèles LM tel qu’abordés dans le chapitre 7. La distance de Cook peut ainsi être utilisée pour détecter les potentielles valeurs aberrantes et le facteur d’inflation de la variance (VIF) pour détecter la multicolinéarité. Les conditions d’application particulières sont détaillées dans les sections dédiées à chaque modèle.
8.1.4 Résidus et déviance
Dans la section sur la régression linéaire simple, nous avons présenté la notion de résidu, soit l’écart entre la valeur observée (réelle) de Y et la valeur prédite par le modèle. Pour un modèle GLM, ces résidus traditionnels (aussi appelés résidus naturels) ne sont pas très informatifs si la variable à modéliser est binaire, multinomiale ou même de comptage. Lorsque l’on travaille avec des GLM, nous préférons utiliser trois autres formes de résidus, soit les résidus de Pearson, les résidus de déviance et les résidus simulés.
Les résidus de Pearson sont une forme ajustée des résidus classiques, obtenus par la division des résidus naturels par la racine carrée de la variance modélisée. Leur formule varie donc d’un modèle à l’autre puisque l’expression de la variance change en fonction de la distribution du modèle. Pour un modèle GLM gaussien, elle s’écrit :
\[\begin{equation} r_i = \frac{y_i - \mu_i}{\sigma} \tag{8.6} \end{equation}\]
Pour un modèle GLM de Bernoulli, elle s’écrit :
\[\begin{equation} r_i = \frac{y_i - p_i}{\sqrt{p_i(1-p_i)}} \tag{8.7} \end{equation}\]
avec \(\mu_i\) et \(p_i\) les préditions du modèle pour l’observation i.
Les résidus de déviance sont basés sur le concept de likelihood présenté dans la section 2.5.4.2. Pour rappel, le likelihood, ou la vraisemblance d’un modèle, correspond à la probabilité conjointe d’avoir observé les données Y selon le modèle étudié. Pour des raisons mathématiques (voir section 2.5.4.2), le log likelihood est plus souvent calculé. Plus cette valeur est forte, moins le modèle se trompe. Cette interprétation est donc inverse à celle des résidus classiques, c’est pourquoi le log likelihood est généralement multiplié par −2 pour retrouver une interprétation intuitive. Ainsi, pour chaque observation i, nous pouvons calculer :
\[\begin{equation} d_i = \mbox{-2} \times log(P(y_i|M_e)) \tag{8.8} \end{equation}\]
avec \(d_i\) le résidu de déviance et \(P(y_i|M_e)\) la probabilité d’avoir observé la valeur \(y_i\) selon le modèle étudié (\(M_e\)).
La somme de tous ces résidus est appelée la déviance totale du modèle.
\[\begin{equation} D(M_e) = \sum_{i=1}^n \mbox{-2} \times log(P(y_i|M_e)) \tag{8.9} \end{equation}\]
Il s’agit donc d’une quantité représentant à quel point le modèle est erroné vis-à-vis des données. Notez qu’en tant que telle, la déviance n’a pas d’interprétation directe en revanche, elle est utilisée pour calculer des mesures d’ajustement des modèles GLM.
Les résidus simulés sont une avancée récente dans le monde des GLM, ils fournissent une définition et une interprétation harmonisée des résidus pour l’ensemble des modèles GLM. Dans la section sur les LM (voir section 7.2.2), nous avons vu comment interpréter les graphiques des résidus pour détecter d’éventuels problèmes dans le modèle. Cependant, cette technique est bien plus compliquée à mettre en œuvre pour les GLM puisque la forme attendue des résidus varie en fonction de la distribution choisie pour modéliser Y. La façon la plus efficace de procéder est d’interpréter les graphiques des résidus simulés qui ont la particularité d’être identiquement distribués, quel que soit le modèle GLM construit. Ces résidus simulés sont compris entre 0 et 1 et sont calculés de la manière suivante :
À partir du modèle GLM construit, simuler S fois (généralement 1 000) une variable Y’ avec autant d’observation (n) que Y. Cette variable simulée est une combinaison de la prédiction du modèle (coefficient et variables indépendantes) et de sa dispersion (variance). Ces simulations représentent des variations vraisemblables de la variable Y si le modèle est correctement spécifié. En d’autres termes, si le modèle représente bien le phénomène à l’origine de la variable Y, alors les simulations Y’ issues du modèle devraient être proches de la variable Y originale. Pour une explication plus détaillée de ce que signifie simuler des données à partir d’un modèle, référez-vous au bloc attention intitulé Distinction entre simulation et prédiction dans la section 8.1.5.2.
Pour chaque observation, nous obtenons ainsi S valeurs formant une distribution \(Ds_i\), soit les valeurs simulées par le modèle pour cette observation.
Pour chacune de ces distributions, nous calculons la probabilité cumulative d’observer la vraie valeur \(Y_i\) d’après la distribution \(Ds_i\). Cette valeur est comprise entre 0 (toutes les valeurs simulées sont plus grandes que \(Y_i\)) et 1 (toutes les valeurs simulées sont inférieures à \(Y_i\)).
Si le modèle est correctement spécifié, le résultat attendu est que la distribution de ces résidus est uniforme. En effet, il y a autant de chances que les simulations produisent des résultats supérieurs ou inférieurs à \(Y_i\) si le modèle représente bien le phénomène (Dunn et Smyth 1996; Gelman et Hill 2006). Si la distribution des résidus ne suit pas une loi uniforme, cela signifie que le modèle échoue à reproduire le phénomène à l’origine de Y, ce qui doit nous alerter sur sa pertinence.
8.1.5 Vérification l’ajustement
Il existe trois façons de vérifier l’ajustement d’un modèle GLM :
- utiliser des mesures d’ajustement (AIC, pseudo-R2, déviance expliquée, etc.);
- comparer les distributions de la variable originale et celle des prédictions;
- comparer les prédictions du modèle avec les valeurs originales.
Notez d’emblée que vérifier la qualité d’ajustement d’un modèle (ajustement aux données originales) ne revient pas à vérifier la validité d’un modèle (respect des conditions d’application). Cependant, ces deux éléments sont généralement liés, car un modèle mal ajusté a peu de chances d’être valide et inversement.
8.1.5.1 Mesures d’ajustement
Les mesures d’ajustement sont des indicateurs plus ou moins arbitraires dont le principal intérêt est de faciliter la comparaison entre plusieurs modèles similaires. Il est nécessaire de les reporter, car dans certains cas, ils peuvent indiquer que des modèles sont très mal ajustés.
8.1.5.1.1 Déviance expliquée
Rappelons que la déviance d’un modèle est une quantité représentant à quel point le modèle est erroné. L’objectif de l’indicateur de la déviance expliquée est d’estimer le pourcentage de la déviance maximale observable dans les données que le modèle est parvenu à expliquer. La déviance maximale observable dans les données est obtenue en utilisant la déviance totale du modèle nul (notée \(M_n\), soit un modèle dans lequel aucune variable indépendante n’est ajoutée et ne comportant qu’une constante). Cette déviance est maximale puisqu’aucune variable indépendante n’est présente dans le modèle. Nous calculons ensuite le pourcentage de cette déviance totale qui a été contrôlée par le modèle étudié (\(M_e\)).
\[\begin{equation} \mbox{déviance expliquée} = \frac{D(M_n) - D(M_e)}{D(M_n)} = 1- \frac{D(M_e)}{D(M_n)} \tag{8.10} \end{equation}\]
Il s’agit donc d’un simple calcul de pourcentage entre la déviance maximale (\(D(M_n)\)) et la déviance expliquée par le modèle étudié (\(D(M_n )-D(M_e)\)). Cet indicateur est compris entre 0 et 1 : plus il est petit, plus la capacité de prédiction du modèle est faible. Attention, cet indicateur ne tient pas compte de la complexité du modèle. Ajouter une variable indépendante supplémentaire ne fait qu’augmenter la déviance expliquée, ce qui ne signifie pas que la complexification du modèle soit justifiée (voir l’encadré sur le principe de parcimonie, section 7.3.2).
8.1.5.1.2 Pseudo-R2
Le R2 est une mesure d’ajustement représentant la part de la variance expliquée dans un modèle linéaire classique. Cette mesure n’est pas directement transposable au cas des GLM puisqu’ils peuvent être appliqués à des variables non continues et anormalement distribuées. Toutefois, il existe des mesures semblables appelées pseudo-R2, remplissant un rôle similaire. Notez cependant qu’ils ne peuvent pas être interprétés comme le R2 classique (d’une régression linéaire multiple) : ils ne représentent pas la part de la variance expliquée. Ils sont compris dans l’intervalle 0 et 1; plus leurs valeurs s’approchent de 1, plus le modèle est ajusté.
| Nom | Formule | Commentaire |
|---|---|---|
| McFadden | \(1-\frac{loglike(M_e)}{loglike(M_n)}\) | Le rapport des loglikelihood, très proche de la déviance expliquée. |
| McFadden ajusté | \(1-\frac{loglike(M_e)-K}{loglike(M_n)}\) | Version ajustée du R2 de McFadden tenant compte du nombre de paramètres (k) dans le modèle. |
| Efron | \(1-\frac{\sum_{i=1}^n(y_i-\hat{y}_i)^2}{\sum_{i=1}^n(y_i-\bar{y}_i)^2}\) | Rapport entre la somme des résidus classiques au carré (numérateur) et de la somme des écarts au carré à la moyenne (dénominateur). Notez que pour un GLM gaussien, ce pseudo-R2 est identique au R2 classique. |
| Cox & Snell | \(1-e^{-\frac{2}{n}({loglike(M_e) - loglike(M_n))}}\) | Transformation de la déviance afin de la mettre sur une échelle de 0 à 1 (mais ne pouvant atteindre exactement 1). |
| Nagelkerke | \(\frac{1-e^{-\frac{2}{n}({loglike(M_e) - loglike(M_n))}}}{1-e^{\frac{2*loglike(M_n)}{n}}}\) | Ajustement du R2 de Cox et Snell pour que l’échelle de valeurs possibles puisse comporter 1 (attention, car les valeurs de ce R2 tendent à être toujours plus fortes que les autres). |
En dehors du pseudo-R2 de McFadden ajusté, aucune de ces mesures ne tient compte de la complexité du modèle. Il est cependant important de les reporter, car des valeurs très faibles indiquent vraisemblablement un modèle avec une moindre capacité informative. À l’inverse, des valeurs trop fortes pourraient indiquer un problème de surajustement (voir encadré sur le principe de parcimonie, section 7.3.2).
8.1.5.1.3 Critère d’information d’Akaike (AIC)
Probablement l’indicateur le plus répandu, sa formule est relativement simple, car il s’agit seulement d’un ajustement de la déviance :
\[\begin{equation} AIC = D(M_e) + 2K \tag{8.11} \end{equation}\]
avec K le nombre de paramètres à estimer dans le modèle (coefficients, paramètres de distribution, etc.).
L’AIC n’a pas d’interprétation directe, mais permet de comparer deux modèles imbriqués (voir section 7.3.2). Plus l’AIC est petit, mieux le modèle est ajusté. L’idée derrière cet indicateur est relativement simple. Si la déviance D est grande, alors le modèle est mal ajusté. Ajouter des paramètres (des coefficients pour de nouvelles variables X, par exemple) ne peut que réduire D, mais cette réduction n’est pas forcément suffisamment grande pour justifier la complexification du modèle. L’AIC pondère donc D en lui ajoutant 2 fois le nombre de paramètres du modèle. Un modèle plus simple (avec moins de paramètres) parvenant à une même déviance est préférable à un modèle complexe (principe de parcimonie ou du rasoir d’Ockham), ce que permet de « quantifier » l’AIC. Attention, l’AIC ne peut pas être utilisé pour comparer des modèles non imbriqués. Notez que d’autres indicateurs similaires comme le WAIC, le BIC et le DIC sont utilisés dans un contexte d’inférence bayésienne. Retenez simplement que ces indicateurs sont conceptuellement proches du AIC et s’interprètent (à peu de choses près) de la même façon.
8.1.5.2 Comparaison des distributions originales et prédites
Une façon rapide de vérifier si un modèle est mal ajusté est de comparer la forme de la distribution originale et celle capturée par le modèle. L’idée est la suivante : si le modèle est bien ajusté aux données, il est possible de se servir de celui-ci pour générer de nouvelles données dont la distribution ressemble à celle des données originales. Si une différence importante est observable, alors les résultats du modèle ne sont pas fiables, car le modèle échoue à reproduire le phénomène étudié. Cette lecture graphique ne permet pas de s’assurer que le modèle est valide ou bien ajusté, mais simplement d’écarter rapidement les mauvais candidats. Notez que cette méthode ne s’applique pas lorsque la variable modélisée est binaire, multinomiale ou ordinale. Le graphique à réaliser comprend donc la distribution de la variable dépendante Y (représentée avec un histogramme ou un graphique de densité) et plusieurs distributions simulées à partir du modèle. Cette approche est plus répandue dans la statistique bayésienne, mais elle reste pertinente dans l’approche fréquentiste. Il est rare de reporter ces figures, mais elles doivent faire partie de votre diagnostic.
Distinction entre simulation et prédiction
Notez ici que simuler des données à partir d’un modèle et effectuer des prédictions à partir d’un modèle sont deux opérations différentes. Prédire une valeur à partir d’un modèle revient simplement à appliquer son équation de régression à des données. Si nous réutilisons les mêmes données, la prédiction renvoie toujours le même résultat, il s’agit de la partie systématique (ou déterministe) du modèle. Pour illustrer cela, admettons que nous avons ajusté un modèle GLM de type gaussien (fonction de lien identitaire) avec trois variables continues \(X_1\), \(X_2\) et \(X_3\) et des coefficients respectifs de 0,5, 1,2 et 1,8 ainsi qu’une constante de 7. Nous pouvons utiliser ces valeurs pour prédire la valeur attendue de \(Y\) quand \(X_1= 3\), \(X_2= 5\) et \(X_3 = 5\) :
\(\mbox{Prédiction} = \mbox{7 + 3}\times \mbox{0,5 + 5}\times \mbox{1,2 + 5}\times\mbox{1,8 = 23,5}\)
En revanche, simuler des données à partir d’un modèle revient à ajouter la dimension stochastique (aléatoire) du modèle. Puisque notre modèle GLM est gaussien, il comporte un paramètre \(\sigma\) (son écart-type); admettons, pour cet exemple, qu’il est de 1,2. Ainsi, avec les données précédentes, il est possible de simuler un ensemble infini de valeurs dont la distribution est la suivante : \(Normal(\mu = \mbox{23,5, } \sigma = \mbox{1,2})\). 95 % du temps, ces valeurs simulées se trouveront dans l’intervalle \(\mbox{[21,1-25,9]}\) (\(\mu - 2\sigma \text{; } \mu + 2\sigma\)), puisque cette distribution est normale. Les valeurs simulées dépendent donc de la distribution choisie pour le modèle et de l’ensemble des paramètres du modèle, pas seulement de l’équation de régression.
Si vous aviez à ne retenir qu’une seule phrase de ce bloc, retenez que la prédiction ne se réfère qu’à la partie systématique du modèle (équation de régression), alors que la simulation incorpore la partie stochastique (aléatoire) de la distribution du modèle. Deux prédictions effectuées sur des données identiques donnent nécessairement des résultats identiques, ce qui n’est pas le cas pour la simulation.
8.1.5.3 Comparaison des prédictions du modèle avec les valeurs originales
Les prédictions d’un modèle devraient être proches des valeurs réelles observées. Si ce n’est pas le cas, alors le modèle n’est pas fiable et ses paramètres ne sont pas informatifs. Dépendamment de la nature de la variable modélisée (quantitative ou qualitative), plusieurs approches peuvent être utilisées pour quantifier l’écart entre valeurs réelles et valeurs prédites.
8.1.5.3.1 Pour une variable quantitative
La mesure la plus couramment utilisée pour une variable quantitative est l’erreur moyenne quadatrique (Root Mean Square Error – RMSE en anglais).
\[\begin{equation} RMSE = \sqrt{\frac{\sum_{i=1}^n(y_i - \hat{y_i})^2}{n}} \tag{8.12} \end{equation}\]
Il s’agit de la racine carrée de la moyenne des écarts au carré entre valeurs réelles et prédites. Le RMSE est exprimé dans la même unité que la donnée originale et nous donne une indication sur l’erreur moyenne de la prédiction du modèle. Admettons, par exemple, que nous modélisons les niveaux de bruit environnemental en ville en décibels et que notre modèle de régression ait un RMSE de 3,5. Cela signifierait qu’en moyenne notre modèle se trompe de 3,5 décibels (erreur pouvant être négative ou positive), ce qui serait énorme (3 décibels correspond à une multiplication par deux de l’intensité sonore) et nous amènerait à reconsidérer la fiabilité du modèle. Notez que l’usage d’une moyenne quadratique plutôt qu’une moyenne arithmétique permet de donner plus d’influence aux larges erreurs et donc de pénaliser davantage des modèles faisant parfois de grosses erreurs de prédiction. Le RMSE est donc très sensible à la présence de valeurs aberrantes. À la place de la moyenne quadratique, il est possible d’utiliser la simple moyenne arithmétique des valeurs absolues des erreurs (MAE). Cette mesure est cependant moins souvent utilisée :
\[\begin{equation} MAE = \frac{\sum_{i=1}^n|y_i - \hat{y_i|}}{n} \tag{8.13} \end{equation}\]
Ces deux mesures peuvent être utilisées pour comparer la capacité de prédiction de deux modèles appliqués aux mêmes données, même s’ils ne sont pas imbriqués. Elles ne permettent cependant pas de prendre en compte la complexité du modèle. Un modèle plus complexe aura toujours des valeurs de RMSE et de MAE plus faibles.
8.1.5.3.2 Pour une variable qualitative
Lorsque l’on modélise une variable qualitative, une erreur revient à prédire la mauvaise catégorie pour une observation. Il est ainsi possible de compter, pour un modèle, le nombre de bonnes et de mauvaises prédictions et d’organiser cette information dans une matrice de confusion. Cette dernière prend la forme suivante pour un modèle binaire :
| Valeur prédite / Valeur réelle | A | B | Total (%) |
|---|---|---|---|
| A | 15 | 3 | 18 (41,9) |
| B | 5 | 20 | 25 (51,1) |
| Total (%) | 20 (46,6) | 23 (53,5) | 43 (81,4) |
En colonne du tableau 8.2, nous avons les catégories observées et en ligne, les catégories prédites. La diagonale représente les prédictions correctes. Dans le cas présent, le modèle a bien catégorisé 35 (15 + 20) observations sur 43, soit une précision totale de 81,4 %; huit sont mal classifiées (18,6 %); cinq avec la modalité A ont été catégorisées comme des B, soit 20 % des A, et seuls trois B ont été catégorisées comme des A (13 %).
La matrice ci-dessus (tableau 8.2) ne comporte que deux catégories possibles puisque la variable Y modélisée est binaire. Il est facile d’étendre le concept de matrice de confusion au cas des variables avec plus de deux modalités (multinomiale). Le tableau 8.3 est un exemple de matrice de confusion multinomiale.
| Valeur prédite / Valeur réelle | A | B | C | D | Total (%) |
|---|---|---|---|---|---|
| A | 15 | 3 | 1 | 5 | 24 (18,7) |
| B | 5 | 20 | 2 | 12 | 39 (30,4) |
| C | 2 | 10 | 25 | 8 | 45 (35,2) |
| D | 1 | 0 | 5 | 14 | 20 (15,6) |
| Total (%) | 23 (18,1) | 33 (25,7) | 33 (25,7) | 39 (30,5) | 128 |
Trois mesures pour chaque catégorie peuvent être utilisées pour déterminer la capacité de prédiction du modèle :
- La précision (precision en anglais), soit le nombre de fois où une catégorie a été correctement prédite, divisée par le nombre de fois où la catégorie a été prédite.
- Le rappel (recall en anglais), soit le nombre de fois où une catégorie a été correctement prédite divisée par le nombre de fois où elle se trouve dans les données originales.
- Le score F1 est la moyenne harmonique entre la précision et le rappel, soit :
\[\begin{equation} \text{F1} = 2 \times \frac{\text{précision} \times \text{rappel}}{\text{précision} + \text{rappel}} \tag{8.14} \end{equation}\]
Il est possible de calculer les moyennes pondérées des différents indicateurs (macro-indicateurs) afin de disposer d’une valeur d’ensemble pour le modèle. La pondération est faite en fonction du nombre de cas observé de chaque catégorie; l’idée étant qu’il est moins grave d’avoir des indicateurs plus faibles pour des catégories moins fréquentes. Cependant, il est tout à fait possible que cette pondération ne soit pas souhaitable. C’est par exemple le cas dans de nombreuses études en santé portant sur des maladies rares où l’attention est concentrée sur ces catégories peu fréquentes.
Le coefficient de Kappa (variant de 0 à 1) peut aussi être utilisé pour quantifier la fidélité générale de la prédiction du modèle. Il est calculé avec l’équation (8.15) :
\[\begin{equation} k = \frac{Pr(a)-Pr(e)}{1-Pr(e)} \tag{8.15} \end{equation}\]
avec \(Pr(a)\) la proportion d’accord entre les catégories observées et les catégories prédites, et \(Pr(e)\) la probabilité d’un accord alétoire entre les catégories observées et les catégories prédites (équation (8.16))
\[\begin{equation} Pr(e) = \sum^{J}_{j=1} \frac{Cnt_{prédit}(j)}{n\times2} \times \frac{Cnt_{réel}(j)}{n\times2} \tag{8.16} \end{equation}\]
avec n le nombre d’observations, \(Cnt_{prédit}(j)\) le nombre de fois où le modèle prédit la catégorie j et \(Cnt_{réel}(j)\) le nombre de fois où la catégorie j a été observée.
Pour l’interprétation du coefficient de Kappa, référez-vous au tableau 8.4.
| K | Interprétation |
|---|---|
| < 0 | Désaccord |
| 0 - 0,20 | Accord très faible |
| 0,21 - 0,40 | Accord faible |
| 0,41 - 0,60 | Accord modéré |
| 0,61 - 0,80 | Accord fort |
| 0,81 - 1 | Accord presque parfait |
Enfin, un test statistique basé sur la distribution binomiale peut être utilisé pour vérifier que le modèle atteint un niveau de précision supérieur au seuil de non-information. Ce seuil correspond à la proportion de la modalité la plus présente dans le jeu de données. Dans la matrice de confusion utilisée dans le tableau 8.4, ce seuil est de 30,5 % (catégorie D), ce qui signifie qu’un modèle prédisant tout le temps la catégorie D aurait une précision de 30,5 % pour cette catégorie. Il est donc nécessaire que notre modèle fasse mieux que ce seuil.
Dans le cas de la matrice de confusion du tableau 8.3, nous obtenons donc les valeurs affichées dans le tableau 8.5.
| précision | rappel | F1 | |
|---|---|---|---|
| A | 65,2 | 31,3 | 42,3 |
| B | 60,6 | 25,6 | 36,0 |
| C | 75,8 | 27,8 | 40,7 |
| D | 35,9 | 35,0 | 35,4 |
| macro | 57,8 | 30,0 | 38,2 |
| Kappa | 0,44 | ||
| Valeur de p (précision > NIR) | < 0,0001 |
À la lecture du tableau 8.5, nous remarquons que :
- la catégorie D est la moins bien prédite des quatre catégories (faible précision et faible rappel);
- la catégorie C a une forte précision, mais un faible rappel, ce qui signifie que de nombreuses observations étant originalement des A, B ou D ont été prédites comme des C. Ce constat est également vrai pour la catégorie B;
- le coefficient de Kappa indique un accord modéré entre les valeurs originales et la prédiction;
- la probabilité que la précision du modèle ne dépasse pas le seuil de non-information est inférieure à 0,001, indiquant que le modèle à une précision supérieure à ce seuil.
8.1.6 Comparaison de deux modèles GLM
Tel qu’abordé dans le chapitre sur les régressions linéaires classiques, il est courant de comparer plusieurs modèles imbriqués (section 7.3.2). Cette procédure permet de déterminer si l’ajout d’une ou de plusieurs variables contribue à significativement améliorer le modèle. Il est possible d’appliquer la même démarche aux GLM à l’aide du test de rapport de vraisemblance (likelihood ratio test). Le principe de base de ce test est de comparer le likelihood de deux modèles GLM imbriqués; la valeur de ce test se calcule avec l’équation suivante :
\[\begin{equation} LR = 2(loglik(M_2) - loglik(M_1)) \tag{8.17} \end{equation}\]
avec \(M_2\) un modèle reprenant toutes les variables du modèle \(M_1\), impliquant donc que \(loglik(M_2) >= loglik(M_1)\).
Avec ce test, nous supposons que le modèle \(M_2\), qui comporte plus de paramètres que le modèle \(M_1\), devrait être mieux ajusté aux données. Si c’est bien le cas, la différence entre les loglikelihood de deux modèles devrait être supérieure à zéro. La valeur calculée LR suit une distribution du khi-deux avec un nombre de degrés de liberté égal au nombre de paramètres supplémentaires dans le modèle \(M_2\) comparativement à \(M_1\). Avec ces deux informations, il est possible de déterminer la valeur de p associée à ce test et de déterminer si \(M_2\) est significativement mieux ajusté que \(M_1\) aux données. Notez qu’il existe aussi deux autres tests (test de Wald et test de Lagrange) ayant la même fonction. Il s’agit, dans les deux cas, d’approximation du test de rapport des vraisemblances dont la puissance statistique est inférieure au test de rapport de vraisemblance (Neyman, Pearson et Pearson 1933).
Dans les prochaines sections, nous décrivons les modèles GLM les plus couramment utilisés. Il en existe de nombreuses variantes que nous ne pouvons pas toutes décrire ici. L’objectif est de comprendre les rouages de ces modèles afin de pouvoir, en cas de besoin, transposer ces connaissances sur des modèles plus spécifiques. Pour faciliter la lecture de ces sections, nous vous proposons une carte d’identité de chacun des modèles présentés. Elles contiennent l’ensemble des informations pertinentes à retenir pour chaque modèle.