11.1 Introduction
Puisque les modèles GAM sont une extension des modèles GLM, ils peuvent s’appliquer à des modèles pour des variables indépendantes qualitatives, de comptage ou continues. Nous l’appliquons ici, à titre d’illustration, à une variable indépendante continue. Pour rappel, la formule décrivant un modèle linéaire généralisé (GLM) utilisant une distribution normale et une fonction de lien identitaire est la suivante :
\[\begin{equation} \begin{aligned} &Y \sim Normal(\mu,\sigma)\\ &g(\mu) = \beta_0 + \beta X\\ &g(x) = x \end{aligned} \tag{11.1} \end{equation}\]
Les coefficients \(\beta\) permettent de quantifier l’effet des variables indépendantes (X) sur la moyenne (l’espérance) (\(\mu\)) de la variable dépendante (Y). Un coefficient \(\beta_k\) négatif indique que, si la variable \(X_k\) augmente, alors la variable Y tend à diminuer et inversement, si le coefficient est positif. L’inconvénient de cette formulation est que le modèle est capable de capter uniquement des relations linéaires entre ces variables. Or, il existe de nombreuses situations dans lesquelles une variable indépendante a un lien non linéaire avec une variable dépendante; voici quelques exemples :
- Si nous mesurons le niveau de bruit émis par une source sonore (variable dépendante) à plusieurs endroits et que nous tentons de prédire l’intensité sonore en fonction de la distance à la source (variable indépendante), nous pouvons nous attendre à observer une relation non linéaire entre les deux. En effet, le son étant une énergie se dispersant selon une sphère dans l’espace, son intensité est inversement proportionnelle au carré de la distance avec la source sonore.
- La concentration de la pollution atmosphérique en ville suit généralement des patrons temporels et spatiaux influencés directement par la météorologie et les activités humaines. Autrement dit, il serait absurde d’introduire l’espace de façon linéaire (avec un gradient nord-sud ou est-ouest), ou le moment de la journée de façon linéaire (comme si la pollution augmentait du matin au soir ou inversement). En guise d’exemple, la figure 11.1, tirée de Gelb et Apparicio (2020), illustre bien ces variations temporelles pour deux polluants (le dioxyde d’azote et l’ozone).
Figure 11.1: Patron journalier du dioxyde d’azote et de l’ozone à Paris
11.1.1 Non linéarité fonctionnelle
Il existe de nombreuses façons d’introduire des relations non linéaires dans un modèle. La première et la plus simple à mettre en oeuvre est de transformer la variable indépendante à l’aide d’une fonction inverse, exponentielle, logarithmique ou autre.
Prenons un premier exemple avec une variable Y que nous tentons de prédire avec une variable X, présenté à la figure 11.2. Si nous ajustons une droite de régression à ces données (en bleu), nous constatons que l’augmentation de X est associée à une augmentation de Y. Cependant, la droite de régression est très éloignée des données et ne capte qu’une petite partie de la relation. Une lecture attentive permet de constater que l’effet de X sur Y augmente de plus en plus rapidement à mesure que X augmente. Cette forme est caractéristique d’une relation exponentielle. Nous pouvons donc transformer la variable X avec la fonction exponentielle afin d’obtenir un meilleur ajustement (en rouge).
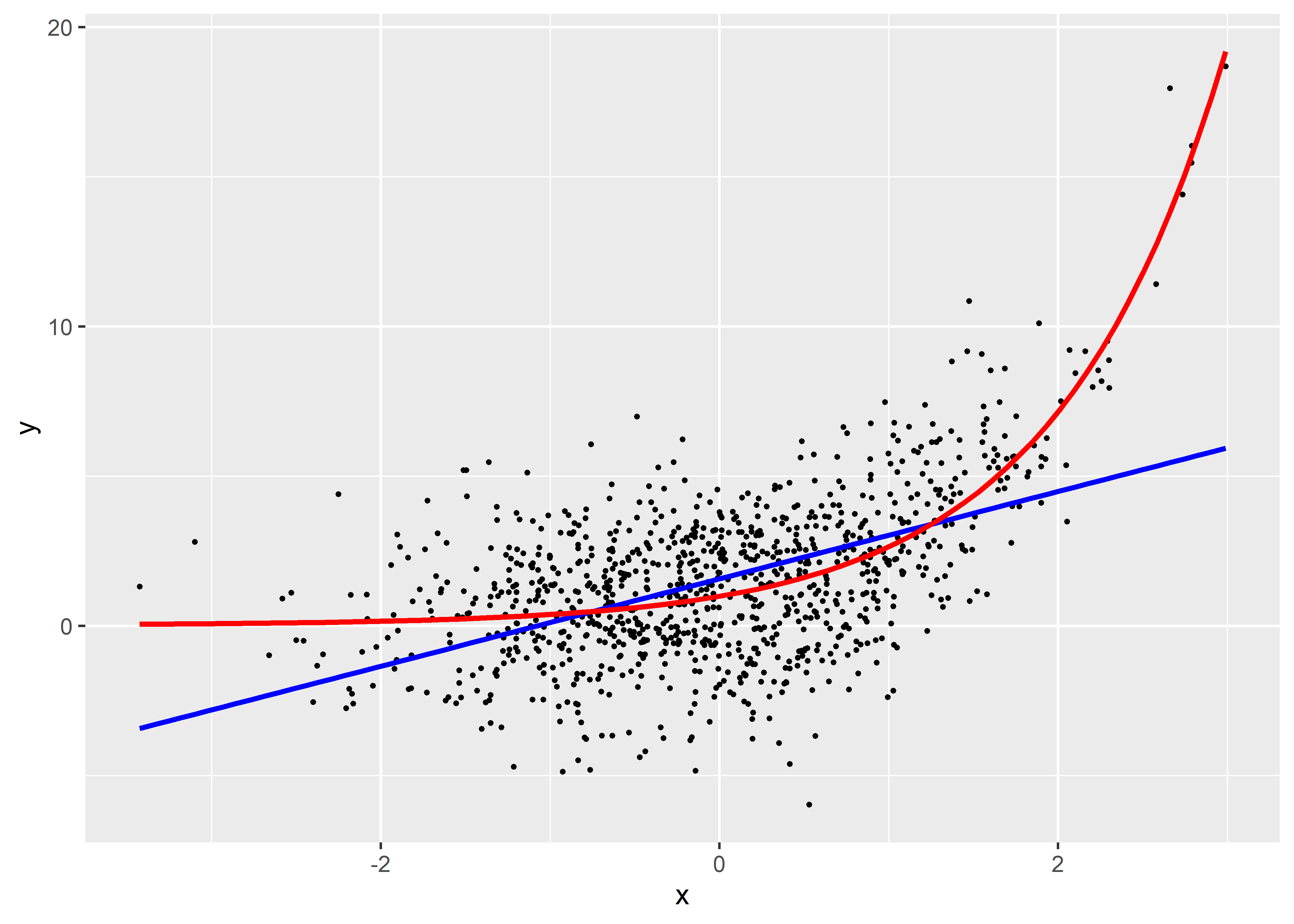
Figure 11.2: Relation non linéaire exponentielle
La figure 11.3 illustre trois autres situations avec les fonctions logarithmique, logistique inverse et racine carrée. Cette approche peut donner des résultats intéressants si vous disposez d’une bonne justification théorique sur la forme attendue de la relation entre X et Y.
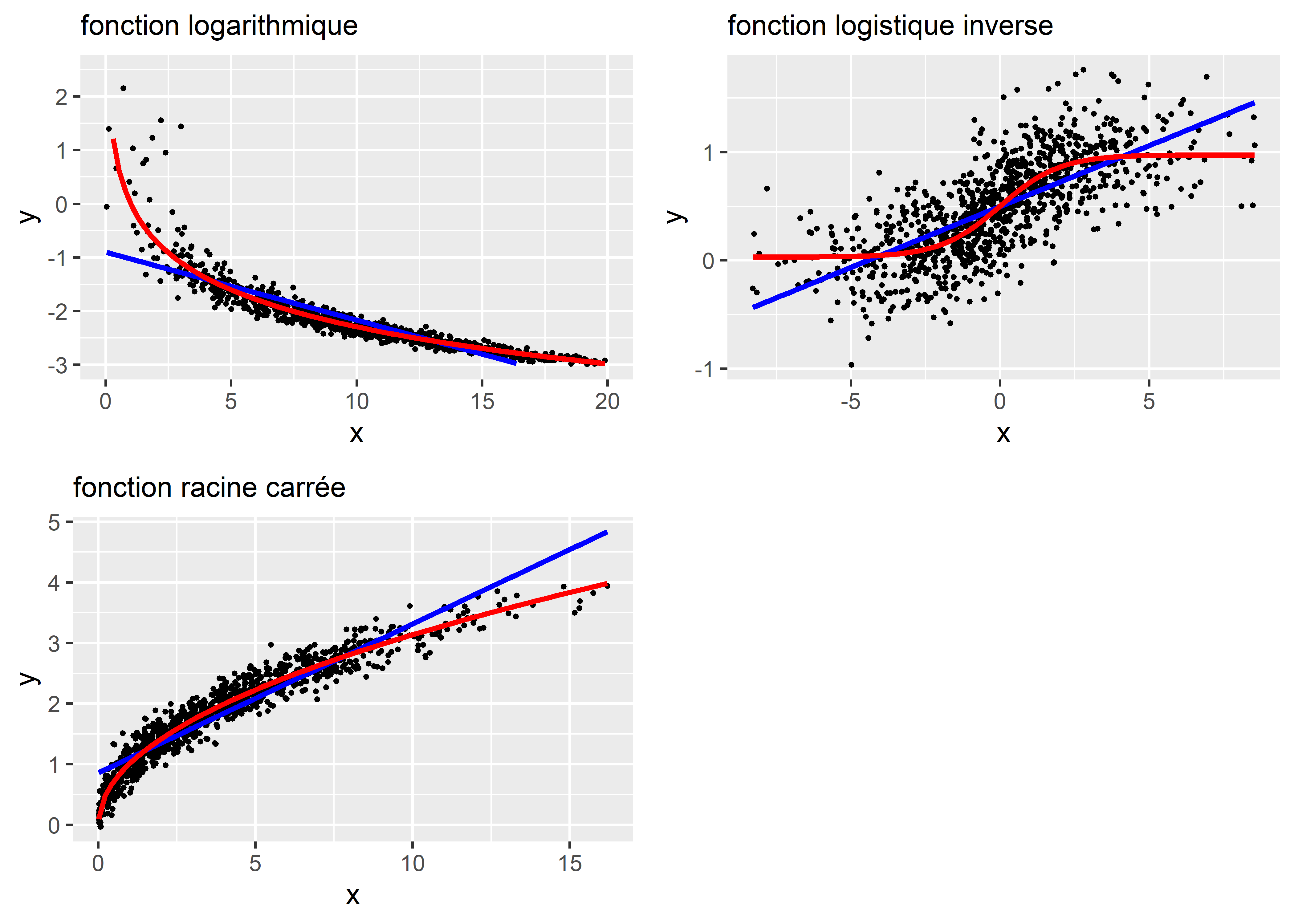
Figure 11.3: Autres relations non linéaires
Il existe également des cas de figure dans lesquels aucune fonction ne donne de résultats pertinents, tel qu’illustré à la figure 11.4. Nous constatons facilement qu’aucune des fonctions proposées n’est capable de bien capter la relation entre les deux variables. Puisque cette relation est complexe, il convient alors d’utiliser une autre stratégie pour la modéliser.
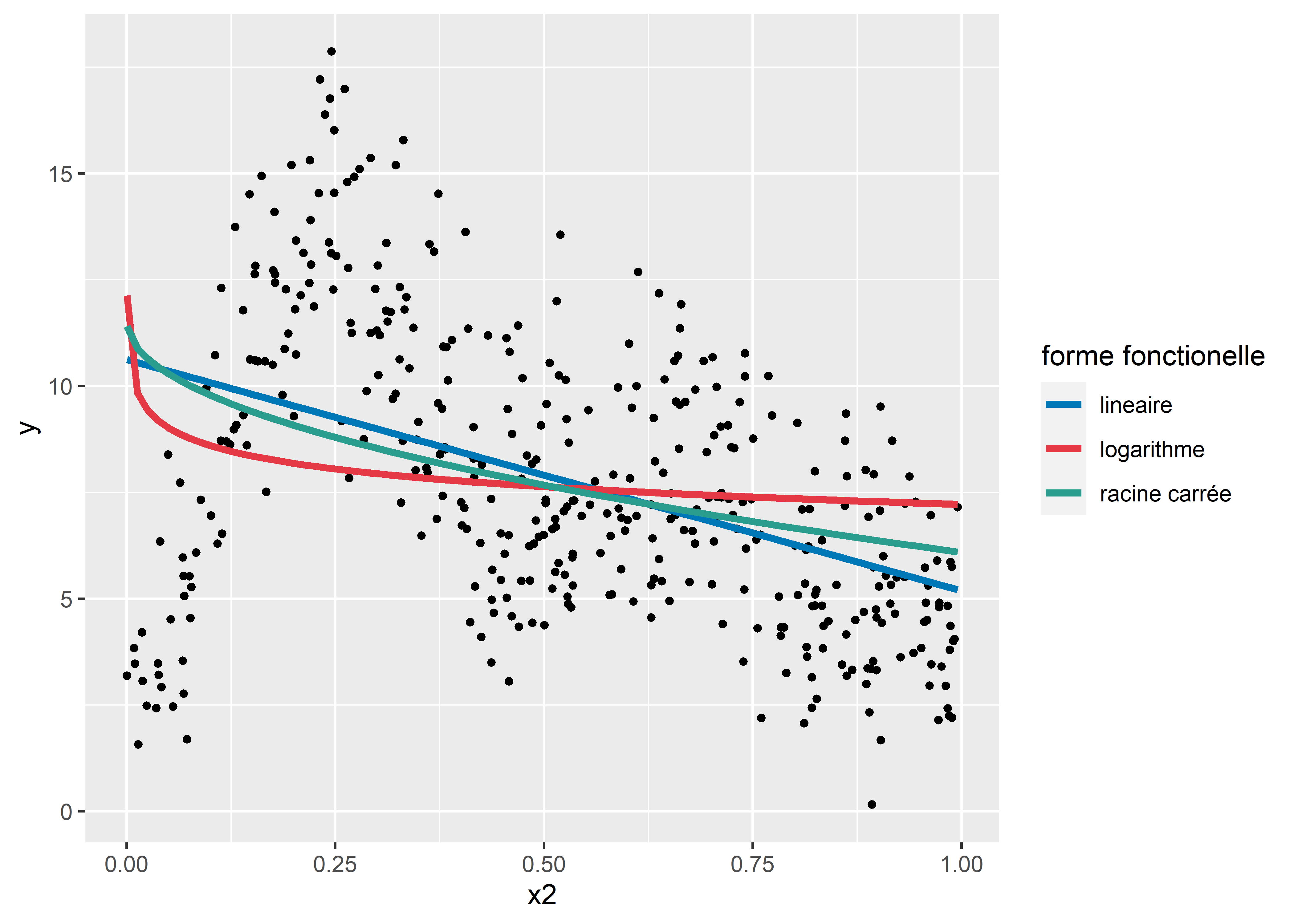
Figure 11.4: Relation non linéaire plus complexe
11.1.2 Non linéarité avec des polynomiales
Nous avons vu, dans le chapitre sur la régression simple (section 7.5.1.1), qu’il est possible d’utiliser des polynomiales pour ajuster des relations non linéaires. Pour rappel, il s’agit simplement d’ajouter à un modèle la variable X à différents exposants (\(X+X^2+\dots+X^k\)). Chaque exposant supplémentaire (chaque ordre supplémentaire) permet au modèle d’ajuster une relation plus complexe. Rien de tel qu’un graphique pour illustrer le tout (figure 11.5).
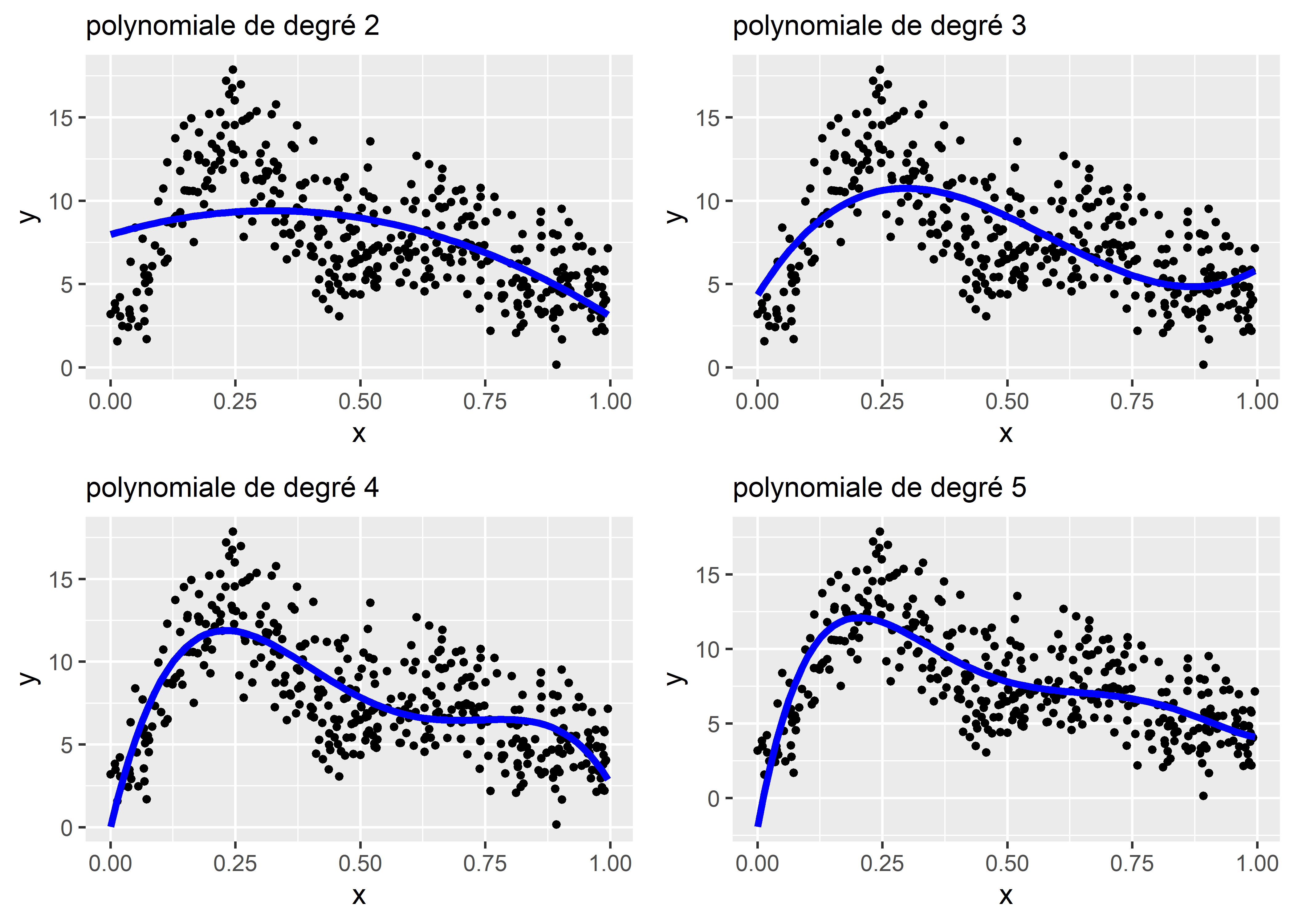
Figure 11.5: Visualisation de plusieurs polynomiales
L’enjeu est de sélectionner le bon nombre de degrés de la polynomiale pour le modèle. Chaque degré supplémentaire constitue une nouvelle variable dans le modèle, et donc un paramètre supplémentaire. Un trop faible nombre de degrés produit des courbes trop simplistes, alors qu’un nombre trop élevé conduit à un surajustement (overfitting en anglais) du modèle. La figure 11.6 illustre ces deux situations.
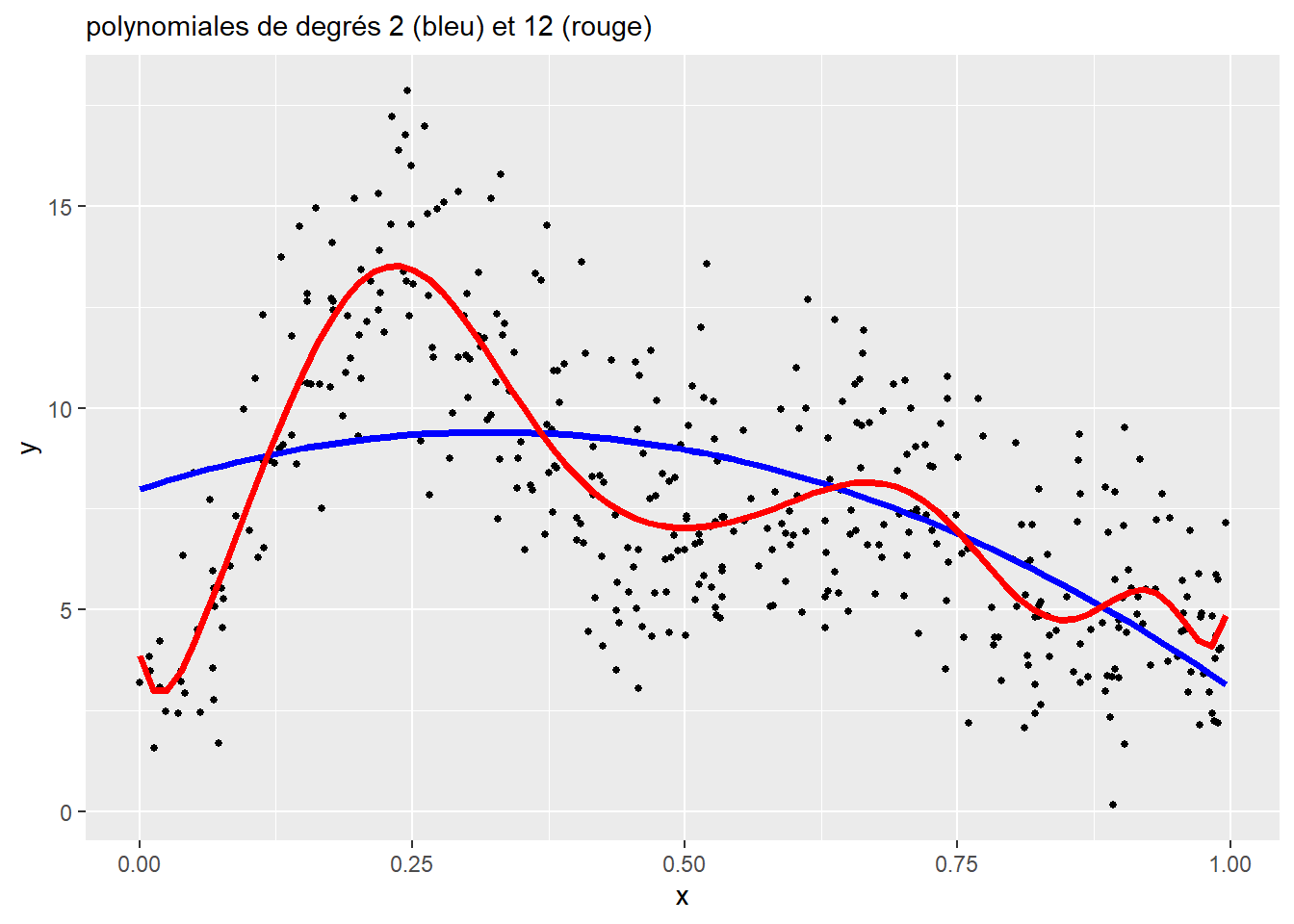
Figure 11.6: Sur et sous-ajustement d’une polynomiale
Un des problèmes inhérents à l’approche des polynomiales est la difficulté d’interprétation. En effet, les coefficients ne sont pas directement interprétables et seule une figure représentant les prédictions du modèle permet d’avoir une idée de l’effet de la variable X sur la variable Y.
11.1.3 Non linéarité par segments
Un compromis intéressant offrant une interprétation simple et une relation potentiellement complexe consiste à découper la variable X en segments, puis d’ajuster un coefficient pour chacun de ces segments. Nous obtenons ainsi une ligne brisée et des coefficients faciles à interpréter (figure 11.7). Nous ne présentons pas d’exemple d’application dans R, mais sachez que le package segmented permets d’ajuster ce type de modèle.
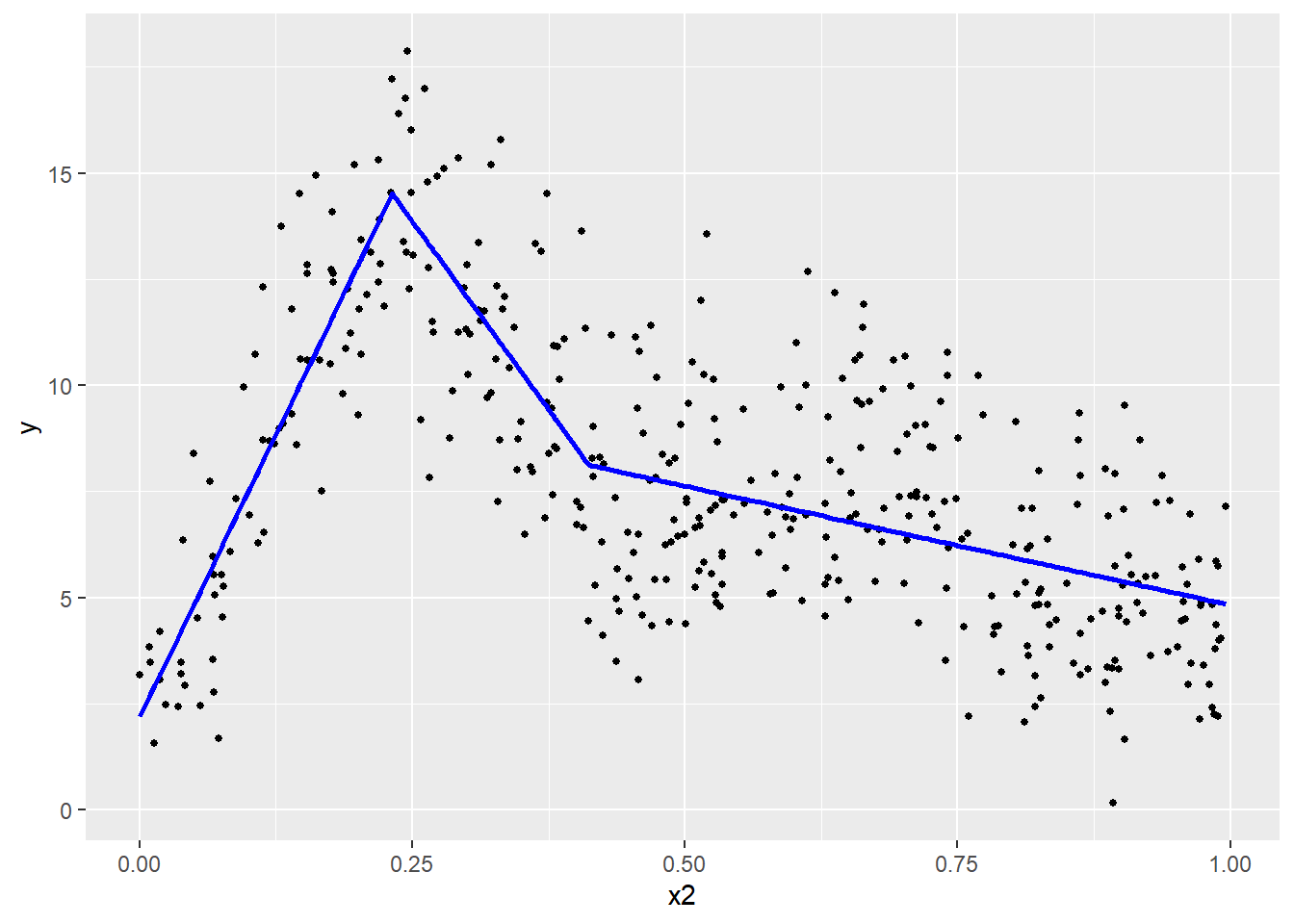
Figure 11.7: Régression par segment
L’enjeu est alors de déterminer le nombre de points et la localisation de points de rupture. L’inconvénient majeur de cette approche est qu’en réalité, peu de phénomènes sont marqués par des ruptures très nettes.
À la figure 11.7, nous avons divisé la variable X en trois segments (\(k_1\), \(k_2\) et \(k_3\)), définis respectivement avec les intervalles suivants : [0,00-0,22], [0,22-0,41] et [0,41-1,00]. Concrètement, cela revient à diviser la variable X en trois nouvelles variables \(X_{k1}\), \(X_{k2}\), et \(X_{k3}\). La valeur de \(X_{ik}\) est égale à \(x_i\) si \(x_i\) se trouve dans l’intervalle propre à k, et à 0 autrement. Ici, nous obtenons trois coefficients :
- le premier est positif, une augmentation de X sur le premier segment est associée à une augmentation de Y;
- le second est négatif, une augmentation de X sur le second segment est associée à une diminution de Y;
- le troisième est aussi négatif, une augmentation de X sur le troisième segment est associée à une diminution de Y, mais moins forte que pour le second segment.
11.1.4 Non linéarité avec des splines
La dernière approche, et certainement la plus flexible, est d’utiliser ce que l’on appelle une spline pour capter des relations non linéaires. Une spline est une fonction créant des variables supplémentaires à partir d’une variable X et d’une fonction de base. Ces variables supplémentaires, appelées bases (basis en anglais), sont ajoutées au modèle; la sommation de leurs valeurs multipliées par leurs coefficients permet de capter les relations non linéaires entre une variable dépendante et une variable indépendante. Le nombre de bases et leur localisation (plus souvent appelé nœuds) permettent de contrôler la complexité de la fonction non linéaire.
Prenons un premier exemple simple avec une fonction de base triangulaire (tent basis en anglais). Nous créons ici une spline avec sept nœuds répartis équitablement sur l’intervalle de valeurs de la variable X. Les sept bases qui en résultent sont présentées à la figure 11.8. Dans cette figure, chaque sommet d’un triangle correspond à un nœud et chaque triangle correspond à une base.
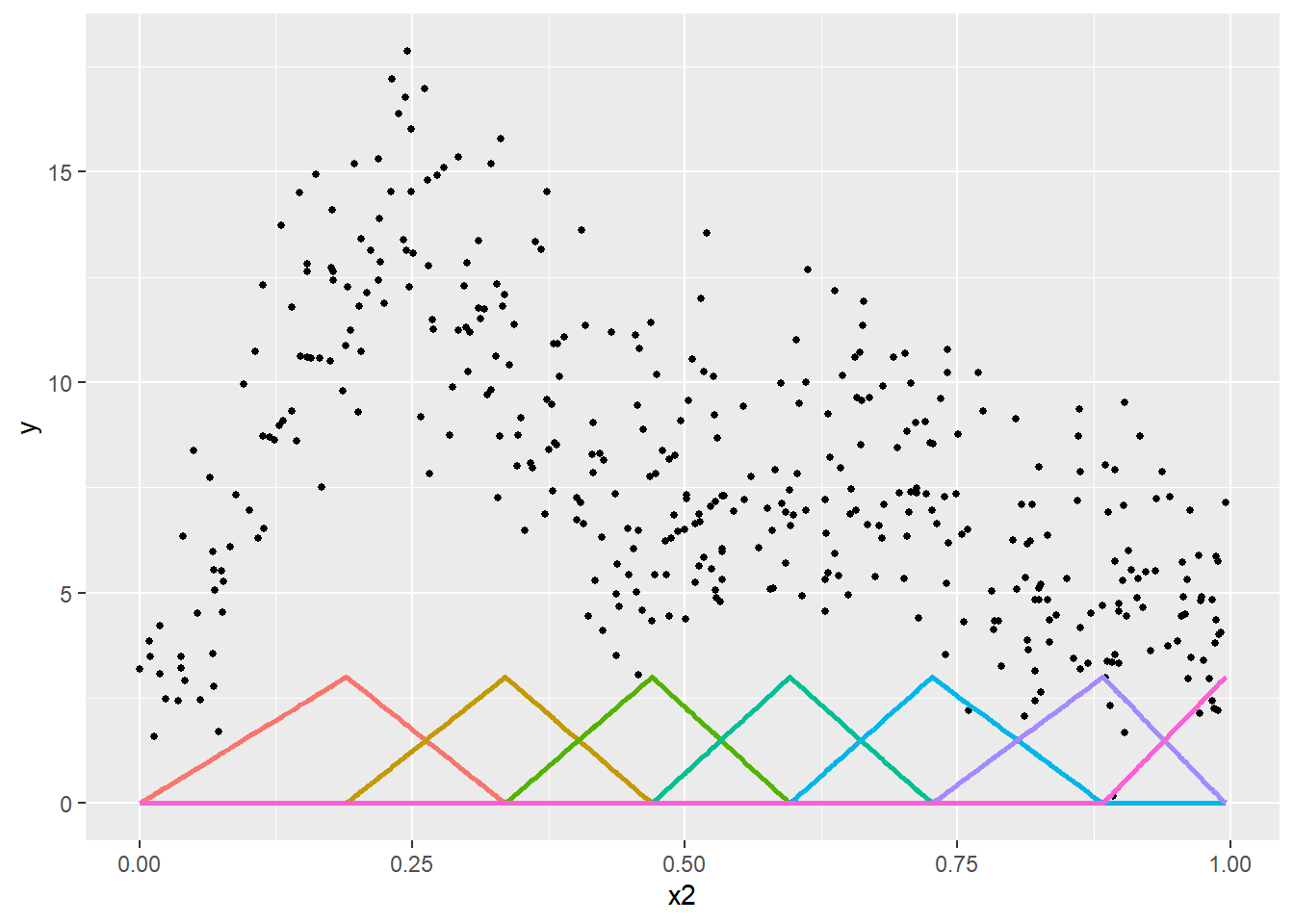
Figure 11.8: Bases de la spline triangulaire
En ajoutant ces bases dans notre modèle de régression, nous pouvons ajuster un coefficient pour chacune et le représenter en multipliant ces bases par les coefficients obtenus avec une simple régression linéaire (figure 11.9).
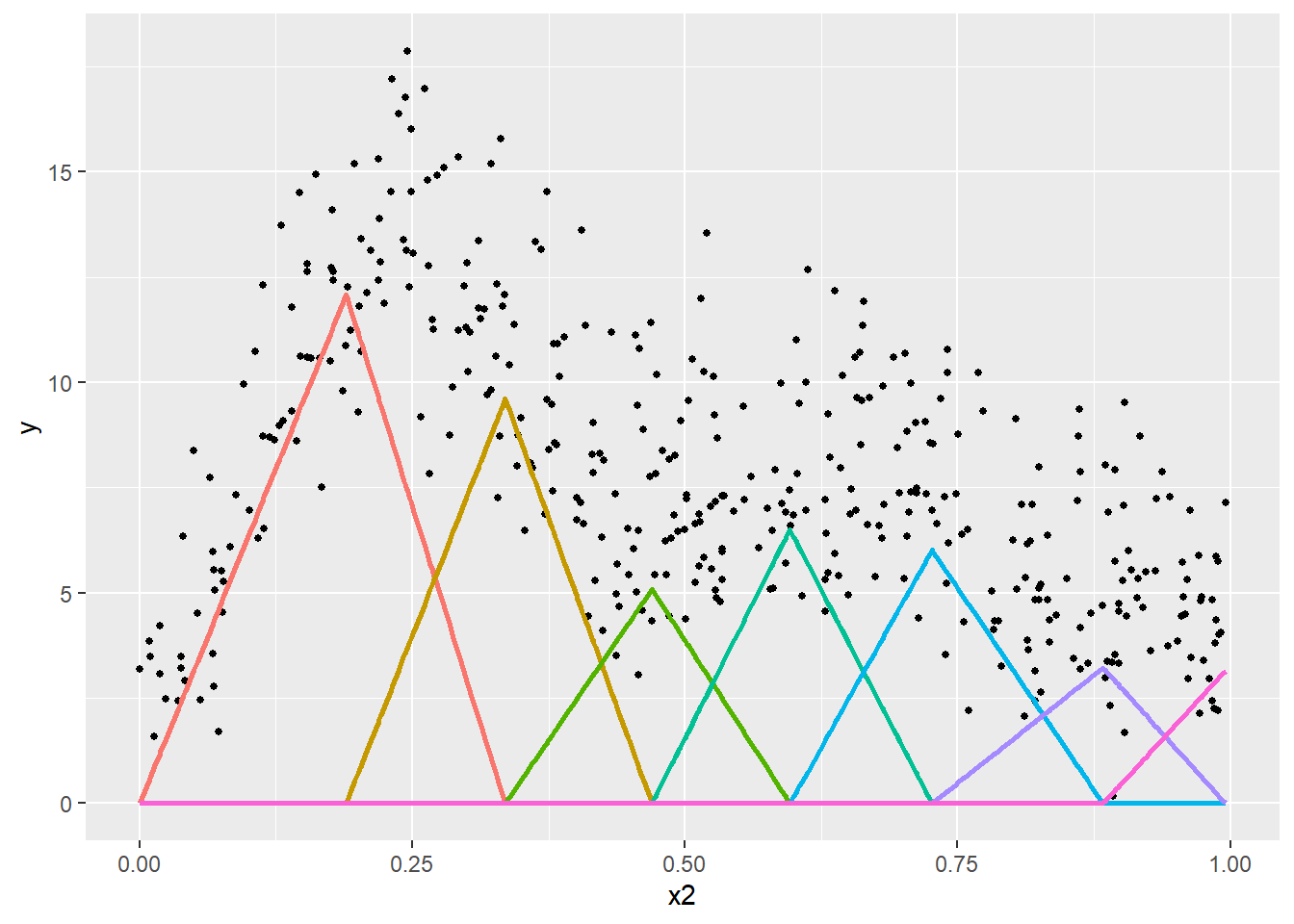
Figure 11.9: Spline triangulaire multipliée par ces coefficients
Nous remarquons ainsi que les bases correspondant à des valeurs plus fortes de Y ont reçu des coefficients plus élevés. Pour reconstituer la fonction non linéaire, il suffit d’additionner ces bases multipliées par leurs coefficients, soit la ligne bleue à la figure 11.10.
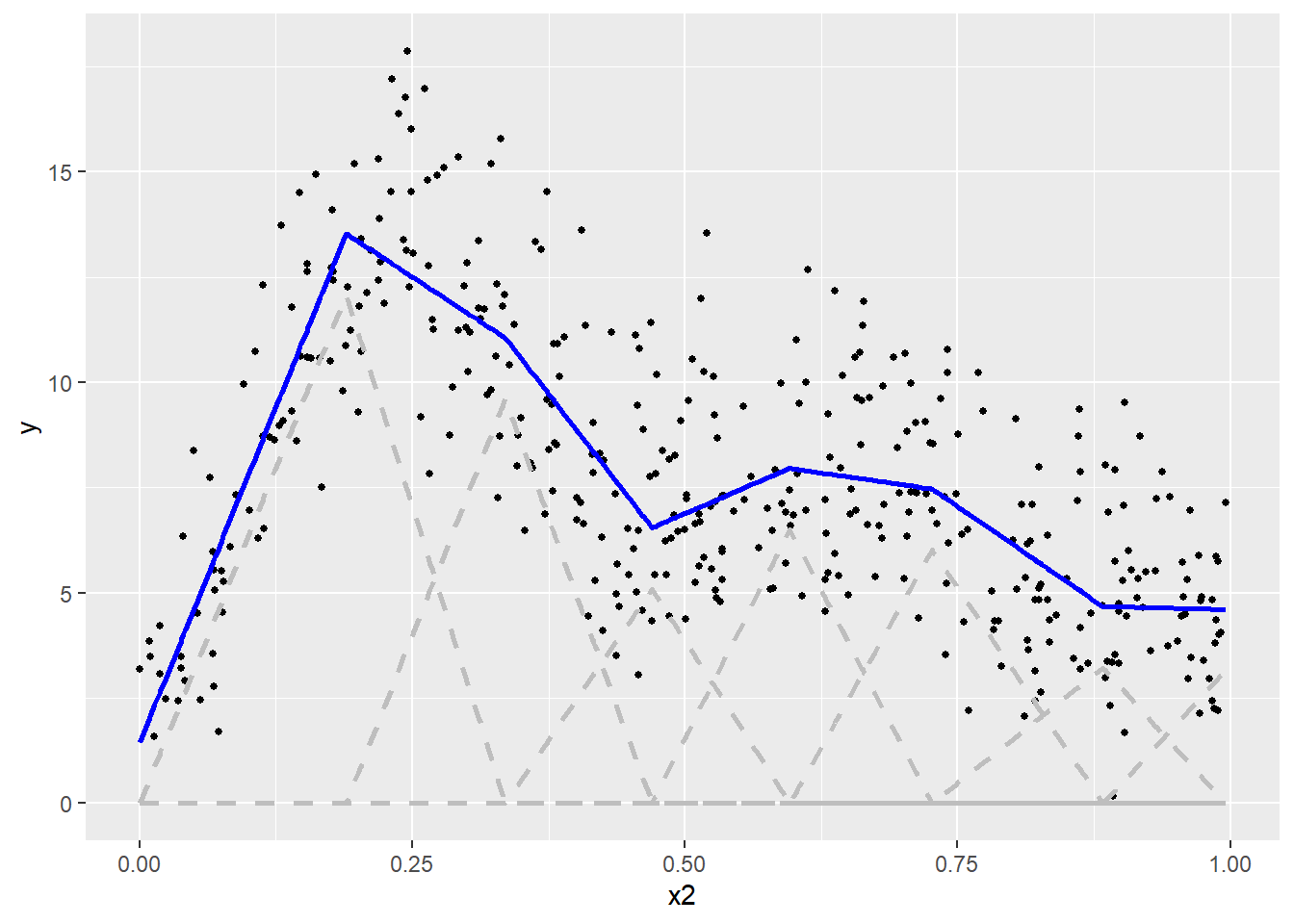
Figure 11.10: Spline triangulaire
La fonction de base triangulaire est intéressante pour présenter la logique qui sous-tend les splines, mais elle est rarement utilisée en pratique. On lui préfère généralement d’autre formes donnant des résultats plus lisses comme les B-spline quadratiques, B-spline cubiques, M-spline, Duchon spline, etc.
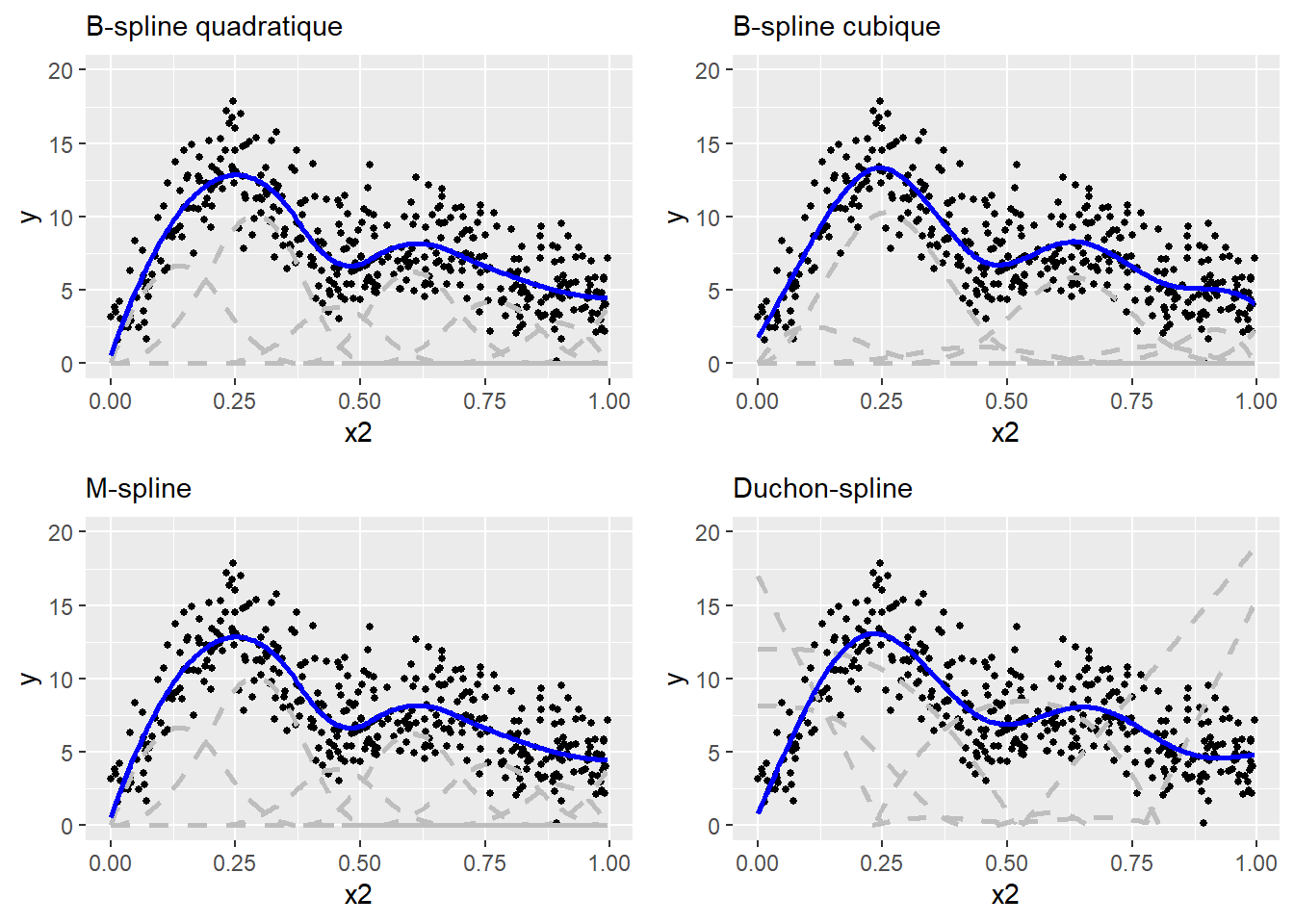
Figure 11.11: Comparaison de différentes bases
Les approches que nous venons de décrire sont regroupées sous l’appellation de modèles additifs. Dans les prochaines sous-sections, nous nous concentrons davantage sur les splines du fait de leur plus grande flexibilité.