8.3 Modèles GLM pour des variables de comptage
Dans cette section, nous présentons les principaux modèles utilisés pour modéliser des variables de comptage. Il peut s’agir de variables comme le nombre d’accidents à une intersection, le nombre de cafés par quartier, le nombre de cas d’une maladie donnée par entité géographique, etc.
8.3.1 Modèle de Poisson
Le modèle GLM de base pour modéliser une variable de comptage est le modèle de Poisson. Pour rappel, la distribution de Poisson a un seul paramètre: \(\lambda\). Il représente le nombre moyen d’évènements observés sur l’intervalle de temps d’une observation, ainsi que la dispersion de la distribution. En conséquence, \(\lambda\) doit être un nombre strictement positif; autrement dit, nous ne pouvons pas observer un nombre négatif d’évènements. Il est donc nécessaire d’utiliser une fonction de lien pour contraindre l’équation de régression sur l’intervalle \([0 ,+\infty]\). La fonction la plus utilisée est le logarithme naturel (log) dont la réciproque est la fonction exponentielle (exp).
| Type de variable dépendante | Variable de comptage |
| Distribution utilisée | Poisson |
| Formulation |
\(Y \sim Poisson(\lambda)\) \(g(\lambda) = \beta_0 + \beta X\) \(g(x) =log(x)\) |
| Fonction de lien | log |
| Paramètre modélisé | \(\lambda\) |
| Paramètres à estimer | \(\beta_0\), \(\beta\) |
| Conditions d’application | Absence d’excès de zéros, absence de sur-dispersion ou de sous-dispersion |
8.3.1.1 Interprétation des paramètres
Les coefficients du modèle expriment l’effet du changement d’une unité des variables X sur \(\lambda\) (le nombre de cas) dans l’échelle logarithmique (log-scale). Pour rappel, l’échelle logarithmique est multiplicative : si nous convertissons les coefficients dans leur échelle originale avec la fonction exponentielle, leur effet n’est plus additif, mais multiplicatif. Prenons un exemple concret, admettons que nous avons ajusté un modèle de Poisson à une variable de comptage Y avec deux variables \(X_1\) et \(X_2\) et que nous avons obtenus les coefficients suivants :
\(\beta_0 = 1,8 \text{; } \beta_1 = 0,5 \text{; } \beta_2 = -1,5\)
L’interprétation basique (sur l’échelle logarithmique) est la suivante : une augmentation d’une unité de la variable \(X_1\) est associée avec une augmentation de 0,5 du logarithme du nombre de cas attendus. Une augmentation d’une unité de la variable \(X_2\) est associée avec une réduction de 1,5 unité du logarithme du nombre de cas attendus. Avec la conversion avec la fonction exponentielle, nous obtenons alors :
- \(exp\mbox{(0,5) = 1,649}\), soit une multiplication par 1,649 du nombre de cas attendu (aussi appelé taux d’incident) à chaque augmentation d’une unité de \(X_1\);
- \(exp\mbox{(-1,5) = 0,223}\), soit une division par 4,54 (1/0,223) du nombre de cas attendu (aussi appelé taux d’incident) à chaque augmentation d’une unité de \(X_2\).
Utilisons maintenant notre équation pour effectuer une prédiction si \(X_1 = 1\) et \(X_2 = 1\).
\(\lambda = exp(\mbox{1,8} + (\mbox{0,5}\times 1) + (\mbox{-1,5}\times1)) = \mbox{2,225}\)
Si nous augmentons \(X_1\) d’une unité, nous obtenons alors :
\(\lambda = exp(1,8 + (\mbox{0,5}\times 2) + (\mbox{-1,5}\times1)) = \mbox{3,670}\)
En ayant augmenté d’une unité \(X_1\), nous avons multiplié notre résultat par 1,649 (\(\mbox{2,225} \times \mbox{1,649 = 3,670}\)).
Notez que ces effets se multiplient entre eux. Si nous augmentons à la fois \(X_1\) et \(X_2\) d’une unité chacune, nous obtenons : \(\lambda = exp(1,8 + (\mbox{0,5} \times 2) + (\mbox{-1,5} \times 2)) = \mbox{0,818}\), ce qui correspond bien à \(\mbox{2,225} \times \mbox{1,649} \text{ (effet de }X_1\text{)} \times \mbox{0,223} \text{ (effet de }X_2\text{)} = \mbox{0,818}\).
Il existe des fonctions dans R qui calculent ces prédictions à partir des équations des modèles. Il est cependant essentiel de bien saisir ce comportement multiplicatif induit par la fonction de lien log.
8.3.1.1.1 Conditions d’application
Puisque la distribution de Poisson n’a qu’un seul paramètre, le modèle GLM de Poisson est exposé au même problème potentiel de sur-dispersion que les modèles binomiaux de la section précédente. Référez-vous à la section 8.2.1.2 pour davantage de détails sur le problème posé par la sur-dispersion. Pour détecter une potentielle sur-dispersion dans un modèle de Poisson, il est possible, dans un premier temps, de calculer le ratio entre la déviance du modèle et son nombre de degrés de liberté (SAS Institute Inc 2020b). Ce ratio doit être proche de 1, s’il est plus grand, le modèle souffre de sur-dispersion.
\[\begin{equation} \hat{\phi} = \frac{D(modele)}{N-p} \tag{8.19} \end{equation}\]
avec \(N\) et \(p\) étant respectivement les nombres d’observations et de paramètres. Il est également possible de tester formellement si la sur-dispersion est significative avec un test de dispersion.
La question de l’excès de zéros a été abordée dans la section 2.4.3.7 du chapitre 2. Il s’agit d’une situation où un plus grand nombre de zéros sont présents dans les données que ce que suppose la distribution de Poisson. Dans ce cas, il convient d’utiliser la distribution de Poisson avec excès de zéros.
8.3.1.2 Exemple appliqué dans R
Pour cet exemple, nous reproduisons l’analyse effectuée dans l’article de Cloutier et al. (2014). L’enjeu de cette étude était de modéliser le nombre de piétons blessés autour de plus de 500 carrefours dans les quartiers centraux de Montréal. Pour cela, trois types de variables étaient utilisées : des variables décrivant l’intersection, des variables décrivant les activités humaines dans un rayon d’un kilomètre autour de l’intersection et des variables représentant le trafic routier autour de l’intersection. Un effet direct de ce type d’étude est bien évidemment l’établissement de meilleures pratiques d’aménagement réduisant les risques encourus par les piétons lors de leurs déplacements en ville. Le tableau 8.21 présente l’ensemble des variables utilisées dans l’analyse.
| Nom de la variable | Signification | Type de variable | Mesure |
|---|---|---|---|
| Feux_auto | Présence de feux de circulation | Variable binaire | 0 = absence; 1 = présence |
| Feux_piet | Présence de feux de traversée pour les piétons | Variable binaire | 0 = absence; 1 = présence |
| Pass_piet | Présence d’un passage piéton | Variable binaire | 0 = absence; 1 = présence |
| Terreplein | Présence d’un terre-plein central | Variable binaire | 0 = absence; 1 = présence |
| Apaisement | Présence de mesure d’apaisement de la circulation | Variable binaire | 0 = absence; 1 = présence |
| LogEmploi | Logarithme du nombre d’emplois dans un rayon d’un kilomètre | Variable continue | Logarithme du nombre d’emploi. Utilisation du logarithme, car la variable est fortement asymétrique |
| Densite_pop | Densité de population dans un rayon d’un kilomètre | Variable continue | Habitants par hectare |
| Entropie | Diversité des occupations du sol dans un rayon d’un kilomètre (indice d’entropie) | Variable continue | Mesure de 0 à 1; 0 = spécialisation parfaite; 1 = diversité parfaite |
| DensiteInter | Densité d’intersections dans un rayon d’un kilomètre (connexité) | Variable continue | Nombre d’intersection par km2 |
| Artere | Présence d’une artère à l’intersection | Variable binaire | 0 = absence; 1 = présence |
| Long_arterePS | Longueur d’artère dans un rayon d’un kilomètre | Variable continue | Exprimée en mètres |
| NB_voies5 | Présence d’une cinq voies à l’intersection | Variable binaire | 0 = absence; 1 = présence |
La distribution originale de la variable est décrite à la figure 8.23. Les barres grises représentent la distribution du nombre d’accidents et les barres rouges une distribution de Poisson ajustée sans variable indépendante (modèle nul). Ce premier graphique peut laisser penser qu’un modèle de Poisson n’est pas nécessairement le plus adapté considérant le grand nombre d’intersections pour lesquelles nous n’avons aucun accident. Cependant, rappelons que la variable Y n’a pas besoin de suivre une distribution de Poisson. Dans un modèle GLM, l’hypothèse que nous formulons est que la variable dépendante (Y) conditionnée par les variables indépendantes (X) suit une certaine distribution (ici Poisson).
# Chargement des données
data_accidents <- read.csv("data/glm/accident_pietons.csv", sep = ";")
# Ajustement d'une distribution de Poisson sans variable indépendante
library(fitdistrplus)
model_poisson <- fitdist(data_accidents$Nbr_acci,distr = "pois")
# Création d'un graphique pour comparer les deux distributions
dfpoisson <- data.frame(x=c(0:19),
y=dpois(0:19, model_poisson$estimate)
)
counts <- data.frame(table(data_accidents$Nbr_acci))
names(counts) <- c("nb_accident",'frequence')
counts$nb_accident <- as.numeric(as.character(counts$nb_accident))
counts$prop <- counts$frequence / sum(counts$frequence)
ggplot() +
geom_bar(aes(x=nb_accident, weight = prop, fill = "real"), width = 0.6, data = counts)+
geom_bar(aes(x=x, weight = y, fill = "adj"), width = 0.15, data = dfpoisson)+
scale_x_continuous(limits = c(-0.5,7), breaks = c(0:7))+
scale_fill_manual(name = "",
breaks = c("real","adj"),
labels = c("distribution originale", "distribution de Poisson"),
values = c("real" = rgb(0.4,0.4,0.4), "adj" = "red"))+
labs(subtitle = "",
x = "nombre d'accidents",
y = "")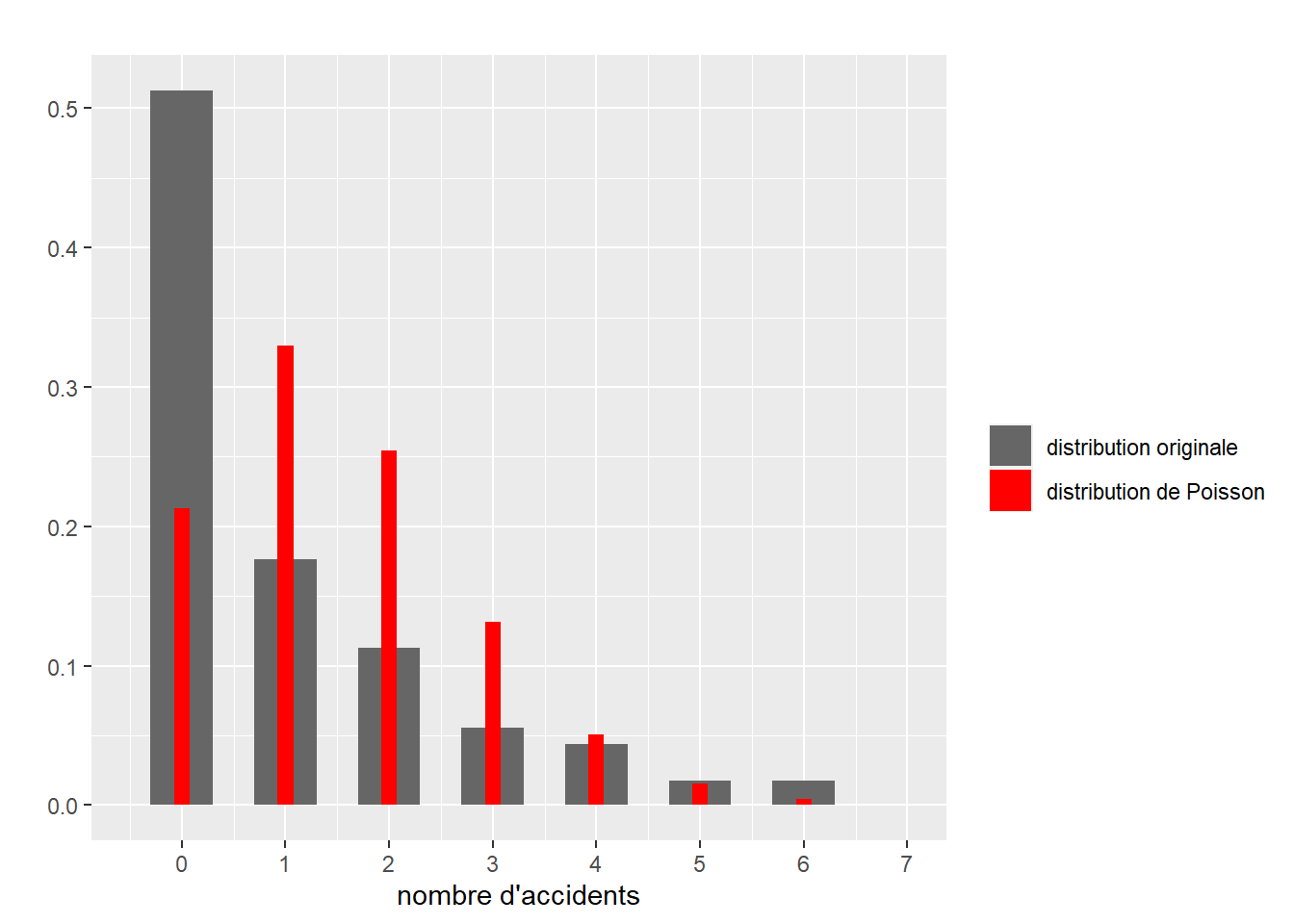
Figure 8.23: Distribution originale du nombre d’accidents par intersection
Vérification des conditions d’application
Comme précédemment, notre première étape est de vérifier l’absence de multicolinéarité excessive avec la fonction vif du package car.
vif(glm(Nbr_acci ~ Feux_auto + Feux_piet + Pass_piet + Terreplein + Apaisement +
LogEmploi + Densite_pop + Entropie + DensiteInter +
Long_arterePS + Artere + NB_voies5,
family = poisson(link="log"),
data = data_accidents))## Feux_auto Feux_piet Pass_piet Terreplein Apaisement LogEmploi Densite_pop
## 2.861708 1.518668 2.321213 1.221683 1.059722 4.763692 1.153096
## Entropie DensiteInter Long_arterePS Artere NB_voies5
## 1.770904 2.040457 4.467841 1.887728 1.520514Toutes les valeurs de VIF sont inférieures à 5. Notons tout de même que le logarithme de l’emploi et la longueur d’artère dans un rayon d’un kilomètre ont des valeurs de VIF proches de 5. La seconde étape du diagnostic consiste à calculer et à visualiser les distances de Cook.
# Ajustement d'une première version du modèle
modele <- glm(Nbr_acci ~ Feux_auto + Feux_piet + Pass_piet + Terreplein + Apaisement +
LogEmploi + Densite_pop + Entropie + DensiteInter +
Long_arterePS + Artere + NB_voies5,
family = poisson(link="log"),
data = data_accidents)
# Calcul des distances de Cook
cooksd <- cooks.distance(modele)
df <- data.frame(
cook = cooksd,
oid = 1:length(cooksd)
)
ggplot(data = df)+
geom_point(aes(x = oid, y = cook), size = 0.5, alpha = 0.5)+
labs(x = "",
y = "Distance de Cook")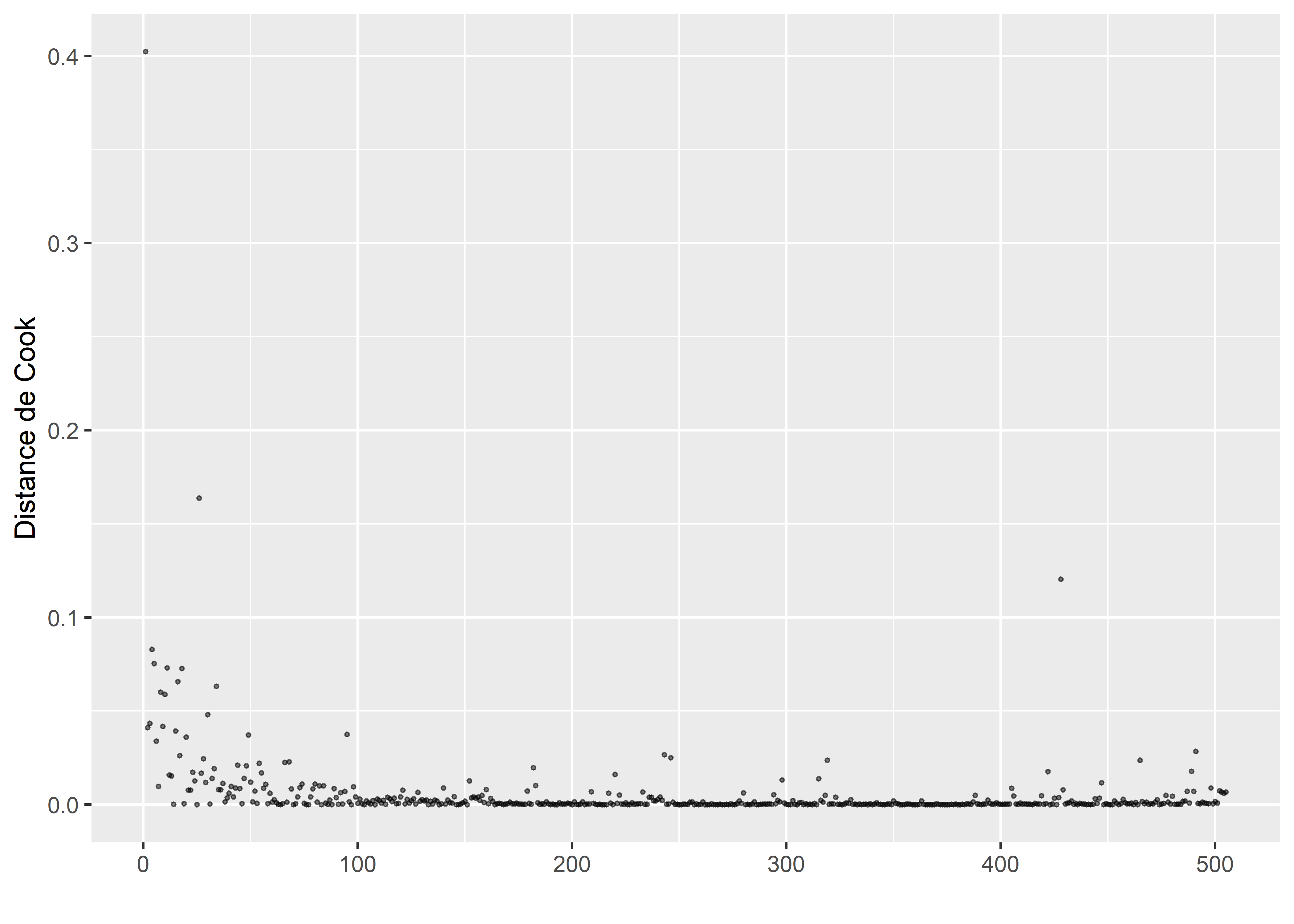
Figure 8.24: Distances de Cook pour le modèle de Poisson
La figure 8.24 signale la présence de trois observations avec des valeurs extrêmement fortes de distance de Cook. Nous les isolons dans un premier temps pour les analyser.
cas_etrange <- subset(data_accidents, cooksd>0.1)
print(cas_etrange)## Nbr_acci Feux_auto Feux_piet Pass_piet Terreplein Apaisement EmpTotBuffer Densite_pop Entropie
## 1 19 1 1 1 1 0 7208.538 5980.923 0.8073926
## 26 7 0 0 1 0 0 1342.625 2751.012 0.0000000
## 428 0 1 1 1 0 1 13122.560 14148.827 0.6643891
## DensiteInter Long_arterePS Artere NB_voies5 log_acci catego_acci catego_acci2 Arret VAG sum_app
## 1 42.41597 6955.00 1 1 2.995732 1 1 0 1 4
## 26 73.35344 2849.66 0 0 2.079442 1 1 1 1 3
## 428 109.25066 4634.20 0 0 0.000000 0 0 0 0 3
## LogEmploi AccOrdinal PopHa
## 1 8.883021 2 5.980923
## 26 7.202382 2 2.751012
## 428 9.482088 0 14.148827Les deux premiers cas sont des intersections avec de nombreux accidents (respectivement 19 et 7) qui risquent de perturber les estimations du modèle. Le troisième cas ne comprend en revanche aucun accident. Puisqu’il ne s’agit que de trois observations et que leurs distances de Cook sont très nettement supérieures aux autres, nous les retirons du modèle.
data2 <- subset(data_accidents, cooksd<0.1)
# Ajustement d'une première version du modèle
modele <- glm(Nbr_acci ~ Feux_auto + Feux_piet + Pass_piet + Terreplein + Apaisement +
LogEmploi + Densite_pop + Entropie + DensiteInter +
Long_arterePS + Artere + NB_voies5,
family = poisson(link="log"),
data = data2)
# Calcul des distances de Cook
cooksd <- cooks.distance(modele)
df <- data.frame(
cook = cooksd,
oid = 1:length(cooksd)
)
ggplot(data = df)+
geom_point(aes(x = oid, y = cook), size = 0.5, alpha = 0.5)+
labs(x = "",
y = "distance de Cook")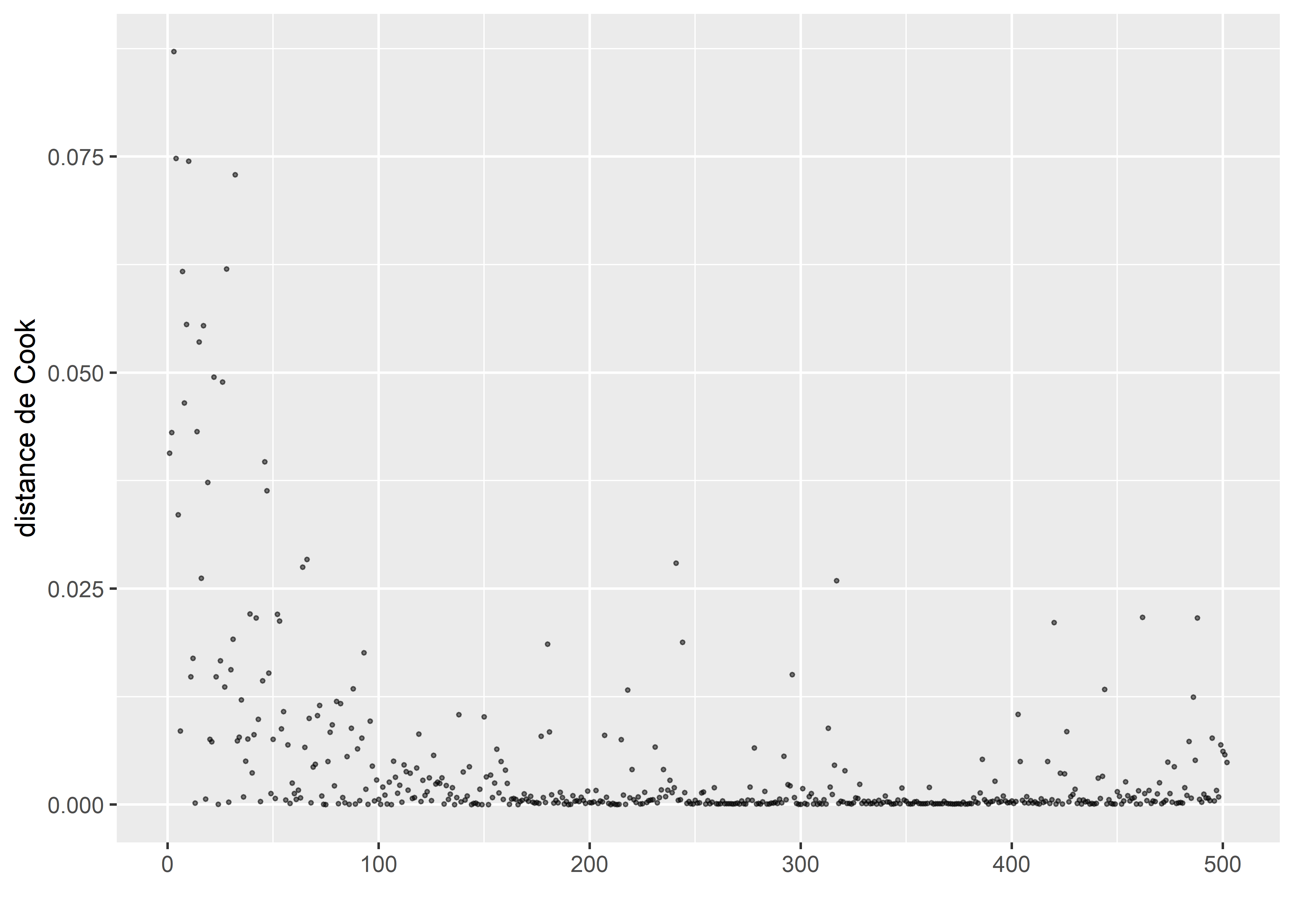
Figure 8.25: Distances de Cook pour le modèle de Poisson après avoir retiré les valeurs aberrantes
La figure 8.25 montre que nous n’avons plus d’observations fortement influentes dans le modèle après avoir retiré les trois observations identifiées précédemment. Nous devons à présent vérifier l’absence de sur-dispersion.
# Calcul du rapport entre déviance et nombre de degrés de liberté du modèle
deviance(modele)/(nrow(data2) - modele$rank)## [1] 1.674691Le rapport entre la déviance et le nombre de degrés de liberté du modèle est nettement supérieur à 1, indiquant une sur-dispersion excessive. Nous pouvons confirmer ce résultat avec la fonction dispersiontest du package AER.
library(AER)
# Test de sur-dispersion
dispersiontest(modele)##
## Overdispersion test
##
## data: modele
## z = 5.2737, p-value = 6.686e-08
## alternative hypothesis: true dispersion is greater than 1
## sample estimates:
## dispersion
## 1.891565Contrairement à la forme classique d’un modèle de Poisson pour laquelle la dispersion attendue est de 1, le test nous indique qu’une dispersion de 1,89 serait mieux ajustée aux données.
Il est également possible d’illuster cet écart à l’aide d’un graphique représentant les valeurs réelles, les valeurs prédites, ainsi que la variance (sous forme de barres d’erreurs) attendue par le modèle (figure 8.26). Nous constatons ainsi que les valeurs réelles (en rouge) ont largement tendance à dépasser la variance attendue par le modèle, surtout pour les valeurs les plus faibles de la distribution.
# Extraction des prédictions du modèle
lambdas <- predict(modele, type = "response")
# Création d'un DataFrame pour contenir la prédiction et les vraies valeurs
df1 <- data.frame(
lambdas = lambdas,
reals = data2$Nbr_acci
)
# Calcul de l'intervalle de confiance à 95 % selon la distribution de Poisson
# et stockage dans un second DataFrame
seqa <- seq(0,round(max(lambdas)),1)
df2 <- data.frame(
lambdas = seqa,
lower = qpois(p = 0.025, lambda = seqa),
upper = qpois(p = 0.975, lambda = seqa)
)
# Affichage des valeurs réelles et prédites (en rouge)
# et de leur variance selon le modèle (en noir)
ggplot() +
geom_errorbar(data = df2,
mapping = aes(x = lambdas, ymin = lower, ymax = upper),
width = 0.2, color = rgb(0.4,0.4,0.4)) +
geom_point(data = df1,
mapping = aes(x = lambdas, y = reals),
color ="red", size = 0.5) +
labs(x = 'valeurs prédites',
y = "valeurs réelles")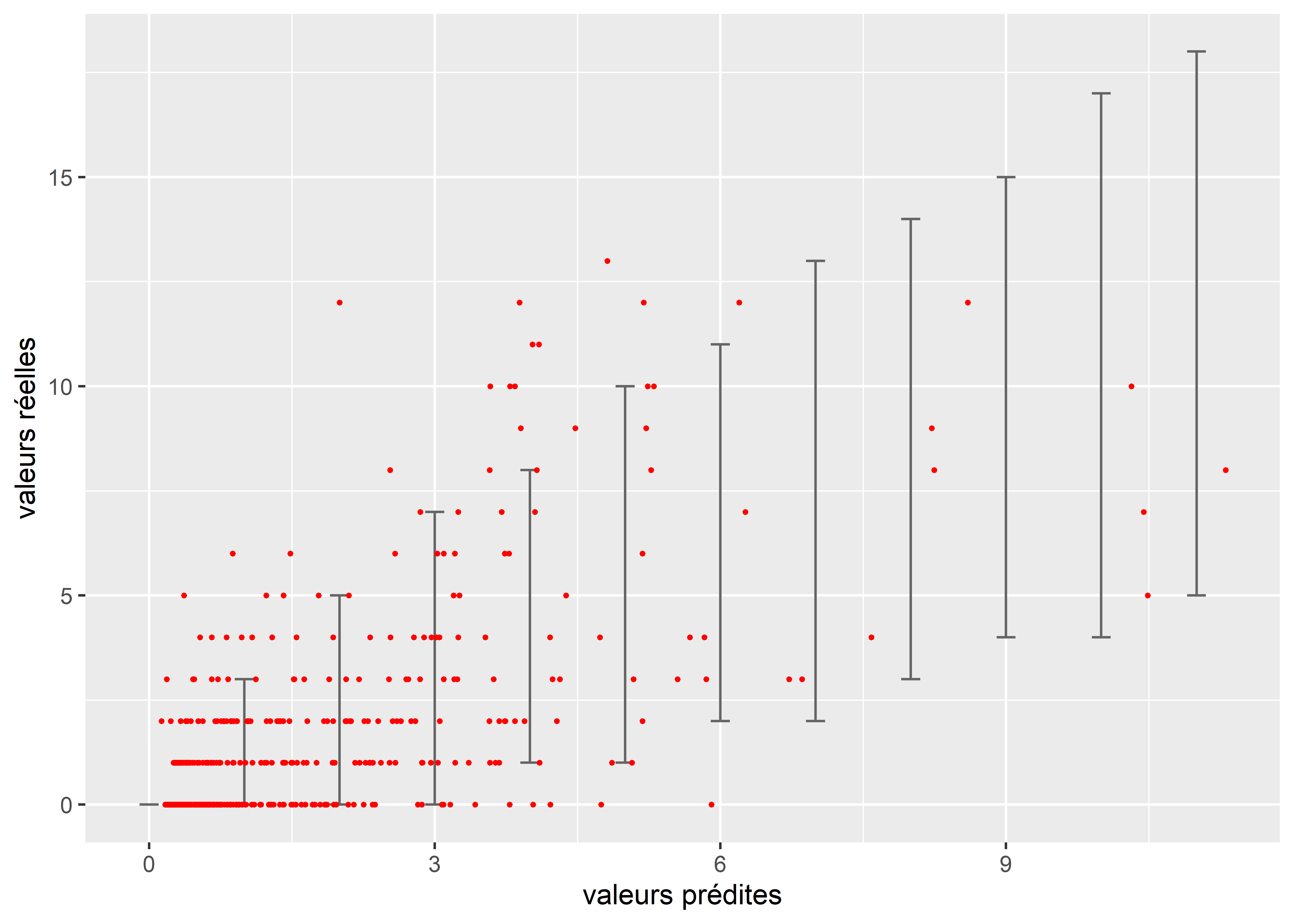
Figure 8.26: Représentation de la sur-dispersion des données dans le modèle de Poisson
Pour tenir compte de cette particularité des données, nous modifions légèrement le modèle pour utiliser une distribution de quasi-Poisson, intégrant spécifiquement un paramètre de dispersion. Cet ajustement ne modifie pas l’estimation des coefficients du modèle, mais modifie le calcul des erreurs standards et par extension les valeurs de p pour les rendre moins sensibles au problème de sur-dispersion. Une autre approche aurait été de calculer une version robuste des erreurs standards avec le package sandwich comme nous l’avons fait dans la section 8.2.1 sur le modèle binomial. Après réajustement du modèle, le nouveau paramètre de dispersion estimé est de 1,92.
Les quasi-distributions
Les distributions binomiale et de Poisson ne disposent chacune que d’un paramètre décrivant à la fois leur dispersion et leur espérance. Elles manquent donc de flexibilité et échouent parfois à représenter fidèlement des données avec une forte variance. Il existe donc d’autres distributions, respectivement les distributions quasi-binomiale et quasi-Poisson comprenant chacune un paramètre supplémentaire pour contrôler la dispersion. Bien que cette solution soit attrayante, il ne faut pas perdre de vue que la sur ou la sous dispersion peuvent être causées par l’absence de certaines variables explicatives, la sur-représentation de zéros, ou encore une séparation parfaite de la variable dépendante causée par une variable indépendante.
modele2 <- glm(Nbr_acci ~ Feux_auto + Feux_piet + Pass_piet + Terreplein + Apaisement +
LogEmploi + Densite_pop + Entropie + DensiteInter +
Long_arterePS + Artere + NB_voies5,
family = quasipoisson(link="log"),
data = data2)Nous pouvons à présent comparer la distribution originale des données et les simulations issues du modèle. Notez que contrairement à la distribution de Poisson simple, il n’existe pas dans R de fonction pour simuler des valeurs issues d’une distribution de quasi-Poisson. Il est cependant possible d’exploiter sa proximité théorique avec la distribution binomiale négative pour définir notre propre fonction de simulation. La figure 8.27 permet de comparer la distribution originale (en gris) et l’intervalle de confiance à 95 % des simulations (en rouge). Nous remarquons que le modèle semble capturer efficacement la forme générale de la distribution originale. À titre de comparaison, nous pouvons effectuer le même exercice avec la distribution de Poisson classique (le code n’est pas montré pour éviter les répétitions). La figure 8.28 montre qu’un simple modèle de Poisson est très éloigné de la distribution originale de Y.
# Définition d'une fonction pour simuler des données quasi-Poisson
rqpois <- function(n, lambda, disp) {
rnbinom(n = n, mu = lambda, size = lambda/(disp-1))
}
# Extraction des valeurs prédites par le modèle
preds <- predict(modele2, type="response")
# Génération de 1000 simulations pour chaque prédiction
disp <- summary(modele2)$dispersion
nsim <- 1000
cols <- lapply(1:length(preds),function(i){
lambda <- preds[[i]]
sims <- round(rqpois(n = nsim, lambda = lambda, disp = disp))
return(sims)
})
mat_sims <- do.call(rbind, cols)
# Préparation des données pour le graphique (valeurs réelles)
counts <- data.frame(table(data2$Nbr_acci))
names(counts) <- c("nb_accident",'frequence')
counts$nb_accident <- as.numeric(as.character(counts$nb_accident))
counts$prop <- counts$frequence / sum(counts$frequence)
# Préparation des données pour le graphique (valeurs simulées)
df1 <- data.frame(count = 0:25)
count_sims <- lapply(1:nsim, function(i){
sim <- mat_sims[,i]
cnt <- data.frame(table(sim))
df2 <- merge(df1,cnt, by.x="count", by.y = "sim", all.x = T, all.y=F)
df2$Freq <- ifelse(is.na(df2$Freq),0,df2$Freq)
return(df2$Freq)
})
count_sims <- do.call(cbind,count_sims)
df_sims <- data.frame(
val = 0:25,
med = apply(count_sims, MARGIN = 1, median),
lower = apply(count_sims, MARGIN = 1, quantile, probs = 0.025),
upper = apply(count_sims, MARGIN = 1, quantile, probs = 0.975)
)
ggplot() +
geom_bar(aes(x=nb_accident, weight = frequence), width = 0.6, data = counts)+
geom_errorbar(aes(x = val, ymin = lower, ymax = upper),
data = df_sims, color = "red", width = 0.6)+
geom_point(aes(x = val, y = med), color = "red", size = 1.3, data = df_sims)+
scale_x_continuous(limits = c(-0.5,7), breaks = c(0:7))+
xlim(-1,12)+
labs(subtitle = "",
x = "nombre d'accidents",
y = "nombre d'occurrences")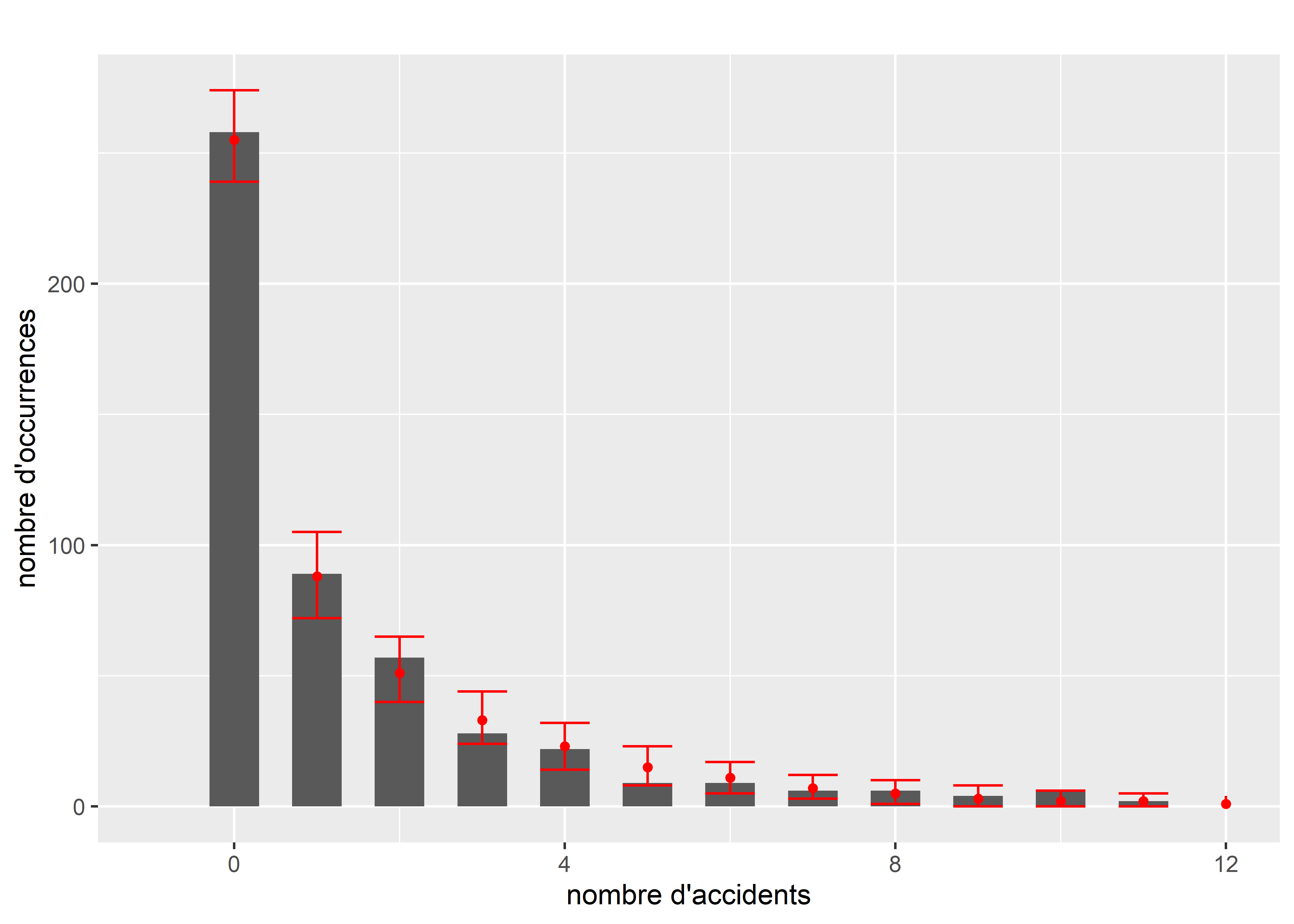
Figure 8.27: Comparaison de la distribution originale et des simulations pour le modèle de quasi-Poisson
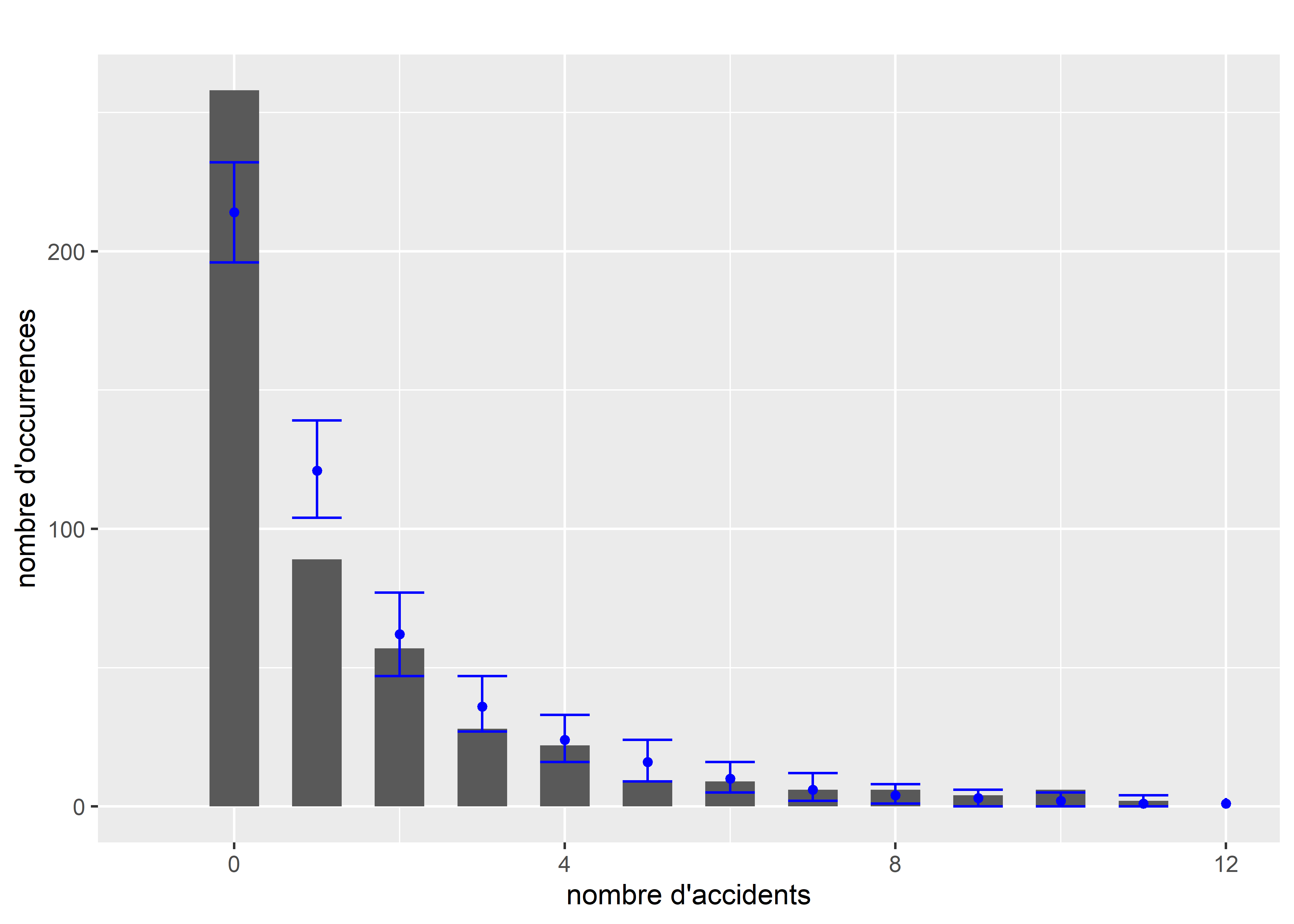
Figure 8.28: Comparaison de la distribution originale et des simulations pour le modèle de Poisson
La prochaine étape du diagnostic est l’analyse des résidus simulés. La figure 8.29 indique que les résidus du modèle suivent bien une distribution uniforme et qu’aucune valeur aberrante n’est observable.
# Génération de 1000 simulations pour chaque prédiction
disp <- 1.918757 # trouvable dans le summary(modele2)
nsim <- 1000
cols <- lapply(1:length(preds),function(i){
lambda <- preds[[i]]
sims <- rqpois(n = nsim, lambda = lambda, disp = disp)
return(sims)
})
mat_sims <- do.call(rbind, cols)
sim_res <- createDHARMa(simulatedResponse = mat_sims,
observedResponse = data2$Nbr_acci,
fittedPredictedResponse = modele2$fitted.values,
integerResponse = T)
plot(sim_res)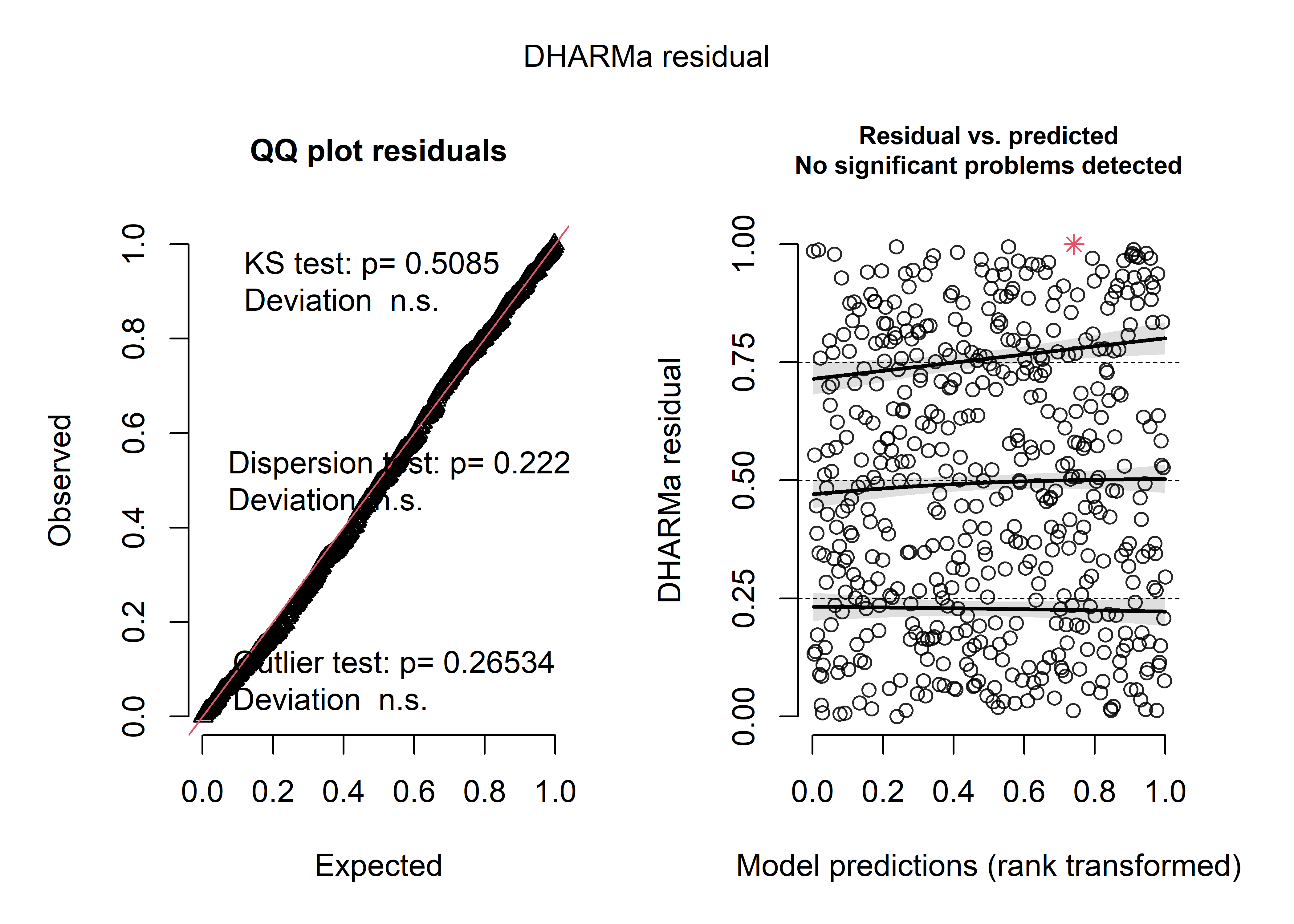
Figure 8.29: Analyse globale des résidus simulés pour le modèle de quasi-Poisson
Pour affiner notre diagnostic, nous pouvons également comparer les résidus simulés et chaque variable indépendante. La figure 8.30 n’indique aucune relation problématique entre nos variables indépendantes et les résidus.
par(mfrow=c(3,4))
vars <- c("Feux_auto", "Feux_piet", "Pass_piet", "Terreplein", "Apaisement",
"LogEmploi", "Densite_pop", "Entropie", "DensiteInter",
"Long_arterePS", "Artere", "NB_voies5")
for(v in vars){
plotResiduals(sim_res, data2[[v]], xlab = v, main = "", ylab = "résidus")
}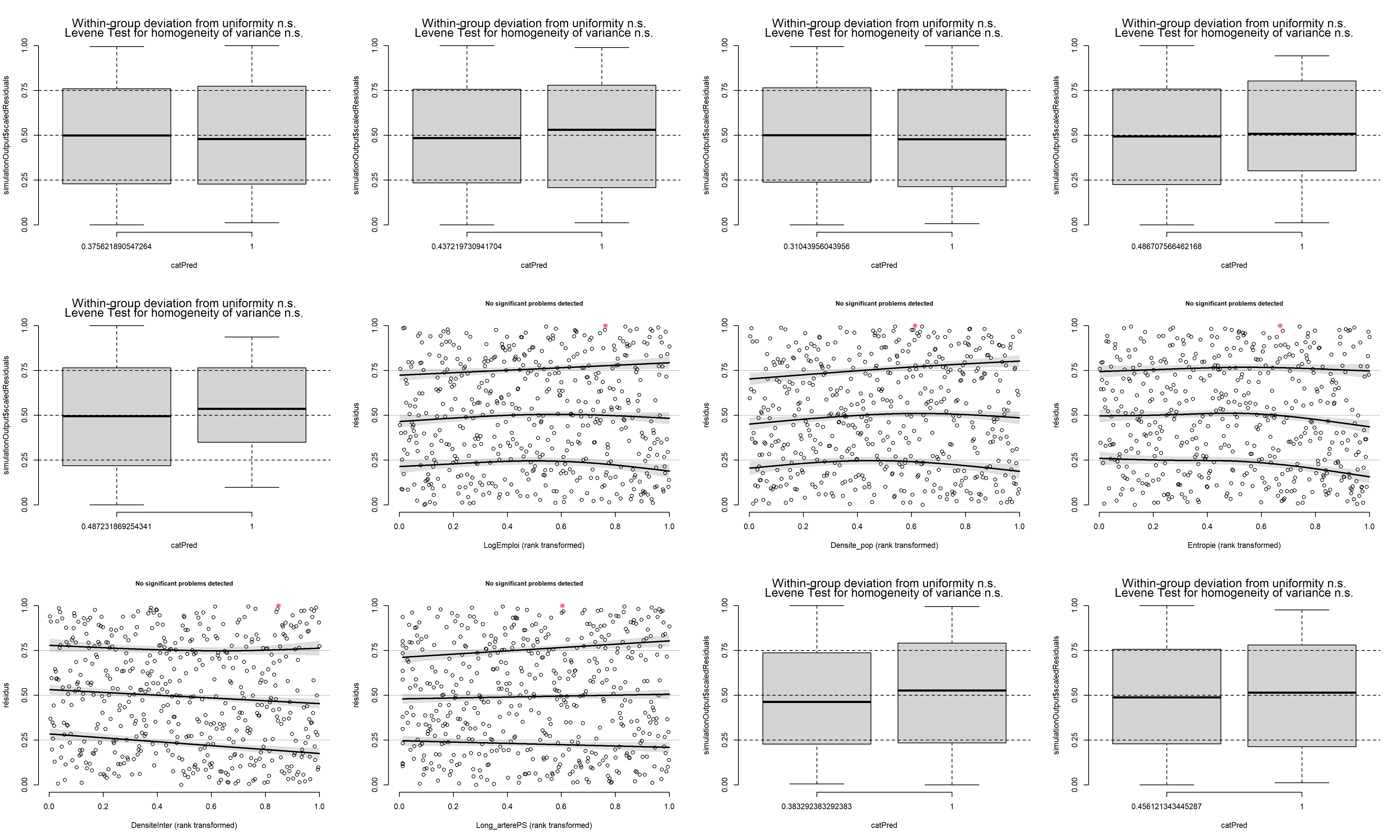
Figure 8.30: Comparaison des résidus simulés et de chaque variable indépendante
Maintenant que l’ensemble des diagnostics a été effectué, nous pouvons passer à la vérification de la qualité d’ajustement.
Vérification de la qualité d’ajustement
Pour le calcul des pseudo-R2, notez qu’il n’existe pas à proprement parler de loglikelihood pour les quasi-distributions. Pour contourner ce problème, il est possible d’utiliser le loglikelihood d’un simple modèle de Poisson (puisque les coefficients ne changent pas), mais il est important de garder à l’esprit que ces pseudo-R2 seront d’autant plus faibles que la sur-dispersion originale était forte.
modelnull <- glm(Nbr_acci ~ 1,
family = poisson(link="log"),
data = data2)
rsqs(loglike.full = logLik(modele),
loglike.null = logLik(modelnull),
full.deviance = deviance(modele),
null.deviance = deviance(modelnull),
nb.params = modele$rank,
n = nrow(data2))## $`deviance expliquee`
## [1] 0.4805998
##
## $`McFadden ajuste`
## 'log Lik.' 0.3258375 (df=13)
##
## $`Cox and Snell`
## 'log Lik.' 0.7789704 (df=13)
##
## $Nagelkerke
## 'log Lik.' 0.787958 (df=13)Le modèle parvient ainsi à expliquer 48 % de la déviance totale. Il obtient un R2 ajusté de McFadden de 0,33 et un R2 de Cox et Snell de 0,78.
# Calcul du RMSE
sqrt(mean((predict(modele2, type = "response") - data2$Nbr_acci)**2))## [1] 1.838026# Nombre moyen d'accidents
mean(data2$Nbr_acci)## [1] 1.503984L’erreur quadratique moyenne du modèle est de 1,84, ce que signifie qu’en moyenne le modèle se trompe d’environ deux accidents pour chaque intersection. Cette valeur est relativement élevée si nous la comparons avec le nombre moyen d’accidents, soit 1,5. Cela s’explique certainement par le grand nombre de zéros dans la variable Y qui tendent à tirer les prédictions vers le bas.
Interprétation des résultats
L’ensemble des coefficients du modèle sont accessibles via la fonction summary. Puisque la fonction de lien du modèle est la fonction log, il est pertinent de convertir les coefficients avec la fonction exp afin de pouvoir les interpréter sur l’échelle originale (nombre d'accidents) plutôt que l’échelle logarithmique (log(nombre d'accidents)). N’oubliez pas que ces effets sont multiplicatifs une fois transformés avec la fonction exp. Nous pouvons également utiliser les erreurs standards pour calculer des intervalles de confiance à 95 % des exponentiels des coefficients. Le tableau 8.22 présente l’ensemble des informations pertinentes pour l’interprétation des résultats.
# Calcul des coefficients en exponentiel et des intervalles de confiance
tableau <- summary(modele2)$coefficients
coeffs <- tableau[,1]
err.std <- tableau[,2]
expcoeff <- exp(coeffs)
exp2.5 <- exp(coeffs - 1.96*err.std)
exp975 <- exp(coeffs - 1.96*err.std)
pvals <- tableau[,4]
tableauComplet <- cbind(coeffs,err.std,expcoeff,exp2.5,exp975,pvals)
# print(tableauComplet)| Variable | Coeff. | exp(Coeff.) | Val.p | IC 2,5 % exp(Coeff.) | IC 97,5 % exp(Coeff.) | Sign. |
|---|---|---|---|---|---|---|
| Constante | -3,680 | 0,030 | 0,000 | 0,010 | 0,090 | *** |
| Feux_auto | 1,100 | 3,000 | 0,000 | 1,970 | 4,660 | *** |
| Feux_piet | 0,330 | 1,390 | 0,009 | 1,090 | 1,790 | ** |
| Pass_piet | 0,340 | 1,400 | 0,149 | 0,880 | 2,200 | |
| Terreplein | -0,360 | 0,700 | 0,099 | 0,440 | 1,050 | . |
| Apaisement | 0,290 | 1,330 | 0,157 | 0,880 | 1,950 | |
| LogEmploi | 0,230 | 1,260 | 0,017 | 1,040 | 1,520 |
|
| Densite_pop | 0,000 | 1,000 | 0,000 | 1,000 | 1,000 | *** |
| Entropie | -0,420 | 0,660 | 0,271 | 0,320 | 1,390 | |
| DensiteInter | 0,000 | 1,000 | 0,410 | 1,000 | 1,010 | |
| Long_arterePS | 0,000 | 1,000 | 0,684 | 1,000 | 1,000 | |
| Artere | 0,030 | 1,030 | 0,842 | 0,780 | 1,360 | |
| NB_voies5 | 0,640 | 1,890 | 0,000 | 1,460 | 2,440 | *** |
Parmi les variables décrivant les aménagements de l’intersection, nous constatons que les présences d’un feu de circulation et d’un feu de traversée pour les piétons multiplient le nombre attendu d’accidents à une intersection par 3,0 et 1,39. Par contre, les présences d’un passage piéton, d’un terre-plein ou de mesures d’apaisement n’ont pas d’effets significatifs (valeurs de p > 0,05). Concernant les variables décrivant l’environnement à proximité des intersections, nous observons que la concentration d’emplois et la densité de population contribuent toutes les deux à augmenter le nombre d’accidents à une intersection, bien que leurs effets soient limités. Enfin, la présence d’une rue à cinq voies à l’intersection augmente le nombre d’accidents attendu à l’intersection de 89 %. Nous ne détaillons pas plus les résultats, car nous utilisons le même jeu de données dans les prochaines sections.
8.3.2 Modèle binomial négatif
Dans le cas où une variable de comptage est marquée par une sur ou sous-dispersion, la distribution de Poisson n’est pas en mesure de capturer efficacement sa variance. Pour contourner ce problème, il est possible d’utiliser la distribution binomiale négative plutôt que la distribution de Poisson (ou quasi-Poisson). Cette distribution peut être décrite comme une généralisation de la distribution de Poisson : elle inclut un second paramètre \(\theta\) contrôlant la dispersion. L’intérêt premier de ce changement de distribution est que l’interprétation des paramètres est la même pour les deux modèles, tout en contrôlant directement l’effet d’une potentielle sur ou sous-dispersion.
| Type de variable dépendante | Variable de comptage |
| Distribution utilisée | Négative binomiale |
| Formulation |
\(Y \sim NB(\mu,\theta)\) \(g(\mu) = \beta_0 + \beta X\) \(g(x) =log(x)\) |
| Fonction de lien | log |
| Paramètre modélisé | \(\mu\) |
| Paramètres à estimer | \(\beta_0\), \(\beta\) et \(\theta\) |
| Conditions d’application | Absence d’excès de zéros, respect du lien variance-moyenne |
8.3.2.1 Conditions d’application
Les conditions d’application d’un modèle binomial négatif sont presque les mêmes que celles d’un modèle de Poisson. La seule différence est que la condition d’absence de sur ou sous-dispersion est remplacée par une condition de respect du lien espérance-variance. En effet, dans un modèle binomial négatif, le paramètre de dispersion \(\theta\) est combiné avec \(\mu\) (l’espérance) pour exprimer la dispersion de la distribution. Dans le package mgcv que nous utilisons dans l’exemple, le lien entre \(\mu\), \(\theta\) et la variance est le suivant :
\[\begin{equation} variance = \mu + \mu^{\frac{2}{\theta}} \tag{8.20} \end{equation}\]
Il s’agit donc d’un modèle hétéroscédastique : sa variance n’est pas fixe, mais varie en fonction de sa propre espérance. Si celle-ci augmente, la variance augmente (comme pour un modèle de Poisson), et l’intensité de cette augmentation est contrôlée par le paramètre \(\theta\). Si cette condition n’est pas respectée, l’analyse des résidus simulés révélera un problème de dispersion.
8.3.2.2 Exemple appliqué dans R
Dans l’exemple précédent avec le modèle de Poisson, nous avons observé une certaine sur-dispersion que nous avons contournée en utilisant un modèle de quasi-Poisson. Dans l’article original, les auteurs ont opté pour un modèle binomial négatif, ce que nous reproduisons ici. Les variables utilisées sont les mêmes que pour le modèle de Poisson. Nous utilisons le package mgcv et sa fonction gam pour ajuster le modèle.
Vérification des conditions d’application
Nous avons vu précédemment que nos variables indépendantes ne sont pas marquées par une multicolinéarité forte. Il n’est pas nécessaire de recalculer les valeurs de VIF puisque nous utilisons les mêmes données. La première étape du diagnostic est donc de calculer les distances de Cook.
library(mgcv)
# Chargement des données
data_accidents <- read.csv("data/glm/accident_pietons.csv", sep = ";")
# Ajustement d'une première version du modèle
modelnb <- gam(Nbr_acci ~ Feux_auto + Feux_piet + Pass_piet +
Terreplein + Apaisement +
LogEmploi + Densite_pop + Entropie + DensiteInter +
Long_arterePS + Artere + NB_voies5,
family = nb(link="log"),
data = data_accidents)
# Calcul et affichage des distances de Cook
cooksd <- cooks.distance(modelnb)
df <- data.frame(
cook = cooksd,
oid = 1:length(cooksd)
)
ggplot(data = df)+
geom_point(aes(x = oid, y = cook), size = 0.5, color = rgb(0.4,0.4,0.4)) +
labs(x = "", y = "distance de Cook")+
theme(axis.ticks.x = element_blank(),
axis.text.x = element_blank())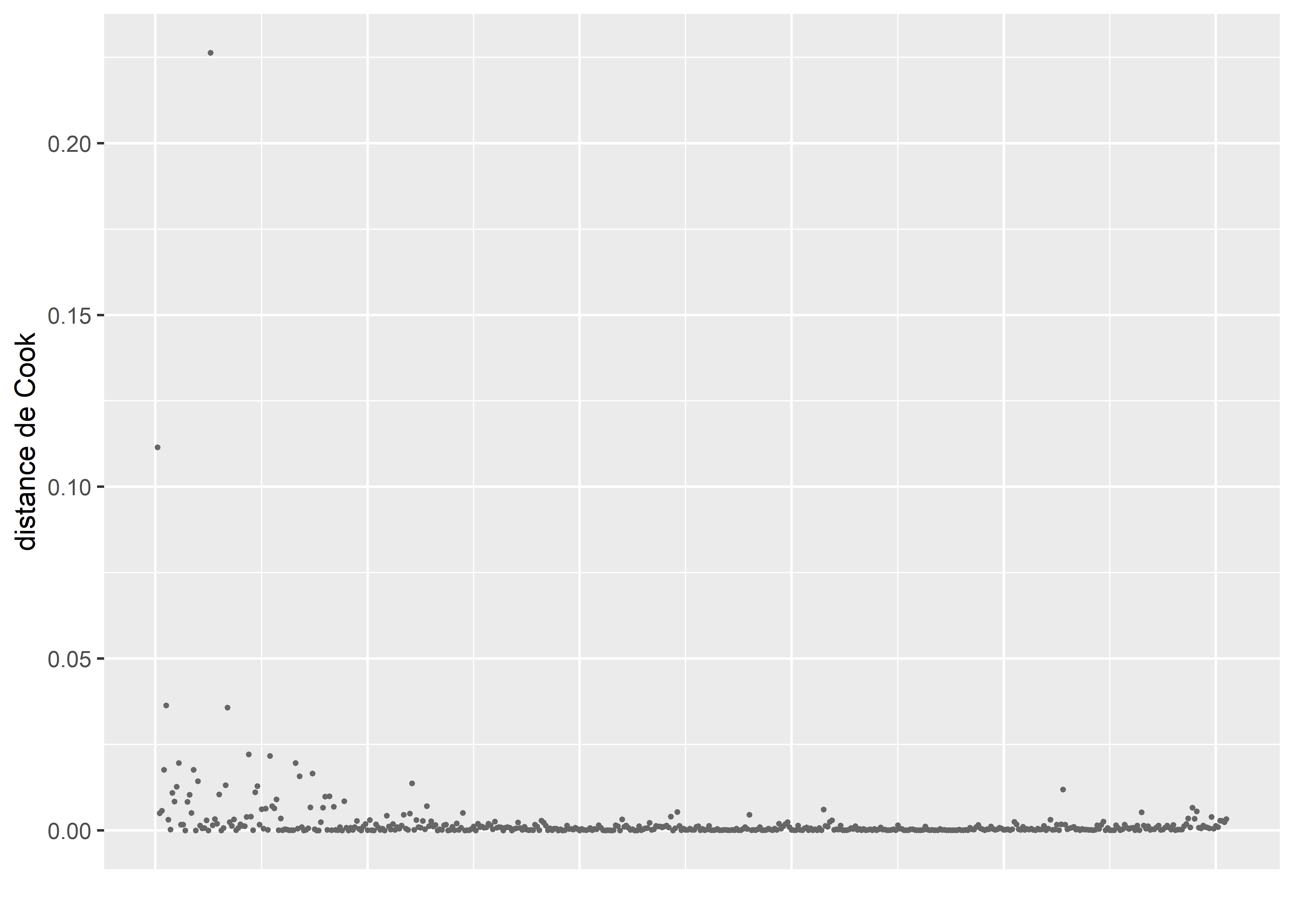
Figure 8.31: Distances de Cook pour le modèle binomial négatif
Nous observons, dans la figure 8.31, que quatre observations se distinguent très nettement des autres.
cas_etrange <- subset(data_accidents, cooksd > 0.03)
print(cas_etrange)## Nbr_acci Feux_auto Feux_piet Pass_piet Terreplein Apaisement EmpTotBuffer Densite_pop Entropie
## 1 19 1 1 1 1 0 7208.538 5980.923 0.8073926
## 5 12 1 0 1 0 0 8585.350 8655.430 0.7607852
## 26 7 0 0 1 0 0 1342.625 2751.012 0.0000000
## 34 6 0 0 1 0 0 12516.410 8950.942 0.4300549
## DensiteInter Long_arterePS Artere NB_voies5 log_acci catego_acci catego_acci2 Arret VAG sum_app
## 1 42.41597 6955.00 1 1 2.995732 1 1 0 1 4
## 5 89.11495 6412.27 0 0 2.564949 1 1 0 1 4
## 26 73.35344 2849.66 0 0 2.079442 1 1 1 1 3
## 34 74.91879 8443.01 1 0 1.945910 1 1 1 0 3
## LogEmploi AccOrdinal PopHa
## 1 8.883021 2 5.980923
## 5 9.057813 2 8.655430
## 26 7.202382 2 2.751012
## 34 9.434796 2 8.950942Il s’agit à nouveau de quatre observations avec un grand nombre d’accidents. Nous décidons de les retirer du jeu de données pour ne pas fausser les résultats concernant l’ensemble des autres intersections. Dans une analyse plus détaillée, il serait judicieux de chercher à comprendre pourquoi ces quatre observations sont particulièrement accidentogènes.
data2 <- subset(data_accidents, cooksd < 0.03)
# Ajustement d'une première version du modèle
modelnb <- gam(Nbr_acci ~ Feux_auto + Feux_piet + Pass_piet +
Terreplein + Apaisement +
LogEmploi + Densite_pop + Entropie + DensiteInter +
Long_arterePS + Artere + NB_voies5,
family = nb(link="log"),
data = data2)
# Calcul et affichage des distances de Cook
cooksd <- cooks.distance(modelnb)
df <- data.frame(
cook = cooksd,
oid = 1:length(cooksd)
)
ggplot(data = df)+
geom_point(aes(x = oid, y = cook), size = 0.5, color = rgb(0.4,0.4,0.4)) +
labs(x = "", y = "distance de Cook")+
theme(axis.ticks.x = element_blank(),
axis.text.x = element_blank())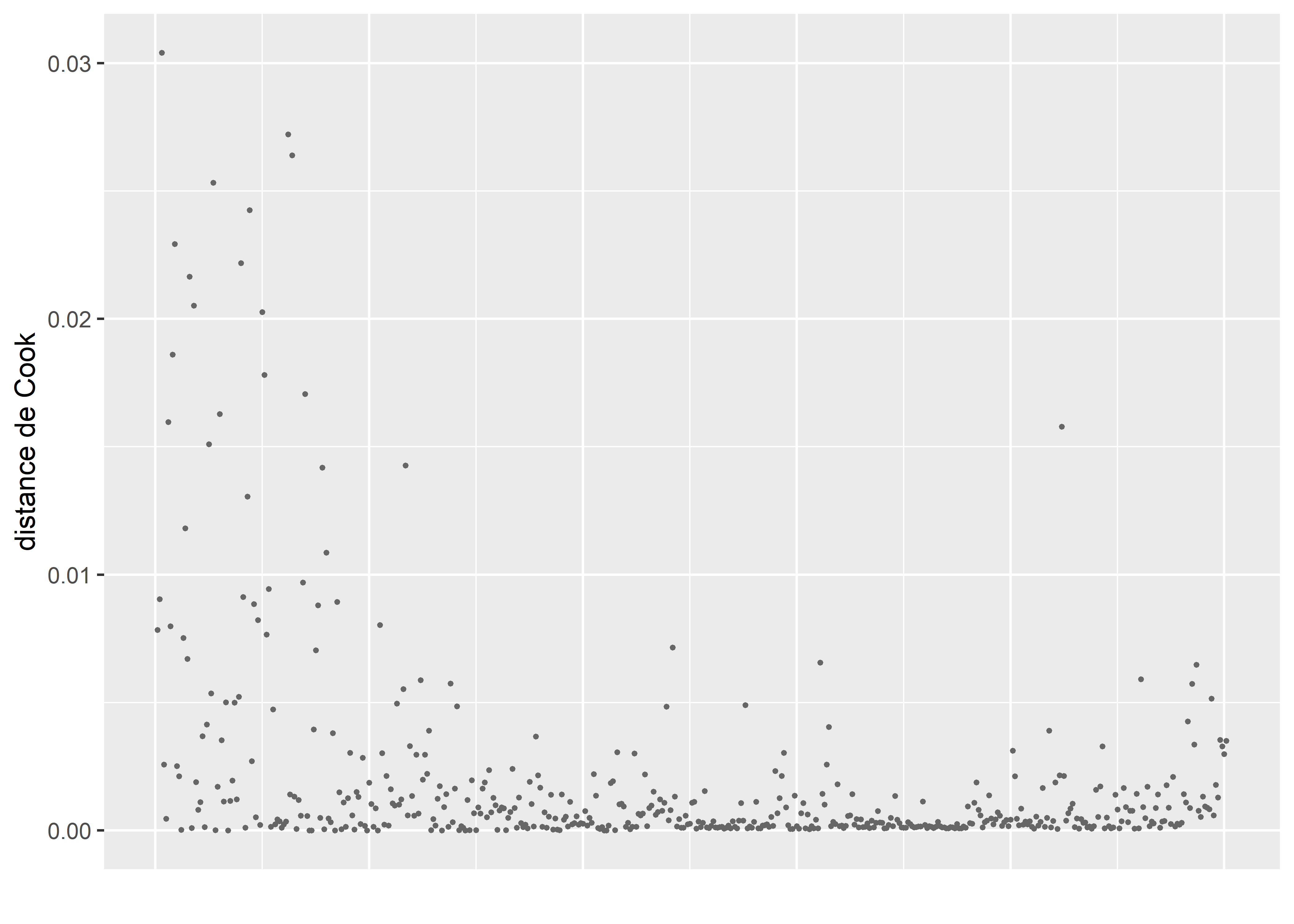
Figure 8.32: Distances de Cook pour le modèle binomial négatif (après avoir retiré quatre observations fortement influentes)
Après avoir retiré ces quatre observations, les distances de Cook (figure 8.32) ne révèlent plus d’observations fortement influentes dans le modèle. La prochaine étape du diagnostic est donc d’analyser les résidus simulés.
# Extraction de la valeur de theta
theta <- modelnb$family$getTheta(T)
nsim <- 1000
# Extraction des valeurs prédites par le modèle
mus <- predict(modelnb, type = "response")
# Calcul des simulations
cols <- lapply(1:length(mus),function(i){
mu <- mus[[i]]
sims <- rnbinom(n = nsim, mu = mu, size = theta)
return(sims)
})
mat_sims <- do.call(rbind, cols)
# Calcul des résidus simulés
sim_res <- createDHARMa(simulatedResponse = mat_sims,
observedResponse = data2$Nbr_acci,
fittedPredictedResponse = mus,
integerResponse = T)
# Affichage du diagnostic
plot(sim_res)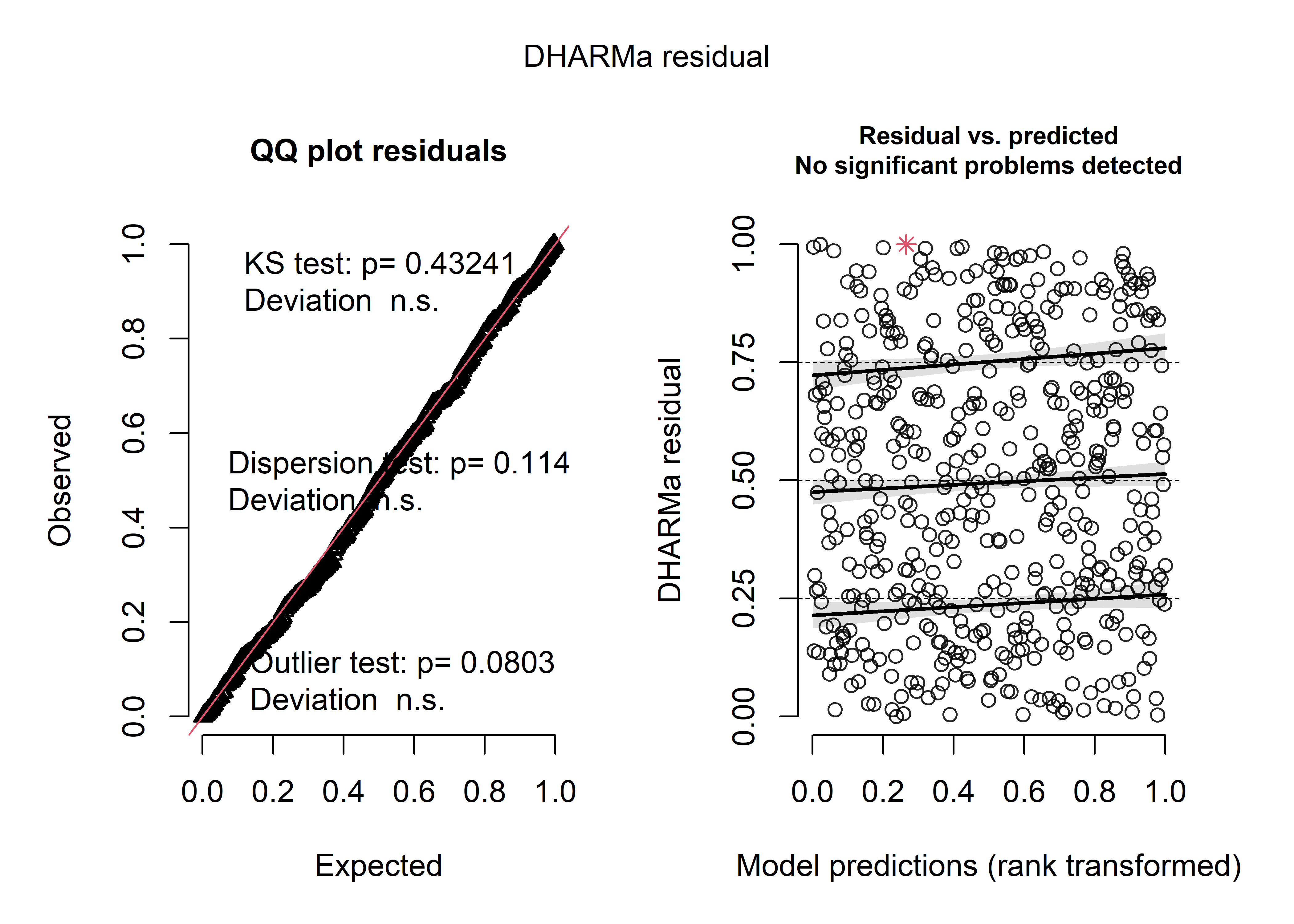
Figure 8.33: Diagnostic général des résidus simulés pour le modèle binomial négatif
La figure 8.33 présentant le diagnostic des résidus simulés, montre que ces derniers suivent bien une distribution uniforme et aucun problème de dispersion ni de valeurs aberrantes. La figure 8.34 permet de comparer la distribution originale de la variable Y et les simulations issues du modèle (intervalles de confiance représentés en bleu). Nous constatons que le modèle parvient bien à reproduire la distribution originale, et ce, même pour les valeurs les plus extrèmes de la distribution.
# Extraction des valeurs prédites par le modèle
mus <- predict(modelnb, type="response")
# Génération de 1000 simulations pour chaque prédiction
theta <- modelnb$family$getTheta(T)
nsim <- 1000
cols <- lapply(1:length(mus),function(i){
mu <- mus[[i]]
sims <- round(rnbinom(n = nsim, mu = mu, size = theta))
return(sims)
})
mat_sims <- do.call(rbind, cols)
# Préparation des données pour le graphique (valeurs réelles)
counts <- data.frame(table(data2$Nbr_acci))
names(counts) <- c("nb_accident",'frequence')
counts$nb_accident <- as.numeric(as.character(counts$nb_accident))
counts$prop <- counts$frequence / sum(counts$frequence)
# Préparation des données pour le graphique (valeurs simulées)
df1 <- data.frame(count = 0:25)
count_sims <- lapply(1:nsim, function(i){
sim <- mat_sims[,i]
cnt <- data.frame(table(sim))
df2 <- merge(df1,cnt, by.x="count", by.y = "sim", all.x = T, all.y=F)
df2$Freq <- ifelse(is.na(df2$Freq),0,df2$Freq)
return(df2$Freq)
})
count_sims <- do.call(cbind,count_sims)
df_sims <- data.frame(
val = 0:25,
med = apply(count_sims, MARGIN = 1, median),
lower = apply(count_sims, MARGIN = 1, quantile, probs = 0.025),
upper = apply(count_sims, MARGIN = 1, quantile, probs = 0.975)
)
# Affichage du graphique
ggplot() +
geom_bar(aes(x=nb_accident, weight = frequence), width = 0.6, data = counts)+
geom_errorbar(aes(x = val, ymin = lower, ymax = upper),
data = df_sims, color = "blue", width = 0.6)+
geom_point(aes(x = val, y = med), color = "blue", size = 1.3, data = df_sims)+
scale_x_continuous(limits = c(-0.5,7), breaks = c(0:7))+
xlim(-1,12)+
labs(subtitle = "",
x = "nombre d'accidents",
y = "nombre d'occurrences")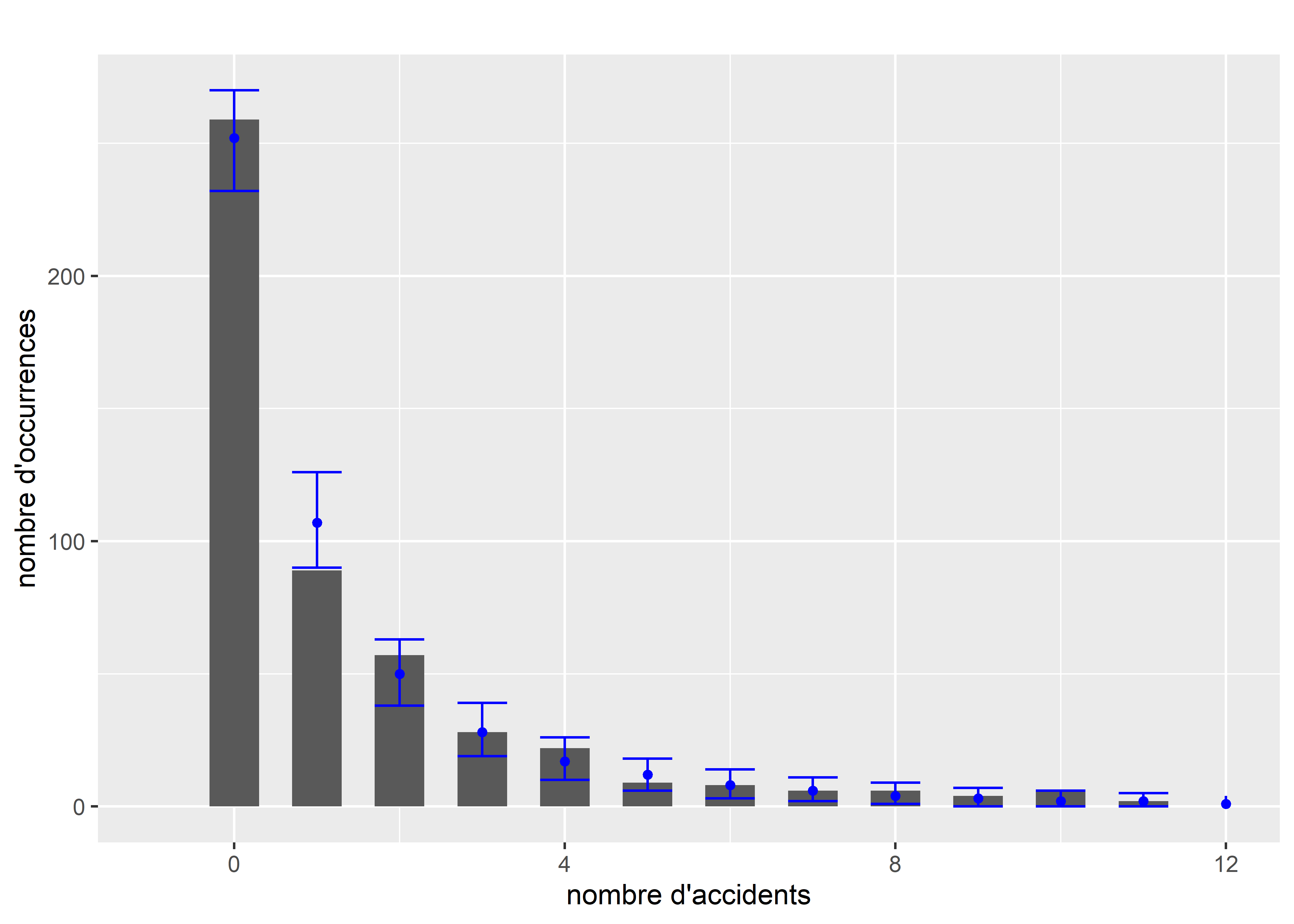
Figure 8.34: Comparaison de la distribution originale et des simulations pour le modèle binomial négatif
À titre de comparaison, nous pouvons à nouveau réaliser le graphique permettant de visualiser si la variance attendue par le modèle est proche de celle effectivement observée dans les données. Nous avons constaté avec ce graphique, lorsque nous ajustions un modèle de Poisson, que la variance des données était trop grande comparativement à celle attendue par le modèle (figure 8.26).
# Extraction des prédictions du modèle
mus <- predict(modelnb, type = "response")
# Création d'un DataFrame pour contenir la prédiction et les vraies valeurs
df1 <- data.frame(
mus = mus,
reals = data2$Nbr_acci
)
# Calcul de l'intervalle de confiance à 95 % selon la distribution de Poisson
# et stockage dans un second DataFrame
seqa <- seq(0,round(max(mus)),1)
df2 <- data.frame(
mus = seqa,
lower = qnbinom(p = 0.025, mu = seqa, size = theta),
upper = qnbinom(p = 0.975, mu = seqa, size = theta)
)
# Affichage des valeurs réelles et prédites (en rouge)
# et de leur variance selon le modèle (en noir)
ggplot() +
geom_errorbar(data = df2,
mapping = aes(x = mus, ymin = lower, ymax = upper),
width = 0.2, color = rgb(0.4,0.4,0.4)) +
geom_point(data = df1,
mapping = aes(x = mus, y = reals),
color ="red", size = 0.5) +
labs(x = 'valeurs prédites',
y = "valeurs réelles")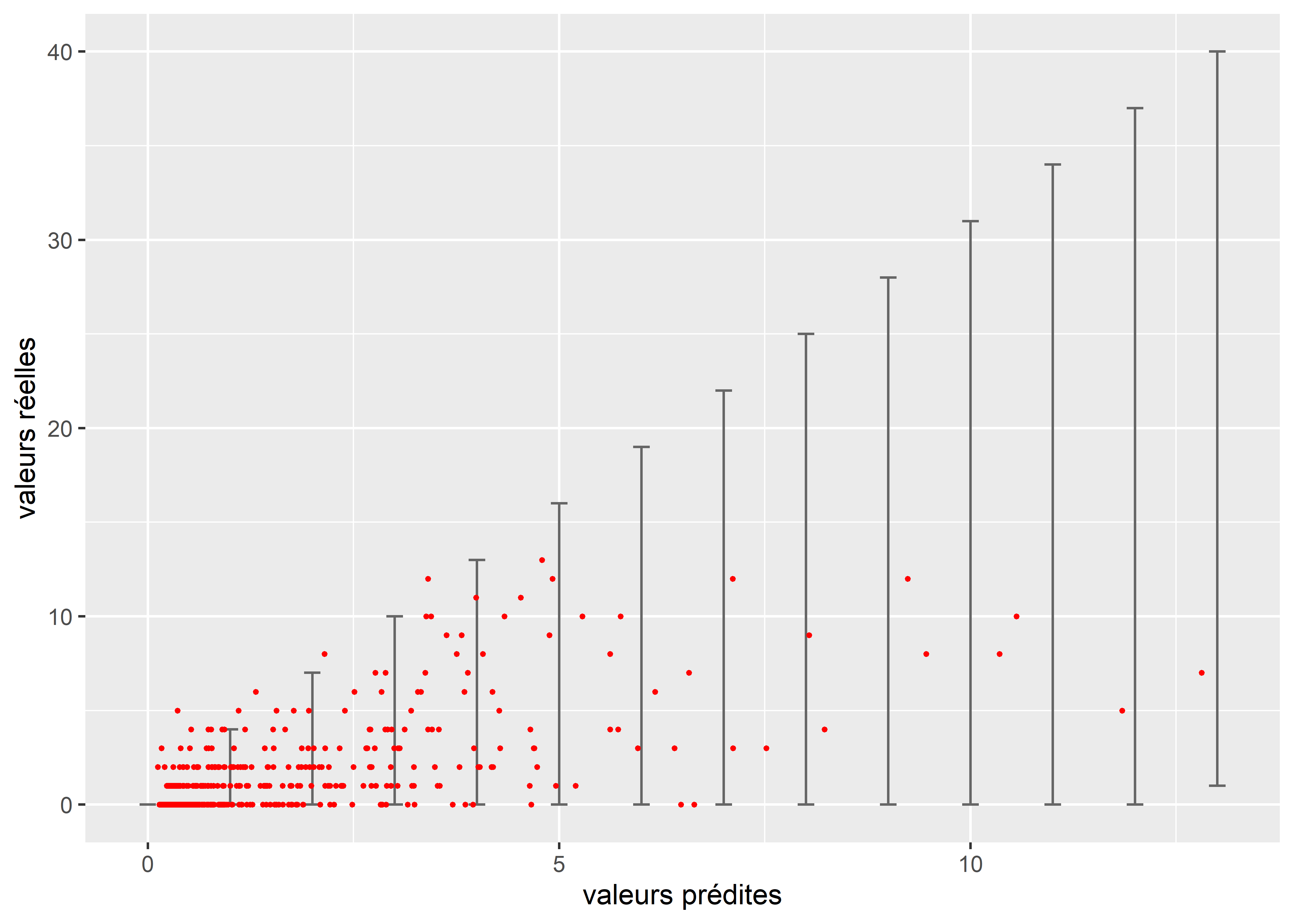
Figure 8.35: Représentation de la sur-dispersion des données dans le modèle de Poisson
Nous pouvons ainsi constater à la figure 8.35 que le modèle binomial négatif autorise une variance bien plus large que le modèle de Poisson et est ainsi mieux ajusté aux données.
Vérification de la qualité d’ajustement
# Calcul des pseudo R2
rsqs(loglike.full = logLik(modelnb),
loglike.null = logLik(modelnull),
full.deviance = deviance(modelnb),
null.deviance = modelnb$null.deviance,
nb.params = modelnb$rank,
n = nrow(data2))## $`deviance expliquee`
## [1] 0.458052
##
## $`McFadden ajuste`
## 'log Lik.' 0.384353 (df=14)
##
## $`Cox and Snell`
## 'log Lik.' 0.8304773 (df=14)
##
## $Nagelkerke
## 'log Lik.' 0.8399731 (df=14)# Calcul du RMSE
sqrt(mean((predict(modelnb, type = "response") - data2$Nbr_acci)**2))## [1] 1.825278Le modèle parvient à expliquer 45 % de la déviance. Il obtient un R2 ajusté de McFadden de 0,14 et un R2 de Nagelkerke de 0,42. L’erreur moyenne quadratique de la prédiction est de 1,82, ce qui est identique au modèle de Poisson ajusté précédemment.
Interprétation des résultats
Il est possible d’accéder à l’ensemble des coefficients du modèle via la fonction summary. À nouveau, les coefficients doivent être convertis avec la fonction exponentielle (du fait de la fonction de lien log) et interprétés comme des effets multiplicatifs. Le tableau 8.24 présente les coefficients estimés par le modèle. Les résultats sont très similaires à ceux du modèle de quasi-Poisson original. Nous notons cependant que la variable représentant la présence d’un feu pour piéton n’est plus significative au seuil de 0,05.
| Variable | Coeff. | exp(Coeff.) | Val.p | IC 2,5 % exp(Coeff.) | IC 97,5 % exp(Coeff.) | Sign. |
|---|---|---|---|---|---|---|
| Constante | -3,880 | 0,020 | 0,000 | 0,010 | 0,080 | *** |
| Feux_auto | 1,130 | 3,100 | 0,000 | 2,030 | 4,710 | *** |
| Feux_piet | 0,350 | 1,420 | 0,016 | 1,060 | 1,900 |
|
| Pass_piet | 0,220 | 1,240 | 0,300 | 0,830 | 1,880 | |
| Terreplein | -0,340 | 0,710 | 0,155 | 0,440 | 1,140 | |
| Apaisement | 0,240 | 1,270 | 0,315 | 0,790 | 2,030 | |
| LogEmploi | 0,230 | 1,260 | 0,025 | 1,030 | 1,550 |
|
| Densite_pop | 0,000 | 1,000 | 0,000 | 1,000 | 1,000 | *** |
| Entropie | -0,170 | 0,840 | 0,669 | 0,380 | 1,860 | |
| DensiteInter | 0,000 | 1,000 | 0,925 | 0,990 | 1,010 | |
| Long_arterePS | 0,000 | 1,000 | 0,587 | 1,000 | 1,000 | |
| Artere | 0,110 | 1,110 | 0,497 | 0,820 | 1,510 | |
| NB_voies5 | 0,700 | 2,010 | 0,000 | 1,480 | 2,750 | *** |
8.3.3 Modèle de Poisson avec excès fixe de zéros
Dans le cas où la variable Y comprendrait significativement plus de zéros que ce que suppose une distribution de Poisson, il est possible d’utiliser la distribution de Poisson avec excès de zéros. Pour rappel, cette distribution ajoute un paramètre p contrôlant pour la proportion de zéros dans la distribution. Du point de vue conceptuel, cela revient à formuler l’hypothèse suivante : dans les données que nous avons observées, deux processus distincts sont à l’œuvre. Le premier est issu d’une distribution de Poisson et l’autre produit des zéros qui s’ajoutent aux données. Les zéros produits par la distribution de Poisson sont appelés les vrais zéros, alors que ceux produits par le second phénomène sont appelés les faux zéros.
| Type de variable dépendante | Variable de comptage |
| Distribution utilisée | Poisson avec excès de zéros |
| Formulation |
\(Y \sim ZIP(\mu,\theta)\) \(g(\lambda) = \beta_0 + \beta X\) \(g(x) =log(x)\) |
| Fonction de lien | log |
| Paramètre modélisé | \(\lambda\) |
| Paramètres à estimer | \(\beta_0\), \(\beta\) et p |
| Conditions d’application | Absence de sur-dispersion |
Dans cette formulation, p est fixé. Nous n’avons donc aucune information sur ce qui produit les zéros supplémentaires, mais seulement leur proportion totale dans le jeu de données.
8.3.3.1 Interprétation des paramètres
L’interprétation des paramètres est identique à celle d’un modèle de Poisson. Le paramètre p représente la proportion de faux zéros dans la variable Y une fois que les variables indépendantes sont contrôlées.
8.3.3.2 Exemple appliqué dans R
La variable de comptage des accidents des piétons que nous avons utilisée dans les deux exemples précédents semble être une bonne candidate pour une distribution de Poisson avec excès de zéros. En effet, nous avons pu constater une sur-dispersion dans le modèle de Poisson original, ainsi qu’un nombre important d’intersections sans accident. Tentons donc d’améliorer notre modèle en ajustant un excès fixe de zéros. Nous utilisons la fonction gamlss du package gamlss.
library(gamlss)
modelzi <- gamlss(formula = Nbr_acci ~ Feux_auto + Feux_piet + Pass_piet +
Terreplein + Apaisement + LogEmploi + Densite_pop +
Entropie + DensiteInter + Long_arterePS + Artere + NB_voies5,
sigma.formula = ~1,
family = ZIP(mu.link = "log", sigma.link="logit"),
data = data_accidents)## GAMLSS-RS iteration 1: Global Deviance = 1516.53
## GAMLSS-RS iteration 2: Global Deviance = 1514.656
## GAMLSS-RS iteration 3: Global Deviance = 1514.52
## GAMLSS-RS iteration 4: Global Deviance = 1514.508
## GAMLSS-RS iteration 5: Global Deviance = 1514.506
## GAMLSS-RS iteration 6: Global Deviance = 1514.506modelnull <- glm(formula = Nbr_acci ~ 1,
family = poisson(link="log"),
data = data_accidents)
# Constante pour p
coeff_p <- modelzi$sigma.coefficients
cat("Coefficient pour p =", round(coeff_p,4))## Coefficient pour p = -1.4376# Calcul de la déviance expliquée
1 - deviance(modelzi) / deviance(modelnull)## [1] 0.08267513# Calcul de la probabilité de base p d'être un faux 0
# en appliquant l'inverse de la fonction logistique
exp(-coeff_p) / (1+exp(-coeff_p))## (Intercept)
## 0.80809Nous constatons immédiatement que le modèle avec excès fixe de zéros est peu ajusté aux données. Cette version du modèle ne parvient à capter que 8 % de la déviance, ce qui s’explique facilement, car nous n’avons donné aucune variable au modèle pour distinguer les vrais et les faux zéros. Pour cela, nous devons passer au prochain modèle : Poisson avec excès ajusté de zéros. Notons tout de même que d’après ce modèle, 81 % des observations seraient des faux zéros.
8.3.4 Modèle de Poisson avec excès ajusté de zéros
Nous avons vu dans le modèle précédent, que l’excès de zéro était conceptualisé comme la combinaison de deux phénomènes, l’un issu d’une distribution de Poisson que nous souhaitons modéliser, et l’autre générant des zéros supplémentaires. Il est possible d’aller plus loin que de simplement contrôler la proportion de zéros supplémentaires en modélisant explicitement ce second processus en ajoutant une deuxième équation au modèle. Cette deuxième équation a pour enjeu de modéliser p (la proportion de 0) à l’aide de variables indépendantes, ces dernières pouvant se retrouver dans les deux parties du modèle. L’idée étant que, pour chaque observation, le modèle évalue sa probabilité d’être un faux zéro (partie binomiale), et le nombre attendu d’accidents.
| Type de variable dépendante | Variable de comptage |
| Distribution utilisée | Poisson avec excès de zéros |
| Formulation |
\(Y \sim ZIP(\mu,\theta)\) \(g(\mu) = \beta_0 + \beta X\) \(s(p) = \alpha_0 + \alpha_X\) \(g(x) =log(x)\) \(s(x) = log(\frac{x}{1-x})\) |
| Fonction de lien | log et logistique |
| Paramètre modélisé | \(\mu\) et p |
| Paramètres à estimer | \(\beta_0\), \(\beta\), \(\alpha_0\) et \(\alpha\) |
| Conditions d’application | Absence de sur-dispersion |
8.3.4.1 Interprétation des paramètres
L’interprétation des paramètres \(\beta_0\) et \(\beta\) est identique à celle d’un modèle de Poisson. Les paramètres \(\alpha_0\) et \(\alpha\) sont identiques à ceux d’un modèle binomial. Plus spécifiquement, ces derniers paramètres modélisent la probabilité d’observer des valeurs supérieures à zéro.
8.3.4.2 Exemple appliqué
Nous avons vu, dans l’exemple précédent, que l’utilisation du modèle avec excès fixe de zéros pour les données d’accident des piétons aux intersections ne donnait pas de résultats satisfaisants. Nous tentons ici d’améliorer le modèle en ajoutant les variables indépendantes significatives du modèle Poisson dans la seconde équation de régression destinée à détecter les faux zéros.
Vérification des conditions d’application
Pour un modèle de Poisson avec excès de zéros, il n’est pas possible de calculer les distances de Cook. Nous devons donc directement passer à l’analyse des résidus simulés.
# Ajuster une première version du modèle
modelza <- gamlss(formula = Nbr_acci ~ Feux_auto + Feux_piet + Pass_piet +
Terreplein + Apaisement + LogEmploi + Densite_pop +
Entropie + DensiteInter + Long_arterePS + Artere + NB_voies5,
sigma.formula = ~1 + Feux_auto + Feux_piet + Densite_pop + NB_voies5,
family = ZIP(mu.link = "log", sigma.link="logit"),
data = data_accidents)## GAMLSS-RS iteration 1: Global Deviance = 1505.155
## GAMLSS-RS iteration 2: Global Deviance = 1488.658
## GAMLSS-RS iteration 3: Global Deviance = 1483.304
## GAMLSS-RS iteration 4: Global Deviance = 1482.085
## GAMLSS-RS iteration 5: Global Deviance = 1481.868
## GAMLSS-RS iteration 6: Global Deviance = 1481.832
## GAMLSS-RS iteration 7: Global Deviance = 1481.827
## GAMLSS-RS iteration 8: Global Deviance = 1481.825
## GAMLSS-RS iteration 9: Global Deviance = 1481.825# Extraire la prédiction des valeurs lambda
lambdas <- predict(modelza, type = "response", what = "mu")
# Extraire la prédiction des valeurs p
ps <- predict(modelza, type = "response", what = "sigma")
# Calculer la combinaison de ces deux éléments
preds <- lambdas * ps
# Effectuer les 1000 simulations
nsim <- 1000
cols <- lapply(1:length(lambdas),function(i){
lambda <- lambdas[[i]]
p <- ps[[i]]
sims <- rZIP(n = nsim, mu = lambda, sigma = p)
return(sims)
})
mat_sims <- do.call(rbind, cols)
# Calculer les résidus simulés
sim_res <- createDHARMa(simulatedResponse = mat_sims,
observedResponse = data_accidents$Nbr_acci,
fittedPredictedResponse = preds,
integerResponse = T)plot(sim_res)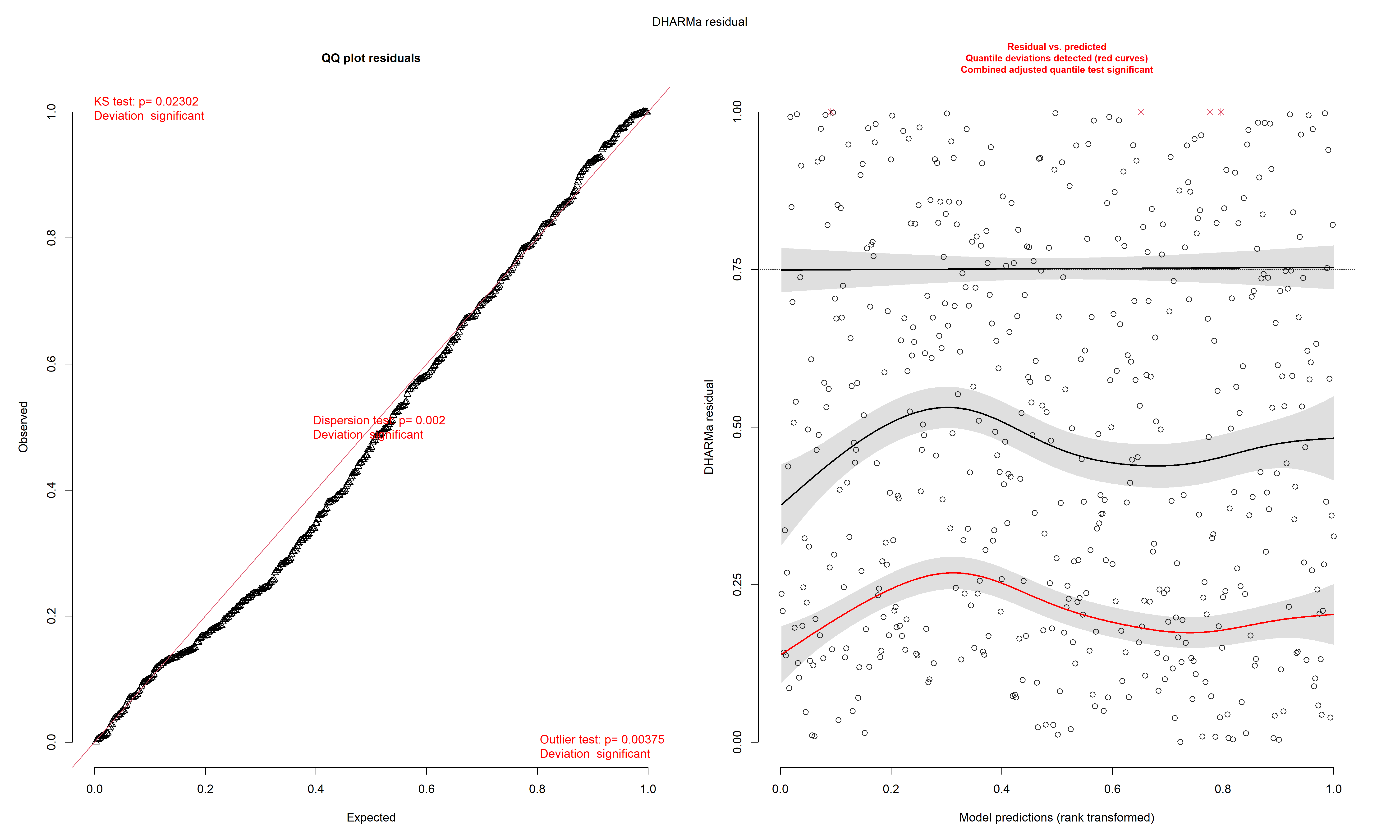
Figure 8.36: Diagnostic général des résidus simulés du modèle de Poisson avec excès de zéros ajusté
La figure 8.36 indique deux problèmes importants dans le modèle : la présence de valeurs aberrantes ainsi qu’un potentiel problème de dispersion. Nous commençons donc par identifier ces valeurs aberrantes.
# Identification des outliers
isOutlier <- outliers(sim_res,return = "logical",lowerQuantile = 0.001,
upperQuantile = 0.999)
cas_etrange <- subset(data_accidents, isOutlier)
print(cas_etrange)## Nbr_acci Feux_auto Feux_piet Pass_piet Terreplein Apaisement EmpTotBuffer Densite_pop Entropie
## 1 19 1 1 1 1 0 7208.538 5980.923 0.8073926
## 2 13 1 1 1 0 0 15198.958 11696.805 0.6432018
## 5 12 1 0 1 0 0 8585.350 8655.430 0.7607852
## 26 7 0 0 1 0 0 1342.625 2751.012 0.0000000
## 483 0 0 0 1 0 0 2665.846 7208.356 0.6251996
## DensiteInter Long_arterePS Artere NB_voies5 log_acci catego_acci catego_acci2 Arret VAG sum_app
## 1 42.41597 6955.00 1 1 2.995732 1 1 0 1 4
## 2 86.50445 9581.51 1 0 2.639057 1 1 0 1 4
## 5 89.11495 6412.27 0 0 2.564949 1 1 0 1 4
## 26 73.35344 2849.66 0 0 2.079442 1 1 1 1 3
## 483 44.49561 1684.07 0 0 0.000000 0 0 1 1 4
## LogEmploi AccOrdinal PopHa
## 1 8.883021 2 5.980923
## 2 9.628982 2 11.696805
## 5 9.057813 2 8.655430
## 26 7.202382 2 2.751012
## 483 7.888277 0 7.208356Nous retirons des données les quelques observations pouvant avoir une trop forte influence sur le modèle. Après réajustement, la figure 8.37 nous informe que nous n’avons plus de valeurs aberrantes restantes ni de fort problème de dispersion. En revanche, le premier quantile des résidus tant à être plus faible que ce que nous aurions pu nous attendre d’une distribution uniforme. Ce constat laisse penser que le modèle a du mal à bien identifier les faux zéros. Ce résultat n’est pas étonnant, car aucune variable n’avait été identifiée à cette fin dans l’article original (Cloutier et al. 2014) qui utilisait un modèle binomial négatif.
data2 <- subset(data_accidents, isOutlier==FALSE)
# Ajuster une première version du modèle
modelza <- gamlss(formula = Nbr_acci ~ Feux_auto + Feux_piet + Pass_piet +
Terreplein + Apaisement + LogEmploi + Densite_pop +
Entropie + DensiteInter + Long_arterePS + Artere + NB_voies5,
sigma.formula = ~1 + Feux_auto + Feux_piet + Densite_pop + NB_voies5,
family = ZIP(mu.link = "log", sigma.link="logit"),
data = data2)## GAMLSS-RS iteration 1: Global Deviance = 1397.751
## GAMLSS-RS iteration 2: Global Deviance = 1386.151
## GAMLSS-RS iteration 3: Global Deviance = 1382.5
## GAMLSS-RS iteration 4: Global Deviance = 1381.285
## GAMLSS-RS iteration 5: Global Deviance = 1380.893
## GAMLSS-RS iteration 6: Global Deviance = 1380.777
## GAMLSS-RS iteration 7: Global Deviance = 1380.745
## GAMLSS-RS iteration 8: Global Deviance = 1380.736
## GAMLSS-RS iteration 9: Global Deviance = 1380.733
## GAMLSS-RS iteration 10: Global Deviance = 1380.732# Extraire la prédiction des valeurs lambda
lambdas <- predict(modelza, type = "response", what = "mu")
# Extraire la prédiction des valeurs p
ps <- predict(modelza, type = "response", what = "sigma")
# Calculer la combinaison de ces deux éléments
preds <- lambdas * ps
# Effectuer les 1000 simulations
nsim <- 1000
cols <- lapply(1:length(lambdas),function(i){
lambda <- lambdas[[i]]
p <- ps[[i]]
sims <- rZIP(n = nsim, mu = lambda, sigma = p)
return(sims)
})
mat_sims <- do.call(rbind, cols)
# Calculer les résidus simulés
sim_res <- createDHARMa(simulatedResponse = mat_sims,
observedResponse = data2$Nbr_acci,
fittedPredictedResponse = preds,
integerResponse = T)
plot(sim_res)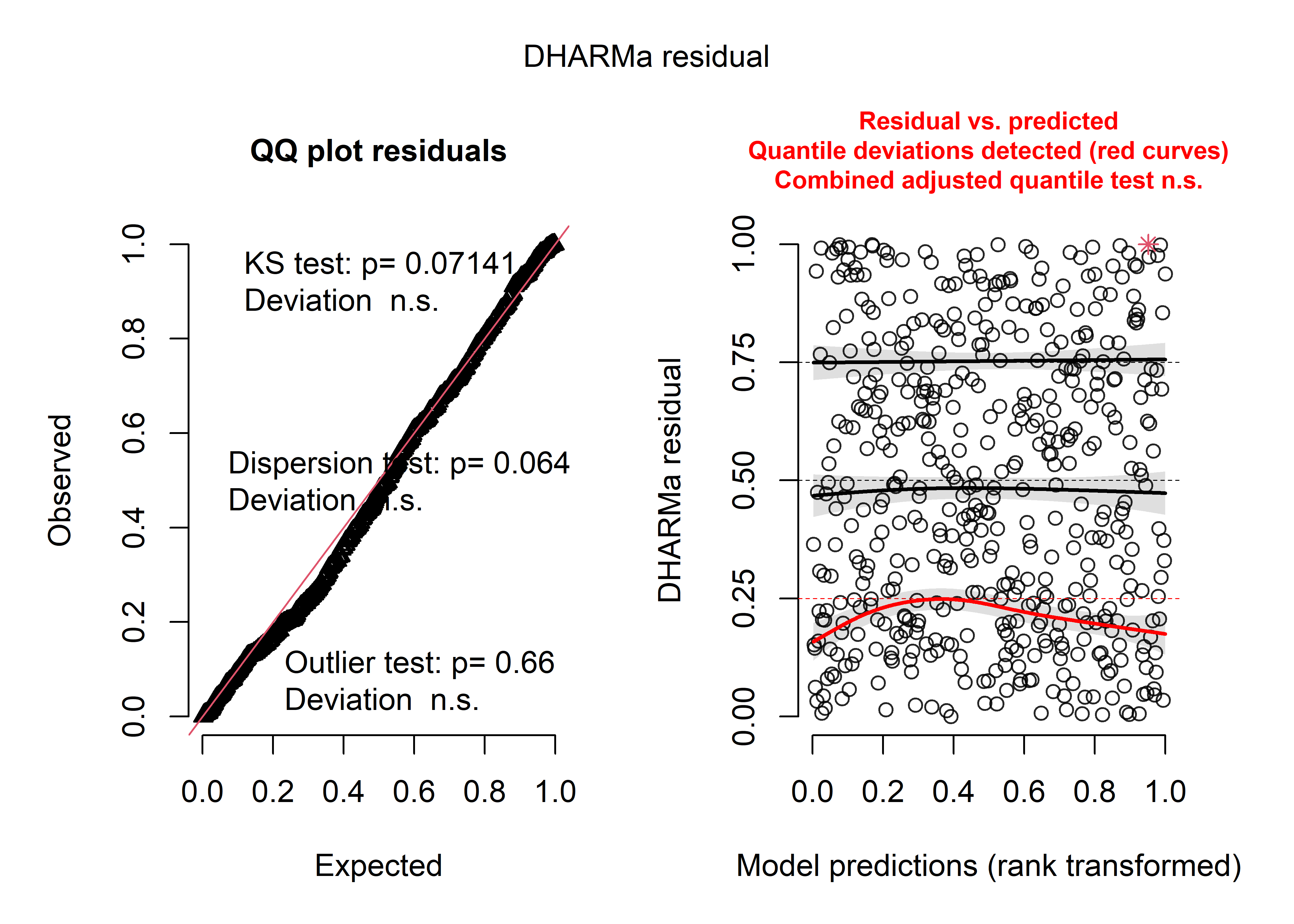
Figure 8.37: Diagnostic général des résidus simulés du modèle de Poisson avec excès de zéros ajusté (sans valeurs aberrantes)
Nous pouvons une fois encore comparer des simulations issues du modèle et de la distribution originale de la variable Y. La figure 8.38 montre clairement que les simulations du modèle (en bleu) sont très éloignées dans la distribution originale (en gris), ce qui remet directement en question la pertinence de ce modèle.
# Extraire la prédiction des valeurs lambda
lambdas <- predict(modelza, type = "response", what = "mu")
# Extraire la prédiction des valeurs p
ps <- predict(modelza, type = "response", what = "sigma")
# Génération de 1000 simulations pour chaque prédiction
nsim <- 1000
cols <- lapply(1:length(lambdas),function(i){
lambda <- lambdas[[i]]
p <- ps[[1]]
sims <- round(rZIP(nsim,mu=lambda, sigma = p))
return(sims)
})
mat_sims <- do.call(rbind, cols)
# Préparation des données pour le graphique (valeurs réelles)
counts <- data.frame(table(data2$Nbr_acci))
names(counts) <- c("nb_accident",'frequence')
counts$nb_accident <- as.numeric(as.character(counts$nb_accident))
counts$prop <- counts$frequence / sum(counts$frequence)
# Préparation des données pour le graphique (valeurs simulées)
df1 <- data.frame(count = 0:25)
count_sims <- lapply(1:nsim, function(i){
sim <- mat_sims[,i]
cnt <- data.frame(table(sim))
df2 <- merge(df1,cnt, by.x="count", by.y = "sim", all.x = T, all.y=F)
df2$Freq <- ifelse(is.na(df2$Freq),0,df2$Freq)
return(df2$Freq)
})
count_sims <- do.call(cbind,count_sims)
df_sims <- data.frame(
val = 0:25,
med = apply(count_sims, MARGIN = 1, median),
lower = apply(count_sims, MARGIN = 1, quantile, probs = 0.025),
upper = apply(count_sims, MARGIN = 1, quantile, probs = 0.975)
)
# Affichage du graphique
ggplot() +
geom_bar(aes(x=nb_accident, weight = frequence), width = 0.6, data = counts)+
geom_errorbar(aes(x = val, ymin = lower, ymax = upper),
data = df_sims, color = "blue", width = 0.6)+
geom_point(aes(x = val, y = med), color = "blue", size = 1.3, data = df_sims)+
scale_x_continuous(limits = c(-0.5,7), breaks = c(0:7))+
xlim(-1,12)+
labs(subtitle = "",
x = "nombre d'accidents",
y = "nombre d'occurrences")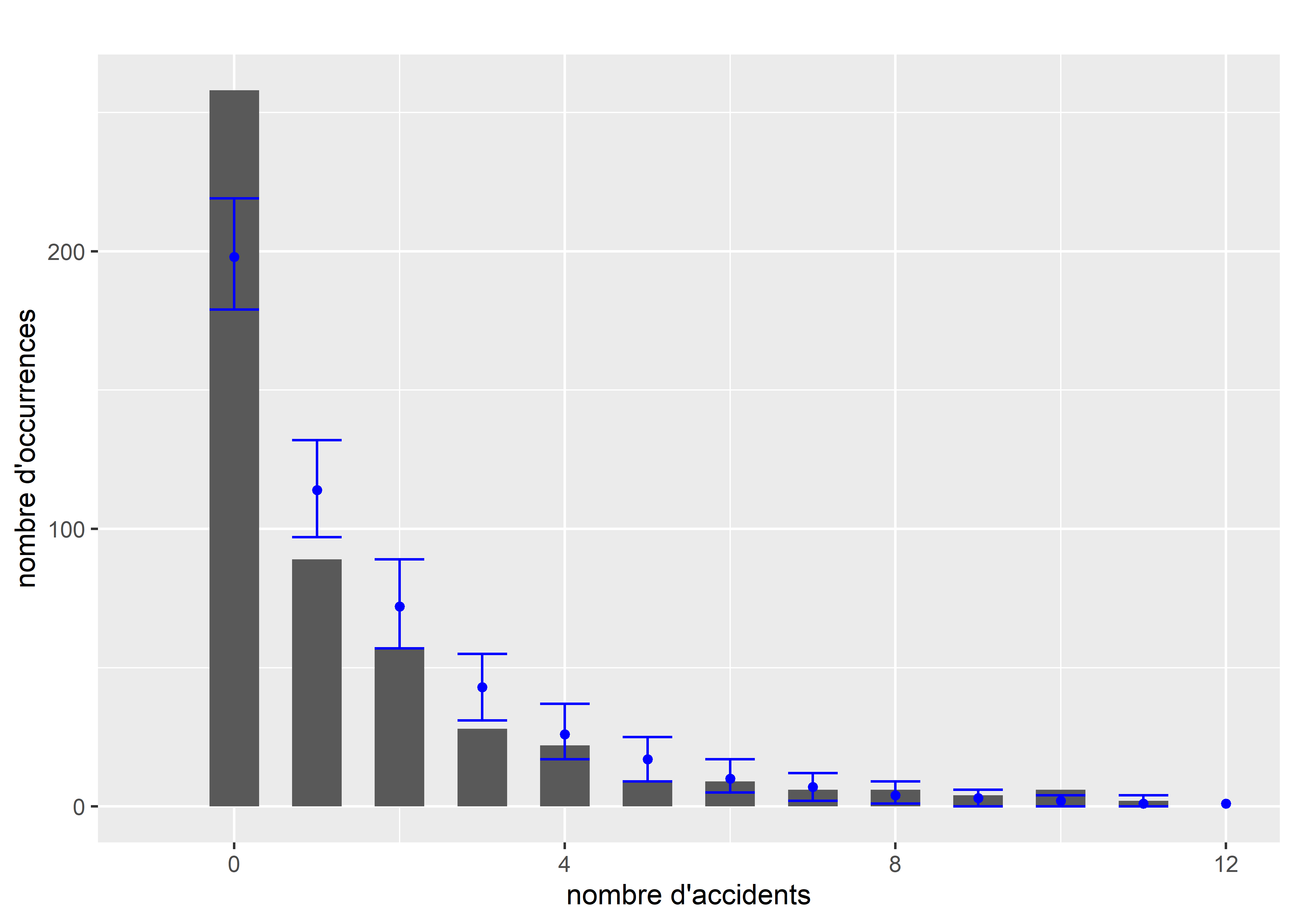
Figure 8.38: Comparaison de la distribution originale et des simulations pour le modèle de Poisson avec excès de zéros ajusté
Vérification la qualité d’ajustement
modelenull <- glm(Nbr_acci ~ 1,
family = poisson(link="log"),
data = data2)
# Calcul des R2
rsqs(loglike.full = logLik(modelza),
loglike.null = logLik(modelenull),
full.deviance = deviance(modelza),
null.deviance = deviance(modelenull),
nb.params = modelza$sigma.df + modelza$mu.df,
n = nrow(data2)
)## $`deviance expliquee`
## [1] 0.08807561
##
## $`McFadden ajuste`
## 'log Lik.' 0.3484515 (df=18)
##
## $`Cox and Snell`
## 'log Lik.' 0.7955335 (df=18)
##
## $Nagelkerke
## 'log Lik.' 0.805948 (df=18)# Calcul du RMSE
sqrt(mean((preds - data2$Nbr_acci)**2))## [1] 2.576983Le modèle avec excès de zéro ajusté ne parvient à expliquer que 11 % de la déviance totale. Il obtient toutefois des valeurs de R2 assez hautes (McFadden ajusté : 0,36, Nagerlkerke : 0,82). Son RMSE est très élevé (2,6), comparativement à celui que nous avons obtenu avec le modèle binomial négatif (1,9). Considérant ces éléments, ce modèle est nettement moins informatif que le modèle binomial négatif et ne devrait pas être retenu. Nous montrons tout de même ici comment interpréter ces résultats.
Interprétation des résultats
L’ensemble des coefficients du modèle sont accessibles avec la fonction summary. Les coefficients dédiés à la partie Poisson (appelée Mu dans le résumé) doivent être analysés et interprétés de la même manière que s’ils provenaient d’un modèle de Poisson. Les coefficients appartenant à la partie logistique (appelé Sigma dans le résumé) doivent être analysés et interprétés de la même manière que s’ils provenaient d’un modèle logistique.
# Extraction des résultats
base_table <- summary(modelza)## ******************************************************************
## Family: c("ZIP", "Poisson Zero Inflated")
##
## Call: gamlss(formula = Nbr_acci ~ Feux_auto + Feux_piet +
## Pass_piet + Terreplein + Apaisement + LogEmploi +
## Densite_pop + Entropie + DensiteInter + Long_arterePS +
## Artere + NB_voies5, sigma.formula = ~1 + Feux_auto +
## Feux_piet + Densite_pop + NB_voies5, family = ZIP(mu.link = "log",
## sigma.link = "logit"), data = data2)
##
## Fitting method: RS()
##
## ------------------------------------------------------------------
## Mu link function: log
## Mu Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) -2.472e+00 5.483e-01 -4.508 8.21e-06 ***
## Feux_auto 5.628e-01 1.909e-01 2.948 0.003359 **
## Feux_piet 3.905e-01 1.102e-01 3.545 0.000431 ***
## Pass_piet 3.389e-01 1.926e-01 1.760 0.079087 .
## Terreplein -3.318e-01 1.667e-01 -1.991 0.047078 *
## Apaisement 2.164e-01 1.534e-01 1.411 0.158933
## LogEmploi 1.638e-01 7.644e-02 2.142 0.032668 *
## Densite_pop 7.841e-05 1.533e-05 5.116 4.51e-07 ***
## Entropie -1.308e-01 3.094e-01 -0.423 0.672799
## DensiteInter 3.677e-03 2.082e-03 1.766 0.078108 .
## Long_arterePS 8.103e-06 2.054e-05 0.395 0.693332
## Artere 3.142e-02 1.156e-01 0.272 0.785871
## NB_voies5 4.761e-01 1.055e-01 4.511 8.10e-06 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## ------------------------------------------------------------------
## Sigma link function: logit
## Sigma Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 1.1597263 0.5259636 2.205 0.02793 *
## Feux_auto -1.6591393 0.6038115 -2.748 0.00622 **
## Feux_piet 0.0653804 0.7645555 0.086 0.93189
## Densite_pop -0.0001252 0.0000532 -2.353 0.01903 *
## NB_voies5 -1.4651605 0.8694733 -1.685 0.09261 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## ------------------------------------------------------------------
## No. of observations in the fit: 500
## Degrees of Freedom for the fit: 18
## Residual Deg. of Freedom: 482
## at cycle: 10
##
## Global Deviance: 1380.732
## AIC: 1416.732
## SBC: 1492.595
## ******************************************************************# Multiplication par 1000 des coefficients de population
# (effet pour 1000 habitants)
base_table[8,1] <- 1000 * base_table[8,1]
base_table[8,2] <- 1000 * base_table[8,2]
base_table[17,1] <- 1000 * base_table[17,1]
base_table[17,2] <- 1000 * base_table[17,2]
# Multiplication par 1000 des coefficients de longueur artère
# (effet pour 1 km)
base_table[11,1] <- 1000 * base_table[11,1]
base_table[11,2] <- 1000 * base_table[11,2]
# Calcul des exponentiels des variables indépendantes
# et des intervalles de confiance
expcoeff <- exp(base_table[,1])
expcoeff2.5 <- exp(base_table[,1] - 1.96 * base_table[,2])
expcoeff97.5 <- exp(base_table[,1] + 1.96 * base_table[,2])
base_table <- cbind(base_table, expcoeff, expcoeff2.5,expcoeff97.5)
# Calculer une colonne indiquant le niveau de significativité
sign <- case_when(
base_table[,4] < 0.001 ~ "***",
base_table[,4] >= 0.001 & base_table[,4]<0.01 ~ "**",
base_table[,4] >= 0.01 & base_table[,4]<0.05 ~ "*",
base_table[,4] >= 0.05 & base_table[,4]<0.1 ~ ".",
TRUE ~ ""
)
# Arrondir à trois décimales
base_table <- round(base_table,3)
# Enlever les colonnes de valeurs de t et d'erreur standard
base_table <- base_table[,c(1,4,5,6,7)]
base_table <- cbind(base_table, sign)
# Remplacer les 0 dans la colonne pval
base_table[,2] <- ifelse(base_table[,2]=="0","<0.001",base_table[,2])
# Séparer le tout en deux tableaux
part_poiss <- base_table[1:13,]
part_logit <- base_table[14:18,]
# Mettre les bons noms de colonnes
colnames(part_poiss) <- c("Coeff.","Val.p","Exp(Coeff.)",
"IC 2,5 % exp(Coeff.)","IC 97,5 % exp(Coeff.)", "Sign.")
colnames(part_logit) <- c("Coeff.","Val.p","RC","IC 2,5 % RC","IC 97,5 % RC", "Sign.")Nous rapportons les résultats de ce modèle de Poisson avec excès de zéro ajusté dans les tableaux 8.27 et 8.28.
| Variable | Coeff. | Val.p | Exp(Coeff.) | IC 2,5 % exp(Coeff.) | IC 97,5 % exp(Coeff.) | Sign. |
|---|---|---|---|---|---|---|
| (Intercept) | -2.472 | <0.001 | 0.084 | 0.029 | 0.247 | *** |
| Feux_auto | 0.563 | 0.003 | 1.756 | 1.208 | 2.552 | ** |
| Feux_piet | 0.391 | <0.001 | 1.478 | 1.191 | 1.834 | *** |
| Pass_piet | 0.339 | 0.079 | 1.403 | 0.962 | 2.047 | . |
| Terreplein | -0.332 | 0.047 | 0.718 | 0.518 | 0.995 |
|
| Apaisement | 0.216 | 0.159 | 1.242 | 0.919 | 1.677 | |
| LogEmploi | 0.164 | 0.033 | 1.178 | 1.014 | 1.368 |
|
| Densite_pop | 0.078 | <0.001 | 1.082 | 1.05 | 1.115 | *** |
| Entropie | -0.131 | 0.673 | 0.877 | 0.478 | 1.609 | |
| DensiteInter | 0.004 | 0.078 | 1.004 | 1 | 1.008 | . |
| Long_arterePS | 0.008 | 0.693 | 1.008 | 0.968 | 1.05 | |
| Artere | 0.031 | 0.786 | 1.032 | 0.823 | 1.294 | |
| NB_voies5 | 0.476 | <0.001 | 1.61 | 1.309 | 1.98 | *** |
| Variable | Coeff. | Val.p | RC | IC 2,5 % RC | IC 97,5 % RC | Sign. |
|---|---|---|---|---|---|---|
| (Intercept) | 1.16 | 0.028 | 3.189 | 1.138 | 8.941 |
|
| Feux_auto | -1.659 | 0.006 | 0.19 | 0.058 | 0.621 | ** |
| Feux_piet | 0.065 | 0.932 | 1.068 | 0.239 | 4.777 | |
| Densite_pop | -0.125 | 0.019 | 0.882 | 0.795 | 0.979 |
|
| NB_voies5 | -1.465 | 0.093 | 0.231 | 0.042 | 1.27 | . |
Nous observons ainsi que la présence d’un feu de circulation divise par 5 les chances de rentrer dans la catégorie d’intersection où des accidents peuvent se produire. De même, la densité de population réduit les chances de passer dans cette catégorie de 11 %.
Concernant les coefficients pour la partie Poisson du modèle, nous observons que les présences d’un feu de circulation et d’un feu pour piéton contribuent à multiplier respectivement par 2 et 1,5 le nombre attendu d’accidents à une intersection. De même, la présence d’un axe de circulation à cinq voies augmente de 57 % le nombre d’accidents. Enfin, la densité de population est aussi associée à une augmentation du nombre d’accidents : pour 1 000 habitants supplémentaires autour de l’intersection, nous augmentons le nombre d’accidents attendu de 9 %.
8.3.5 Conclusion sur les modèles destinés à des variables de comptage
Dans cette section, nous avons vu que modéliser une variable de comptage ne doit pas toujours être réalisé avec une simple distribution de Poisson. Il est nécessaire de tenir compte de la sur ou sous-dispersion potentielle ainsi que de l’excès de zéros. Nous n’avons cependant pas couvert tous les cas. Il est en effet possible d’ajuster des modèles avec une distribution binomiale négative avec excès de zéros (avec le package gamlss), ainsi que des modèles de Hurdle. Ces derniers ont une approche différente de celle proposée par les distributions ajustées pour tenir compte de l’excès de zéro que nous détaillons dans l’encadré « pour aller plus loin » ci-dessous. Le processus de sélection du modèle peut être résumé avec la figure 8.39. Notez que même en suivant cette procédure, rien ne garantit que votre modèle final reflète bien les données que vous étudiez. L’analyse approfondie des résidus et des prédictions du modèle est la seule façon de déterminer si oui ou non le modèle est fiable.
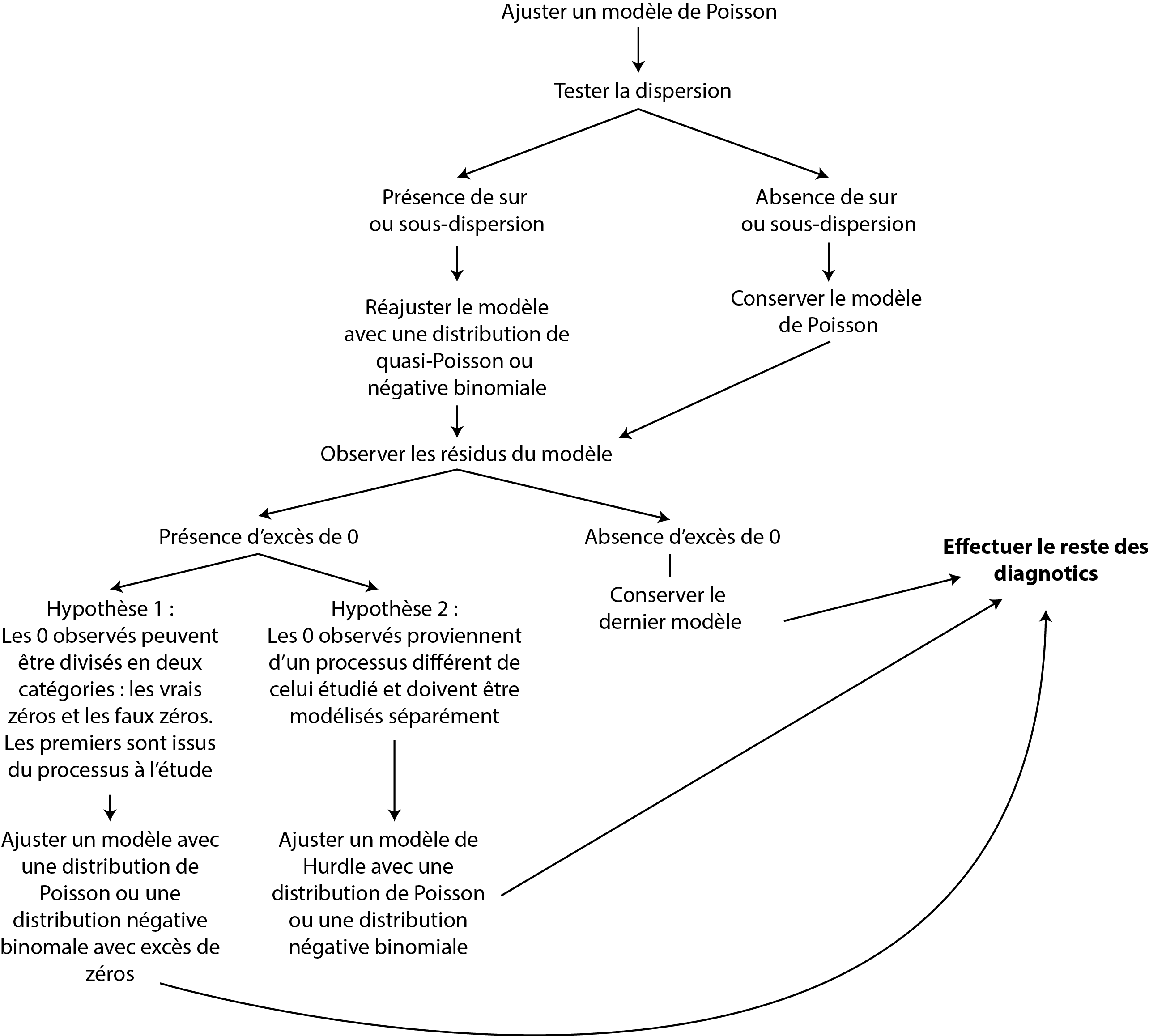
Figure 8.39: Processus de sélection d’un modèle pour une variable de comptage
Modèle de Hurdle versus modèle avec excès de zéro
Les modèles de Hurdle sont une autre catégorie de modèles GLM. Ils peuvent être décrits avec la formulation suivante :
\[\begin{equation}\left\{\begin{array}{c} Y \sim \text {Binomial}(p) \text { si } y=0 \\ \text { logit }(p)=\beta_{a} X_{a} \\ Y \sim \text { TrPoisson}(\lambda) \text { si } y>0 \\ \log (\lambda)=\beta_{b} X_{b} \end{array}\right. \tag{8.21} \end{equation}\]
Nous constatons qu’un modèle de Hurdle utilise deux distributions, la première est une distribution binomiale dont l’objectif est de prédire si les observations sont à 0 ou au-dessus de 0. La seconde est une distribution strictement positive (supérieure à 0), il peut s’agir d’une distribution tronquée de Poisson, tronquée binomiale négative, Gamma, log-normale ou autre, dépendamment du phénomène modélisé. Puisque le modèle fait appel à deux distributions, deux équations de régression sont utilisées, l’une pour prédire p (la probabilité d’observer une valeur au-dessus de 0) et l’autre l’espérance (moyenne) de la seconde distribution.
En d’autres termes, un modèle de Hurdle modélise les données à zéro et les données au-delà de 0 comme deux processus différents (chacun avec sa propre distribution). Cette approche se distingue des modèles avec excès de zéros qui utilisent une seule distribution pour décrire l’ensemble des données. D’après un modèle avec excès de zéro, il existe de vrais et de faux zéros que l’on tente de distinguer. Dans un modèle de Hurdle, l’idée est que les zéros constituent une limite. Nous modélisons la probabilité de dépasser cette limite et ensuite la magnitude du dépassement de cette limite.
Prenons un exemple pour rendre la distinction plus concrète. Admettons que nous utilisons un capteur capable de mesurer la concentration de particules fines dans l’air. D’après les spécifications du fabricant, le capteur est capable de mesurer des taux de concentration à partir de 0,001 µg/m3. Dans une ville avec des niveaux de concentration très faibles, il est très fréquent que le capteur enregistre des valeurs à zéro. Considérant ce phénomène, il serait judicieux de modéliser le processus avec un modèle de Hurdle Gamma puisque les 0 représentent une limite qui n’a pas été franchie : le seuil de détection du capteur. Nous traitons donc différemment les secteurs au-dessous et au-dessus de ce seuil. Si nous reprenons notre exemple sur les accidents des piétons à des intersections, il est plus judicieux, dans ce cas, de modéliser le phénomène avec un modèle avec excès de zéro puisque nous pouvons observer zéro accident à une intersection dangereuse (vrai zéro) et zéro accident à une intersection sur laquelle aucun piéton ne traverse jamais (faux zéro).