7.5 Introduction de variables explicatives particulières

7.5.1 Exploration des relations non linéaires

7.5.1.1 Variable indépendante avec une fonction polynomiale

Dans la section 4.1, nous avons vu que la relation entre deux variables continues n’est pas toujours linéaire; elle peut être aussi curvilinéaire. Pour explorer les relations curvilinéaires, nous introduisons la variable indépendante sous la forme polynomiale d’ordre 2 (voir le prochain encadré). L’équation de régression s’écrit alors :

\[\begin{equation} Y = b_{0} + b_{1}X_{1} + b_{11}X_{1}^2 + b_{2}X_{2} +\ldots+ b_{k}X_{k} + e \tag{7.21} \end{equation}\]

Dans l’équation (7.21), la première variable indépendante est introduite dans le modèle de régression à la fois dans sa forme originelle et mise au carré : \(b_{1}X_{1} + b_{11}X_{1}^2\). Un coefficient différent est ajusté pour chacune de ces deux versions de la variable \(X_{1}\).

La démographie est probablement la discipline des sciences sociales qui a le plus recours aux régressions polynomiales. En effet, la variable âge est souvent introduite comme variable explicative dans sa forme originale et mise au carré. L’objectif est de vérifier si l’âge partage ou non une relation curvilinéaire avec un phénomène donné : par exemple, il pourrait y être associé positivement jusqu’à un certain seuil (45 ans par exemple), puis négativement à partir de ce seuil.

Régression polynomiale et nombre d’ordres.

Sachez qu’il est aussi possible de construire des régressions polynomiales avec plus deux ordres. Par exemple, une régression polynomiale d’ordre 3 comprend une variable dans sa forme originelle, puis mise au carré et au cube. Cela a l’inconvénient d’augmenter corollairement le nombre de coefficients. Nous verrons au chapitre 11 qu’il existe une solution plus élégante et efficace : le recours aux modèles de régressions linéaires généralisés additifs avec des splines. Dans le cadre de cette section, nous nous limitons à des régressions polynomiales d’ordre 2.

\[\begin{equation} \mbox{Ordre 2 : } Y = b_{0} + b_{1}X_{1} + b_{11}X_{}^2 + b_{2}X_{2} +\ldots+ b_{k}X_{k} + e \tag{7.22} \end{equation}\]

\[\begin{equation} \mbox{Ordre 3 : } Y = b_{0} + b_{1}X_{1} + b_{11}X_{}^2 + b_{111}X_{}^3 + b_{2}X_{2} +\ldots+ b_{k}X_{k} + e \tag{7.23} \end{equation}\]

\[\begin{equation} \mbox{Ordre 4 : } Y = b_{0} + b_{1}X_{1} + b_{11}X_{}^2 + b_{111}X_{}^3 + b_{1111}X_{}^4 + b_{2}X_{2} +\ldots+ b_{k}X_{k} + e \tag{7.24} \end{equation}\]

Pour construire une régression polynomiale dans R, il est possible d’utiliser deux fonctions de R :

  • I(VI^2) avec VI qui est la variable indépendante sur laquelle est appliquée la mise au carré.
  • poly(VI,2) qui utilise une forme polynomiale orthogonale pour éviter les problèmes de corrélation entre les deux termes, c’est-à-dire entre VI et VI2.

Ces deux méthodes produisent les mêmes résultats pour les autres variables dépendantes et pour la qualité d’ajustement du modèle (R2, F, etc.). Nous privilégions la seconde fonction pour éviter de détecter à tort des problèmes de multicolinéarité excessive.

Appliquons cette démarche à la variable AgeMedian (âge médian des bâtiments) afin de vérifier si elle partage ou non une relation curvilinéaire avec la couverture végétale de l’îlot. À la lecture des résultats pour les deux modèles, les constats suivants peuvent être avancés :

  • Le R2 ajusté passe de 0,4179 à 0,4378 du modèle 1 au modèle 2, ce qui signale un gain de variance expliquée.
  • Le F incrémentiel entre les deux modèles s’élève à 362,64 et est significatif (p < 0,001). Nous pouvons donc en conclure que le second modèle est plus performant que le premier, ce qui signale que la forme curvilinéaire pour AgeMedian (modèle 2) est plus efficace que la forme linéaire (modèle 1).
  • Dans le premier modèle, le coefficient de régression pour AgeMedian n’est pas significatif. L’âge médian des bâtiments n’est donc pas associé linéairement avec la variable dépendante.
  • Dans le second modèle, la valeur du coefficient de poly(AgeMedian, 2)1 est positive et celle de poly(AgeMedian, 2)2 est négative et significative. Cela indique qu’il existe une relation linéaire en forme de U inversé. Si le premier coefficient avait été négatif et le second positif, nous aurions alors conclu que la forme curvilinéaire prend la forme d’un U.
# régression linéaire
modele1 <- lm(VegPct ~ HABHA+AgeMedian+Pct_014+Pct_65P+Pct_MV+Pct_FR, data = DataFinal)

# régression polynomiale
modele2 <- lm(VegPct ~ HABHA+poly(AgeMedian,2)+Pct_014+Pct_65P+Pct_MV+Pct_FR, data = DataFinal)

# affichage des résultats du modèle 1
summary(modele1)
## 
## Call:
## lm(formula = VegPct ~ HABHA + AgeMedian + Pct_014 + Pct_65P + 
##     Pct_MV + Pct_FR, data = DataFinal)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -48.876  -9.757  -0.232   9.499 103.830 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 26.355774   0.882235  29.874   <2e-16 ***
## HABHA       -0.070401   0.002202 -31.975   <2e-16 ***
## AgeMedian    0.010790   0.006369   1.694   0.0902 .  
## Pct_014      1.084478   0.032179  33.702   <2e-16 ***
## Pct_65P      0.400531   0.018835  21.265   <2e-16 ***
## Pct_MV      -0.031112   0.010406  -2.990   0.0028 ** 
## Pct_FR      -0.348256   0.011640 -29.918   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 14.16 on 10203 degrees of freedom
## Multiple R-squared:  0.4182, Adjusted R-squared:  0.4179 
## F-statistic:  1223 on 6 and 10203 DF,  p-value: < 2.2e-16
# affichage des résultats du modèle 1
summary(modele2)
## 
## Call:
## lm(formula = VegPct ~ HABHA + poly(AgeMedian, 2) + Pct_014 + 
##     Pct_65P + Pct_MV + Pct_FR, data = DataFinal)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -49.659  -9.361  -0.159   9.034 105.160 
## 
## Coefficients:
##                       Estimate Std. Error t value Pr(>|t|)    
## (Intercept)          2.968e+01  7.535e-01  39.383  < 2e-16 ***
## HABHA               -7.107e-02  2.164e-03 -32.839  < 2e-16 ***
## poly(AgeMedian, 2)1  1.134e+01  1.598e+01   0.710  0.47788    
## poly(AgeMedian, 2)2 -2.721e+02  1.429e+01 -19.043  < 2e-16 ***
## Pct_014              9.969e-01  3.196e-02  31.198  < 2e-16 ***
## Pct_65P              3.219e-01  1.896e-02  16.972  < 2e-16 ***
## Pct_MV              -2.888e-02  1.023e-02  -2.823  0.00476 ** 
## Pct_FR              -3.562e-01  1.145e-02 -31.116  < 2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 13.92 on 10202 degrees of freedom
## Multiple R-squared:  0.4382, Adjusted R-squared:  0.4378 
## F-statistic:  1137 on 7 and 10202 DF,  p-value: < 2.2e-16
# test de Fisher pour comparer les modèles
anova(modele1, modele2)
## Analysis of Variance Table
## 
## Model 1: VegPct ~ HABHA + AgeMedian + Pct_014 + Pct_65P + Pct_MV + Pct_FR
## Model 2: VegPct ~ HABHA + poly(AgeMedian, 2) + Pct_014 + Pct_65P + Pct_MV + 
##     Pct_FR
##   Res.Df     RSS Df Sum of Sq      F    Pr(>F)    
## 1  10203 2046427                                  
## 2  10202 1976182  1     70245 362.64 < 2.2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Construction d’un graphique des effets marginaux

Pour visualiser la relation linéaire et curvilinéaire, nous vous proposons de réaliser un graphique des effets marginaux à partir de la syntaxe ci-dessous.

Les graphiques des effets marginaux permettent de visualiser l’impact d’une variable indépendante sur la variable dépendante d’une régression. Nous nous basons pour cela sur les prédictions effectuées par le modèle. Admettons que nous nous intéressons à l’effet de la variable X1 sur la variable Y. Il est possible de créer de nouvelles données fictives pour lesquelles l’ensemble des autres variables X sont fixées à leur moyenne respective, et seule X1 est autorisée à varier. En utilisant l’équation de régression du modèle sur ces données fictives, nous pouvons observer l’évolution de la valeur prédite de Y quand X1 augmente ou diminue, et ce, toutes choses étant égales par ailleurs (puisque toutes les autres variables ont une valeur fixe). Cette approche est particulièrement intéressante pour décrire des effets non linéaires obtenus avec des polynomiales, mais aussi des interactions comme nous le verrons plus tard. Elle est également utilisée dans les modèles linéaires généralisés (GLM) et additifs (GAM) (chapitres 8 et 11). Notez qu’il est aussi important de représenter, sur ce type de graphique, l’incertitude de la prédiction. Pour cela, il est possible de construire des intervalles de confiance à 95 % autour de la prédiction en utilisant l’erreur standard de la prédiction (renvoyée par la fonction predict).

library(ggplot2)
# Statistique sur la variable AgeMedian qui varie de 0 à 226 ans
summary(DataFinal$AgeMedian)
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
##    0.00   37.25   49.00   52.11   61.00  226.00
# Création d'un DataFrame temporaire
# remarquez que les autres variables indépendantes sont constantes :
# nous leur avons attribué leur moyenne correspondante
df <- data.frame(
  HABHA = mean(DataFinal$HABHA),
  AgeMedian= seq(0,200, by = 2),
  AgeMedian2 = seq(0,200, by = 2)**2,
  Pct_014= mean(DataFinal$Pct_014),
  Pct_65P= mean(DataFinal$Pct_65P),
  Pct_MV= mean(DataFinal$Pct_MV),
  Pct_FR= mean(DataFinal$Pct_FR)
)

# calcul de la valeur de t pour un intervalle à 95 %
n <- length(modele1$fitted.values) 
k <- length(modele1$coefficients)-1
t95 <- qt(p=1 - (0.05/2),  df=n-k-1)

# Calcul des valeurs prédites pour le 1er modèle
# avec l'intervalle de confiance à 95 %
predsM1 <- predict(modele1,se = T, newdata = df)
df$predM1 <- predsM1$fit
df$lowerM1 <- predsM1$fit - t95*predsM1$se.fit
df$upperM1 <- predsM1$fit + t95*predsM1$se.fit

# Calcul des valeurs prédites pour le 2e modèle
# avec l'intervalle de confiance à 95 %
predsM2 <- predict(modele2,se = T, newdata = df)
df$predM2 <- predsM2$fit
df$lowerM2 <- predsM2$fit - t95*predsM2$se.fit
df$upperM2 <- predsM2$fit + t95*predsM2$se.fit

# Graphique
ggplot(data = df) + 
  geom_ribbon(aes(x = AgeMedian, ymin = lowerM1, ymax = upperM1), 
             fill = rgb(0.1,0.1,0.1,0.4)) + 
  geom_path(aes(x = AgeMedian, y = predM1), color = 'blue', size = 1)+
  
  geom_ribbon(aes(x = AgeMedian, ymin = lowerM2, ymax = upperM2), 
              fill = rgb(0.1,0.1,0.1,0.4)) + 
  geom_path(aes(x = AgeMedian, y = predM2), color = 'red', size = 1)+
  
  labs(title="Effet marginal de l'âge médian des bâtiments sur la",
       subtitle = "couverture végétale des îlots de l'île de Montréal",
       caption = "bleu : relation linéaire; rouge : curvilinéaire",
       x = "Âge médian des bâtiments",
       y = "Couverture végétale (%)")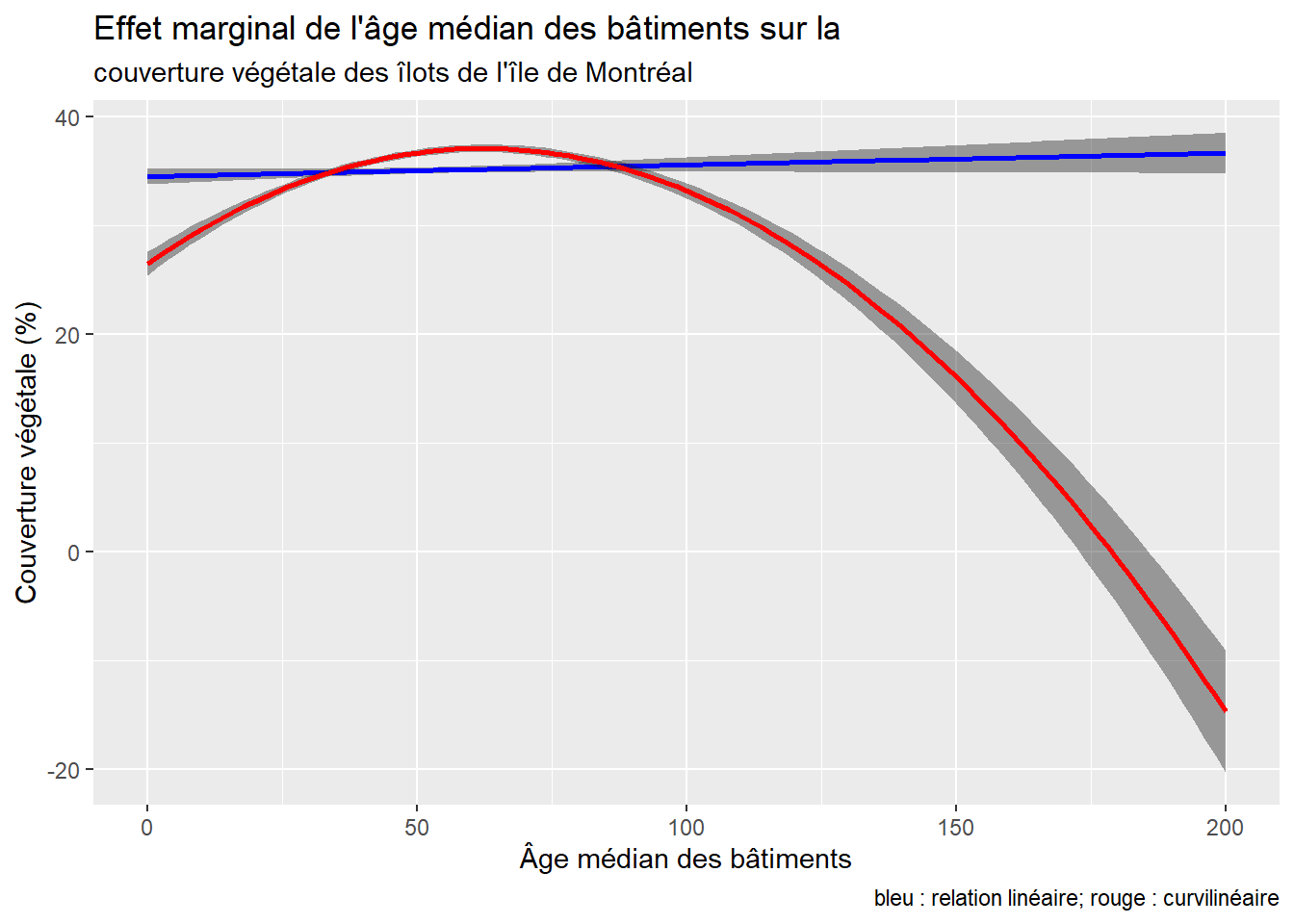
Relations linéaire et curvilinéaire

Figure 7.2: Relations linéaire et curvilinéaire

La figure 7.2 démontre bien que la relation linéaire n’est pas significative : la pente est extrêmement faible, ce qui signale que l’effet de l’âge médian est presque nul (B = 0,0108, p = 0,0902). En revanche, la relation curvilinéaire est plus intéressante : la couverture végétale croît quand l’âge médian des bâtiments dans l’îlot augmente de 0 à 60 ans environ, puis elle décroît.

7.5.1.2 Variable indépendante sous forme logarithmique

Une autre manière d’explorer une relation non linéaire est d’intégrer la variable sous forme logarithmique (Hanck et al. 2019, 212‑218). L’interprétation du coefficient de régression est alors plus complexe : un 1 % d’augmentation de la variable \(X_k\) entraîne un changement de \(\mbox{0,01} \times \beta_k\) de la variable dépendante. Autrement dit, il n’est plus exprimé dans les unités de mesure originales des deux variables.

Au tableau 7.4, le coefficient de -6,855 pour la variable logHABHA s’interprète alors comme suit : un changement de 1 % de la variable densité de population entraîne une diminution de \(\mbox{0,01} \times -\mbox{6,855 =} -\mbox{0,07}\) de la couverture végétale dans l’île, toutes choses étant égales par ailleurs.

Tableau 7.4: Modèle avec une variable indépendante sous forme logarithmique
Variable Coef. Erreur type Valeur de T P coef. 2,5 % coef. 97,5 %
Constante 52,831 1,001 52,780 0,000 50,868 54,793 ***
logHABHA -6,855 0,168 -40,730 0,000 -7,185 -6,525 ***
AgeMedian ordre 1 11,985 15,586 0,770 0,442 -18,568 42,537
AgeMedian ordre 2 -286,144 13,942 -20,520 0,000 -313,473 -258,816 ***
Pct_014 0,941 0,031 30,090 0,000 0,879 1,002 ***
Pct_65P 0,306 0,019 16,550 0,000 0,270 0,343 ***
Pct_MV -0,036 0,010 -3,650 0,000 -0,056 -0,017 ***
Pct_FR -0,344 0,011 -31,210 0,000 -0,366 -0,323 ***

Puisque l’interprétation du coefficient de régression de \(log(\beta_k)\) est plus complexe, il convient de s’assurer que son apport au modèle est justifié, et ce, de deux façons :

  • Comparez les mesures d’ajustement des deux modèles (surtout les R2 ajustés). Si le R2 ajusté du modèle avec \(log(\beta_k)\) est plus élevé que celui avec \(\beta_k\), alors la transformation logarithmique fait de votre variable indépendante un meilleur prédicteur, toutes choses étant égales par ailleurs.
  • Construisez les graphiques des effets marginaux de votre variable afin de vérifier si la relation qu’elle partage avec votre VD est plutôt logarithmique que linéaire (figure 7.3). Notez que cette approche graphique peut aussi ne donner aucune indication lorsque vos données sont très dispersées ou que la relation est faible entre votre variable dépendante et indépendante.
library(ggpubr)
library(ggplot2)
library(ggeffects)

# Modèles
modele1a <- lm(VegPct ~ HABHA+poly(AgeMedian,2)+
              Pct_014+Pct_65P+Pct_MV+Pct_FR, data = DataFinal)

modele1b <- lm(VegPct ~ log(HABHA)+poly(AgeMedian,2)+
              Pct_014+Pct_65P+Pct_MV+Pct_FR, data = DataFinal)


# Valeurs prédites
fit1a <- ggpredict(modele1a, terms = "HABHA")
fit1b <- ggpredict(modele1b, terms = "HABHA")


# Graphiques
G1a <- ggplot(fit1a, aes(x, predicted)) +
      geom_point(data = DataFinal, mapping = aes(x=HABHA, y = VegPct),
                 size = 0.2, color = rgb(0.1,0.1,0.1,0.4)) + 
      geom_ribbon(aes(ymin = conf.low, ymax = conf.high), alpha = .3, fill ="red")+
      geom_line(color = "red") +
      labs(title="Variable non transformée",
           y="VD: valeur prédite",
           x = "Habitants km2") + 
  ylim(0,100) + xlim(0,600)

G1b <- ggplot(fit1b, aes(x, predicted)) +
      geom_point(data = DataFinal, mapping = aes(x=HABHA, y = VegPct),
                 size = 0.2, color = rgb(0.1,0.1,0.1,0.4)) + 
      geom_ribbon(aes(ymin = conf.low, ymax = conf.high), alpha = .3, fill ="red")+
      geom_line(color = "red") +
      labs(title="Variable transformée (log)",
           y="VD: valeur prédite",
           x = "Habitants km2")

G1aG1b <- ggarrange(G1a, G1b, nrow = 1)
G1aG1b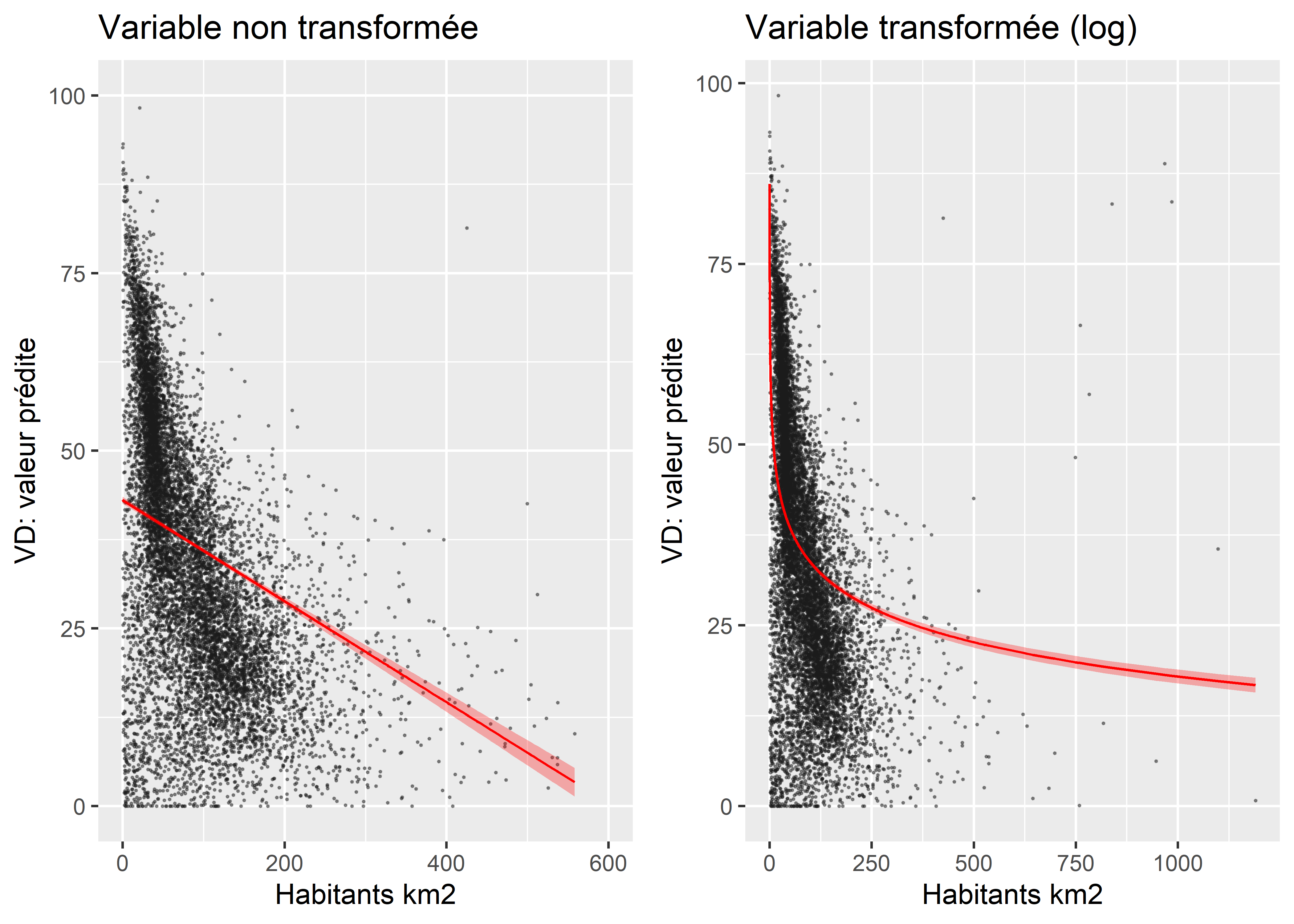
Effet marginal de la densité de population

Figure 7.3: Effet marginal de la densité de population

7.5.2 Variable indépendante qualitative dichotomique

Il est très fréquent d’introduire une variable qualitative dichotomique comme variable explicative ou de contrôle dans un modèle. À titre de rappel, une variable dichotomique comprend deux modalités (section 2.1.2).

Dans le modèle ci-dessous, nous voulons vérifier si un îlot situé sur le territoire de la ville de Montréal a proportionnellement moins de végétation qu’un îlot situé dans une autre municipalité de l’île de Montréal, toutes choses étant égales par ailleurs. Pour ce faire, nous créons une variable binaire dénommée VilleMtl qui prend la valeur de 1 pour les îlots de la ville de Montréal et 0 pour ceux d’une autre municipalité.

Nous obtenons ainsi un coefficient de régression pour VilleMtl de -7,699 (tableau 7.5). Cela signifie que si toutes les autres variables indépendantes du modèle étaient constantes, alors un îlot de la ville de Montréal aurait en moyenne une valeur de -7,7 % de moins de végétation comparativement à un îlot situé dans une autre municipalité.

# Création d'une variable muette pour Montréal (0 ou 1)
DataFinal$VilleMtl <- ifelse(DataFinal$SDRNOM == "Montréal", 1, 0)

# Modèle avec la variable dichtonomique
modele3 <- lm(VegPct ~ VilleMtl+log(HABHA)+poly(AgeMedian,2)+
              Pct_014+Pct_65P+Pct_MV+Pct_FR, data = DataFinal)
Tableau 7.5: Modèle avec une variable dichotomique
Variable Coef. Erreur type Valeur de T P coef. 2,5 % coef. 97,5 %
Constante 57,676 1,009 57,140 0,000 55,697 59,654 ***
VilleMtl -7,699 0,377 -20,430 0,000 -8,438 -6,960 ***
log(HABHA) -6,174 0,168 -36,680 0,000 -6,504 -5,844 ***
AgeMedian ordre 1 -14,871 15,334 -0,970 0,332 -44,929 15,186
AgeMedian ordre 2 -280,251 13,668 -20,500 0,000 -307,044 -253,459 ***
Pct_014 0,794 0,031 25,230 0,000 0,732 0,856 ***
Pct_65P 0,270 0,018 14,810 0,000 0,234 0,306 ***
Pct_MV -0,028 0,010 -2,890 0,004 -0,047 -0,009 **
Pct_FR -0,294 0,011 -26,550 0,000 -0,316 -0,273 ***

Bien interpréter un coefficient d’une variable dichotomique

Nous avons vu que le coefficient de régression (\(\beta_k\)) indique le changement de la variable dépendante (Y), lorsque la variable indépendante augmente d’une unité, toutes choses étant égales par ailleurs.

Pour une variable dichotomique, le coefficient indique le changement de Y quand les observations appartiennent à la modalité qui a la valeur de 1 (ici la ville de Montréal), comparativement à celle qui a la valeur de 0 (autres municipalités de l’île de Montréal), toutes choses étant égales par ailleurs.

La modalité qui a la valeur de 0 est alors appelée modalité ou catégorie de référence.

Autrement dit, si la variable avait été codée : 0 pour la ville de Montréal et 1 pour les autres municipalités, alors le coefficient aurait été de 7,699.

Pour éviter d’oublier quelle est la modalité de référence (valeur de 0), nous verrons plus tard (dans la section mise en œuvre des modèles de régression dans R (section 7.7) qu’il peut être préférable de définir un facteur avec la fonction as.factor et d’indiquer la catégorie de référence avec la fonction relevel(x, ref).

Comme pour une variable indépendante introduite avec une fonction polynomiale, il peut être très intéressant d’illustrer l’effet marginal de la variable dichotomique avec un graphique qui montre l’écart entre les moyennes des deux modalités, une fois contrôlées les autres variables indépendantes (figure 7.4). Notez que dans ce graphique, les barres d’erreurs situées au sommet des rectangles représentent les intervalles à 95 % des prédictions du modèle.

Effet marginal d'une variable dichotomique

Figure 7.4: Effet marginal d’une variable dichotomique

7.5.3 Variable indépendante qualitative polytomique

Il est possible d’introduire une variable qualitative polytomique comme variable explicative ou de contrôle dans un modèle. À titre de rappel, une variable polytomique comprend plus de deux modalités, qu’elle soit nominale ou ordinale (section 2.1.2).

En guise d’exemple, une variable qualitative pourrait être : différents groupes de population (groupes d’âge, minorités visibles, catégories socioprofessionnelles, etc.), différents territoires ou régions (ville centrale, première couronne, deuxième couronne, etc.), une variable continue transformée en quatre ou cinq catégories ordinales selon les quartiles ou les quintiles.

7.5.3.1 Comment construire un modèle de régression avec une variable explicative qualitative polytomique?

Prenons l’exemple d’un modèle de régression comprenant deux variables indépendantes : l’une continue (X1), l’autre qualitative (X2) avec quatre modalités (A, B, C et D). L’introduction de la variable qualitative dans le modèle revient à :

  • Transformer chaque modalité en variable muette (binaire). Nous avons ainsi quatre nouvelles variables binaires : X2A, X2B, X2C et X2D. Par exemple, pour X2A, les observations de la modalité A se verront affecter la valeur de 1 versus 0 pour les autres observations. La même démarche s’applique à X2B, X2C et X2D (voir tableau 7.6).
Tableau 7.6: Transformation d’une variable qualitative en variables muettes pour chaque modalité
obs Y X1 X2 X2A X2B X2C X2D
1 44,69 22,97 A 1 0 0 0
2 27,65 19,54 A 1 0 0 0
3 65,50 17,87 A 1 0 0 0
4 56,06 25,55 B 0 1 0 0
5 56,35 23,77 B 0 1 0 0
6 36,09 21,42 B 0 1 0 0
7 41,13 21,40 C 0 0 1 0
8 49,46 24,27 C 0 0 1 0
9 49,31 26,90 D 0 0 0 1
10 42,23 21,83 D 0 0 0 1

  • Toutes les modalités transformées en variables muettes sont introduites dans le modèle comme variables indépendantes sauf celle servant de catégorie de référence. Pourquoi sauf une? Si nous mettions toutes les modalités en variable muette, alors chaque observation serait repérée par une valeur de 1, « il y aurait alors une parfaite multicolinéarité et aucune solution unique pour les coefficients de régression ne pourrait être trouvée » (Bressoux 2010, 128).

  • Par exemple, si nous choisissons la modalité A comme catégorie de référence, l’équation de régression s’écrit alors :

\[\begin{equation} Y = b_{0} + b_{1}X_{1} + b_{2B}X_{2B} + b_{2C}X_{2C} + b_{2D}X_{2D}+ e \tag{7.25} \end{equation}\]

  • Vous aurez compris que choisir la modalité D comme catégorie de référence revient à écrire l’équation suivante :

\[\begin{equation} Y = b_{0} + b_{1}X_{1} + b_{2A}X_{2A} + b_{2B}X_{2B} + b_{2C}X_{2C} + e \tag{7.26} \end{equation}\]

7.5.3.2 Comment interpréter les coefficients des modalités d’une variable explicative qualitative polytomique

Les coefficients des différentes modalités s’interprètent en fonction de la catégorie de référence. Dans l’exemple ci-dessous, nous avons inclus la ville de Montréal comme catégorie de référence (tableau 7.7). Toutes choses étant égales par ailleurs, nous pouvons alors constater que  :

  • en moyenne, les îlots résidentiels de Senneville et de Baie-D’Urfé ont respectivement 23,235 % et 21,400 % plus de végétation que ceux de la ville de Montréal.
  • la seule municipalité comprenant en moyenne moins de végétation dans ses îlots résidentiels est Montréal-Est (-13,334 %)
  • nous remarquons aussi que les îlots des municipalités de Sainte-Anne-de-Bellevue, de Montréal-Ouest et de Côte-Saint-Luc ne présentent pas significativement moins ou plus de végétation que ceux de la ville de Montréal (leurs valeurs de p sont supérieures à 0,05).

Par conséquent, les valeurs de t et de p pour une modalité permettent de vérifier si elle est ou non significativement différente de la catégorie de référence.

Tableau 7.7: Modèle avec une variable polytomique (ville de Montréal en catégorie de référence)
Variable Coef. Erreur type Valeur de T P
Constante 48,193 0,992 48,580 0,000 ***
log(HABHA) -5,836 0,168 -34,840 0,000 ***
AgeMedian ordre 1 -11,807 15,648 -0,750 0,451
AgeMedian ordre 2 -266,469 13,613 -19,570 0,000 ***
Pct_014 0,794 0,032 25,190 0,000 ***
Pct_65P 0,277 0,018 15,130 0,000 ***
Pct_MV -0,036 0,010 -3,740 0,000 ***
Pct_FR -0,279 0,011 -25,340 0,000 ***
Municipalité
ref : Montréal – – – – –
Baie-D’Urfé 21,400 1,635 13,090 0,000 ***
Beaconsfield 14,112 0,893 15,810 0,000 ***
Côte-Saint-Luc 0,172 1,035 0,170 0,868
Dollard-Des Ormeaux 7,960 0,748 10,640 0,000 ***
Dorval 11,157 0,971 11,490 0,000 ***
Hampstead 3,080 1,599 1,930 0,054 .
Kirkland 6,937 1,014 6,840 0,000 ***
Mont-Royal 12,699 0,894 14,210 0,000 ***
Montréal-Est -13,334 1,920 -6,940 0,000 ***
Montréal-Ouest 3,306 1,819 1,820 0,069 .
Pointe-Claire 9,896 0,866 11,430 0,000 ***
Sainte-Anne-de-Bellevue 0,342 1,904 0,180 0,858
Senneville 23,235 3,793 6,130 0,000 ***
Westmount 2,255 1,088 2,070 0,038

Utilisons maintenant comme référence la municipalité qui avait le coefficient le plus fort dans le modèle précédent, soit Senneville (tableau 7.8). Bien entendu, les coefficients des variables continues et de la constante ne changent pas. Par contre, les coefficients de toutes les municipalités sont négatifs puisque la municipalité de Senneville est celle qui a proportionnellement le plus de végétation dans ses îlots, toutes choses étant égales par ailleurs.

Tableau 7.8: Modèle avec une variable polytomique (Senneville en catégorie de référence)
Variable Coef. Erreur type Valeur de T P
Constante 71,429 3,846 18,570 0,000 ***
log(HABHA) -5,836 0,168 -34,840 0,000 ***
AgeMedian ordre 1 -11,807 15,648 -0,750 0,451
AgeMedian ordre 2 -266,469 13,613 -19,570 0,000 ***
Pct_014 0,794 0,032 25,190 0,000 ***
Pct_65P 0,277 0,018 15,130 0,000 ***
Pct_MV -0,036 0,010 -3,740 0,000 ***
Pct_FR -0,279 0,011 -25,340 0,000 ***
Municipalité
ref : Senneville – – – – –
Baie-D’Urfé -1,835 4,093 -0,450 0,654
Beaconsfield -9,123 3,866 -2,360 0,018
Côte-Saint-Luc -23,064 3,918 -5,890 0,000 ***
Dollard-Des Ormeaux -15,275 3,852 -3,970 0,000 ***
Dorval -12,078 3,891 -3,100 0,002 **
Hampstead -20,156 4,094 -4,920 0,000 ***
Kirkland -16,298 3,911 -4,170 0,000 ***
Mont-Royal -10,537 3,875 -2,720 0,007 **
Montréal -23,235 3,793 -6,130 0,000 ***
Montréal-Est -36,570 4,231 -8,640 0,000 ***
Montréal-Ouest -19,930 4,187 -4,760 0,000 ***
Pointe-Claire -13,339 3,865 -3,450 0,001 ***
Sainte-Anne-de-Bellevue -22,893 4,225 -5,420 0,000 ***
Westmount -20,980 3,927 -5,340 0,000 ***

À l’inverse, si nous utilisons Montréal-Est comme modalité de référence, soit la municipalité avec le coefficient le plus faible dans le premier modèle, tous les coefficients deviendront positifs (tableau 7.9).

Tableau 7.9: Modèle avec une variable polytomique (Montréal-Est en catégorie de référence)
Variable Coef. Erreur type Valeur de T P
Constante 34,859 2,109 16,530 0,000 ***
log(HABHA) -5,836 0,168 -34,840 0,000 ***
AgeMedian ordre 1 -11,807 15,648 -0,750 0,451
AgeMedian ordre 2 -266,469 13,613 -19,570 0,000 ***
Pct_014 0,794 0,032 25,190 0,000 ***
Pct_65P 0,277 0,018 15,130 0,000 ***
Pct_MV -0,036 0,010 -3,740 0,000 ***
Pct_FR -0,279 0,011 -25,340 0,000 ***
Municipalité
ref : Montréal-Est – – – – –
Baie-D’Urfé 34,735 2,495 13,920 0,000 ***
Beaconsfield 27,446 2,091 13,130 0,000 ***
Côte-Saint-Luc 13,506 2,167 6,230 0,000 ***
Dollard-Des Ormeaux 21,294 2,053 10,370 0,000 ***
Dorval 24,491 2,134 11,480 0,000 ***
Hampstead 16,414 2,478 6,620 0,000 ***
Kirkland 20,272 2,159 9,390 0,000 ***
Mont-Royal 26,033 2,101 12,390 0,000 ***
Montréal 13,334 1,920 6,940 0,000 ***
Montréal-Ouest 16,640 2,628 6,330 0,000 ***
Pointe-Claire 23,230 2,087 11,130 0,000 ***
Sainte-Anne-de-Bellevue 13,676 2,687 5,090 0,000 ***
Senneville 36,570 4,231 8,640 0,000 ***
Westmount 15,590 2,196 7,100 0,000 ***

Comment choisir la catégorie de référence?

Plusieurs options sont possibles. Vous pouvez retenir :

  • la modalité comprenant le plus d’observations;
  • la modalité avec la plus forte valeur pour la variable dépendante;
  • la modalité avec la plus faible valeur pour la variable dépendante;
  • la modalité qui fait le plus de sens avec votre cadre théorique. Prenons l’exemple d’une variable qualitative comprenant plusieurs groupes d’âge (15-29 ans, 30-39 ans, 40-49 ans, 50-54 ans, 65 ans et plus). Si votre étude porte sur les jeunes et que vous souhaitez comparer leur situation comparativement aux autres groupes d’âge, toutes choses étant égales par ailleurs, sélectionnez bien évidemment la modalité des 15 à 29 ans comme catégorie de référence.

Mais surtout, évitez de choisir une catégorie comprenant très peu d’observations.

7.5.3.3 Effet marginal d’une variable explicative qualitative polytomique

Comme pour une variable dichotomique, il est possible d’illustrer l’effet marginal de la variable qualitative dichotomique avec un graphique. Quelle que soit la catégorie de référence choisie, le graphique est le même. La figure 7.5 illustre ainsi la valeur moyenne, avec son intervalle de confiance à 95 %, de la végétation dans les îlots résidentiels de chacune des municipalités de la région de Montréal, ceteris paribus.

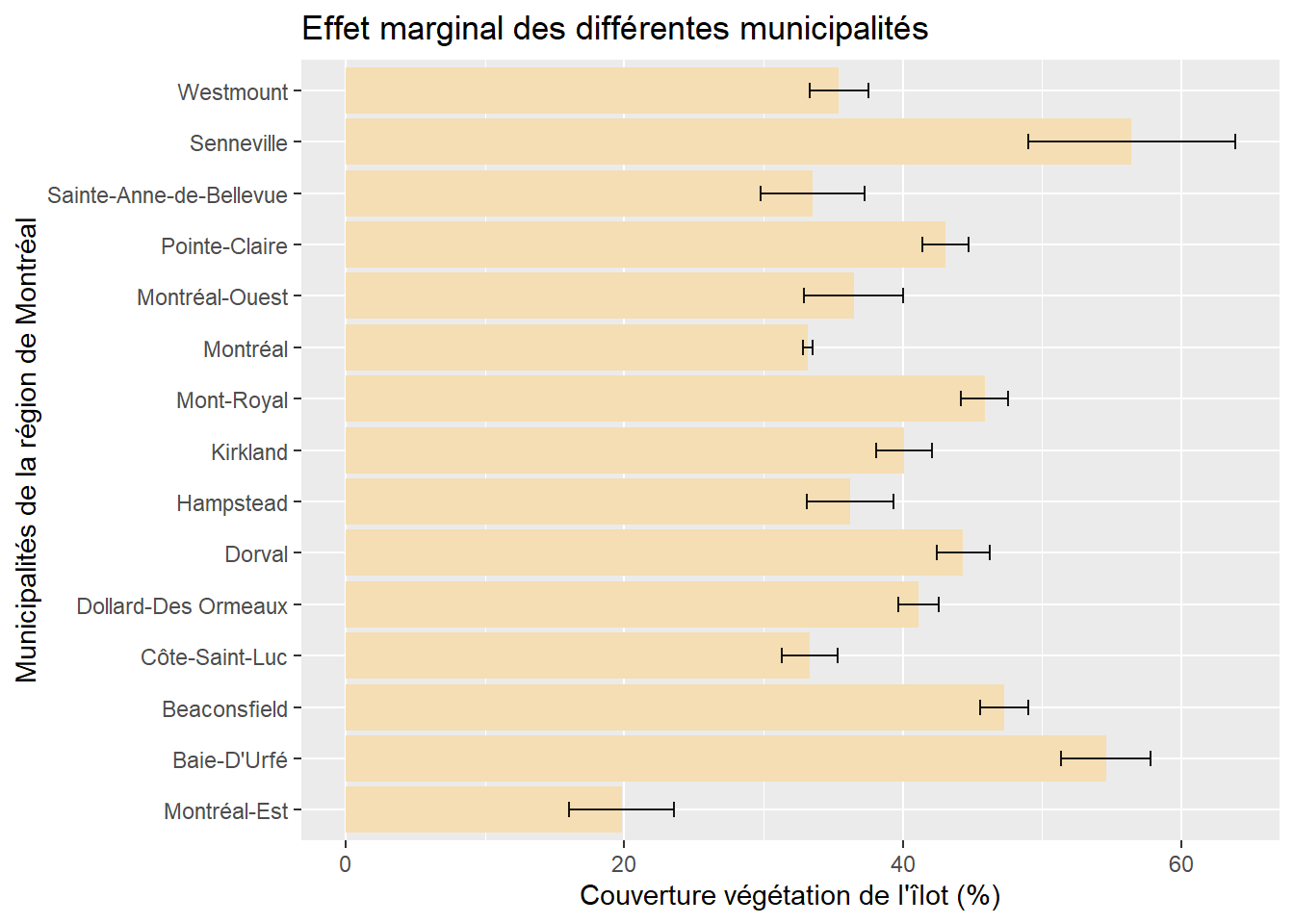
Effet marginal d'une variable polytomique

Figure 7.5: Effet marginal d’une variable polytomique

7.5.4 Variables d’interaction

7.5.4.1 Variable d’interaction entre deux variables continues

Une interaction entre deux variables indépendantes continues consiste à simplement les multiplier (\(X_1 \times X_2\)). Le modèle s’écrit alors :

\[\begin{equation} Y = \beta_{0} + \beta_{1}X_{1} + \beta_{2}X_{2} + \beta_{3}(X_{1}\times X_{2}) +\ldots+ \beta_{k}X_{k} + e\tag{7.27} \end{equation}\]

Un nouveau coefficient (\(\beta_{3}\)) s’ajoute pour l’interaction (la multiplication) entre les deux variables continues. Pourquoi ajouter une interaction entre deux variables? L’objectif est d’évaluer l’effet d’une augmentation de \(\beta_{1}\) en fonction d’un niveau donné de \(\beta_{2}\) et inversement. Cela permet ainsi de répondre à la question suivante : l’effet de la variable \(\beta_{1}\) est-il influencé par la variable \(\beta_{2}\) et inversement?

Prenons un exemple concret pour illustrer le tout. Premièrement, nous ajoutons DistCBDkm comme VI, soit la distance au centre-ville exprimée en kilomètres. Notez que pour ne pas surspécifier le modèle, les variables dichotomique VilleMtl ou polytomique Municipalité ont été préalablement ôtées. Le coefficient (B = 0,659, p < 0,001) signale que plus nous nous éloignons du centre-ville, plus la couverture végétale des îlots augmente significativement. En guise d’exemple, toutes choses étant égales par ailleurs, un îlot situé à dix kilomètres du centre-ville aura en moyenne 6,59 % plus de végétation (tableau 7.10).

Tableau 7.10: Modèle avec la distance au centre-ville (km)
Variable Coef. Erreur type Valeur de T P
Constante 41,061 1,085 37,830 0,000 ***
log(HABHA) -5,555 0,172 -32,300 0,000 ***
AgeMedian ordre 1 176,921 16,582 10,670 0,000 ***
AgeMedian ordre 2 -298,735 13,560 -22,030 0,000 ***
Pct_014 0,763 0,031 24,440 0,000 ***
Pct_65P 0,321 0,018 17,860 0,000 ***
Pct_MV -0,018 0,010 -1,880 0,060 .
Pct_FR -0,288 0,011 -26,260 0,000 ***
DistCBDkm 0,659 0,027 24,460 0,000 ***

Dans ce modèle (tableau 7.10), les pourcentages d’enfants de moins de 15 ans et de 65 ans et plus (Pct_014 et Pct_65P) sont associés positivement à la variable dépendante tandis que le pourcentage de personnes à faible revenu (Pct_FR) est associé négativement.

Que se passe-t-il si nous introduisons une variable d’interaction entre DistCBDkm et Pct_FR (tableau 7.11)? L’effet du pourcentage de personnes à faible revenu (%) est significatif et négatif lorsqu’il est mis en interaction avec la distance au centre-ville. Cela indique que plus l’îlot est éloigné du centre-ville, plus Pct_FR a un effet négatif sur la couverture végétale (B = −0,011, p < 0,001).

Tableau 7.11: Modèle avec une variable d’interaction entre deux VI continues
Variable Coef. Erreur type Valeur de T P
Constante 38,382 1,137 33,760 0,000 ***
log(HABHA) -5,505 0,172 -32,080 0,000 ***
AgeMedian ordre 1 160,523 16,672 9,630 0,000 ***
AgeMedian ordre 2 -310,666 13,610 -22,830 0,000 ***
Pct_014 0,786 0,031 25,130 0,000 ***
Pct_65P 0,345 0,018 18,960 0,000 ***
Pct_MV -0,018 0,010 -1,820 0,069 .
Pct_FR -0,191 0,017 -11,500 0,000 ***
DistCBDkm 0,821 0,034 24,060 0,000 ***
DistCBDkmX_Pct_FR -0,011 0,001 -7,700 0,000 ***

À nouveau, il est possible de représenter l’effet de cette interaction à l’aide d’un graphique des effets marginaux. Notez cependant que nous devons représenter l’effet simultané de deux variables indépendantes sur notre variable dépendante, ce qu’il est possible de faire avec une carte de chaleur. La figure 7.6 représente donc l’effet moyen de l’interaction sur la prédiction dans le premier panneau, ainsi que l’intervalle de confiance à 95 % de la prédiction dans les deuxième et troisième panneaux.

Nous constatons ainsi que le modèle prédit des valeurs de végétation les plus faibles lorsque le pourcentage de personnes à faible revenu est élevé et que la distance au centre-ville est élevée (en haut à droite à la figure 7.6). En revanche, les valeurs les plus élevées de végétation sont atteintes lorsque la distance au centre-ville est élevée et que le pourcentage de personnes à faible revenu est faible (en bas à droite). Il semble donc que l’éloignement au centre-ville soit associé avec une augmentation de la densité végétale, mais que cette augmentation puisse être mitigée par l’augmentation parallèle du pourcentage de personnes à faible revenu.

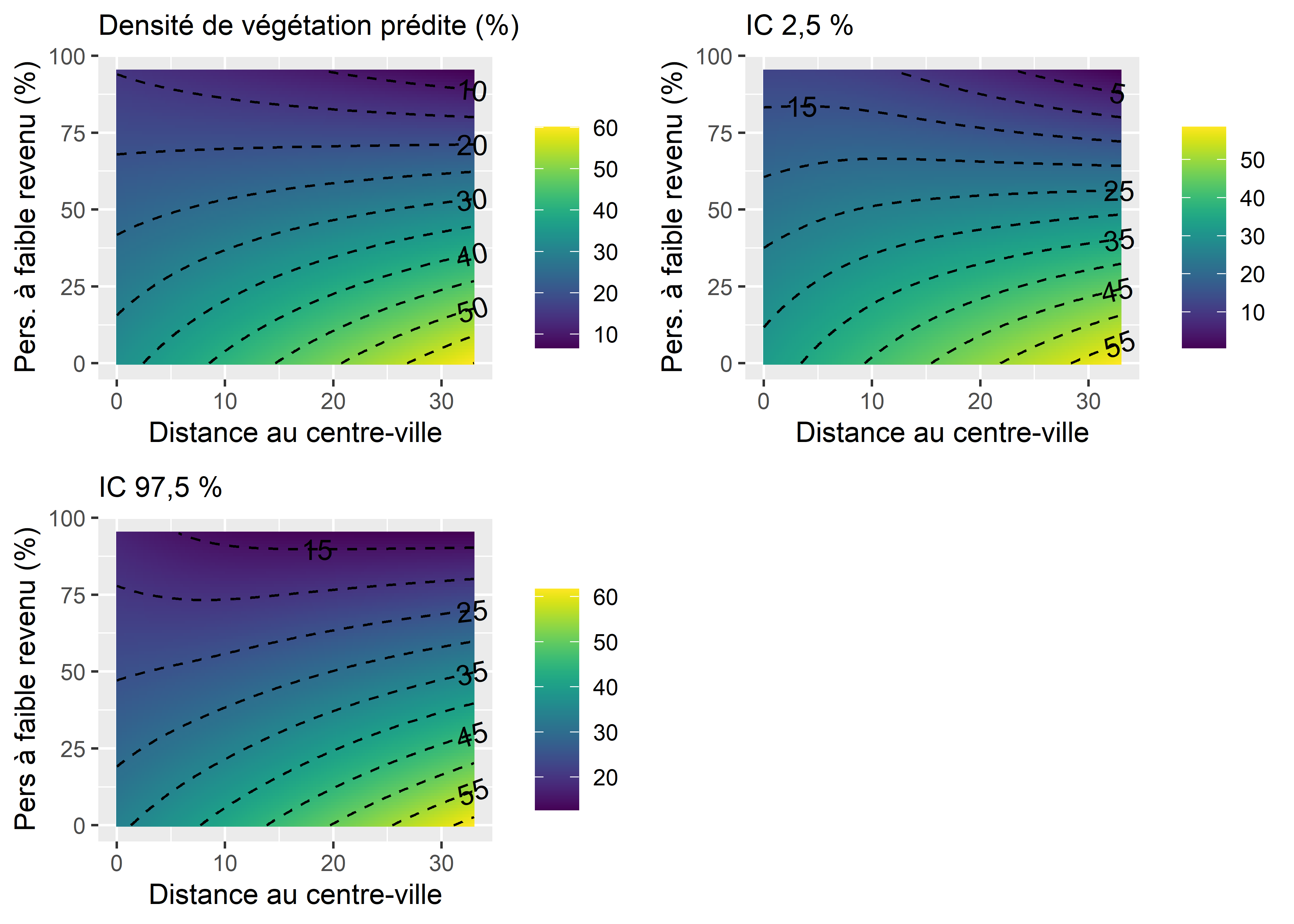
Effet marginal de l'interaction entre deux variables continues

Figure 7.6: Effet marginal de l’interaction entre deux variables continues

Notez que dans la figure 7.6, la relation entre les deux variables indépendantes et la variable dépendante apparaît non linéaire du fait de l’interaction. À titre de comparaison, si nous utilisons les prédictions du modèle 5 (sans interaction), nous obtenons les prédictions présentées à la figure 7.7. Vous pouvez constater sur cette figure sans interaction que les deux effets des variables indépendantes sont linéaires puisque toutes les lignes sont parallèles.

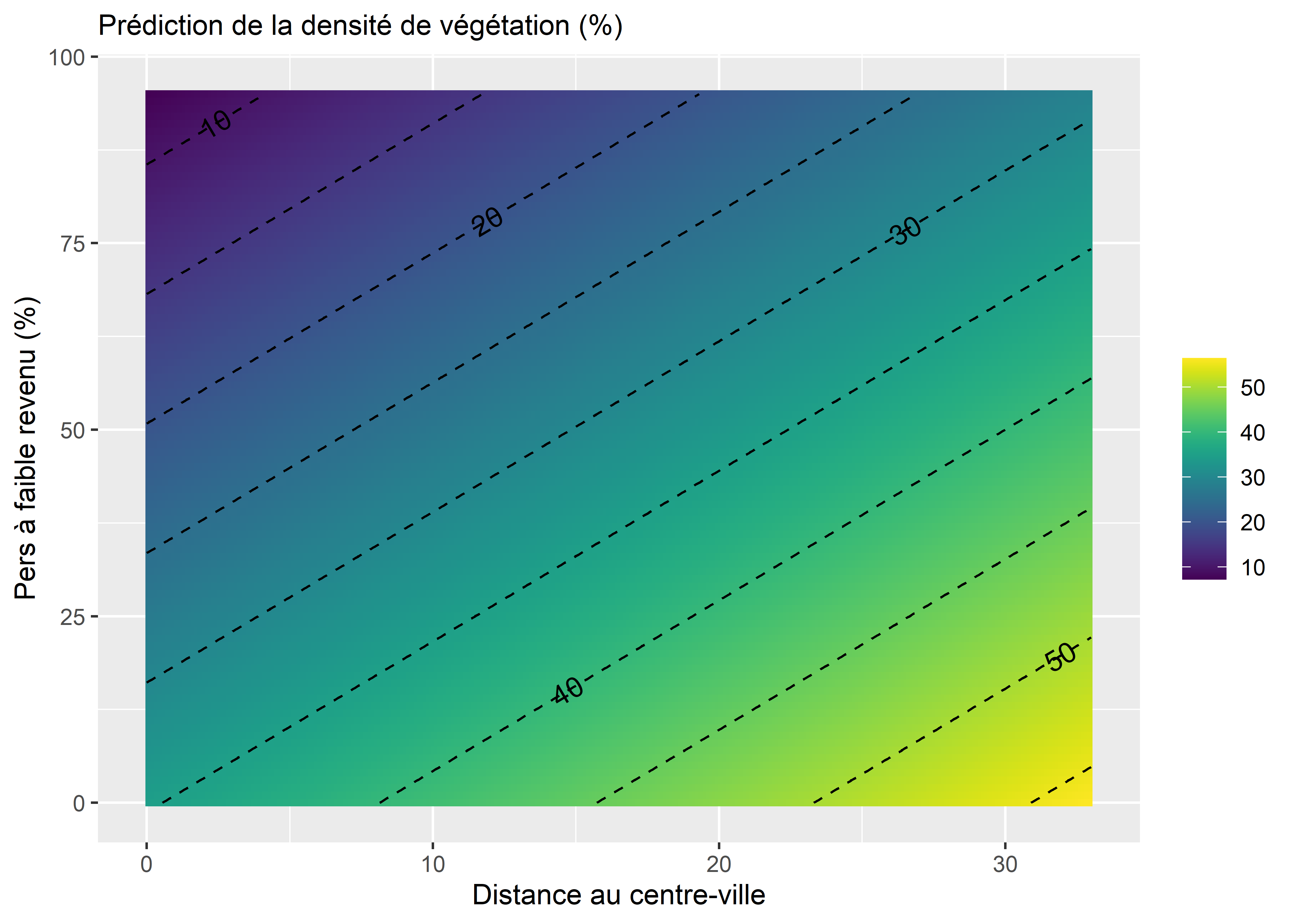
Effets marginaux de deux variables continues en cas d'absence d'interaction

Figure 7.7: Effets marginaux de deux variables continues en cas d’absence d’interaction

7.5.4.2 Variable d’interaction entre une variable continue et une variable dichotomique

Une interaction entre une VI continue et une VI dichotomique consiste aussi à les multiplier (\(X_1 \times D_2\)); le modèle s’écrit alors :

\[\begin{equation} Y = \beta_{0} + \beta_{1}X_{1} + \beta_{2}D_{2} + \beta_{3}(X_{1}\times D_{2}) +\ldots+ \beta_{k}X_{k} + e\tag{7.28} \end{equation}\]

Pour interpréter le coefficient \(B_3\), il convient alors de bien connaître le nom de la modalité ayant la valeur de 1 (0 étant la modalité de référence). Dans le modèle présenté au tableau 7.12, nous avons multiplié la variable dichotomique ville de Montréal (VilleMtl) avec le pourcentage de personnes à faible revenu (Pct_FR). Les résultats de ce modèle démontrent que, toutes choses étant égales par ailleurs :

  • à chaque augmentation d’une unité du pourcentage à faible revenu (Pct_FR), le pourcentage de la couverture végétale diminue significativement de −0,444;
  • comparativement à un îlot situé dans une autre municipalité de l’île de Montréal, un îlot de la ville de Montréal a en moyenne −9,804 de couverture végétale;
  • à chaque augmentation d’une unité de Pct_FR pour un îlot de la Ville Montréal, la couverture végétale augmente de 0,166 comparativement à une autre municipalité de l’île. En d’autres termes, le Pct_FR sur le territoire de la ville de Montréal est associé à une diminution de la couverture végétale moins forte que les autres municipalités, comme illustré à la figure 7.8 (pentes en rouge et en bleu).
Tableau 7.12: Modèle avec les variables d’interaction entre une VI continue et une VI dichotomique
Variable Coef. Erreur type Valeur de T P
Constante 59,275 1,053 56,300 0,000 ***
log(HABHA) -6,160 0,168 -36,640 0,000 ***
AgeMedian ordre 1 -20,719 15,354 -1,350 0,177
AgeMedian ordre 2 -278,141 13,656 -20,370 0,000 ***
Pct_014 0,789 0,031 25,100 0,000 ***
Pct_65P 0,278 0,018 15,200 0,000 ***
Pct_MV -0,030 0,010 -3,030 0,002 **
Pct_FR -0,444 0,030 -14,550 0,000 ***
VilleMtl -9,804 0,549 -17,850 0,000 ***
VilleMtlX_Pct_FR 0,166 0,032 5,260 0,000 ***

L’interaction entre une variable qualitative et une variable quantitative peut être représentée par un graphique des effets marginaux. La pente (coefficient) de la variable quantitative varie en fonction des deux catégories de la variable qualitative dichotomique.

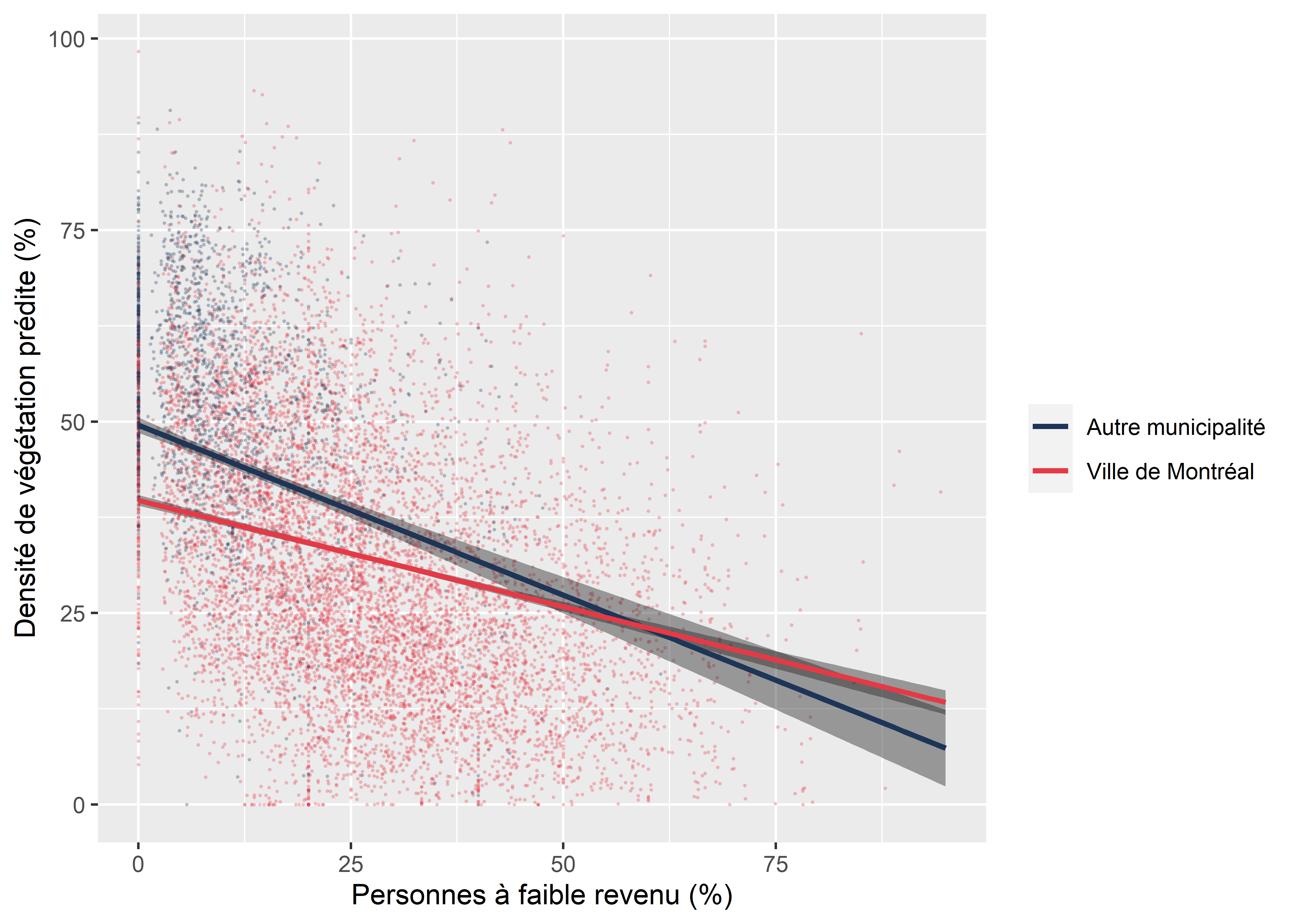
Graphique de l’effet marginal de l’interaction entre une variable quantitative et qualitative

Figure 7.8: Graphique de l’effet marginal de l’interaction entre une variable quantitative et qualitative

7.5.4.3 Variable d’interaction entre deux variables dichotomiques

Variable d’interaction entre deux variables dichotomiques

Nous avons vu qu’il est possible d’introduire une variable d’interaction entre deux variables continues ou entre une variable continue et une autre dichotomique. Sachez qu’il est aussi possible d’introduire une interaction entre deux variables dichotomiques. Sur le sujet, vous pouvez consulter la section 8.3 de l’excellent ouvrage de Hanck et al. (2019).

Références

Bressoux, Pascal. 2010. Modélisation statistique appliquée aux sciences sociales. De boeck.
Hanck, Christoph, Martin Arnold, Alexander Gerber et Martin Schmelzer. 2019. Introduction to econometrics with R. s.n. https://www.econometrics-with-r.org/ITER.pdf.