5.4 Interprétation d’un tableau de contingence
Nous vous proposons une démarche très simple pour vérifier l’association entre deux variables qualitatives avec les deux étapes suivantes :
Nous posons l’hypothèse nulle (H0), soit l’indépendance entre les deux variables.
Si la valeur du khi-deux total du tableau de contingence est inférieure à la valeur critique du khi-deux avec p = 0,05 et le nombre de degrés de liberté de la table T, alors il y a bien indépendance. La valeur de p est alors supérieure à 0,05. L’analyse s’arrête donc là! Autrement dit, il n’est pas nécessaire d’analyser le contenu de votre tableau de contingence puisqu’il n’y pas d’association significative entre les modalités des deux variables. Vous pouvez simplement signaler que selon les résultats du test du khi-deux, il n’y a pas d’association significative entre les deux variables (\(\chi\) = … avec p= …).
S’il y a dépendance (\(khi_{observé}^2 > khi_{critique}^2\)), trouvez les cellules ij où les contributions au khi-deux sont les plus fortes, c’est-à-dire où les associations entre les modalités i de la variable en ligne et les modalités j de la variable en colonne sont les plus marquées. Pour ces cellules, le phénomène ij est surreprésenté si la déviation est positive ou sous-représenté si la déviation est négative. Commentez ces associations et utilisez les pourcentages en ligne ou en colonne pour appuyer vos propos.
Pour repérer rapidement les cellules où les contributions au khi-deux sont les plus fortes, vous pouvez construire un graphique avec la fonction mosaic du package vcd. À la figure 5.1, la taille des rectangles représente les effectifs entre les deux modalités tandis que les associations sont représentées comme suit :
en gris lorsqu’elles ne sont pas significatives, en rouge pour des déviations significatives et négatives et en bleu pour des déviations significatives et positives.
library(vcd)
mosaic(~ Taille+Periode,
data=dataHLM,shade=TRUE, legend=TRUE,
labeling= labeling_border(rot_labels = c(45, 90),
just_labels = c("left", "center")))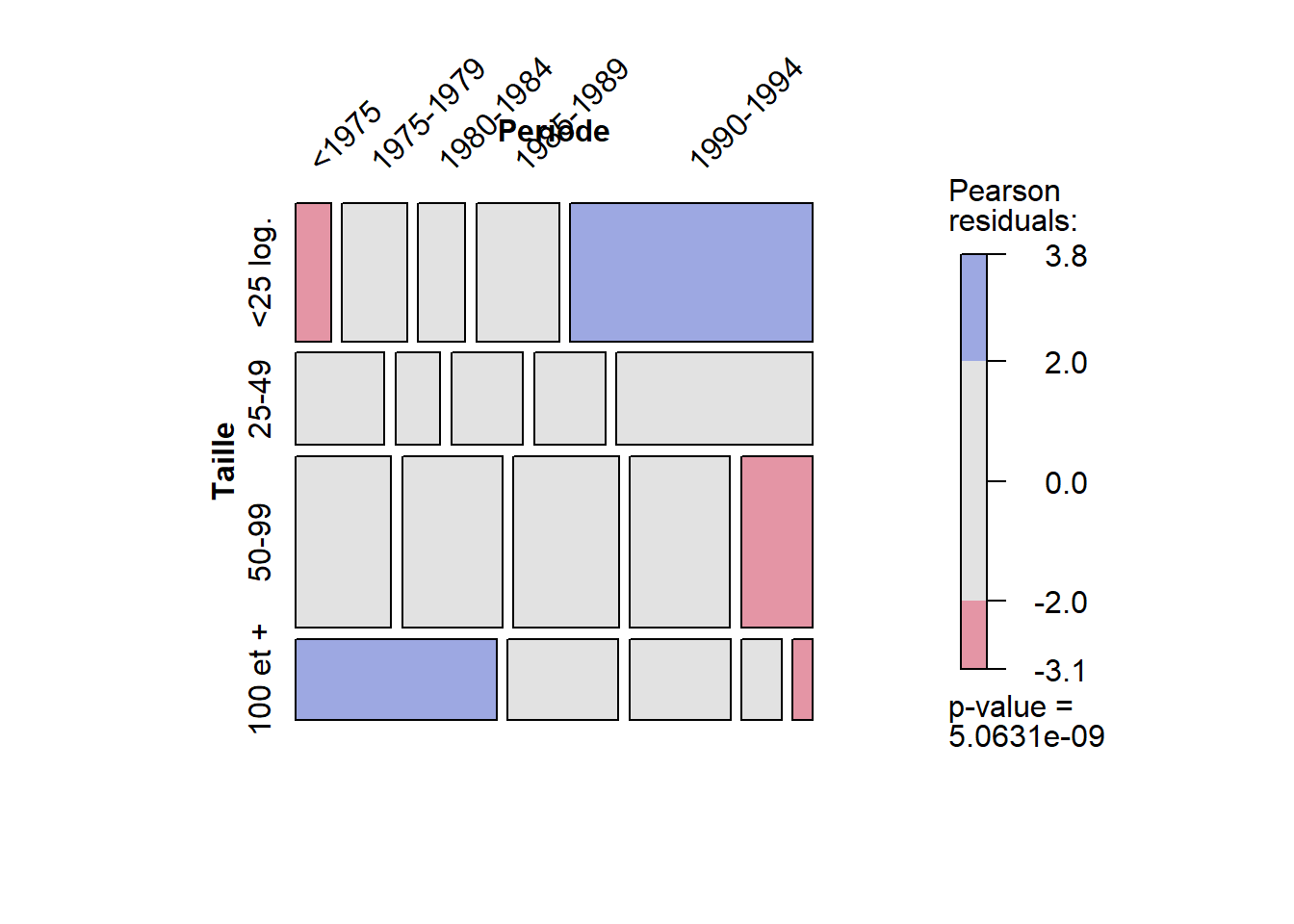
Figure 5.1: Figure avec la fonction mosaic du package vcd
Exemple d’interprétation. « Les résultats du test du khi-deux signalent qu’il existe des associations entre les modalités de la taille et de la période de construction des projets d’habitation (\(\chi\) = 63,5, p < 0,001). Les fortes contributions au khi-deux et le signe positif ou négatif des déviations correspondantes permettent de repérer cinq associations majeures entre les modalités de taille et de période de construction des projets HLM : 1) la répulsion entre les projets d’habitation de moins de 25 logements et la période de construction 1964-1974; 2) l’attraction entre les projets d’habitation de 100 logements et plus et la période de construction de 1969-1974; 3) l’attraction entre les projets d’habitation de moins de 25 logements et la période de construction de 1990-1994; 4) la répulsion entre les projets d’habitation de 50 à 99 logements et la période de construction 1990-1994; 5) la répulsion entre les projets d’habitation de 100 logements et plus et la période de construction 1990-1994. On observe donc une tendance bien marquée dans l’évolution du type de construction entre 1970 et 1994 : entre 1969 et 1974, on a construit de grandes habitations dépassant souvent 100 logements; du milieu des années 1970 à la fin des années 1980, on privilégie la construction d’habitations de taille plus modeste, entre 50 et 100 logements; tandis qu’au début des années 1990, on opte plutôt pour des habitations de taille réduite (moins de 50 logements). Quelques chiffres à l’appui : sur les 56 habitations réalisées entre 1969 et 1974, 20 ont plus de 100 logements, 20 comprennent entre 50 et 99 logements et seules 10 ont moins de 25 logements. Près de la moitié des habitations construites entre 1975 et 1989 regroupent 50 à 99 logements (43,8 % pour la période 1975-1979, 45,8 % pour 1980-1984 et 44,7 % pour 1985-1989). Par contre, 51 % des habitations érigés à partir de 1990 disposent de moins de 25 logements » (Apparicio (2002), p. 117-118). Notez que cette évolution décroissante est aussi soutenue par le coefficient négatif de la corrélation polychorique.
Vous pouvez aussi construire un graphique pour appuyer vos constats, soit avec les pourcentages en ligne ou en colonne (figure 5.2 tirée de Apparicio (2002)).

Figure 5.2: Taille des projets d’habitation à loyer modique selon la période de construction
Comment rapporter succinctement les résultats d’un test du khi-deux?
Le test du khi-deux a été réalisé pour examiner la relation entre la taille et la période de construction des habitations HLM. Cette relation est significative : \(\chi^2\)(12, N = 279) = 63,5, p < 0,001. Plus les projets ont été construits récemment, plus ils sont de taille réduite.
Pour un texte en anglais, consultez https://www.socscistatistics.com/tutorials/chisquare/default.aspx.