8.4 Modèles GLM pour des variables continues

Comme nous l’avons vu dans la section 2.4, il existe un grand nombre de distributions permettant de décrire une grande diversité de variables continues. Il serait fastidieux de toutes les présenter, nous revenons donc seulement sur les plus fréquentes.

8.4.1 Modèle GLM gaussien

Comme nous l’avons vu en introduction, le modèle GLM gaussien est le plus simple puisqu’il correspond à la transposition de la régression linéaire classique (des moindres carrés) dans la forme des modèles généralisés.

Tableau 8.29: Carte d’identité du modèle gaussien
Type de variable dépendante	Variable continue dans l’intervalle \(]-\infty ; + \infty[\)
Distribution utilisée	Normale
Formulation	\(Y \sim Normal(\mu,\sigma)\) \(g(\mu) = \beta_0 + \beta X\) \(g(x) = x\)
Fonction de lien	Identitaire
Paramètre modélisé	\(\mu\)
Paramètres à estimer	\(\beta_0\), \(\beta\) et \(\sigma\)
Conditions d’application	Homoscédasticité

8.4.1.1 Conditions d’application

Les conditions d’application sont les mêmes que celles d’une régression linéaire classique. La condition de l’homoscédasticité (homogénéité de la variance) est due au fait que la variance du modèle est contrôlée par un seul paramètre fixe \(var(y) = \sigma\) (l’écart-type de la distribution normale). À titre de comparaison, rappelons que dans un modèle de Poisson, la variance est égale à la moyenne (\(var(y) = E(y)\)) alors que dans un modèle binomial négatif, la variance est fonction de la moyenne et d’un paramètre \(\theta\) (\(var(y) = E(y) + E(y)^{\frac{2}{\theta}}\)). Pour ces deux exemples, la variance augmente au fur et à mesure que la moyenne augmente.

8.4.1.2 Interprétation des paramètres

L’interprétation des paramètres est la même que pour une régression linéaire classique :

\(\beta_0\) : la constante, soit la moyenne attendue de la variable Y lorsque les valeurs de toutes les variables X sont 0.
\(\beta\) : les coefficients de régression qui quantifient l’effet d’une augmentation d’une unité des variables X sur la moyenne de la variable Y.
\(\sigma\) : l’écart-type de Y après avoir contrôlé les variables X. Il peut s’interpréter comme l’incertitude restante après modélisation de la moyenne de Y. Concrètement, si vous utilisez votre équation de régression pour prédire une nouvelle valeur de Y : \(\hat{Y}\), l’intervalle de confiance à 95 % de cette prédiction est (\(\hat{Y} - 3\sigma\text{ ; }\hat{Y} + 3\sigma\)). Vous noterez donc que plus \(\sigma\) est grand, plus grande est l’incertitude de la prédiction.

8.4.1.3 Exemple appliqué dans R

Pour cet exemple, nous reprenons le modèle LM que nous avons présenté dans la section 7.7. À titre de rappel, l’objectif est de modéliser la densité végétale dans les secteurs de recensement de Montréal. Pour cela, nous utilisons des variables relatives aux populations vulnérables physiologiquement ou socioéconomiquement, tout en contrôlant l’effet de la forme urbaine. Parmi ces dernières, l’âge médian des bâtiments est ajouté au modèle avec une polynomiale d’ordre deux, et la densité d’habitants est transformée avec la fonction logarithmique.

Vérification des conditions d’application

La première étape de la vérification des conditions d’application est bien sûr de s’assurer de l’absence de multicolinéarité excessive.

# Chargement des données
load("data/lm/DataVegetation.RData")
# Calcul du VIF
library(car)
vif(glm(VegPct ~ log(HABHA)+poly(AgeMedian,2)+
                       Pct_014+Pct_65P+Pct_MV+Pct_FR, data = DataFinal))

##                        GVIF Df GVIF^(1/(2*Df))
## log(HABHA)         1.289495  1        1.135559
## poly(AgeMedian, 2) 1.387429  2        1.085307
## Pct_014            1.517957  1        1.232054
## Pct_65P            1.304094  1        1.141969
## Pct_MV             1.480275  1        1.216666
## Pct_FR             1.729646  1        1.315160

Puisque l’ensemble des valeurs de VIF sont inférieures à deux, nos données ne sont pas marquées par une multicolinéarité problématique. La seconde étape du diagnostic consiste à calculer et à afficher les distances de Cook.

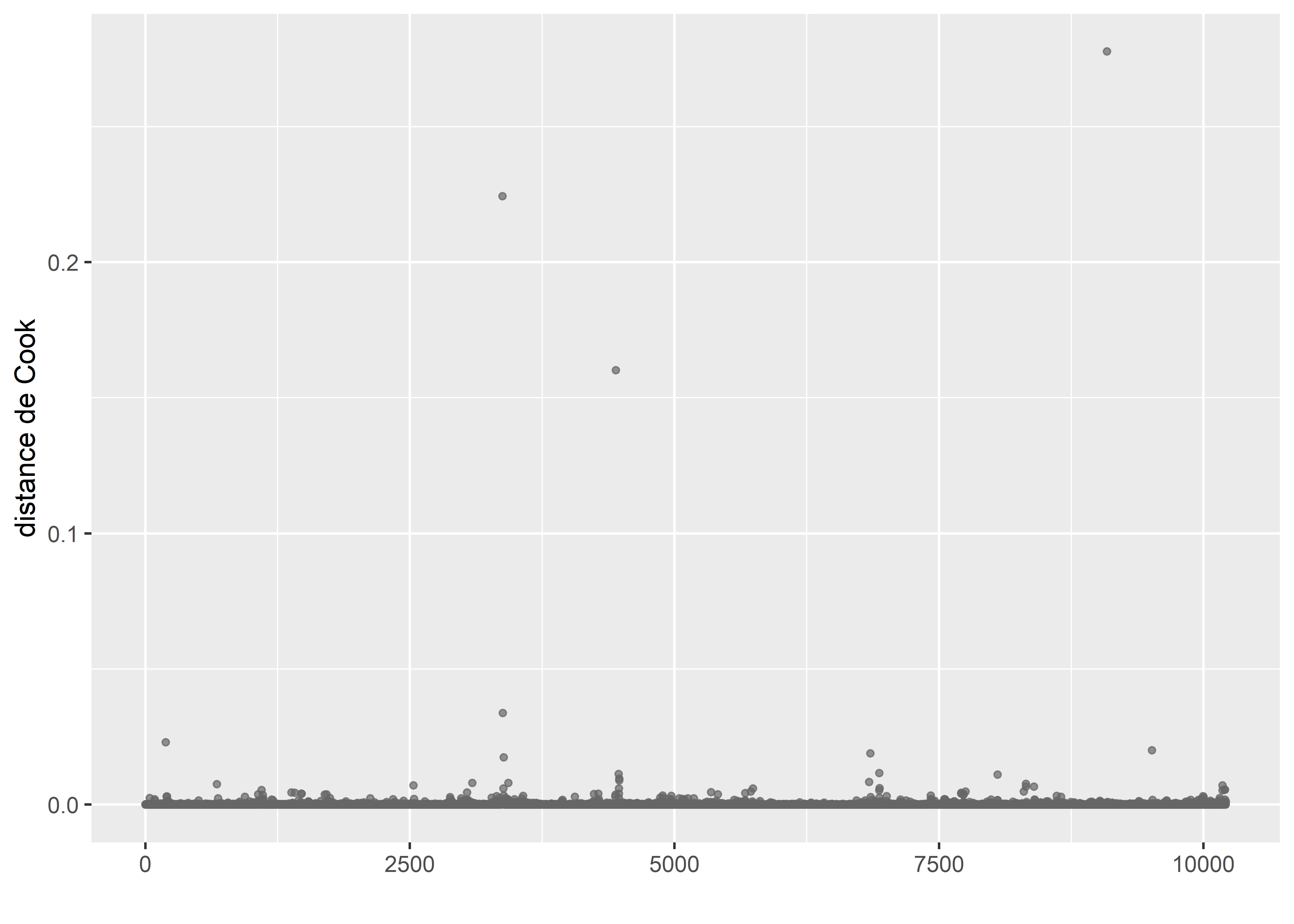
Figure 8.40: Distances de Cook pour le modèle gaussien

La figure 8.40 indique clairement que quatre observations sont très influentes dans le modèle.

# Sélection des cas étranges
cas_etranges <- subset(DataFinal, cooksd > 0.03)
print(cas_etranges)

##      VegPct ArbPct V250Pct V500Pct A250Pct A500Pct      HABHA AgeMedian Pct_014 Pct_65P Pct_MV Pct_FR
## 3374 10.481  5.478  18.987  13.744   2.908   2.704  74.835867       226    4.76   14.29  23.81  14.29
## 3378  0.000  0.000  12.709  12.505   2.116   2.324  88.006946       206    6.25   12.50  25.00  12.50
## 4446 23.162  5.209  31.437  31.535   8.672   9.108 313.142733       206   14.40   16.87  53.50  42.39
## 9088 85.767 27.583  78.195  83.492  42.999  51.074   2.070472       207   12.00   24.00  12.00  16.00
##      DistCBDkm   SDRNOM
## 3374     0.748 Montréal
## 3378     0.706 Montréal
## 4446     8.678 Montréal
## 9088    28.440 Montréal

Il s’agit de quatre îlots dans Montréal avec des logements très anciens : plus de 200 ans, alors que la moyenne est de 52 ans pour le reste de la zone d’étude. Le fait que nous ayons dans le modèle une polynomiale d’ordre 2 pour cette variable intensifie l’influence de ces valeurs extrêmes. Par conséquent, nous décidons de simplement les supprimer. Nous verrons plus tard qu’une alternative envisageable est de changer la distribution du modèle pour une distribution de Student (plus robuste aux valeurs extrêmes).

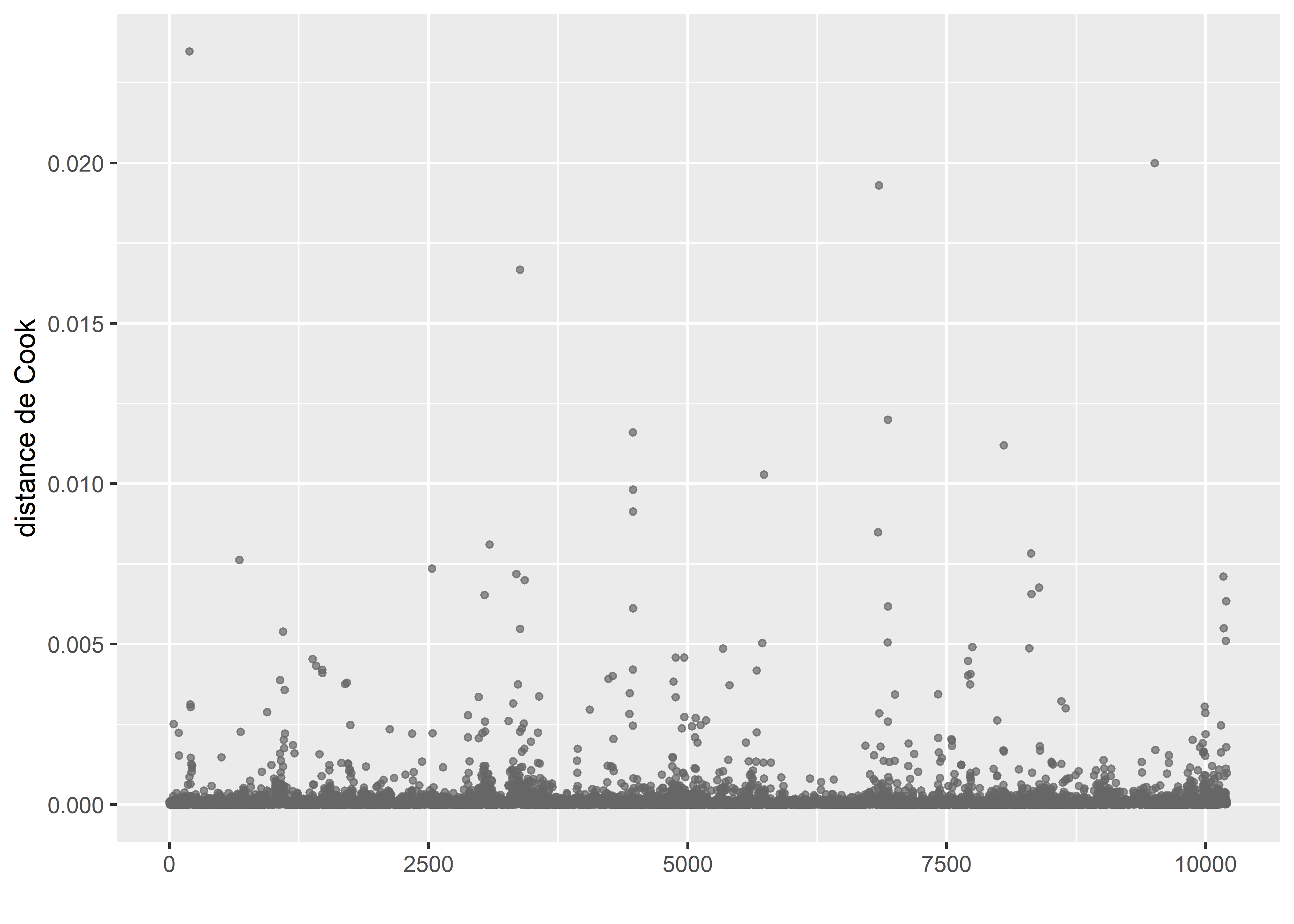
Figure 8.41: Distances de Cook pour le modèle gaussien après suppression des observations influentes

Une fois ces observations retirées, les nouvelles distances de Cook (figure 8.41) ne révèlent plus d’observations fortement influentes. Nous pouvons passer à l’analyse des résidus simulés. La figure 8.42 démontre que la distribution des résidus est significativement différente d’une distribution uniforme, que des valeurs aberrantes sont encore présentes et qu’il existe un lien entre résidus et prédiction dans le modèle.

# Extraction des prédictions du modèle
mus <- predict(modele, type = 'response')
modsigma <- sigma(modele)
# Extraction de l'écart type du modèle
# Génération de 1000 simulations pour chaque prédiction
nsim <- 1000
cols <- lapply(1:length(mus),function(i){
  mu <- mus[[i]]
  sims <- rnorm(nsim, mean=mu, sd = modsigma)
  return(sims)
})
mat_sims <- do.call(rbind, cols)
# Calculer les résidus simulés
sim_res <- createDHARMa(simulatedResponse = mat_sims, 
                            observedResponse = DataFinal2$VegPct,
                            fittedPredictedResponse = mus,
                            integerResponse = F)
plot(sim_res)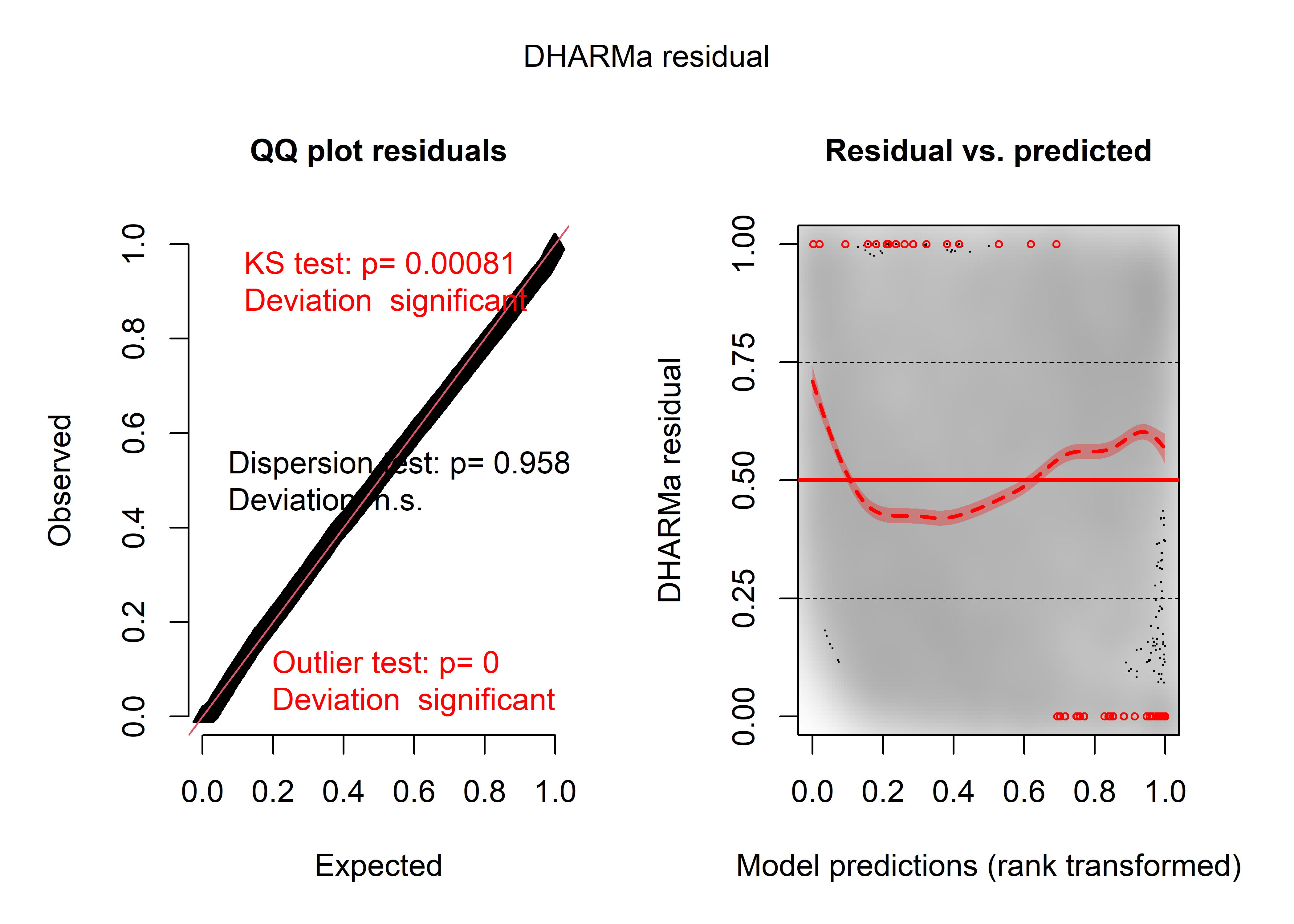

Figure 8.42: Diagnostic général des résidus simulés pour le modèle gaussien

Pour mieux cerner ce problème, nous pouvons, dans un premier temps, comparer la distribution originale des données et les simulations issues du modèle. La figure 8.43 montre clairement que la distribution normale est mal ajustée aux données. Ces dernières sont légèrement asymétriques et ne peuvent pas être inférieures à zéro, ce que la distribution normale ne parvient pas à reproduire.

df <- reshape2::melt(mat_sims[,1:30])
ggplot() + 
  geom_histogram(data = DataFinal2, mapping = aes(x = VegPct, y = ..density..),
                 color = "black", fill = "white", bins = 50)+
  geom_density(data = df, aes(x = value, group = Var2), 
               color = rgb(0.4,0.4,0.4,0.4), fill = rgb(0,0,0,0))+
  labs(x = "Pourcentage de végétation dans l'îlot (%)",
  y = "Densité")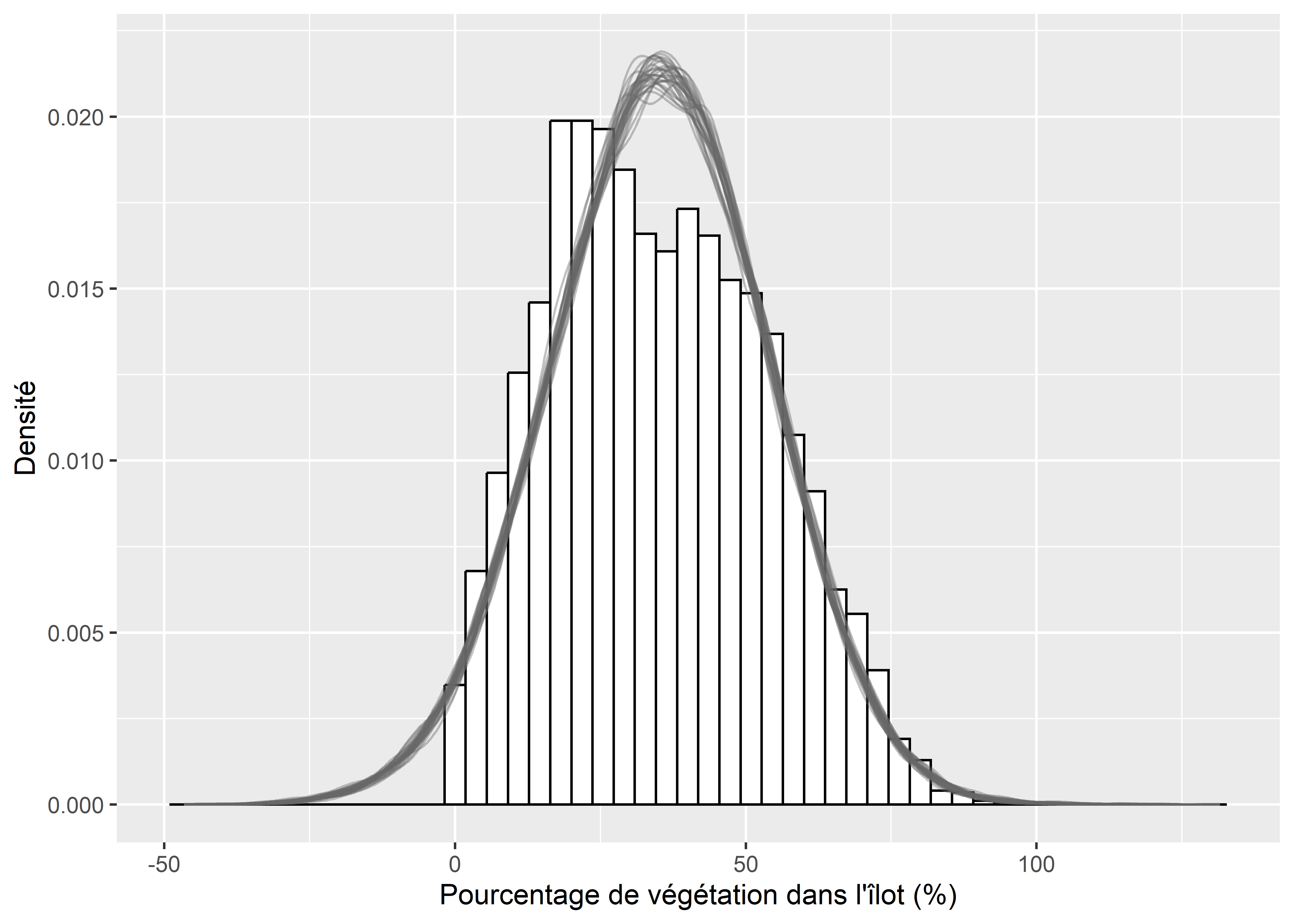

Figure 8.43: Comparaison de la distribution originale de la variable et des simulations issues du modèle

Il est également possible de vérifier si la condition d’homogénéité de la variance s’applique bien aux données.

# Extraction des prédictions du modèle
mus <- predict(modele, type = "response")
sigma_model <- sigma(modele)
# Création d'un DataFrame pour contenir les prédictions et les vraies valeurs
df1 <- data.frame(
  mus = mus,
  reals = DataFinal2$VegPct
)
# Calcul de l'intervalle de confiance à 95 % selon la distribution normale
# et stockage dans un second DataFrame
seqa <- seq(0,100,10)
df2 <- data.frame(
  mus = seqa,
  lower = qnorm(p = 0.025, mean = seqa, sd = sigma_model),
  upper = qnorm(p = 0.975, mean = seqa, sd = sigma_model)
)

# Affichage des valeurs réelles et prédites (en rouge)
# et de leur variance selon le modèle (en noir)
ggplot() + 
  geom_point(data = df1, 
             mapping = aes(x = mus, y = reals),
             color ="red", size = 0.5) + 
  geom_errorbar(data = df2,
                mapping = aes(x = mus, ymin = lower, ymax = upper),
                width = 0.2, color = rgb(0.4,0.4,0.4)) + 
  labs(x = 'valeurs prédites',
       y = "valeurs réelles")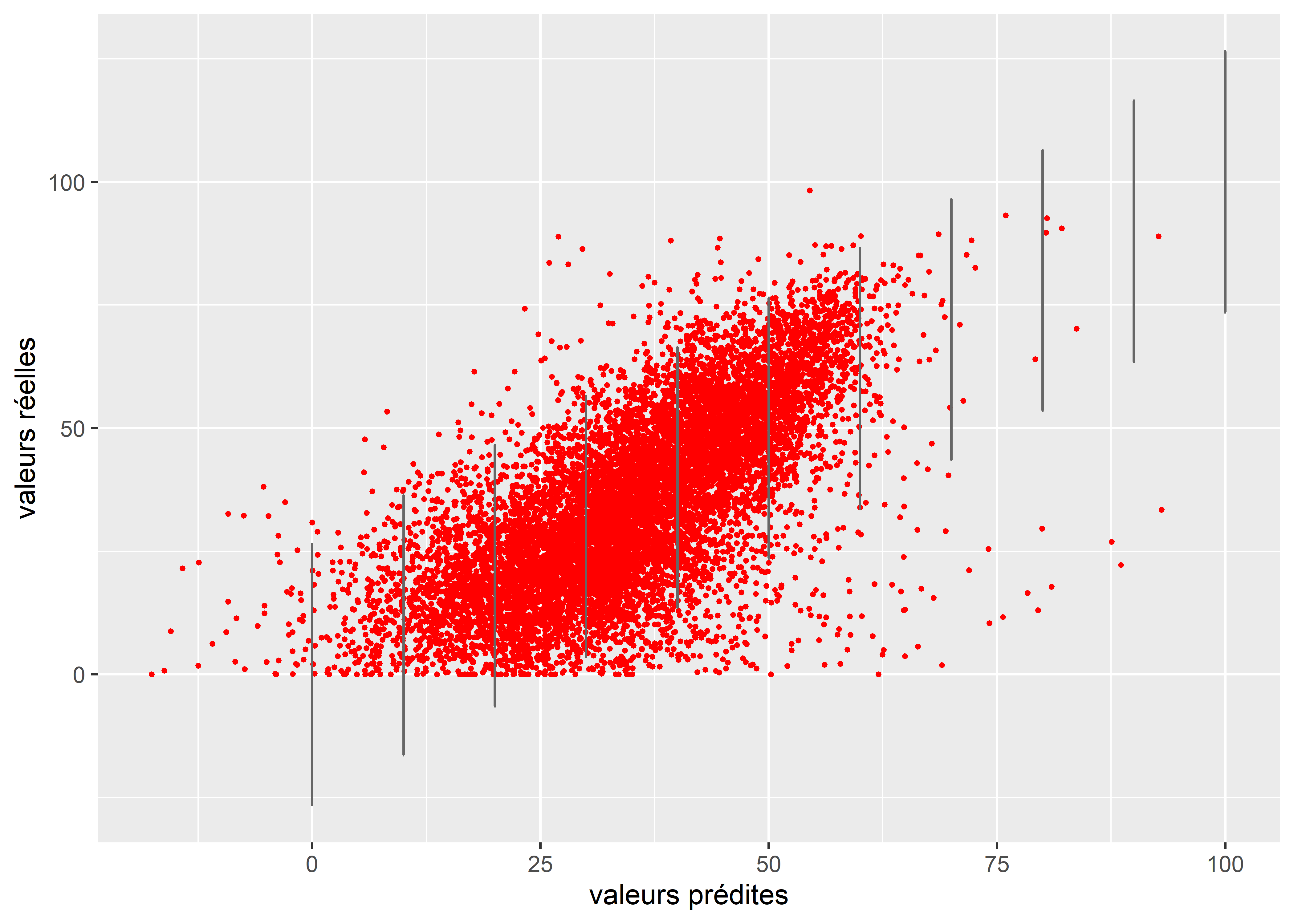

Figure 8.44: Comparaison de la distribution originale de la variable et des simulations issues du modèle

À nouveau, nous constatons à la figure 8.44 que le modèle s’attend à trouver des valeurs négatives pour la concentration de végétation, ce qui n’est pas possible dans notre cas. En revanche, il semble que la variance soit bien homogène puisque la dispersion des observations semble suivre à peu près la dispersion attendue par le modèle (en noir).

Malgré ces différents constats indiquant clairement qu’un modèle gaussien est un choix sous-optimal pour ces données, nous poursuivons l’analyse de ce modèle.

Vérification de la qualité d’ajustement

# Ajustement d'un modèle nul
modelenull <- glm(VegPct ~ 1,
                  data = DataFinal2, 
                  family = gaussian())
# Calcul des pseudo R2
rsqs(loglike.full = logLik(modele),
     loglike.null = logLik(modelenull),
     full.deviance = deviance(modele),
     null.deviance = deviance(modelenull), 
     nb.params = modele$rank,
     n = nrow(DataFinal2)
     )

## $`deviance expliquee`
## [1] 0.4706321
## 
## $`McFadden ajuste`
## 'log Lik.' 0.07310662 (df=9)
## 
## $`Cox and Snell`
## 'log Lik.' 0.4706321 (df=9)
## 
## $Nagelkerke
## 'log Lik.' 0.4707122 (df=9)

Le modèle parvient à expliquer 47 % de la déviance totale, mais obtient un R² ajusté de McFadden de seulement 0,07.

# Calcul du RMSE
sqrt(mean((predict(modele, type = "response") - DataFinal2$VegPct)**2))

## [1] 13.49885

L’erreur quadratique moyenne et de 13,5 points de pourcentage, ce qui indique que le modèle a une assez faible capacité prédictive.

Interprétation des résultats

L’ensemble des coefficients du modèle sont accessibles via la fonction summary; le tableau 8.30 présente les résultats pour les coefficients du modèle.

Tableau 8.30: Résultats du modèle gaussien
Variable	Coeff.	Err.std	Val.z	val.p	IC coeff 2,5 %	IC coeff 97,5 %	Sign.
Constante	53,606	1,000	53,640	0,000	51,647	55,565	***
AgeMedian ordre 1	2,732	15,560	0,180	0,861	-27,772	33,237
AgeMedian ordre 2	-320,869	14,000	-22,910	0,000	-348,318	-293,420	***
Pct_014	0,915	0,030	29,310	0,000	0,853	0,976	***
Pct_65P	0,280	0,020	15,050	0,000	0,243	0,316	***
Pct_MV	-0,042	0,010	-4,190	0,000	-0,061	-0,022	***
Pct_FR	-0,340	0,010	-30,940	0,000	-0,362	-0,318	***

Les résultats de la régression linéaire multiple ont déjà été interprétés dans la section 7.7.1, nous ne commenterons pas ici les résultats du modèle GLM gaussien qui sont identiques.

8.4.2 Modèle GLM avec une distribution de Student

Pour rappel, la distribution de Student ressemble à une distribution normale (section 2.4.3.11). Elle est symétrique autour de sa moyenne et a également une forme de cloche. Cependant, elle dispose de queues lourdes, ce qui signifie qu’elle permet de représenter des phénomènes présentant davantage de valeurs extrêmes qu’une distribution normale. Pour contrôler le poids des queues, la distribution de Student intègre un troisième paramètre : \(\nu\) (nu). Lorsque \(\nu\) tends vers l’infini, la distribution de Student tend vers une distribution normale (figure 8.45).

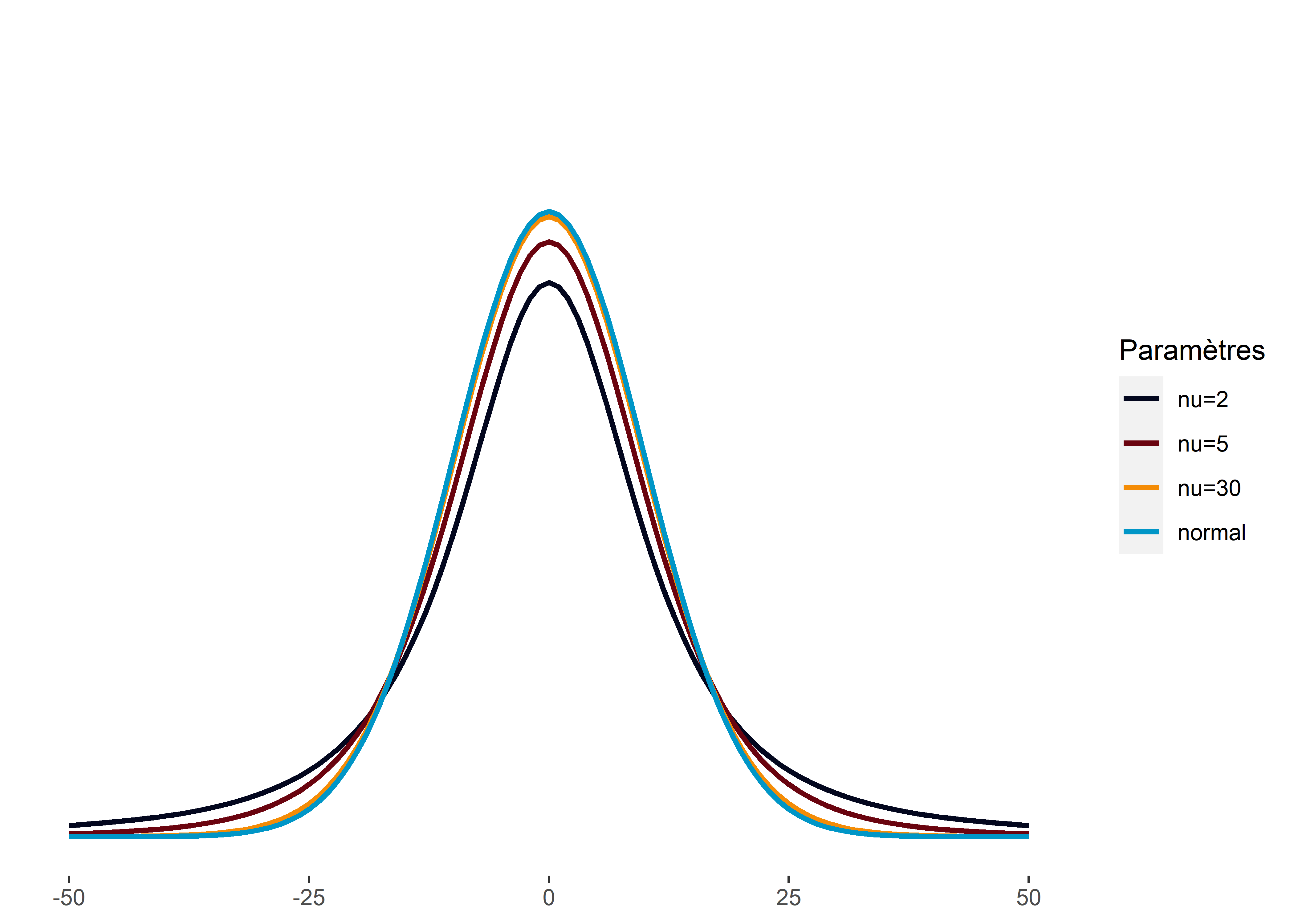
Figure 8.45: Effet du paramètre nu sur une distribution de Student

Comme vous pouvez le constater dans la carte d’identité au tableau 8.31, le modèle GLM de Student est très proche du modèle GLM gaussien. Nous modélisons explicitement la moyenne de la distribution et son paramètre de dispersion (variance) est laissé fixe. Ce GLM est même souvent utilisé comme une version « robuste » du modèle gaussien du fait de sa capacité à intégrer explicitement l’effet des observations extrêmes. En effet, dans un modèle gaussien, les observations extrêmes (aussi appelées observations aberrantes) vont davantage influencer les paramètres du modèle que pour un modèle utilisant une distribution de Student.

Tableau 8.31: Carte d’identité du modèle de Student
Type de variable dépendante	Variable continue dans l’intervalle \(]-\infty ; + \infty[\)
Distribution utilisée	Student
Formulation	\(Y \sim Student(\mu,\sigma,\nu)\) \(g(\mu) = \beta_0 + \beta X\) \(g(x) = x\)
Fonction de lien	Identitaire
Paramètre modélisé	\(\mu\)
Paramètres à estimer	\(\beta_0\), \(\beta\), \(\sigma\) et \(\nu\)
Conditions d’application	Homoscédasticité

8.4.2.1 Conditions d’application

Les conditions d’application sont les mêmes que pour un modèle GLM gaussien, à ceci prêt que le modèle utilisant la distribution de Student est moins sensible aux observations extrêmes.

8.4.2.2 Interprétation des paramètres

L’interprétation des paramètres est la même que pour un modèle gaussien puisque nous modélisons la moyenne de la distribution et que la fonction de lien est la fonction identitaire. Le seul paramètre supplémentaire est \(\nu\), qui n’a en soit aucune interprétation pratique. Notez simplement que si \(\nu\) est supérieur à 30, un simple modèle GLM gaussien serait sûrement suffisant.

8.4.2.3 Exemple appliqué dans R

Nous proposons ici de simplement réajuster le modèle gaussien présenté dans la section précédente en utilisant une distribution de Student. Nous utilisons pour cela la fonction gam du package mgcv avec le paramètre family=scat pour utiliser une distribution de Student. Les valeurs de VIF ont déjà été calculées dans l’exemple précédent, nous pouvons donc passer directement au calcul des distances de Cook.

# Chargement des données
load("data/lm/DataVegetation.RData")
# Ajustement du modèle
modele <- gam(VegPct ~ log(HABHA)+poly(AgeMedian,2)+
                       Pct_014+Pct_65P+Pct_MV+Pct_FR, data = DataFinal,
              family = scat)

# Calcul des distances de Cook
cooksd <- cooks.distance(modele)
# Affichage des valeurs
df <- data.frame(
  cook = cooksd,
  oid = 1:length(cooksd)
)
ggplot(data = df) + 
  geom_point(aes(x = oid, y = cook), color = rgb(0.4,0.4,0.4,0.7), size = 1) + 
  labs(x="", y = "distance de Cook")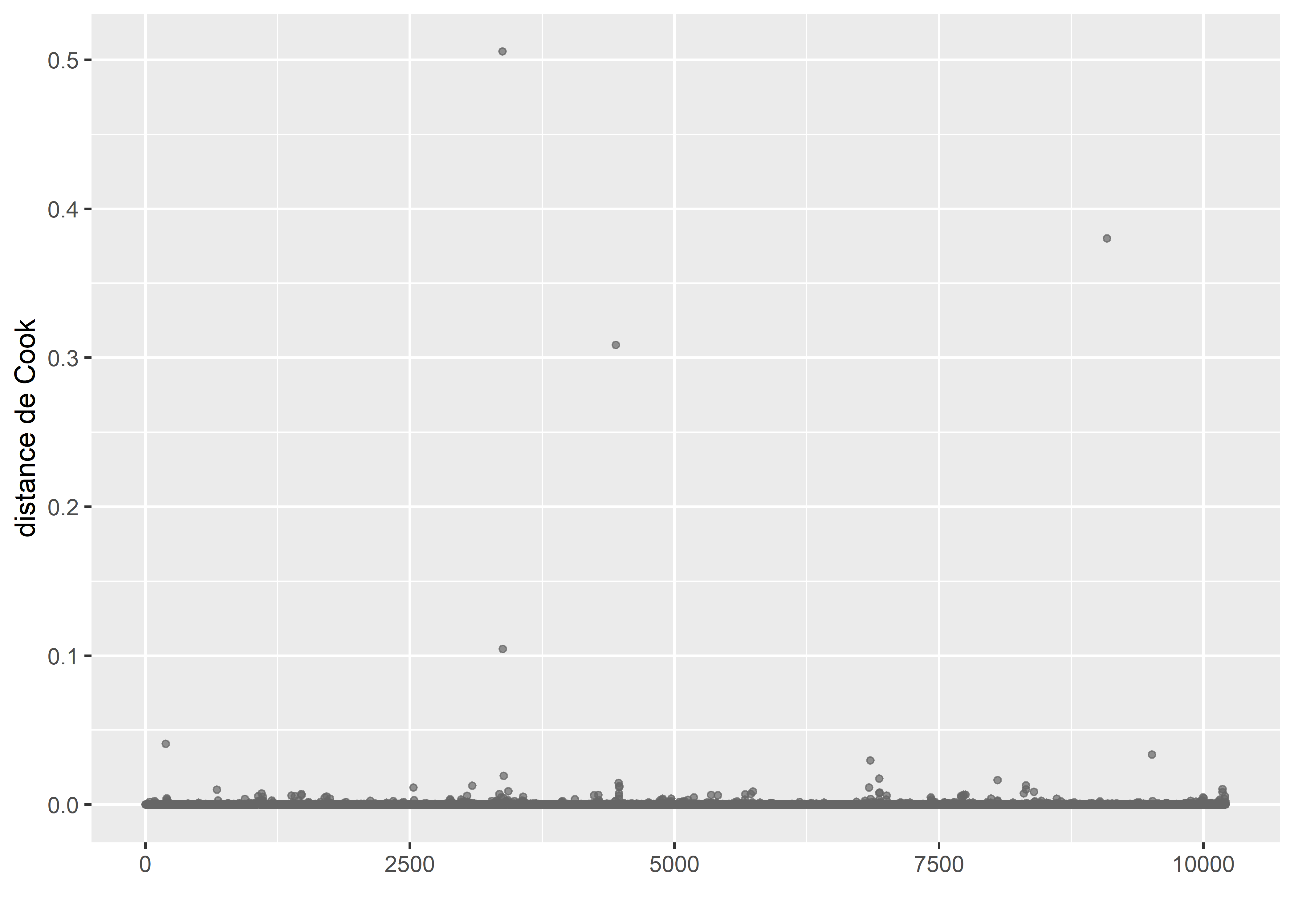

Figure 8.46: Distances de Cook pour un modèle GLM avec une distribution de Student

Nous retrouvons les quatre observations avec des distances de Cook très fortes que nous avons identifiées dans le modèle gaussien. Nous décidons donc de les enlever pour les mêmes raisons que précédemment.

# Chargement des données
DataFinal2 <- subset(DataFinal, cooksd<0.1)
# Ajustement du modèle
modele <- gam(VegPct ~ log(HABHA)+poly(AgeMedian,2)+
                       Pct_014+Pct_65P+Pct_MV+Pct_FR, data = DataFinal2,
              family = scat)

# Calcul des distances de Cook
cooksd <- cooks.distance(modele)
# Affichage des valeurs
df <- data.frame(
  cook = cooksd,
  oid = 1:length(cooksd)
)
ggplot(data = df) + 
  geom_point(aes(x = oid, y = cook), color = rgb(0.4,0.4,0.4,0.7), size = 1) + 
  labs(x="", y = "distance de Cook")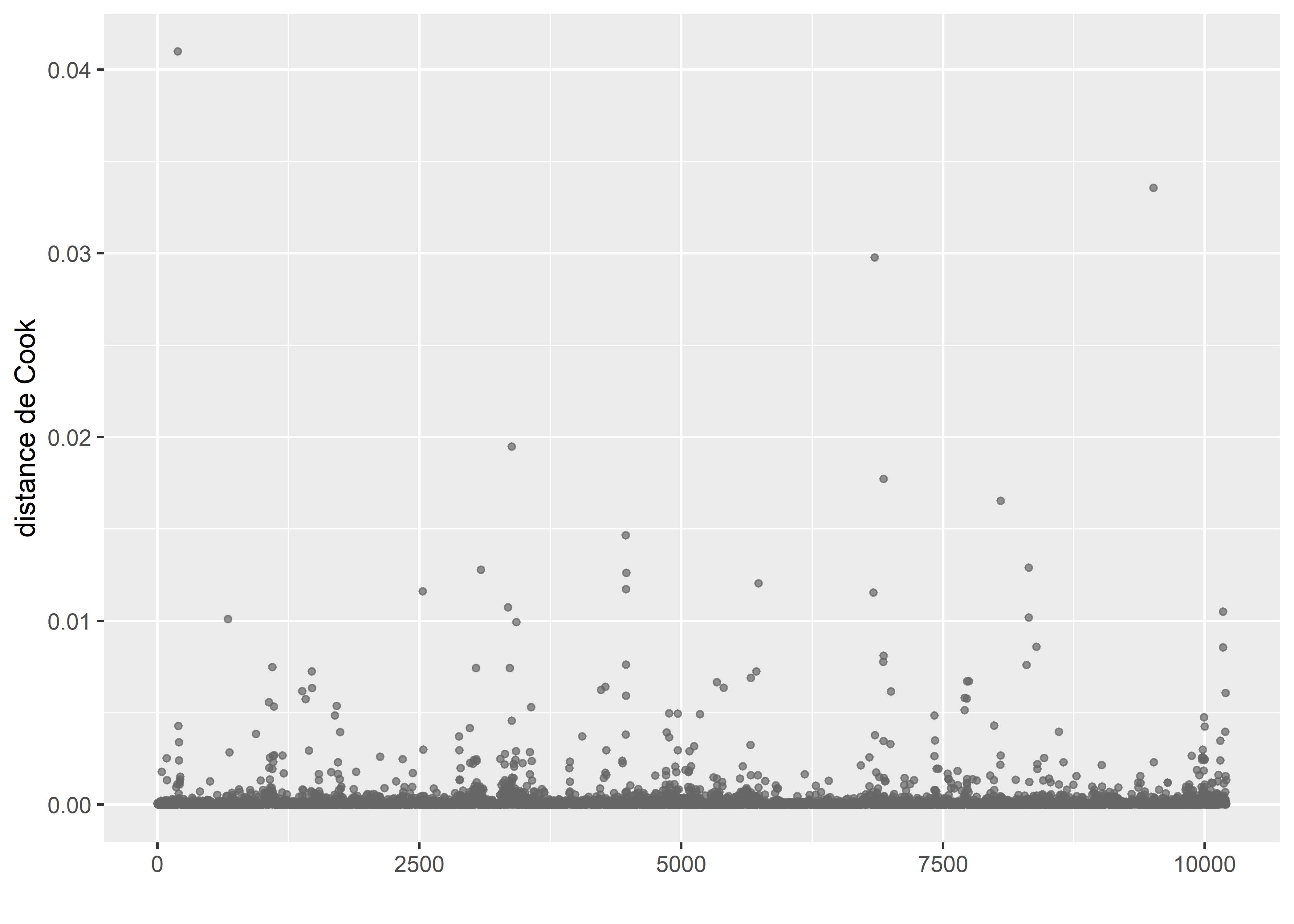

Figure 8.47: Distances de Cook pour un modèle GLM avec une distribution de Student après suppression des valeurs fortement influentes

Nous pouvons à présent vérifier si les résidus simulés se comportent tel qu’attendu.

# Extraction des prédictions du modèle
mus <- predict(modele, type = 'response')
# Affichage des paramètres nu et sigma
modele$family$family

## [1] "Scaled t(6.333,11.281)"

sigma_model <- 11.281
nu_model <- 6.333
library(LaplacesDemon) # pour simuler des données d'une distribution de Student
# Génération de 1000 simulations pour chaque prédiction
nsim <- 1000
cols <- lapply(1:length(mus),function(i){
  mu <- mus[[i]]
  sims <- rst(nsim, mu=mu, sigma = sigma_model, nu = nu_model)
  return(sims)
})
mat_sims <- do.call(rbind, cols)
# Calculer les résidus simulés
sim_res <- createDHARMa(simulatedResponse = mat_sims, 
                            observedResponse = DataFinal2$VegPct,
                            fittedPredictedResponse = mus,
                            integerResponse = F)
plot(sim_res)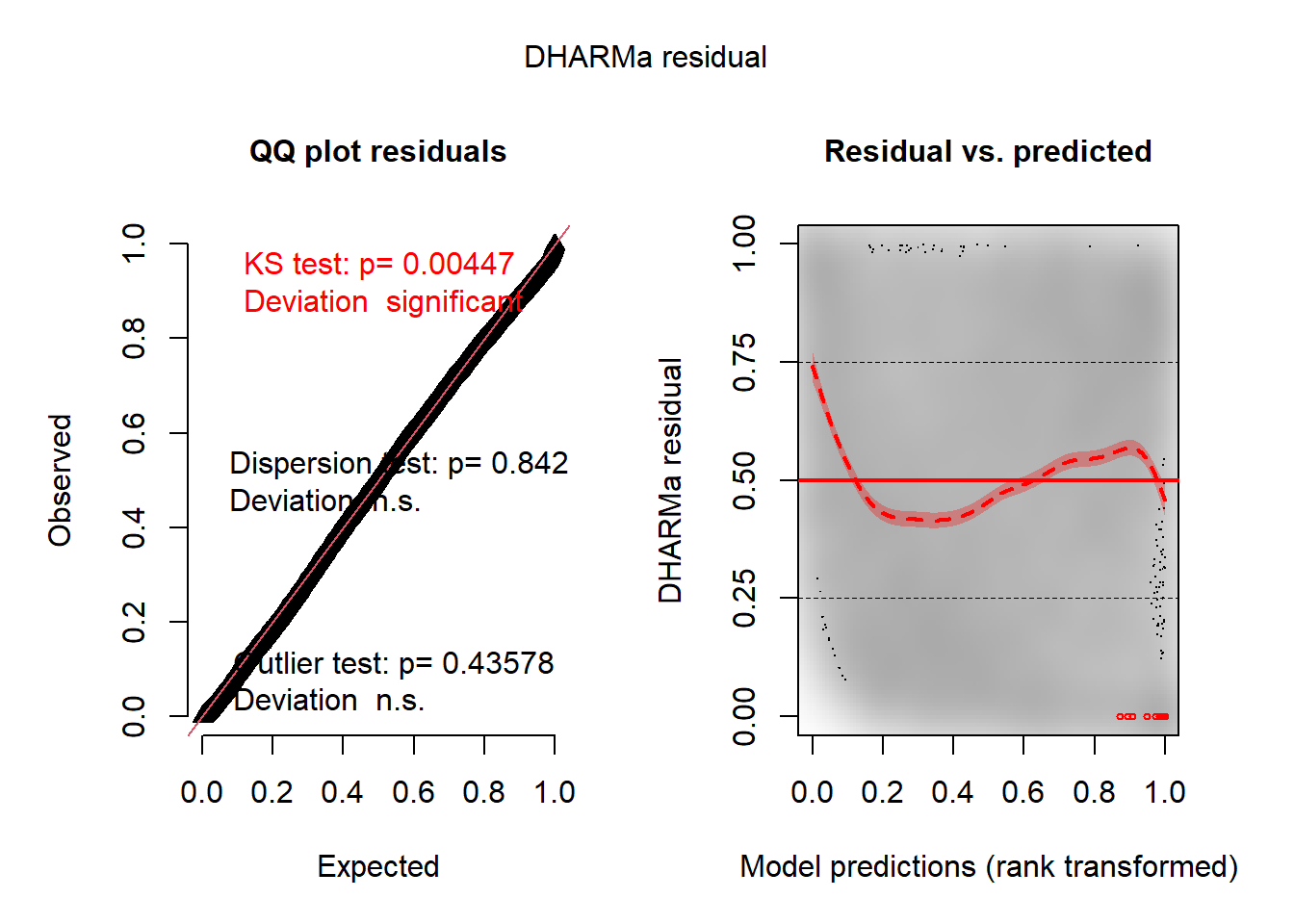

Figure 8.48: Diagnostic général des résidus simulés pour le GLM avec distribution de Student

Il semble que nous obtenons des résultats similaires à ceux du modèle gaussien: les résidus divergent significativement d’une distribution uniforme (figure 8.48). Le graphique quantile-quantile n’est parfois pas très adapté pour discerner une déviation de la distribution uniforme, nous pouvons dans ce cas afficher un histogramme des résidus pour en avoir le coeur net (figure 8.49).

ggplot()+
  geom_histogram(aes(x = residuals(sim_res)), bins = 50, color = "white") + 
  labs(x = "effectifs", y = "résidus simulés")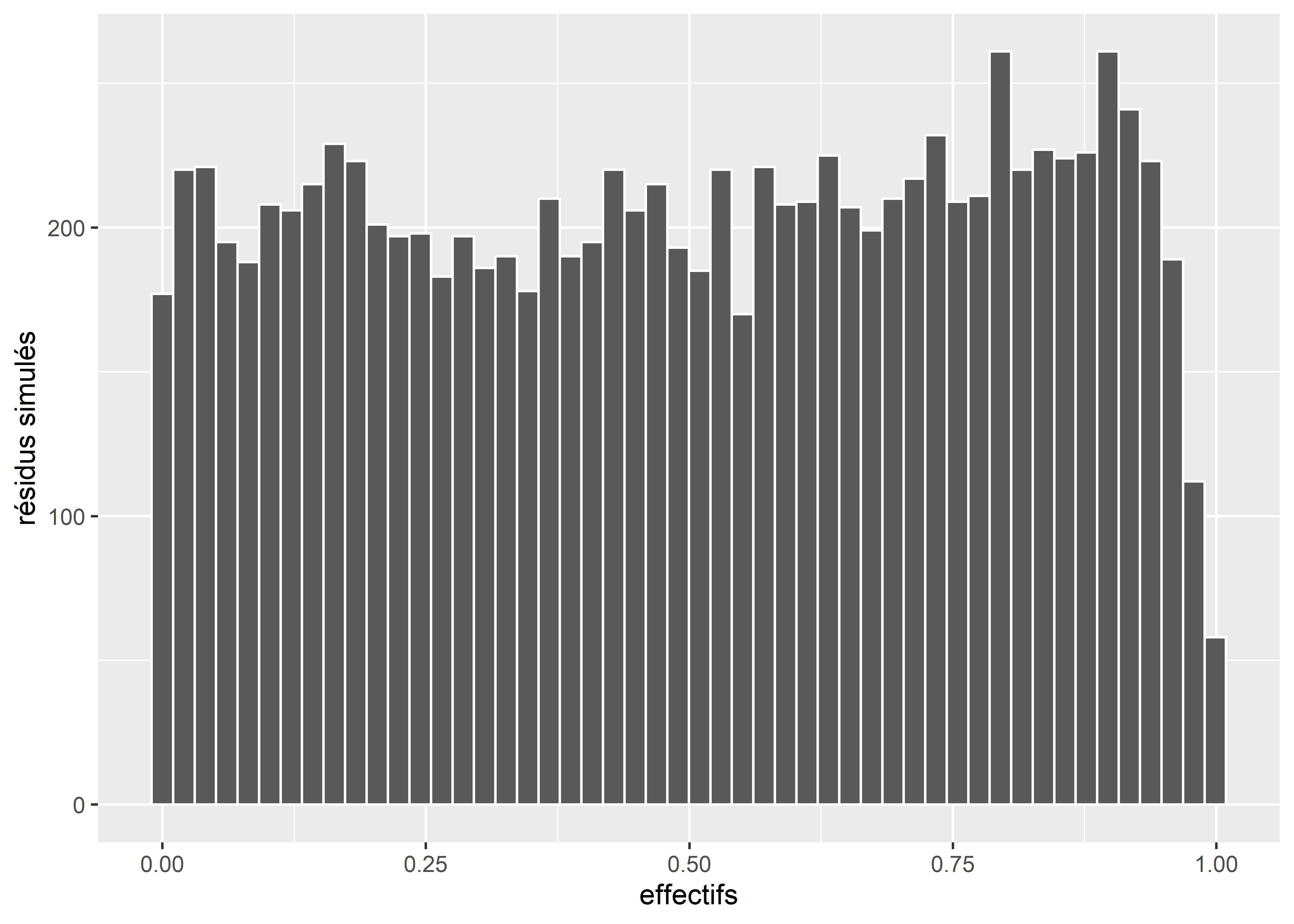

Figure 8.49: Distribution des résidus simulés du modèle GLM avec distribution de Student

Pour cet exercice, il est intéressant de comparer les formes des simulations issues du modèle gaussien et du modèle de Student pour bien distinguer la différence entre les deux.

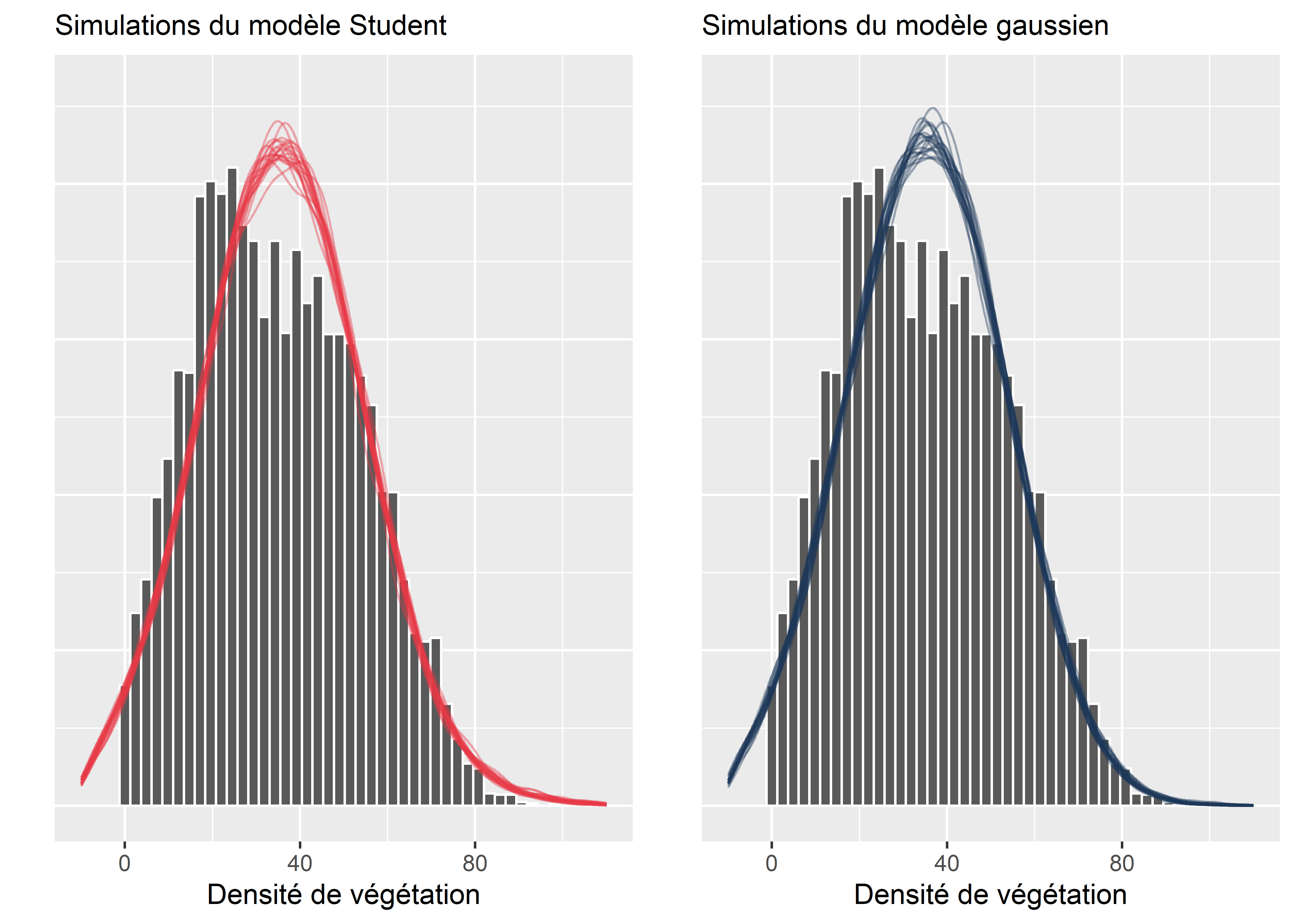
Figure 8.50: Simulations issues des modèles gaussien et de Student, comparées aux données originales

Nous constatons ainsi que la différence entre les deux modèles est ici très mince, voire inexistante. Le seul élément que nous pouvons noter est que le modèle de Student à une courbe (une queue de distribution) moins aplatie vers la droite. Cela lui permettrait de mieux tenir compte de cas extrêmes avec de fortes densités de végétation (ce qui concerne donc très peu d’observations puisque cette variable a un maximum de 100).

Pour déterminer si le modèle de Student est plus pertinent à retenir que le modèle gaussien, nous pouvons ajuster un second modèle de Student pour lequel nous forçons artificiellement \(\nu\) à être très élevé. Pour rappel, quand \(\nu\) tend vers l’infini, la distribution de Student tend vers une distribution normale. Nous forçons ici \(\nu\) à être supérieur à 100 pour créer un second modèle de Student se comportant quasiment comme un modèle gaussien et calculons les AIC des deux modèles.

# Calcul d'un modèle de Student identitique à un modèle gaussien
modele2 <- gam(VegPct ~ log(HABHA)+poly(AgeMedian,2)+
                   Pct_014+Pct_65P+Pct_MV+Pct_FR, data = DataFinal2,
               family = scat(min.df = 100))
# Calcul des deux AIC
AIC(modele)

## [1] 81771.92

AIC(modele2)

## [1] 82057.79

Le second AIC (modèle gaussien) est plus élevé, indiquant que le modèle est moins bien ajusté aux données. Dans le cas présent, il est plus pertinent de retenir le modèle de Student même si les écarts entre ces deux modèles sont minimes. Ce résultat n’est pas surprenant puisque la variable Y (pourcentage de végétation dans les îlots de l’île de Montréal) est relativement compacte et comporte peu / pas de valeurs pouvant être qualifiées de valeurs extrêmes.

Nous ne détaillons pas ici l’interprétation des coefficients du modèle (présentés au tableau 8.32) puisqu’ils s’interprètent de la même façon qu’un modèle GLM et qu’un modèle de régression linéaire multiple.

Tableau 8.32: Résultats du modèle Student
Variable	Coeff.	Err.std	Val.z	val.p	IC coeff 2,5 %	IC coeff 97,5 %	Sign.
Constante	65,096	0,940	69,110	0,000	63,250	66,943	***
log(HABHA)	-9,502	0,160	-60,160	0,000	-9,811	-9,192	***
Pct_014	0,866	0,030	29,450	0,000	0,808	0,924	***
Pct_65P	0,237	0,020	13,540	0,000	0,203	0,272	***
Pct_MV	-0,015	0,010	-1,650	0,099	-0,034	0,003	.
Pct_FR	-0,301	0,010	-29,040	0,000	-0,321	-0,280	***

8.4.3 Modèle GLM avec distribution Gamma

Pour rappel, la distribution Gamma est strictement positive (\([0;+\infty[\)), asymétrique, et a une variance proportionnelle à sa moyenne (hétéroscedastique). Dans la section sur les distributions, nous avons vu que la distribution Gamma (section 2.4.3.15) est formulée avec deux paramètres : sa forme (\(\alpha\) ou shape) et son échelle (\(b\) ou scale). Ces deux paramètres n’ont pas une interprétation intuitive, mais il est possible avec un peu de jonglage mathématique d’arriver à une reparamétrisation intéressante. Cela est détaillé dans l’encadré ci-dessous; notez toutefois qu’il n’est pas nécessaire de maîtriser le contenu de cet encadré pour lire la suite de cette section sur les modèles GLM avec une distribution Gamma.

Reparamétrisation d’une distribution Gamma pour un GLM

Si nous disposons d’une variable Y, suivant une distribution Gamma telle que \(Y \sim Gamma(\alpha,b)\) avec \(\alpha\) le paramètre de forme et \(b\) le paramètre d’échelle, alors, l’espérance et la variance de Y peuvent être définies comme suit :

\[\begin{equation} \begin{aligned} &E(Y) = \alpha \times b \\ &Var(Y) = \alpha \times b^2\\ \end{aligned} \tag{8.22} \end{equation}\]

En d’autres termes, l’espérance (l’équivalent de la moyenne pour une distribution normale) de notre variable Y est égale au produit des paramètres de forme et d’échelle.

Avec ces propriétés, il est possible de redéfinir la fonction de densité de la distribution Gamma et d’arriver à une nouvelle formulation : \(Y \sim Gamma(\mu,\alpha)\). \(\mu\) est donc l’espérance de Y (interprétable comme sa moyenne, soit sa valeur attendue) et \(\alpha\) permet de capturer la dispersion de la distribution Gamma. Par extension des relations présentées ci-dessus, il est possible de reformuler la variance en fonction de \(\mu\) et de \(\alpha\).

\[\begin{equation} \begin{aligned} &Var(Y) = \alpha \times b^2\\ &\mu = \alpha \times b \text{ soit }b = \frac{\mu}{a}\\ &Var(Y) = \alpha \times (\frac{\mu}{\alpha})^2 \text{ soit } Var(Y) = \frac{\mu^2}{\alpha}\\ \end{aligned} \tag{8.23} \end{equation}\]

Nous observons donc que la variance dans un modèle Gamma augmente de façon quadratique avec la moyenne, mais est tempérée par le paramètre de forme. Nous en concluons qu’un paramètre de forme plus grand produit une distribution moins étalée.

Dans ce contexte, \(\mu\) doit être strictement positif : la valeur attendue moyenne d’une distribution Gamma doit être positive par définition puisqu’une distribution Gamma ne peut pas produire de valeurs négatives. Il est donc logique d’utiliser la fonction logarithmique comme fonction de lien, puisque sa contrepartie (la fonction exponentielle) ne produit que des résultats positifs.

Pour résumer, nous nous retrouvons donc avec un modèle qui prédit, sur une échelle logarithmique, l’espérance (~moyenne) d’une distribution Gamma. Notez qu’il existe d’autres façons de spécifier un modèle GLM avec une distribution Gamma, mais celle-ci est la plus intuitive.

Tableau 8.33: Carte d’identité du modèle Gamma
Type de variable dépendante	Variable continue dans l’intervalle \(]0 ; + \infty[\)
Distribution utilisée	Gamma
Formulation	\(Y \sim Gamma(\mu,\alpha)\) \(g(\mu) = \beta_0 + \beta X\) \(g(x) = log(x)\)
Fonction de lien	log
Paramètre modélisé	\(\mu\)
Paramètres à estimer	\(\beta_0\), \(\beta\), et \(\alpha\)
Conditions d’application	\(Variance = \frac{\mu^2}{\alpha}\)

8.4.3.1 Interprétation des paramètres

Puisque le modèle utilise la fonction de lien log, alors les coefficients \(\beta\) expriment l’augmentation de l’espérance (la valeur attendue de Y, ce qui est proche de l’idée de moyenne) de la variable Y sur une échelle logarithmique (comme dans un modèle de Poisson). Il est possible de convertir les coefficients dans l’échelle originale de la variable Y en utilisant la fonction exponentielle (l’inverse de la fonction log), mais ces coefficients représentent alors des effets multiplicatifs et non des effets additifs. Prenons un exemple, admettons que le coefficient \(\beta_1\), associé à la variable \(X_1\) soit de 1,5. Cela signifie qu’une augmentation d’une unité de \(X_1\), augmente le log de l’espérance de Y de 1,5 unité. L’exponentielle du coefficient est 4,48, ce qui signifie qu’une augmentation d’une unité entraîne une multiplication par 4,48 de la valeur attendue de Y (l’espérance de Y). Le paramètre de forme (\(\alpha\)) n’a pas d’interprétation pratique, bien qu’il soit utilisé dans les différents tests des conditions d’application du modèle et dans le calcul de sa déviance.

8.4.3.2 Conditions d’application

Dans un modèle GLM gaussien, la variance est capturée par un paramètre \(\sigma\) et est constante, produisant la condition d’homoscédasticité des résidus. Dans un modèle Gamma, la variance varie en fonction de l’espérance et du paramètre de forme selon la relation : \(Var(Y) = \frac{E(Y)^2}{\alpha}\). Les résidus sont donc par nature hétéroscédastiques dans un modèle Gamma et doivent suivre cette relation.

8.4.3.3 Exemple appliqué dans R

Pour cet exemple, nous nous intéressons à la durée de déplacement en milieu urbain. Ce type d’analyse permet notamment de mieux comprendre les habitudes de déplacement de la population et d’orienter les politiques de transport. Plusieurs travaux concluent que les durées de déplacement en milieu urbain varient en fonction du motif du déplacement, du mode de transport utilisé, des caractéristiques socio-économiques de l’individu et des caractéristiques du trajet lui-même (Anastasopoulos et al. 2012; Frank et al. 2008). Nous modélisons ici la durée en minute d’un ensemble de déplacements effectués par des Montréalais en 2017 et enregistrés avec l’application MTL Trajet proposée par la Ville de Montréal. Ces données sont disponibles sur le site web des données ouvertes de Montréal et son anonymisées. Nous ne disposons donc d’aucune information individuelle. Compte tenu du très grand nombre d’observations (plus de 185 000), nous avons dû effectuer quelques opérations de tri et nous avons ainsi supprimé:

les trajets utilisant de multiples modes de transport (sauf en combinaison avec la marche à pied, par exemple, un trajet effectué à pied et en transport en commun a été recatégorisé comme un trajet en transport en commun uniquement). Les déplacements multimodaux se distinguent largement des déplacements unimodaux dans la littérature scientifique;
les trajets de nuit (seuls les trajets démarrant dans l’intervalle de 7 h à 21 h ont été conservés);
les trajets dont le point de départ est un arrondissement / municipalité pour lequel moins de 150 trajets ont été enregistrés (trop peu d’observations);
les trajets de plus de deux heures (cas rares, considérés comme des données aberrantes);
les trajets dont le point de départ est à moins de 100 mètres du point d’arrivée (formant des boucles plutôt que des déplacements).

Nous arrivons ainsi à un total de 24 969 observations. Pour modéliser ces durées de déplacement, nous utilisons les variables indépendantes présentées dans le tableau 8.34.

Tableau 8.34: Variables indépendantes utilisées dans le modèle Gamma
Nom de la variable	Signification	Type de variable	Mesure
Mode	Mode de déplacement	Variable catégorielle	Transport collectif; piéton; vélo et véhicule individuel
Motif	Motif du déplacement	Variable catégorielle	Travail; loisir; magasinage et éducation
HeureDep	Heure de départ	Variable catégorielle	De 7 h à 21 h
ArrondDep	Arrondissement de départ	Variable catégorielle	Nom de l’arrondissement dont part le trajet
LogDist	Logarithme de la distance à vol d’oiseau en km	Variable continue	Logarithme de la distance à vol d’oiseau en km entre le point de départ et d’arrivée
MemeArrond	L’arrivée du trajet se situe-t-elle dans le même arrondissement que celui du départ?	Variable binaire	Oui ou non
Semaine	Le trajet a-t-il été effectué en semaine ou en fin de semaine?	Variable binaire	Semaine ou fin de semaine

Les temps de trajet forment une variable strictement positive et très vraisemblablement asymétrique. En effet, nous nous attendons à observer une certaine concentration de valeurs autour d’une moyenne, et davantage de trajets avec de courtes durées que de trajets avec de longues durées. Pour nous en assurer, réalisons un histogramme de la distribution de notre variable Y et comparons la avec des distributions normale et Gamma.

# Chargement des données
dataset <- read.csv("data/glm/DureeTrajets.csv", stringsAsFactors = F)
arrondMTL <- c("Mercier-Hochelaga-Maisonneuve", "Villeray-Saint-Michel-Parc-Extension", 
               "Ville-Marie", "Verdun", "Saint-Leonard", "Saint-Laurent", 
               "Rosemont-La Petite-Patrie", "Riviere-des-Prairies-Pointe-aux-Trembles", 
               "Pierrefonds-Roxboro", "Outremont", "Montreal-Nord", "Le Sud-Ouest", 
               "Le Plateau-Mont-Royal", "Lachine" , "Ahuntsic-Cartierville",
               "Anjou" ,"Cote-des-Neiges-Notre-Dame-de-Grace", "LaSalle"  
)
dataset <- subset(dataset,dataset$ArrondDep %in% arrondMTL)
# Définissons 7 h du matin comme la référence pour la variable Heure de départ
dataset$HeureDep <- relevel(
  factor(dataset$HeureDep, levels = as.character(7:21)),
  ref = "7")
# Comparaison de la distribution originale avec une distribution 
# normale et une distribution Gamma
library(fitdistrplus)
model_gamma <- fitdist(dataset$Duree, distr = "gamma")
ggplot(data = dataset) + 
  geom_histogram(aes(x=Duree, y = ..density..), bins = 40, color = "white")+
  stat_function(fun = dgamma, color = 'red', size = 0.8, 
                args = as.list(model_gamma$estimate))+
  stat_function(fun = dnorm, color = 'blue', size = 0.8, 
                args = list(mean = mean(dataset$Duree), 
                            sd = sd(dataset$Duree)))+
  labs(x = 'Temps de déplacement (minutes)',
       y = '',
       subtitle = "modèles Gamma et gaussien")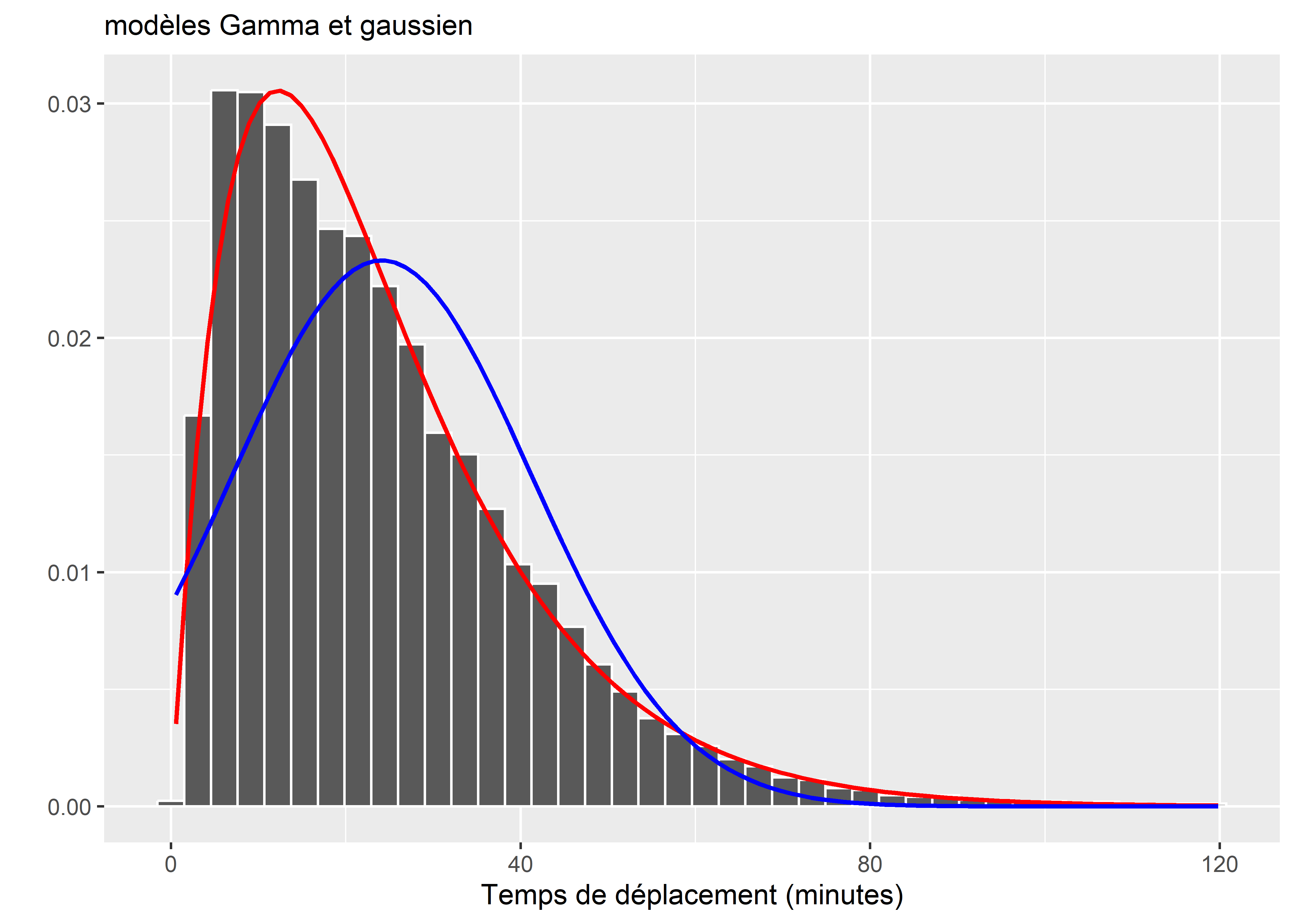

Figure 8.51: Distribution des temps de trajet diurne à Montréal

La figure 8.51 permet de constater l’asymétrie de la distribution des temps de trajet et qu’un modèle Gamma (ligne rouge) a plus de chance d’être adapté aux données qu’un modèle gaussien (ligne bleue).

Vérification des conditions d’application

Comme pour les modèles précédents, nous commençons par la vérification de l’absence de multicolinéarité.

## Calcul du VIF
vif(glm(Duree ~ Mode + Motif + HeureDep + LogDist +
          ArrondDep + MemeArrond + Jour,
        data = dataset,
        family = Gamma(link="log")))

##                GVIF Df GVIF^(1/(2*Df))
## Mode       2.103392  3        1.131931
## Motif      1.934997  3        1.116298
## HeureDep   1.791009 14        1.021032
## LogDist    2.665998  1        1.632789
## ArrondDep  1.439499 17        1.010772
## MemeArrond 2.151113  1        1.466667
## Jour       1.330091  6        1.024055

L’ensemble des valeurs de VIF sont inférieures à trois, indiquant donc l’absence de multicolinéarité excessive. Nous pouvons donc ajuster une première version du modèle (ici avec le package VGAM et la fonction vglm) et calculer les distances de Cook.

# Calcul du modèle avec VGAM
modele <- vglm(Duree ~ Mode + Motif + HeureDep + LogDist +
                 ArrondDep+ MemeArrond + Semaine,
               data = dataset,
               family=gamma2(lmu = "loglink"))
# Calcul des distances de Cook
hats <- hatvaluesvlm(modele)[,1]
res <- residuals(modele,type = "pearson")[,1]
disp <- modele@coefficients[[2]]**-1
nbparams <- modele@rank
cooksd <- (res/(1 - hats))^2 * hats/(disp * nbparams)
df <- data.frame(
  cook = cooksd,
  oid = 1:length(cooksd)
)
# Représentation des distances de Cook
ggplot(data = df)+
  geom_point(aes(x = oid, y = cook), size = 0.5, color = rgb(0.4,0.4,0.4,0.4)) + 
  geom_hline(yintercept = 0.003, color = "red") +
  labs(x = "", y = "distance de Cook")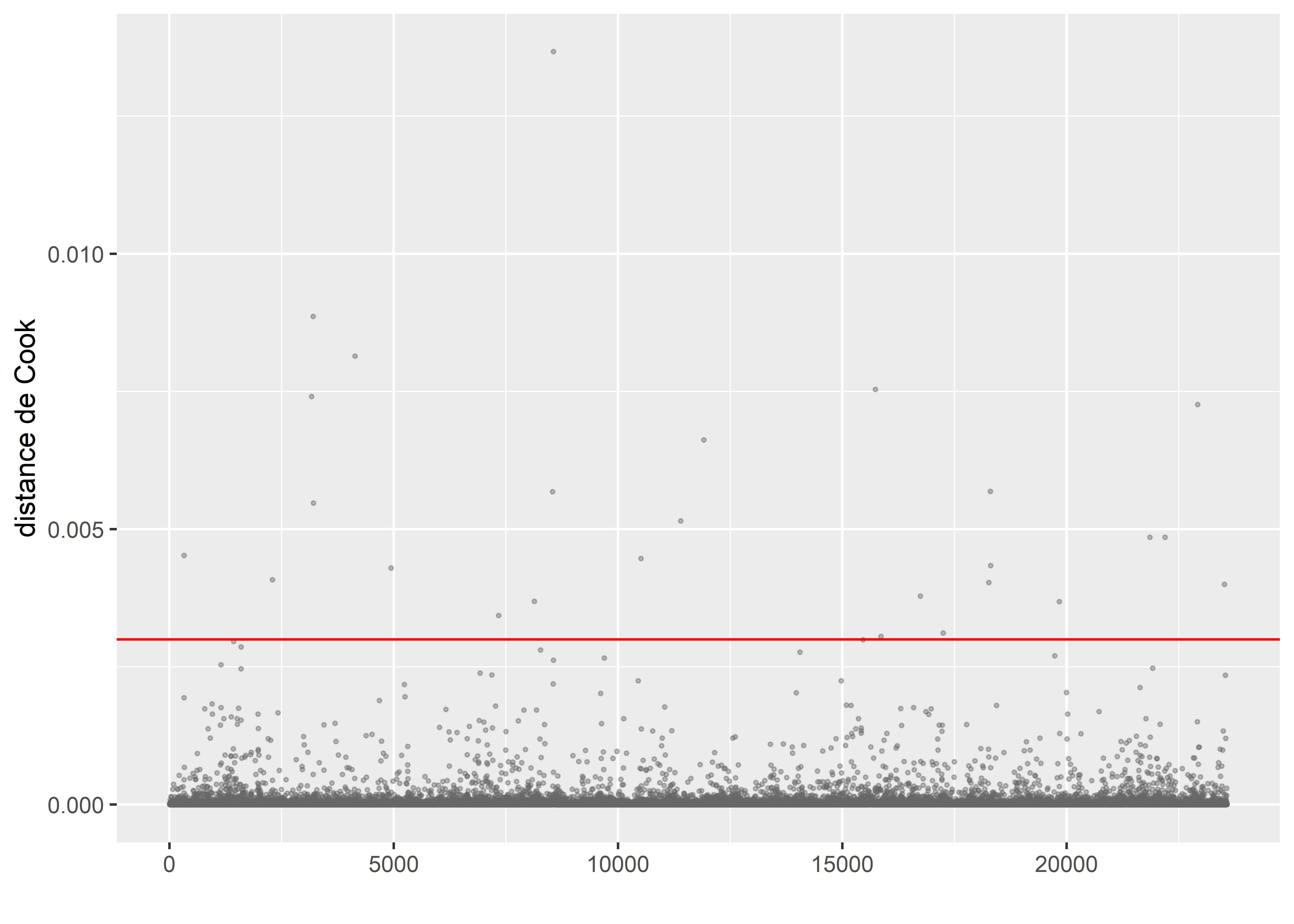

Figure 8.52: Distances de Cook pour le modèle Gamma

Puisque nous disposons d’un (très) grand nombre d’observations, nous pouvons nous permettre de retirer les quelques observations fortement influentes (distance de Cook > 0,003 dans notre cas) qui apparaissent dans la figure 8.52. Nous retirons ainsi 28 observations et réajustons le modèle.

# Retirer les valeurs influentes
dataset2 <- subset(dataset, cooksd<0.003)
# Calcul du modèle avec VGAM
modele <- vglm(Duree ~ Mode + Motif + HeureDep + LogDist +
                 ArrondDep+ MemeArrond + Semaine,
               data = dataset2,
               family=gamma2(lmu = "loglink"))

Nous constatons ainsi que dans la nouvelle version du modèle (figure 8.53), aucune valeur particulièrement influente ne semble être présente.

# Calcul des distances de Cook
hats <- hatvaluesvlm(modele)[,1]
res <- residuals(modele,type = "pearson")[,1]
disp <- modele@coefficients[[2]]**-1
nbparams <- modele@rank
cooksd <- (res/(1 - hats))^2 * hats/(disp * nbparams)
df <- data.frame(
  cook = cooksd,
  oid = 1:length(cooksd)
)
# Représentation des distances de Cook
ggplot(data = df)+
  geom_point(aes(x = oid, y = cook), size = 0.5, color = rgb(0.4,0.4,0.4,0.4)) +
  labs(x = "", y = "distance de Cook")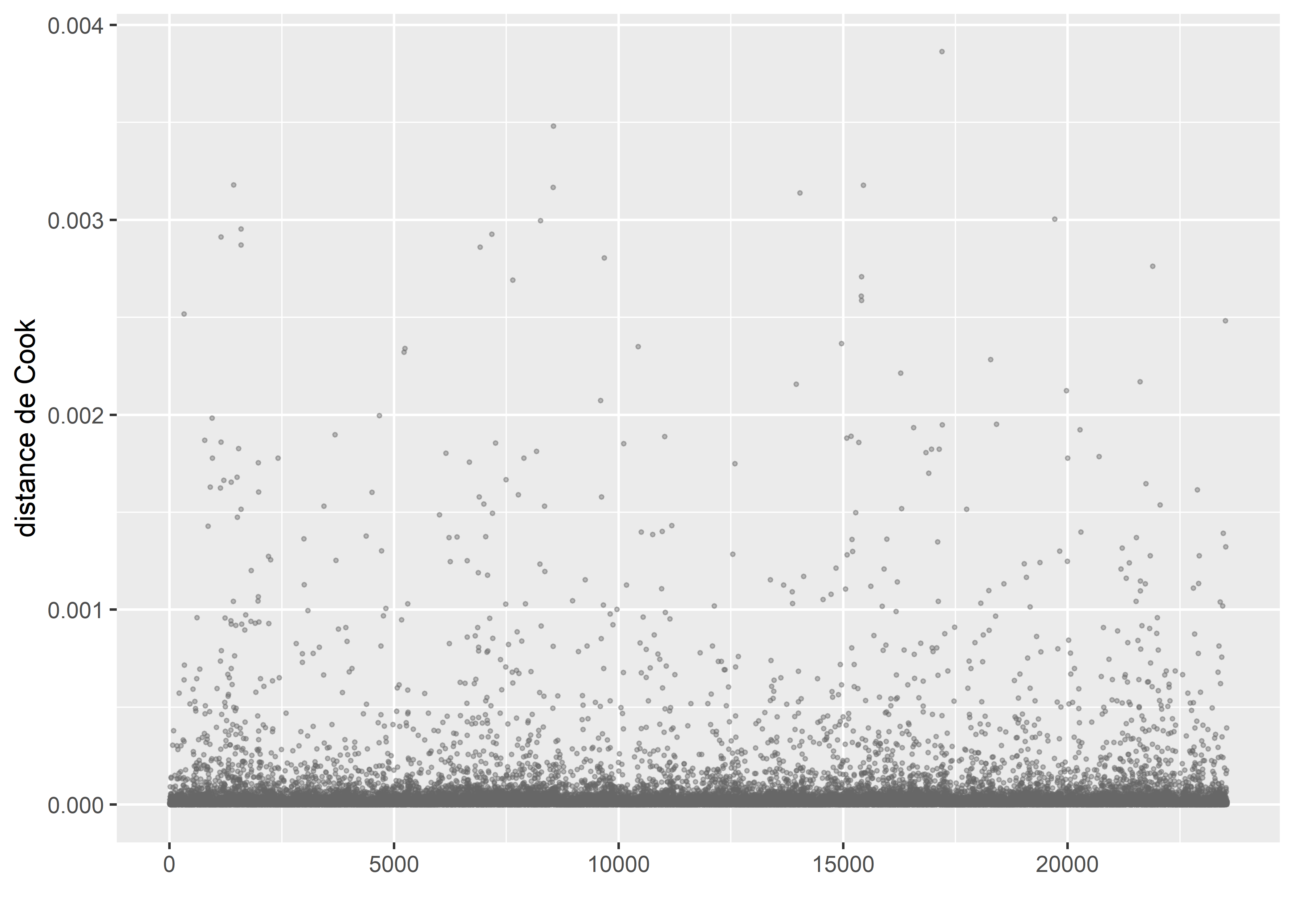

Figure 8.53: Distances de Cook pour le modèle Gamma (sans les observations fortement influentes)

# Extraction des prédictions du modèle (mu)
mus <- modele@fitted.values
# Extration du paramètre de forme
shape <- exp(modele@coefficients[[2]])
# Calcul des simulations
nsim <- 1000
cols <- lapply(1:length(mus),function(i){
  mu <- mus[[i]]
  sims <- rgamma(n = nsim,shape = shape, scale = mu/shape)
  return(sims)
})
mat_sims <- do.call(rbind, cols)
# Représentation graphique de 20 simulations
df2 <- reshape2::melt(mat_sims[,0:20])
ggplot() + 
  geom_histogram(aes(x = Duree, y = ..density..),
                 data = dataset, bins = 100, color = "black", fill = "white") + 
  geom_density(aes(x = value, y=..density.., group = Var2), data = df2, 
               fill = rgb(0,0,0,0), color = rgb(0.9,0.22,0.27,0.4), size = 1)+
  xlim(0,200)+
  labs(X="durée (minutes)", y="densité")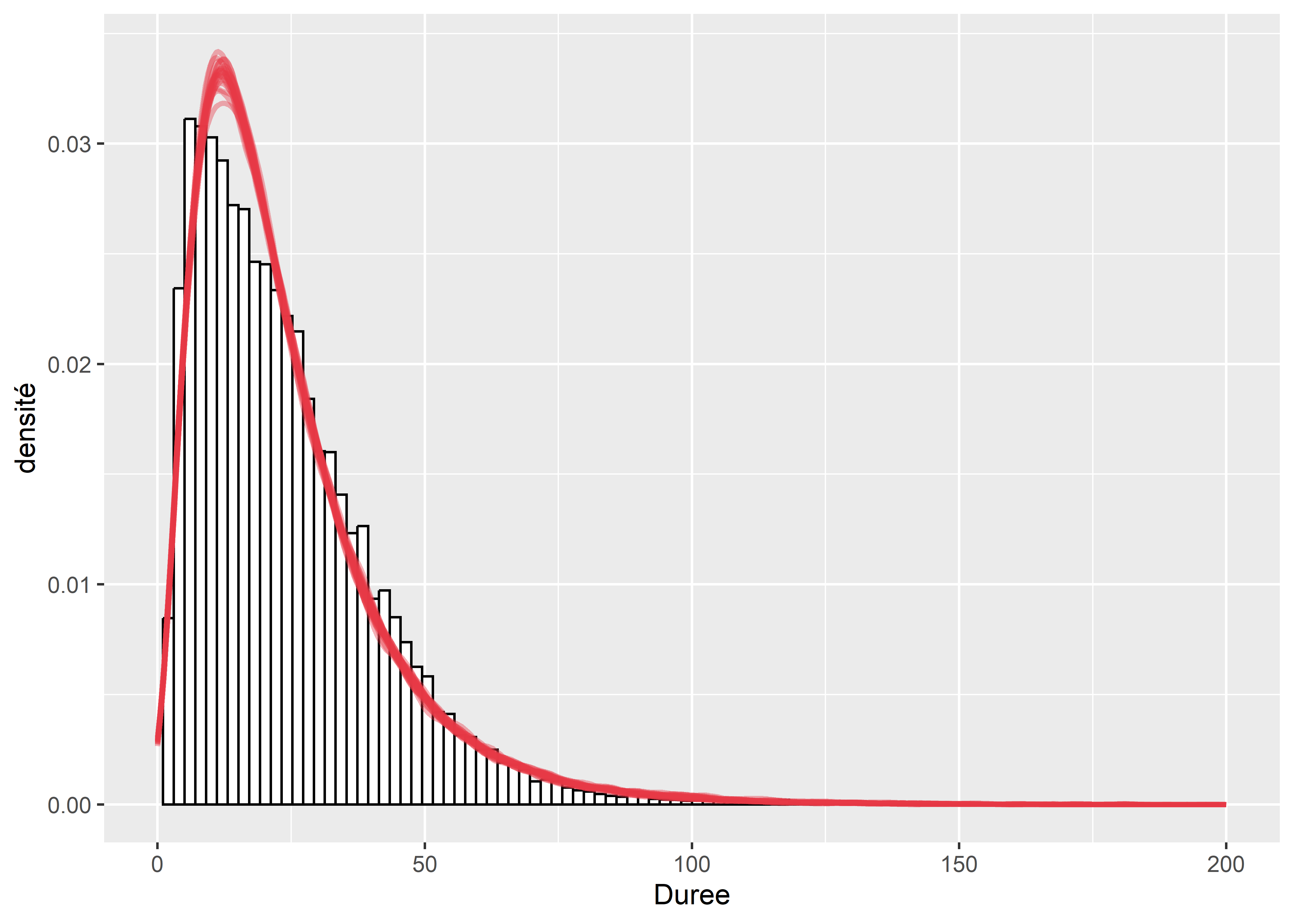

Figure 8.54: Comparaison de la distribution originale et de simulations issues du modèle Gamma

Avant de calculer les résidus simulés, nous comparons la distribution originale des données et des simulations issues du modèle. La figure 8.54 permet de constater que le modèle semble bien capturer l’essentiel de la forme de la variable Y originale. Nous notons un léger décalage entre la pointe des deux distributions, laissant penser que les valeurs prédites par le modèle tendent à être légèrement plus grandes que les valeurs réelles. Pour mieux appréhender ce constat, nous passons à l’analyse des résidus simulés.

# DHarma tests
sim_res <- createDHARMa(simulatedResponse = mat_sims, 
                            observedResponse = dataset2$Duree,
                            fittedPredictedResponse = modele@fitted.values[,1],
                            integerResponse = F)
ggplot() + 
  geom_histogram(aes(x = residuals(sim_res)), bins = 100, color = "white") + 
  labs(x = "résidus simulés",
        y = "effectifs")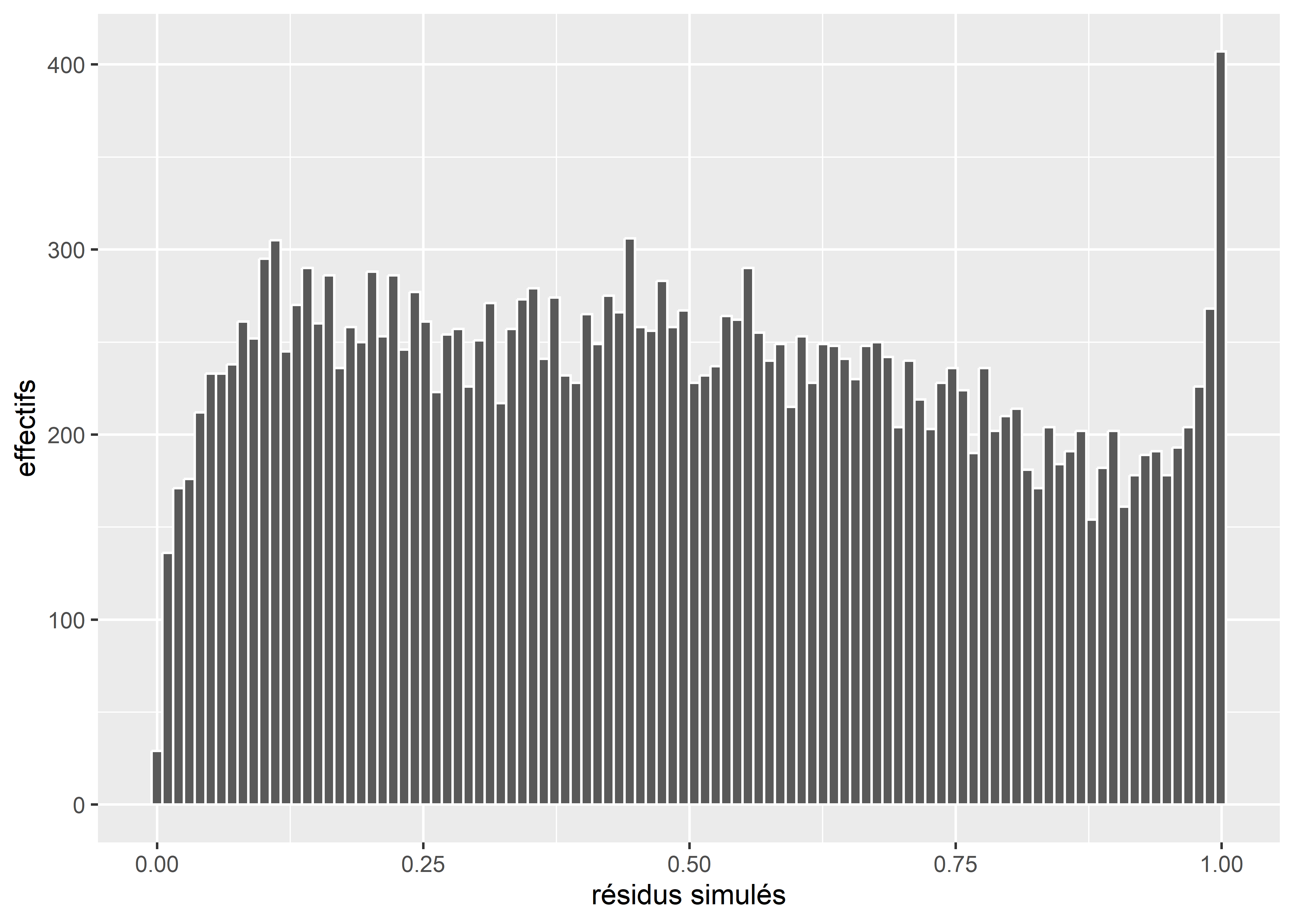

Figure 8.55: Distribution des résidus simulés du modèle Gamma

Nul besoin d’un test statistique pour constater que ces résidus (figure 8.55) ne suivent pas une distribution uniforme. Nous observons une nette surreprésentation de résidus à 1 et une nette sous-représentation de résidus à 0. Il y a donc de nombreuses observations dans notre modèle pour lesquelles les simulations sont systématiquement trop fortes et il n’y en a pas assez pour lesquelles les simulations seraient systématiquement trop faibles.

plot(sim_res)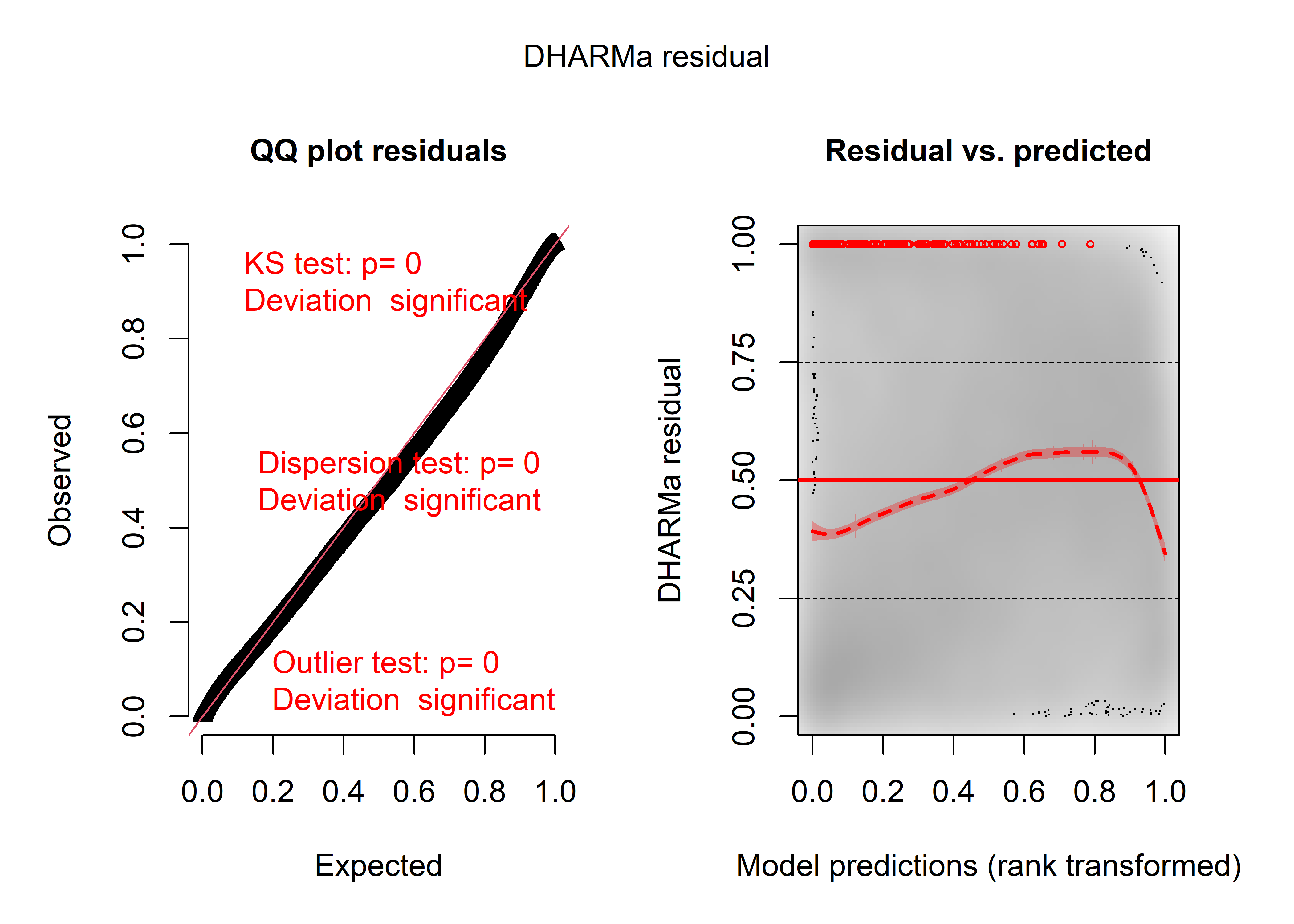

Figure 8.56: Diagnostic général des résidus simulés du modèle Gamma

La figure 8.56 indique que le modèle souffre à la fois d’un problème de dispersion (la relation espérance-variance n’est donc pas respectée) et est affecté par des valeurs aberrantes. Considérant que nous avons encore un très grand nombre d’observations, nous faisons le choix de retirer celles pour lesquelles la méthode des résidus simulés estime qu’elles sont des valeurs aberrantes dans au moins 1 % des simulations, soit environ 620 observations.

# Sélection des valeurs aberrantes au seuil 0.01
sim_outliers <- outliers(sim_res, 
                         lowerQuantile = 0.01,
                         upperQuantile = 0.99, 
                         return = "logical")
table(sim_outliers)

## sim_outliers
## FALSE  TRUE 
## 22908   638

# Retirer ces observations des données
dataset3 <- subset(dataset2, sim_outliers==FALSE)
# Réajuster le modèle
modele <- vglm(Duree ~ Mode + Motif + HeureDep + 
                 LogDist + ArrondDep + MemeArrond + Semaine,
               data = dataset3,
               model = T,
               family=gamma2)
modele2 <- vglm(Duree ~ Mode + Motif + HeureDep + ArrondDep + MemeArrond + Semaine,
               data = dataset3,
               model = T,
               family=gamma2)
# Extraction des prédictions du modèle (mu)
mus <- modele@fitted.values
# Extration du paramètre de forme
shape <- exp(modele@coefficients[[2]])
# Calcul des simulations
nsim <- 1000
cols <- lapply(1:length(mus),function(i){
  mu <- mus[[i]]
  sims <- rgamma(n = nsim,shape = shape, scale = mu/shape)
  return(sims)
})
mat_sims <- do.call(rbind, cols)
# Calcul des résidus simulés
sim_res <- createDHARMa(simulatedResponse = mat_sims, 
                            observedResponse = dataset3$Duree,
                            fittedPredictedResponse = modele@fitted.values[,1],
                            integerResponse = F)
plot(sim_res)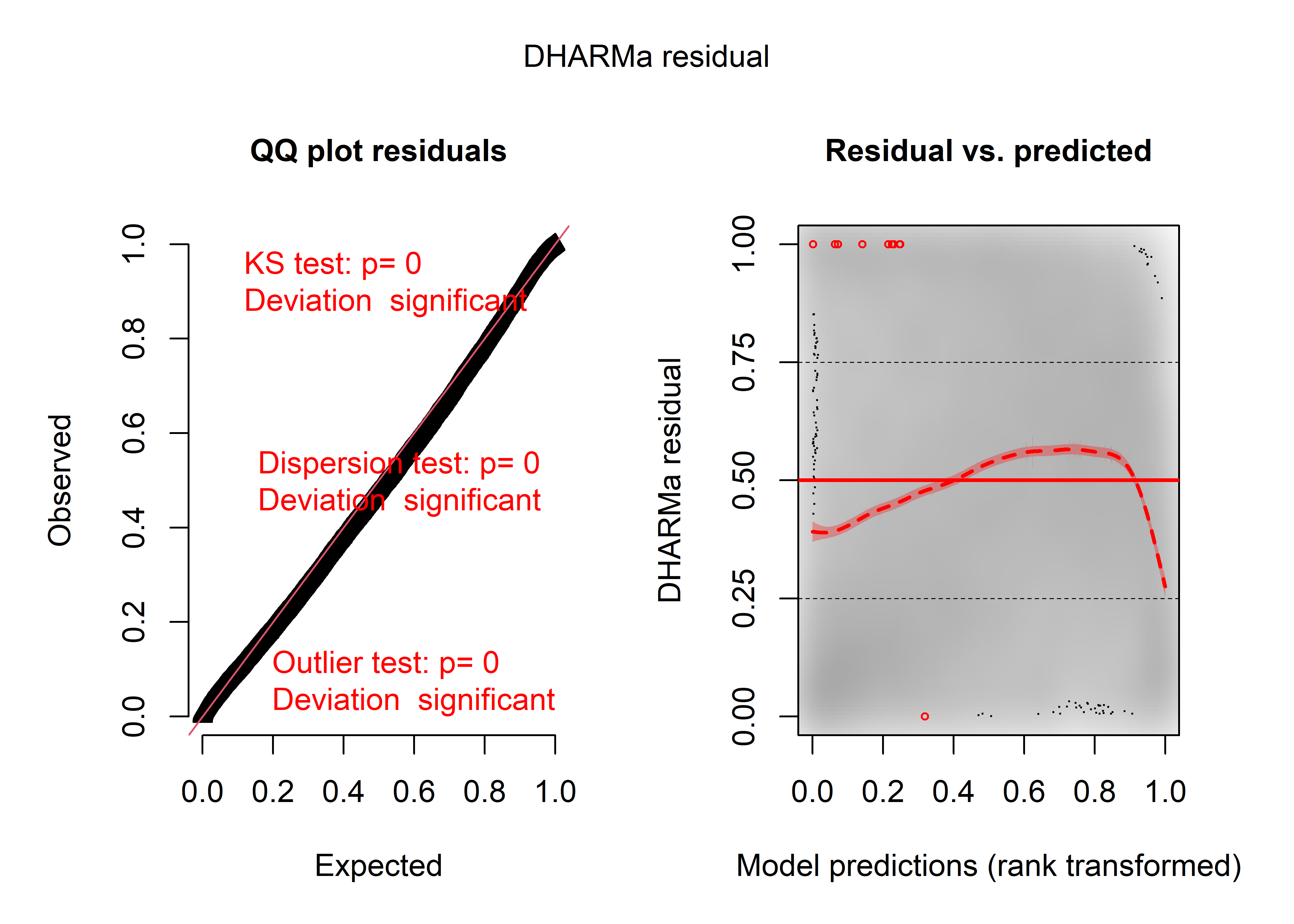

Figure 8.57: Diagnostic général des résidus simulés du modèle Gamma (après suppression d’environ 620 valeurs aberrantes)

La figure 8.57 indique que les résidus simulés ne suivent toujours pas une distribution uniforme et qu’il existe une relation prononcée (panneau de droite) entre les résidus et les valeurs prédites. Cette dernière laisse penser que des variables indépendantes importantes ont été omises dans le modèle, ce qui n’est pas surprenant compte tenu du fait que nous ne disposons d’aucune donnée socioéconomique sur les individus ayant réalisé les trajets. Nos données sont également potentiellement affectées par la présence de dépendance spatiale.

Nous pouvons comparer graphiquement la variance observée dans les données et la variance attendue par le modèle. La figure 8.58 montre clairement que la variance des données tend à être plus grande qu’attendue quand les temps de trajet sont courts, mais diminue trop vite quand les temps de trajet augmentent. D’autres distributions pourraient être envisagées pour ajuster notre modèle : Lognormal, Weibull, etc.

# Extraction des prédictions du modèle
mus <- predict(modele, type = "response")[,1]
# Création d'un DataFrame pour contenir la prédiction et les vraies valeurs
df1 <- data.frame(
  mus = mus,
  reals = dataset3$Duree
)
# Calcul de l'intervalle de confiance à 95 % selon la distribution Gamma
# et stockage dans un second DataFrame
seqa <- seq(10,120,10)
shape <- exp(modele@coefficients[[2]])
df2 <- data.frame(
  mus = seqa,
  lower = qgamma(p = 0.025, shape = shape, scale = seqa/shape),
  upper = qgamma(p = 0.975, shape = shape, scale = seqa/shape)
)
# Affichage des valeurs réelles et prédites (en rouge)
# et de leur variance selon le modèle (en noir)
ggplot() + 
  geom_point(data = df1, 
             mapping = aes(x = mus, y = reals),
             color =rgb(0.9,0.22,0.27,0.4), size = 0.5) + 
  geom_errorbar(data = df2,
                mapping = aes(x = mus, ymin = lower, ymax = upper),
                width = 0.2, color = rgb(0.4,0.4,0.4)) + 
  labs(x = 'valeurs prédites',
       y = "valeurs réelles")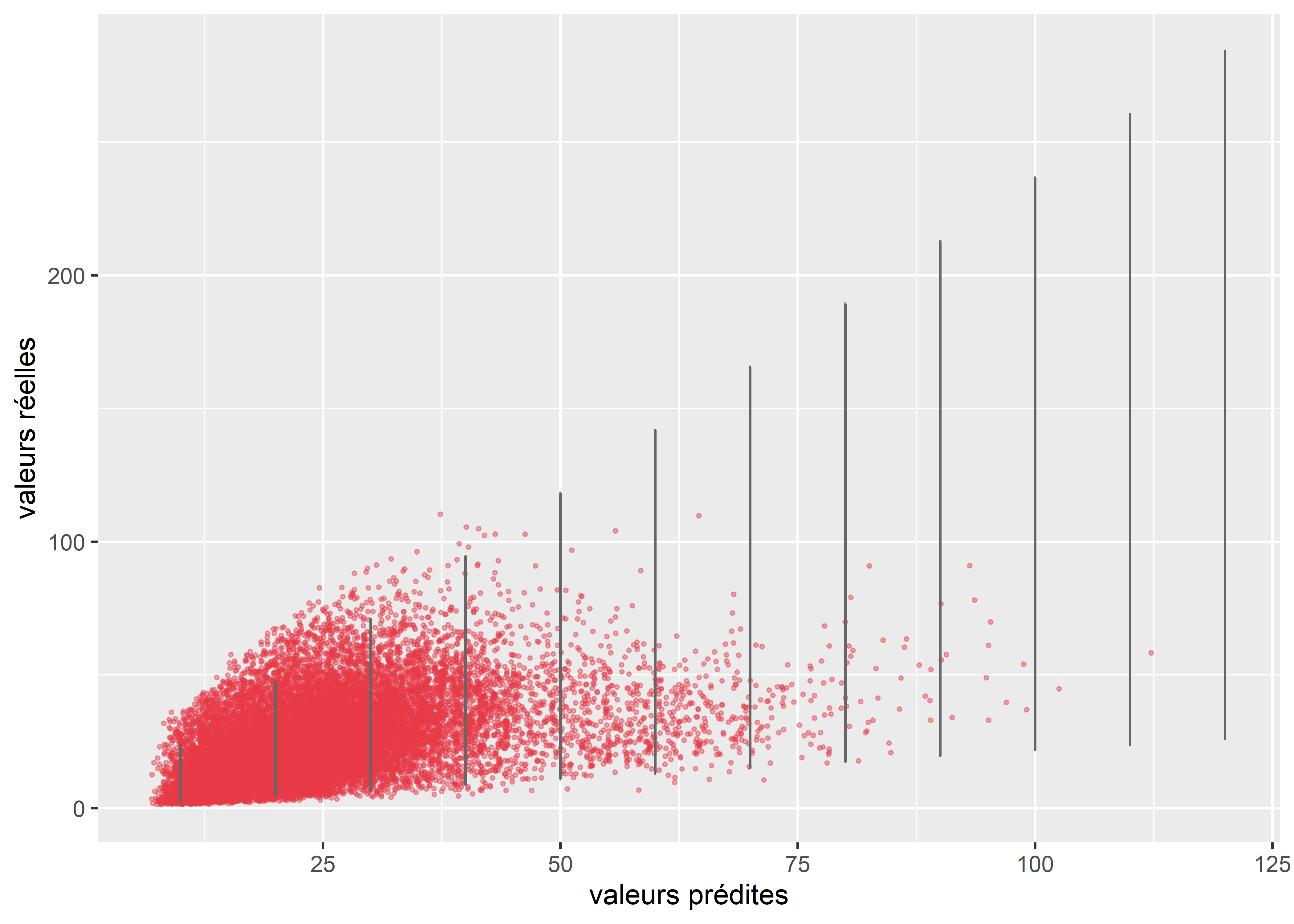

Figure 8.58: Comparaison de la variance attendue par le modèle et la variance observée dans les données pour le modèle Gamma

À ce stade, nous disposons de suffisamment d’éléments pour douter des résultats du modèle. Nous poursuivons tout de même notre analyse afin d’illustrer l’estimation de la qualité d’ajustement d’un tel modèle et son interprétation.

Analyse de la qualité d’ajustement

# Ajustement d'un modele nul
modele.null <- vglm(Duree ~1,
               data = dataset3,
               model = T,
               family=gamma2)
# Calcul des pseudos R2
rsqs(loglike.full = logLik(modele),
     loglike.null = logLik(modele.null),
     full.deviance = logLik(modele) * -2,
     null.deviance = logLik(modele.null) * -2,
     nb.params = modele2@rank,
     n = nrow(dataset3)
     )

## $`deviance expliquee`
## [1] 0.05082912
## 
## $`McFadden ajuste`
## [1] 0.05038095
## 
## $`Cox and Snell`
## [1] 0.3336696
## 
## $Nagelkerke
## [1] 0.3337831

# Calcul du RMSE
preds <- predict(modele, type="response")[,1]
sqrt(mean((preds - dataset3$Duree)**2))

## [1] 13.33416

Le modèle n’explique que 5 % de la déviance et obtient des valeurs de R² ajusté de McFadden, de Cox et Snell et de Nagelkerke de respectivement 0,05, 0,33 et 0,33. La moyenne de l’erreur quadratique est de seulement 13,4 indiquant que le modèle se trompe en moyenne de seulement 13,4 minutes. La capacité de prédiction du modèle est donc limitée sans être catastrophique.

Interprétation des résultats

Pour rappel, la fonction de lien dans notre modèle est la fonction log. Chaque coefficient représente donc l’effet de l’augmentation d’une unité des variables indépendantes sur le logarithme de l’espérance de notre variable dépendante. Si nous transformons nos coefficients avec la fonction exponentielle (exp), nous obtenons, pour chaque augmentation d’une unité des variables indépendantes, la multiplication de l’espérance de notre variable dépendante.

Puisque nos trajets peuvent provenir de nombreux arrondissements, nous proposons de représenter l’exponentiel de leurs coefficients avec un graphique. Nous pouvons d’ailleurs comparer les exponentiels des coefficients et les effets marginaux pour simplifier l’interprétation.

# Extraction des coefficient du modèle
coeffs <- modele@coefficients
# Calcul des interval de confiance des coefficients
conf <- confint(modele)
# Passage en exponentiel
df <- exp(cbind(coeffs, conf))
# Extraction des coefficients pour les arrondissements
dfArrond <- data.frame(df[grepl("ArrondDep",row.names(df), fixed = T),])
names(dfArrond) <- c("coeff", "lower","upper")
dfArrond$Arrondissement <- gsub("ArrondDep","",rownames(dfArrond),fixed = T)
# Graphique des exponentiels des coefficients
P1 <- ggplot(data = dfArrond) + 
  geom_vline(xintercept = 1, color = "red")+
  geom_errorbarh(aes(y = reorder(Arrondissement, coeff), xmin = upper, xmax = lower),
                 height = 0)+
  geom_point(aes(y = reorder(Arrondissement, coeff), x = coeff)) + 
  geom_text(aes(x = upper, y = reorder(Arrondissement, coeff),
                label = paste("coeff. : ",round(coeff,2),sep="")),
                size = 3, nudge_x = 0.07)+
  labs(x = "Coefficient multiplicateur (ref : Ahuntsic-Cartierville)",
       y = "",
       subtitle = "Exponentiels des coefficients du modèle")+
  xlim(c(0.75,1.46))
# Création d'un DataFrame fictif pour les effets marginaux
dfpred <- expand.grid(
  LogDist = mean(dataset3$LogDist),
  Motif = 'education',
  HeureDep = '7',
  MemeArrond = 'Different',
  ArrondDep = unique(dataset3$ArrondDep),
  Mode = 'pieton','velo','transport collectif',
  Semaine = 'lundi au vendredi'
)
# Utiliser le modèle pour effectuer des prédictions (échelle log)
lin_pred <- predict(modele,dfpred, se = T)
mu_lin_pred <- lin_pred$fitted.values[,1]
se_lin_pred <- lin_pred$se.fit[,1]
dfpred2 <- data.frame(
  pred = exp(mu_lin_pred),
  lower = exp(mu_lin_pred- 1.96*se_lin_pred),
  upper = exp(mu_lin_pred+ 1.96*se_lin_pred)
)
dfpred2 <- cbind(dfpred2, dfpred)
# Réaliser le graphique des effets marginaux
P2 <- ggplot(data = dfpred2) + 
  geom_col(aes(x = pred, y = ArrondDep)) + 
  geom_errorbarh(aes(xmin = lower, xmax = upper, y = ArrondDep)) + 
  labs(x = "Temps de déplacement prédit", y="",
       subtitle = "Prédiction du modèle")
ggarrange(P1,P2, ncol = 1, nrow = 2)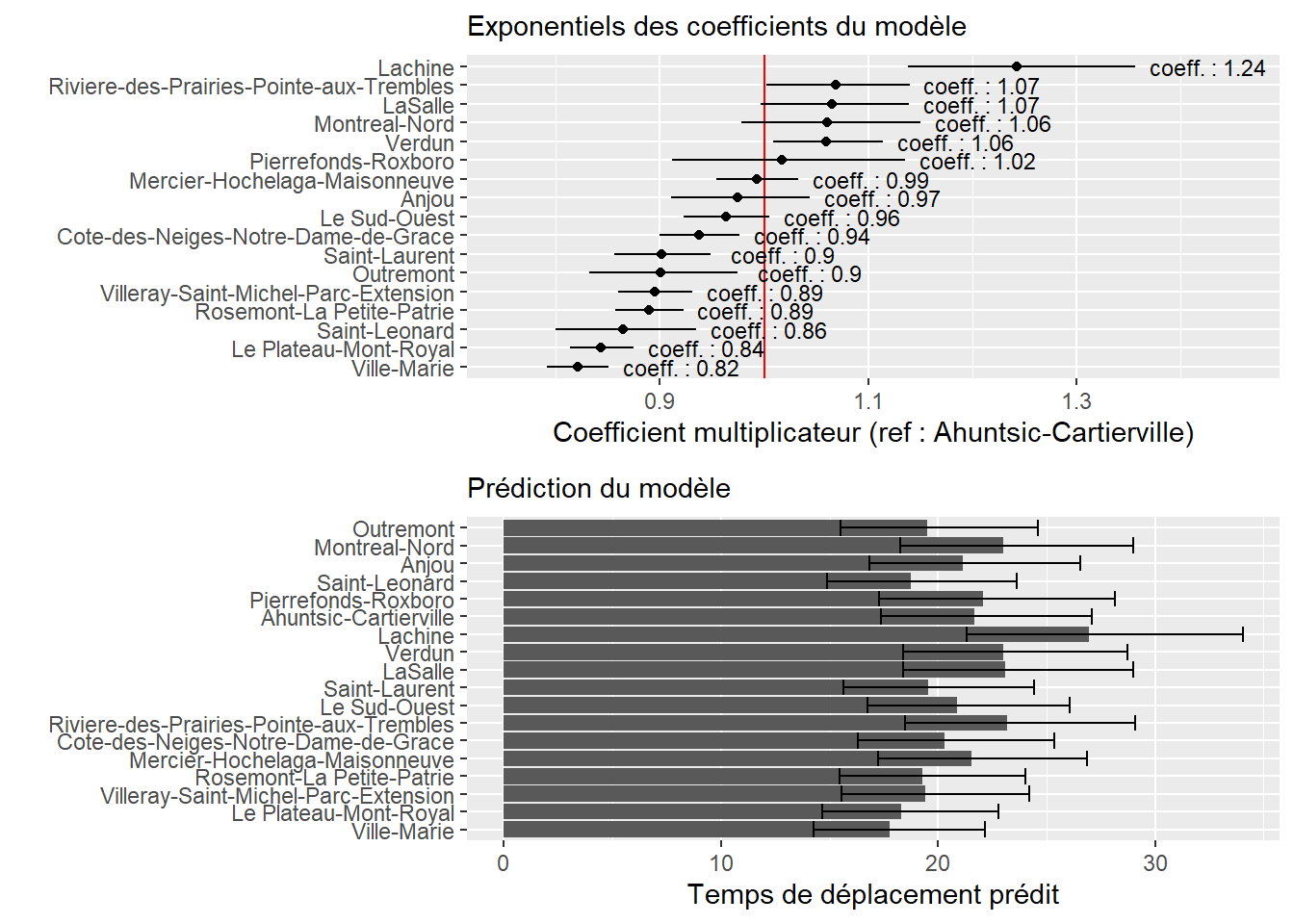

Figure 8.59: Effet de l’arrondissement de départ sur les temps de trajet à Montréal

La figure 8.59 permet de constater que les arrondissements Ville-Marie et Plateau-Mont-Royal se distinguent avec des trajets plus courts (environ 20 % plus courts en moyenne que les trajets partant d’Ahuntsic-Cartierville). À l’inverse, Lachine est de loin l’arrondissement avec les trajets les plus longs (25 % plus longs en moyenne que les trajets partant d’Ahuntsic-Cartierville).

Nous appliquons la même méthode de visualisation à la variable Heure de départ des trajets.

# Extraction des valeurs pour les heures de départ
dfHeures <- data.frame(df[grepl("HeureDep",row.names(df), fixed = T),])
names(dfHeures) <- c("coeff", "lower","upper")
dfHeures$Heure <- gsub("HeureDep","",rownames(dfHeures),fixed = T)
# Rajouter des 0 et des h pour de jolies légendes
dfHeures$Heure <- paste(dfHeures$Heure,"h",sep=" ")

# Afficher le graphique
ggplot(data = dfHeures) + 
  geom_hline(yintercept = 1, color = "red")+
  geom_errorbar(aes(x = Heure, ymin = upper, ymax = lower), width = 0)+
  geom_point(aes(x = Heure, y = coeff)) + 
  geom_text(aes(y = upper, x = Heure, label = round(coeff,2)), size = 3, nudge_y = 0.07)+
  labs(x = "Coefficient multiplicateur (ref : 7 h)",
       y = "")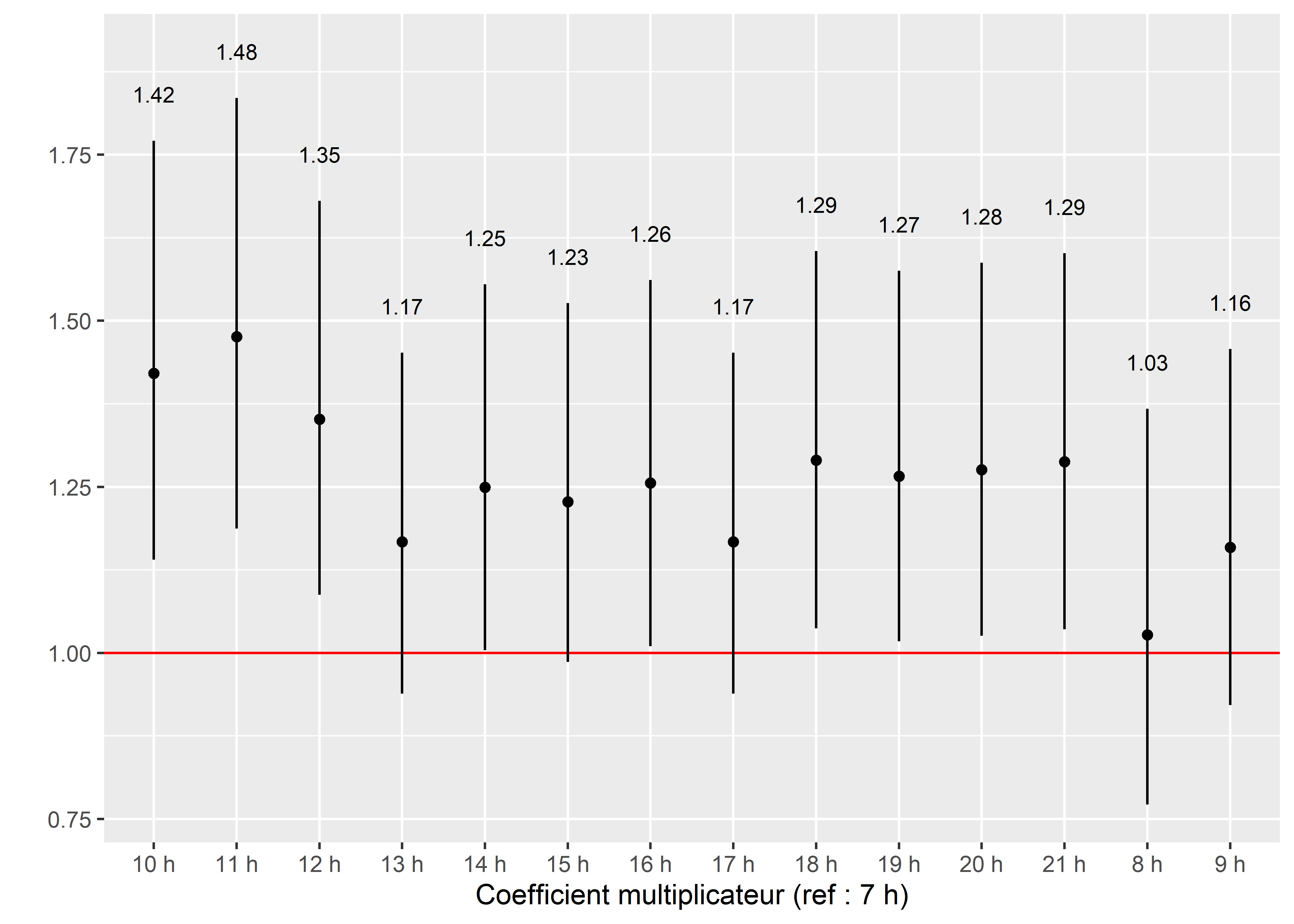

Figure 8.60: Effet de l’heure de départ sur les temps de trajet à Montréal

Nous pouvons ainsi observer, à la figure 8.60, que les trajets effectués à 10 h, 11 h et 12 h sont les plus longs de la journée, entre 30 et 40 % plus longs que ceux effectués à 7 h et 8 h qui constituent les trajets les plus courts.

Le reste des coefficients (ainsi que le paramètre de forme) sont affichés dans le tableau 8.35. Comparativement à un trajet effectué à pied, un trajet en transport en commun dure en moyenne 52 % plus longtemps (1,53 fois plus long), alors que les déplacements en véhicule individuel et en vélo sont respectivement 28 % et 23 % moins longs. Aucune différence n’est observable entre les déplacements effectués en semaine ou pendant la fin de semaine.

Tableau 8.35: Résultats pour le modèle GLM Gamma
Variable	Coeff.	Exp(Coeff.)	Val.p	IC 2,5 % exp(Coeff.)	IC 97,5 % exp(Coeff.)	Sign.
Constante	2,925	18,637	0,000	14,924	23,266	***
Mode
ref : pieton	–	–	–	–	–	–
transport collectif	0,424	1,527	0,000	1,489	1,567	***
vehicule individuel	-0,318	0,727	0,000	0,709	0,746	***
velo	-0,258	0,772	0,000	0,754	0,792	***
Motif
ref : education	–	–	–	–	–	–
loisir	-0,011	0,989	0,508	0,956	1,022
magasinage	-0,113	0,893	0,000	0,863	0,924	***
travail	-0,062	0,940	0,000	0,912	0,969	***
LogDist	0,333	1,395	0,000	1,381	1,411	***
MemeArrond
ref : Different	–	–	–	–	–	–
Meme	-0,038	0,963	0,001	0,943	0,984	***
Semaine
ref : lundi au vendredi	–	–	–	–	–	–
samedi et dimanche	0,002	1,002	0,852	0,981	1,023

shape	1,150	3,158	0,000	3,105	3,212	***

Les déplacements ayant comme motif le magasinage et le travail ont tendance à être en moyenne plus courts de 11 % et 6 % respectivement, comparativement aux déplacements effectués pour l’éducation ou le loisir (différence non significative entre loisir et éducation). Sans surprise, la distance entre le point de départ et d’arrivée du trajet (LogDist) affecte sa durée de façon positive. Considérant qu’il est difficile d’interpréter des log de kilomètre (dû à une transformation de la variable originale), nous représentons l’effet de cette variable avec la prédiction du modèle à la figure. Nous utilisons pour cela le cas suivant: déplacement à pied à 7 h en semaine, ayant pour motif éducation, dont le point de départ se situe dans l’arrondissement Ahuntsic et donc le point d’arrivée est dans un autre arrondissement. Seule la distance du trajet varie de 1 à 40 km. À titre de comparaison, nous représentons aussi, pour les mêmes conditions, le cas d’une personne à vélo (en vert) et d’une personne utilisant le transport en commun (en bleu). Les lignes en pointillés représentent les intervalles de confiance à 95 % des prédictions (figure 8.61).

# Création d'un DataFrame fictif pour la prédiction
dfpred <- expand.grid(
  Dist = seq(1,40, 0.5),
  Motif = 'education',
  HeureDep = '7',
  MemeArrond = 'Different',
  ArrondDep = 'Ahuntsic-Cartierville',
  Mode = c('pieton','velo','transport collectif'),
  Semaine = 'lundi au vendredi'
)
# Mise en log de la variable de distance
dfpred$LogDist <- log(dfpred$Dist)
# Calcul des prédictions et de leur erreur standard (échelle log)
lin_pred <- predict(modele,dfpred, se = T)
# Calcul des intervalles de confiance et mise en exponentielle des prédictions
dfpred$pred <- exp(lin_pred$fitted.values[,1])
dfpred$lower <- exp(lin_pred$fitted.values[,1] -1.96*lin_pred$se.fit[,1])
dfpred$upper <- exp(lin_pred$fitted.values[,1] +1.96*lin_pred$se.fit[,1])
# Ajoutons les accents pour le graphiques
dfpred$Mode <- as.character(dfpred$Mode)
dfpred$Mode2 <- case_when(dfpred$Mode == "pieton" ~ "piéton",
                         dfpred$Mode == "velo" ~ "vélo",
                         TRUE ~ dfpred$Mode)
# Affichage des résultats
ggplot(data = dfpred) + 
  geom_path(aes(x = Dist, y = lower, color = Mode2), linetype = "dashed")+
  geom_path(aes(x = Dist, y = upper, color = Mode2), linetype = "dashed")+
  geom_path(aes(x = Dist, y = pred, color = Mode2), size = 1) + 
  labs(y = "temps de trajet prédit (minutes)",
       x = "distance à vol d'oiseau (km)")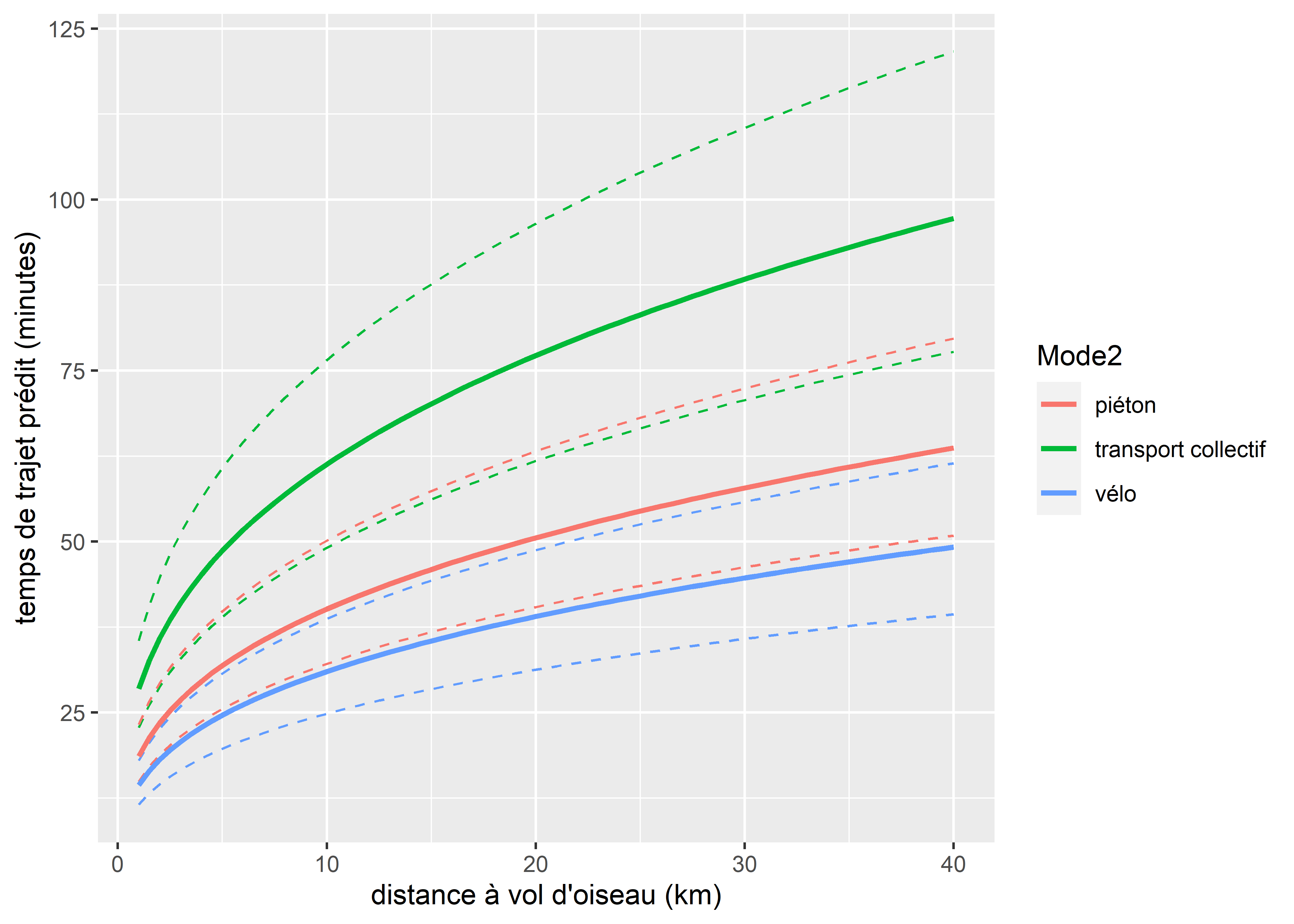

Figure 8.61: Effet de la distance à vol d’oiseau sur les temps de trajet à Montréal

8.4.4 Modèle GLM avec une distribution bêta

Pour rappel, la distribution bêta est une distribution définie sur l’intervalle \([0,1]\), elle est donc particulièrement utile pour décrire des proportions, des pourcentages ou des probabilités. Dans la section 2.4.3.16 sur les distributions, nous avons présenté la paramétrisation classique de la distribution avec les paramètres \(a\) et \(b\) étant tous les deux des paramètres de forme. Ces deux paramètres n’ont pas d’interprétation pratique, mais il est possible (comme pour la distribution Gamma) de reparamétrer la distribution bêta avec un paramètre de centralité (espérance) et de dispersion.

Notez également que si la distribution bêta autorise la présence de 0 et de 1, le modèle GLM utilisant cette distribution doit les exclure des valeurs possibles s’il utilise la fonction de lien logistique. En effet, cette fonction à la forme suivante :

\[\begin{equation} logit(x) = log(\frac{x}{1-x})\\ \tag{8.24} \end{equation}\]

Nous pouvons constater que si \(x = 1\), alors le dénominateur de la fraction est 0, or il est impossible de diviser par 0. Si \(x = 0\), alors nous obtenons \(log(0)\) ce qui est également impossible au plan mathématique.

Dans le cas de figure où des 0 et/ou des 1 sont présents dans les données, quatre options sont possibles pour contourner le problème :

Si les observations à 0 ou 1 sont très peu nombreuses, il est envisageable de les retirer des données.
Si la variable mesurée le permet, il est possible de remplacer les 0 et les 1 par des valeurs très proches (0,0001 et 0,9999 par exemple) sans dénaturer excessivement les données initiales.
Plutôt que d’utiliser une valeur arbitraire, Smithson et Verkuilen (2006) recommande de recalculer la variable \(Y \in [0;1]\) avec la formule (8.25);
Employer un modèle Hurdle à trois équations, la première prédisant la probabilité d’observer \(Y > 0\), la seconde, la probabilité d’observer \(Y = 1\) et la dernière prédisant les valeurs de Y pour \(0>Y>1\).

\[\begin{equation} Y' = \frac{Y(N-1)+s}{N} \tag{8.25} \end{equation}\]

Avec N le nombre d’observations, Y’ la variable Y transformée et s une constante. Plus cette dernière est élevée, plus la variable Y’ a des valeurs éloignée de 0 et 1. la valeur de 0,5 est recommandée par les auteurs.

Reparamétrisation de la distribution bêta

Pour une distribution bêta telle que définie par \(Y \sim Beta(a,b)\), l’espérance de cette distribution et sa variance sont données par :

\[\begin{equation} \begin{aligned} &E(Y) = \frac{a}{a+b} \\ &Var(Y) = \frac{a \times b}{(a+b)^2(a+b+1)}\\ \end{aligned} \tag{8.26} \end{equation}\]

Pour reparamétrer cette distribution, nous définissons un nouveau paramètre \(\phi\) (phi) tel que:

\[\begin{equation} \begin{aligned} &a = \phi * E(Y) \\ &b = \phi - a \\ &Var(Y) = \frac{E(Y) \times (1-E(Y))}{1+\phi} \end{aligned} \tag{8.27} \end{equation}\]

De cette manière, il est possible d’exprimer la distribution bêta en fonction de son espérance (sa valeur attendue, ce qui s’interprète approximativement comme une moyenne) et d’un paramètre \(\phi\) intervenant dans le calcul de sa variance. Vous noterez d’ailleurs que la variance de cette distribution dépend de sa moyenne, impliquant à nouveau une hétéroscédasticité intrinsèque.

Pour résumer, nous nous retrouvons donc avec un modèle qui prédit l’espérance d’une distribution bêta avec une fonction de lien logistique. La variance de cette distribution est fonction de cette moyenne et d’un second paramètre \(\phi\). Ces informations sont résumées dans la fiche d’identité du modèle (tableau 8.36).

Tableau 8.36: Carte d’identité du modèle bêta
Type de variable dépendante	Variable continue dans l’intervalle \(]0,1[\)
Distribution utilisée	Student
Formulation	\(Y \sim Beta(\mu,\phi)\) \(g(\mu) = \beta_0 + \beta X\) \(g(x) = log(\frac{x}{1-x})\)
Fonction de lien	log
Paramètre modélisé	\(\mu\)
Paramètres à estimer	\(\beta_0\), \(\beta\), et \(\phi\)
Conditions d’application	\(Variance = \frac{\mu \times (1-\mu)}{1+\phi}\)

8.4.4.1 Conditions d’application

Comme pour un modèle Gamma, la seule condition d’application spécifique à un modèle avec distribution bêta est que la variance des résidus suit la forme attendue par la distribution bêta.

8.4.4.2 Interprétation des coefficients

Puisque le modèle utilise la fonction de lien logistique, les exponentiels des coefficients \(\beta\) du modèle peuvent être interprétés comme des rapports de cotes (voir la section 8.2.1 sur le modèle GLM binomial). Admettons ainsi que nous avons obtenu pour une variable indépendante \(X_1\) le coefficient \(\beta_1\) de 0,12. Puisque le coefficient est positif, cela signifie qu’une augmentation de \(X_1\) conduit à une augmentation de l’espérance de Y. L’exponentiel de 0,12 est 1,13, ce qui signifie qu’une augmentation d’une unité de \(X_1\) multiplie par 1,13 (augmente de 13 %) les chances d’une augmentation de Y. Pour ce type de modèle, il est particulièrement important de calculer ses prédictions afin d’en faciliter l’interprétation.

8.4.4.3 Exemple appliqué dans R

Afin de présenter le modèle GLM avec une distribution bêta, nous utilisons un jeu de données que nous avons construit pour l’île de Montréal. Nous nous intéressons à la question des îlots de chaleur urbains au niveau des aires de diffusion (AD – entités spatiales du recensement canadien comprenant entre 400 et 700 habitants). Pour cela, nous avons calculé dans chaque AD le pourcentage de sa surface classifiée comme îlot de chaleur dans la carte des îlots de chaleur/fraicheur réalisée par l’INSPQ et le CERFO.

La question que nous nous posons est la suivante : les populations vulnérables socioéconomiquement et/ou physiologiquement sont-elles systématiquement plus exposées à la nuisance que représentent les îlots de chaleur? Cette question se rattache donc au champ de la recherche sur la justice environnementale et plus spécifiquement sur sa dimension spatiale (à savoir l’équité environnementale, à distinguer des dimensions procédurale et de reconnaissance). Plusieurs études se sont d’ailleurs déjà penchées sur la question des îlots de chaleur abordée sous l’angle de l’équité environnementale (Harlan et al. 2007; Sanchez et Reames 2019; Huang, Zhou et Cadenasso 2011). Nous modélisons donc pour chaque AD (n = 3 158) de l’île de Montréal la proportion de sa surface couverte par des îlots de chaleur. Nos variables indépendantes sont divisées en deux catégories : variables environnementales et variables socio-économiques. Les premières sont des variables de contrôle, il s’agit de la densité de végétation dans l’AD (ajoutée avec une polynomiale d’ordre deux) et de l’arrondissement dans lequel elle se situe. Ces deux paramètres affectent directement les chances d’observer des îlots de chaleur, mais nous souhaitons isoler leurs effets (toutes choses étant égales par ailleurs) de ceux des variables socio-économiques. Ces dernières ont pour objectif de cibler les populations vulnérables sur le plan physiologique (personnes âgées et enfants de moins de 14 ans) ou socio-économique (minorités visibles et faible revenu). L’ensemble de ces variables sont présentées dans le tableau 8.37. Notez que, puisque le modèle avec distribution bêta ne peut pas prendre en compte des valeurs exactes de 1 ou 0, nous les avons remplacées respectivement par 0,99 et 0,01. Cette légère modification n’altère que marginalement les données, surtout si nous considérons qu’elles sont agrégées au niveau des AD et proviennent originalement d’imagerie satellitaire.

Tableau 8.37: Variables indépendantes utilisées dans le modèle bêta
Nom de la variable	Signification	Type de variable	Mesure
A65PlusPct	Population de 65 ans et plus	Variable continue	Pourcentage de la population ayant 65 ans et plus
A014Pct	Population de 14 ans et moins	Variable continue	Pourcentage de la population ayant 14 ans et moins
PopFRPct	Population à faible revenu	Variable continue	Pourcentage de la population à faible revenu
PopMVPct	Minorités visibles	Variable continue	Pourcentage de la population faisant partie des minorités visibles
VegPct	Végétation	Variable continue	Pourcentage de la surface de l’AD couverte par de la végétation
Arrond	Arrondissements	Variable continue	Arrondissement de l’Île de Montréal

Vérification des conditions d’application

Sans surprise, nous commençons par charger nos données et nous nous assurons de l’absence de multicolinéarité excessive entre nos variables indépendantes.

## Chargement des données
dataset <- read.csv("data/glm/data_chaleur.csv",fileEncoding = "utf8")
## Calcul des valeurs de vif
vif(glm(hot ~
          A65Pct + A014Pct + PopFRPct + PopMVPct +
          poly(prt_veg, degree = 2)  + Arrond,
        data = dataset))

##                               GVIF Df GVIF^(1/(2*Df))
## A65Pct                    1.609917  1        1.268825
## A014Pct                   2.206072  1        1.485285
## PopFRPct                  2.162036  1        1.470386
## PopMVPct                  2.370269  1        1.539568
## poly(prt_veg, degree = 2) 2.619552  2        1.272204
## Arrond                    7.899208 32        1.032820

La seule variable semblant poser un problème de multicolinéarité est la variable Arrond. Cependant, du fait de sa nature multinomiale, elle regroupe en réalité 32 coefficients (voir la colonne Df). Il faut donc utiliser la règle habituelle de 5 sur le carré de la troisième colonne (GVIF^(1/(2*Df))) du tableau (Fox et Monette 1992), soit 1,032820^2 = 1,066717, ce qui est bien inférieur à la limite de 5. Nous n’avons donc pas de problème de multicolinéarité excessive. Nous pouvons passer au calcul des distances de Cook. Pour ajuster notre modèle, nous utilisons le package mgcv et la fonction gam avec le paramètre family = betar(link = "logit").

# Ajustement d'une première version du modèle
modele <- gam(hot ~
                A65Pct + A014Pct + PopFRPct + PopMVPct +
                poly(prt_veg, degree=2) + Arrond,
              data = dataset, family = betar(link = "logit"))
# Calcul des distances de Cook
df <- data.frame(
  cooksd = cooks.distance(modele),
  oid = 1:nrow(dataset)
)
# Affichage des distances de Cook
ggplot(data = df)+
  geom_point(aes(x = oid, y = cooksd),
             color = rgb(0.4,0.4,0.4,0.4), size = 0.5)+
  labs(x = "", y = "Distance de Cook")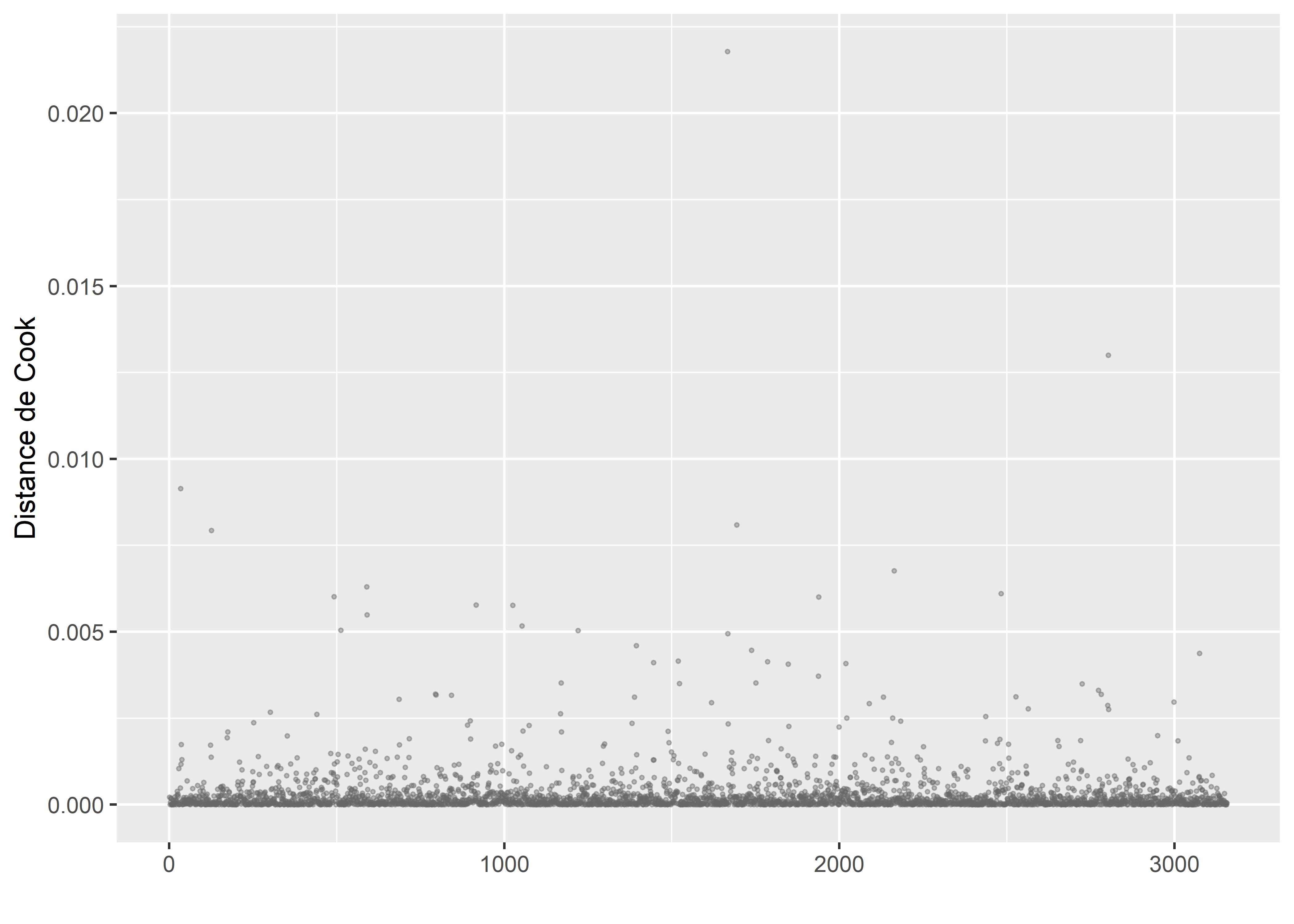

Figure 8.62: Distances de Cook pour le modèle GLM bêta

Nous pouvons observer à la figure 8.62 que seulement deux observations se distinguent très nettement des autres. Nous les isolons donc dans un premier temps.

cas_etranges <- subset(dataset, df$cooksd >= 0.01)
print(cas_etranges[,23:ncol(cas_etranges)])

##      A014Pct A65Pct PopFRPct PopMVPct      Km2    HabKm2 Shape_Leng Shape_Area   prt_hot  prt_veg
## 1666   11.78  26.77     6.38    11.65 6.458460   72.3083  21153.055  6458456.6  1.824483 90.11691
## 2803   15.54  31.07    24.17    52.17 0.134013 5283.0879   1651.471   134012.5 40.117994 60.15745
##      dist_cntr     Arrond  hot
## 1666 29.181345 Senneville 0.02
## 2803  4.178823  Westmount 0.40

Ces deux observations n’ont pas de points communs marqués, et ne semblent pas avoir de valeurs particulièrement fortes sur les différentes variables indépendantes ou la variable dépendante. Nous décidons donc de les supprimer et de recalculer les distances de Cook.

# Suppression des deux observations très influentes
dataset2 <- subset(dataset, df$cooksd < 0.01)
modele2 <- gam(hot ~
                A65Pct + A014Pct + PopFRPct + PopMVPct +
                I(prt_veg**2) + prt_veg + Arrond,
              data = dataset2, family = betar(link = "logit"), methode = "REML")
# Calcul des distances de Cook
df2 <- data.frame(
  cooksd = cooks.distance(modele2),
  oid = 1:nrow(dataset2)
)
# Affichage des distances de Cook
ggplot(data = df2)+
  geom_point(aes(x = oid, y = cooksd),
             color = rgb(0.4,0.4,0.4,0.4), size = 0.5)+
  labs(x = "", y = "Distance de Cook")

Figure 8.63: Distances de Cook pour le modèle GLM bêta (suppression de deux observations influentes)

Après réajustement (figure 8.63) nous constatons à nouveau qu’une observation est extrêmement éloignée des autres. Nous la retirons également, car cette différence est si forte qu’elle risque de polluer le modèle.

# Suppression de l'observation très étonnante
dataset3 <- subset(dataset2, df2$cooksd<max(df2$cooksd))
# Réajustement du modèle
modele3 <- gam(hot ~
                A65Pct + A014Pct + PopFRPct + PopMVPct +
                I(prt_veg**2) + prt_veg + Arrond,
              data = dataset3, family = betar(link = "logit"), methode = "REML")
# Calcul des distances de Cook
df3 <- data.frame(
  cooksd = cooks.distance(modele3),
  oid = 1:nrow(dataset3)
)
# Affichage des distances de Cook
ggplot(data = df3)+
  geom_point(aes(x = oid, y = cooksd),
             color = rgb(0.4,0.4,0.4,0.4), size = 0.5)+
  labs(x = "", y = "Distance de Cook")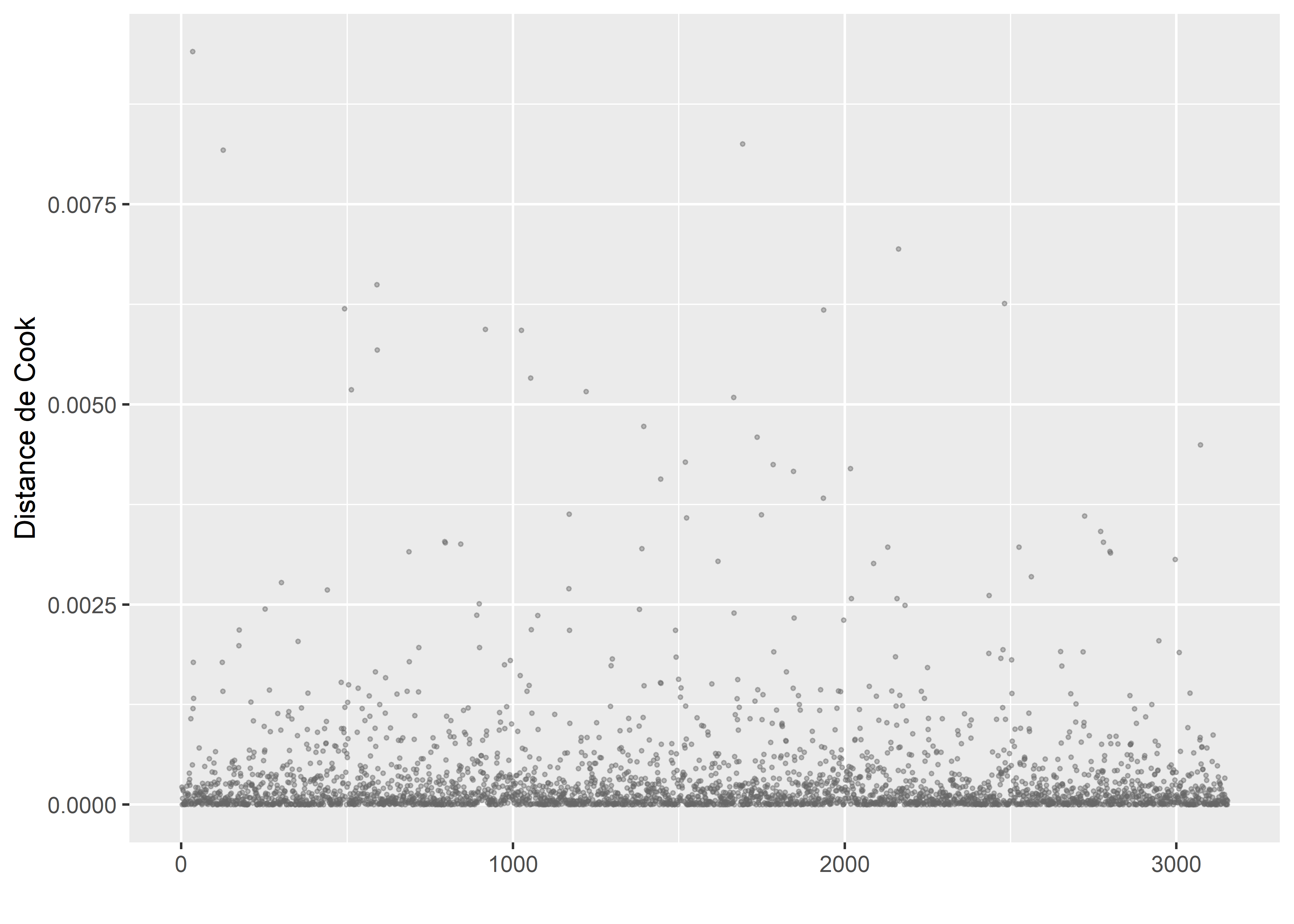

Figure 8.64: Distances de Cook pour le modèle GLM bêta (suppression de trois observations influentes)

Tout semble aller pour le mieux après ce second passage (figure 8.64). Si nous avions continué à observer des valeurs aussi influentes, nous aurions dû commencer à sérieusement questionner nos données ou notre modèle. La prochaine étape du diagnostic est donc l’analyse des résidus simulés.

# Extraction de phi
modele3$family$family

## [1] "Beta regression(14.612)"

phi <- 14.612
# Réalisation des simulations
nsim <- 1000
mus <- modele3$fitted.values
cols <- lapply(1:length(mus),function(i){
  mu <- mus[[i]]
  p <- mu * phi
  q <- (1-mu)*phi
  sims <- rbeta(n = nsim,shape1 = p, shape2 = q)
  return(sims)
})
mat_sims <- do.call(rbind, cols)
# Calcul des résidus simulés
sim_res <- createDHARMa(simulatedResponse = mat_sims,
                           observedResponse = dataset3$hot,
                           fittedPredictedResponse = modele3$fitted.values,
                           integerResponse = F)
plot(sim_res)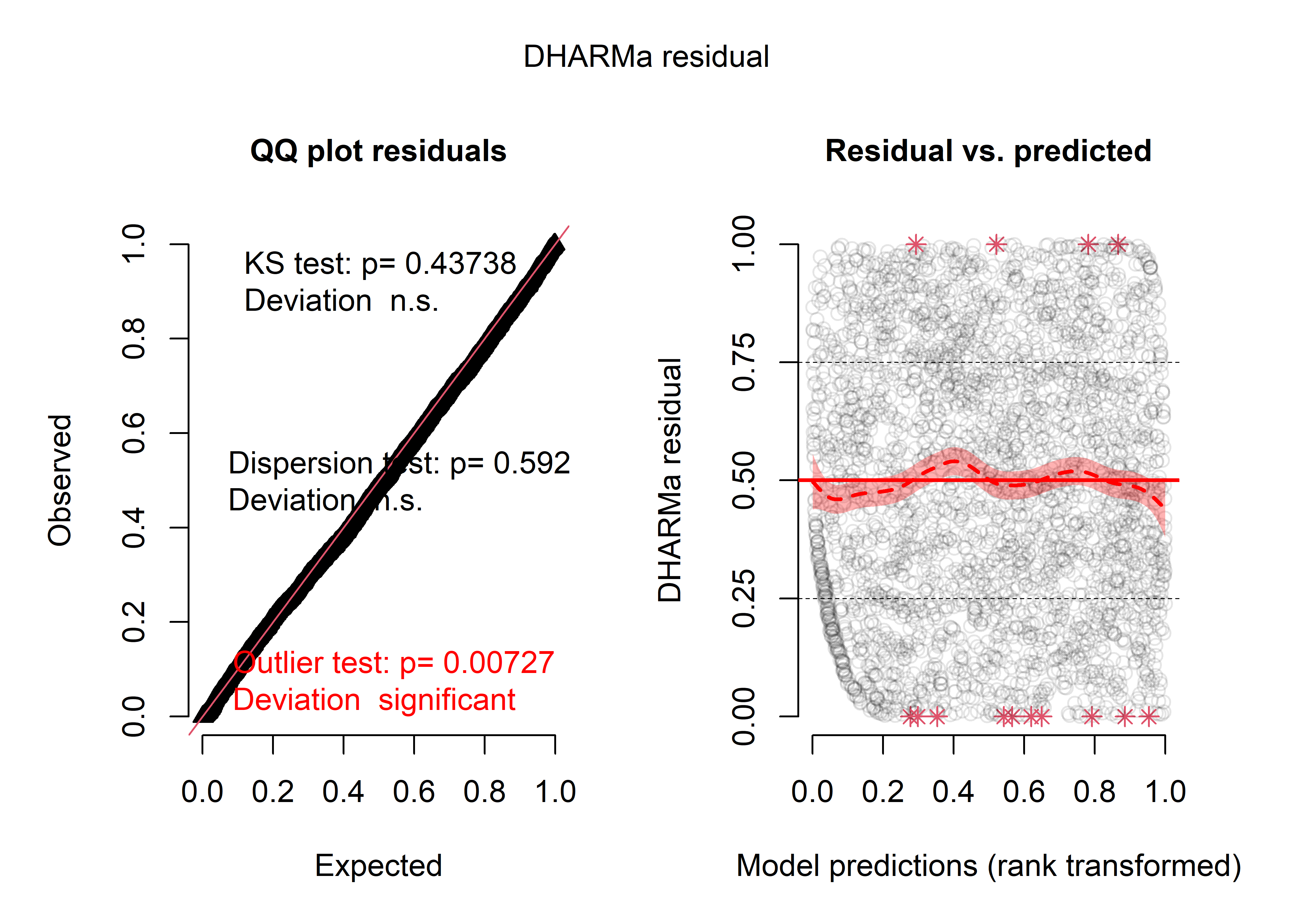

Figure 8.65: Diagnostic général des résidus simulés du modèle bêta

La figure 8.65 indique que les résidus suivent bien une distribution uniforme. Le test des valeurs aberrantes n’est pas significatif au seuil de 0,01 (nous retenons ce seuil considérant le grand nombre de simulations et d’observations de notre jeu de données), nous décidons donc de ne pas supprimer davantage d’observations. Le panneau de droite indique une relation non linéaire instable, mais essentiellement centrée sur la ligne droite attendue. Pour plus de détails, nous calculons ces résidus simulés avec chacune des variables indépendantes.

# Préparons un plot multiple
par(mfrow=c(2,3))
vars <- c("A65Pct", "A014Pct", "PopFRPct", "PopMVPct", "prt_veg")
for(v in vars){
  plotResiduals(sim_res, dataset3[[v]], main = "", xlab = v)
}
plotResiduals(sim_res, dataset3[["prt_veg"]]**2, xlab = "prt_veg^2", main = "")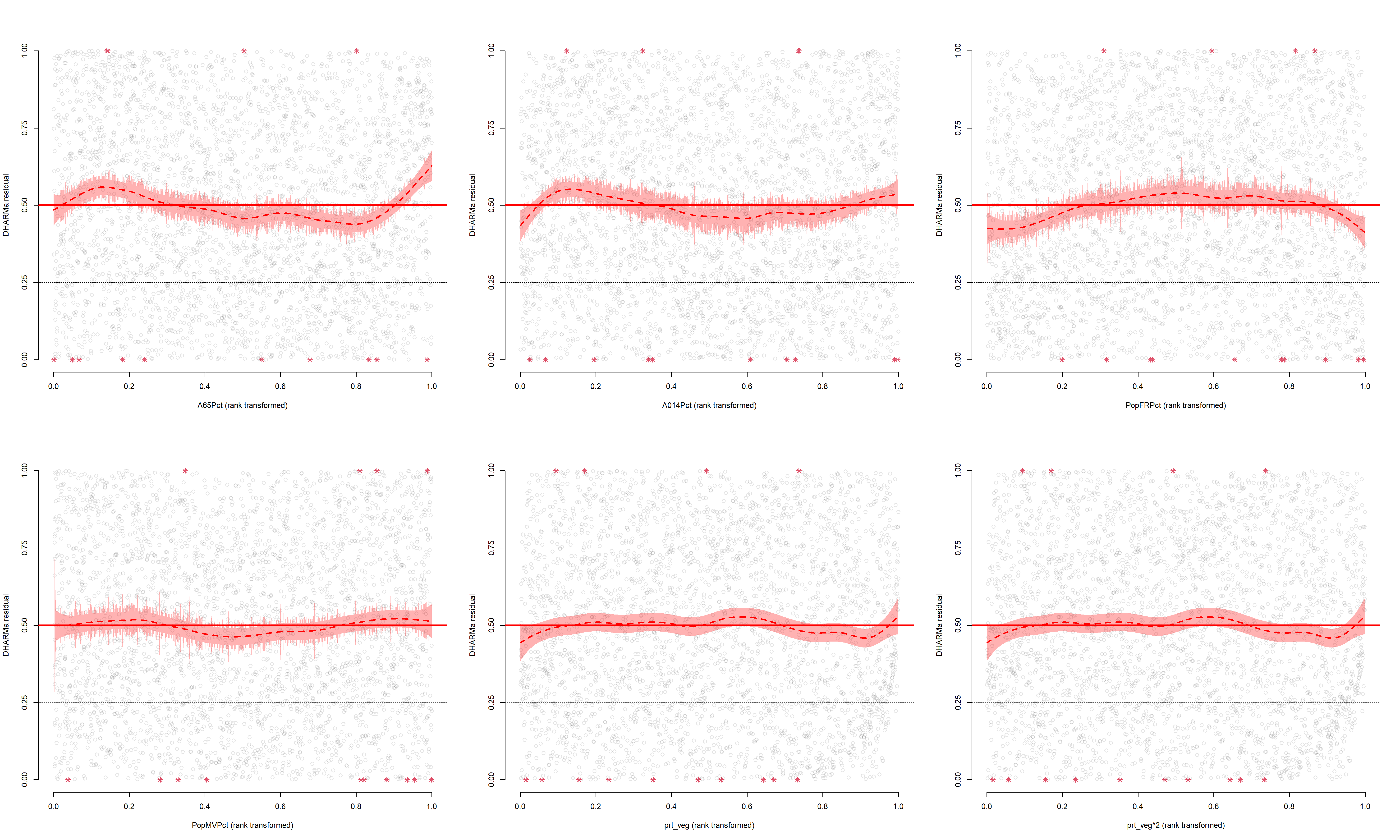

Figure 8.66: Relation entre chaque variable indépendante et les résidus simulés du modèle bêta

La figure 8.66 indique des relations marginales et négligeables entre nos variables indépendantes et nos résidus simulés. Concernant la variable Arrond (figure 8.67), nous observons une situation plus particulière. Pour quelques arrondissements, les résidus simulés sont nettement plus forts ou plus faibles. Notre hypothèse est que cet effet est provoqué par l’introduction de cette variable dans notre modèle comme un effet fixe alors que sa nature devrait nous inciter à l’introduire comme un effet aléatoire. Nous n’avons pas encore présenté ces concepts ici, mais nous le ferons dans le chapitre 9. En attendant, nous conservons le modèle tel quel et passons à l’analyse de sa qualité d’ajustement.

df <- data.frame(
  resid = residuals(sim_res),
  Arrond = dataset3$Arrond
)
ggplot(data = df) + 
  geom_boxplot(aes(x = Arrond, y = resid))+
  theme(axis.text.x = element_blank(),
        axis.ticks.x = element_blank()
        )+
  labs(x = "Arrondissements", y = "Résidus simulés")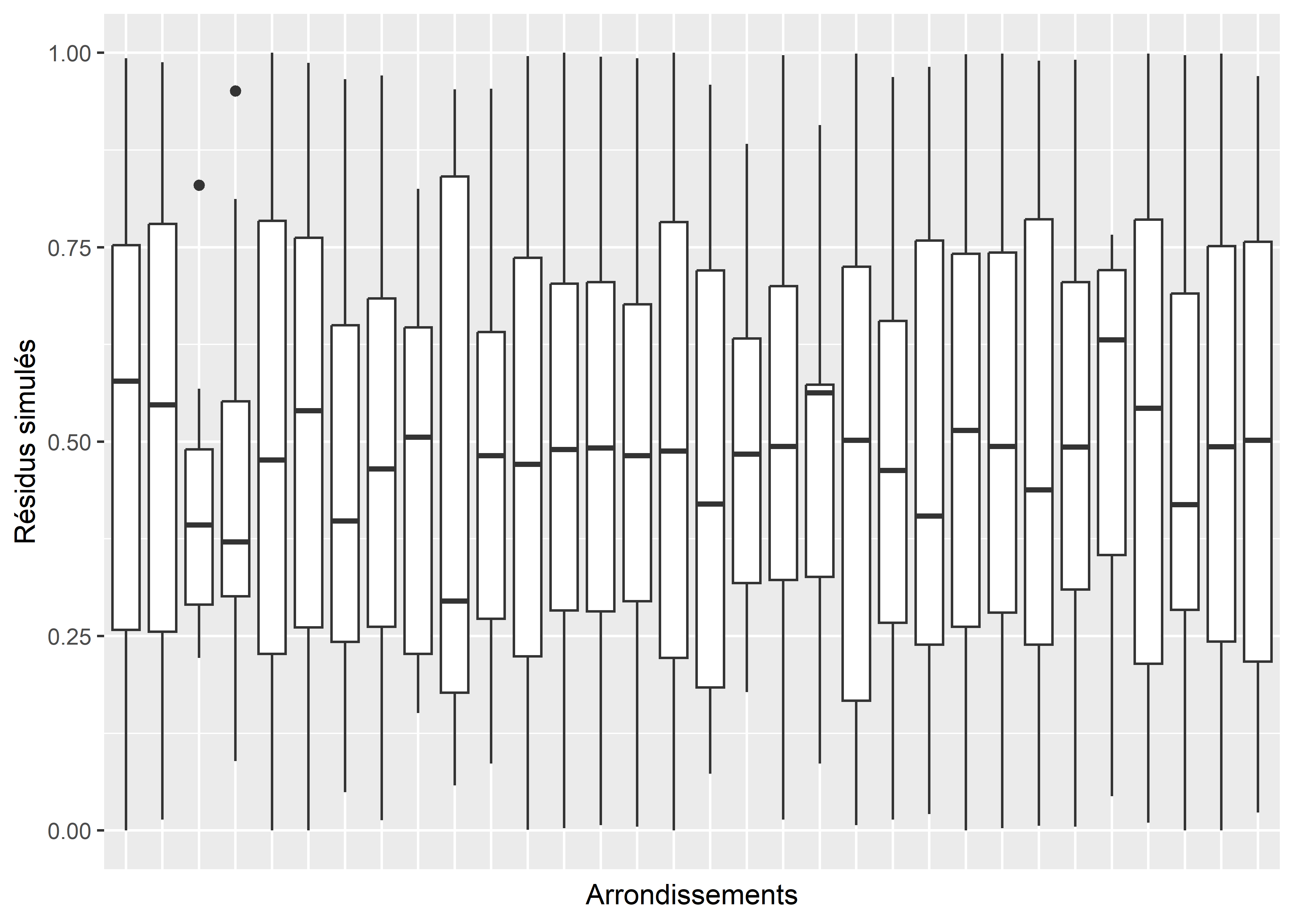

Figure 8.67: Relation entre la variable Arrondissement et les résidus simulés du modèle bêta

Analyse de la qualité d’ajustement

Dans un premier temps, nous comparons la distribution originale des données à des simulations issues du modèle.

# Extraction de 20 simulations
df2 <- data.frame(mat_sims[,1:20])
df3 <- reshape2::melt(df2)
ggplot() +
  geom_histogram(aes(x = hot, y = ..density..),
                 data = dataset3, bins = 100, color = "black", fill = "white") +
  geom_density(aes(x = value, y=..density.., group = variable), data = df3,
               fill = rgb(0,0,0,0), color = rgb(0.2,0.2,0.2,0.3), size = 1) + 
  labs(x = "résidus simulés", y = "densité")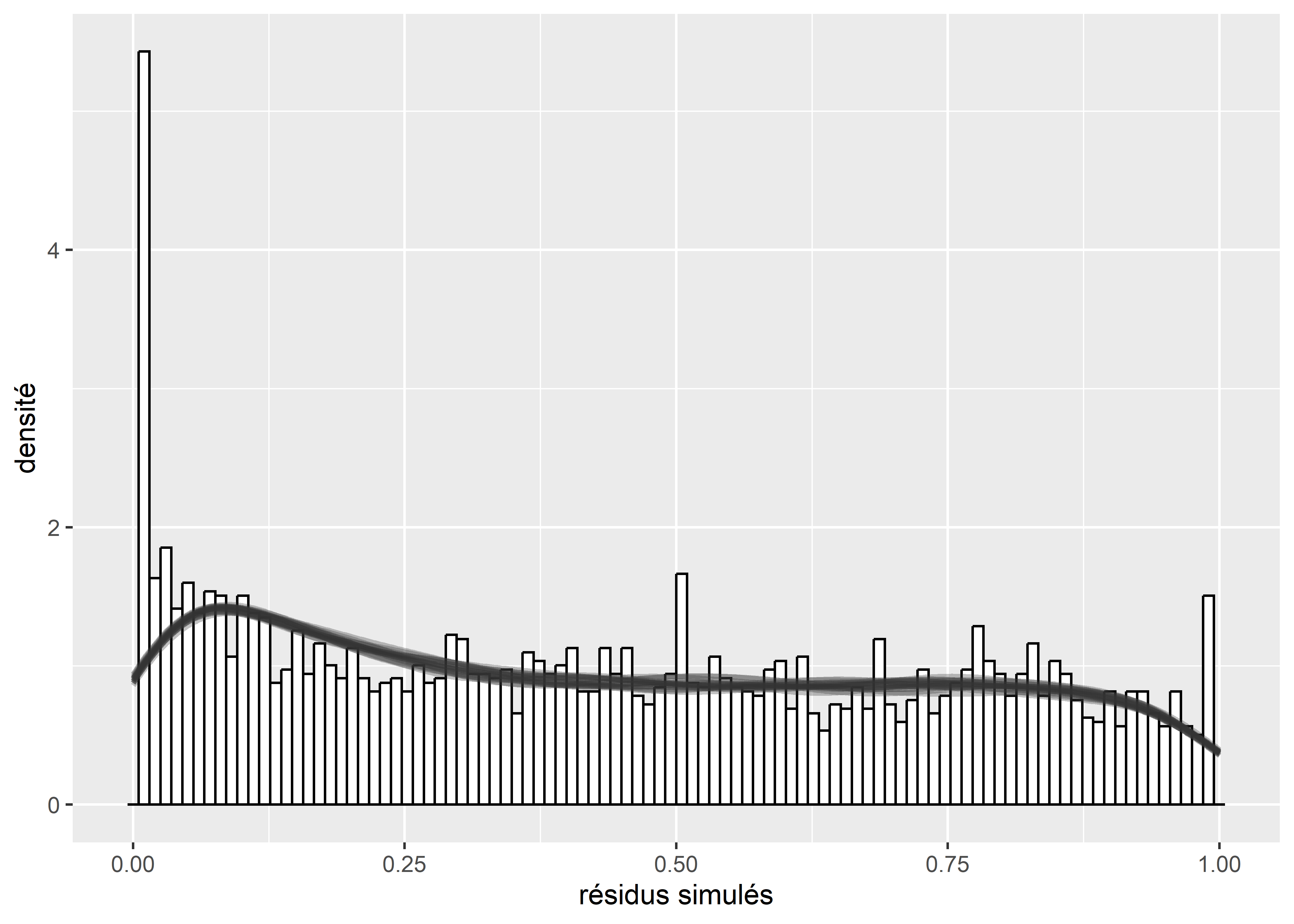

Figure 8.68: Comparaison entre la distribution originale et les simulations issues du modèle

Nous constatons à la figure 8.68 que le modèle est parvenu à reproduire la forme générale de la distribution originale : un plus grand nombre de valeurs proches de zéro, suivies d’une répartition presque homogène dans les valeurs comprises entre 0,15 et 0,8, suivies par un plus faible nombre de valeurs quand Y est supérieur à 0,8. Il semble en revanche manquer un certain nombre de valeurs extrêmes proches de 0 (absence d’îlot de chaleur) et proches de 1 (couverture à 100 % par des îlots de chaleur).

# Calcul des pseudo R2
rsqs(loglike.full = modele3$deviance/-2,
     loglike.null = modele3$null.deviance/-2,
     full.deviance = modele3$deviance,
     null.deviance = modele3$null.deviance,
     nb.params = modele3$rank,
     n = nrow(dataset3))

## $`deviance expliquee`
## [1] 0.9017396
## 
## $`McFadden ajuste`
## [1] 0.8992329
## 
## $`Cox and Snell`
## [1] 0.999828
## 
## $Nagelkerke
## [1] 0.9998949

# Calcul du RMSE
sqrt(mean((modele3$fitted.values - modele3$y)**2))

## [1] 0.1025719

Le modèle parvient à expliquer 90 % de la déviance totale et obtient des pseudo-R² très élevés. Il obtient cependant un RMSE de 0,10 soit une erreur quadratique moyenne de 10 % dans la prédiction, ce qui est tout de même important. Le modèle ne semble pas souffrir particulièrement de sur-ajustement comme les pseudo-R² auraient pu nous le laisser penser.

L’ensemble des coefficients du modèle sont accessibles via la fonction summary. Pour rappel, il est nécessaire de les convertir avec la fonction exponentielle pour pouvoir les interpréter en termes de rapport de cotes. À nouveau, nous proposons de construire dans un premier temps une figure pour observer l’effet des arrondissements.

# Identifier les coefficients pour les arrondissements
test <- grepl("Arrond",names(modele3$coefficients), fixed = T)
# Extraire les coefficients et les erreurs standards
coeffs <- modele3$coefficients[test]
err.std <- summary(modele3)$se[test]
# Créer un DataFrame avec les rapports de cote et les intervalles de confiance
df <- data.frame(
  Arrond = gsub("Arrond","",names(coeffs), fixed = T),
  coeffs = coeffs,
  err.std = err.std,
  RC = exp(coeffs),
  lowerRC = exp(coeffs-1.96*err.std),
  upperRC = exp(coeffs+1.96*err.std)
)
# Retrouver l'arrondissement de référence
allArrond <- unique(dataset3$Arrond)
refArrond <- setdiff(allArrond, df$Arrond)
# Créer le graphique
ggplot(data = df) + 
  geom_errorbarh(aes(xmin = lowerRC, xmax = upperRC, y = reorder(Arrond,RC)))+
  geom_point(aes(x = RC, y = reorder(Arrond,RC)))+
  geom_vline(xintercept = 1, color = "red")+
  geom_text(aes(x = upperRC, y = reorder(Arrond, RC), 
                label = paste("RC : ",round(RC,2),sep="")), size = 3, nudge_x = 0.3)+
  labs(x = paste("Rapport de cote (rouge : ",refArrond,')',sep=''),
       y = 'Arrondissement')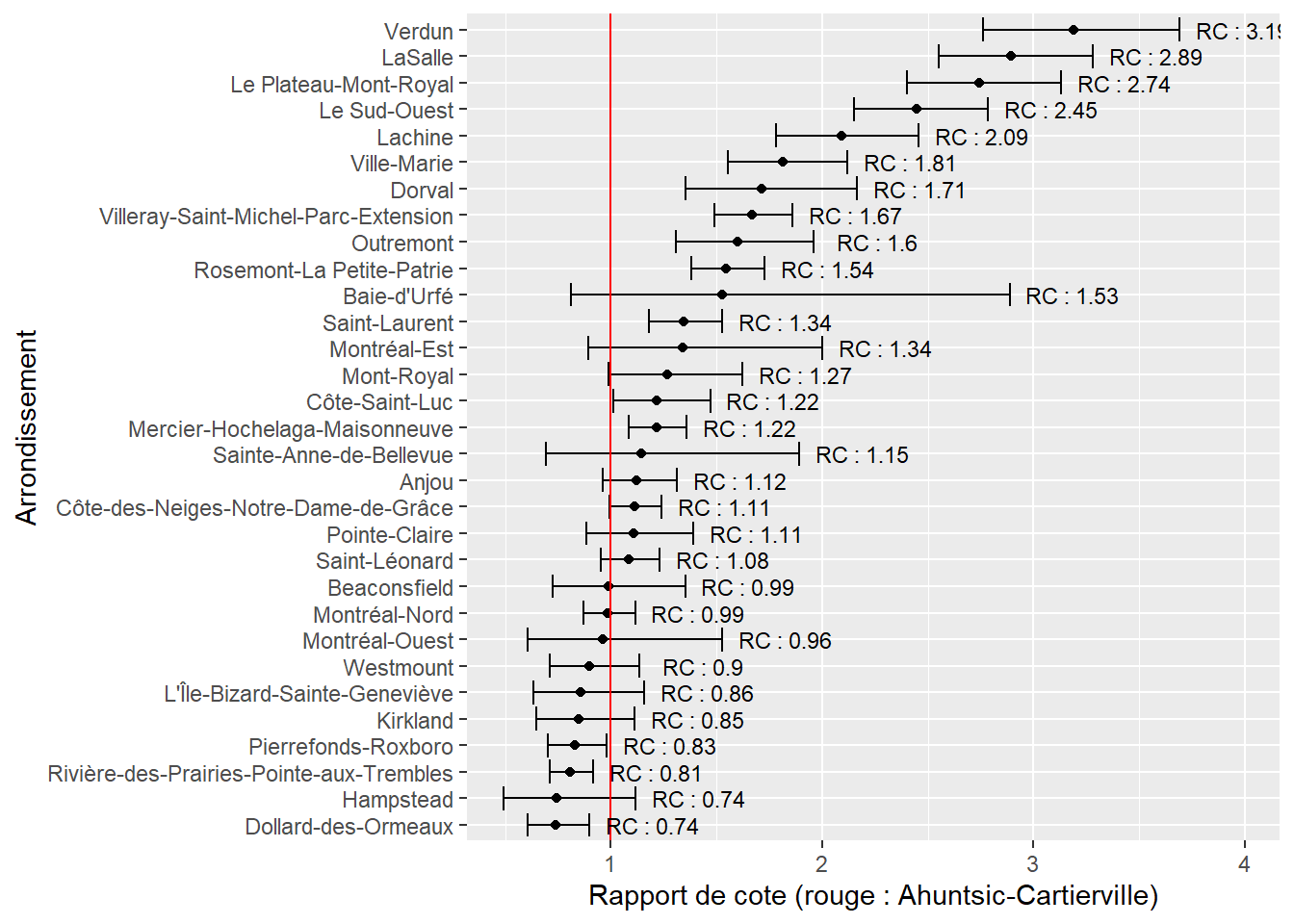

Figure 8.69: Rapports de cote pour les arrondissements dans le modèle bêta

Nous constatons ainsi que seuls quelques arrondissements ont une différence d’exposition aux îlots de chaleur significative au seuil de 0,05 comparativement à Ahuntsic-Cartierville (figure 8.69). Pour l’essentiel, il s’agit d’arrondissements pour lesquels nous observons des rapports de cotes supérieurs à 1. Verdun, Lasalle et le Plateau-Mont-Royal sont les arrondissements les plus touchés avec des chances d’observer des niveaux supérieurs de densité d’îlots de chaleur multipliés par 3,19, 2,89 et 2,74. Le reste des coefficients sont affichés dans le tableau 8.38.

Nous notons ainsi que le seul groupe associé avec une augmentation significative des chances d’observer une augmentation de la densité d’îlot de chaleur est le groupe des personnes à faible revenu (1,4 % de chance supplémentaire à chaque augmentation d’un point de pourcentage de la variable indépendante). Pour mieux cerner la taille de cet effet, nous représentons l’effet marginal de ce coefficient en maintenant toutes les autres variables à leur moyenne. Nous calculons également ces effets marginaux pour trois arrondissements différents : Verdun (RC le plus fort), Ahuntsic-Cartierville (la référence) et Dollard-des-Ormeaux (RC le plus faible). Nous réalisons également un second graphique pour visualiser l’effet non linéaire de la variable pourcentage de végétation. La figure 8.70 nous indique ainsi que le rôle de l’arrondissement est plus important que celui du pourcentage de personnes à faible revenu. Cependant, nous constatons que passer de 0 % de personnes à faible revenu dans une AD à 75 % est associé avec une multiplication de la surface couverte par des îlots de chaleur par environ 1,5 (toutes choses égales par ailleurs). Le rôle de la végétation dans la réduction de la surface des îlots de chaleur est très net et non linéaire. L’essentiel de la réduction est observé entre 0 et 50 % de végétation dans une AD, au-delà de ce seuil, la réduction des îlots de chaleur par la végétation est moins flagrante. Il semblerait donc exister à Montréal une forme d’iniquité systématique pour les populations à faible revenu, qui seraient davantage exposées aux îlots de chaleur. Cependant, compte tenu de la dépendance spatiale et de l’hétéroscésadicité observées plus haut, des ajustements devraient être apportés au modèle pour confirmer ou infirmer ce résultat.

Tableau 8.38: Résultats pour le modèle GLM bêta
Variable	Coeff.	RC	Val.p	IC 2,5 % RC	IC 97,5 % RC	Sign.
Constante	3,468	32,059	0,000	25,636	40,085	***
A65Pct	-0,002	0,998	0,243	0,996	1,001
A014Pct	-0,006	0,994	0,035	0,988	1,000
PopFRPct	0,013	1,014	0,000	1,011	1,016	***
PopMVPct	-0,003	0,997	0,000	0,995	0,998	***
prt_veg	-0,137	0,872	0,000	0,865	0,879	***

# Créer un DataFrame pour la prédiction
df <- expand.grid(
  A65Pct = mean(dataset3$A65Pct),
  A014Pct = mean(dataset3$A014Pct),
  PopFRPct = seq(0,75, 1),
  PopMVPct = mean(dataset3$PopMVPct),
  prt_veg = mean(dataset3$prt_veg),
  Arrond = c("Verdun",'Ahuntsic-Cartierville','Dollard-des-Ormeaux')
)
# Effectuer les prédiction sur l'échelle log
pred <- predict(modele3, df, se=T, type = "link")
# Calculer les prédictions et leurs intervalles de confiance
ilink <- modele3$family$linkinv
df$pred <- ilink(pred$fit)
df$lower <- ilink(pred$fit - 1.96* pred$se.fit)
df$upper <- ilink(pred$fit + 1.96* pred$se.fit)
# Afficher le résultat
P1 <- ggplot(data = df)+
  geom_path(aes(x = PopFRPct, y = pred, color = Arrond), size =1) + 
  geom_path(aes(x = PopFRPct, y = lower, color = Arrond), linetype="dashed") +
  geom_path(aes(x = PopFRPct, y = upper, color = Arrond), linetype="dashed")+
  labs(x = "Personnes à faible revenu (%)", 
       y = "Surface de l'AD couverte par des îlots de chaleur (%)",
       color = 'Arrondissement')+
  ylim(0,1)
# Pour la végétation
df2 <- expand.grid(
  A65Pct = mean(dataset3$A65Pct),
  A014Pct = mean(dataset3$A014Pct),
  PopFRPct = mean(dataset3$PopFRPct),
  PopMVPct = mean(dataset3$PopMVPct),
  prt_veg = seq(0,95,1),
  Arrond = c("Verdun",'Ahuntsic-Cartierville','Dollard-des-Ormeaux')
)
# Effectuer les prédiction sur l'échelle log
pred2 <- predict(modele3, df2, se=T, type = "link")
# Calculer les prédictions et leurs intervalles de confiance
df2$pred <- ilink(pred2$fit)
df2$lower <- ilink(pred2$fit - 1.96* pred2$se.fit)
df2$upper <- ilink(pred2$fit + 1.96* pred2$se.fit)
# Afficher le résultat
P2 <- ggplot(data = df2)+
  geom_path(aes(x = prt_veg, y = pred, color = Arrond), size =1) + 
  geom_path(aes(x = prt_veg, y = lower, color = Arrond), linetype="dashed") +
  geom_path(aes(x = prt_veg, y = upper, color = Arrond), linetype="dashed")+
  labs(x = "Couverture végétale (%)", y = '', color = 'Arrondissement')+
  ylim(0,1)
ggarrange(P1,P2, common.legend = T)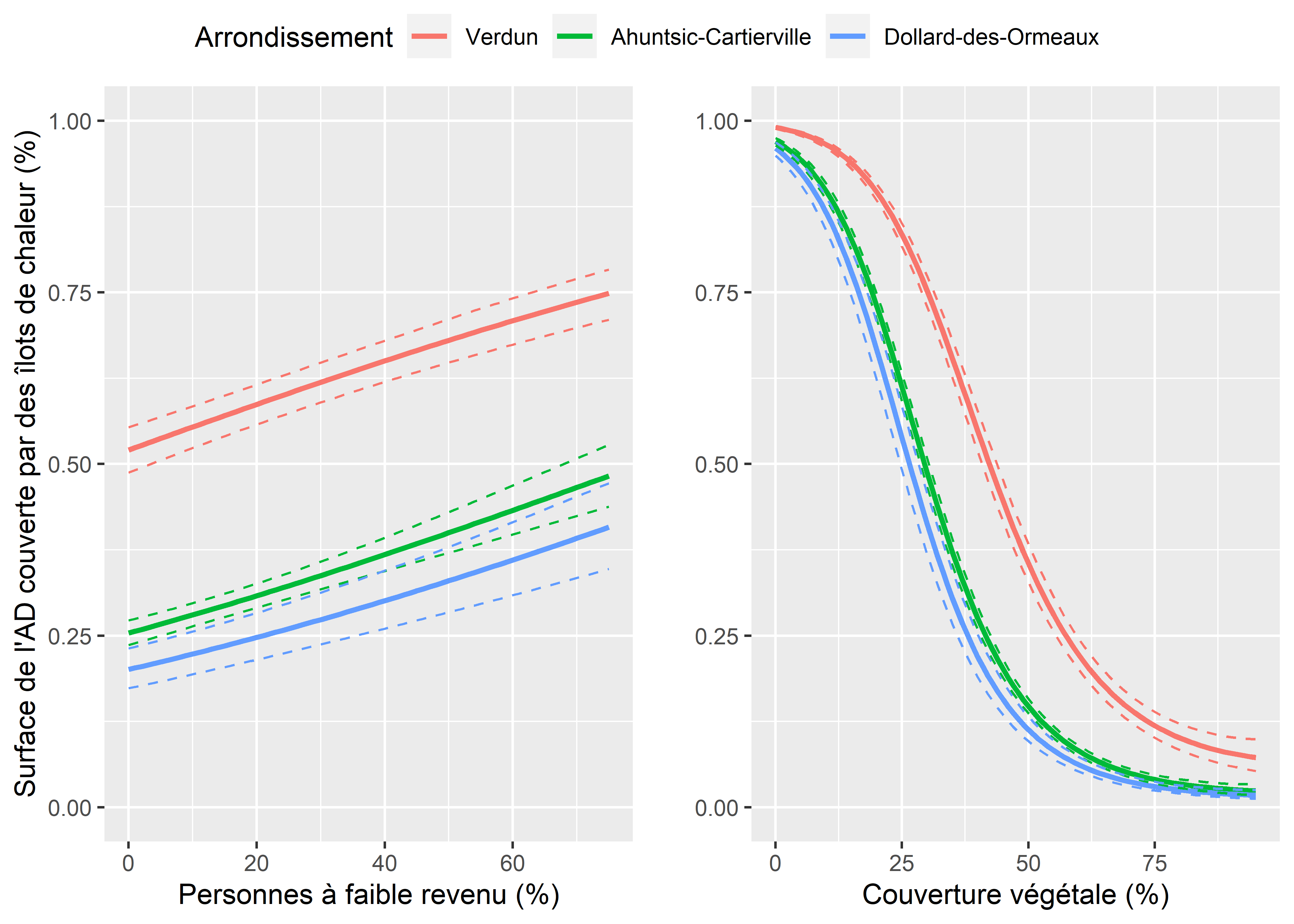

Figure 8.70: Effets marginaux des variables pourcentage de personnes à faible revenu et densité de végétation

Références

Anastasopoulos, Panagiotis C, John E Haddock, Matthew G Karlaftis et Fred L Mannering. 2012. « Analysis of urban travel times: Hazard-based approach to random parameters. » Transportation research record 2302 (1): 121‑129. https://doi.org/10.3141%2F2302-13.

Fox, John et Georges Monette. 1992. « Generalized collinearity diagnostics. » Journal of the American Statistical Association 87 (417): 178‑183. https://doi.org/10.2307/2290467.

Frank, Lawrence, Mark Bradley, Sarah Kavage, James Chapman et T Keith Lawton. 2008. « Urban form, travel time, and cost relationships with tour complexity and mode choice. » Transportation 35 (1): 37‑54. https://doi.org/10.1007/s11116-007-9136-6.

Harlan, Sharon L, Anthony J Brazel, G Darrel Jenerette, Nancy S Jones, Larissa Larsen, Lela Prashad et William L Stefanov. 2007. « In the shade of affluence: the inequitable distribution of the urban heat island. » Research in Social Problems and Public Policy 15: 173‑202. http://dx.doi.org/10.1016/S0196-1152(07)15005-5.

Huang, Ganlin, Weiqi Zhou et ML Cadenasso. 2011. « Is everyone hot in the city? Spatial pattern of land surface temperatures, land cover and neighborhood socioeconomic characteristics in Baltimore, MD. » Journal of environmental management 92 (7): 1753‑1759. https://doi.org/10.1016/j.jenvman.2011.02.006.

Sanchez, Lino et Tony G Reames. 2019. « Cooling Detroit: A socio-spatial analysis of equity in green roofs as an urban heat island mitigation strategy. » Urban Forestry & Urban Greening 44: 126331. https://doi.org/10.1016/j.ufug.2019.04.014.

Smithson, Michael et Jay Verkuilen. 2006. « A better lemon squeezer? Maximum-likelihood regression with beta-distributed dependent variables. » Psychological methods 11 (1): 54. https://doi.org/10.1037/1082-989x.11.1.54.