8.2 Modèles GLM pour des variables qualitatives
Nous abordons en premier les principaux GLM utilisés pour modéliser des variables binaires, multinomiales et ordinales. Prenez bien le temps de saisir le fonctionnement du modèle logistique binomial, car il sert de base pour les trois autres modèles présentés.
8.2.1 Modèle logistique binomial
Le modèle logistique binomial est une généralisation du modèle de Bernoulli que nous avons présenté dans l’introduction de cette section. Le modèle logistique binomiale couvre donc deux cas de figure :
- La variable observée est binaire (0 ou 1). Dans ce cas, le modèle logistique binomiale devient un simple modèle de Bernoulli.
- La variable observée est un comptage (nombre de réussites) et nous disposons d’une autre variable avec le nombre de réplications de l’expérience. Par exemple, pour chaque intersection d’un réseau routier, nous pourrions avoir le nombre de décès à vélo (variable Y de comptage) et le nombre de collisions vélo / automobile (variable quantifiant le nombre d’expériences, chaque collision étant une expérience). Spécifiquement, nous tentons de prédire le paramètre p de la distribution binomiale à l’aide de notre équation de régression et de la fonction logistique comme fonction de lien. Notez ici que cette fonction de lien influence directement l’interprétation des paramètres du modèle. Pour rappel, cette fonction est définie comme :
\[\begin{equation} g(x) = ln(\frac{x}{1-x}) \end{equation}\]
avec \(ln\) le logarithme naturel.
Au-delà de sa propriété mathématique assurant que \(g(x) \in \mathopen[0,1\mathclose]\), cette fonction offre une interprétation intéressante. La partie \(\frac{x}{1-x}\) est une cote et s’interprète en termes de chances d’observer un évènement. Par exemple, dans le cas des accidents de cyclistes, si la probabilité d’observer un décès suite à une collision est de 0,1, alors la cote de cet évènement est \(\frac{\frac{1}{10}}{\frac{9}{10}} = \frac{1}{9}\) soit un contre neuf. Dans un modèle GLM logistique, les coefficients ajustés pour les variables indépendantes représentent des logarithmes de rapport de cote, car ils comparent les chances d’observer l’évènement (y = 1) en fonction des valeurs des variables indépendantes.
| Type de variable dépendante | Variable binaire (0 ou 1) ou comptage de réussite à une expérience (ex : 3 réussites sur 5 expériences) |
| Distribution utilisée | Binomiale |
| Formulation |
\(Y \sim Binomial(p)\) \(g(p) = \beta_0 + \beta X\) \(g(x) = log(\frac{x}{1-x})\) |
| Fonction de lien | Logistique |
| Paramètre modélisé | p |
| Paramètres à estimer | \(\beta_0\), \(\beta\) |
| Conditions d’application | Non-séparation complète, absence de sur-dispersion ou de sous-dispersion |
8.2.1.1 Interprétation des paramètres
Les seuls paramètres à estimer du modèle sont les coefficients \(\beta\) et la constante \(\beta_0\). La fonction de lien logistique transforme la valeur de ces coefficients, en conséquence, ils ne peuvent plus être interprétés directement. \(\beta_0\) et \(\beta\) sont exprimés dans une unité particulière: des logarithmes de rapports de cote (log odd ratio). Le rapport de cote est relativement facile à interpréter contrairement à son logarithme. Pour l’obtenir, il suffit d’utiliser la fonction exponentielle (l’inverse de la fonction logarithme) pour passer des log rapport de cote à de simples rapports de cote. Donc si \(exp(\beta)\) est inférieur à 1, il réduit les chances d’observer l’évènement et inversement si \(exp(\beta)\) est supérieur à 1.
Par exemple, admettons que nous ayons un coefficient \(\beta_1\) de 1,2 pour une variable \(X_1\) dans une régression logistique. Il est nécessaire d’utiliser son exponentiel pour l’interpréter de façon intuitive. \(exp\mbox{(1,2)} = \mbox{3,32}\), ce qui signifie que lorsque \(X_1\) augmente d’une unité, les chances d’observer 1 plutôt que 0 comme valeur de Y sont multipliées par 3,32. Admettons maintenant que \(\beta_1\) vaille −1,2, nous calculons donc \(exp\mbox{(-1,2) = 0,30}\), ce qui signifie qu’à chaque augmentation d’une unité de \(X_1\), les chances d’observer 1 plutôt que 0 comme valeur de Y sont multipliées par 0,30. En d’autres termes,les chances d’observer 1 plutôt que 0 sont divisées par 3,33 (\(\mbox{1}/\mbox{0,30} = \mbox{3,33}\)), soit une diminution de 70 % (\(\mbox{1}-\mbox{0,3} = \mbox{0,7}\)) des chances d’observer 1 plutôt que 0.
Les rapports de cotes
Le rapport de cote ou rapport des chances est une mesure utilisée pour exprimer l’effet d’un facteur sur une probabilité. Il est très utilisé dans le domaine de la santé, mais aussi des paris. Prenons un exemple concret avec le port du casque à vélo. Si sur 100 accidents impliquant des cyclistes portant un casque, nous observons seulement 3 cas de blessures graves à la tête, contre 15 dans un second groupe de 100 cyclistes ne portant pas de casque, nous pouvons calculer le rapport de cote suivant :
\[\begin{equation} \frac{p(1-q)}{q(1-p)} = \frac{\mbox{0,15} \times (\mbox{1}-\mbox{0,03})}{\mbox{0,03} \times (\mbox{1}-\mbox{0,15})} = \mbox{5,71} \end{equation}\]
avec p la probabilité d’observer le phénomène (ici la blessure grave à la tête) dans le groupe 1 (ici les cyclistes sans casque) et q la probabilité d’observer le phénomène dans le groupe 2 (ici les cyclistes avec un casque). Ce rapport de cote indique que les cyclistes sans casques ont 5,71 fois plus de risques de se blesser gravement à la tête lors d’un accident comparativement aux cyclistes portant un casque.
8.2.1.2 Conditions d’application
La non-séparation complète signifie qu’aucune des variables X n’est, à elle seule, capable de parfaitement distinguer les deux catégories 0 et 1 de la variable Y. Dans un tel cas de figure, les algorithmes d’ajustement utilisés pour estimer les paramètres des modèles sont incapables de converger. Notez aussi l’absurdité de créer un modèle pour prédire une variable Y si une variable X est capable à elle seule de la prédire à coup sûr. Ce problème est appelé un effet de Hauck-Donner. Il est assez facile de le repérer, car la plupart du temps les fonctions de R signalent ce problème (message d’erreur sur la convergence). Sinon, des valeurs extrêmement élevées ou faibles pour certains rapports de cote peuvent aussi indiquer un effet de Hauck-Donner.
La sur-dispersion est un problème spécifique aux distributions n’ayant pas de paramètre de dispersion (binomiale, de Poisson, exponentielle, etc.), pour lesquelles la variance dépend directement de l’espérance. La sur-dispersion désigne une situation dans laquelle les résidus (ou erreurs) d’un modèle sont plus dispersés que ce que suppose la distribution utilisée. À l’inverse, il est aussi possible (mais rare) d’observer des cas de sous-dispersion (lorsque la dispersion des résidus est plus petite que ce que suppose la distribution choisie). Ce cas de figure se produit généralement lorsque le modèle parvient à réaliser une prédiction trop précise pour être crédible. Si vous rencontrez une forte sous-dispersion, cela signifie souvent que l’une de vos variables indépendantes provoque une séparation complète. La meilleure option, dans ce cas, est de supprimer la variable en question du modèle. La variance attendue d’une distribution binomiale est \(nb \times p \times(1-p)\), soit le produit entre le nombre de tirages, la probabilité de réussite et la probabilité d’échec. À titre d’exemple, si nous considérons une distribution binomiale avec un seul tirage et 50 % de chances de réussite, sa variance serait : \(1 \times \mbox{0,5} \times \mbox{(1}-\mbox{0,5}) = \mbox{0,25}\).
Plusieurs raisons peuvent expliquer la présence de sur-dispersion dans une modèle:
- il manque des variables importantes dans le modèle, conduisant à un mauvais ajustement et donc une sur-dispersion des erreurs;
- les observations ne sont pas indépendantes, impliquant qu’une partie de la variance n’est pas contrôlée et augmente les erreurs;
- la probabilité de succès de chaque expérience varie d’une répétition à l’autre (différentes distributions).
La conséquence directe de la sur-dispersion est la sous-estimation de la variance des coefficients de régression. En d’autres termes, la sur-dispersion conduit à sous-estimer notre incertitude quant aux coefficients obtenus et réduit les valeurs de p calculées pour ces coefficients. Les risques de trouver des résultats significatifs à cause des fluctuations d’échantillonnage augmentent.
Pour détecter une sur-dispersion ou une sous-dispersion dans un modèle logistique binomial, il est possible d’observer les résidus de déviance du modèle. Ces derniers sont supposés suivre une distribution du khi-deux avec n−k degrés de liberté (avec n le nombre d’observations et k le nombre de coefficients dans le modèle). Par conséquent, la somme des résidus de déviance d’un modèle logistique binomiale divisée par le nombre de degrés de liberté devrait être proche de 1. Une légère déviation (jusqu’à 0,15 au-dessus ou au-dessous de 1) n’est pas alarmante; au-delà, il est nécessaire d’ajuster le modèle.
Notez que si la variable Y modélisée est exactement binaire (chaque expérience est indépendante et n’est composée que d’un seul tirage) et que le modèle utilise donc une distribution de Bernoulli, le test précédent pour détecter une éventuelle sur-dispersion n’est pas valide. Hilbe (2009) parle de sur-dispersion implicite pour le modèle de Bernoulli et recommande notamment de toujours ajuster les erreurs standards des modèles utilisant des distributions de Bernoulli, binomiale et de Poisson. L’idée ici est d’éviter d’être trop optimiste face à l’incertitude du modèle sur les coefficients et de l’ajuster en conséquence. Pour cela, il est possible d’utiliser des quasi-distributions ou des estimateurs robustes (Zeileis 2004). Notez que si le modèle ne souffre pas de sur ou sous-dispersion, ces ajustements produisent des résultats équivalents aux résultats non ajustés.
8.2.1.3 Exemple appliqué dans R
Présentation des données
Pour illustrer le modèle logistique binomial, nous utilisons ici un jeu de données proposé par l’Union européenne : l’enquête de déplacement sur la demande pour des systèmes de transports innovants. Pour cette enquête, un échantillon de 1 000 individus représentatifs de la population a été constitué dans chacun des 26 États membres de l’UE, soit un total de 26 000 observations. Pour chaque individu, plusieurs informations ont été collectées relatives à la catégorie socioprofessionnelle, le mode de transport le plus fréquent, le temps du trajet de son déplacement le plus fréquent et son niveau de sensibilité à la cause environnementale. Nous modélisons ici la probabilité qu’un individu déclare utiliser le plus fréquemment le vélo comme moyen de transport. Les variables explicatives sont résumées au tableau 8.7. Il existe bien évidemment un grand nombre de facteurs individuels qui influence la prise de décision sur le mode de transport. Les résultats de ce modèle ne doivent donc pas être pris avec un grand sérieux; il est uniquement construit à des fins pédagogiques, sans cadre conceptuel solide.
| Nom de la variable | Signification | Type de variable | Mesure |
|---|---|---|---|
| Pays | Pays de résidence | Variable multinomiale | Le nom d’un des 26 pays membres de l’UE |
| Sexe | Sexe biologique | Variable binaire | Homme ou femme |
| Age | Âge biologique | Variable continue | L’âge en nombre d’années variant de 16 à 84 ans dans le jeu de données |
| Education | Niveau d’éducation maximum atteint | Variable multinomiale | Premier cycle, secondaire inférieur (classes supérieures de l’école élémentaire), secondaire, troisième cycle |
| StatutEmploi | Employé ou non | Variable binaire | Employé ou non |
| Revenu | Niveau de revenu autodéclaré | Variable multinomiale | Très faible revenu, faible revenu, revenu moyen, revenu élevé, revenu très élevé, sans reponse |
| Residence | Lieu de résidence | Variable multinomiale | Zone rurale, petite ou moyenne ville (moins de 250 000 habitants), grande ville (entre 250 000 et 1 million d’habitants) , aire métropolitaine (plus d’un million d’habitants) |
| Duree | Durée du voyage le plus fréquent autodéclarée (en minutes) | Variable continue | Nombre de minutes |
| ConsEnv | Préoccupation environnementale | Variable ordinale | Échelle de Likert de 1 à 10 |
Vérification des conditions d’application
La première étape de la vérification des conditions d’application est de calculer les valeurs du facteur d’inflation de variance (VIF) pour s’assurer de l’absence de multicolinéarité trop forte entre les variables indépendantes. L’ensemble des valeurs de VIF sont inférieures à 5, indiquant l’absence de multicolinéarité excessive dans le modèle.
library(car)
# Chargement des données
dfenquete <- read.csv("data/glm/enquete_transport_UE.csv", encoding = 'UTF-8')
dfenquete$Pays <- relevel(as.factor(dfenquete$Pays), ref = "Allemagne")
# Vérification du VIF
model1 <- glm(y ~
Pays + Sexe + Age + Education + StatutEmploi + Revenu +
Residence + Duree + ConsEnv,
family = binomial(link="logit"),
data = dfenquete
)
vif(model1)## GVIF Df GVIF^(1/(2*Df))
## Pays 1.794797 27 1.010890
## Sexe 1.028618 1 1.014208
## Age 1.060256 1 1.029687
## Education 1.428872 3 1.061285
## StatutEmploi 1.151879 1 1.073256
## Revenu 1.220934 5 1.020162
## Residence 1.130526 3 1.020658
## Duree 1.042638 1 1.021096
## ConsEnv 1.090987 1 1.044503La seconde étape de vérification est le calcul des distances de Cook et l’identification d’éventuelles valeurs aberrantes (figure 8.4).
# Calcul et représentation des distances de Cook
cookd <- data.frame(
dist = cooks.distance(model1),
oid = 1:nrow(dfenquete)
)
ggplot(cookd) +
geom_point(aes(x = oid, y = dist ), color = rgb(0.1,0.1,0.1,0.4), size = 1)+
geom_hline(yintercept = 0.002, color = "red")+
labs(x = "observations", y = "distance de Cook") +
theme(axis.text.x = element_blank(),
axis.ticks.x = element_blank())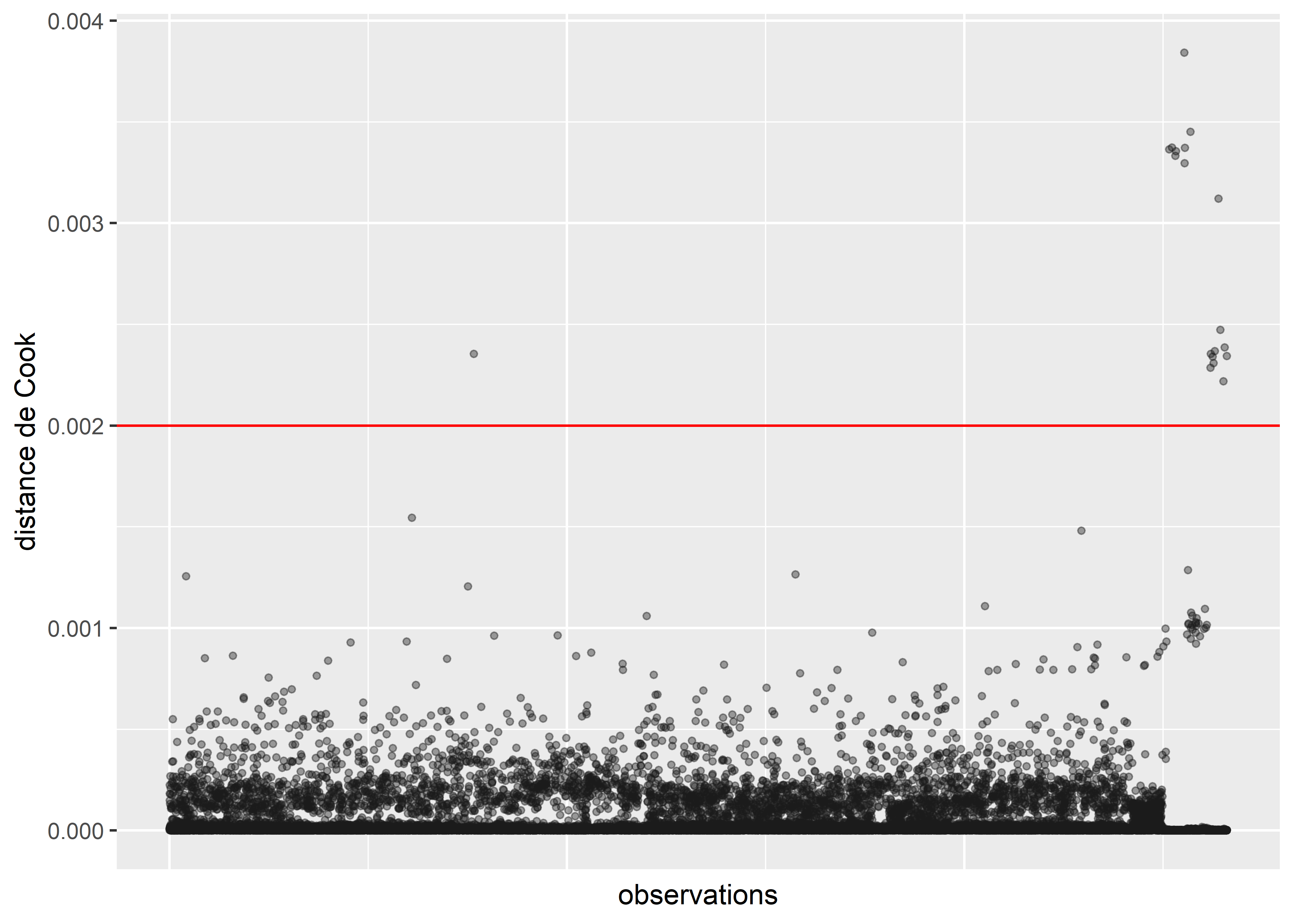
Figure 8.4: Distances de Cook pour le modèle binomial avec toutes les observations
Le calcul de la distance de Cook révèle un ensemble d’observations se démarquant nettement des autres (délimitées dans la figure 8.4 par la ligne rouge). Nous les isolons dans un premier temps pour les analyser.
# Isoler les observations avec de très fortes valeurs de Cook
# valeur seuil choisie : 0,002
cas_etranges <- subset(dfenquete, cookd$dist>=0.002)
cat(nrow(cas_etranges),'observations se démarquant dans le modèle')## 19 observations se démarquant dans le modèleprint(cas_etranges)## X y Pays Sexe Age Education Statut_emploi Revenu Residence
## 7660 7660 1 Slovaquie homme 50 universite Employed moyen zone rurale
## 25150 25150 1 Malte homme 16 secondaire Not Employed moyen zone rurale
## 25227 25227 1 Malte femme 53 secondaire inferieur Not Employed moyen zone rurale
## 25309 25309 1 Malte femme 32 secondaire Employed moyen petite-moyenne ville
## 25322 25322 1 Malte homme 38 universite Employed eleve zone rurale
## 25536 25536 1 Malte homme 27 universite Employed tres eleve petite-moyenne ville
## 25541 25541 1 Malte homme 38 secondaire inferieur Employed moyen zone rurale
## 25549 25549 1 Malte homme 31 universite Employed sans reponse petite-moyenne ville
## 25690 25690 1 Luxembourg homme 32 universite Employed tres eleve petite-moyenne ville
## 26190 26190 1 Chypre homme 24 secondaire Not Employed moyen grande ville
## 26201 26201 1 Chypre homme 25 secondaire Employed faible zone rurale
## 26244 26244 1 Chypre homme 32 secondaire Employed tres faible petite-moyenne ville
## 26269 26269 1 Chypre homme 60 secondaire Not Employed moyen petite-moyenne ville
## 26303 26303 1 Chypre homme 59 secondaire Not Employed moyen zone rurale
## 26393 26393 1 Chypre homme 30 premier cycle Employed tres eleve petite-moyenne ville
## 26444 26444 1 Chypre femme 52 universite Employed eleve petite-moyenne ville
## 26516 26516 1 Chypre homme 21 universite Not Employed moyen petite-moyenne ville
## 26549 26549 1 Chypre homme 28 universite Employed tres faible petite-moyenne ville
## 26600 26600 1 Chypre homme 36 secondaire Employed moyen petite-moyenne ville
## Duree mode_pref StatutEmploi ConsEnv
## 7660 775 velo employe 7
## 25150 15 velo sans emploi 3
## 25227 45 marche sans emploi 5
## 25309 25 marche employe 4
## 25322 30 marche employe 10
## 25536 14 velo employe 10
## 25541 5 marche employe 8
## 25549 60 velo employe 10
## 25690 720 velo employe 6
## 26190 20 velo sans emploi 5
## 26201 20 velo employe 5
## 26244 18 velo employe 4
## 26269 5 velo sans emploi 7
## 26303 7 velo sans emploi 8
## 26393 61 velo employe 5
## 26444 120 velo employe 3
## 26516 25 velo sans emploi 8
## 26549 15 velo employe 2
## 26600 8 velo employe 1À la lecture des valeurs pour ces 19 cas étranges, nous remarquons que la plupart des observations proviennent de Malte et de Chypre. Ces deux petites îles constituent des cas particuliers en Europe et devraient vraisemblablement faire l’objet d’une analyse séparée. Nous décidons donc de les retirer du jeu de données. Deux autres observations étranges sont observables en Slovaquie et au Luxembourg. Dans les deux cas, les répondants ont renseigné des temps de trajet fantaisistes de respectivement 775 et 720 minutes. Nous les retirons donc également de l’analyse.
# Retirer les observations aberrantes
dfenquete2 <- subset(dfenquete, (dfenquete$Pays %in% c("Malte", "Chypre")) == F &
dfenquete$Duree < 400)
# Réajuster le modèle
model2 <- glm(y ~
Pays + Sexe + Age + Education + StatutEmploi + Revenu +
Residence + Duree + ConsEnv,
family = binomial(link="logit"),
data = dfenquete2)
# Recalculer la distance de Cook
cookd <- data.frame(
dist = cooks.distance(model2),
oid = 1:nrow(dfenquete2)
)
ggplot(cookd) +
geom_point(aes(x = oid, y = dist ), color = rgb(0.1,0.1,0.1,0.4), size = 1)+
labs(x = "observations", y = "distance de Cook") +
theme(axis.text.x = element_blank(),
axis.ticks.x = element_blank())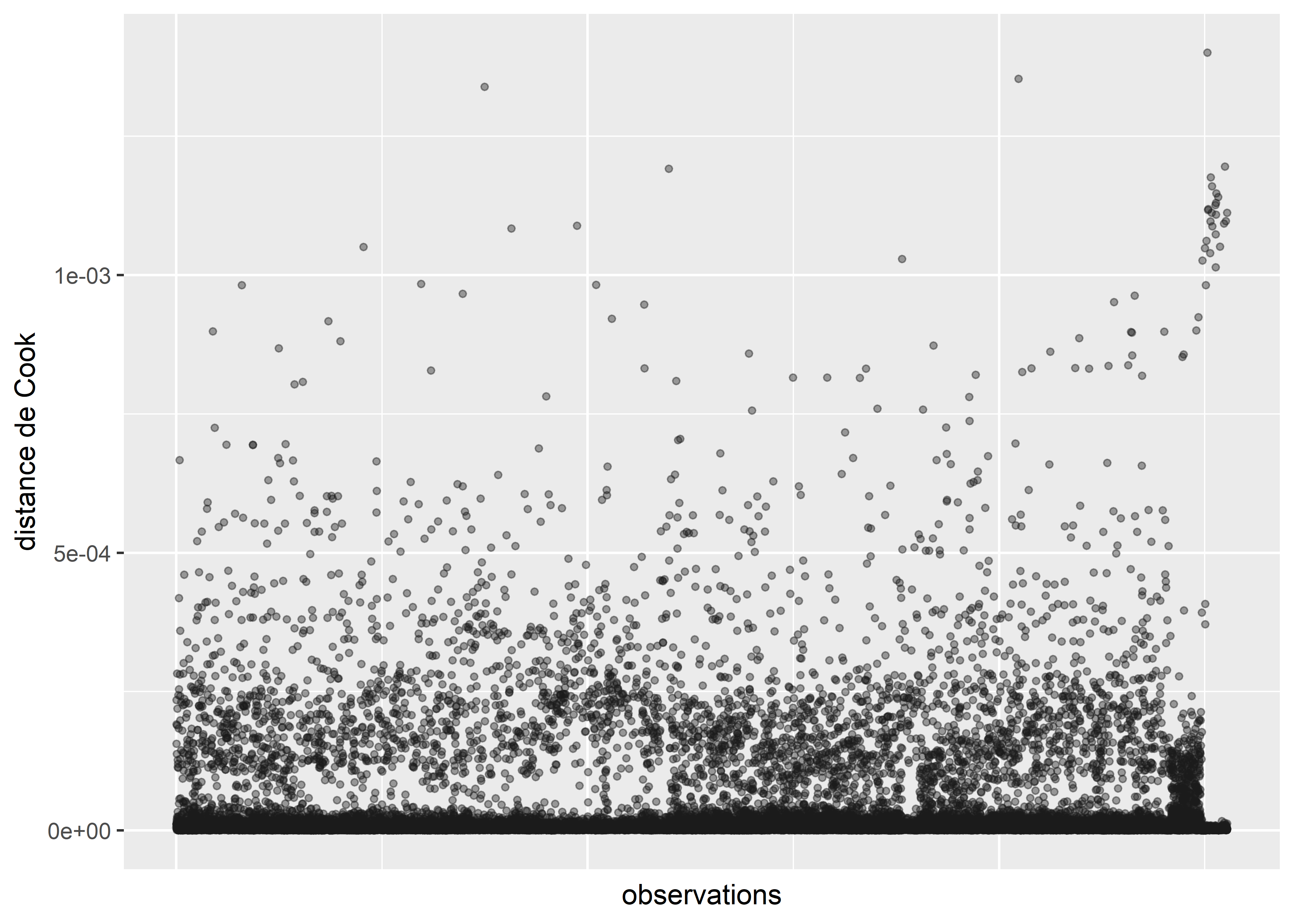
Figure 8.5: Distances de Cook pour le modèle binomial sans les valeurs aberrantes
Après avoir retiré ces valeurs aberrantes, nous n’observons plus de nouveaux cas singuliers avec les distances de Cook (figure 8.5).
La prochaine étape de vérification des conditions d’application est l’analyse des résidus simulés. Nous commençons donc par calculer ces résidus et afficher leur histogramme (figure 8.6).
library(DHARMa)
# Extraire les probabilités prédites par le modèle
probs <- predict(model2, type = "response")
# Calculer 1000 simulations a partir du modele ajuste
sims <- lapply(1:length(probs), function(i){
p <- probs[[i]]
vals <- rbinom(n = 1000, size = 1,prob = p)
})
matsim <- do.call(rbind,sims)
# Utiliser le package DHARMa pour calculer les résidus simulés
sim_res <- createDHARMa(simulatedResponse = matsim,
observedResponse = dfenquete2$y,
fittedPredictedResponse = probs,
integerResponse = T)
ggplot()+
geom_histogram(aes(x = residuals(sim_res)),
bins = 30, fill = "white", color = rgb(0.3,0.3,0.3))+
labs(x="résidus simulés", y="fréquence")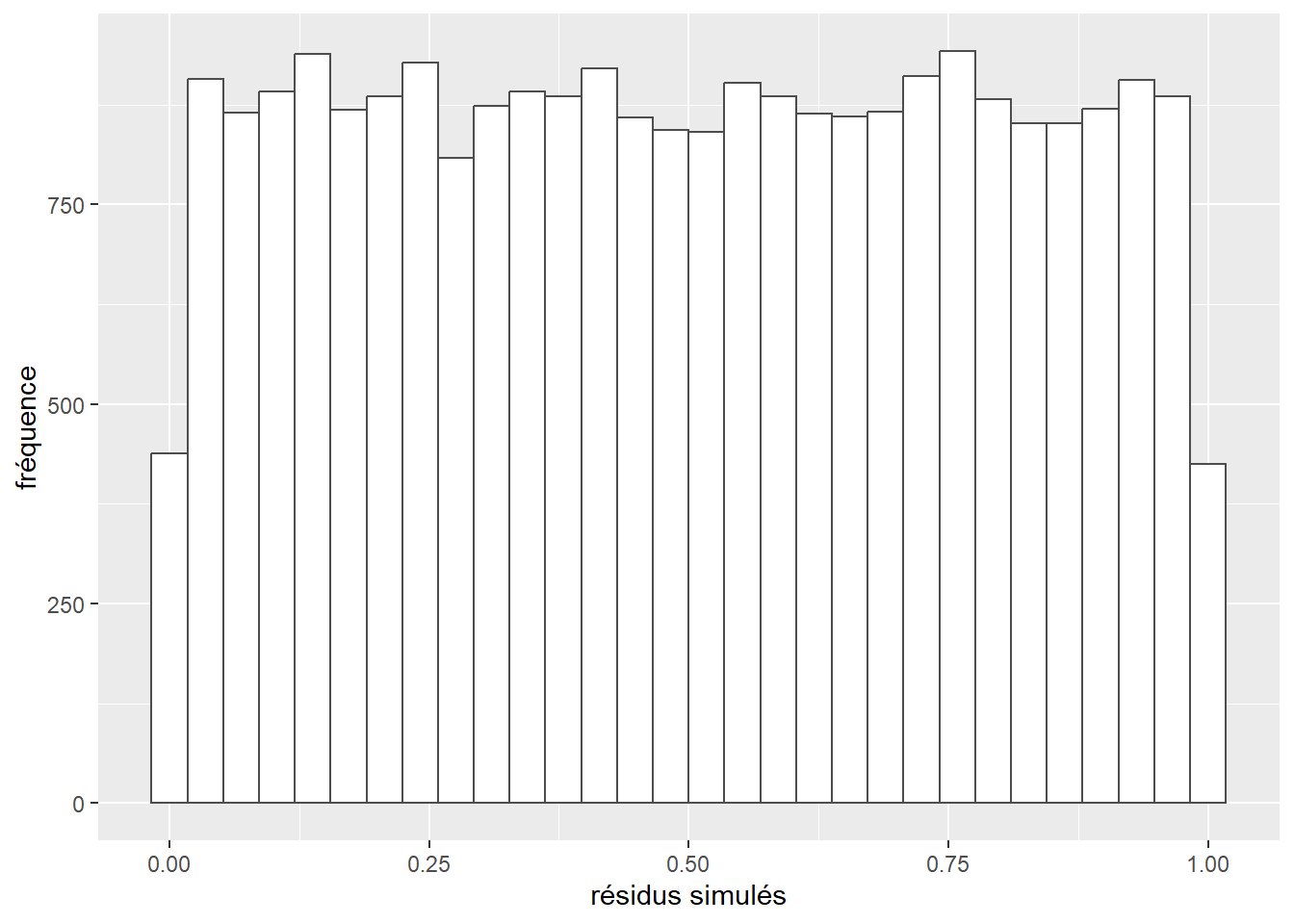
Figure 8.6: Distribution des résidus simulés pour le modèle binomial
L’histogramme indique clairement que les résidus simulés suivent une distribution uniforme (figure 8.6). Il est possible d’aller plus loin dans le diagnostic en utilisant la fonction plot sur l’objet sim_res. La partie de droite de la figure ainsi obtenue (figure 8.7) est un diagramme de quantiles-quantiles (ou Q-Q plot). Les points du graphique sont supposés suivre une ligne droite matérialisée par la ligne rouge. Une déviation de cette ligne indique un éloignement des résidus de leur distribution attendue. Trois tests sont également réalisés par la fonction :
- Le premier (Test de Kolmogorov-Smirnov, KS test) permet de tester si les points dévient significativement de la ligne droite. Dans notre cas, la valeur de p n’est pas significative, indiquant que les résidus ne dévient pas de la distribution uniforme.
- Le second test permet de vérifier la présence de sur ou sous-dispersion. Dans notre cas, ce test n’est pas significatif, n’indiquant aucun problème de sur-dispersion ou de sous-dispersion.
- Le dernier test permet de vérifier si des valeurs aberrantes sont présentes dans les résidus. Une valeur non significative indique une absence de valeurs aberrantes.
Le second graphique permet de comparer les résidus et les valeurs prédites. L’idéal est donc d’observer une ligne droite horizontale au milieu du graphique qui indiquerait une absence de relation entre les valeurs prédites et les résidus (ce que nous observons bien ici).
plot(sim_res)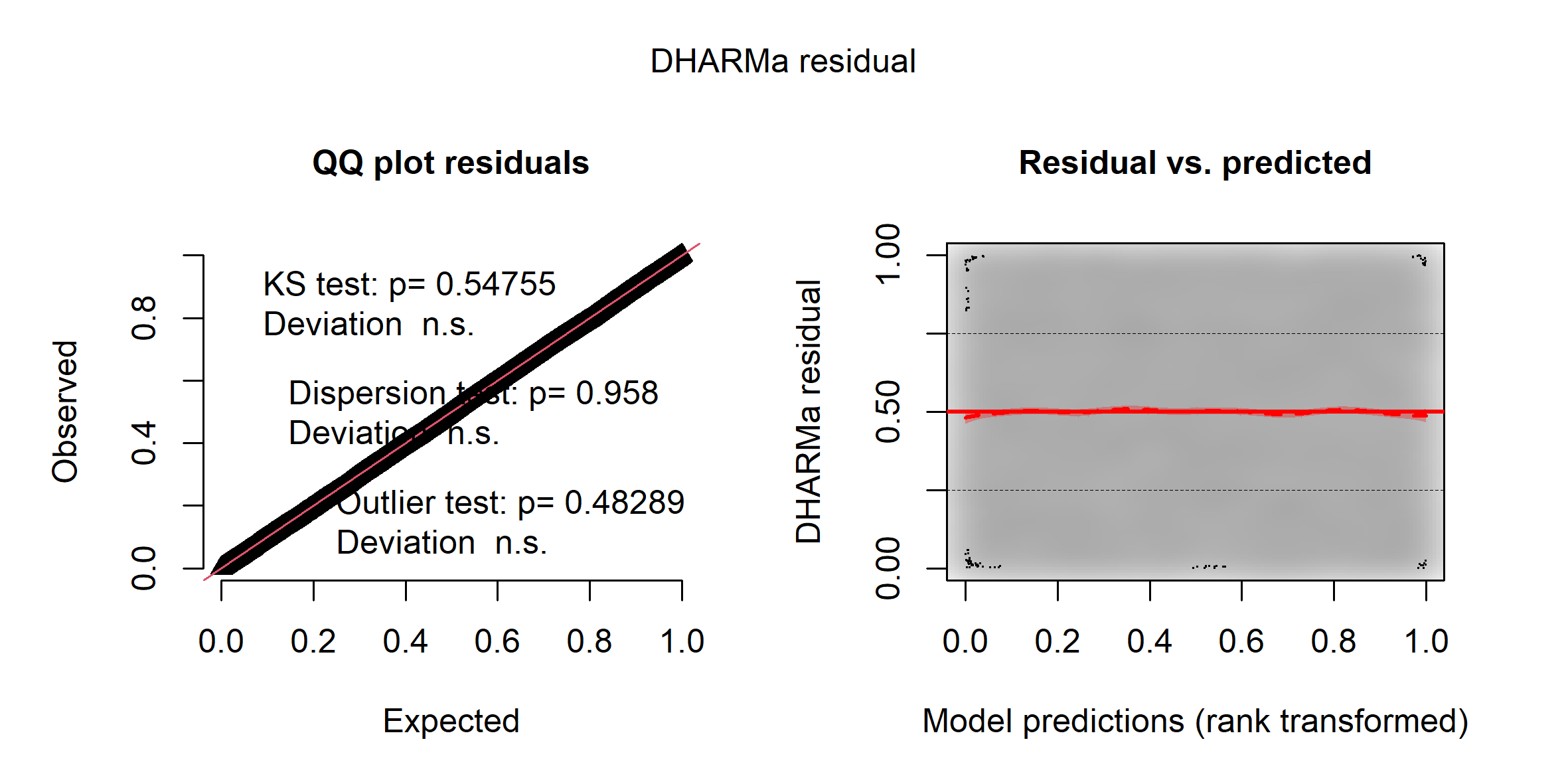
Figure 8.7: Diagnostic des résidus simulés par le package DHARMa
L’analyse approfondie des résidus nous permet donc de conclure que le modèle respecte les conditions d’application et que nous pouvons passer à la vérification de la qualité d’ajustement du modèle.
Vérification de la qualité d’ajustement
Pour calculer les différents R2 d’un modèle GLM, nous proposons la fonction suivante :
rsqs <- function(loglike.full, loglike.null,full.deviance, null.deviance, nb.params, n){
# Calcul de la déviance expliquée
explained_dev <- 1-(full.deviance / null.deviance)
K <- nb.params
# R2 de McFadden ajusté
r2_faddenadj <- 1- (loglike.full - K) / loglike.null
Lm <- loglike.full
Ln <- loglike.null
# R2 de Cox and Snell
Rcs <- 1 - exp((-2/n) * (Lm-Ln))
# R2 de Nagelkerke
Rn <- Rcs / (1-exp(2*Ln/n))
return(
list("deviance expliquee" = explained_dev,
"McFadden ajuste" = r2_faddenadj,
"Cox and Snell" = Rcs,
"Nagelkerke" = Rn
)
)
}Nous l’utilisons pour l’ensemble des modèles GLM de ce chapitre. Dans le cas du modèle binomial, nous obtenons :
# Ajuster un modele null avec seulement une constante
model2.null <- glm(y ~1,
family = binomial(link="logit"),
data = dfenquete2)
# Calculer les R2
rsqs(loglike.full = as.numeric(logLik(model2)), # loglikelihood du modèle complet
loglike.null = as.numeric(logLik(model2.null)), # loglikelihood du modèle nul
full.deviance = deviance(model2), # déviance du modèle complet
null.deviance = deviance(model2.null), # déviance du modèle nul
nb.params = model2$rank, # nombre de paramètres dans le modèle
n = nrow(dfenquete2) # nombre d'observations
)## $`deviance expliquee`
## [1] 0.0876057
##
## $`McFadden ajuste`
## [1] 0.08357379
##
## $`Cox and Snell`
## [1] 0.0689509
##
## $Nagelkerke
## [1] 0.1236597La déviance expliquée par le modèle est de 8,8 %, les pseudos R2 de McFadden (ajusté), d’Efron et de Nagelkerke sont respectivement 0,084, 0,069 et 0,124. Toutes ces valeurs sont relativement faibles et indiquent qu’une large partie de la variabilité de Y reste inexpliquée.
Pour vérifier la qualité de prédiction du modèle, nous devons comparer les catégories prédites et les catégories réelles de notre variable dépendante et construire une matrice de confusion. Cependant, un modèle GLM binomial prédit la probabilité d’appartenance au groupe 1 (ici les personnes utilisant le vélo pour effectuer leur déplacement le plus fréquent). Pour convertir ces probabilités prédites en catégories prédites, il faut choisir un seuil de probabilité au-delà duquel nous considérons que la valeur attendue est 1 (cycliste) plutôt que 0 (autre). Un exemple naïf serait de prendre le seuil 0,5, ce qui signifierait que si le modèle prédit qu’une observation a au moins 50 % de chance d’être une personne à vélo, alors nous l’attribuons à cette catégorie. Cependant, cette méthode est rarement optimale; il est donc plus judicieux de fixer le seuil de probabilité en trouvant le point d’équilibre entre la sensibilité (proportion de 1 correctement identifiés) et la spécificité (proportion de 0 correctement identifiés). Ce point d’équilibre est identifiable graphiquement en calculant la spécificité et la sensibilité de la prédiction selon toutes les valeurs possibles du seuil.
library(ROCR)
# Obtention des prédictions du modèle
prob <- predict(model2, type = "response")
# Calcul de la sensibilité et de la spécificité (package ROCR)
predictions <- prediction(prob, dfenquete2$y)
sens <- data.frame(x=unlist(ROCR::performance(predictions, "sens")@x.values),
y=unlist(ROCR::performance(predictions, "sens")@y.values))
spec <- data.frame(x=unlist(ROCR::performance(predictions, "spec")@x.values),
y=unlist(ROCR::performance(predictions, "spec")@y.values))
# Trouver numériquement la valeur seuil (minimiser la différence absolue
# entre sensibilité et spécificité)
real <- dfenquete2$y
find_cutoff <- function(seuil){
pred <- ifelse(prob>seuil,1,0)
sensi <- sum(real==1 & pred==1) / sum(real==1)
spec <- sum(real==0 & pred==0) / sum(real==0)
return(abs(sensi-spec))
}
prob_seuil <- optimize(find_cutoff,interval = c(0,1), maximum = F)$minimum
cat("Le seuil de probabilité à retenir équilibrant",
"la sensibilité et la spécificité est de",prob_seuil)## Le seuil de probabilité à retenir équilibrant la sensibilité et la spécificité est de 0.14785# Affichage du graphique
ggplot() +
geom_line(data = sens, mapping = aes(x = x, y = y)) +
geom_line(data = spec, mapping = aes(x = x,y = y,col="red")) +
scale_y_continuous(sec.axis = sec_axis(~., name = "Spécificité")) +
labs(x='Seuil de probabilité', y="Sensibilité") +
geom_vline(xintercept = prob_seuil, color = "black", linetype = "dashed") +
annotate(geom = "text", x = prob_seuil, y = 0.01, label = round(prob_seuil,3))+
theme(axis.title.y.right = element_text(colour = "red"), legend.position="none")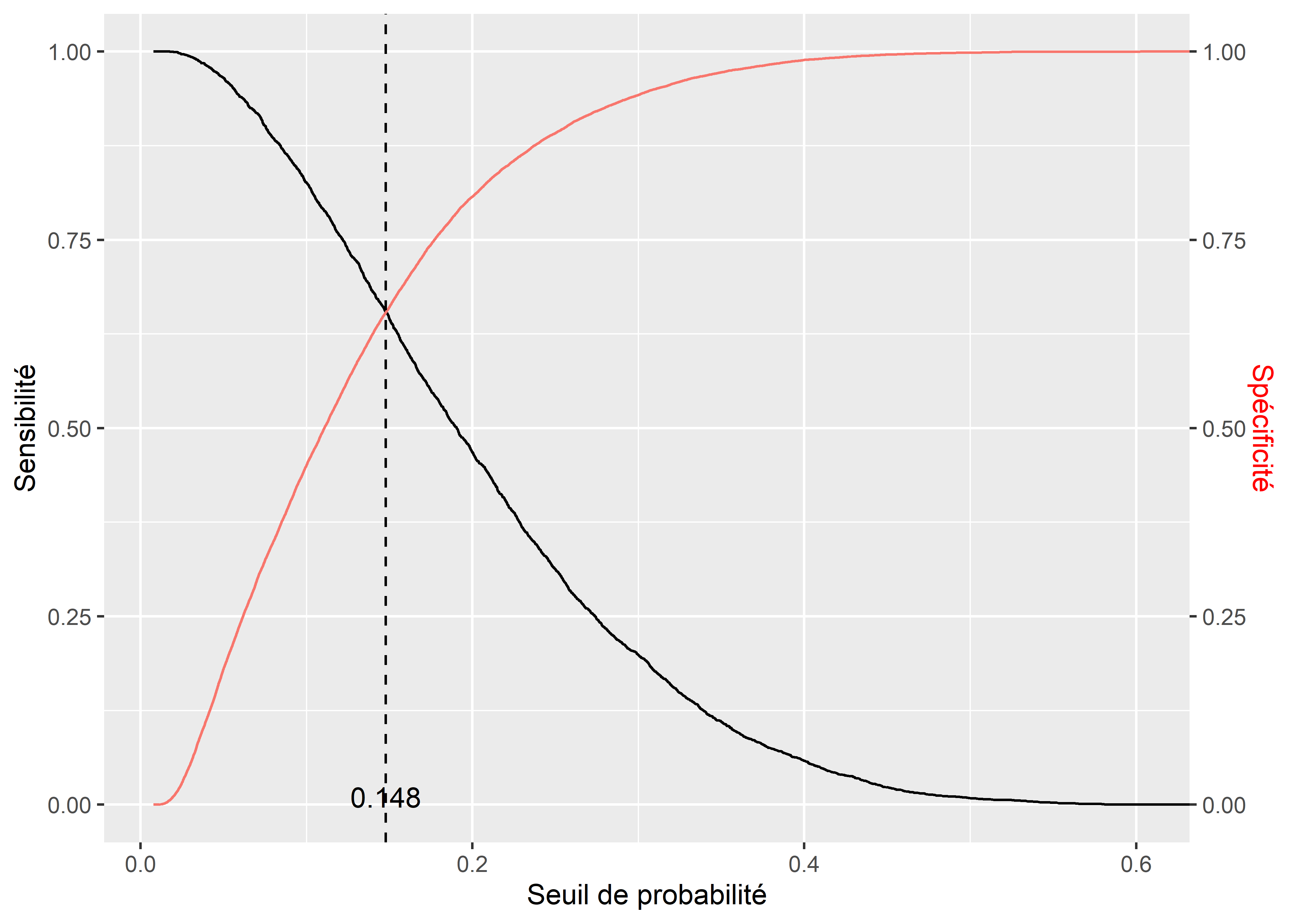
Figure 8.8: Point d’équilibre entre sensibilité et spécificité
Nous constatons à la figure 8.8 que si la valeur du seuil est 0 %, alors la prédiction a une sensibilité parfaite (le modèle prédit toujours 1, donc tous les 1 sont détectés); à l’inverse, si le seuil choisi est 100 %, alors la prédiction à une spécificité parfaite (le modèle prédit toujours 0, donc tous les 0 sont détectés). Dans notre cas, la valeur d’équilibre est d’environ 0,148, donc si le modèle prédit une probabilité au moins égale à 14,8 % qu’un individu utilise le vélo pour son déplacement le plus fréquent, nous devons l’attribuer à la catégorie cycliste. Avec ce seuil, nous pouvons convertir les probabilités prédites en classes prédites et construire notre matrice de confusion.
library(caret) # pour la matrice de confusion
# Calcul des catégories prédites
ypred <- ifelse(predict(model2,type="response")>0.148,1,0)
info <- confusionMatrix(as.factor(dfenquete2$y), as.factor(ypred))
# Affichage des valeurs brutes de la matrice de confusion
print(info)## Confusion Matrix and Statistics
##
## Reference
## Prediction 0 1
## 0 14355 7576
## 1 1251 2365
##
## Accuracy : 0.6545
## 95% CI : (0.6486, 0.6603)
## No Information Rate : 0.6109
## P-Value [Acc > NIR] : < 2.2e-16
##
## Kappa : 0.1783
##
## Mcnemar's Test P-Value : < 2.2e-16
##
## Sensitivity : 0.9198
## Specificity : 0.2379
## Pos Pred Value : 0.6546
## Neg Pred Value : 0.6540
## Prevalence : 0.6109
## Detection Rate : 0.5619
## Detection Prevalence : 0.8585
## Balanced Accuracy : 0.5789
##
## 'Positive' Class : 0
## Les résultats proposés par le package caret sont exhaustifs; nous vous proposons ici une façon de les présenter dans deux tableaux : l’un présente la matrice de confusion (tableau 8.8) et l’autre, les indicateurs de qualité de prédiction (tableau 8.9).
| 0 (réel) | 1 (réel) | Total | % | |
|---|---|---|---|---|
| 0 (prédit) | 14355 | 7576 | 21931 | 85.8 |
| 1 (prédit) | 1251 | 2365 | 3616 | 14.2 |
| Total | 15606 | 9941 | 25547 | |
| % | 61.1 | 38.9 |
D’après ces indicateurs, nous constatons que le modèle a une capacité de prédiction relativement faible, mais tout de même significativement supérieure au seuil de non-information. La valeur de rappel pour la catégorie 1 (cycliste) est faible, indiquant que le modèle a manqué un nombre important de cyclistes lors de sa prédiction.
| Précision | Rappel | F1 | |
|---|---|---|---|
| 0 | 0.65 | 0.92 | 0.76 |
| 1 | 0.65 | 0.24 | 0.35 |
| macro | 0.65 | 0.65 | 0.6 |
| Kappa | 0.18 | ||
| Valeur de p (précision > NIR) | < 0,0001 |
Interprétation des résultats du modèle
L’interprétation des résultats d’un modèle binomial passe par la lecture des rapports de cotes (exponentiel des coefficients) et de leurs intervalles de confiance. Nous commençons donc par calculer la version robuste des erreurs standards des coefficients :
library(sandwich) # pour calculer les erreurs standards robustes
covModel2 <- vcovHC(model2, type = "HC0") # méthode HC0, basée sur les résidus
stdErrRobuste <- sqrt(diag(covModel2)) # extraire la diagonale
# Extraction des coefficients
coeffs <- model2$coefficients
# Recalcul des scores Z
zvalRobuste <- coeffs / stdErrRobuste
# Recalcul des valeurs de P
pvalRobuste <- 2 * pnorm(abs(zvalRobuste), lower.tail = FALSE)
# Calcul des rapports de cote
oddRatio <- exp(coeffs)
# Calcul des intervalles de confiance à 95 % des rapports de cote
lowerBound <- exp(coeffs - 1.96 * stdErrRobuste)
upperBound <- exp(coeffs + 1.96 * stdErrRobuste)
# Étoiles pour les valeurs de p
starsp <- case_when(pvalRobuste <= 0.001 ~ "***",
pvalRobuste > 0.001 & pvalRobuste <= 0.01 ~ "**",
pvalRobuste > 0.01 & pvalRobuste <= 0.05 ~ "*",
pvalRobuste > 0.05 & pvalRobuste <= 0.1 ~ ".",
TRUE ~ ""
)
# Compilation des résultats dans un tableau
tableau_binom <- data.frame(
coefficients = coeffs,
rap.cote = oddRatio,
err.std = stdErrRobuste,
score.z = zvalRobuste,
p.val = pvalRobuste,
rap.cote.2.5 = lowerBound,
rap.cote.97.5 = upperBound,
sign = starsp
)Considérant que la variable Pays a 24 modalités, il est plus judicieux de présenter ses 23 rapports de cotes sous forme d’un graphique. Nous avons choisi l’Allemagne comme catégorie de référence puisqu’elle fait partie des pays avec une importante part modale pour le vélo sans pour autant constituer un cas extrême comme le Danemark.
# Isoler les ligne du tableau récapitualtif pour les pays
paysdf <- subset(tableau_binom, grepl("Pays",row.names(tableau_binom), fixed = T))
#paysdf$Pays <- gsub("Pays","",row.names(paysdf),fixed=T)
paysdf$Pays <- substr(row.names(paysdf), 5, nchar(row.names(paysdf)))
ggplot(data = paysdf) +
geom_vline(xintercept = 1, color = "red")+ #afficher la valeur de référence
geom_errorbarh(aes(xmin = rap.cote.2.5, xmax = rap.cote.97.5,
y = reorder(Pays, rap.cote)), height = 0)+
geom_point(aes(x = rap.cote, y = reorder(Pays, rap.cote))) +
geom_text(aes(x = rap.cote.97.5, y = reorder(Pays, rap.cote),
label = paste("RC : ",round(rap.cote,2),sep="")),
size = 3, nudge_x = 0.25)+
labs(x = "Rapports de cote", y = "Pays (référence : Allemagne)")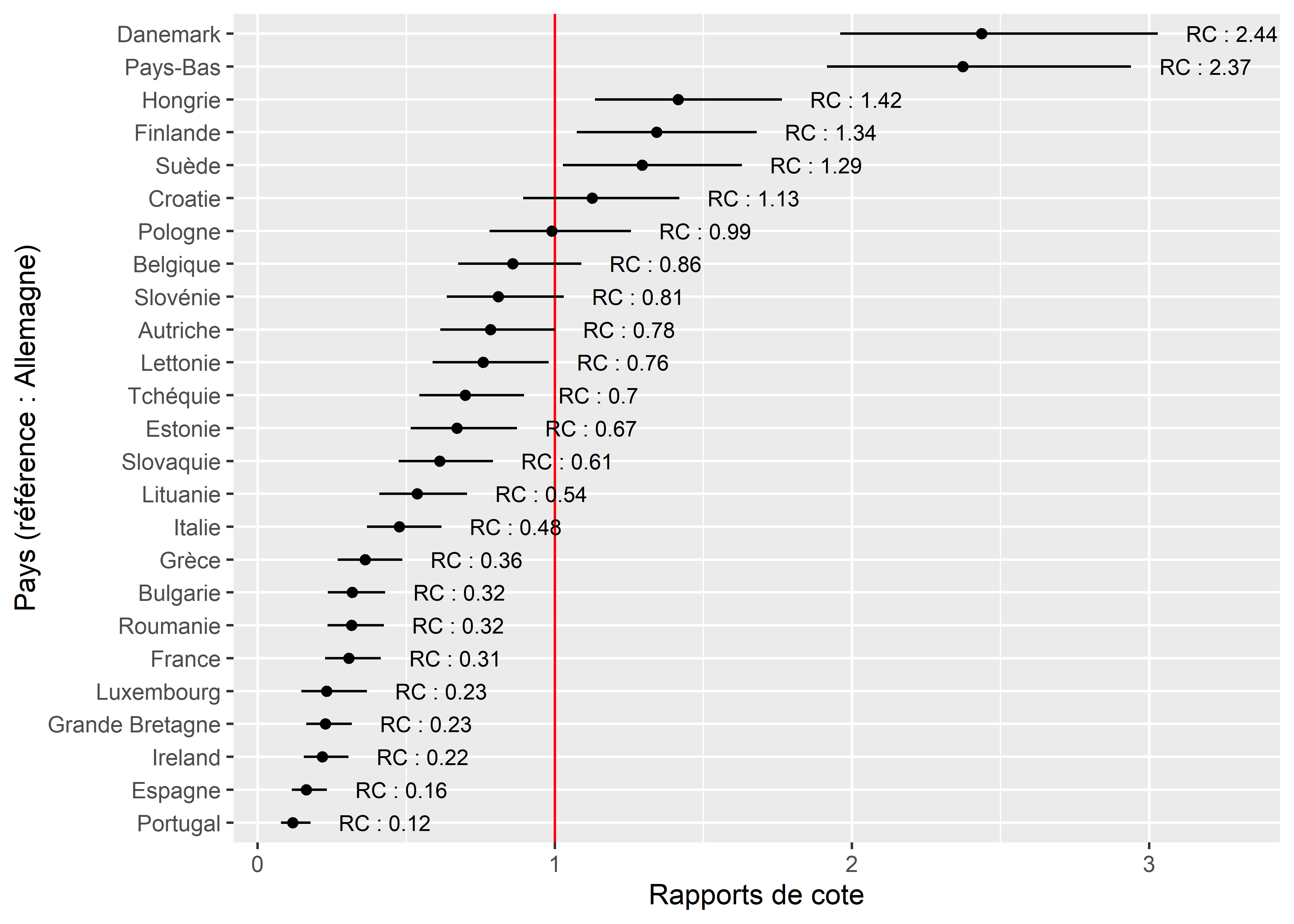
Figure 8.9: Rapports de cote pour les différents pays de l’UE
Dans la figure 8.9, la barre horizontale pour chaque pays représente l’intervalle de confiance de son rapport de cotes (le point); plus cette ligne est longue, plus grande est l’incertitude autour de ce paramètre. Lorsque les lignes de deux pays se chevauchent, cela signifie qu’il n’y a pas de différence significative au seuil 0,05 entre les rapports de cotes des deux pays. La ligne rouge tracée à x = 1, représente le rapport de cotes du pays de référence (ici l’Allemagne). Nous constatons ainsi que comparativement à un individu vivant en Allemagne, ceux vivant au Danemark et aux Pays-Bas ont 2,4 fois plus de chances d’utiliser le vélo pour leur déplacement le plus fréquent. Les Pays de l’Ouest (France, Luxembourg, Royaume-Uni, Irlande) et du Sud (Grèce, Italie, Espagne, Portugal) ont en revanche des rapports de cotes plus faibles. En France, les chances qu’un individu utilise le vélo pour son trajet le plus fréquent sont 3,22 (1/0,31) fois plus faibles que si l’individu vivait en Allemagne.
Pour le reste des coefficients et des rapports de cotes, nous les rapportons dans le tableau 8.10.
| Variable | Coefficient | Rapport de cote | Err.std | Val.z | P | RC 2,5 % | RC 97,5 % |
|---|---|---|---|---|---|---|---|
| Constante | -2,497 | 0,082 | 0,183 | -13,674 | 0,000 | 0,058 | 0,118 |
| Sexe | |||||||
| ref : femme | – | – | – | – | – | – | – |
| homme | 0,372 | 1,451 | 0,038 | 9,803 | 0,000 | 1,347 | 1,562 |
| Age | -0,009 | 0,991 | 0,002 | -5,361 | 0,000 | 0,988 | 0,994 |
| Education | |||||||
| ref : premier cycle | – | – | – | – | – | – | – |
| secondaire | 0,193 | 1,213 | 0,105 | 1,836 | 0,066 | 0,987 | 1,490 |
| secondaire inferieur | 0,301 | 1,351 | 0,114 | 2,649 | 0,008 | 1,081 | 1,687 |
| universite | 0,146 | 1,157 | 0,108 | 1,349 | 0,177 | 0,936 | 1,432 |
| StatutEmploi | |||||||
| ref : employe | – | – | – | – | – | – | – |
| sans emploi | 0,257 | 1,293 | 0,043 | 6,045 | 0,000 | 1,190 | 1,405 |
| Revenu | |||||||
| ref : eleve | – | – | – | – | – | – | – |
| faible | 0,077 | 1,080 | 0,072 | 1,067 | 0,286 | 0,938 | 1,244 |
| moyen | 0,042 | 1,043 | 0,065 | 0,639 | 0,523 | 0,917 | 1,185 |
| sans reponse | 0,217 | 1,242 | 0,102 | 2,120 | 0,034 | 1,016 | 1,517 |
| tres eleve | -0,120 | 0,887 | 0,188 | -0,637 | 0,524 | 0,613 | 1,283 |
| tres faible | 0,240 | 1,271 | 0,086 | 2,776 | 0,006 | 1,073 | 1,505 |
| Residence | |||||||
| ref : aire metropolitaine | – | – | – | – | – | – | – |
| grande ville | 0,273 | 1,314 | 0,070 | 3,911 | 0,000 | 1,146 | 1,507 |
| petite-moyenne ville | 0,277 | 1,319 | 0,061 | 4,503 | 0,000 | 1,169 | 1,487 |
| zone rurale | -0,119 | 0,888 | 0,069 | -1,713 | 0,087 | 0,775 | 1,017 |
| Duree | -0,001 | 0,999 | 0,001 | -0,981 | 0,326 | 0,998 | 1,001 |
| ConsEnv | 0,102 | 1,108 | 0,010 | 10,502 | 0,000 | 1,087 | 1,130 |
Les chances pour un individu d’utiliser le vélo pour son trajet le plus fréquent sont augmentées de 45 % s’il s’agit d’un homme plutôt qu’une femme. Pour l’âge, nous constatons un effet relativement faible puisque chaque année supplémentaire réduit les chances qu’un individu utilise le vélo comme mode de transport pour son trajet le plus fréquent de 0,9 % \(((\mbox{0,991}-\mbox{1})\times\mbox{100})\). Le fait d’être sans emploi augmente les chances d’utiliser le vélo de 29 % comparativement au fait d’avoir un emploi. Concernant le niveau d’éducation, seul le coefficient pour le groupe des personnes de la catégorie « secondaire inférieure » est significatif, indiquant que les personnes de ce groupe ont 35 % de chances en plus d’utiliser le vélo comme mode de transport pour leur déplacement le plus fréquent comparativement aux personnes de la catégorie « premier cycle ». Pour le revenu, seul le groupe avec de très faibles revenus se distingue significativement du groupe avec un revenu élevé avec un rapport de cotes de 1,27, soit 27 % de chances en plus d’utiliser le vélo.
Comparativement à ceux vivant dans une aire métropolitaine, les personnes vivant dans de petites, moyennes et grandes villes ont des chances accrues d’utiliser le vélo comme mode de déplacement pour leur trajet le plus fréquent. En revanche, nous n’observons aucune différence entre la probabilité d’utiliser le vélo dans une métropole et en zone rurale. La figure 8.10 permet de clairement visualiser cette situation. Rappelons que la référence est la situation : vivre dans une région métropolitaine, représentée par la ligne verticale rouge. Plusieurs pistes d’interprétation peuvent être envisagées pour ce résultat :
- En métropole et dans les zones rurales, les distances domicile-travail tendent à être plus grandes que dans les petites, moyennes et grandes villes.
- En métropole, le système de transport en commun est davantage développé et entre donc en concurrence avec les modes de transport actifs.
# Isoler les lignes du tableau récapitualtif pour les lieux de résidence
residdf <- subset(tableau_binom, grepl("Residence",row.names(tableau_binom), fixed = T))
residdf$resid <- gsub("Residence","",row.names(residdf),fixed=T)
ggplot(data = residdf) +
geom_vline(xintercept = 1, color = "red")+ #afficher la valeur de référence
geom_errorbarh(aes(xmin = rap.cote.2.5, xmax = rap.cote.97.5, y = resid), height = 0)+
geom_point(aes(x = rap.cote, y = resid)) +
geom_text(aes(x = rap.cote.97.5, y = resid,
label = paste("RC : ",round(rap.cote,2),sep="")),
size = 3, nudge_x = 0.1)+
labs(x = "Rapports de cotes",
y = "Lieu de résidence (référence : aire métropolitaine)")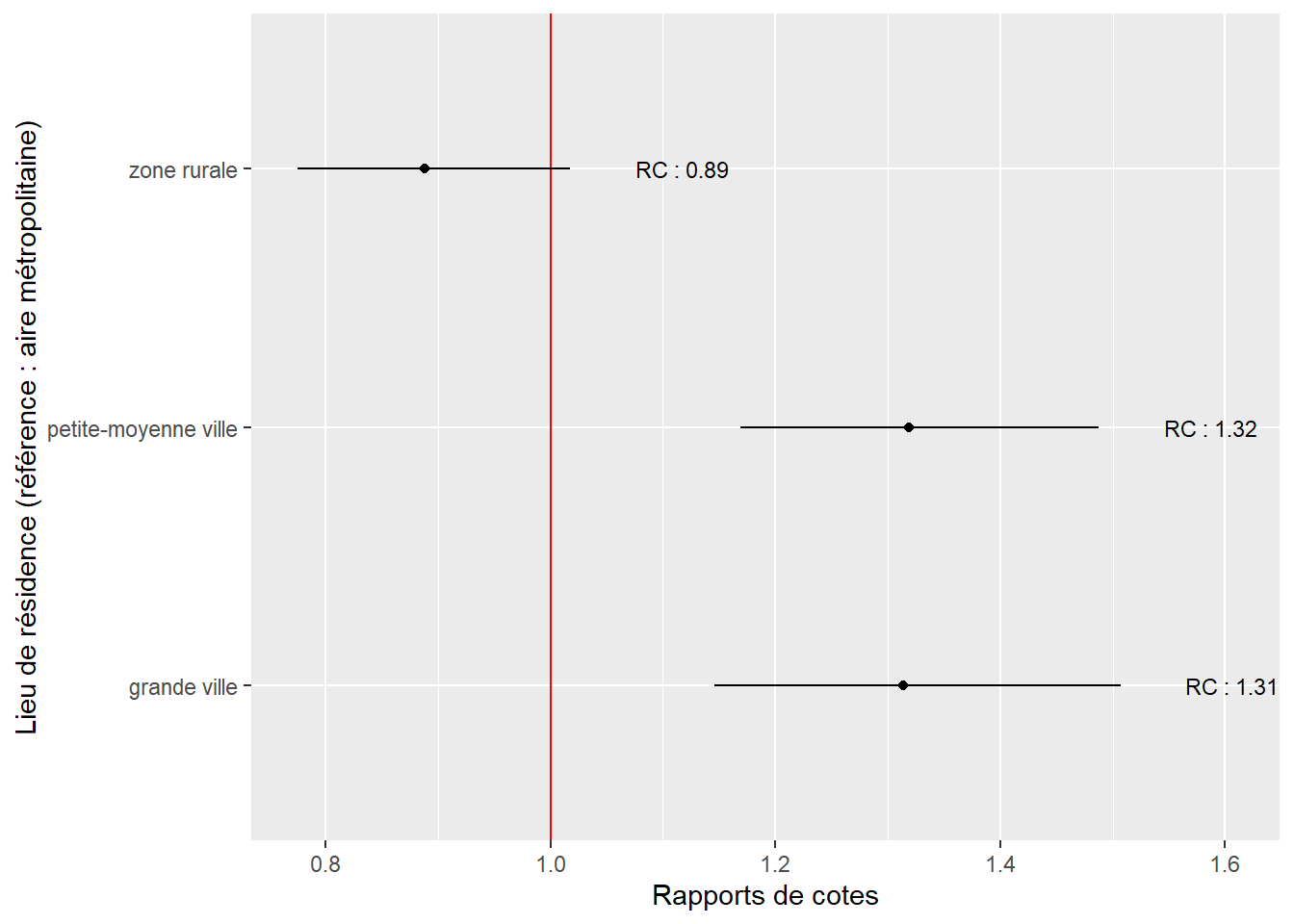
Figure 8.10: Rapports de cote pour les différents lieux de résidence
Il est aussi intéressant de noter que la durée des trajets ne semble pas influencer la probabilité d’utiliser le vélo. Enfin, une conscience environnementale plus affirmée semble être associée avec une probabilité supérieure d’utiliser le vélo pour son déplacement le plus fréquent, avec une augmentation des chances de 11 % pour chaque point supplémentaire sur l’échelle de Likert.
Afin de simplifier la présentation de certains résultats, il est possible de calculer exactement les prédictions réalisées par le modèle. Un bon exemple ici est le cas de la variable âge. À quelle différence pouvons-nous nous attendre entre deux individus identiques ayant seulement une différence d’âge de 15 ans?
Prenons comme individu un homme de 30 ans, vivant dans une grande ville allemande, ayant un niveau d’éducation de niveau secondaire, employé, dans la tranche de revenu moyen, déclarant effectuer un trajet de 45 minutes et ayant rapporté un niveau de conscience environnementale de 5 (sur 10). Nous pouvons prédire la probabilité qu’il utilise le vélo pour son trajet le plus fréquent en utilisant la formule suivante :
\(logit(p) = -\mbox{2,497} + \mbox{1} \times \mbox{0,372} + \mbox{30} \times -\mbox{0,009} + \mbox{1} \times \mbox{0,193} + \mbox{1} \times \mbox{0,042} + \mbox{1} \times \mbox{0,273} + \mbox{45} \times -\mbox{0,001} + \mbox{5} \times \mbox{0,102}\)
\(p = exp(-\mbox{2,497} + \mbox{1} \times \mbox{0,372} + \mbox{30} \times -\mbox{0,009} + \mbox{1} \times \mbox{0,193} + \mbox{1} \times \mbox{0,042} + 1 \times \mbox{0,273} + 45 \times -\mbox{0,001} + \mbox{5} \times \mbox{0,102})/(\mbox{1}+exp(-\mbox{2,497} + 1 \times \mbox{0,372} + \mbox{30} \times-\mbox{0,009} + 1 \times \mbox{0,193} + 1 \times \mbox{0,042} + \mbox{1} \times \mbox{0,273} + \mbox{45} \times -\mbox{0,001} + 5 \times \mbox{0,102})) = \mbox{0,194}\)
Il y aurait 19,4 % de chances pour que cette personne soit cycliste. Comme cette probabilité dépasse le seuil que nous avons sélectionné, cette personne serait classée comme cycliste. Si nous augmentons son âge de 15 ans, nous obtenons :
\(p = exp(-\mbox{2,497} + \mbox{1} \times \mbox{0,372} + \mbox{45} \times \mbox{-0,009} + \mbox{1} \times \mbox{0,193} + \mbox{1} \times \mbox{0,042} + \mbox{1} \times \mbox{0,273} + \mbox{45} \times -\mbox{0,001} + \mbox{5} \times \mbox{0,102}) / (\mbox{1}+exp(-\mbox{2,497} + \mbox{1} \times \mbox{0,372} + \mbox{45} \times -\mbox{0,009} + \mbox{1} \times \mbox{0,193} + \mbox{1} \times \mbox{0,042} + \mbox{1} \times \mbox{0,273} + \mbox{45} \times -\mbox{0,001} + \mbox{5} \times \mbox{0,102})) = \mbox{0,174}\)
soit une réduction de 2 points de pourcentages. Il est également possible de représenter cette évolution sur un graphique pour montrer l’effet sur l’étendue des valeurs possibles. Sur ces graphiques des effets marginaux, il est essentiel de représenter l’incertitude quant à la prédiction. En temps normal, la fonction predict calcule directement l’erreur standard de la prédiction et cette dernière peut être utilisée pour calculer l’intervalle de confiance de la prédiction. Cependant, nous voulons ici utiliser nos erreurs standards robustes. Nous devons donc procéder par simulation pour déterminer l’intervalle de confiance à 95 % de nos prédictions. Cette opération nécessite de réaliser plusieurs opérations manuellement dans R.
# Créer un jeu de données fictif pour la prédiction
mat <- model.matrix(model2$terms, model2$model)
age2seq <- seq(20,80)
mat2 <- matrix(mat[1,], nrow=length(age2seq), ncol=length(mat[1,]), byrow=TRUE)
colnames(mat2) <- colnames(mat)
mat2[,"Age"] <- age2seq
mat2[,"PaysBelgique"] <- 0
mat2[,"Duree"] <- 45
mat2[,"ConsEnv"] <- 5
mat2[,"StatutEmploisans emploi"] <- 0
mat2[,"Residencegrande ville"] <- 1
mat2[,"Educationsecondaire"] <- 1
mat2[,"Sexehomme"] <- 1
mat2[,"Revenumoyen"] <- 1
mat2[,"Revenufaible"] <- 0
# Calculer la prédiction comme un log de rapport de cote (avec les erreurs standards)
# en multipliant les coefficient par les valeurs des données fictives
coeffs <- model2$coefficients
pred <- coeffs %*% t(mat2)
# Simulation de prédictions (toujours en log de rapport de cote)
# Étape 1 : simuler 1000 valeurs pour chaque coefficient
sim_coeffs <- lapply(1:length(coeffs), function(i){
coef <- coeffs[[i]]
std.err <- stdErrRobuste[[i]]
vals <- rnorm(n = 1000, mean = coef, sd = std.err)
return(vals)
})
mat_sim_coeffs <- do.call(rbind,sim_coeffs)
# Étape 2 : effectuer les prédictions à partir des coefficients simulés
sim_preds <- lapply(1:ncol(mat_sim_coeffs),function(i){
temp_coefs <- mat_sim_coeffs[,i]
temp_pred <- as.vector(temp_coefs %*% t(mat2))
return(temp_pred)
})
mat_sim_preds <- do.call(cbind,sim_preds)
# Étape 3 : extraire les intervalles de confiances pour les simulations
intervals <- apply(mat_sim_preds,MARGIN = 1, FUN = function(vec){
return(quantile(vec,probs = c(0.025, 0.975)))
})
# Étape 4 : récupérer tous ces éléments dans un DataFrame
df <- data.frame(
Age = seq(20,80),
pred = as.vector(pred),
lower = as.vector(intervals[1,]),
upper = as.vector(intervals[2,])
)
# Étape 5 : appliquer l'inverse de la fonction de lien pour
# obtenir les prédictions en termes de probabilité
ilink <- family(model2)$linkinv
df$prob_pred <- ilink(df$pred)
df$prob_lower <- ilink(df$lower)
df$prob_upper <- ilink(df$upper)
# Étape 6 : représenter le tout sur un graphique
ggplot(df) +
geom_ribbon(aes(x = Age, ymax = prob_upper, ymin = prob_lower),
fill = rgb(0.1,0.1,0.1,0.4)) +
geom_path(aes(x = Age, y = prob_pred), color = "blue", size = 1) +
geom_hline(yintercept = 0.15, linetype = "dashed", size = 0.7) +
labs(x = "Âge", y = "Probabilité prédite (intervalle de confiance à 95 %)")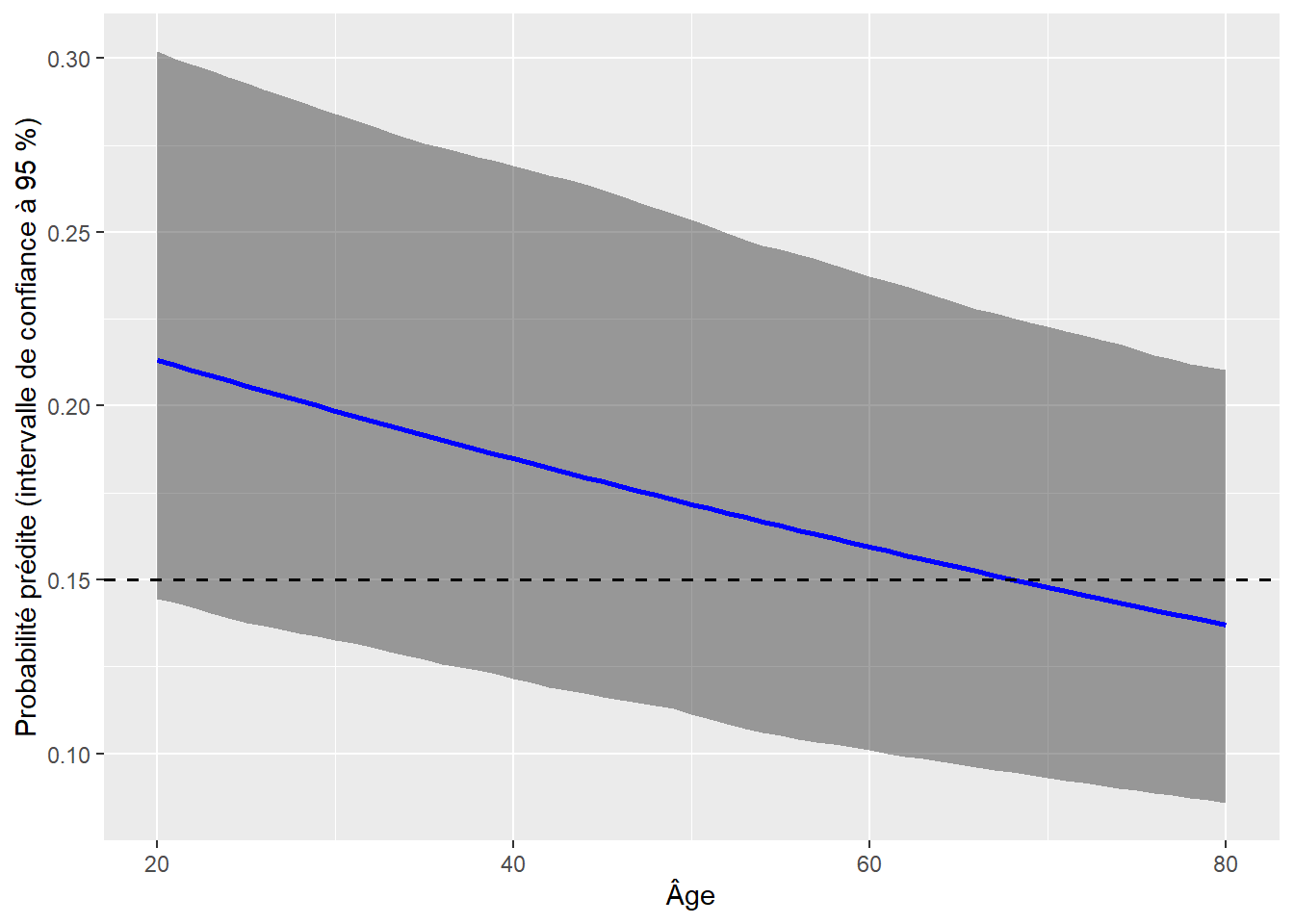
Figure 8.11: Effet de l’âge sur la probabilité d’utiliser le vélo comme moyen de déplacement pour son trajet le plus fréquent
La figure 8.11 permet de bien constater la diminution de la probabilité d’utiliser le vélo pour son trajet le plus fréquent avec l’âge, mais cette réduction est relativement ténue. Dans le cas utilisé en exemple, l’individu ne serait plus classé cycliste qu’après 67 ans.
8.2.2 Modèle probit binomial
Le modèle GLM probit binomial est pour ainsi dire le frère du modèle logistique binomial. La seule différence entre les deux réside dans l’utilisation d’une autre fonction de lien: probit plutôt que logistique. La fonction de lien probit (Φ) correspond à la fonction cumulative de la distribution normale et a également une forme de S. Cette version du modèle est plus souvent utilisée par les économistes. Le principal changement réside dans l’interprétation des coefficients \(\beta_0\) et \(\beta\). Du fait de la transformation probit, ces derniers indiquent le changement en termes de scores Z de la probabilité modélisée. Vous conviendrez qu’il ne s’agit pas d’une échelle très intuitive; la plupart du temps, seuls la significativité et le signe (positif ou négatif) des coefficients sont interprétés.
| Type de variable dépendante | Variable binaire (0 ou 1) ou comptage de réussite à une expérience (ex : 3 réussites sur 5 expériences) |
| Distribution utilisée | Binomiale |
| Formulation |
\(Y \sim Binomial(p)\) \(g(p) = \beta_0 + \beta X\) \(g(x) = \Phi^-1(x)\) |
| Fonction de lien | probit |
| Paramètre modélisé | p |
| Paramètres à estimer | \(\beta_0\), \(\beta\) |
| Conditions d’application | Non-séparation complète, absence de sur-dispersion ou de sous-dispersion |
8.2.3 Modèle logistique des cotes proportionnelles
Le modèle logistique des cotes proportionnelles (aussi appelé modèle logistique cumulatif) est utilisé pour modéliser une variable qualitative ordinale. Un exemple classique de ce type de variable est une échelle de satisfaction (très insatisfait, insatisfait, mitigé, satisfait, très satisfait) qui peut être recodée avec des valeurs numériques (0, 1, 2, 3, 4; ces échelons étant notés j). Il n’existe pas à proprement parler de distribution pour représenter ces données, mais avec une petite astuce, il est possible de simplement utiliser la distribution binomiale. Cette astuce consiste à poser l’hypothèse de la proportionnalité des cotes, soit que le passage de la catégorie 0 à la catégorie 1 est proportionnel au passage de la catégorie 1 à la catégorie 2 et ainsi de suite. Si cette hypothèse est respectée, alors les coefficients du modèle pourront autant décrire le passage de la catégorie satisfait à celle très satisfait que le passage de insatisfait à mitigé. Si cette hypothèse n’est pas respectée, il faudrait des coefficients différents pour représenter les passages d’une catégorie à l’autre (ce qui est le cas pour le modèle multinomial présenté dans la section 8.2.4).
| Type de variable dépendante | Variable qualitative ordinale avec j catégories |
| Distribution utilisée | Binomiale |
| Formulation |
\(Y \sim Binomial(p)\) \(g(p \leq j) = \beta_{0j} + \beta X\) \(g(x) = log(\frac{x}{1-x})\) |
| Fonction de lien | logistique |
| Paramètre modélisé | p |
| Paramètres à estimer | \(\beta\) et j-1 constantes \(\beta_{0j}\) |
| Conditions d’application | Non-séparation complète, absence de sur-dispersion ou de sous-dispersion, Proportionnalité des cotes |
Ainsi, dans le modèle logistique binomial vu précédemment, nous modélisons la probabilité d’observer un évènement \(P(Y = 1)\). Dans un modèle logistique ordinal, nous modélisons la probabilité cumulative d’observer l’échelon j de notre variable ordinale \(P(Y \leq j)\). L’intérêt de cette reformulation est que nous conservons la facilité d’interprétation du modèle logistique binomial classique avec les rapports de cotes, à ceci prêt qu’ils représentent maintenant la probabilité de passer à un échelon supérieur de Y. La différence pratique est que notre modèle se retrouve avec autant de constantes qu’il y a de catégories à prédire moins une, chacune de ces constantes contrôlant la probabilité de base de passer de la catégorie j à la catégorie j + 1.
8.2.3.1 Conditions d’application
Les conditions d’application sont les mêmes que pour un modèle binomial, avec bien sûr l’ajout de l’hypothèse sur la proportionnalité des cotes. Selon cette hypothèse, l’effet de chaque variable indépendante est identique sur la probabilité de passer d’un échelon de la variable Y au suivant. Afin de tester cette condition, deux approches sont envisageables :
- Utiliser l’approche de Brant (1990). Il s’agit d’un test statistique comparant les résultats du modèle ordinal avec ceux d’une série de modèles logistiques binomiaux (1 pour chaque catégorie possible de Y).
- Ajuster un modèle ordinal sans l’hypothèse de proportionnalité des cotes et effectuer un test de ratio des likelihood pour vérifier si le premier est significativement mieux ajusté.
Si certaines variables ne respectent pas cette condition d’application, trois options sont possibles pour y remédier :
- Supprimer la variable du modèle (à éviter si cette variable est importante dans votre cadre théorique).
- Autoriser la variable à avoir un effet différent entre chaque palier (possible avec le package
VGAM). - Changer de modèle et opter pour un modèle des catégories adjacentes. Il s’agit du cas particulier où toutes les variables sont autorisées à changer à chaque niveau. Ne pas confondre ce dernier modèle et le modèle multinomial (section 8.2.4)), puisque le modèle des catégories adjacentes continue à prédire la probabilité de passer à une catégorie supérieure.
8.2.3.2 Exemple appliqué dans R
Pour cet exemple, nous analysons un jeu de données proposé par Inside Airbnb, une organisation sans but lucratif collectant des données des annonces sur le site d’Airbnb pour alimenter le débat sur l’effet de cette société sur les quartiers. Plus spécifiquement, nous utilisons le jeu de données pour Montréal compilé le 30 juin 2020. Nous modélisons ici le prix par nuit des logements, ce type d’exercice est appelé modélisation hédonique. Il est particulièrement utilisé en économie urbaine pour évaluer les déterminants du marché immobilier et prédire son évolution. Le cas d’Airbnb a déjà été étudié dans plusieurs articles (Teubner, Hawlitschek et Dann 2017; Wang et Nicolau 2017; Zhang et al. 2017). Il en ressort notamment que le niveau de confiance inspiré par l’hôte, les caractéristiques intrinsèques du logement et sa localisation sont les principales variables indépendantes de son prix. Nous construisons donc notre modèle sur cette base. Notez que nous avons décidé de retirer les logements avec des prix supérieurs à 250 $ par nuit qui constituent des cas particuliers et qui devraient faire l’objet d’une analyse à part entière. Nous avons également retiré les observations pour lesquelles certaines données sont manquantes, et obtenons un nombre final de 9 051 observations.
La distribution originale du prix des logements dans notre jeu de données est présentée à la figure 8.12.
# Charger le jeu de données
data_airbnb <- read.csv("data/glm/airbnb_data.csv")
# Afficher la distribution du prix
ggplot(data = data_airbnb) +
geom_histogram(aes(x = price), bins = 30,
color = "white", fill = "#1d3557", size = 0.02)+
labs(x="Prix (en dollars)", y="Fréquence")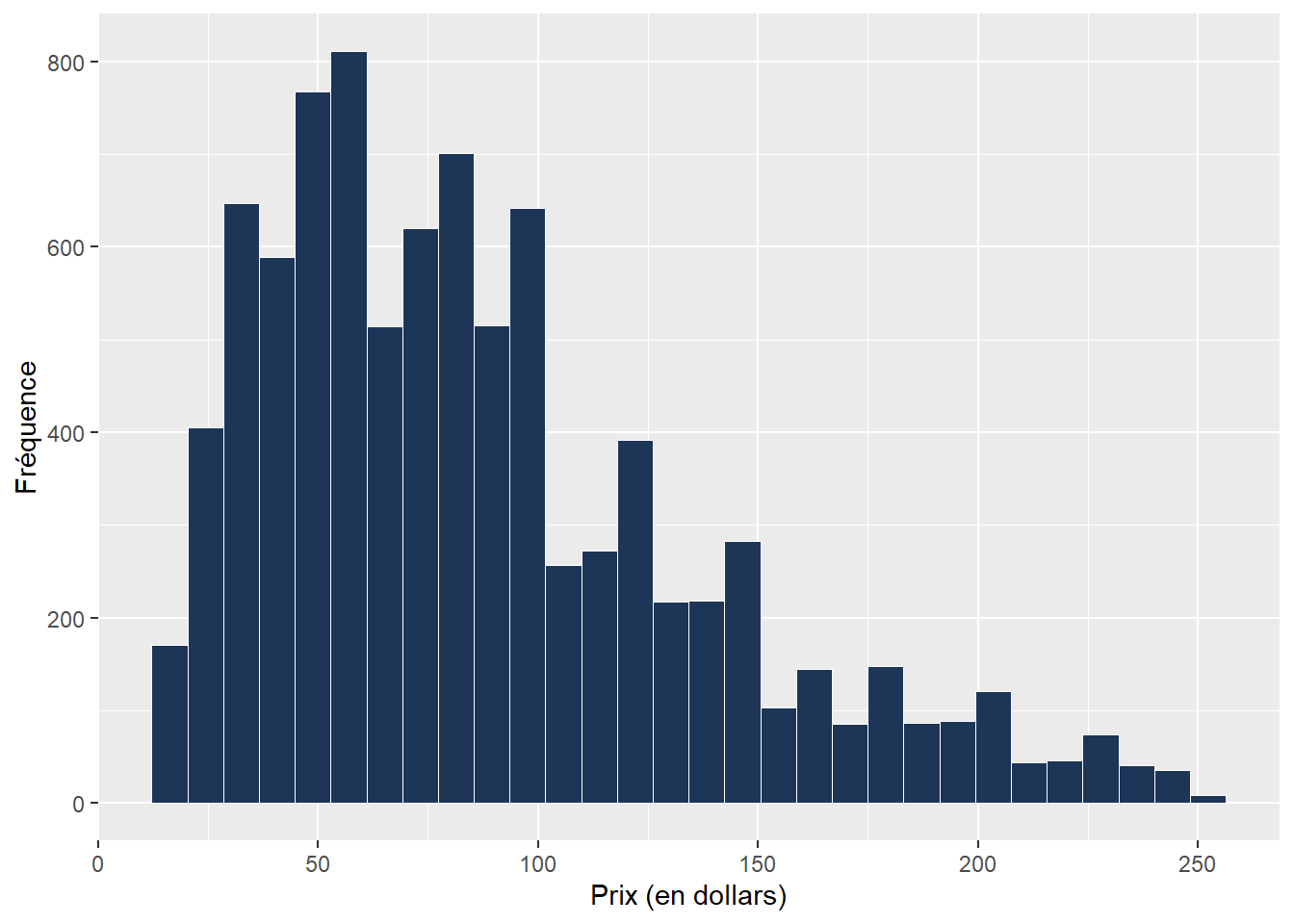
Figure 8.12: Distribution des prix des logements Airbnb
Nous avons ensuite découpé le prix des logements en trois catégories : inférieur à 50 $, de 50 $ à 99 $ et de 100 $ à 249 $. Ces catégories forment une variable ordinale de trois échelons que nous modélisons à partir de trois catégories de variables :
- les caractéristiques propres au logement;
- les caractéristiques environnementales autour du logement;
- les notes obtenues par le logement sur le site d’Airbnb.
# Afficher le nombre de logement par catégories
table(data_airbnb$fac_price_cat)##
## 1 2 3
## 2212 3911 2928Le tableau 8.13 présente l’ensemble des variables utilisées dans le modèle.
| Nom de la variable | Description | Type de variable | Mesure |
|---|---|---|---|
| beds | Nombre de lits dans le logement | Variable de comptage | Nombre de lits dans le logement |
| Garden_or_backyard | Présence d’un jardin ou d’une arrière-cour | Variable binaire | Oui ou non |
| private | Le logement est entièrement à disposition du locataire ou seulement une pièce | Variable binaire | Privé ou partagé |
| Free_street_parking | Une place de stationnement gratuite est disponible sur la rue | Variable binaire | Oui ou non |
| Host_greets_you | L’hôte accueille personnellement les locataires | Variable binaire | Oui ou non |
| prt_veg_500m | Végétation dans les environs du logement | Variable continue | Pourcentage de surface végétale dans un rayon de 500 mètres autour du logement |
| has_metro_500m | Présence d’une station de métro à proximité du logement | Variable binaire | Présence d’une station de métro dans un rayon de 500 mètres autour du logement |
| commercial_1km | Commerce dans les environs du logement | Variable continue | Pourcentage de surface dédiée au commerce (mode d’occupation du sol) dans un rayon d’un kilomètre autour du logement |
| cat_review | Évaluation de la qualité du logement par les usagers | Variable ordinale | Note obtenue par le logement sur une échelle allant de 1 (très mauvais) à 5 (parfait) |
| host_total_listings_count | Nombre total de logements détenus par l’hôte sur Airbnb | Variable de comptage | Nombre total de logements détenus par l’hôte sur Airbnb |
Vérification des conditions d’application
Avant d’ajuster le modèle, il convient de vérifier l’absence de multicolinéarité excessive entre les variables indépendantes.
# Notez que la fonction vif ne s'intéresse qu'aux variables indépendantes.
# Vous pouvez ainsi utiliser la fonction glm avec la fonction vif
# pour n'importe quel modèle glm
vif(glm(price ~ beds +
Garden_or_backyard + Host_greets_you + Free_street_parking +
prt_veg_500m + has_metro_500m + commercial_1km +host_total_listings_count +
private + cat_review, data = data_airbnb))## beds Garden_or_backyard Host_greets_you Free_street_parking
## 1.123595 1.079324 1.046884 1.142189
## prt_veg_500m has_metro_500m commercial_1km host_total_listings_count
## 1.532536 1.239516 1.225301 1.058232
## private cat_review
## 1.143932 1.015778Toutes les valeurs de VIF sont inférieures à 2, indiquant une absence de multicolinéarité excessive. Nous pouvons alors ajuster le modèle et analyser les distances de Cook afin de vérifier la présence ou non d’observations très influentes. Pour ajuster le modèle, nous utilisons le package VGAM et la fonction vglm qui nous donnent accès à la famille cumulative pour ajuster des modèles logistiques ordinaux. Notez que le fonctionnement de base de cette famille est de modéliser \(P(Y\leq1),P(Y\leq2),...,P(Y\leq J)\) avec J le nombre de catégories. Cependant, nous voulons ici modéliser la probabilité de passer à une catégorie supérieure de prix. Pour cela, il est nécessaire de spécifier le paramètre reverse = TRUE pour la famille cumulative (voir help(cumulative) pour plus de détails).
library(VGAM)
modele <- vglm(fac_price_cat ~ beds +
Garden_or_backyard + Free_street_parking +
prt_veg_500m + has_metro_500m + commercial_1km +
private + cat_review + host_total_listings_count ,
family = cumulative(link="logitlink", # fonction de lien
parallel = TRUE, # cote proportionelle
reverse = TRUE),
data = data_airbnb, model = T)Notez que, puisque la variable Y a trois catégories différentes et que nous modélisons la probabilité de passer à une catégorie supérieure, chaque observation a alors deux (3-1) valeurs de résidus différentes. Par conséquent, nous calculons deux distances de Cook différentes que nous devons analyser conjointement. Malheureusement, la fonction cook.distance ne fonctionne pas avec les objets vglm, nous devons donc les calculer manuellement.
# Extraction des résidus
res <- residuals(modele, type = "pearson")
# Extraction de la hat matrix (nécessaire pour calculer la distance de Cook)
hat <- hatvaluesvlm(modele)
# Calcul des distances de Cook
cooks <- lapply(1:ncol(res),function(i){
r <- res[,i]
h <- hat[,i]
cook <- (r/(1 - h))^2 * h/(1 * modele@rank)
})
# Structuration dans un DataFrame
matcook <- data.frame(do.call(cbind, cooks))
names(matcook) <- c("dist1","dist2")
matcook$oid <- 1:nrow(matcook)
# Afficher les distances de Cook
plot1 <- ggplot(data = matcook) +
geom_point(aes(x = oid, y = dist1), size = 0.2, color = rgb(0.1,0.1,0.1,0.4)) +
labs(x = "", y = "", subtitle = "distance de Cook P(Y>=2)")+
theme(axis.ticks.x = element_blank(),
axis.text.x = element_blank())
plot2 <- ggplot(data = matcook) +
geom_point(aes(x = oid, y = dist2), size = 0.2, color = rgb(0.1,0.1,0.1,0.4)) +
labs(x = "", y = "", subtitle = "distance de Cook P(Y>=3)")+
theme(axis.ticks.x = element_blank(),
axis.text.x = element_blank())
ggarrange(plot1, plot2, ncol = 2, nrow = 1)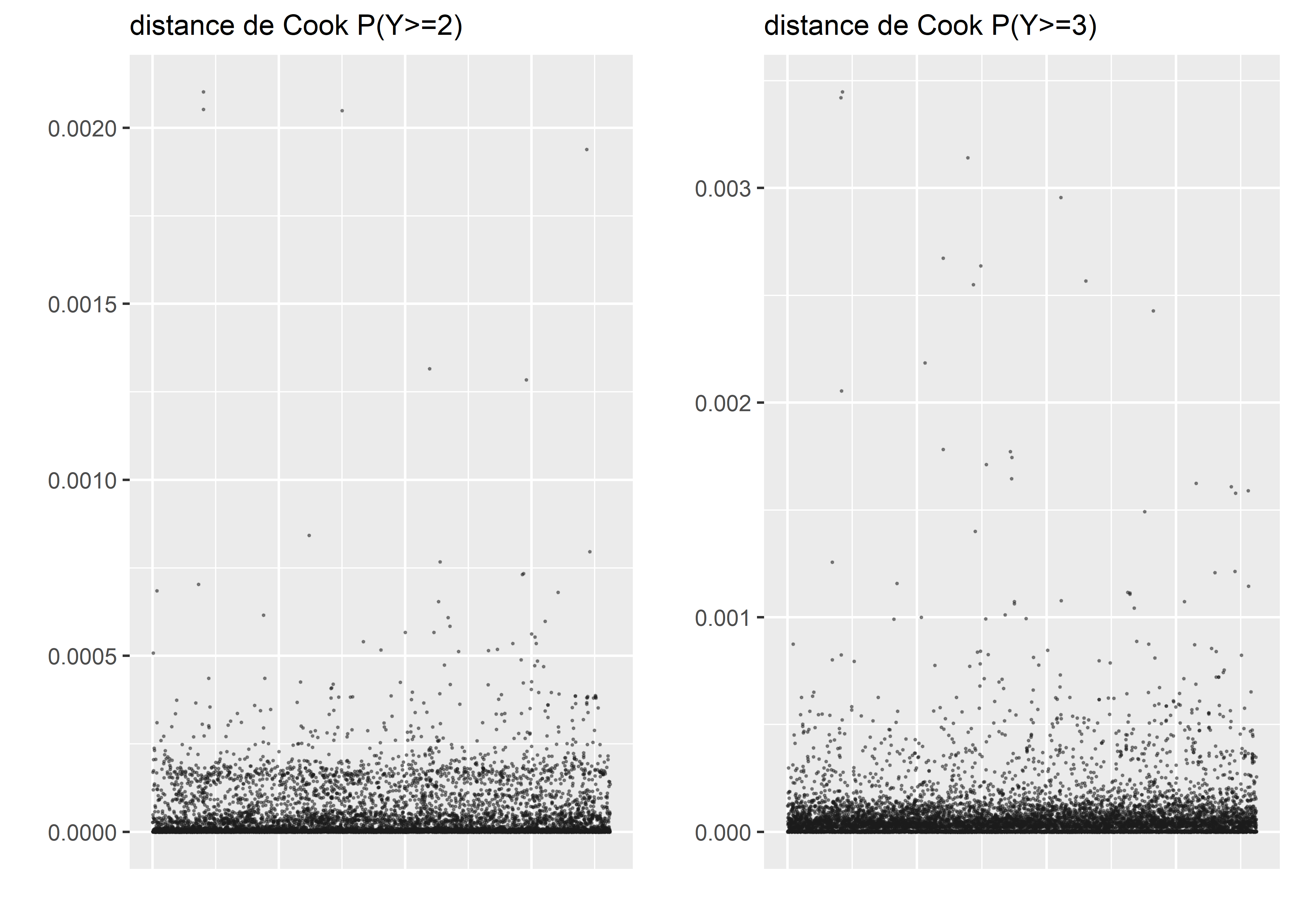
Figure 8.13: Distances de Cook pour le modèle logistique des cotes proportionnelles
Les distances de Cook (figure 8.13) nous permettent d’identifier quelques observations potentiellement trop influentes, mais elles semblent être différentes d’un graphique à l’autre. Nous décidons donc de ne pas retirer d’observations à ce stade et de passer à l’analyse des résidus simulés. Pour effectuer des simulations à partir de ce modèle, nous nous basons sur les probabilités d’appartenance prédites par le modèle.
# Extraire les probabilités prédites
predicted <- predict(modele,type = "response")
round(head(predicted,n = 4),3)## 1 2 3
## 1 0.706 0.267 0.028
## 2 0.073 0.461 0.466
## 3 0.687 0.283 0.030
## 4 0.049 0.383 0.568Nous constatons ainsi que, pour la première observation, la probabilité prédite d’appartenir au groupe 1 est de 69,4 %, de 27,7 % pour le groupe 2 et de 2,9 % pour le groupe 3. Si nous effectuons 1 000 simulations, nous pouvons nous attendre à ce qu’en moyenne, sur ces 1 000 simulations, 694 indiqueront 1 comme catégorie prédite, 277 indiqueront 2 et seulement 29 indiqueront 3.
# Nous effectuerons 1000 simulations
nsim <- 1000
# Lancement des simulations pour chaque observation (lignes dans predicted)
simulations <- lapply(1:nrow(predicted), function(i){
probs <- predicted[i,]
sims <- sample(c(1,2,3), size = nsim, replace = T, prob = probs)
return(sims)
})
# Combiner les prédictions dans un tableau
matsim <- do.call(rbind, simulations)
# Observons si nos simulations sont proches de ce que nous attendions
table(matsim[1,])##
## 1 2 3
## 713 268 19À partir de ces simulations de prédiction, nous pouvons réaliser un diagnostic des résidus simulés grâce au package DHARMa.
library(DHARMa)
# Extraction de la prédiction moyenne du modèle
pred_cat <- unique(data_airbnb$fac_price_cat)[max.col(predicted)]
# Préparer les données avec le package DHARMa
sim_res <- createDHARMa(simulatedResponse = matsim,
observedResponse = as.numeric(data_airbnb$fac_price_cat),
fittedPredictedResponse = as.numeric(pred_cat),
integerResponse = T)
# Afficher le graphique de diagnostic général
plot(sim_res)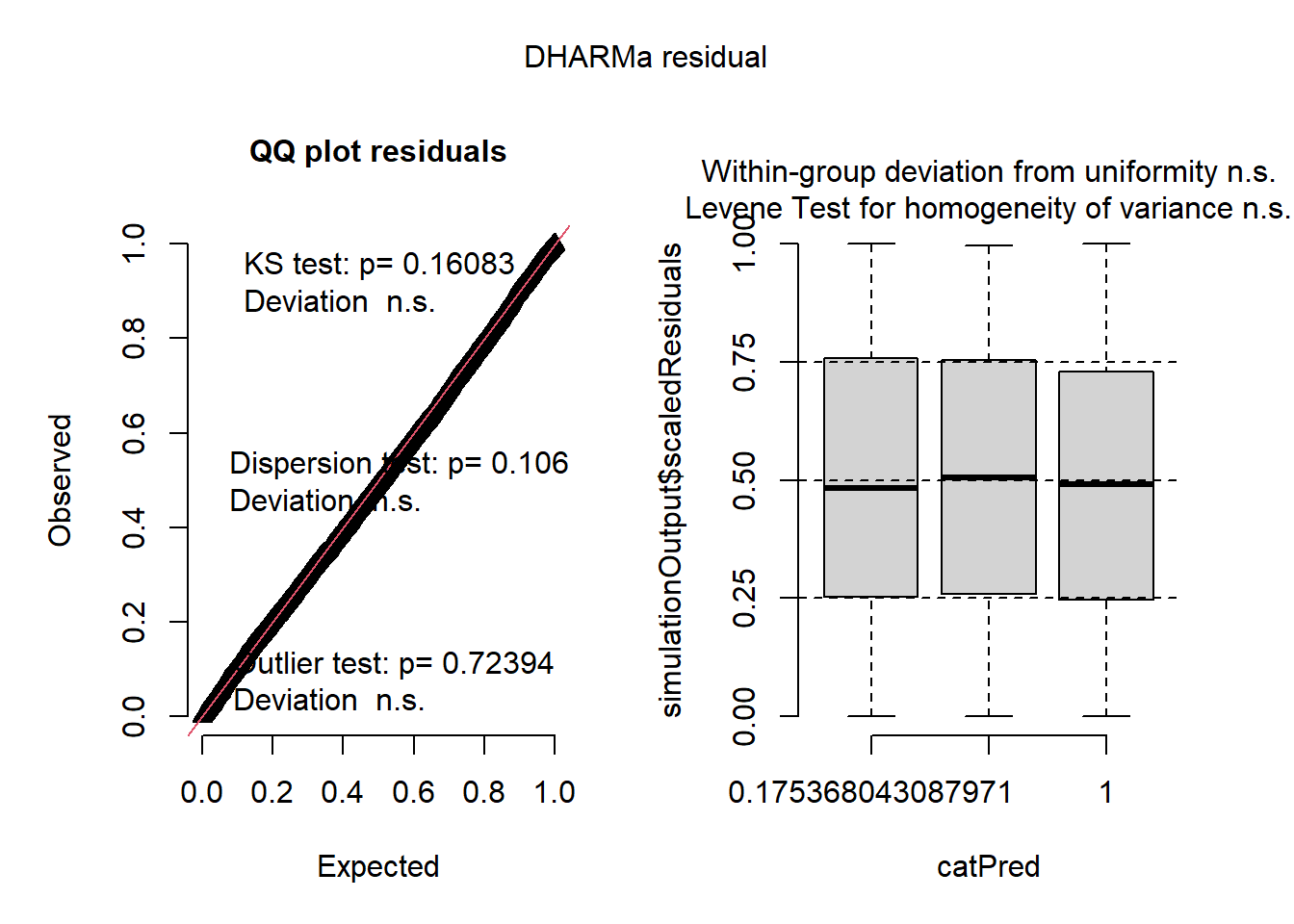
Figure 8.14: Diagnostic général des résidus simulés du modèle des cotes proportionnelles
La figure 8.14 nous indique que les résidus simulés suivent bien une distribution uniforme et qu’aucune valeur aberrante n’est observable. Pour affiner notre diagnostic, nous vérifions également si aucune relation ne semble exister entre chaque variable indépendante et les résidus.
# Préparons un plot multiple
par(mfrow=c(3,4))
vars <- c("nombre de lits" = "beds",
"couvert végétal" = "prt_veg_500m",
"commercial" = "commercial_1km",
"nb logements hôte" = "host_total_listings_count",
"jardin" = "Garden_or_backyard",
"accueil" = "Host_greets_you",
"stationnement gratuit" = "Free_street_parking",
"métro" = "has_metro_500m",
"logement privé" = "private",
"évaluation" = "cat_review")
for(name in names(vars)){
v <- vars[[name]]
plotResiduals(sim_res, data_airbnb[[v]], rank = F, quantreg = F, main = "",
xlab = name, ylab = "résidus")
}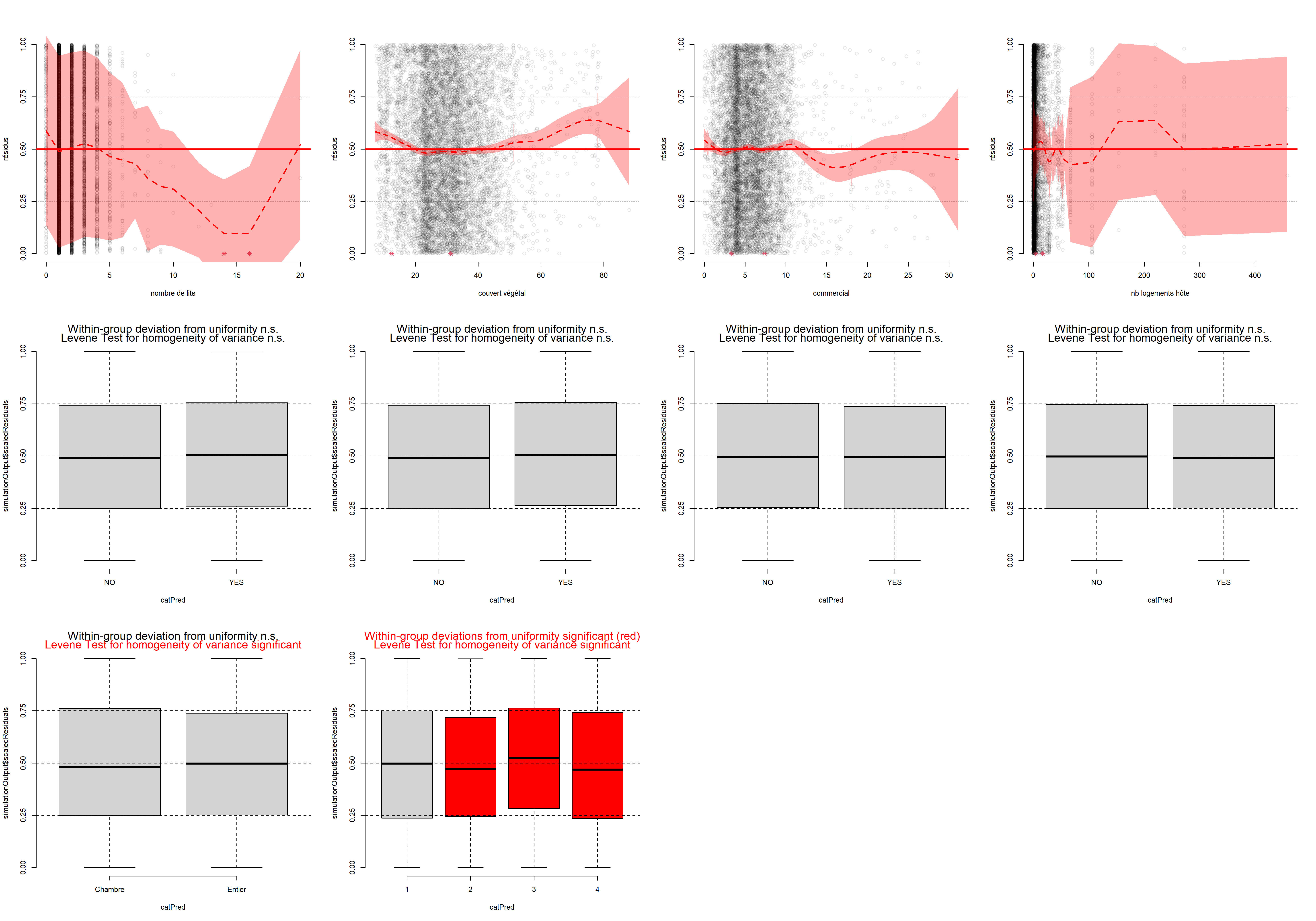
Figure 8.15: Diagnostic des variables indépendantes et des résidus simulés du modèle des cotes proportionnelles
La fonction plotResiduals du package DHARMa produit des graphiques peu esthétiques, mais pratiques pour effectuer ce type de diagnostic.
La figure 8.15 indique qu’aucune relation marquée n’existe entre nos variables indépendantes et nos résidus simulés, sauf pour la variable nombre de lits. En effet, nous pouvons constater que les résidus ont tendance à être toujours plus faibles quand le nombre de lits augmente. Cet effet est sûrement lié au fait qu’au-delà de cinq lits, le logement en question est vraisemblablement un dortoir. Il pourrait être judicieux de retirer ces observations de l’analyse, considérant qu’elles sont peu nombreuses et constituent un type de logement particulier.
data_airbnb2 <- subset(data_airbnb, data_airbnb$beds <=5)
modele2 <- vglm(fac_price_cat ~ beds +
Garden_or_backyard + Free_street_parking +
prt_veg_500m + has_metro_500m + commercial_1km +
private + cat_review + host_total_listings_count ,
family = cumulative(link="logitlink", # fonction de lien
parallel = TRUE, # cote proportionelle
reverse = TRUE),
data = data_airbnb2, model = T)Nous pouvons ensuite recalculer les résidus simulés pour observer si cette tendance a été corrigée. La figure 8.16 montre qu’une bonne partie du problème a été corrigée; cependant, il semble tout de même que les résidus soient plus forts pour les logements avec un seul lit.
# Nous effectuerons 1000 simulations
nsim <- 1000
predicted <- predict(modele2, type = "response")
# Lancement des simulations pour chaque observation (lignes dans predicted)
simulations <- lapply(1:nrow(predicted), function(i){
probs <- predicted[i,]
sims <- sample(c(1,2,3), size = nsim, replace = T, prob = probs)
return(sims)
})
# Combiner les prédictions dans un tableau
matsim <- do.call(rbind, simulations)
# Extraction de la prédiction moyenne du modèle
pred_cat <- unique(data_airbnb2$fac_price_cat)[max.col(predicted)]
# Préparer les donnees avec le package DHARMa
sim_res <- createDHARMa(simulatedResponse = matsim,
observedResponse = as.numeric(data_airbnb2$fac_price_cat),
fittedPredictedResponse = as.numeric(pred_cat),
integerResponse = T)par(mfrow=c(3,4))
vars <- c("nombre de lits" = "beds",
"couvert végétal" = "prt_veg_500m",
"commercial" = "commercial_1km",
"nb logements hôte" = "host_total_listings_count",
"jardin" = "Garden_or_backyard",
"accueil" = "Host_greets_you",
"stationnement gratuit" = "Free_street_parking",
"métro" = "has_metro_500m",
"logement privé" = "private",
"évaluation" = "cat_review")
for(name in names(vars)){
v <- vars[[name]]
plotResiduals(sim_res, data_airbnb2[[v]], rank = F, quantreg = F, main = "",
xlab = name, ylab = "résidus")
}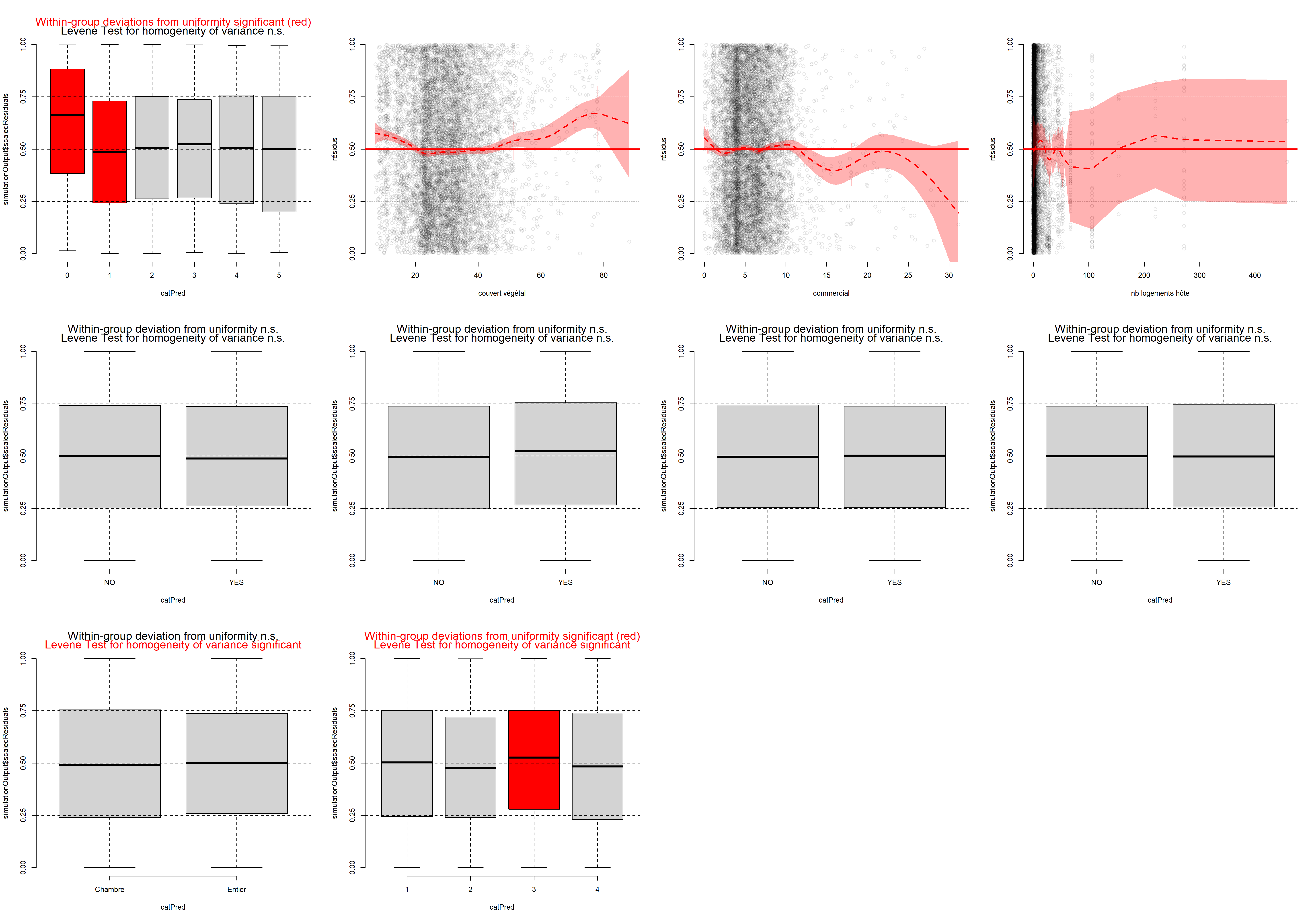
Figure 8.16: Diagnostic des variables indépendantes et des résidus simulés du modèle des cotes proportionnelles (après correction)
La prochaine étape du diagnostic est de vérifier l’absence de séparation parfaite provoquée par une de nos variables indépendantes. Le package VGAM propose pour cela la fonction hdeff.
tests <- hdeff(modele2)
problem <- table(tests)
problem## tests
## FALSE
## 11La fonction nous informe qu’aucune de nos variables indépendantes ne provoque de séparation parfaite : toutes les valeurs renvoyées par la fonction hdeff sont égales à FALSE.
Il ne nous reste donc plus qu’à vérifier que l’hypothèse de proportionnalité des cotes est respectée, soit que l’effet de chacune des variables indépendantes est bien le même pour passer de la catégorie 1 à 2 que pour passer de la catégorie 2 à 3. Pour cela, deux approches sont possibles : le test de Brant ou la réalisation d’une séquence de tests de rapport de vraisemblance.
Le package brant propose une implémentation du test de Brant, mais celle-ci ne peut être appliquée qu’à des modèles construits avec la fonction polr du package MASS. Nous avons donc récupéré le code source de la fonction brant du package brant et apporté quelques modifications pour qu’elle soit utilisable sur un objet vglm. Cette nouvelle fonction, appelée brant.vglm, est disponible dans le code source de ce livre.
tableau_brant <- round(brant.vglm(modele2),3)## ------------------------------------------------------------
## Test for X2 df probability
## ------------------------------------------------------------
## Omnibus 113.72 9 0
## beds 0.63 1 0.43
## Garden_or_backyardYES 0.16 1 0.69
## Free_street_parkingYES 0.84 1 0.36
## prt_veg_500m 6.49 1 0.01
## has_metro_500mYES 0.02 1 0.89
## commercial_1km 0.01 1 0.92
## privateEntier 93.56 1 0
## cat_review 0.63 1 0.43
## host_total_listings_count 1.51 1 0.22
## ------------------------------------------------------------
##
## H0: Parallel Regression Assumption holdsCe premier tableau nous indique que seule la variable indiquant si le logement est disponible en entier ou partagé contrevient à l’hypothèse de proportionnalité des cotes (la seule valeur p significative). Pour confirmer cette observation, nous pouvons réaliser un ensemble de tests de rapport de vraisemblance. Pour chaque variable du modèle, nous créons un second modèle dans lequel cette variable est autorisée à varier pour chaque catégorie et nous comparons les niveaux d’ajustement des modèles. Nous avons implémenté cette procédure dans la fonction parallel.likelihoodtest.vglm disponible dans le code source de ce livre.
tableau_likelihood <- parallel.likelihoodtest.vglm(modele2, verbose = FALSE)
print(tableau_likelihood)## variable non parallele AIC loglikelihood p.val loglikelihood ratio test
## 1 beds 15304 -7640 0.271
## 2 Garden_or_backyard 15305 -7641 0.417
## 3 Free_street_parking 15301 -7639 0.079
## 4 prt_veg_500m 15296 -7636 0.007
## 5 has_metro_500m 15303 -7640 0.191
## 6 commercial_1km 15305 -7640 0.271
## 7 private 15215 -7595 0.000
## 8 cat_review 15306 -7641 0.430
## 9 host_total_listings_count 15304 -7640 0.257Les résultats de cette seconde série de tests confirment les précédents, la variable concernant le type de logement doit être autorisée à varier en fonction de la catégorie. Ce second tableau nous indique que la variable concernant la densité de végétation pourrait aussi être amenée à varier en fonction du groupe, mais ce changement a un effet très marginal (différence entre les valeurs d’AIC de seulement 8 points). Nous ajustons donc un nouveau modèle autorisant la variable private à changer en fonction de la catégorie prédite.
modele3 <- vglm(fac_price_cat ~ beds +
Garden_or_backyard + Host_greets_you + Free_street_parking +
prt_veg_500m + has_metro_500m + commercial_1km +
private + cat_review + host_total_listings_count,
family = cumulative(link="logitlink",
parallel = FALSE ~ private ,
reverse = TRUE),
data = data_airbnb2, model = T)Vérification l’ajustement du modèle
Maintenant que toutes les conditions d’application ont été passées en revue, nous pouvons passer à la vérification de l’ajustement du modèle.
modelenull <- vglm(fac_price_cat ~ 1,
family = cumulative(link="logitlink",
parallel = TRUE,
reverse = TRUE),
data = data_airbnb2, model = T)
rsqs(loglike.full = logLik(modele3),
loglike.null = logLik(modelenull),
full.deviance = deviance(modele3),
null.deviance = deviance(modelenull),
nb.params = modele3@rank,
n = nrow(data_airbnb2)
)## $`deviance expliquee`
## [1] 0.2087098
##
## $`McFadden ajuste`
## [1] 0.2073552
##
## $`Cox and Snell`
## [1] 0.3606848
##
## $Nagelkerke
## [1] 0.4085924Le modèle final parvient à expliquer 21 % de la déviance originale. Il obtient un R2 ajusté de McFadden de 0,21, et des R2 de Cox et Snell et de Nagelkerke de respectivement 0,36 et 0,41. Construisons à présent la matrice de confusion de la prédiction du modèle (nous utilisons ici la fonction nice_confusion_matrix également disponible dans le code source de ce livre).
preds_probs <- fitted(modele3)
pred_cat <- c(1,2,3)[max.col(preds_probs)]
library(caret)
matrices <- nice_confusion_matrix(data_airbnb2$fac_price_cat,pred_cat)
# Afficher la matrice de confusion
print(matrices$confusion_matrix)## rowsnames 1 2 3 rs rp
## colsnames "" "1 (reel)" "2 (reel)" "3 (reel)" "Total" "%"
## 1 "1 (predit)" "1576" "736" "168" "2480" "27.7"
## 2 "2 (predit)" "579" "2385" "1331" "4295" "48"
## 3 "3 (predit)" "49" "771" "1360" "2180" "24.3"
## "Total" "2204" "3892" "2859" "8955" NA
## "%" "24.6" "43.5" "31.9" NA NA# Afficher les indicateurs de qualité de prédiction
print(matrices$indicators)## rnames precision rappel F1
## 1 "1" "0.64" "0.72" "0.67"
## 2 "2" "0.56" "0.61" "0.58"
## 3 "3" "0.62" "0.48" "0.54"
## macro_scores "macro" "0.6" "0.59" "0.59"
## "Kappa" "0.37" NA NA
## "Valeur de p (precision > NIR)" "0" NA NALe modèle a une précision totale de 61 % (61 % des observations ont été correctement prédites). La catégorie 1 a de loin la meilleure précision (72 %) et la 3 a la pire (48 %), ce qui indique qu’il manque vraisemblablement des variables indépendantes contribuant à prédire les prix des logements les plus chers. Le coefficient de Kappa () indique un niveau d’accord entre modéré et faible, mais le modèle parvient à une prédiction significativement supérieure au seuil de non-information. Si l’ajustement du modèle est imparfait, il est suffisamment fiable pour nous donner des renseignements pertinents sur le phénomène étudié.
Interprétation des résultats
L’ensemble des coefficients du modèle sont accessibles via la fonction summary. À partir des coefficients et de leurs erreurs standards, il est possible de calculer les rapports de cotes ainsi que leurs intervalles de confiances.
tableau <- summary(modele3)@coef3
rappCote <- exp(tableau[,1])
rappCote2.5 <- exp(tableau[,1] - 1.96 * tableau[,2])
rappCote97.5 <- exp(tableau[,1] + 1.96 * tableau[,2])
tableau <- cbind(tableau, rappCote, rappCote2.5, rappCote97.5)
print(round(tableau,3))## Estimate Std. Error z value Pr(>|z|) rappCote rappCote2.5 rappCote97.5
## (Intercept):1 -1.203 0.137 -8.768 0.000 0.300 0.230 0.393
## (Intercept):2 -3.240 0.151 -21.516 0.000 0.039 0.029 0.053
## beds 0.748 0.027 28.143 0.000 2.113 2.006 2.226
## Garden_or_backyardYES 0.120 0.067 1.795 0.073 1.128 0.989 1.287
## Host_greets_youYES 0.094 0.060 1.548 0.122 1.098 0.975 1.236
## Free_street_parkingYES -0.015 0.046 -0.320 0.749 0.985 0.900 1.078
## prt_veg_500m -0.026 0.003 -10.182 0.000 0.975 0.970 0.980
## has_metro_500mYES 0.063 0.048 1.326 0.185 1.065 0.970 1.170
## commercial_1km 0.008 0.008 0.955 0.340 1.008 0.992 1.024
## privateEntier:1 2.445 0.062 39.241 0.000 11.533 10.207 13.031
## privateEntier:2 1.576 0.081 19.573 0.000 4.834 4.128 5.660
## cat_review 0.200 0.021 9.563 0.000 1.222 1.173 1.273
## host_total_listings_count -0.002 0.001 -2.094 0.036 0.998 0.996 1.000Pour faciliter la lecture des résultats, nous proposons le tableau 8.14.
| Variable | Coefficient | RC | P | RC 2,5 % | RC 97,5 % | sign. |
|---|---|---|---|---|---|---|
| (Intercept):1 | -1,200 | 0,300 | 0,000 | 0,230 | 0,395 | *** |
| (Intercept):2 | -3,240 | 0,039 | 0,000 | 0,029 | 0,052 | *** |
| beds | 0,750 | 2,113 | 0,000 | 2,014 | 2,226 | *** |
| Garden_or_backyard | ||||||
| ref : NO | – | – | – | – | – | – |
| YES | 0,120 | 1,128 | 0,073 | 0,990 | 1,284 | . |
| Host_greets_you | ||||||
| ref : NO | – | – | – | – | – | – |
| YES | 0,090 | 1,098 | 0,122 | 0,980 | 1,234 | |
| Free_street_parking | ||||||
| ref : NO | – | – | – | – | – | – |
| YES | -0,010 | 0,985 | 0,749 | 0,896 | 1,083 | |
| prt_veg_500m | -0,030 | 0,975 | 0,000 | 0,970 | 0,980 | *** |
| has_metro_500m | ||||||
| ref : NO | – | – | – | – | – | – |
| YES | 0,060 | 1,065 | 0,185 | 0,970 | 1,174 | |
| commercial_1km | 0,010 | 1,008 | 0,340 | 0,990 | 1,020 | |
| cat_review | 0,200 | 1,222 | 0,000 | 1,174 | 1,271 | *** |
| host_total_listings_count | 0,000 | 0,998 | 0,036 | 1,000 | 1,000 |
|
| Effets par niveau | ||||||
| private | ||||||
| ref : Chambre | – | – | – | – | – | – |
| Entier:1 | 2,450 | 11,533 | 0,000 | 10,176 | 13,066 | *** |
| Entier:2 | 1,580 | 4,834 | 0,000 | 4,137 | 5,641 | *** |
Sans surprise, chaque lit supplémentaire contribue à augmenter les chances que le logement soit dans une catégorie de prix supérieure (multiplication par deux à chaque lit supplémentaire). En revanche, la présence d’un stationnement gratuit, d’un jardin et l’accueil en personne par l’hôte n’ont pas d’effets significatifs. Comme l’indiquent les articles mentionnés en début de section, les revues positives augmentent la probabilité d’appartenir à une catégorie supérieure de prix. Pour chaque point supplémentaire sur l’échelle de 1 à 5, la probabilité d’appartenir à une catégorie de prix supérieure augmente de 22,2 %. Il est intéressant de noter que le fait de disposer du logement entier plutôt que d’une simple chambre augmente davantage les chances de passer du groupe de prix 1 à 2 (multiplication par 2,45) que du groupe 2 à 3 (multiplication par 1,58). Il semble également que si l’hôte possède plusieurs logements, la probabilité d’avoir une classe de prix supérieure diminue légèrement. Cependant, l’effet est trop petit pour pouvoir se livrer à des interprétations.
Les variables environnementales ont peu d’effet : le pourcentage de surface commerciale dans un rayon d’un kilomètre et la présence d’une station de métro ne sont pas significatifs. En revanche, une augmentation de la surface végétale dans un rayon de 500 mètres tend à réduire la probabilité d’appartenir à une classe supérieure. Notre hypothèse concernant ce résultat est que cette variable représente un effet associé à la localisation des Airbnb, les plus centraux ayant tendance à être plus dispendieux, mais avec un environnement moins vert et inversement. Pour l’illustrer, prédisons les probabilités d’appartenance aux différents niveaux de prix d’un logement avec les caractéristiques suivantes : entièrement privé, 2 lits, un jardin, une place de stationnement gratuite, l’hôte ne dispose que d’un logement sur Airbnb et accueille les arrivants en personne, 10 % de surface commerciale dans un rayon d’un kilomètre, noté 2 comme catégorie de revue, absence de métro dans un rayon de 500 mètres.
# Créer un jeu de données pour effectuer des prédictions
df <- data.frame(
prt_veg_500m = seq(5,90),
beds = 2,
Garden_or_backyard = "YES",
Host_greets_you = "YES",
Free_street_parking = "YES",
has_metro_500m = "NO",
commercial_1km = 10,
private = "Entier",
cat_review = 2,
host_total_listings_count = 1
)
# Effectuer les prédictions (dans l'échelle log)
preds <- predict(modele3, newdata = df, type = "link", se.fit=T)
# Définir l'inverse de la fonction de lien
ilink <- function(x){exp(x)/(1+exp(x))}
# Calculer les probabilités et leurs intervalles de confiance
df[["P[Y>=2]"]] <- ilink(preds$fitted.values[,1])
df[["P[Y>=2] 2,5"]] <- ilink(preds$fitted.values[,1] - 1.96 * preds$se.fit[,1])
df[["P[Y>=2] 97,5"]] <- ilink(preds$fitted.values[,1] + 1.96 * preds$se.fit[,1])
df[["P[Y>=3]"]] <- ilink(preds$fitted.values[,2])
df[["P[Y>=3] 2,5"]] <- ilink(preds$fitted.values[,2] - 1.96 * preds$se.fit[,2])
df[["P[Y>=3] 97,5"]] <- ilink(preds$fitted.values[,2] + 1.96 * preds$se.fit[,2])
df[["P[Y=1]"]] = 1-df[["P[Y>=2]"]]
df[["P[Y=1] 2,5" ]] = 1-df[["P[Y>=2] 2,5"]]
df[["P[Y=1] 97,5"]] = 1-df[["P[Y>=2] 97,5"]]
# Afficher les résultats
ggplot(data = df) +
geom_ribbon(aes(x = prt_veg_500m,
ymin = `P[Y>=2] 2,5`,
ymax = `P[Y>=2] 97,5`),fill ="#f94144", alpha = 0.4)+
geom_path(aes(x = prt_veg_500m, y = `P[Y>=2]`,color="Y2")) +
geom_ribbon(aes(x = prt_veg_500m,
ymin = `P[Y>=3] 2,5`,
ymax = `P[Y>=3] 97,5`), fill ="#90be6d", alpha = 0.4)+
geom_path(aes(x = prt_veg_500m, y = `P[Y>=3]`, color = "Y3" )) +
geom_ribbon(aes(x = prt_veg_500m,
ymin = `P[Y=1] 2,5`,
ymax = `P[Y=1] 97,5`),fill ="#277da1" , alpha = 0.4)+
geom_path(aes(x = prt_veg_500m, y = `P[Y=1]`, color = "Y1")) +
scale_color_manual(name = "Probabilités prédites",
breaks = c("Y1", "Y2", "Y3"),
labels = c("P[Y=1]", "P[Y>=2]", "P[Y>=3]"),
values = c("Y2" = "#f94144", "Y3" = "#90be6d",
"Y1" = "#277da1")) +
labs(x = "Densité de végétation (%)",
y = "Probabilité",
subtitle = "Y1 : moins de 50 $; Y2 : 50 à 99 $; Y3 : 100 à 249 $")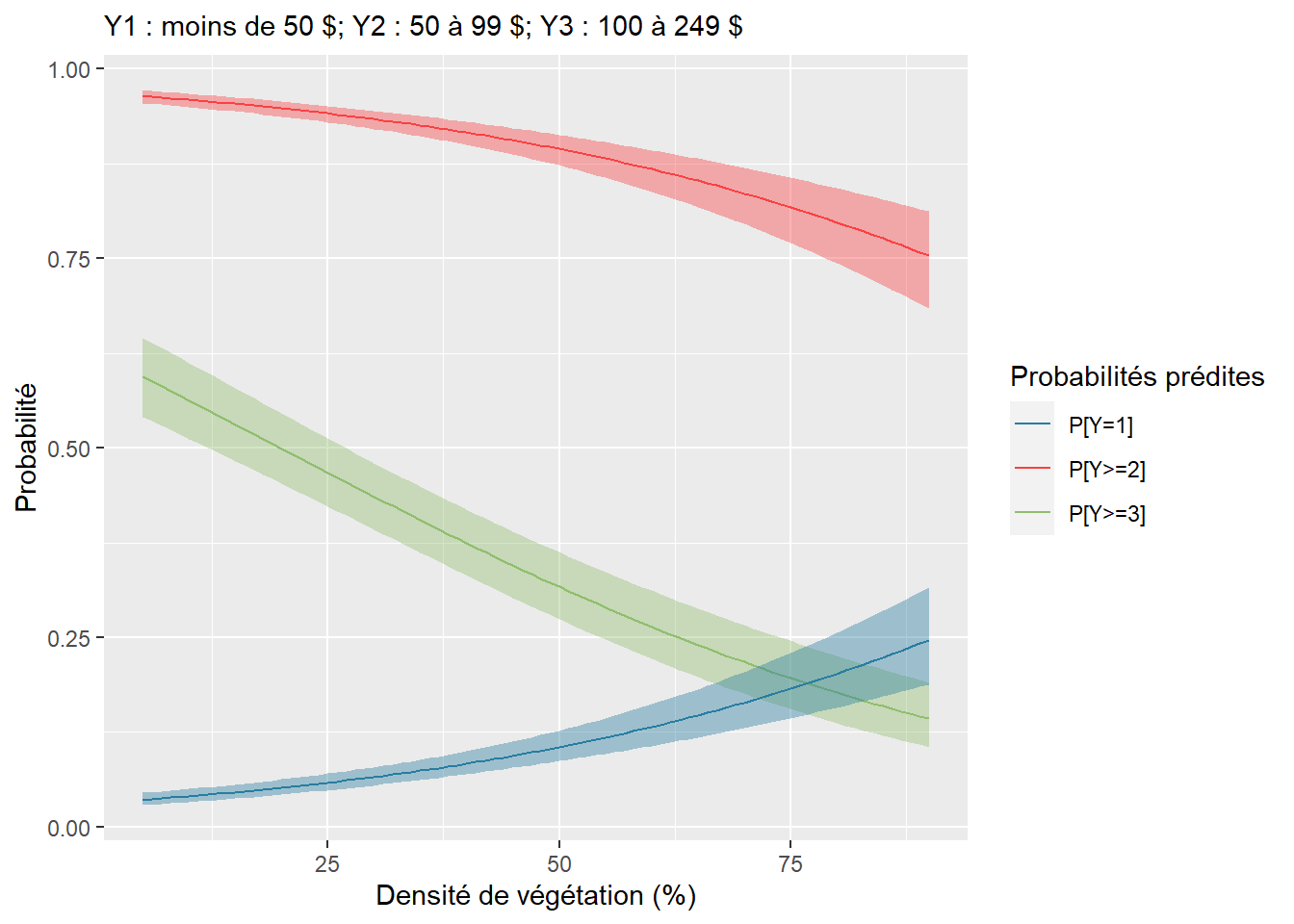
Figure 8.17: Prédiction de la probabilité d’appartenance aux trois catégories de prix en fonction de la densité de végétation
Nous constatons, à la figure 8.17, que les probabilités d’appartenir aux niveaux 2 et 3 diminuent à mesure qu’augmente le pourcentage de végétation. La probabilité d’appartenir à la classe 2 et plus (en rouge) passe de plus de 95 % en cas d’absence de végétation et à environ 75 % avec 80 % de végétation dans un rayon de 500 mètres. Comme vous pouvez le constater, la probabilité \(P[Y=1]\) est la symétrie de \(P[Y>=2]\) puisque \(P[Y=1]+P[Y>=2] = 1\).
8.2.4 Modèle logistique multinomial
La régression logistique multinomiale est utilisée pour modéliser une variable Y qualitative multinomiale, c’est-à-dire une variable dont les modalités ne peuvent pas être ordonnées. Dans le modèle précédent, nous avons vu qu’il était possible de modéliser une variable ordinale avec une distribution binomiale en formulant l’hypothèse de la proportionnalité des cotes. Avec une variable multinomiale, cette hypothèse ne tient plus, car les catégories ne sont plus ordonnées. Il faut donc formuler le modèle différemment.
L’idée derrière un modèle multinomial est de choisir une catégorie de référence, puis de modéliser les probabilités d’appartenir à chaque autre catégorie plutôt qu’à cette catégorie de référence (tableau 8.15). Si nous avons K catégories possibles dans notre variable Y, nous obtenons K-1 comparaisons. Chaque comparaison est modélisée avec sa propre équation, ce qui génère de nombreux paramètres. Par exemple, admettons que notre variable Y a cinq catégories et que nous disposons de six variables X prédictives. Nous avons ainsi 4 (5-1) équations de régression avec 7 paramètres (6 coefficients et une constante), soit 28 coefficients à analyser.
Considérant cette tendance à la multiplication des coefficients, il est fréquent de recourir à une méthode appelée Analyse de type 3 pour limiter au maximum le nombre de variables indépendantes (VI) dans le modèle. L’idée de cette méthode est de recalculer plusieurs versions du modèle dans lesquelles une variable indépendante est retirée, puis de réaliser un test de rapport de vraisemblance en comparant ce nouveau modèle (complet moins une VI) au modèle complet (toutes les VI) pour vérifier si la variable en question améliore significativement le modèle. Il est alors possible de retirer toutes les variables dont l’apport est négligeable si elles sont également peu intéressantes du point de vue théorique.
| Type de variable dépendante | Variable qualitative multinomiale avec K catégories |
| Distribution utilisée | Binomiale |
| Formulation |
\(Y \sim Binomial(p)\) \(g(p = k\text{ avec }ref = a) = \beta_{0k} + \beta X_{k}\) \(g(x) = \frac{log(x)}{1-x}\) |
| Fonction de lien | Logistique |
| Paramètre modélisé | p |
| Paramètres à estimer | \(\beta_{0k}\), \(\beta\)k pour \(k \in [2,...,K]\) |
| Conditions d’application | Non-séparation complète, absence de sur-dispersion ou de sous-dispersion, Indépendance des alternatives non pertinentes |
8.2.4.1 Conditions d’application
Les conditions d’application sont les mêmes que pour un modèle binomial, avec l’ajout de l’hypothèse sur l’indépendance des alternatives non pertinentes. Cette dernière suppose que le choix entre deux catégories est indépendant des catégories proposées. Voici un exemple simple pour illustrer cette hypothèse: admettons que nous disposons d’une trentaine de personnes et que nous leur demandons la couleur de leurs yeux. Cette variable ne serait pas affectée par la présence de nouvelles couleurs en dehors de notre échantillon. En revanche, si nous leur demandons de choisir un mode de transport parmi une liste pour se rendre à leur lieu de travail, leur réponse serait nécessairement affectée par la liste des modes de transport disponibles. Les tests développés pour vérifier cette hypothèse sont connus pour leur faible fiabilité. Il est plus pertinent de décider théoriquement si cette hypothèse est valide ou non. Dans le cas contraire, il est possible d’utiliser une classe de modèle logistique plus rare: le modèle logistique imbriqué.
Notez également que le grand nombre de paramètres dans ce type de modèle implique de disposer d’un plus grand nombre d’observations afin d’avoir suffisamment d’information dans chaque catégorie pour ajuster tous les paramètres.
Pour vérifier la présence de sur-dispersion, il est possible, dans le cas du modèle multinomial, de calculer le rapport entre le khi-deux de Pearson et le nombre de degrés de liberté du modèle. Si ce rapport est supérieur à 1 (des valeurs jusqu’à 1,15 ne sont pas problématiques), alors le modèle souffre de sur-dispersion (SAS Institute Inc 2020a). Le khi-deux de Pearson est simplement la somme des résidus de Pearson au carré dans le cas d’un modèle GLM.
\[\begin{equation} \chi^2 = \sum_{i=1}^N\sum_{c=1}^K{\frac{(y_{ic} - p_{ic})^2}{p_{ic}}} \tag{8.18} \end{equation}\]
Avec \(y_{ic}\) 1 si l’observation i appartient à la catégorie c, 0 autrement, \(p_{ic}\) la probabilité prédite pour l’observation i d’appartenir à la catégorie c, N le nombre d’observations et K le nombre de catégories.
Le ratio est ensuite calculé comme suit: \(\frac{\chi^2}{(N - p)(K-1)}\), avec N le nombre d’observations et K le nombre de modalités dans la variable Y. Si ce ratio est égal ou supérieur à 1, alors le modèle souffre de sur-dispersion, si le ratio est inférieur à 1, le modèle souffre de sous-dispersion. Un léger écart (> 0,15) n’est pas considéré comme problématique.
Le modèle logistique imbriqué
Du fait de sa proximité avec les modèles à effets mixtes que nous abordons au chapitre 9, nous ne détaillons pas ici le modèle logistique imbriqué, mais présentons plutôt son principe général. Il s’agit d’une généralisation du modèle logistique multinomial basé sur l’idée que certaines catégories pourraient être regroupées dans des « nids » (nest en anglais). Dans ces groupes, les erreurs peuvent être corrélées, indiquant ainsi que si une catégorie est manquante, une autre catégorie du même groupe sera préférée. Un paramètre \(\lambda\) contrôle spécifiquement cette corrélation et permet de mesurer sa force une fois le modèle ajusté. Il peut être pertinent de comparer un modèle imbriqué à un modèle multinomial pour déterminer lequel des deux est le mieux ajusté aux données.
8.2.4.2 Exemple appliqué dans R
Pour cet exemple, nous reproduisons une partie de l’analyse effectuée dans l’étude de McFadden (2016). Cet article s’intéresse aux écarts entre les croyances des individus et les connaissances scientifiques sur les sujets des OGM et du réchauffement climatique. Les auteurs utilisent pour cela des données issues d’une enquête auprès de 961 individus formant un échantillon représentatif de la population des États-Unis. Les données issues de cette enquête sont téléchargeables sur le site de l’éditeur, ce qui nous permet ici de reproduire l’analyse effectuée par les auteurs. Deux questions sont centrales dans l’enquête :
- Dans quelle mesure êtes-vous en accord ou en désaccord avec la phrase suivante : les plantations génétiquement modifiées sont sans danger pour la consommation ?
- Dans quelle mesure êtes-vous en accord ou en désaccord avec la phrase suivante : la Terre se réchauffe du fait des activités humaines ?
Pour ces deux questions, les répondants devaient sélectionner leur degré d’accord sur une échelle de Likert allant de 1 (fortement en désaccord) à 5 (fortement en accord). Les réponses à ces deux questions ont été utilisées pour former une variable multinomiale à quatre modalités :
- A. Les individus sont en accord avec les deux propositions.
- B. Les individus sont en désaccord sur les OGM, mais en accord sur le réchauffement climatique.
- C. Les individus sont en accord sur les OGM, mais en désaccord sur le réchauffement climatique.
- D. Les individus sont en désaccord avec les deux propositions.
Un modèle logistique multinomial a été utilisé pour déterminer quels facteurs contribuent à la probabilité d’appartenir à ces différentes catégories. Les variables indépendantes présentes dans le modèle sont détaillées dans le tableau 8.16. Les auteurs avaient notamment conclu que :
- Les effets des connaissances (réelles ou perçues) sur l’appartenance aux différentes catégories n’étaient pas uniformes et pouvaient varier en fonction du sujet.
- L’orientation politique avait une influence significative sur les croyances.
- Les répondants avec de plus hauts résultats au test de cognition CRT avaient plus souvent des opinions divergentes de la communauté scientifique.
| Nom de la variable | signification | Type de variable | Mesure |
|---|---|---|---|
| PercepOGM | La recherche scientifique supporte ma vision sur la sécurité des plantes OGM | Variable ordinale | Échelle de Likert de 1 (fortement en désaccord) à 5 (fortement en accord) |
| PercepRechClim | La recherche scientifique supporte ma vision sur le réchauffement climatique | Variable ordinale | Échelle de Likert de 1 (fortement en désaccord) à 5 (fortement en accord) |
| ConnaisOGM | Niveau de connaissance sur les OGM | Variable ordinale | Nombre de réponses sur trois questions portant sur les OGM |
| ConnaisRechClim | Niveau de connaissance sur le réchauffement climatique | Variable ordinale | Nombre de réponses sur trois questions portant sur le réchauffement climatique |
| CRT | Score obtenu au Cognitive Reflection Test, utilisé pour déterminer la propension à faire preuve d’esprit d’analyse plutôt que choisir des réponses intuitives | Variable ordinale | Nombre de réponses sur trois questions pièges |
| Parti | Orientation politique du répondant | Variable multinomiale | Républicain, démocrate et autre |
| Sexe | Sexe du répondant | Variable binaire | Femme ou homme |
| Age | Âge du répondant | Variable continue | Âge du répondant |
| Revenu | Niveau de revenu du répondant | Variable ordinale | Échelle de 1 (moins de 20 000 $) à (140 000 $ et plus) |
Vérification des conditions d’application
Avant d’ajuster le modèle, nous commençons par vérifier l’absence de multicolinéarité excessive entre les variables indépendantes. Toutes les valeurs de VIF sont inférieures à 2, indiquant bien une absence de multicolinéarité.
data_quest <- read.csv("data/glm/enquete_PublicOpinion_vs_Science.csv")
# Choix des valeurs de références dans les facteurs
data_quest$Parti <- relevel(as.factor(data_quest$Parti), ref = "Democrate")
data_quest$Sexe <- relevel(as.factor(data_quest$Sexe), ref = "homme")
vif(glm(SCIGM ~ PercepOGM + PercepRechClim + ConnaisOGM + ConnaisRechClim +
CRT + Parti + AGE + Sexe + Revenu, data = data_quest))## GVIF Df GVIF^(1/(2*Df))
## PercepOGM 1.092693 1 1.045320
## PercepRechClim 1.177495 1 1.085125
## ConnaisOGM 1.150662 1 1.072689
## ConnaisRechClim 1.158438 1 1.076307
## CRT 1.155371 1 1.074882
## Parti 1.130817 2 1.031212
## AGE 1.071655 1 1.035208
## Sexe 1.064918 1 1.031949
## Revenu 1.049499 1 1.024451La seconde étape est d’ajuster le modèle et de vérifier l’absence de sur ou sous-dispersion. Pour ajuster le modèle, nous utilisons à nouveau la fonction vglm du package VGAM, avec le paramètre family = multinomial(). Le ratio entre la statistique de Pearson et le nombre de degrés de liberté du modèle indique une absence de sur ou sous-dispersion (1,04).
# Ajustement du modèle
modele <- vglm(Y ~ PercepOGM + PercepRechClim + ConnaisOGM + ConnaisRechClim +
CRT + Parti + AGE + Sexe + Revenu,
data = data_quest,
family = multinomial(refLevel="A"), model = T)
# Calcul du Khi2 de Pearson
pred <- predict(modele, type= "response")
cat_predict <- colnames(pred)[max.col(pred)]
freq_real <- table(data_quest$Y)
freq_pred <- table(cat_predict)
khi2 <- sum(residuals(modele, type = "pearson")^2)
N <- nrow(data_quest)
p <- modele@rank
r <- length(freq_real)
ratio <- khi2 / ((N-p)*(r-1))
print(ratio)## [1] 1.045889La troisième étape de la vérification des conditions d’application est l’analyse des distances de Cook. À nouveau, puisque le modèle évalue la probabilité d’appartenir à \(K-1\) catégorie, nous pouvons calculer \(K-1\) résidus par observation et par extension \(K-1\) distances de Cook. Aucune observation ne semble se détacher nettement dans la figure 8.18. Nous décidons donc pour le moment de conserver toutes les observations.
# Extraction des résidus
res <- residuals(modele, type = "pearson")
# Extraction de la hat matrix (nécessaire pour calculer la distance de Cook)
hat <- hatvaluesvlm(modele)
# Calcul des distances de Cook
vals <- c("A","B","C","D")
cooks <- lapply(1:ncol(res),function(i){
r <- res[,i]
h <- hat[,i]
cook <- (r/(1 - h))^2 * h/(1 * modele@rank)
df <- data.frame(
oid = 1:length(cook),
cook = cook
)
plot <- ggplot(data = df)+
geom_point(aes(x = oid, y = cook), size = 0.2, color = rgb(0.1,0.1,0.1,0.4)) +
labs(x = "", y = "", subtitle = paste("distance de Cook P(",vals[[1]]," VS ",vals[[i+1]],")",sep=""))+
theme(axis.ticks.x = element_blank(),
axis.text.x = element_blank())
return(plot)
})
ggarrange(plotlist = cooks, ncol = 2, nrow = 2)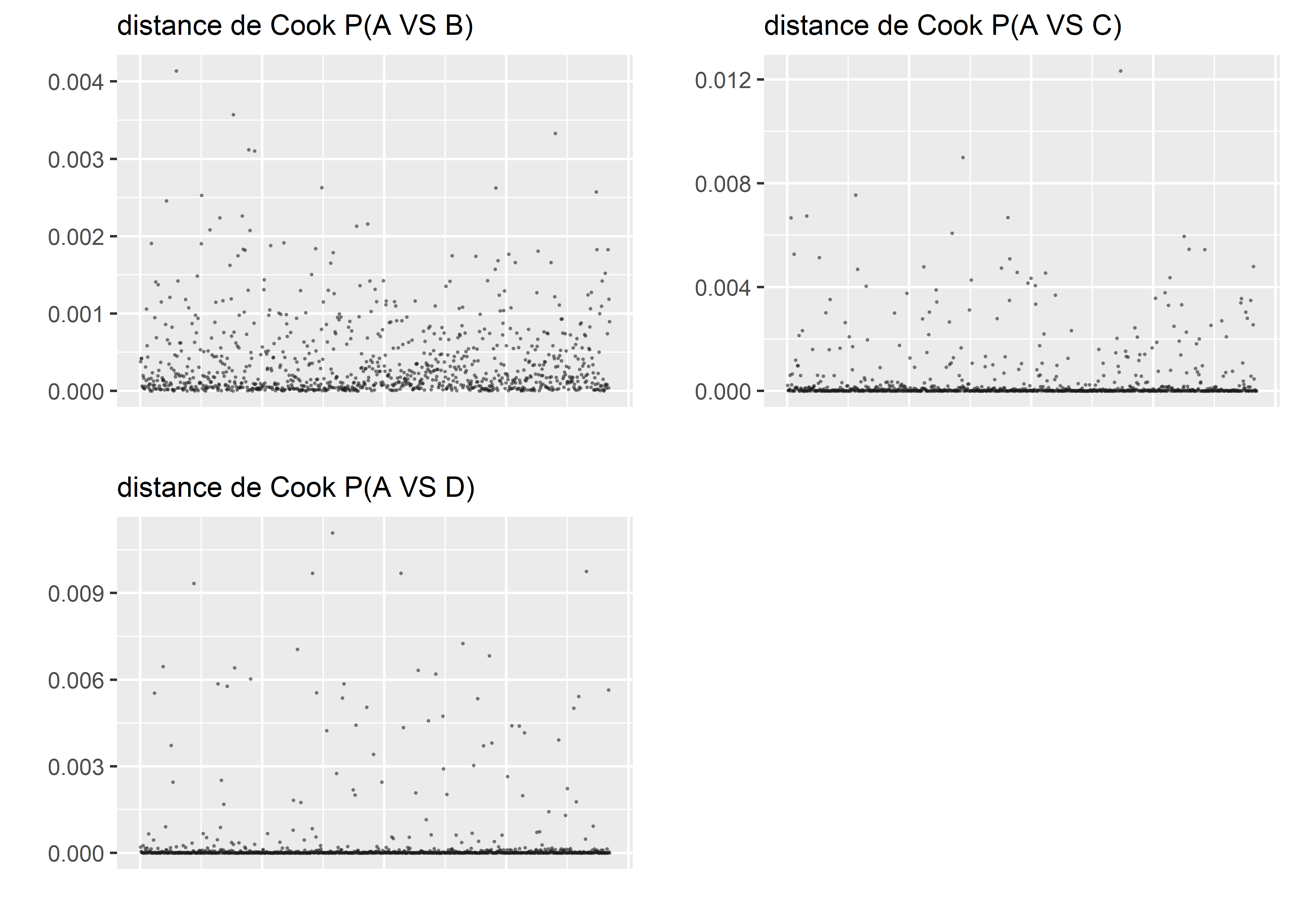
Figure 8.18: Distances de Cook pour le modèle logistique multinomial
Avant de passer à l’analyse de résidus simulés, il est pertinent de réaliser une analyse de type 3 afin de retirer les variables indépendantes dont l’apport au modèle est négligeable. La fonction AnalyseType3 (disponible dans le code source de ce livre) permet d’effectuer cette opération automatiquement pour un objet de type vglm.
tableau <- AnalyseType3(modele, data_quest, verbose = FALSE)## *************************************
## Type 3 Analysis of Effects
## *************************************
## AIC model complet : 1855
## loglikelihood model complet : 1789
## variable retiree AIC loglikelihood p.val
## 1 PercepOGM 1879 1819 0
## 2 PercepRechClim 1941 1881 0
## 3 ConnaisOGM 1910 1850 0
## 4 ConnaisRechClim 1862 1802 0.0059
## 5 CRT 1860 1800 0.0125
## 6 Parti 1879 1825 0
## 7 AGE 1852 1792 0.4469
## 8 Sexe 1875 1815 0
## 9 Revenu 1850 1790 0.7718L’analyse de type 3 nous permet de déterminer que l’âge et le revenu sont deux variables dont la contribution au modèle est marginale. À titre de rappel, l’analyse de type 3 permet de comparer si le modèle complet (avec l’ensemble des variables indépendantes) est statistiquement mieux ajusté que le modèle avec l’ensemble des variables, sauf une. Or, dans notre cas, le modèle complet n’est pas statistiquement mieux ajusté que le modèle complet sans la variable Age (p = 0,44) et que le modèle complet sans la variable Revenu (p = 0,77). Cela signifie donc que ces deux variables n’ont pas un apport significatif au modèle et peuvent par conséquent être ôtées par parcimonie. Nous décidons donc de les retirer afin d’alléger les tableaux de coefficients que nous présentons plus loin. Nous pouvons également en conclure que ces deux variables ne jouent aucun rôle dans la propension à être en désaccord avec la recherche scientifique. Nous réajustons le modèle en conséquence.
modele2 <- vglm(Y ~ PercepOGM + PercepRechClim + ConnaisOGM + ConnaisRechClim +
CRT + Parti + Sexe,
data = data_quest,
family = multinomial(refLevel="A"), model = T)Nous pouvons à présent passer à l’analyse des résidus simulés. Le problème avec ce modèle est que sa variable Y est qualitative alors que la méthode d’analyse des résidus du package DHARMa ne peut traiter que des variables quantitatives, binaires ou ordinales. Pour rappel, il est possible d’envisager la prédiction d’un modèle logistique multinomial comme la prédiction d’une série de modèles logistiques binomiaux. En représentant nos prédictions de cette façon, nous pouvons à nouveau utiliser le package DHARMa pour analyser nos résidus. Veuillez noter que cette approche n’est pas optimale et que cette section du livre peut être amenée à changer.
La figure 8.19 indique que les résidus suivent bien une distribution uniforme et qu’aucune valeur aberrante n’est observable.
# Extraire les prédictions du modèle
categories <- c("B","C","D")
predicted <- predict(modele2, type = "link")
nsim <- 1000
ilink <- function(x){exp(x)/(1+exp(x))}
# Boucler sur chacune des catégories en dehors de la référence
data_sims <- lapply(1:ncol(predicted),function(i){
categorie <- categories[[i]]
# Extraire les observation de la catégorie i et de la référence
test <- data_quest$Y %in% c("A",categorie)
# Calculer les probabilité d'appartenance à i
values <- predicted[test,i]
probs <- ilink(values)
# Extraire les valeurs réelles et les convertir en 0 / 1
real <- data_quest[test,]$Y
real <- ifelse(real=="A",0,1)
# Enregistrer ces différents éléments
all_probs <- cbind(1-probs,probs)
sub_data <- subset(data_quest,test)
return(list("real" = real, "probs" = all_probs, "data" = sub_data))
})
# Extraire les probabilités prédites
all_probs <- do.call(rbind, lapply(data_sims, function(i){i$probs}))
# Extraire les vrais catégories
all_real <- unlist(lapply(data_sims, function(i){i$real}))
# Effectuer les simulations
simulations <- lapply(1:nrow(all_probs), function(i){
probs <- all_probs[i,]
sims <- sample(c(0,1), size = nsim, replace = T, prob = probs)
return(sims)
})
matsim <- do.call(rbind, simulations)
# Calculer les résidus simulés
sim_res <- createDHARMa(simulatedResponse = matsim,
observedResponse = all_real,
fittedPredictedResponse = all_probs[,2],
integerResponse = T)
# Afficher les résultats
plot(sim_res)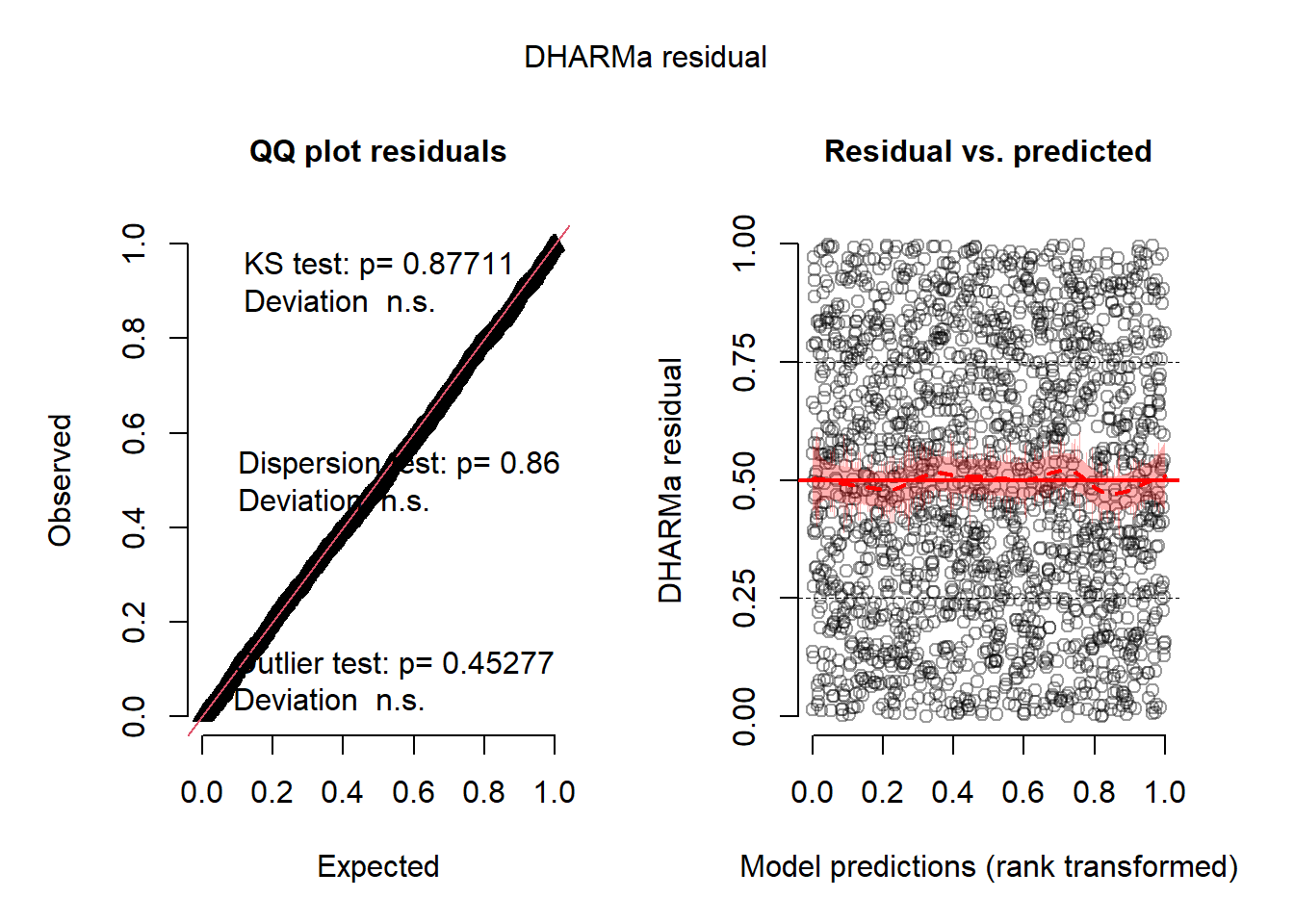
Figure 8.19: Diagnostic général des résidus simulés pour le modèle multinomial
La figure 8.20 permet d’affiner le diagnostic en s’assurant de l’absence de relation entre les variables indépendantes et les résidus. Il est possible de remarquer des irrégularités pour les variables de perception (premier et second panneaux). Dans les deux cas, la catégorie 1 (fort désaccord) se démarque nettement des autres catégories. Nous proposons donc de les recoder comme des variables binaires : en désaccord / pas en désaccord pour minimiser cet effet.
# Recomposer les données pour coller au format
# étendu de la prediction
etend_data <- do.call(rbind, lapply(data_sims, function(i){i$data}))
par(mfrow=c(3,3))
vars <- c("PercepOGM", "PercepRechClim", "ConnaisOGM",
"ConnaisRechClim", "CRT", "Parti", "Sexe")
for(v in vars){
plotResiduals(sim_res, etend_data[[v]], xlab= v, ylab = "résidus")
}
Figure 8.20: Diagnostic des variables indépendantes et des résidus simulés pour le modèle multinomial
Nous réajustons donc le modèle et recalculons nos résidus ajustés (masqué ici pour alléger le document). La figure 8.21 nous confirme que le problème a été corrigé.
# Convertir les variables ordinales et variables binaires
data_quest$PercepOGMDes <- ifelse(data_quest$PercepOGM %in% c(1,2), 1,0)
data_quest$PercepRechClimDes <- ifelse(data_quest$PercepRechClim %in% c(1,2), 1,0)
# Réajuster le modèle
modele3 <- vglm(Y ~ PercepOGMDes + PercepRechClimDes +
ConnaisOGM + ConnaisRechClim +
CRT + Parti + Sexe,
data = data_quest,
family = multinomial(refLevel="A"), model = T)
Figure 8.21: Diagnostic général des résidus simulés pour le modèle multinomial (version 3)
Profitons du fait que nous utilisons le package VGAM pour vérifier l’absence d’effet de Hauck-Donner qui indiquerait que des variables indépendantes provoquent des séparations parfaites.
test <- hdeff(modele3)
test[test==TRUE]## (Intercept):2 (Intercept):3
## TRUE TRUELa fonction nous informe que les constantes permettant de comparer le groupe C au groupe A, et le groupe D au groupe A provoquent des séparations parfaites. Cela s’explique notamment par le faible nombre d’observations tombant dans ces catégories. Considérant que comparativement à la catégorie A, être dans les catégories B, C, ou D signifie remettre en cause au moins un consensus scientifique, il peut être raisonnable de fixer la constante pour qu’elle soit la même pour les trois comparaisons. Ainsi, les chances de passer de A à un autre groupe ne dépenderaient pas du groupe en question, mais uniquement des variables indépendantes. Pour cela, nous pouvons forcer le modèle à n’ajuster qu’une seule constante avec la syntaxe suivante :
modele4 <- vglm(Y ~ PercepOGMDes + PercepRechClimDes +
ConnaisOGM + ConnaisRechClim +
CRT + Parti + Sexe,
data = data_quest,
family = multinomial(refLevel="A",
parallel = TRUE ~1), model = T)
test <- hdeff(modele4)
print(table(test))## test
## FALSE
## 25# Calcul du khi2 de Pearson
pred <- predict(modele4, type= "response")
cat_predict <- colnames(pred)[max.col(pred)]
freq_real <- table(data_quest$Y)
freq_pred <- table(cat_predict)
khi2 <- sum(residuals(modele4, type = "pearson")^2)
N <- nrow(data_quest)
p <- modele4@rank
r <- length(freq_real)
ratio <- khi2 / ((N)*(r-1)-p)
print(ratio)## [1] 1.010319Nous n’avons donc plus de séparation complète ni de sur ou sous-dispersion et les résidus simulés de la quatrième version du modèle sont toujours acceptables (figure 8.22).
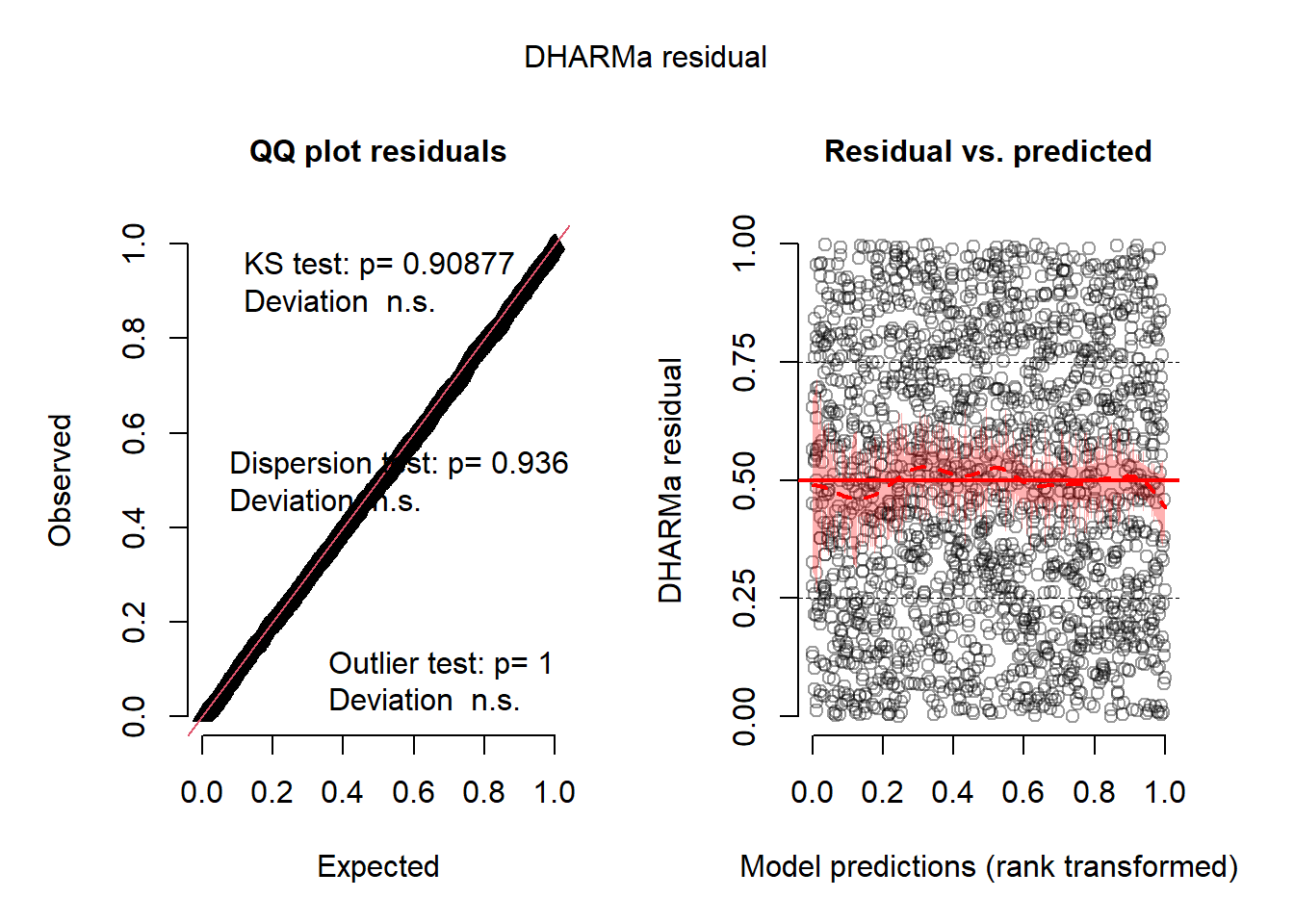
Figure 8.22: Diagnostic général des résidus simulés pour le modèle multinomial (version 4)
Vérification l’ajustement du modèle
Puisque les conditions d’application du modèle sont respectées, nous pouvons à présent vérifier sa qualité d’ajustement.
modelenull <- vglm(Y ~ 1 ,
data = data_quest,
family = multinomial(refLevel="A",
parallel = TRUE ~ 1 + CRT)
, model = T)
rsqs(loglike.full = logLik(modele4),
loglike.null = logLik(modelenull),
full.deviance = deviance(modele4),
null.deviance = deviance(modelenull),
nb.params = modele4@rank,
n = nrow(data_quest)
)## $`deviance expliquee`
## [1] 0.1750071
##
## $`McFadden ajuste`
## [1] 0.1530715
##
## $`Cox and Snell`
## [1] 0.3397248
##
## $Nagelkerke
## [1] 0.3746843Le modèle parvient à expliquer 17,5 % de la déviance totale. Il obtient un R2 ajusté de McFadden de 0,15, et des R2 de Cox et Snell et de Nagelkerke de respectivement 0,34 et 0,37. Passons à la construction de la matrice de confusion pour analyser la capacité de prédiction du modèle.
preds <- predict(modele4, type = "response")
pred_cats <- colnames(preds)[max.col(preds)]
real <- data_quest$Y
matrices <- nice_confusion_matrix(real, pred_cats)
# Afficher la matrice de confusion
print(matrices$confusion_matrix)## rowsnames A B C D rs rp
## colsnames "" "A (reel)" "B (reel)" "C (reel)" "D (reel)" "Total" "%"
## A "A (predit)" "482" "168" "75" "29" "754" "78.5"
## B "B (predit)" "31" "88" "9" "20" "148" "15.4"
## C "C (predit)" "10" "6" "18" "6" "40" "4.2"
## D "D (predit)" "3" "4" "3" "9" "19" "2"
## "Total" "526" "266" "105" "64" "961" NA
## "%" "54.7" "27.7" "10.9" "6.7" NA NA# Afficher les indicateurs de qualité de prédiction
print(matrices$indicators)## rnames precision rappel F1
## A "A" "0.64" "0.92" "0.75"
## B "B" "0.59" "0.33" "0.43"
## C "C" "0.45" "0.17" "0.25"
## D "D" "0.47" "0.14" "0.22"
## macro_scores "macro" "0.6" "0.62" "0.57"
## "Kappa" "0.27" NA NA
## "Valeur de p (precision > NIR)" "0" NA NALa précision globale (macro) du modèle est de 60 % et dépasse significativement le seuil de non-information. L’indicateur de Kappa indique un accord modéré entre la prédiction et les valeurs réelles. Les catégories C et D sont les catégories avec la plus faible précision, indiquant ainsi que le modèle a tendance à manquer les prédictions pour les individus en désaccord avec le consensus scientifique sur le réchauffement climatique. Les indices de rappel sont également très faibles pour les catégories B, C et D, indiquant que très peu d’observations appartenant originalement à ces groupes ont bien été classées dans ces groupes. La capacité de prédiction du modèle est donc relativement faible.
Interprétation des résultats
Puisque nous disposons de quatre catégories dans notre variable Y, nous obtenons au final trois tableaux de coefficients. Il est possible de visualiser l’ensemble des coefficients du modèle avec la fonction summary, nous proposons les tableaux 8.17, 8.18 et 8.19 pour présenter l’ensemble des résultats.
| Variable | Coefficient | RC | val.p | RC 2,5 % | RC 97,5 % | sign. |
|---|---|---|---|---|---|---|
| PercepOGMDes | 1,940 | 6,989 | 0,000 | 4,221 | 11,588 | *** |
| PercepRechClimDes | 0,430 | 1,532 | 0,305 | 0,677 | 3,456 | |
| ConnaisOGM | -0,330 | 0,718 | 0,000 | 0,607 | 0,852 | *** |
| ConnaisRechClim | 0,180 | 1,197 | 0,084 | 0,980 | 1,462 | . |
| CRT | 0,350 | 1,417 | 0,016 | 1,073 | 1,878 |
|
| Parti | ||||||
| ref : Democrate | – | – | – | – | – | – |
| autre | 0,660 | 1,934 | 0,001 | 1,310 | 2,858 | *** |
| Republicain | 0,650 | 1,910 | 0,003 | 1,259 | 2,915 | ** |
| Sexe | ||||||
| ref : homme | – | – | – | – | – | – |
| femme | 1,280 | 3,581 | 0,000 | 2,535 | 5,053 | *** |
Le tableau 8.17 compare donc le groupe A (en accord avec la recherche scientifique sur les deux sujets) et le groupe B (en désaccord sur la question des OGM). Les résultats indiquent que le fait de se percevoir en désaccord avec le consensus scientifique sur la question des OGM multiplie par sept les chances d’appartenir au groupe B comparativement au groupe A. Cependant, pour chaque bonne réponse supplémentaire sur les questions testant les connaissances sur les OGM, les chances d’appartenir au groupe B comparativement au groupe A diminue de 28 %. Ainsi, un individu ayant répondu correctement aux trois questions verrait ses chances réduites de 63 % d’appartenir au groupe B (\(exp(-\text{0,33}\times\text{3})\)). Il est intéressant de noter que les variables concernant le réchauffement climatique n’ont pas d’effet significatif ici. La variable CRT indique qu’à chaque bonne réponse supplémentaire au test de cognition, les chances d’appartenir au groupe B augmentent de 42 %. Un individu qui aurait répondu aux trois questions du test aurait donc 2,9 fois plus de chances d’appartenir au groupe B qu’au groupe A. Concernant le parti politique, comparativement à une personne se déclarant plus proche du parti démocrate, les personnes proches du parti républicain ou d’un autre parti ont près de deux fois plus de chances d’appartenir au groupe B. Enfin, une femme, comparativement à un homme, a 3,6 fois plus de chance d’appartenir au groupe B.
| variable | Coefficient | RC | val.p | RC 2,5 % | RC 97,5 % | sign. |
|---|---|---|---|---|---|---|
| PercepOGMDes | -0,180 | 0,834 | 0,705 | 0,326 | 2,138 | |
| PercepRechClimDes | 2,060 | 7,821 | 0,000 | 3,819 | 16,119 | *** |
| ConnaisOGM | -0,110 | 0,896 | 0,287 | 0,733 | 1,094 | |
| ConnaisRechClim | 0,280 | 1,323 | 0,024 | 1,041 | 1,682 |
|
| CRT | 0,240 | 1,275 | 0,149 | 0,914 | 1,768 | |
| Parti | ||||||
| ref : Democrate | – | – | – | – | – | – |
| autre | -0,190 | 0,828 | 0,496 | 0,482 | 1,433 | |
| Republicain | 0,920 | 2,512 | 0,000 | 1,584 | 4,015 | *** |
| Sexe | ||||||
| ref : homme | – | – | – | – | – | – |
| femme:1 | -0,450 | 0,640 | 0,040 | 0,419 | 0,980 |
|
Le tableau 8.18 compare les groupes A et C (en désaccord sur le réchauffement climatique). Il est intéressant de noter ici que se percevoir en désaccord avec la recherche scientifique est associé avec une forte augmentation des chances d’appartenir au groupe C. Cependant, un plus grand nombre de bonnes réponses aux questions sur le réchauffement climatique est également associé avec une augmentation des chances (30 % à chaque bonne réponse supplémentaire) d’appartenir au groupe C. Le CRT n’a cette fois-ci pas d’effet. Se déclarer proche du parti républicain, comparativement au parti démocrate, multiplie les chances par 2,5 d’appartenir au groupe C. Comparativement au tableau précédent, le fait d’être une femme diminue les chances de 36 % d’appartenir au groupe C.
| variable | Coefficient | RC | val.p | RC 2,5 % | RC 97,5 % | sign. |
|---|---|---|---|---|---|---|
| PercepOGMDes | 1,500 | 4,488 | 0,000 | 2,270 | 8,935 | *** |
| PercepRechClimDes | 2,440 | 11,501 | 0,000 | 5,312 | 25,028 | *** |
| ConnaisOGM | -0,480 | 0,621 | 0,000 | 0,492 | 0,787 | *** |
| ConnaisRechClim | 0,130 | 1,140 | 0,399 | 0,844 | 1,553 | |
| CRT | 0,340 | 1,409 | 0,119 | 0,914 | 2,160 | |
| Parti | ||||||
| ref : Democrate | – | – | – | – | – | – |
| autre | 0,190 | 1,211 | 0,531 | 0,664 | 2,203 | |
| Republicain | 0,630 | 1,872 | 0,038 | 1,041 | 3,387 |
|
| Sexe | ||||||
| ref : homme | – | – | – | – | – | – |
| femme:1 | -0,110 | 0,896 | 0,664 | 0,543 | 1,477 |
Le dernier tableau 8.19 compare le groupe A au groupe D (en désaccord sur les deux sujets). Les variables les plus importantes sont une fois encore le fait de se sentir en désaccord avec la recherche scientifique et le degré de connaissance sur les OGM. La variable concernant le parti politique est significative au seuil 0,05 et exprime toujours une tendance accrue pour les individus du parti républicain à appartenir au groupe D.
Nos propres conclusions corroborent celles de l’article original. Une des conclusions intéressantes est que le rejet du consensus scientifique ne semble pas nécessairement être associé à un déficit d’information ni à une plus faible capacité analytique, mais relèverait davantage d’une polarisation politique. Notez que cette littérature sur les croyances et la confiance dans la recherche est complexe, si le sujet vous intéresse, la discussion de l’article de McFadden (2016) est un bon point de départ.
8.2.5 Conclusion sur les modèles pour des variables qualitatives
Nous avons vu dans cette section, les trois principales formes de modèles GLM pour modéliser une variable binaire (modèle binomial), une variable ordinale (modèle de cotes proportionnel) et une variable multinomiale (modèle multinomial). Pour ces trois modèles, nous avons vu que la distribution utilisée est toujours la distribution binomiale et la fonction de lien logistique. Les coefficients obtenus s’interprètent comme des rapports de cotes, une fois qu’ils sont transformés avec la fonction exponentielle.