9.6 Mise en œuvre des GLMM dans R
Pour cet exemple de GLMM, nous proposons d’analyser à nouveau les données présentées dans la section 6.2.1.1 sur le modèle logistique binomial. Pour rappel, nous modélisions la probabilité qu’un individu utilise le vélo comme mode de transport pour son trajet le plus fréquent en utilisant une enquête réalisée auprès d’environ 26 000 Européens. Initialement, nous avons intégré les pays comme un effet fixe. Or, nous savons à présent qu’il serait plus judicieux de les traiter comme un effet aléatoire. Nous comparons deux modèles, un pour lequel seulement la constante varie par pays et un second dans lequel la pente pour l’âge varie également par pays. L’hypothèse étant que l’effet de l’âge sur l’utilisation du vélo pourrait être réduit dans certains pays où la culture du vélo est plus présente. Cette hypothèse implique également la présence potentielle d’une corrélation inverse entre la constante et la pente de chaque pays : dans un pays où la probabilité de base d’utiliser le vélo est plus élevée, l’effet de l’effet de l’âge est probablement réduit.
Pour ajuster ces modèles, nous utilisons le package lme4, permettant d’ajuster des modèles GLMM avec des distributions gaussienne, Gamma, de Poisson et binomial. Lorsque d’autres distributions sont nécessaires, il est possible de se tourner vers le package gamlss. Notez cependant que les effets aléatoires de gamlss sont estimés avec une méthode appelée PQL très flexible, mais qui peut produire des résultats erronés dans certains cas (Bolker et al. 2009).
Afin de limiter les répétitions, nous ne recalculons pas ici le VIF et nous excluons d’emblée les observations aberrantes (provenant de Malte ou de Chypre ou avec des temps de trajets supérieurs à 400 minutes).
9.6.1 Ajustement du modèle avec uniquement une constante aléatoire
Nous commençons donc par ajuster un premier modèle avec une constante aléatoire en fonction du pays. Dans la plupart des packages intégrant des effets aléatoires, la syntaxe suivante est utilisée pour stipuler une constante aléatoire : + (1|Pays). Concrètement, nous tentons d’ajuster le modèle décrit par l’équation (9.11).
\[\begin{equation} \begin{aligned} &Y \sim Binomial(p)\\ &g(p) = \beta_0 + \beta_1 x_1 + \upsilon \\ &\upsilon \sim Normal(0, \sigma_{\upsilon}) \\ &g(x) = log(\frac{x}{1-x}) \end{aligned} \tag{9.11} \end{equation}\]
Il s’agit simplement d’un modèle logistique binomial dans lequel nous avons ajouté une constante aléatoire : \(\upsilon\). Dans notre cas, elle varie avec la variable Pays. La syntaxe dans R pour produire ce modèle est la suivante.
# Chargement des données
dfenquete <- read.csv("data/glm/enquete_transport_UE.csv", encoding = "UTF-8")
dfenquete$Pays <- relevel(as.factor(dfenquete$Pays), ref = "Allemagne")
# Retirer les observations aberrantes
dfenquete2 <- subset(dfenquete, (dfenquete$Pays %in% c("Malte", "Chypre")) == F &
dfenquete$Duree < 400)
# Ajustement du modèle
library(lme4)
# Nécessité ici de centrer et réduire ces variables pour permettre au modèle de converger
dfenquete2$Age2 <- scale(dfenquete2$Age,center = T, scale = T)
dfenquete2$Duree2 <- scale(dfenquete2$Duree,center = T, scale = T)
modele1 <- glmer(y ~Sexe + Age2 + Education + StatutEmploi + Revenu +
Residence + Duree2 + ConsEnv + (1|Pays),
family = binomial(link="logit"),
control = glmerControl(optimizer = "bobyqa"),
data = dfenquete2)Nous nous concentrons ici sur l’interprétation des résultats du modèle et nous réalisons l’ensemble des diagnostics dans une section dédiée en fin de chapitre. Notez cependant que le diagnostic devrait précéder l’interprétation comme nous l’avons vu dans le chapitre sur les modèles GLM.
Vous constaterez que nous avons centré-réduit les variables Age et Duree. Il est souvent nécessaire de réaliser cette étape en amont pour s’assurer que le modèle converge sans trop de difficulté. Dans notre cas, si ces deux variables sont laissées dans leur échelle d’origine, la fonction glmer ne parvient pas à ajuster le modèle. Notez que cette transformation nous permet d’obtenir les coefficients standardisés, s’exprimant alors en écarts-types. La fonction summary nous donne accès à un premier ensemble d’informations.
summary(modele1)## Generalized linear mixed model fit by maximum likelihood (Laplace Approximation) ['glmerMod']
## Family: binomial ( logit )
## Formula: y ~ Sexe + Age2 + Education + StatutEmploi + Revenu + Residence +
## Duree2 + ConsEnv + (1 | Pays)
## Data: dfenquete2
## Control: glmerControl(optimizer = "bobyqa")
##
## AIC BIC logLik deviance df.resid
## 19176.1 19322.8 -9570.1 19140.1 25529
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -1.1989 -0.4418 -0.3212 -0.2134 7.2461
##
## Random effects:
## Groups Name Variance Std.Dev.
## Pays (Intercept) 0.5949 0.7713
## Number of obs: 25547, groups: Pays, 26
##
## Fixed effects:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.368954 0.212505 -15.854 < 2e-16 ***
## Sexehomme 0.370865 0.037921 9.780 < 2e-16 ***
## Age2 -0.102387 0.018776 -5.453 4.95e-08 ***
## Educationsecondaire 0.188093 0.103183 1.823 0.06832 .
## Educationsecondaire inferieur 0.297587 0.111334 2.673 0.00752 **
## Educationuniversite 0.138666 0.106495 1.302 0.19289
## StatutEmploisans emploi 0.256478 0.042282 6.066 1.31e-09 ***
## Revenufaible 0.073834 0.071648 1.031 0.30277
## Revenumoyen 0.039403 0.065237 0.604 0.54585
## Revenusans reponse 0.215704 0.102298 2.109 0.03498 *
## Revenutres eleve -0.121254 0.185292 -0.654 0.51286
## Revenutres faible 0.237385 0.085705 2.770 0.00561 **
## Residencegrande ville 0.272281 0.069277 3.930 8.48e-05 ***
## Residencepetite-moyenne ville 0.276286 0.061493 4.493 7.02e-06 ***
## Residencezone rurale -0.118963 0.069093 -1.722 0.08511 .
## Duree2 -0.018718 0.019241 -0.973 0.33065
## ConsEnv 0.101757 0.009277 10.969 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1La première partie de ce résumé nous rappelle la formule utilisée pour le modèle et nous indique différents indicateurs de qualité d’ajustement comme l’AIC, le BIC et la déviance. Nous avons ensuite une partie dédiée aux effets aléatoires (Random Effects) et une partie dédiée aux effets fixes (Fixed effects). Cette dernière s’interprète de la même manière que pour un modèle à effets fixes, n’oubliez cependant pas d’utiliser la fonction exponentielle pour obtenir les rapports de cotes (fonction de lien logistique).
9.6.1.1 Rôle joué par l’effet aléatoire
Comme vous pouvez le constater, la section Random Effects ne comprend qu’un seul paramètre : la variance de l’effet pays. Nous pouvons ainsi écrire que l’effet du pays suit une distribution normale avec une moyenne de 0 et une variance \(\sigma^2\) de 0,595. Pour aller plus loin dans cette analyse, nous pouvons calculer le coefficient de corrélation intraclasse (ICC). Cependant, puisque notre modèle est binomial et non gaussien, nous ne disposons pas d’un paramètre de variance au niveau des individus, il est donc possible, à la place, d’utiliser la variance théorique du modèle : \(\frac{\pi^2}{3}\). Nous calculons ainsi notre ICC :
# Extraction de la variance des Pays
var_pays <- VarCorr(modele1)[[1]][[1]]
# Calcul de l'ICC
var_pays / (((pi**2)/3) + var_pays)## [1] 0.1531373Nous pouvons parvenir au même résultat en utilisant la fonction icc du package performance.
library(performance)
# Calcul de l'ICC
icc(modele1)## # Intraclass Correlation Coefficient
##
## Adjusted ICC: 0.153
## Unadjusted ICC: 0.148Notez que cette fonction distingue un ICC ajusté et un ICC conditionnel. Le premier correspond à l’ICC que nous avons présenté jusqu’ici et que nous avons calculé à la main. L’ICC conditionnel inclut dans son estimation la variance présente dans les effets fixes. Un fort écart entre ces deux ICC indique que les effets fixes sont capables de capturer une très forte variance dans les données, ce qui pourrait remettre en cause la pertinence de l’effet aléatoire. Dans notre cas, la différence entre les deux est très faible.
En plus du ICC, nous pouvons calculer les R2 marginal et conditionnel. Pour cela, nous utilisons la fonction r.squaredGLMM du package MuMIn.
library(MuMIn)
r.squaredGLMM(modele1)## R2m R2c
## theoretical 0.03492163 0.1827111
## delta 0.01554532 0.0813336Cette fonction nous renvoie à la fois les R2 obtenus en utilisant la variance théorique du modèle (\(\frac{\pi^2}{3}\) dans notre cas) et la variance estimée par la méthode delta. La seconde est plus conservative, mais les deux résultats indiquent que les effets aléatoires expliquent une part importante de la variance comparativement aux effets fixes. Notez également que la fonction r2 du package performance peut calculer ces deux R2, mais seulement en utilisant la variance théorique.
9.6.1.2 Significativité de l’effet aléatoire
Nous souhaitons déterminer ici si notre effet aléatoire contribue à significativement améliorer le modèle. Pour cela, nous effectuons un test de rapport de vraisemblance entre le modèle sans l’effet aléatoire (un simple GLM ici) et le modèle complet. Nous utilisons pour cela la fonction anova :
# Ajustement d'un modèle sans l'effet aléatoire
model_simple <- glm(y ~Sexe + Age2 + Education + StatutEmploi + Revenu +
Residence + Duree2 + ConsEnv,
family = binomial(link="logit"),
data = dfenquete2)
# Comparaison des deux modèles
anova(modele1,model_simple)## Data: dfenquete2
## Models:
## model_simple: y ~ Sexe + Age2 + Education + StatutEmploi + Revenu + Residence + Duree2 + ConsEnv
## modele1: y ~ Sexe + Age2 + Education + StatutEmploi + Revenu + Residence + Duree2 + ConsEnv + (1 | Pays)
## npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
## model_simple 17 20521 20660 -10243.6 20487
## modele1 18 19176 19323 -9570.1 19140 1347 1 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Le test indique clairement que le modèle complet est mieux ajusté : les valeurs de l’AIC, du BIC et de la déviance sont toutes grandement réduites et le test est largement significatif.
Pour aller plus loin, nous pouvons utiliser une approche par bootstrap pour calculer un intervalle de confiance pour la variance de l’effet aléatoire, l’ICC et le R2 conditionnel. Nous utilisons pour cela la fonction bootMer. Si vous essayez de lancer cette syntaxe, vous constaterez qu’elle prend énormément de temps, ce qui s’explique par le grand nombre de fois où le modèle doit être réajusté. Nous vous recommandons donc de bien enregistrer vos résultats après l’exécution de la fonction avec la fonction save. Notez que pour réduire significativement le temps de calcul, il est possible d’utiliser simultanément plusieurs cœurs de votre processeur, ce que nous faisons ici avec le package snow.
# Définition d'une fonction pour extraire les valeurs qui nous intéressent
extractor <- function(mod){
vari <- VarCorr(mod)[[1]][[1]]
ICC <- vari / (vari + (pi**2/3))
r2cond <- performance::r2(mod)[[1]]
return(c("vari"=vari,"icc"=ICC,"r2cond"=r2cond))
}
# Préparation d'un environnement multitraitement pour accélérer le calcul
library(snow)
# Préparation de huit coeurs (attention si votre machine en a moins!)
cl <- makeCluster(8)
clusterEvalQ(cl,library("lme4"))
valeurs <- bootMer(modele1,FUN = extractor,nsim = 1000,
use.u = F, type="parametric", ncpus = 8,
parallel="snow",
cl = cl)
# Sauvegarde des résultats
save(valeurs,file = 'data/glmm/boot_binom.rda')Nous pouvons à présent analyser l’incertitude de ces différents paramètres. Pour cela, nous devons commencer par observer graphiquement leurs distributions obtenues par bootstrap avec la figure 9.17.
# Chargement de nos valeurs préalablement enregistrées
load('data/glmm/boot_binom.rda')
# Construction de trois graphiques de distribution
df <- data.frame(valeurs$t)
names(df) <- c("variance","icc","R2cond")
breaks1 <- as.vector(quantile(df$variance, probs = c(0.001,0.15,0.5,0.85, 0.999)))
labs1 <- round(breaks1,2)
p1 <- ggplot(df) +
geom_histogram(aes(x = variance), bins = 50, fill = "#e63946", color = "black")+
geom_vline(xintercept = median(df$variance),
color = "black", linetype="dashed", size = 1)+
scale_x_continuous(breaks = breaks1, labels = labs1)+
theme(axis.ticks.y = element_blank(),
axis.text.y = element_blank(), axis.title.y = element_blank())
breaks2 <- as.vector(quantile(df$icc, probs = c(0.001,0.15,0.5,0.85, 0.999)))
labs2 <- round(breaks2,2)
p2 <- ggplot(df) +
geom_histogram(aes(x = icc), bins = 50, fill = "#a8dadc", color = "black")+
geom_vline(xintercept = median(df$icc),
color = "black", linetype="dashed", size = 1)+
scale_x_continuous(breaks = breaks2, labels = labs2)+
theme(axis.ticks.y = element_blank(),
axis.text.y = element_blank(), axis.title.y = element_blank())
breaks3 <- as.vector(quantile(df$R2cond, probs = c(0.001,0.15,0.5,0.85, 0.999)))
labs3 <- round(breaks3,3)
p3 <- ggplot(df) +
geom_histogram(aes(x = R2cond), bins = 50, fill = "#1d3557", color = "black")+
geom_vline(xintercept = median(df$R2cond),
color = "black", linetype="dashed", size = 1)+
scale_x_continuous(breaks = breaks3, labels = labs3)+
theme(axis.ticks.y = element_blank(),
axis.text.y = element_blank(), axis.title.y = element_blank())
ggarrange(p1,p2,p3, nrow = 2, ncol = 2)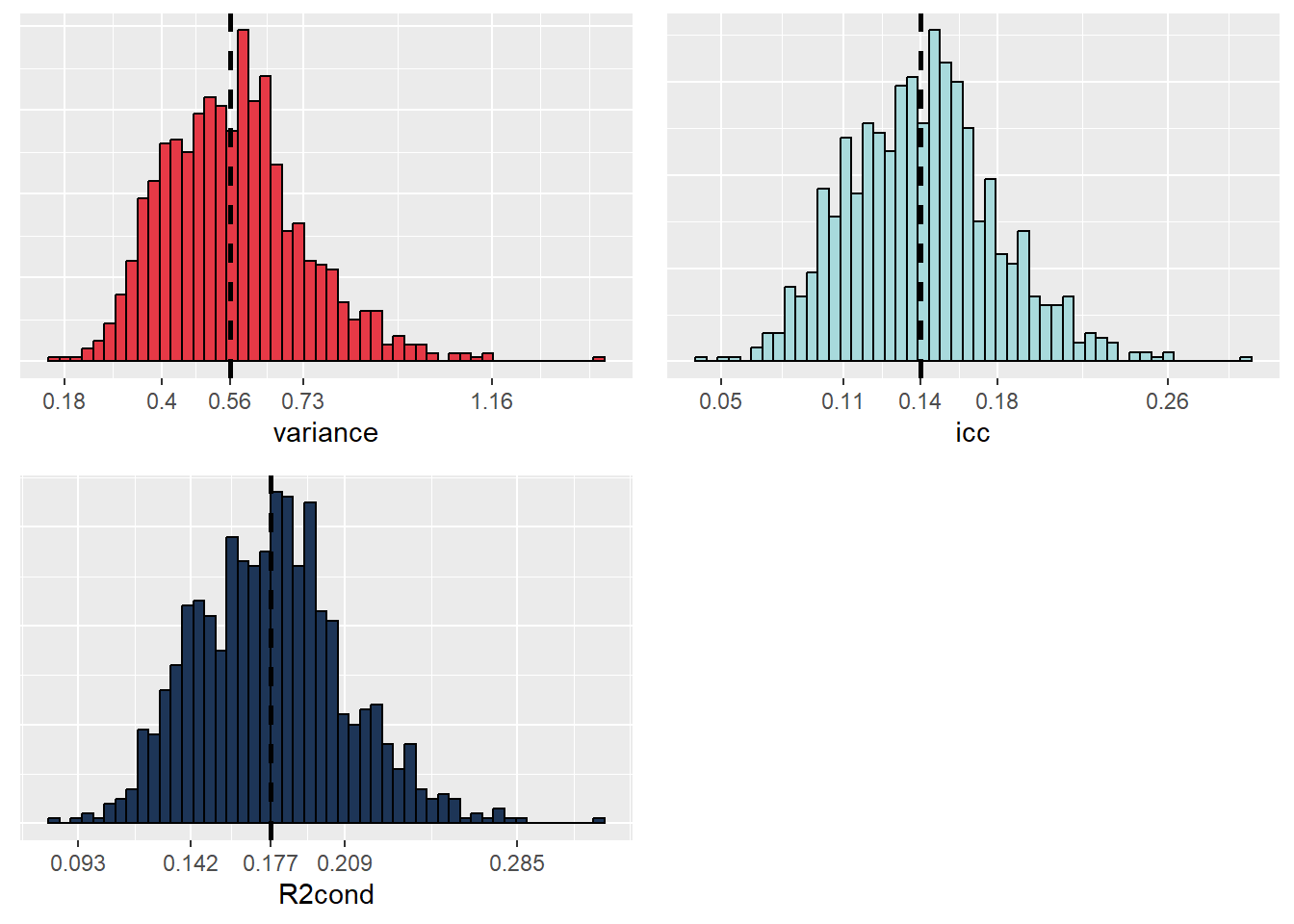
Figure 9.17: Distributions obtenues par bootstrap de la variance de l’effet aléatoire, de l’ICC et du R carré conditionnel
Les trois distributions sont toutes suffisamment éloignées de zéro pour que nous puissions en conclure que ces différentes valeurs sont toutes différentes de zéro. Notez également que les distributions sont relativement symétriques, indiquant que nous disposons de probablement suffisamment d’information dans nos données pour inclure notre effet aléatoire. Des distributions fortement asymétriques indiqueraient, au contraire, une forte difficulté du modèle à estimer le paramètre de variance à partir des données. Dans un article, il n’est pas nécessaire de reporter ces graphiques, mais plus simplement les intervalles de confiance à 95 % et les médianes.
# Intervalle de confiance pour la variance
quantile(df$variance,probs = c(0.0275,0.5,0.975))## 2.75% 50% 97.5%
## 0.3059400 0.5578986 0.9200472# Intervalle de confiance pour l'ICC
quantile(df$icc,probs = c(0.0275,0.5,0.975))## 2.75% 50% 97.5%
## 0.0850824 0.1449928 0.2185428# Intervalle de confiance pour le R2 conditionnel
quantile(df$R2cond,probs = c(0.0275,0.5,0.975))## 2.75% 50% 97.5%
## 0.1208577 0.1772778 0.24626229.6.1.3 Significativité des différentes constantes
Puisque nous avons conclu que l’effet aléatoire contribue significativement au modèle, nous pouvons à présent vérifier si les constantes ajustées pour chaque pays varient significativement les unes des autres. Pour rappel, les pentes et les constantes aléatoires ne sont pas directement estimées par le modèle, mais à posteriori. Il en résulte qu’il n’y a pas de moyen direct de mesurer l’incertitude de ces paramètres, et donc de construire des intervalles de confiance. Une première option pour contourner ce problème est d’effectuer des simulations à partir de la distribution postérieure du modèle. Notez que cette approche s’inspire largement de l’approche statistique bayésienne. Nous utilisons ici le package merTools pour effectuer 1000 simulations et obtenir une erreur standard pour chaque constante aléatoire de chaque pays.
# Simulations et extraction des effets aléatoires
library(merTools)
simsRE <- REsim(modele1,n.sims = 1000, oddsRatio = F)
# Calcul des intervalles de confiance
simsRE$lower <- simsRE$mean - 1.96 * simsRE$sd
simsRE$upper <- simsRE$mean + 1.96 * simsRE$sd
# Variable binaire pour la significativité
simsRE$sign <- case_when(
simsRE$lower<0 & simsRE$upper<0 ~ "inf",
simsRE$lower>0 & simsRE$upper>0 ~ "sup",
TRUE ~ "not"
)
# Représentation des intervalles de confiance
ggplot(simsRE) +
geom_errorbarh(aes(xmin = lower, xmax = upper,
y = reorder(groupID,mean)), size = 0.5, height = 0.5) +
geom_point(aes(x = mean, y = reorder(groupID,mean),
color = sign)) +
scale_color_manual(values = c("inf" = "#0077b6", "sup" = "#e63946", "not"="#000000"),
labels = c("sign. < 0", "sign. > 0", "non sign.")) +
labs(x = "Constante aléatoire", y = "Pays")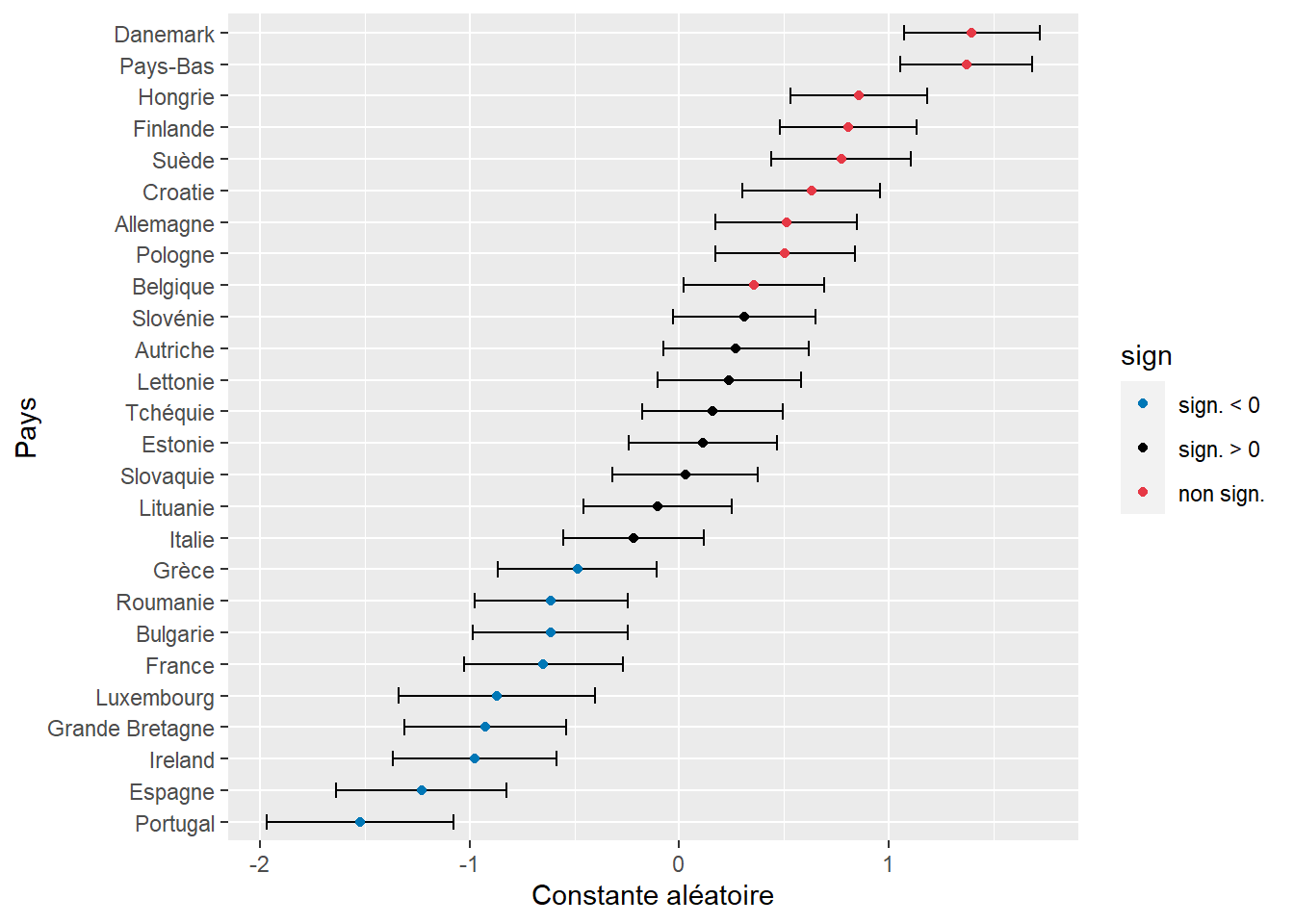
Figure 9.18: Constantes aléatoires estimées par Pays (IC par simulations)
La figure 9.18 permet de repérer en un coup d’oeil les pays pour lesquels la probabilité d’utiliser le vélo comme moyen de transport pour le trajet le plus fréquent est la plus élevée ou la plus faible. Notez cependant que les valeurs représentées sont pour l’instant des logarithmes de rapport de cotes. Nous devons donc les convertir en rapports de cotes avec la fonction exponentielle pour faciliter leur interprétation.
# Conversion en rapports de cote (et arrondissement à trois décimales)
mat <- round(exp(simsRE[c("mean","lower","upper")]),3)
rownames(mat) <- simsRE$groupID
names(mat) <- c("RC","RC.025","RC.975")
print(mat)## RC RC.025 RC.975
## Allemagne 1.667 1.191 2.333
## Autriche 1.311 0.927 1.853
## Belgique 1.428 1.022 1.997
## Bulgarie 0.541 0.374 0.784
## Croatie 1.880 1.354 2.610
## Danemark 4.043 2.926 5.587
## Espagne 0.292 0.194 0.439
## Estonie 1.121 0.787 1.598
## Finlande 2.242 1.621 3.102
## France 0.523 0.357 0.766
## Grande Bretagne 0.396 0.269 0.583
## Grèce 0.615 0.422 0.897
## Hongrie 2.359 1.700 3.273
## Ireland 0.377 0.254 0.558
## Italie 0.805 0.575 1.126
## Lettonie 1.270 0.901 1.790
## Lituanie 0.902 0.632 1.287
## Luxembourg 0.419 0.262 0.670
## Pays-Bas 3.939 2.873 5.400
## Pologne 1.658 1.189 2.311
## Portugal 0.218 0.139 0.340
## Roumanie 0.542 0.376 0.781
## Slovaquie 1.029 0.727 1.455
## Slovénie 1.363 0.969 1.916
## Suède 2.166 1.555 3.018
## Tchéquie 1.172 0.837 1.641Nous observons ainsi qu’une personne vivant en Finlande voit ses chances multipliées par 2,25 d’utiliser le vélo comme mode de transport pour son trajet le plus fréquent comparativement à la moyenne des pays européens. À l’inverse, une personne résidant en France a 47 % de chances de moins d’utiliser le vélo.
Notez cependant que cette approche basée sur des simulations peut poser des problèmes, car elle ne renvoie qu’une erreur standard pour mesurer l’incertitude de nos constantes. Dans les cas où nous ne disposons pas de beaucoup d’observations par groupe, la distribution à posteriori des constantes peut être asymétrique, rendant l’estimation des intervalles de confiance par les erreurs standards inutiles. Il est possible de détecter ce cas de figure quand les médianes et les moyennes renvoyées par la fonction simsRE diffèrent nettement. Une alternative plus robuste est à nouveau d’estimer la variabilité des effets aléatoires par bootstrap. Cette méthode requiert bien plus de temps de calcul que la précédente, nous vous recommandons donc de commencer par la méthode par simulations pour disposer d’un premier aperçu des résultats et d’utiliser ensuite la méthode bootstrap quand votre modèle est dans sa forme finale.
# Création de la fonction d'extraction
extractor2 <- function(mod){
elements <- ranef(mod)$Pays
vec <- elements[,1]
names(vec) <- rownames(elements)
return(vec)
}
# Préparation de l'opération en multitraitement
cl <- makeCluster(8)
clusterEvalQ(cl,library("lme4"))
# Calcul des effets aléatoires en bootstrap
valeurs <- bootMer(modele1,FUN = extractor2,nsim = 1000,
use.u = T, type="parametric", ncpus = 8,
parallel="snow",
cl = cl)
# Sauvegarder des résultats!
save(valeurs,file = 'data/glmm/boot_binom2.rda')Puisque nous disposons des distributions bootstrapées des différents effets aléatoires, nous pouvons directement les représenter dans un graphique (figure 9.19). Les résultats sont très similaires à ceux de la figure 9.18, ce qui s’explique par le grand nombre d’observations et de groupes. Avec moins d’observations, il est recommandé de privilégier l’approche par bootstrap.
# Chargement de nos valeurs bootstrapées
load('data/glmm/boot_binom2.rda')
# Conversion des bootstraps en intervalle de confiance
q025 <- function(x){return(quantile(x,probs = 0.025))}
q975 <- function(x){return(quantile(x,probs = 0.975))}
df <- reshape2::melt(valeurs$t)
df_med <- df %>% group_by(Var2) %>% summarise(
med = median(value),
lower = q025(value),
upper = q975(value))
# Ajout d'une variable pour la couleur si significatif
df_med$sign <- case_when(
df_med$lower<0 & df_med$upper<0 ~ "inf",
df_med$lower>0 & df_med$upper>0 ~ "sup",
TRUE ~ "not"
)
# Affichage des résultats
ggplot(df_med) +
geom_errorbar(aes(xmin = lower, xmax = upper, y = reorder(Var2,med)), width = 0.5) +
geom_point(aes(x = med, y = reorder(Var2,med), color = sign)) +
scale_color_manual(values = c("inf" = "#0077b6", "sup" = "#e63946", "not"="#000000"),
labels = c("sign. < 0", "sign. > 0", "non sign.")) +
labs(x = "Constante aléatoire", y = "Pays")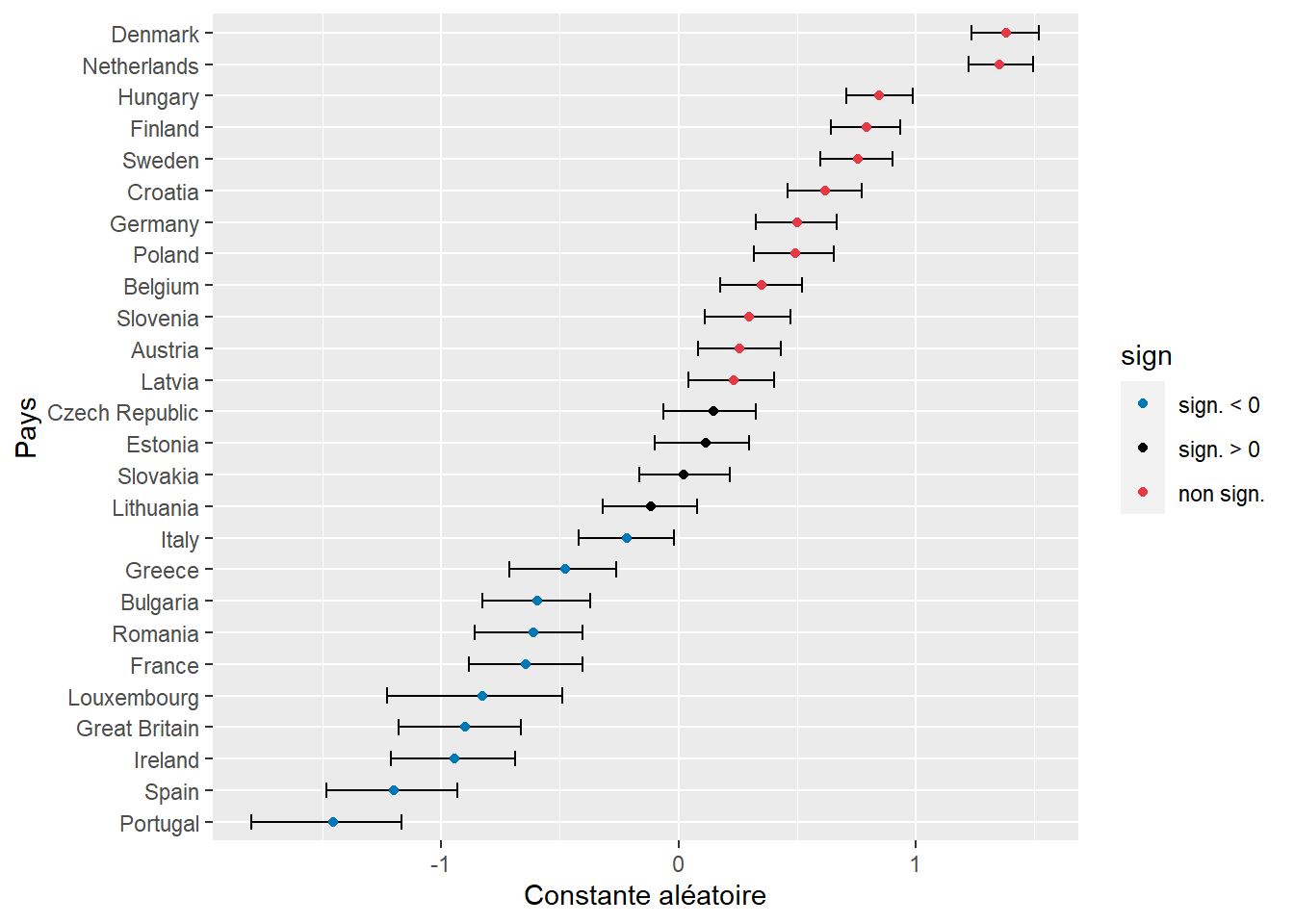
Figure 9.19: Constantes aléatoires estimées par Pays (IC par bootstrap)
9.6.2 Ajustement du modèle avec constantes et pentes aléatoires
Dans le modèle précédent, nous avons ajusté, pour chaque pays, une constante aléatoire afin de vérifier si la probabilité d’utiliser le vélo comme mode de transport principal changeait d’un pays d’Europe à l’autre. Nous souhaitons à présent tester l’hypothèse que l’effet de l’âge sur la probabilité d’utiliser le vélo varie d’un pays à l’autre. Pour cela, nous ajustons des constantes aléatoires par pays. Nous comparons trois modèles, triés ici selon leur niveau de complexité (nombre de paramètres) :
- le modèle avec uniquement des constantes aléatoires;
- le modèle avec des constantes et des pentes aléatoires indépendantes;
- le modèle avec des constantes et des pentes aléatoires corrélées.
Dans le package lme4, les syntaxes pour ajuster ces trois modèles sont les suivantes :
- constantes aléatoires :
+(1|Pays); - constantes et pentes aléatoires indépendantes :
+(1 + Age||Pays); - constantes et pentes aléatoires corrélées :
+(1 + Age|Pays).
Notez qu’il est aussi possible d’ajuster un modèle avec uniquement des pentes aléatoires avec la syntaxe : +(-1 + Age|Pays). Le paramètre -1 sert à retirer explicitement la constante aléatoire du modèle. Ajustons donc nos deux modèles avec pentes et constantes aléatoires.
# Constantes et pentes aléatoires indépendantes
modele2 <- glmer(y ~ Sexe + Age2 + Education + StatutEmploi + Revenu +
Residence + Duree2 + ConsEnv + (1 + Age2||Pays),
family = binomial(link="logit"),
control = glmerControl(optimizer = "bobyqa"),
data = dfenquete2)
# Constantes et pentes aléatoires corrélées
modele3 <- glmer(y ~ Sexe + Age2 + Education + StatutEmploi + Revenu +
Residence + Duree2 + ConsEnv + (1 + Age2|Pays),
family = binomial(link="logit"),
control = glmerControl(optimizer = "bobyqa"),
data = dfenquete2)9.6.2.1 Significativité de l’effet aléatoire
Puisque les trois modèles sont imbriqués, la première étape est de vérifier si les ajouts successifs au modèle de base sont significatifs, ce que nous pouvons tester avec un rapport de vraisemblance.
anova(modele1,modele2,modele3)## Data: dfenquete2
## Models:
## modele1: y ~ Sexe + Age2 + Education + StatutEmploi + Revenu + Residence + Duree2 + ConsEnv + (1 | Pays)
## modele2: y ~ Sexe + Age2 + Education + StatutEmploi + Revenu + Residence + Duree2 + ConsEnv + (1 + Age2 || Pays)
## modele3: y ~ Sexe + Age2 + Education + StatutEmploi + Revenu + Residence + Duree2 + ConsEnv + (1 + Age2 | Pays)
## npar AIC BIC logLik deviance Chisq Df Pr(>Chisq)
## modele1 18 19176 19323 -9570.1 19140
## modele2 19 19171 19325 -9566.3 19133 7.5754 1 0.005917 **
## modele3 20 19172 19335 -9566.1 19132 0.4033 1 0.525385
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Nous constatons ainsi que l’ajout des pentes aléatoires permet d’améliorer significativement le modèle, mais que l’ajout de la corrélation entre les pentes et les constantes aléatoires a un apport très marginal. Nous décidons tout de même de le garder dans un premier temps, car ce paramètre a un intérêt théorique. Affichons le résumé du modèle 3.
summary(modele3)## Generalized linear mixed model fit by maximum likelihood (Laplace Approximation) ['glmerMod']
## Family: binomial ( logit )
## Formula: y ~ Sexe + Age2 + Education + StatutEmploi + Revenu + Residence + Duree2 + ConsEnv + (1 + Age2 | Pays)
## Data: dfenquete2
## Control: glmerControl(optimizer = "bobyqa")
##
## AIC BIC logLik deviance df.resid
## 19172.2 19335.1 -9566.1 19132.2 25527
##
## Scaled residuals:
## Min 1Q Median 3Q Max
## -1.2087 -0.4392 -0.3218 -0.2137 7.1677
##
## Random effects:
## Groups Name Variance Std.Dev. Corr
## Pays (Intercept) 0.594981 0.77135
## Age2 0.007326 0.08559 -0.22
## Number of obs: 25547, groups: Pays, 26
##
## Fixed effects:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.35794 0.21285 -15.776 < 2e-16 ***
## Sexehomme 0.37289 0.03796 9.824 < 2e-16 ***
## Age2 -0.08775 0.02780 -3.157 0.001594 **
## Educationsecondaire 0.17963 0.10376 1.731 0.083420 .
## Educationsecondaire inferieur 0.28700 0.11183 2.566 0.010274 *
## Educationuniversite 0.13012 0.10707 1.215 0.224240
## StatutEmploisans emploi 0.25625 0.04251 6.029 1.65e-09 ***
## Revenufaible 0.07058 0.07179 0.983 0.325574
## Revenumoyen 0.03841 0.06532 0.588 0.556476
## Revenusans reponse 0.20362 0.10262 1.984 0.047245 *
## Revenutres eleve -0.12420 0.18550 -0.670 0.503170
## Revenutres faible 0.23562 0.08592 2.742 0.006103 **
## Residencegrande ville 0.26958 0.06935 3.887 0.000101 ***
## Residencepetite-moyenne ville 0.27570 0.06156 4.479 7.52e-06 ***
## Residencezone rurale -0.11898 0.06916 -1.720 0.085383 .
## Duree2 -0.01889 0.01927 -0.980 0.327063
## ConsEnv 0.10189 0.00929 10.968 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1À nouveau, nous nous intéressons ici principalement à la section Random Effect, puisque les effets fixes s’interprètent exactement comme dans les modèles présentés dans le chapitre 6. Les constantes ont une variance de 0,595 et les pentes de 0,007. La corrélation entre les deux effets est de -0,22. Cette corrélation est négative et relativement faible, ce qui signifie que les pays dans lesquels la constante est forte tendent à avoir un coefficient plus petit pour l’âge, et donc une réduction accrue de la probabilité d’utiliser le vélo avec l’âge. Nous devons cependant encore nous assurer qu’elle est significativement différente de 0. Pour cela, nous devons calculer l’intervalle de confiance des trois paramètres de variance du modèle. Nous utilisons à nouveau une approche par bootstrap et nous enregistrons les résultats.
# Fonction d'extraction des trois paramètres de variance
extractor3 <- function(mod){
vari1 <- VarCorr(mod)[[1]][[1]]
vari2 <- VarCorr(mod)[[1]][[4]]
covari <- VarCorr(mod)[[1]][[2]]
return(c("vari1"=vari1,"vari2"=vari2,"covari"=covari))
}
# Lancement du bootstrap
valeurs <- bootMer(modele3,FUN = extractor3,nsim = 1000,
use.u = F, type="parametric", ncpus = 8,
parallel="snow",
cl = cl,
.progress="txt",PBarg=list(style=3))
# Enregistrement des résultats
save(valeurs,file = 'data/glmm/boot_binom3.rda')À partir des valeurs bootstrapées, nous pouvons représenter les distributions de ces trois paramètres (variance des constantes, variance des pentes et corrélation entre les deux).
# Chargement des résultats
load('data/glmm/boot_binom3.rda')
# Conversion des valeurs de covariance en corrélation
df <- data.frame(
corr_values = valeurs$t[,3] / (sqrt(valeurs$t[,1]) * sqrt(valeurs$t[,2])),
vari_const = valeurs$t[,1],
vari_pente = valeurs$t[,2]
)
# Histogramme pour la variance des constantes
breaks1 <- quantile(df$vari_const,probs=c(0.025,0.5,0.975,0.999))
label1 <- round(breaks1,3)
p1 <- ggplot(df) +
geom_histogram(aes(x = vari_const), color = "black", fill = "white", bins = 30) +
geom_vline(xintercept = median(df$vari_const), color = "red", size = 1, linetype="dashed") +
geom_vline(xintercept = quantile(df$vari_const, probs = 0.025),
color = "blue", size = 0.5, linetype="dashed") +
geom_vline(xintercept = quantile(df$vari_const, probs = 0.975),
color = "blue", size = 0.5, linetype="dashed") +
labs(x = "Variance des constantes", y="")+
scale_x_continuous(breaks = breaks1, labels = label1)
# Histogramme pour la variance des pentes
breaks2 <- quantile(df$vari_pente,probs=c(0.025,0.5,0.975,0.999))
label2 <- round(breaks2,3)
p2 <- ggplot(df) +
geom_histogram(aes(x = vari_pente), color = "black", fill = "white", bins = 30) +
geom_vline(xintercept = median(df$vari_pente), color = "red", size = 1, linetype="dashed") +
geom_vline(xintercept = quantile(df$vari_pente, probs = 0.025),
color = "blue", size = 0.5, linetype="dashed") +
geom_vline(xintercept = quantile(df$vari_pente, probs = 0.975),
color = "blue", size = 0.5, linetype="dashed") +
labs(x = "Variance des pentes", y="")+
scale_x_continuous(breaks = breaks2, labels = label2)
# Histogramme pour la corrélation
breaks3 <- c(-1,-0.5,0,0.5,1,median(df$corr_values))
label3 <- round(breaks3,3)
p3 <- ggplot(df) +
geom_histogram(aes(x = corr_values), color = "black", fill = "white", bins = 30) +
geom_vline(xintercept = median(df$corr_values), color = "red", size = 1, linetype="dashed") +
geom_vline(xintercept = quantile(df$corr_values, probs = 0.025),
color = "blue", size = 0.5, linetype="dashed") +
geom_vline(xintercept = quantile(df$corr_values, probs = 0.975),
color = "blue", size = 0.5, linetype="dashed") +
labs(x = "Corrélation pentes/constantes", y="") +
scale_x_continuous(breaks = breaks3, labels = label3)
ggarrange(p1,p2, p3, ncol = 2, nrow = 2)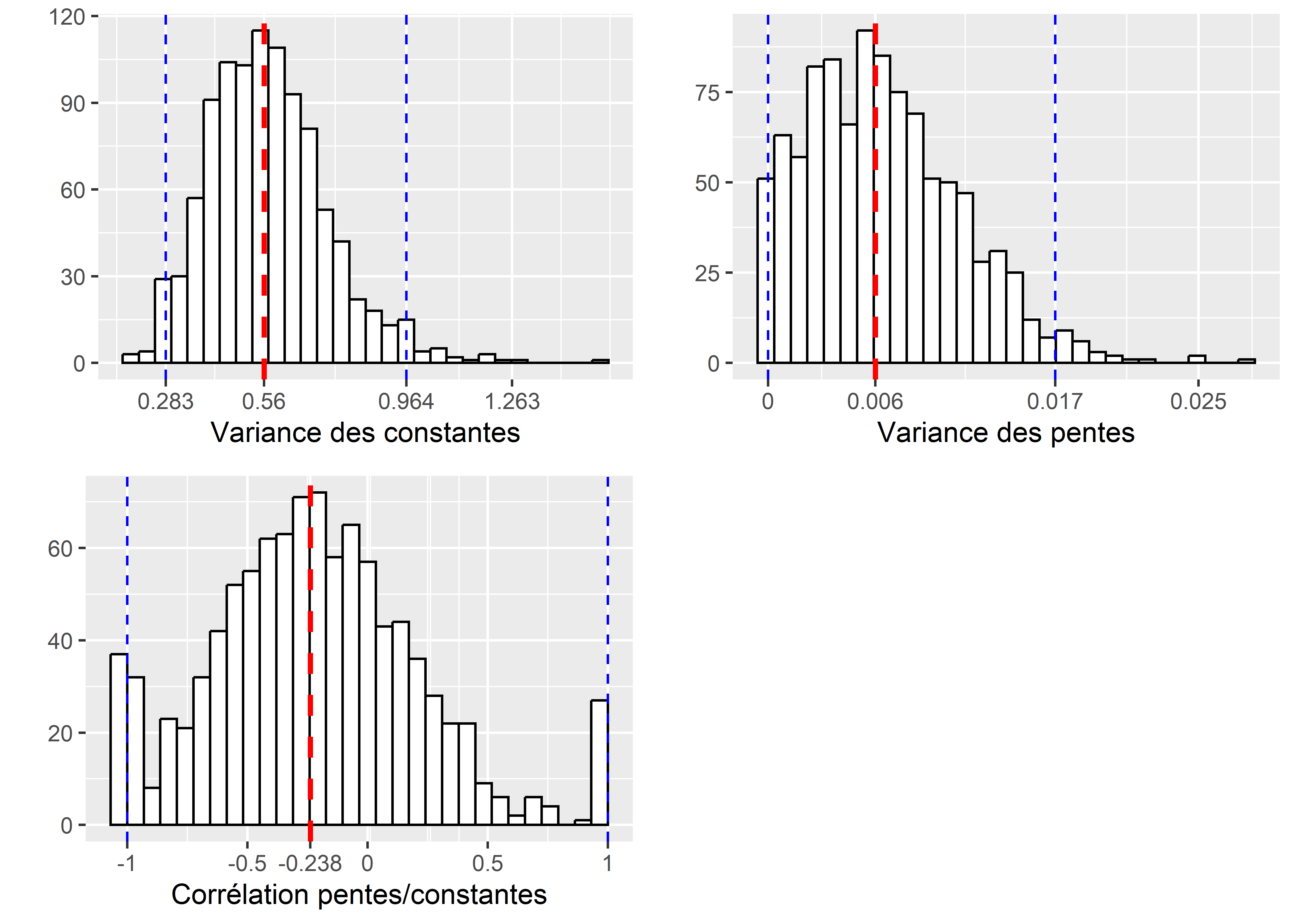
Figure 9.20: Incertitude autour des paramètres de variance obtenue par bootstrap
Nous constatons ainsi, à la figure 9.20, que la variance des constantes aléatoires est significativement différente de zéro (cette valeur n’est pas dans l’intervalle de confiance à 95 % représenté par les lignes verticales bleues) et une médiane de 0,56 (ligne verticale rouge). Pour les pentes, zéro est également à la limite de l’intervalle de confiance, et la distribution asymétrique et étalée nous indique que ce paramètre est fortement incertain dans le modèle. Enfin, la corrélation entre les pentes et les constantes est de loin le paramètre le plus incertain et son intervalle de confiance est franchement à cheval sur zéro, ce qui devrait nous amener à privilégier un modèle sans ce paramètre.
Pour terminer, nous pouvons calculer les R2 marginal et conditionnel du modèle afin de mieux cerner le rôle joué par les effets fixes et les effets aléatoires.
r.squaredGLMM(modele3)## R2m R2c
## theoretical 0.03413720 0.18360270
## delta 0.01419943 0.07636989Les valeurs des R2 marginal et conditionnel du modèle sont similaires à celles que nous avons obtenus avec seulement des constantes aléatoires dans la section précédente, signalant l’apport relativement faible des pentes aléatoires.
9.6.2.2 Analyse des effets aléatoires
Pour analyser facilement les constantes et les pentes aléatoires de chaque pays, nous pouvons représenter graphiquement leurs intervalles de confiance construits à partir des simulations tirées de la distribution a posteriori du modèle.
# Simulations et extraction des effets aléatoires
library(merTools)
simsRE <- REsim(modele3,n.sims = 1000, oddsRatio = F)
# Calcul des intervalles de confiance
simsRE$lower <- simsRE$mean - 1.96 * simsRE$sd
simsRE$upper <- simsRE$mean + 1.96 * simsRE$sd
# Variable binaire pour la significativité
simsRE$sign <- case_when(
simsRE$lower<0 & simsRE$upper<0 ~ "inf",
simsRE$lower>0 & simsRE$upper>0 ~ "sup",
TRUE ~ "not"
)
df1 <- subset(simsRE, grepl("Intercept",simsRE$term,fixed = T))
df2 <- subset(simsRE, grepl("Age2",simsRE$term,fixed = T))
# Représentation des intervalles de confiance
p1 <- ggplot(df1) +
geom_errorbarh(aes(xmin = lower, xmax = upper,
y = reorder(groupID,mean)), size = 0.5, height = 0.5) +
geom_point(aes(x = mean, y = reorder(groupID,mean),
color = sign)) +
scale_color_manual(values = c("inf" = "#0077b6", "sup" = "#e63946", "not"="#000000"),
labels = c("sign. < 0", "non sign.", "sign. > 0")) +
labs(x = "Constante aléatoire", y = "Pays")
p2 <- ggplot(df2) +
geom_errorbarh(aes(xmin = lower, xmax = upper,
y = reorder(groupID,mean)), size = 0.5, height = 0.5) +
geom_point(aes(x = mean, y = reorder(groupID,mean),
color = sign)) +
scale_color_manual(values = c("inf" = "#0077b6", "sup" = "#e63946", "not"="#000000"),
labels = c("sign. < 0", "non sign.", "sign. > 0")) +
labs(x = "Pente aléatoire (âge)", y = "Pays")
ggarrange(p1,p2, common.legend = T, nrow = 1, ncol = 2)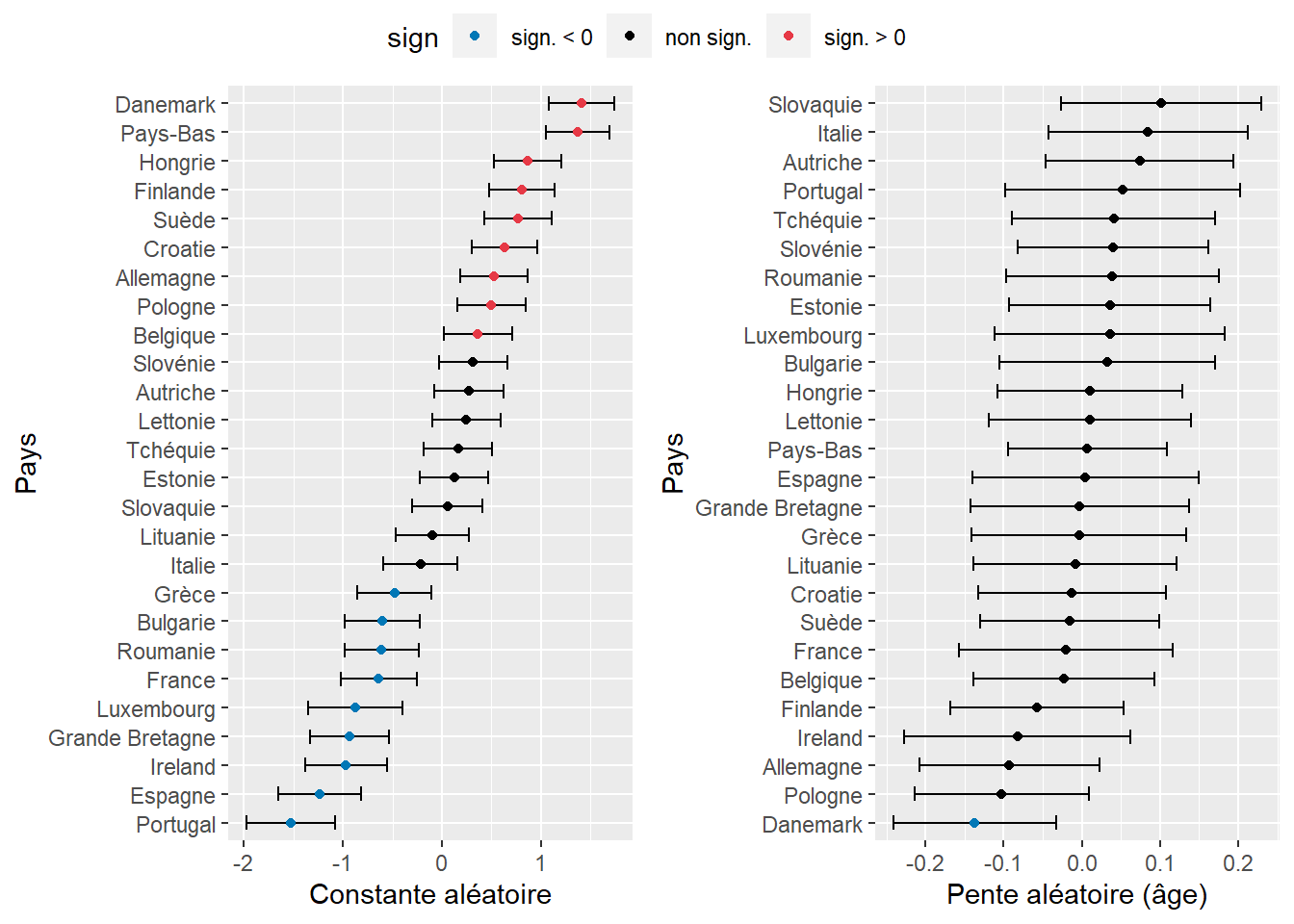
Figure 9.21: Constantes aléatoires estimées par pays (intervalles de confiance obtenus par simulations)
La figure 9.21 nous permet ainsi de constater que l’effet des pays sur les pentes est presque toujours non significatif, sauf pour le Danemark. Son effet négatif (-0,136) indique un renforcement de l’effet général, lui-même négatif (-0,088). Une interprétation possible est qu’au Danemark, l’utilisation du vélo est proportionnellement plus courante par les jeunes que dans le reste des pays de l’Europe.
Pour l’interprétation finale, il est nécessaire d’afficher les valeurs exactes de ces différents paramètres et, dans notre cas, de les convertir en rapports de cotes avec la fonction exponentielle. Pour les pentes aléatoires, il peut être plus facile d’interpréter la somme de l’effet fixe et de l’effet aléatoire.
# Extraction des effets aléatoires obtenus par simulation
mat <- simsRE[c("mean","lower","upper")]
mat$Pays <- simsRE$groupID
mat$effet <- simsRE$term
# Séparation des pentes et des constantes
df1 <- subset(mat, grepl("Intercept",mat$effet, fixed = TRUE))
df2 <- subset(mat, grepl("Age2",mat$effet, fixed = TRUE))
# Conversion en rapports de cotes pour les pentes (+ effet fixe)
df2$RC <- round(exp(df2$mean + fixef(modele3)[[3]]),3)
df2$RC025 <- round(exp(df2$lower + fixef(modele3)[[3]]),3)
df2$RC975 <- round(exp(df2$upper + fixef(modele3)[[3]]),3)
print(head(df2[c("Pays","RC","RC025","RC975")],10))## Pays RC RC025 RC975
## 27 Allemagne 0.835 0.744 0.937
## 28 Autriche 0.986 0.875 1.112
## 29 Belgique 0.895 0.797 1.005
## 30 Bulgarie 0.946 0.824 1.086
## 31 Croatie 0.905 0.802 1.020
## 32 Danemark 0.799 0.720 0.886
## 33 Espagne 0.920 0.796 1.063
## 34 Estonie 0.950 0.835 1.080
## 35 Finlande 0.865 0.774 0.967
## 36 France 0.897 0.783 1.029Nous constatons ainsi qu’au Danemark, les chances pour un individu d’utiliser le vélo sont réduites de 20 % à chaque augmentation de l’âge d’un écart-type, contre seulement 1,5 % en Autriche (non significatif pour ce dernier). Notons ici que l’écart-type de la variable Age est de 11 ans. Nous pouvons à présent analyser les constantes.
# Conversion en rapports de cotes pour les constantes
df1$RC <- round(exp(df1$mean),3)
df1$RC025 <- round(exp(df1$lower),3)
df1$RC975 <- round(exp(df1$upper),3)
print(head(df1[c("Pays","RC","RC025","RC975")],10))## Pays RC RC025 RC975
## 1 Allemagne 1.691 1.207 2.369
## 2 Autriche 1.312 0.925 1.860
## 3 Belgique 1.435 1.015 2.029
## 4 Bulgarie 0.547 0.375 0.799
## 5 Croatie 1.885 1.350 2.630
## 6 Danemark 4.087 2.937 5.686
## 7 Espagne 0.291 0.192 0.440
## 8 Estonie 1.131 0.798 1.602
## 9 Finlande 2.243 1.609 3.125
## 10 France 0.527 0.359 0.774En revanche, les chances pour un individu d’utiliser le vélo comme mode de transport pour son trajet le plus fréquent sont 4 fois supérieures à la moyenne européenne, contre seulement 1,3 fois en Autriche. Notez à nouveau que les intervalles de confiance pour ces pentes et ces constantes pourraient être estimés plus fiablement par bootstrap.
9.6.2.3 Diagnostic des effets aléatoires
Pour rappel, dans un modèle GLMM, les effets aléatoires sont modélisés comme provenant de distributions normales. Nous devons donc vérifier qu’ils respectent cette condition d’application. La figure 9.22 (graphique quantile-quantile) nous permet de constater que les constantes suivent bien une distribution normale, ce qui ne semble pas vraiment être le cas pour les pentes. Considérant que leurs effets sont petits, il serait plus pertinent ici de les retirer du modèle.
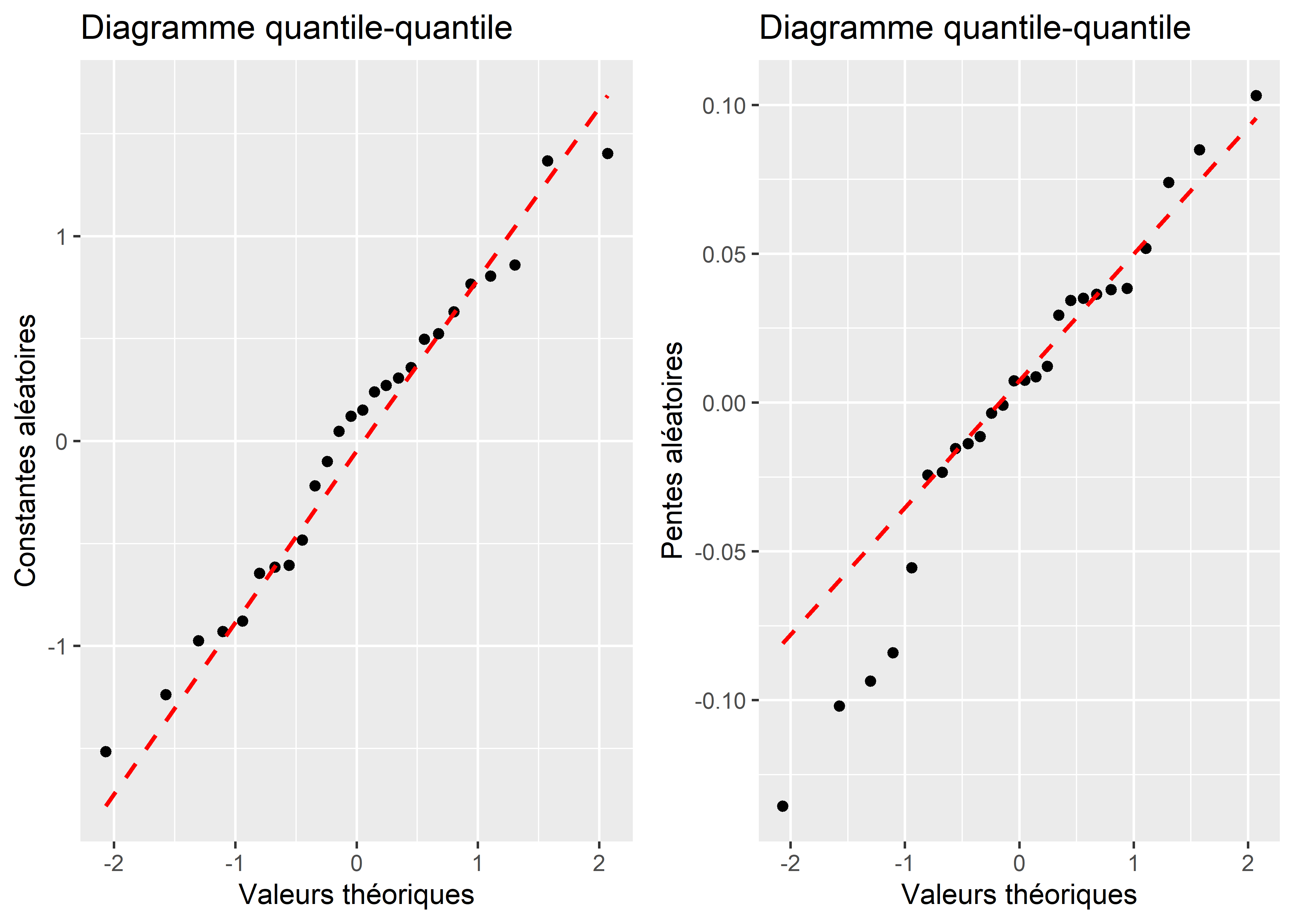
Figure 9.22: Distribution normale univariée des constantes et des pentes aléatoires
Considérant que ce modèle inclut une corrélation entre les constantes et les pentes aléatoires, il est également nécessaire de vérifier si elles suivent conjointement une distribution normale bivariée. La figure 9.23 semble indiquer que c’est le cas.
cor_mat <- VarCorr(modele3)[[1]]
re_effects <- data.frame(ranef(modele3)$Pays)
names(re_effects) <- c("constante","pente")
library(ellipse)
levels <- c(0.05,0.25,0.75,0.95)
els <- lapply(levels, function(i){
el <- data.frame(ellipse(cor_mat,center = c(0,0), level = i))
names(el) <- c("x","y")
return(el)
})
ref_points <- data.frame(data.frame(MASS::mvrnorm(n = 1000, mu = c(0,0), Sigma = cor_mat)))
names(ref_points) <- c("x","y")
ggplot() +
geom_point(aes(x = x, y = y), data = ref_points, alpha = 0.3, size = 0.4) +
geom_path(data = els[[1]], aes(x = x, y = y, color = "a")) +
geom_path(data = els[[2]], aes(x = x, y = y, color = "b")) +
geom_path(data = els[[3]], aes(x = x, y = y, color = "c")) +
geom_path(data = els[[4]], aes(x = x, y = y, color = "d")) +
geom_point(data = re_effects, aes(x = constante, y = pente))+
scale_color_manual(values = c("a"="#90e0ef",
"b"="#00b4d8",
"c"="#0077b6",
"d"="#03045e"),
labels = c("5 %","25 %","75 %","95 %"))+
labs(x = "Constantes", y = "Pentes", color = "quantiles")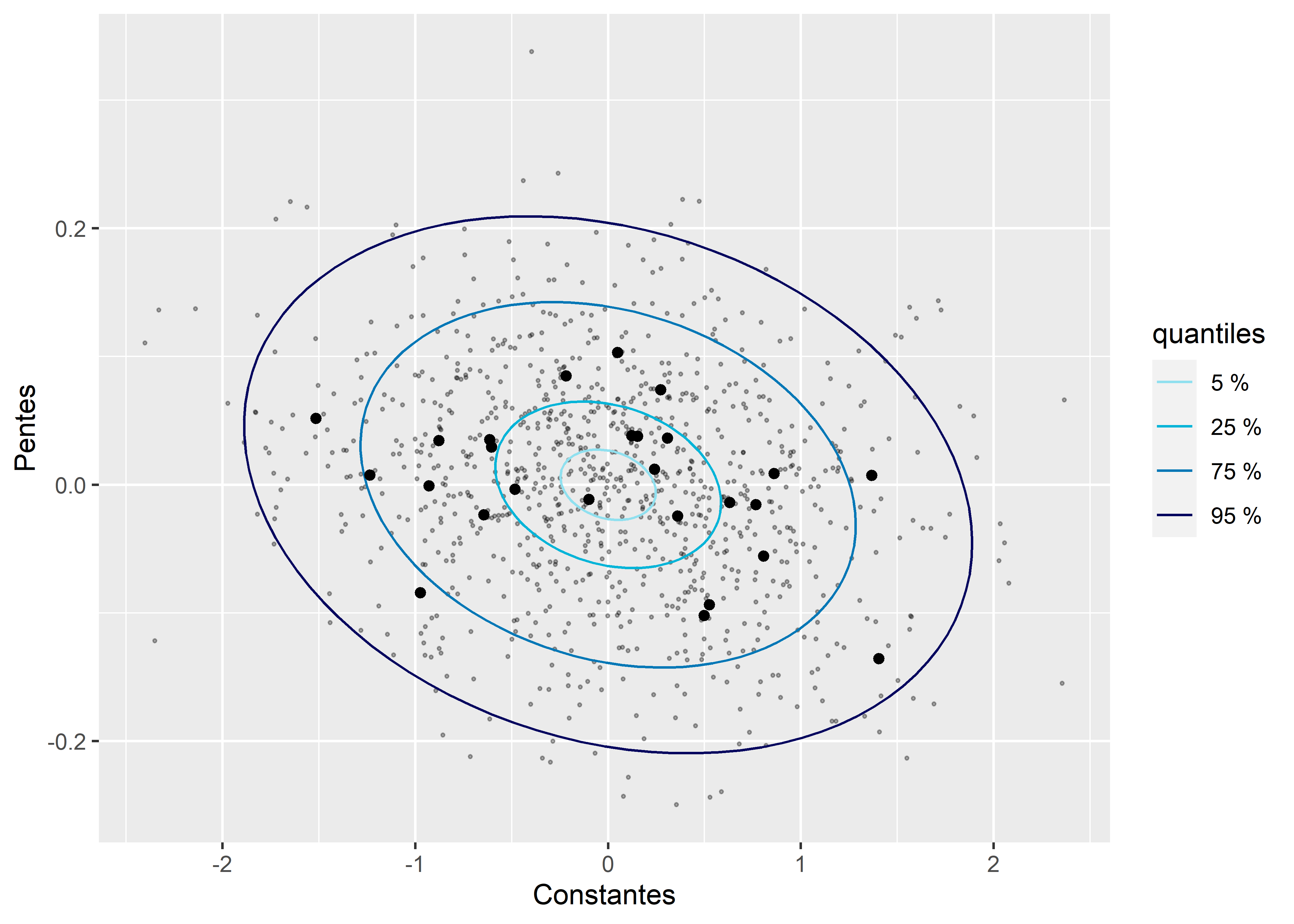
Figure 9.23: Distribution normale bivariée des constantes et des pentes aléatoires
9.6.2.4 Inférence pour les effets fixes
Nous avons mentionné, dans les sections précédentes, que le calcul de valeurs de p pour les effets fixes fait l’objet de controverses pour les modèles GLMM. La méthode offrant le meilleur compromis entre rapidité de calcul et fiabilité est la méthode Satterthwaite implémentée dans le package lmerTest. Pour l’utiliser, il suffit de charger le package lmerTest après lme4, ce qui modifie la fonction summary pour qu’elle utilise directement cette approche.
library(lmerTest)
round(summary(modele3)$coefficients,3)## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -3.358 0.213 -15.776 0.000
## Sexehomme 0.373 0.038 9.824 0.000
## Age2 -0.088 0.028 -3.157 0.002
## Educationsecondaire 0.180 0.104 1.731 0.083
## Educationsecondaire inferieur 0.287 0.112 2.566 0.010
## Educationuniversite 0.130 0.107 1.215 0.224
## StatutEmploisans emploi 0.256 0.043 6.029 0.000
## Revenufaible 0.071 0.072 0.983 0.326
## Revenumoyen 0.038 0.065 0.588 0.556
## Revenusans reponse 0.204 0.103 1.984 0.047
## Revenutres eleve -0.124 0.186 -0.670 0.503
## Revenutres faible 0.236 0.086 2.742 0.006
## Residencegrande ville 0.270 0.069 3.887 0.000
## Residencepetite-moyenne ville 0.276 0.062 4.479 0.000
## Residencezone rurale -0.119 0.069 -1.720 0.085
## Duree2 -0.019 0.019 -0.980 0.327
## ConsEnv 0.102 0.009 10.968 0.000Les deux autres options envisageables sont : effectuer une analyse de type 3 ou calculer les intervalles de confiance par bootstrap. Cependant, elles requièrent beaucoup plus de temps de calcul. Par conséquent, elles ne sont pas présentées ici.