6.2 Relation entre une variable quantitative et une variable qualitative à plus de deux modalités

Existe-t-il une relation entre une variable continue et une variable qualitative comprenant plus de deux modalités? Pour répondre à cette question, nous avons recours à deux méthodes : l’analyse de variance – ANOVA, ANalysis Of VAriance en anglais – et le test non paramétrique de Kruskal-Wallis. La première permet de vérifier si les moyennes de plusieurs groupes d’une population donnée sont ou non significativement différentes; la seconde, si leurs médianes sont différentes.

6.2.1 Analyse de variance

L’analyse de variance (ANOVA) est largement utilisée en psychologie, en médecine et en pharmacologie. Prenons un exemple classique en pharmacologie pour tester l’efficacité d’un médicament. Quatre groupes de population sont constitués :

un premier groupe d’individus pour lequel nous administrons un placebo (un médicament sans substance active), soit le groupe de contrôle ou le groupe témoin;
un second groupe auquel nous administrons le médicament avec un faible dosage;
un troisième avec un dosage moyen;
un quatrième avec un dosage élevé.

La variable continue permet d’évaluer l’évolution de l’état de santé des individus (par exemple, la variation du taux de globules rouges dans le sang avant et après le traitement). Si le traitement est efficace, nous nous attendons alors à ce que les moyennes des deuxième, troisième et quatrième groupes soient plus élevées que celle du groupe de contrôle. Les différences de moyennes entre les second, troisième et quatrième groupes permettent aussi de repérer le dosage le plus efficace. Si nous n’observons aucune différence significative entre les groupes, cela signifie que l’effet du médicament ne diffère pas de l’effet d’un placébo.

L’ANOVA est aussi très utilisée en études urbaines, principalement pour vérifier si un phénomène urbain varie selon plusieurs groupes d’une population donnée ou de régions géographiques. En guise d’exemple, le recours à l’ANOVA permet de répondre aux questions suivantes :

Les moyennes des niveaux d’exposition à un polluant atmosphérique (variable continue) varient-elles significativement selon le mode de transport utilisé (automobile, vélo, transport en commun) pour des trajets similaires en heures de pointe?
Pour une métropole donnée, les moyennes des loyers (variable continue) sont-elles différentes entre les logements de la ville centre versus ceux localisés dans la première couronne et ceux de la seconde couronne?

6.2.1.1 Calcul des trois variances pour l’ANOVA

L’ANOVA repose sur le calcul de trois variances :

la variance totale (VT) de la variable dépendante continue, soit la somme des carrés des écarts à la moyenne de l’ensemble de la population (équation (6.8));
la variance intergroupe (Var_inter) ou variance expliquée (VE), soit la somme des carrés des écarts entre la moyenne de chaque groupe et la moyenne de l’ensemble du jeu de données multipliées par le nombre d’individus appartenant à chacun des groupes (équation (6.9));
la variance intragroupe (Var_intra) ou variance non expliquée (VNE), soit la somme des variances des groupes de la variable indépendante (équation (6.10)).

\[\begin{equation} VT=\sum_{i=1}^n (y_{i}-\overline{y})^2 \tag{6.8} \end{equation}\]

\[\begin{equation} Var_{inter} \mbox{ ou } VE=n_{g_1}\sum_{i\in{g_1}}(\overline{y_{g_1}}-\overline{y})^2 + n_{g_2}\sum_{i\in{g_2}}(\overline{y_{g_2}}-\overline{y})^2 + ... + n_{g_k}\sum_{i\in{g_n}}(\overline{y_{g_k}}-\overline{y})^2 \tag{6.9} \end{equation}\]

\[\begin{equation} Var_{intra} \mbox{ ou } VNE=\sum_{i\in{g_1}}(y_{i}-\overline{y_{g_1}})^2 + \sum_{i\in{g_2}}(y_{i}-\overline{y_{g_2}})^2 + ... + \sum_{i\in{g_n}}(y_{i}-\overline{y_{g_k}})^2 \tag{6.10} \end{equation}\]

où \(\overline{y}\) est la moyenne de l’ensemble de la population; \(\overline{y_{g_1}}\), \(\overline{y_{g_2}}\), \(\overline{y_{g_k}}\) sont respectivement les moyennes des groupes 1 à k (k étant le nombre de modalités de la variable qualitative) et \(n_{g_1}\),\(n_{g_2}\) et \(n_{g_k}\) sont les nombres d’observations dans les groupes 1 à k.

La variance totale (VT) est égale à la somme de la variance intergroupe (expliquée) et la variance intragroupe (non expliquée) (équation (6.11)). Le ratio entre la variance intergroupe (expliquée) et la variance totale est dénommé Eta² (équation (6.12)). Il varie de 0 à 1 et exprime la proportion de la variance de la variable continue qui est expliquée par les différentes modalités de la variable qualitative.

\[\begin{equation} VT = Var_{inter} + Var_{intra} \mbox{ ou } VT = VNE + VE \tag{6.11} \end{equation}\]

\[\begin{equation} \eta^2= \frac{Var_{inter}}{VT} \mbox{ ou } \eta^2= \frac{VE}{VT} \tag{6.12} \end{equation}\]

La décomposition de la variance totale – égale à la somme des variances intragroupe et intergroupe – est fondamentale en statistique. Nous verrons qu’elle est aussi utilisée pour évaluer la qualité d’une partition d’une population en plusieurs groupes dans le chapitre sur les méthodes de classification (chapitre 13). En ANOVA, nous retenons que :

plus la variance intragroupe est faible, plus les différents groupes sont homogènes;
plus la variance intergroupe est forte, plus les moyennes des groupes sont différentes et donc plus les groupes sont dissemblables.

Autrement dit, plus la variance intergroupe (dissimilarité des groupes) est maximisée et corollairement plus la variance intragroupe (homogénéité de chacun des groupes) est minimisée, plus les groupes sont clairement distincts et plus l’ANOVA est performante.

Examinons un premier jeu de données fictives sur la vitesse de déplacement de cyclistes (variable continue exprimée en km/h) et une variable qualitative comprenant trois groupes de cyclistes utilisant soit un vélo personnel (n_A = 5), soit en libre-service (n_B = 7), soit électrique (n_C = 6) (tableau 6.2). D’emblée, nous notons que les moyennes de vitesse des trois groupes sont différentes : 17,6 km/h pour les cyclistes avec leur vélo personnel, 12,3 km/h celles et ceux avec des vélos en libre-service et 23,1 km/h pour les cyclistes avec un vélo électrique. Pour chaque observation, la troisième colonne du tableau représente les écarts à la moyenne globale mis au carré, tandis que les colonnes suivantes représentent la déviation au carré de chaque observation à la moyenne de son groupe d’appartenance. Ainsi, pour la première observation, nous avons \((\mbox{16,900} - \mbox{17,339})^2 = \mbox{0,193}\) et \((\mbox{16,900} - \mbox{17,580})^2~ = \mbox{0,462}\). Les valeurs des trois variances sont les suivantes :

la variance totale (VT) est donc égale à la somme de la troisième colonne (\(\mbox{424,663}\)).
la variance intergroupe (expliquée, VE), elle est égale à \(\mbox{5}\times(\mbox{17,580-17,339})^2+\mbox{7}\times(\mbox{12,257-17,339})^2+\mbox{6}\times(\mbox{23,067-17,339})^2 = \mbox{377,904}\).
la variance intragroupe (non expliquée, VNE) est égale à \(\mbox{11,228+21,537+13,993=46,758}\).

Nous avons donc \(VT = Var_{inter} + Var_{intra}\), soit \(\mbox{424,663 = 377,904 + 46,758}\) et \(\eta_2 = \mbox{377,904 / 424,663 = 0,89}\). Cela signale que 89 % de la variance de la vitesse des cyclistes est expliquée par le type de vélo utilisé.

Tableau 6.2: Données fictives et calcul des trois variances (cas 1)
Type de vélo	km/h	\((y_{i}-\overline{y})^2\)	\((y_{i}-\overline{y_{A}})^2\)	\((y_{i}-\overline{y_{B}})^2\)	\((y_{i}-\overline{y_{C}})^2\)
A. personnel	16,900	0,193	0,462
A. personnel	20,400	9,370	7,952
A. personnel	16,100	1,535	2,190
A. personnel	17,700	0,130	0,014
A. personnel	16,800	0,290	0,608
B. libre-service	13,400	15,515		1,306
B. libre-service	11,300	36,468		0,916
B. libre-service	14,000	11,148		3,038
B. libre-service	12,400	24,393		0,020
B. libre-service	13,700	13,242		2,082
B. libre-service	8,500	78,126		14,116
B. libre-service	12,500	23,415		0,059
C. électrique	22,900	30,926			0,028
C. électrique	26,000	75,015			8,604
C. électrique	23,600	39,202			0,284
C. électrique	21,000	13,404			4,271
C. électrique	22,300	24,613			0,588
C. électrique	22,600	27,679			0,218
grande moyenne	17,339
moyenne groupe A	17,580
moyenne groupe B	12,257
moyenne groupe C	23,067
Variance totale		424,663
Variance intragroupe			11,228	21,537	13,993

Examinons un deuxième jeu de données fictives pour lequel le type de vélo utilisé n’aurait que peu d’effet sur la vitesse des cyclistes (tableau 6.3). D’emblée, les moyennes des trois groupes semblent très similaires (19,3, 17,9 et 18,7). Les valeurs des trois variances sont les suivantes :

la variance totale (VT) est égale à \(\mbox{121,756}\).
la variance intergroupe (expliquée, VE) est égale à \(\mbox{5}\times(\mbox{19,300-18,528})^2+\mbox{7}\times(\mbox{17,871-18,528})^2+\mbox{6}\times(\mbox{18,650-18,528})^2 = \mbox{6,087}\).
la variance intragroupe (non expliquée, VNE) est égale à \(\mbox{9,140+50,254+56,275 = 115,669}\).

Nous avons donc \(VT = Var_{inter} + Var_{intra}\), soit \(\mbox{121,756 = 6,087 + 115,669}\) et \(\eta_2 = \mbox{6,087 / 121,756 = 0,05}\). Cela signale que 5 % de la variance de la vitesse des cyclistes est uniquement expliquée par le type de vélo utilisé.

Tableau 6.3: Données fictives et calcul des trois variances (cas 2)
Type de vélo	km/h	\((y_{i}-\overline{y})^2\)	\((y_{i}-\overline{y_{A}})^2\)	\((y_{i}-\overline{y_{B}})^2\)	\((y_{i}-\overline{y_{C}})^2\)
A. personnel	17,500	1,056	3,24
A. personnel	19,000	0,223	0,09
A. personnel	19,700	1,374	0,16
A. personnel	18,700	0,030	0,36
A. personnel	21,600	9,439	5,29
B. libre-service	13,700	23,307		17,401
B. libre-service	20,800	5,163		8,577
B. libre-service	15,100	11,750		7,681
B. libre-service	18,800	0,074		0,862
B. libre-service	21,500	8,834		13,167
B. libre-service	16,500	4,112		1,881
B. libre-service	18,700	0,030		0,687
C. électrique	16,600	3,716			4,203
C. électrique	16,300	4,963			5,523
C. électrique	15,600	8,572			9,303
C. électrique	20,000	2,167			1,822
C. électrique	24,600	36,872			35,402
C. électrique	18,800	0,074			0,022
grande moyenne	18,528
moyenne groupe A	19,300
moyenne groupe B	17,871
moyenne groupe C	18,650
Variance totale		121,756
Variance intragroupe			9,14	50,254	56,275

6.2.1.2 Test de Fisher

Pour vérifier si les moyennes sont statistiquement différentes (autrement dit, si leur différence est significativement différente de 0), nous avons recours au test F de Fisher. Pour ce faire, nous posons l’hypothèse nulle (H₀), soit que les moyennes des groupes sont égales; autrement dit que la variable qualitative n’a pas d’effet sur la variable continue (indépendance entre les deux variables). L’hypothèse alternative (H₁) est donc que les moyennes sont différentes. Pour nos deux jeux de données fictives ci-dessus comprenant trois groupes, H₀ signifie que \(\overline{y_{A}}=\overline{y_{B}}=\overline{y_{C}}\). La statistique F se calcule comme suit :

\[\begin{equation} F = \frac{\frac{Var{inter}}{k-1}}{\frac{Var{intra}}{n-k}}\mbox{ ou } F = \frac{\frac{VE}{k-1}}{\frac{VNE}{n-k}} \tag{6.13} \end{equation}\]

où \(n\) et \(k\) sont respectivement les nombres d’observations et de modalités de la variable qualitative. L’hypothèse nulle (les moyennes sont égales) est rejetée si la valeur du F calculé est supérieure à la valeur critique de la table F avec les degrés de liberté (k-1, n-k) et un seuil \(\alpha\) (p=0,05 habituellement) (voir la table des valeurs critiques de F, section 15). Notez que nous utilisons rarement la table F puisqu’avec la fonction aov, nous obtenons directement la valeur F et celle de p qui lui est associée. Concrètement, si le test F est significatif (avec p < 0,05), plus la valeur de F est élevée, plus la différence entre les moyennes est élevée.

Appliquons rapidement la démarche du test F à nos deux jeux de données fictives qui comprennent 3 modalités pour la variable qualitative et 18 observations. Avec \(\alpha\) = 0,05, 2 degrés de liberté (3-1) au numérateur et 15 au dénominateur (18-3), la valeur critique de F est de 3,68. Nous en concluons alors que :

pour le cas A, le F calculé est égal à \(\mbox{(377,904 / 2) / (46,758 / 15) = 60,62}\). Il est supérieur à la valeur F critique; les moyennes sont donc statistiquement différentes au seuil 0,05. Autrement dit, nous aurions eu moins de 5 % de chance d’obtenir un échantillon produisant ces résultats si en réalité la différence entre les moyennes était de 0.
pour le cas B, le F calculé est égal à \(\mbox{(6,087 / 2) / (115,669 / 15) = 0,39}\). Il est inférieur à la valeur F critique; les moyennes ne sont donc pas statistiquement différentes au seuil de 0,05.

6.2.1.3 Conditions d’application de l’ANOVA et solutions de rechange

Trois conditions d’application doivent être vérifiées avant d’effectuer une analyse de variance sur un jeu de données :

Normalité des groupes. Le test de Fisher repose sur le postulat que les échantillons (groupes) sont normalement distribués. Pour le vérifier, nous avons recours au test de normalité de Shapiro–Wilk (section 2.5.4.1.3). Rappelez-vous toutefois que ce test est très restrictif, surtout pour de grands échantillons.
Homoscédasticité. La variance dans les échantillons doit être la même (homogénéité des variances). Pour vérifier cette condition, nous utilisons les tests de Levene, de Bartlett ou de Breusch-Pagan.
Indépendance des observations (pseudo-réplication). Chaque individu doit appartenir à un et un seul groupe. En d’autres termes, les observations ne sont pas indépendantes si plusieurs mesures (variable continue) sont faites sur un même individu. Si c’est le cas, nous utiliserons alors une analyse de variance sur des mesures répétées (voir le bloc à la fin du chapitre).

Quelles sont les conséquences si les conditions d’application ne sont pas respectées? La non-vérification des conditions d’application cause deux problèmes distincts : elle affecte la puissance du test (sa capacité à détecter un effet, si celui-ci existe réellement) et le taux d’erreur de type 1 (la probabilité de trouver un résultat significatif alors qu’aucune relation n’existe réellement, soit un faux-positif) (Glass, Peckham et Sanders 1972; Lix, Keselman et Keselman 1996).

Si la distribution est asymétrique plutôt que centrée (comme pour une distribution normale), la puissance et le taux d’erreur de type 1 sont tous les deux peu affectés, car le test est non orienté (la différence de moyennes peut être négative ou positive).
Si la distribution est leptocurtique (pointue, avec des extrémités de la distribution plus importantes), le taux d’erreur de type 1 est peu affecté; en revanche, la puissance du test est réduite. L’inverse s’observe si la distribution est platicurtique (aplatie, c’est-à-dire avec des extrémités de la distribution plus réduites.
Si les groupes ont des variances différentes, le taux d’erreur de type 1 augmente légèrement.
Si les observations ne sont pas indépendantes, à la fois le taux d’erreur de type 1 et la puissance du test sont fortement affectés.
Si les échantillons sont petits, les effets présentés ci-dessus sont démultipliés.
Si plusieurs conditions ne sont pas respectées, les conséquences présentées ci-dessus s’additionnent, voire se combinent.

Que faire quand les conditions d’application relatives à la normalité ou à l’homoscédasticité ne sont vraiment pas respectées? Signalons d’emblée que le non-respect de ces conditions ne change rien à la décomposition de la variance (VT = V_intra+V_inter). Cela signifie que vous pouvez toujours calculer Eta². Par contre, le test de Fisher ne peut pas être utilisé, car il est biaisé comme décrit précédemment. Quatre solutions sont envisageables :

Lorsque les échantillons sont fortement anormalement distribués, certains auteurs vont simplement transformer leur variable en appliquant une fonction logarithme (le plus souvent) ou racine carrée, inverse ou exponentielle, et reporter le test de Fisher calculé sur cette transformation. Attention toutefois! Transformer une variable ne va pas systématiquement la rapprocher d’une distribution normale et complique l’interprétation finale des résultats. Par conséquent, avant de recalculer votre test F, il convient de réaliser un test de normalité de Shapiro–Wilk et un test d’homoscédasticité (Levene, Bartlett ou Breusch-Pagan) sur la variable continue transformée.
Détecter les observations qui contribuent le plus à l’anormalité et à l’hétéroscédasticité (valeurs aberrantes ou extrêmes). Supprimez-les et refaites votre ANOVA en vous assurant que les conditions sont désormais respectées. Notez que supprimer des observations peut être une pratique éthiquement questionnable en statistique. Si vos échantillons sont bien constitués et que la mesure collectée n’est pas erronée, pourquoi donc la supprimer? Si vous optez pour cette solution, prenez soin de comparer les résultats avant et après la suppression des observations. Si les conditions sont respectées après la suppression et que les résultats de l’ANOVA (Eta² et test F de Fisher) sont très semblables, conservez donc les résultats de l’ANOVA initiale et signalez que vous avez procédé aux deux tests.
Lorsque les variances des groupes sont dissemblables, vous pouvez utiliser le test de Welch pour l’ANOVA au lieu du test F de Fisher.
Dernière solution, lorsque les deux conditions ne sont vraiment pas respectées, utilisez le test non paramétrique de Kruskal-Wallis. Par analogie au t de Student, il correspond au test des rangs signés de Wilcoxon. Ce test est décrit dans la section suivante.

Vous l’aurez compris, dans de nombreux cas en statistique, les choix méthodologiques dépendent en partie de la subjectivité des chercheur(e)s. Il faut s’adapter au jeu de données et à la culture statistique en vigueur dans votre champ d’études. N’hésitez pas à réaliser plusieurs tests différents pour évaluer la robustesse de vos conclusions et fiez-vous en premier lieu à ceux pour lesquels votre jeu de données est le plus adapté.

6.2.2 Test non paramétrique de Kruskal-Wallis

Le test non paramétrique de Kruskal-Wallis est une solution de rechange à l’ANOVA classique lorsque le jeu de données présente de graves problèmes de normalité et d’hétéroscédasticité. Cette méthode représente une ANOVA appliquée à une variable continue transformée préalablement en rangs. Du fait de la transformation en rangs, nous ne vérifions plus si les moyennes sont différentes, mais bel et bien si les médianes de la variable continue sont différentes. Pour ce faire, nous utiliserons la fonction kruskal.test.

6.2.3 Mise en œuvre dans R

Dans une étude récente, Apparicio et al. (2018) ont comparé les expositions au bruit et à la pollution atmosphérique aux heures de pointe à Montréal en fonction du mode de transport utilisé. Pour ce faire, trois équipes de trois personnes ont été constituées : une personne à vélo, une autre en automobile et une dernière se déplaçant en transport en commun, équipées de capteurs de pollution, de sonomètres, de vêtements biométriques et d’une montre GPS. Chaque matin, à huit heures précises, les membres de chaque équipe ont réalisé un trajet d’un quartier périphérique de Montréal vers un pôle d’enseignement (université) ou d’emploi localisé au centre-ville. Le trajet inverse était réalisé le soir à 17 h. Au total, une centaine de trajets ont ainsi été réalisés. Des analyses de variance ont ainsi permis de comparer les trois modes (automobile, vélo et transport en commun) en fonction des temps de déplacement, des niveaux d’exposition au bruit, des niveaux d’exposition au dioxyde d’azote et de la dose totale inhalée de dioxyde d’azote. Nous vous proposons ici d’analyser une partie de ces données.

6.2.3.1 Première ANOVA : différences entre les temps de déplacement

Comme première analyse de variance, nous vérifions si les moyennes des temps de déplacement sont différentes entre les trois modes de transport.

Dans un premier temps, nous calculons les moyennes des différents groupes. Nous pouvons alors constater que les moyennes sont très semblables : 37,7 minutes pour l’automobile versus 38,4 et 41,6 pour le vélo et le transport en commun. Aussi, les variances des trois groupes sont relativement similaires.

library("rstatix")
# chargement des DataFrames
load("data/bivariee/dataPollution.RData")
# Statistiques descriptives pour les groupes (moyenne et écart-type)
df_TrajetsDuree %>%                                 # Nom du DataFrame
    group_by(Mode) %>%                                # Variable qualitative
    get_summary_stats(DureeMinute, type = "mean_sd")  # Variable continue

## # A tibble: 3 × 5
##   Mode    variable        n  mean    sd
##   <chr>   <chr>       <dbl> <dbl> <dbl>
## 1 1. Auto DureeMinute    33  37.7  12.8
## 2 2. Velo DureeMinute    33  38.4  15.2
## 3 3. TC   DureeMinute    33  41.6  11.4

Pour visualiser la distribution des données pour les trois groupes, vous pouvez créer des graphiques de densité et en violon (figure 6.4). La juxtaposition des trois distributions montre que les distributions des valeurs pour les trois groupes sont globalement similaires. Cela est corroboré par le fait que les boîtes du graphique en violon sont situées à la même hauteur. Autrement dit, à la lecture des deux graphiques, il ne semble pas y avoir de différences significatives entre les trois groupes en termes de temps de déplacement.

library("ggplot2")
library("ggpubr")
# Graphique de densité
GraphDens <- ggplot(data = df_TrajetsDuree, 
  mapping=aes(x=DureeMinute,colour=Mode,fill=Mode)) +
  geom_density(alpha=0.55,mapping=aes(y=..scaled..))+
    labs(title="a. Graphique de densité",
         x = "Densité",
         y = "Durée du trajet (en minutes)")
# Graphique en violon
GraphViolon <- ggplot(df_TrajetsDuree, aes(x=Mode, y=DureeMinute)) +
  geom_violin(fill="white") +
  geom_boxplot(width=0.1, aes(x=Mode, y=DureeMinute,fill=Mode))+
  labs(title="b. Graphique en violon",
       x = "Mode de transport",
       y = "Durée du trajet (en minutes)")+
  theme(legend.position = "none")
ggarrange(GraphDens, GraphViolon)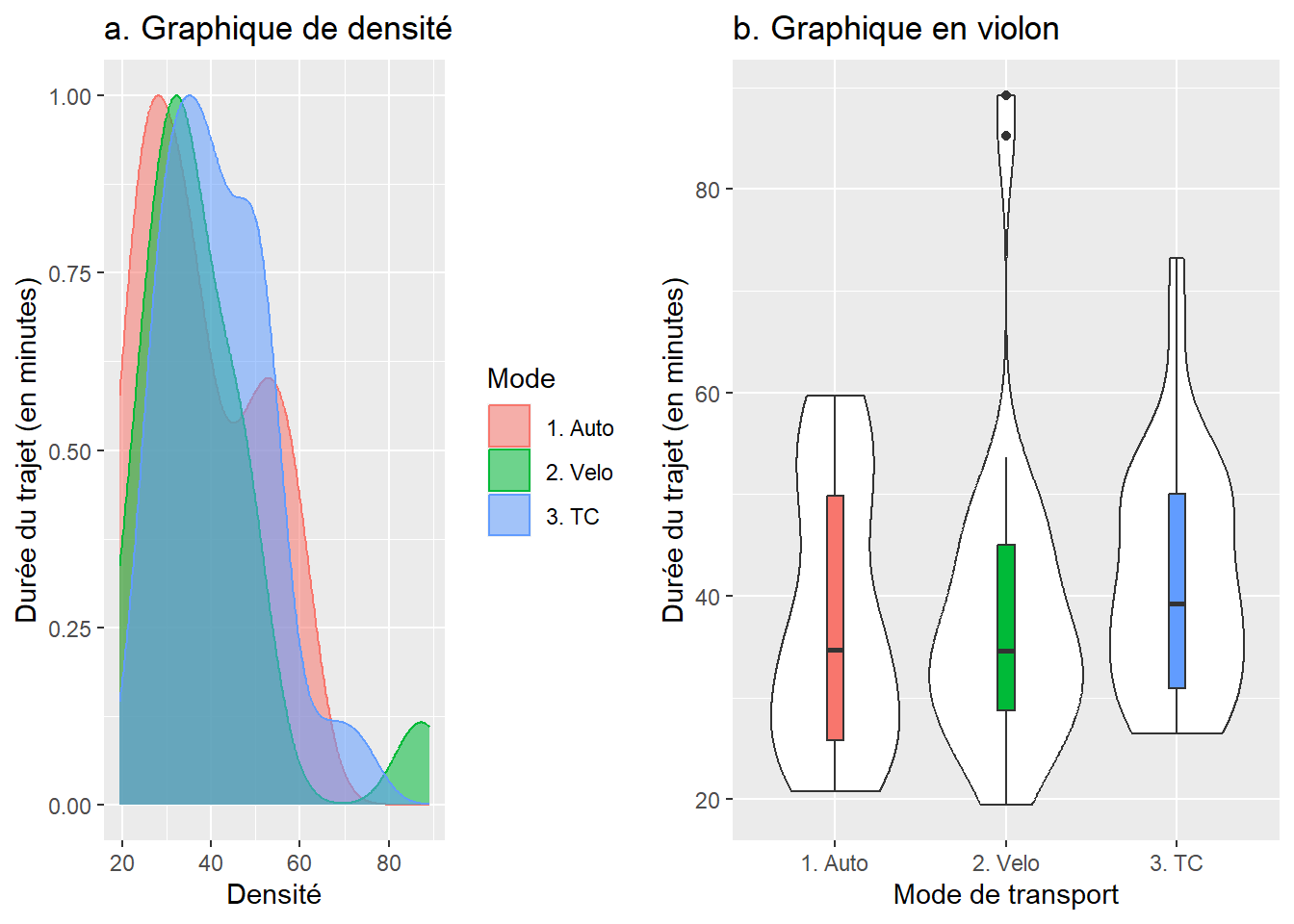

Figure 6.4: Graphiques de densité et en violon

Nous pouvons vérifier si les échantillons sont normalement distribués avec la fonction shapiro_test du package rstatix. À titre de rappel, l’hypothèse nulle (H₀) de ce test est que la distribution est normale. Par conséquent, quand la valeur de p associée à la statistique de Shapiro est supérieure à 0,05, alors nous ne pouvons rejeter l’hypothèse d’une distribution normale (autrement dit, la distribution est anormale). À la lecture des résultats ci-dessous, seul le groupe utilisant le transport en commun présente une distribution proche de la normalité (p = 0,0504). Ce test étant très restrictif, il est fortement conseillé de visualiser le diagramme quantile-quantile pour chaque groupe (graphique QQ plot) (figure 6.5). Ces graphiques sont utilisés pour déterminer visuellement si une distribution empirique (observée sur des données), s’approche d’une distribution théorique (ici la loi normale). Si effectivement les deux distributions sont proches, les points du diagramme devraient tous tomber sur une ligne droite parfaite. Un intervalle de confiance (représenté ici en gris) peut être construit pour obtenir une interprétation plus nuancée. Dans notre cas, seules deux observations pour le vélo et deux autres pour l’automobile s’éloignent vraiment de la ligne droite. Nous pouvons considérer que ces trois distributions s’approchent d’une distribution normale.

library("dplyr")
library("ggpubr")
library("rstatix")
# Condition 1 : normalité des échantillons
# Test pour la normalité des échantillons (groupes) : test de Shapiro
 df_TrajetsDuree %>%          # Nom du DataFrame
   group_by(Mode) %>%         # Variable qualitative
   shapiro_test(DureeMinute)  # Variable continue

## # A tibble: 3 × 4
##   Mode    variable    statistic         p
##   <chr>   <chr>           <dbl>     <dbl>
## 1 1. Auto DureeMinute     0.905 0.00729  
## 2 2. Velo DureeMinute     0.797 0.0000288
## 3 3. TC   DureeMinute     0.936 0.0504

# Graphiques qqplot pour les groupes
ggqqplot(df_TrajetsDuree, "DureeMinute", facet.by = "Mode", 
         xlab="Théorique", ylab="Échantillon")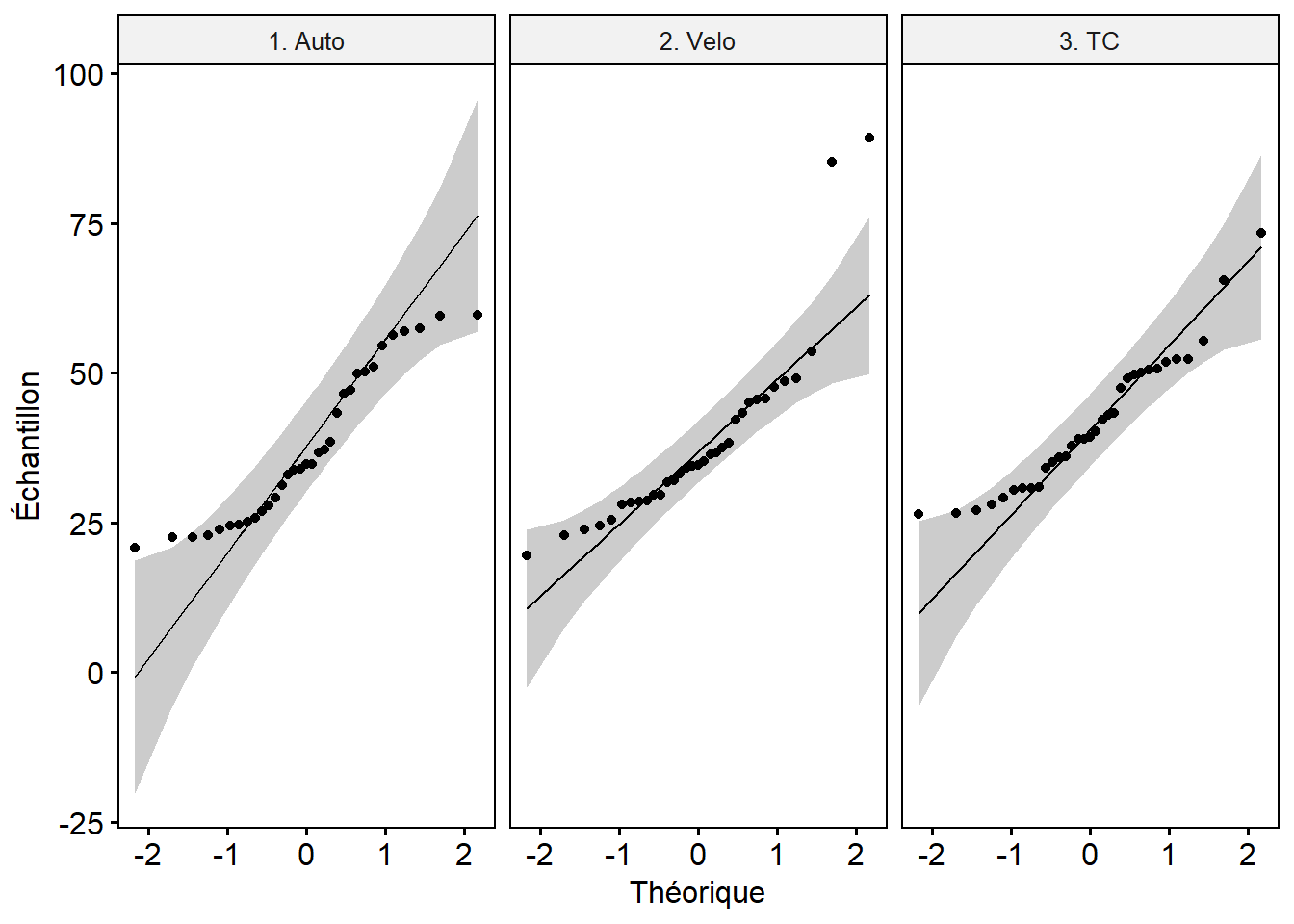

Figure 6.5: QQ Plot pour les groupes

Pour vérifier l’hypothèse d’homogénéité des variances, vous pouvez utiliser les tests de Levene, de Bartlett ou de Breusch-Pagan. Les valeurs de p, toutes supérieures à 0,05, signalent que la condition d’homogénéité des variances est respectée.

library("rstatix")
library("lmtest")
library("car")
# Condition 2 : homogénéité des variances (homocédasticité)
leveneTest(DureeMinute ~ Mode, data = df_TrajetsDuree)

## Levene's Test for Homogeneity of Variance (center = median)
##       Df F value Pr(>F)
## group  2  0.2418 0.7857
##       96

bartlett.test(DureeMinute ~ Mode, data = df_TrajetsDuree)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  DureeMinute by Mode
## Bartlett's K-squared = 2.6718, df = 2, p-value = 0.2629

bptest(DureeMinute ~ Mode, data = df_TrajetsDuree)

## 
##  studentized Breusch-Pagan test
## 
## data:  DureeMinute ~ Mode
## BP = 1.3322, df = 2, p-value = 0.5137

Deux fonctions peuvent être utilisées pour calculer l’analyse de variance : la fonction de base aov(variable continue ~ variable qualitative, data = votre DataFrame) ou bien la fonction anova_test(variable continue ~ variable qualitative, data = votre DataFrame) du package rstatix. Comparativement à aov, l’avantage de la fonction anova_test est qu’elle calcule aussi le Eta².

library("rstatix")
library("car")
library("effectsize")
# ANOVA avec la fonction aov
aov1 <- aov(DureeMinute ~ Mode, data = df_TrajetsDuree)
summary(aov1)

##             Df Sum Sq Mean Sq F value Pr(>F)
## Mode         2    287   143.2    0.82  0.444
## Residuals   96  16781   174.8

# calcul de Eta2 avec la fonction eta_squared du package effectsize
effectsize::eta_squared(aov1)

## # Effect Size for ANOVA
## 
## Parameter | Eta2 |       95% CI
## -------------------------------
## Mode      | 0.02 | [0.00, 1.00]
## 
## - One-sided CIs: upper bound fixed at [1.00].

# ANOVA avec la fonction anova_test du package rstatix
anova_test(DureeMinute ~ Mode, data = df_TrajetsDuree)

## ANOVA Table (type II tests)
## 
##   Effect DFn DFd    F     p p<.05   ges
## 1   Mode   2  96 0.82 0.444       0.017

La valeur de p associée à la statistique F (0,444) nous permet de conclure qu’il n’y a pas de différences significatives entre les moyennes des temps de déplacement des trois modes de transport.

6.2.3.2 Deuxième ANOVA : différences entre les niveaux d’exposition au bruit

Dans ce second exercice, nous analysons les différences d’exposition au bruit. D’emblée, les statistiques descriptives révèlent que les moyennes sont dissemblables : 66,8 dB(A) pour l’automobile versus 68,8 et 74 pour le vélo et le transport en commun. Aussi, la variance du transport en commun est très différente des autres.

library("rstatix")
# chargement des DataFrames
load("data/bivariee/dataPollution.RData")
# Statistiques descriptives pour les groupes (moyenne et écart-type)
 df_Bruit %>%                                 # Nom du DataFrame
   group_by(Mode) %>%                                # Variable qualitative
   get_summary_stats(laeq, type = "mean_sd")  # Variable continue

## # A tibble: 3 × 5
##   Mode    variable     n  mean    sd
##   <chr>   <chr>    <dbl> <dbl> <dbl>
## 1 1. Auto laeq      1094  66.8  4.56
## 2 2. Velo laeq      1124  68.8  4.29
## 3 3. TC   laeq      1207  74.0  6.79

À la lecture des graphiques de densité et en violon (figure 6.6), il semble clair que les niveaux d’exposition au bruit sont plus faibles pour les automobilistes et plus élevés pour les cyclistes et surtout les personnes en transport en commun. En outre, la distribution des valeurs d’exposition au bruit dans le transport en commun semble bimodale. Cela s’explique par le fait que les niveaux de bruit sont beaucoup plus élevés dans le métro que dans les autobus.

library("ggplot2")
library("ggpubr")
# Graphique en densité
GraphDens <- ggplot(data = df_Bruit, 
  mapping=aes(x=laeq,colour=Mode,fill=Mode)) +
  geom_density(alpha=0.55,mapping=aes(y=..scaled..))+
  labs(title="a. graphique de densité",
       x="Exposition au bruit (dB(A))")
# Graphique en violon
GraphViolon <- ggplot(df_Bruit, aes(x=Mode, y=laeq)) +
  geom_violin(fill="white") +
  geom_boxplot(width=0.1, aes(x=Mode, y=laeq,fill=Mode))+
  labs(title="b. Graphique en violon",
       x = "Mode de transport",
       y="Exposition au bruit (dB(A))")+
  theme(legend.position = "none")
ggarrange(GraphDens, GraphViolon)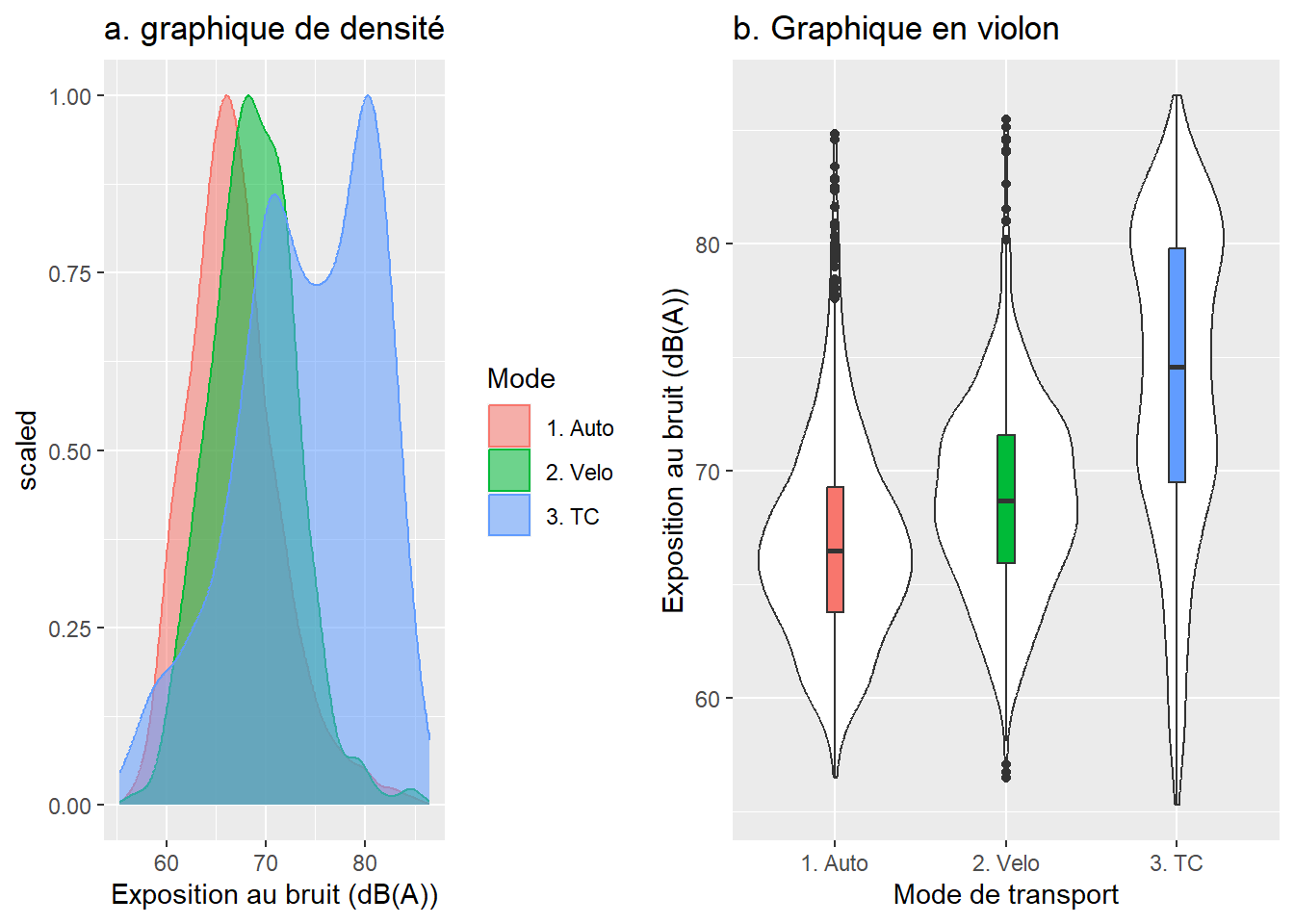

Figure 6.6: Graphique de densité et en violon

Le test de Shapiro et les graphiques QQ plot (figure 6.7) révèlent que les distributions des trois groupes sont anormales. Ce résultat n’est pas surprenant si l’on tient compte de la nature logarithmique de l’échelle décibel.

library("dplyr")
library("ggpubr")
library("rstatix")
# Condition 1 : normalité des échantillons
# Test pour la normalité des échantillons (groupes) : test de Shapiro
df_Bruit %>%          # Nom du DataFrame
  group_by(Mode) %>%         # Variable qualitative
  shapiro_test(laeq)  # Variable continue

## # A tibble: 3 × 4
##   Mode    variable statistic        p
##   <chr>   <chr>        <dbl>    <dbl>
## 1 1. Auto laeq         0.971 4.92e-14
## 2 2. Velo laeq         0.992 5.12e- 6
## 3 3. TC   laeq         0.966 3.34e-16

# Graphiques qqplot pour les groupes
ggqqplot(df_Bruit, "laeq", facet.by = "Mode", xlab="Théorique", ylab="Échantillon")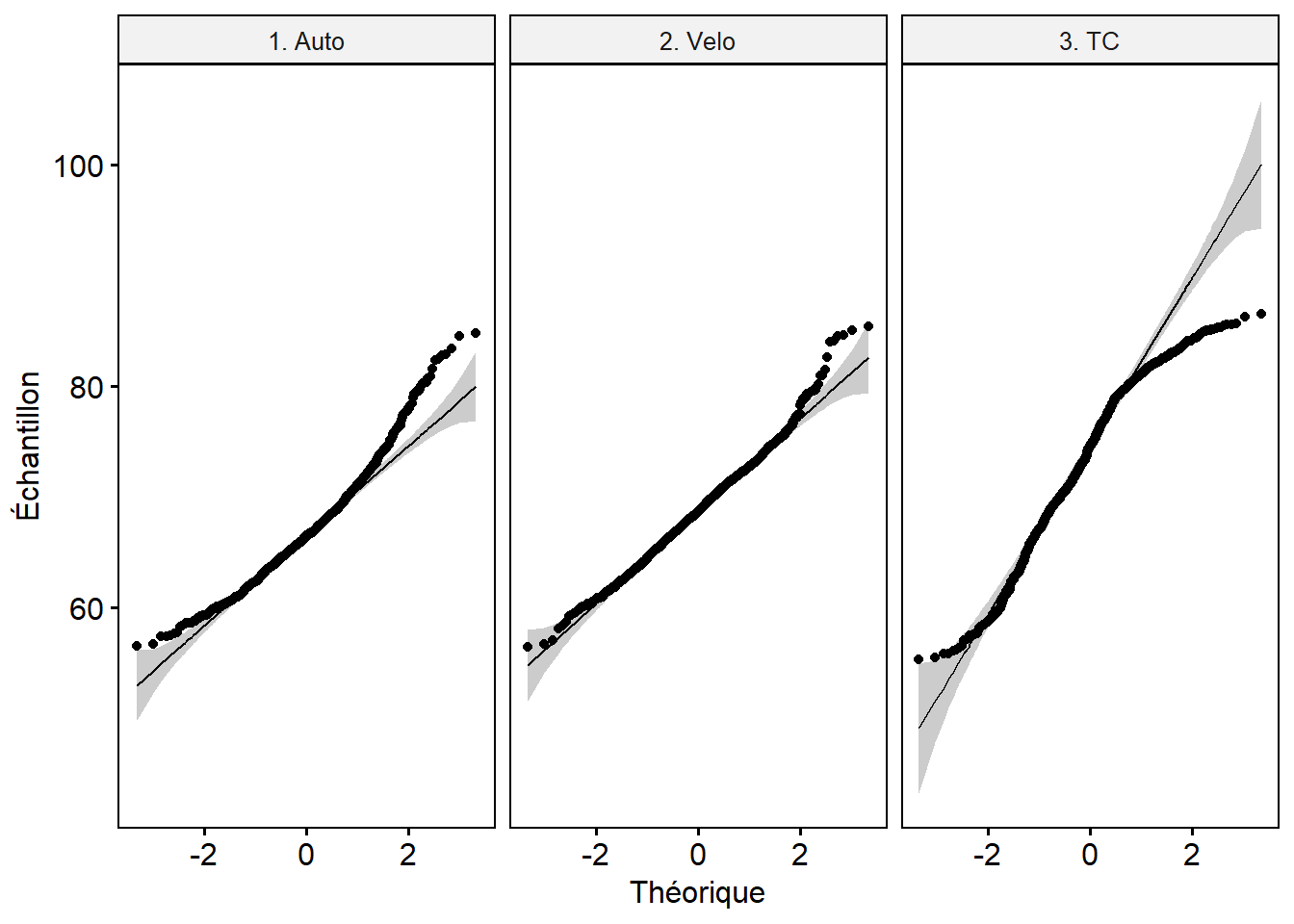

Figure 6.7: QQ Plot pour les groupes

En outre, selon les valeurs des tests de Levene, de Bartlett ou de Breusch-Pagan, les variances ne sont pas égales.

library("rstatix")
library("lmtest")
library("car")
# Condition 2 : homogénéité des variances (homocédasticité)
leveneTest(laeq ~ Mode, data = df_Bruit)

## Levene's Test for Homogeneity of Variance (center = median)
##         Df F value    Pr(>F)    
## group    2   190.3 < 2.2e-16 ***
##       3422                      
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

bartlett.test(laeq ~ Mode, data = df_Bruit)

## 
##  Bartlett test of homogeneity of variances
## 
## data:  laeq by Mode
## Bartlett's K-squared = 306.64, df = 2, p-value < 2.2e-16

bptest(laeq ~ Mode, data = df_Bruit)

## 
##  studentized Breusch-Pagan test
## 
## data:  laeq ~ Mode
## BP = 279.85, df = 2, p-value < 2.2e-16

Étant donné que les deux conditions (normalité et homogénéité des variances) ne sont pas respectées, il est préférable d’utiliser un test non paramétrique de Kruskal-Wallis. Calculons toutefois préalablement l’ANOVA classique et l’ANOVA de Welch puisque les variances ne sont pas égales. Les valeurs de p des deux tests (Fisher et Welch) signalent que les moyennes d’exposition au bruit sont statistiquement différentes entre les trois modes de transport.

library("rstatix")
# ANOVA avec la fonction anova_test du package rstatix
anova_test(laeq ~ Mode, data = df_Bruit)

## ANOVA Table (type II tests)
## 
##   Effect DFn  DFd       F         p p<.05   ges
## 1   Mode   2 3422 544.214 6.12e-206     * 0.241

# ANOVA avec le test de Welch puisque les variances ne sont pas égales
welch_anova_test(laeq ~ Mode, data = df_Bruit)

## # A tibble: 1 × 7
##   .y.       n statistic   DFn   DFd         p method     
## * <chr> <int>     <dbl> <dbl> <dbl>     <dbl> <chr>      
## 1 laeq   3425      446.     2 2248. 9.47e-164 Welch ANOVA

Une fois démontré que les moyennes sont différentes, le test de Tukey est particulièrement intéressant puisqu’il nous permet de repérer les différences de moyennes significatives deux à deux, tout en ajustant les valeurs de p obtenues en fonction du nombre de comparaisons effectuées. Ci-dessous, nous constatons que toutes les paires sont statistiquement différentes et que la différence de moyennes entre les automobilistes et les cyclistes est de 1,9 dB(A) et surtout de 7,1 dB(A) entre les automobilistes et les personnes ayant pris le transport en commun.

aov2 <- aov(laeq ~ Mode, data = df_Bruit)
# Test de Tukey pour comparer les moyennes entre elles
TukeyHSD(aov2, conf.level = 0.95)

##   Tukey multiple comparisons of means
##     95% family-wise confidence level
## 
## Fit: aov(formula = laeq ~ Mode, data = df_Bruit)
## 
## $Mode
##                     diff      lwr      upr p adj
## 2. Velo-1. Auto 1.941698 1.406343 2.477053     0
## 3. TC-1. Auto   7.113506 6.587309 7.639703     0
## 3. TC-2. Velo   5.171808 4.649307 5.694309     0

Le calcul du test non paramétrique de Kruskal-Wallis avec la fonction kruskal.test démontre aussi que les médianes des groupes sont différentes (p < 0,001). De manière comparable au test de Tukey, la fonction pairwise.wilcox.test permet aussi de repérer les différences significatives entre les paires de groupes. Pour conclure, tant l’ANOVA que le test non paramétrique de Kruskal-Wallis indiquent que les trois modes de transport sont significativement différents quant à l’exposition au bruit, avec des valeurs plus faibles pour les automobilistes comparativement aux cyclistes et aux personnes ayant pris le transport en commun.

# Test de Kruskal-Wallis
kruskal.test(laeq ~ Mode, data = df_Bruit)

## 
##  Kruskal-Wallis rank sum test
## 
## data:  laeq by Mode
## Kruskal-Wallis chi-squared = 784.74, df = 2, p-value < 2.2e-16

# Calcul de la moyenne des rangs pour les trois groupes
df_Bruit$laeqRank <- rank(df_Bruit$laeq)
df_Bruit %>%
  group_by(Mode) %>%
  get_summary_stats(laeqRank, type = "mean")

## # A tibble: 3 × 4
##   Mode    variable     n  mean
##   <chr>   <chr>    <dbl> <dbl>
## 1 1. Auto laeqRank  1094 1188.
## 2 2. Velo laeqRank  1124 1572.
## 3 3. TC   laeqRank  1207 2320.

# Comparaison des groupes avec la fonction pairwise.wilcox.test
pairwise.wilcox.test(df_Bruit$laeq, df_Bruit$Mode, p.adjust.method = "BH")

## 
##  Pairwise comparisons using Wilcoxon rank sum test with continuity correction 
## 
## data:  df_Bruit$laeq and df_Bruit$Mode 
## 
##         1. Auto 2. Velo
## 2. Velo <2e-16  -      
## 3. TC   <2e-16  <2e-16 
## 
## P value adjustment method: BH

6.2.4 Comment rapporter les résultats d’une ANOVA et du test de Kruskal-Wallis

Plusieurs éléments doivent être reportés pour détailler les résultats d’une ANOVA ou d’un test de Kruskal-Wallis : la valeur de F, de W (dans le cas d’une ANOVA de Welch) ou du χ2 (Kruskal-Wallis), les valeurs de p, les moyennes ou médianes respectives des groupes et éventuellement un tableau détaillant les écarts intergroupes obtenus avec les tests de Tukey ou Wilcoxon par paires.

Les résultats de l’analyse de variance à un facteur démontrent que le mode de transport utilisé n’a pas d’effet significatif sur le temps de déplacement en heures de pointe à Montréal (F(2,96) = 0,82, p = 0,444). En effet, pour des trajets de dix kilomètres entre un quartier périphérique et le centre-ville, les cyclistes (Moy = 38,4, ET = 15,2) arrivent en moyenne moins d’une minute après les automobilistes (Moy = 37,7, ET = 12,8) et moins de quatre minutes comparativement aux personnes ayant pris le transport en commun (Moy = 41,6, ET = 11,4).
Les résultats de l’analyse de variance à un facteur démontrent que le mode de transport utilisé a un impact significatif sur le niveau d’exposition en heures de pointe à Montréal (F(2,96) = 544, p < 0,001 et Welch(2,96) = 446, p < 0,001). En effet, les personnes en transport en commun (Moy = 74,0, ET = 6,79) et les cyclistes (Moy = 68,8, ET = 4,3) ont des niveaux d’exposition au bruit significativement plus élevés que les automobilistes (Moy = 66,8, ET = 4,56).
Les résultats du test de Kruskal-Wallis démontrent qu’il existe des différences significatives d’exposition au bruit entre les trois modes de transport (χ2(2) = 784,74, p < 0,001) avec des moyennes de rangs de 1094 pour l’automobile, de 1124 pour le vélo et de 1207 pour le transport en commun.

Nous avons vu que l’ANOVA permet de comparer les moyennes d’une variable continue à partir d’une variable qualitative comprenant plusieurs modalités (facteur) pour des observations indépendantes. Il y a donc une seule variable dépendante (continue) et une seule variable indépendante. Sachez qu’il existe de nombreuses extensions de l’ANOVA classique :

une ANOVA à deux facteurs, soit avec une variable dépendante continue et deux variables indépendantes qualitatives (two-way ANOVA en anglais). Nous évaluons ainsi les effets des deux variables (a, b) et de leur interaction (ab) sur une variable continue.
une ANOVA multifacteur avec une variable dépendante continue et plus de deux variables indépendantes qualitatives. Par exemple, avec trois variables qualitatives pour expliquer la variable continue, nous incluons les effets de chaque variable qualitative (a, b, c), ainsi que de leurs interactions (ab, ac, bc, abc).
L’analyse de covariance (ANCOVA, ANalysis of COVAriance en anglais) comprend une variable dépendante continue, une variable indépendante qualitative (facteur) et plusieurs variables indépendantes continues dites covariables. L’objectif est alors de vérifier si les moyennes d’une variable dépendante sont différentes pour plusieurs groupes d’une population donnée, après avoir contrôlé l’effet d’une ou de plusieurs variables continues. Par exemple, pour une métropole donnée, nous pourrions vouloir comparer les moyennes de loyers entre la ville-centre et ceux des première et seconde couronnes (facteur), une fois contrôlée la taille de ces derniers (variable covariée continue). En effet, une partie de la variance des loyers s’explique certainement par la taille des logements.
L’analyse de variance multivariée (MANOVA, Multivariate ANalysis Of VAriance en anglais) comprend deux variables dépendantes continues ou plus et une variable indépendante qualitative (facteur). Par exemple, nous souhaiterions comparer les moyennes d’exposition au bruit et à différents polluants (dioxyde d’azote, particules fines, ozone) (variables dépendantes continues) selon le mode de transport utilisé (automobile, vélo, transport en commun), soit le facteur.
L’analyse de covariance multivariée (MANCOVA, Multivariate ANalysis of COVAriance en anglais), soit une analyse qui comprend deux variables dépendantes continues ou plus (comme la MANOVA) et une variable qualitative comme variable indépendante (facteur) et une covariable continue ou plus.

Pour le test t, nous avons vu qu’il peut s’appliquer soit à deux échantillons indépendants (non appariés), soit à deux échantillons dépendants (appariés). Notez qu’il existe aussi des extensions de l’ANOVA pour des échantillons pairés. Nous parlons alors d’analyse de variance sur des mesures répétées. Par exemple, nous pourrions évaluer la perception du sentiment de sécurité relativement à la pratique du vélo d’hiver pour un échantillon de cyclistes ayant décidé de l’adopter récemment, et ce, à plusieurs moments : avant leur première saison, à la fin de leur premier hiver, à la fin de leur second hiver. Autre exemple, nous pourrions sélectionner un échantillon d’individus (100, par exemple) pour lesquels nous évaluerions leurs perceptions de l’environnement sonore dans différents lieux de la ville. Comme pour l’ANOVA classique (échantillons non appariés), il existe des extensions de l’ANOVA sur des mesures répétées permettant d’inclure plusieurs facteurs (groupes de population); nous mesurons alors une variable continue pour plusieurs groupes d’individus à différents moments ou pour des conditions différentes. Il est aussi possible de réaliser une ANOVA pour des mesures répétées avec une ou plusieurs covariables continues.

Bref, si l’ANOVA était un roman, elle serait certainement « un monde sans fin » de Ken Follett! Notez toutefois que la SUPERNOVA, la BOSSA-NOVA et le CASANOVA ne sont pas des variantes de l’ANOVA!

Références

Apparicio, Philippe, Jérémy Gelb, Mathieu Carrier, Marie-Ève Mathieu et Simon Kingham. 2018. « Exposure to noise and air pollution by mode of transportation during rush hours in Montreal. » Journal of Transport Geography 70: 182‑192. https://doi.org/10.1016/j.jtrangeo.2018.06.007.

Glass, Gene V, Percy D Peckham et James R Sanders. 1972. « Consequences of failure to meet assumptions underlying the fixed effects analyses of variance and covariance. » Review of educational research 42 (3): 237‑288.

Lix, Lisa M, Joanne C Keselman et HJ Keselman. 1996. « Consequences of assumption violations revisited: A quantitative review of alternatives to the one-way analysis of variance F test. » Review of educational research 66 (4): 579‑619. https://doi.org/10.3102/00346543066004579.