2.7 Statistiques descriptives pondérées : pour aller plus loin
Dans la section 2.5, les différentes statistiques descriptives sur des variables quantitatives – paramètres de tendance centrale, de position, de dispersion et de forme – ont été largement abordées. Il est possible de calculer ces différentes statistiques en tenant compte d’une pondération. La statistique descriptive pondérée la plus connue est certainement la moyenne arithmétique pondérée. Son calcul est très simple. Pour chaque observation, deux valeurs sont disponibles :
- \(x_i\), soit la valeur de la variable \(X\) pour l’observation \(i\)
- \(w_i\), soit la valeur de la pondération pour \(i\).
Prenez soin de comparer les deux équations ci-dessous (à gauche, la moyenne arithmétique; à droite, la moyenne arithmétique pondérée). Vous constaterez rapidement qu’il suffit simplement de multiplier chaque observation par sa pondération (numérateur) et de diviser ce produit par la somme des pondérations (dénominateur; et non par \(n\), soit le nombre d’observations comme pour la moyenne arithmétique non pondérée).
\[\begin{equation} \bar{x}=\frac{\sum_{i=1}^n x_i}{n} \text { versus } \bar{m}=\frac{\sum_{i=1}^n w_ix_i}{\sum_{i=1}^nw_i} \tag{2.31} \end{equation}\]
| Observation | \(x_i\) | \(w_i\) | \(x_i \times w_i\) |
|---|---|---|---|
| 1 | 200 | 20 | 4 000 |
| 2 | 225 | 80 | 18 000 |
| 3 | 275 | 50 | 13 750 |
| 4 | 300 | 200 | 60 000 |
| Somme | 1 000 | 350 | 95 750 |
| Moyenne | 250 | ||
| Moyenne pondérée | 274 |
Calcul d’autres statistiques descriptives pondérées
Nous ne reportons pas ici les formules des versions pondérées de toutes les statistiques descriptives. Retenez toutefois le principe suivant permettant de les calculer à partir de l’exemple du tableau 2.12. Pour la variable X, dupliquons respectivement 20, 80, 50, 200 fois les observations 1 à 4. Si nous calculons la moyenne arithmétique sur ces valeurs dupliquées, alors cette valeur est identique à celle de la moyenne arithmétique pondérée. Le même principe reposant sur la duplication des valeurs s’applique à l’ensemble des statistiques descriptives.
Dans un article récent, Alvarenga et al. (2018) évaluent l’accessibilité aux aires de jeux dans les parcs de la Communauté métropolitaine de Montréal (CMM). Pour les 881 secteurs de recensement de la CMM, ils ont calculé la distance à pied à l’aire de jeux la plus proche à travers le réseau de rues. Ce résultat, cartographié à la figure 2.38, permet d’avancer le constat suivant : « la quasi-totalité des secteurs de recensement de l’agglomération de Montréal présente des distances de l’aire de jeux la plus proche inférieures à 500 m, alors que les secteurs situés à plus d’un kilomètre d’une aire de jeux sont très majoritairement localisés dans les couronnes nord et sud de la CMM » (De Alvarenga, Apparicio et Séguin 2018, 238).
Pour chaque secteur de recensement, Alvarenga et al. (2018) disposent des données suivantes :
- \(x_i\), soit la distance à l’aire de jeux la plus proche pour le secteur de recensement i;
- \(w_i\), la pondération, soit le nombre d’enfants de moins de dix ans.
Il est alors possible de calculer les statistiques descriptives de la proximité à l’aire de jeux la plus proche en tenant compte du nombre d’enfants résidant dans chaque secteur de recensement (tableau 2.13). Cet exercice permet de conclure que : « […] globalement, les enfants ont une bonne accessibilité aux aires de jeux sur le territoire de la CMM. […] Les enfants sont en moyenne à un peu plus de 500 m de l’aire de jeux la plus proche (moyenne = 559; médiane = 512). Toutefois, les valeurs percentiles extrêmes signalent que respectivement 10 % et 5 % des enfants résident à près de 800 m et à plus de 1000 m de l’aire de jeux la plus proche » (2018, 236).
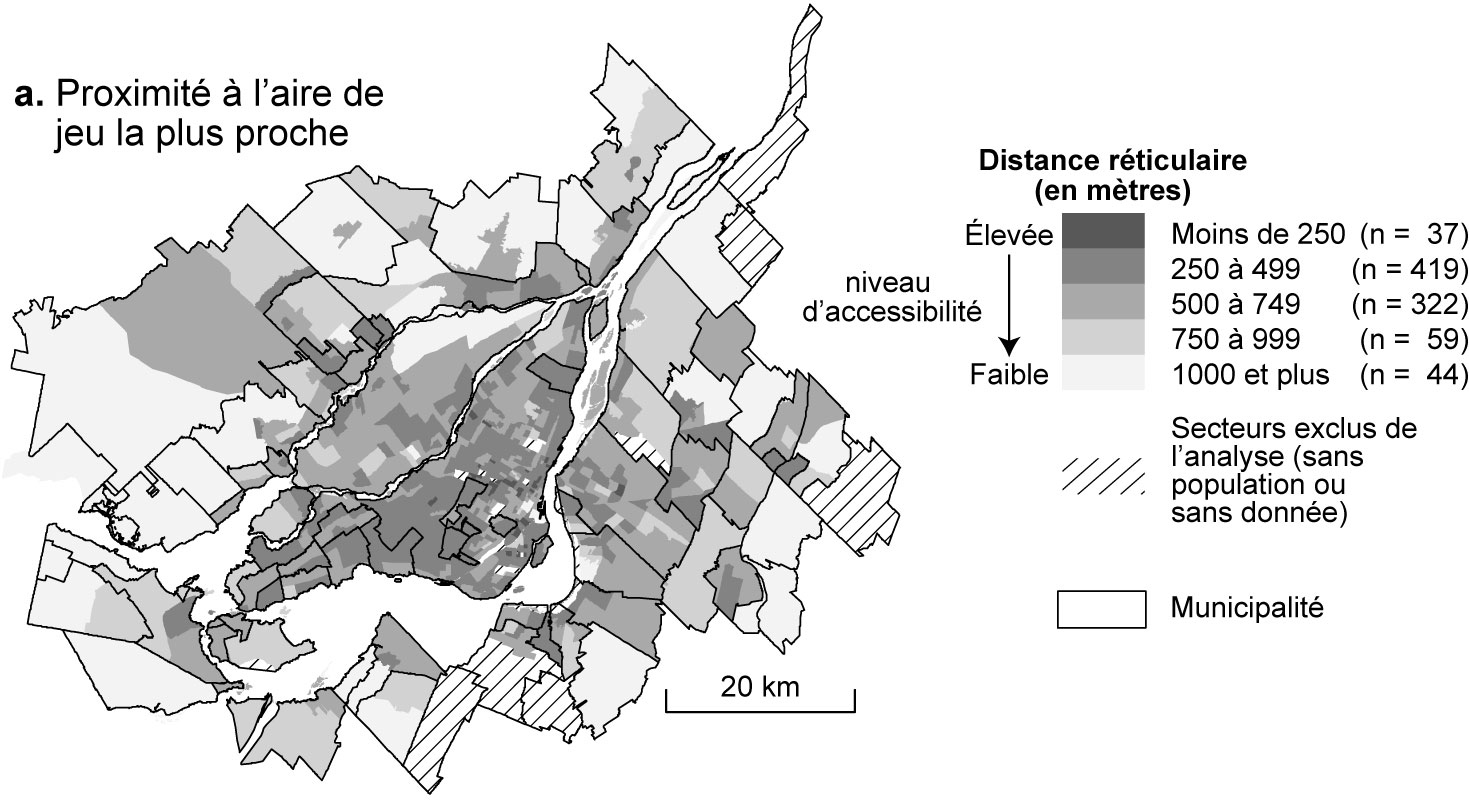
Figure 2.38: Accessibilité aux aires de jeux par secteur de recensement, Communauté métropolitaine de Montréal, 2016
| N | Moyenne | P5 | P10 | Q1 | Médiane | Q3 | P90 | P95 |
|---|---|---|---|---|---|---|---|---|
| 881 | 559 | 282 | 327 | 408 | 512 | 640 | 799 | 1 006 |
De nombreux packages sont disponibles pour calculer des statistiques pondérées, dont notamment Weighted.Desc.Stat et Hmisc utilisés dans la syntaxe ci-dessous.
library(foreign)
library(Hmisc)
library(Weighted.Desc.Stat)
df <- read.dbf("data/bivariee/SR_AireJeux_PopMoins10.dbf")
head(df, n = 5)## SRNOM PopMoins10 AireJeux
## 1 0659.06 380 600.1921
## 2 0410.02 390 324.4396
## 3 0863.01 325 524.3323
## 4 0734.05 875 574.6682
## 5 0073.00 100 352.9505# xi (variable) et wi (pondération)
x <- df$AireJeux
w <- df$PopMoins10
# Calcul des paramètres de position
# Moyenne
Hmisc::wtd.mean(x, w)## [1] 559.8026Weighted.Desc.Stat::w.mean(x, w)## [1] 559.8026# Quartiles et percentile
Hmisc::wtd.quantile(x, weights=w, probs=c(.05, .10, .25, .50, .75, .90, .95))## 5% 10% 25% 50% 75% 90% 95%
## 281.3623 327.3056 406.0759 511.5880 639.4813 798.6559 1011.5493# Paramètres de dispersion avec le package Weighted.Desc.Stat
# Variance, écart-type et coefficient de variation
w.var(x,w)## [1] 82818.18w.sd(x,w)## [1] 287.7815w.cv(x,w)## [1] 0.5140767# Paramètres de forme avec le package Weighted.Desc.Stat
# Skewness et kurtosis
w.skewness(x, w)## [1] 4.735351w.kurtosis(x, w)## [1] 41.17146