9.3 Conditions d’application des GLMM
Puisque les GLMM sont une extension des GLM, ils partagent l’essentiel des conditions d’application de ces derniers. Pour simplifier, si vous ajustez un modèle GLMM avec une distribution Gamma, vous devez réaliser les mêmes tests que ceux pour un simple GLM avec une distribution Gamma.
Une question importante se pose souvent lorsque nous ajustons des modèles GLMM : combien de groupes faut-il au minimum aux différents niveaux? En effet, pour estimer les différentes variances, nous devons disposer de suffisamment de groupes différents. Dans le cas d’un modèle avec uniquement une constante aléatoire, il est fréquent de lire que nous devons disposer au minimum de cinq groupes différents (Gelman et Hill 2006), en dessous de ce minimum, traiter l’effet comme aléatoire plutôt que fixe apporte très peu d’information. De plus, l’estimation des variances pour chaque niveau est très imprécise, donnant potentiellement des valeurs inexactes pour l’ICC et polluant l’interprétation. Avec cinq groupes ou moins, il est certainement plus judicieux d’ajuster seulement un effet fixe. Dans un modèle avec plusieurs effets aléatoires et plusieurs variances / covariances à estimer, ce nombre doit être augmenté proportionnellement, à moins que les effets aléatoires ne soient estimés indépendamment les uns des autres. Notez ici que, si l’enjeu du modèle était d’estimer avec une grande précision les paramètres de variances, il faudrait compter au minimum une centaine de groupes. Il n’est pas nécessaire d’avoir le même nombre d’observations par groupe, car les modèles GLMM partagent l’information entre les groupes. Cependant, dans les groupes avec peu d’observations (inférieur à 15), l’estimation de leur effet propre (BLUP) est très incertaine.
Puisque les GLMM font intervenir la distribution normale aux niveaux supérieurs du modèle, il est nécessaire de vérifier si les hypothèses qu’elle implique sont respectées. Il s’agit essentiellement de deux hypothèses : les effets aléatoires suivent bien une distribution normale (univariée ou multivariée), et la variance au sein des groupes est bien homogène.
9.3.1 Vérification de la distribution des effets aléatoires
Reprenons la formulation d’un modèle simple avec seulement deux niveaux et seulement une constante aléatoire:
\[\begin{equation} \begin{aligned} &Y \sim Normal(\mu,\sigma_e)\\ &g(\mu) = \beta_0 + \beta_1 x_1 + \upsilon \\ &\upsilon \sim Normal(0, \sigma_{\upsilon}) \\ &g(x) = x \end{aligned} \end{equation}\]
Ce modèle formule l’hypothèse que les constantes aléatoires \(\upsilon\) proviennent d’une distribution normale avec une moyenne de 0 et un écart-type \(\sigma_{\upsilon}\). La première étape du diagnostic est donc de vérifier si les constantes aléatoires suivent bien une distribution normale, ce que nous pouvons faire habituellement avec un diagramme quantile-quantile. Si nous reprenons notre exemple avec nos données de performance scolaire des sections précédentes, nous obtenons la figure 9.13. Puisque les points tombent bien approximativement sur la ligne rouge, nous pouvons conclure que cette condition d’application est bien respectée. Notez qu’il est également possible d’utiliser ici un des tests vus dans le chapitre 2 pour tester formellement la distribution des constantes aléatoires, mais nous disposons rarement de suffisamment de valeurs différentes pour qu’un tel test soit pertinent.
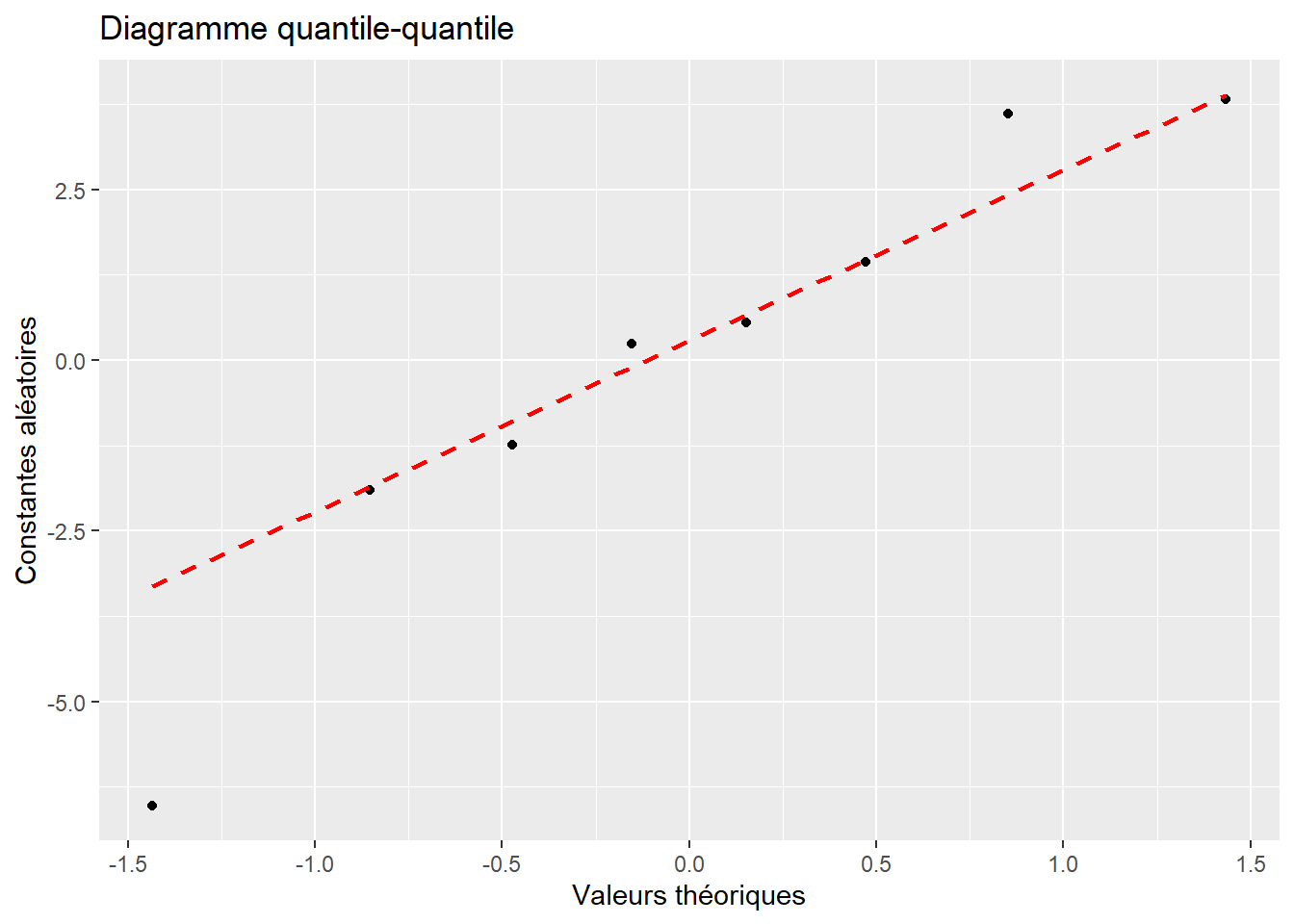
Figure 9.13: Distribution normale univariée des constantes aléatoires
Cette vérification est bien sûr à appliquer à chacun des niveaux (en dehors du niveau de base) du modèle étudié.
Si nous nous intéressons maintenant au modèle avec constantes et pentes aléatoires, nous avons deux cas de figure:
notre modèle inclut une covariance entre les constantes et les pentes; elles proviennent donc d’une distribution normale bivariée.
notre modèle considère les pentes et les constantes comme indépendantes; elles proviennent donc de deux distributions normales distinctes.
Le second cas est de loin le plus simple puisqu’il nous suffit de réaliser un graphique de type quantile-quantile pour les deux effets aléatoires séparément. Dans le premier cas, il nous faut adapter notre stratégie pour vérifier si les deux effets aléatoires suivent conjointement une distribution normale multivariée. Pour cela, nous devons, dans un premier temps, observer séparément la distribution des pentes et des constantes, puisque chaque variable provenant d’une distribution normale multivariée suit elle-même une distribution normale univariée (Burdenski 2000). Nous pouvons, dans un second temps, construire un graphique nous permettant de juger si nos pentes et nos constantes suivent bien la distribution normale bivariée attendue par le modèle. Pour l’illustrer, nous reprenons le modèle sur la performance scolaire intégrant des pentes et des constantes aléatoires avec une covariance estimée entre les deux.
La figure 9.14 représente donc les deux graphiques quantile-quantile univariés. Les deux semblent indiquer que nos effets aléatoires suivent bien chacun une distribution normale. La figure 9.15 montre la distribution normale bivariée attendue par le modèle avec des ellipses représentant différents pourcentiles de cette distribution. Les valeurs des effets aléatoires sont représentées par des points noirs. Seulement 5 % des points noirs devraient se trouver dans la première ellipse et 95 % des points devraient se trouver dans la quatrième ellipse. En revanche, seulement 20 % des points devraient se trouver dans le dernier anneau et seulement 5 % des points en dehors de cet anneau. Il faut donc évaluer si les points sont plus ou moins centrés que ce que nous attendons. Pour simplifier la lecture, il est possible de rajouter des points grisés en arrière-plan représentant des réalisations possibles de cette distribution normale bivariée. Les vrais points noirs devraient avoir une dispersion similaire à celle des points grisés. Dans notre cas, ils semblent suivre un patron cohérent avec notre distribution normale bivariée. Dans le cas contraire, cela signifierait que le modèle doit être révisé.
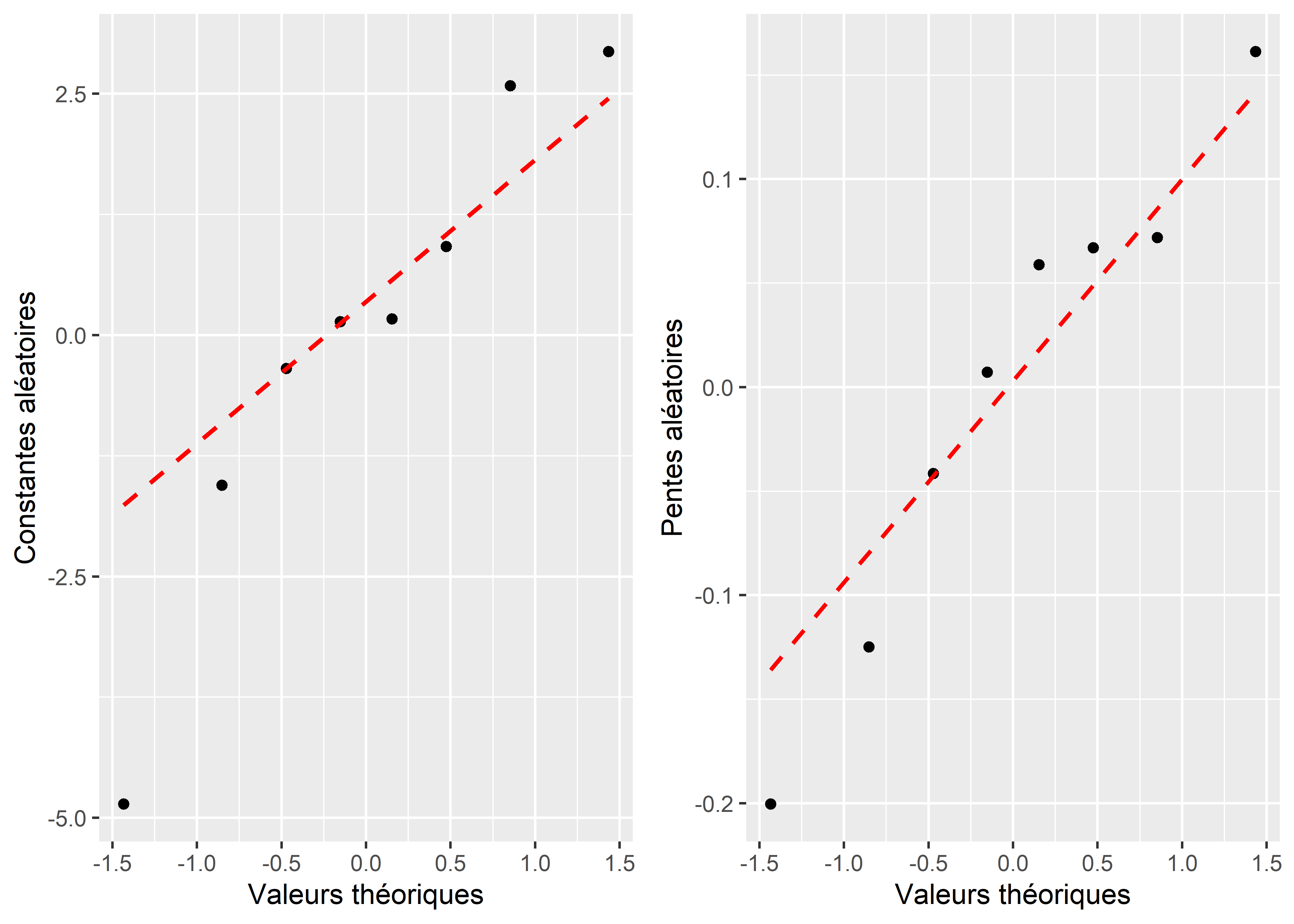
Figure 9.14: Multiples distributions normales univariées des constantes et pentes aléatoires
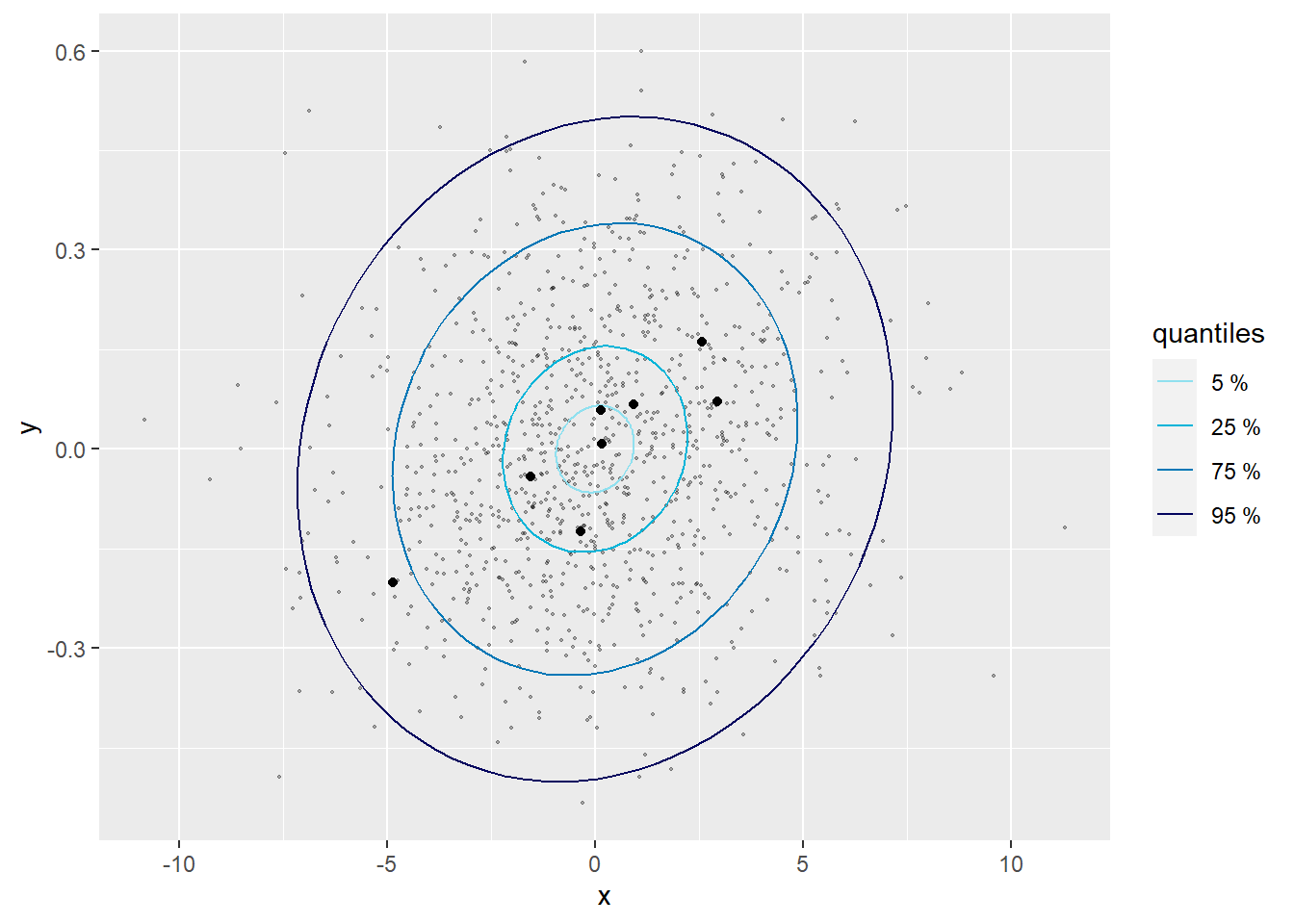
Figure 9.15: Distribution normale bivariée des constantes et des pentes aléatoires
9.3.2 Homogénéité des variances au sein des groupes
Dans le chapitre 8 sur les GLM, nous avons vu que chaque distribution a sa propre définition de la variance. Pour rappel, un modèle gaussien assume une variance constante, un modèle de Poisson assume une variance égale à son espérance, alors qu’un modèle Gamma assume une variance proportionnelle au carré de son espérance divisée par un paramètre de forme, etc. Nous devions donc, pour chaque GLM, vérifier graphiquement si la variance présente dans les données originales était proche de la variance attendue par le modèle. Dans un modèle GLMM, le même exercice doit être fait pour chaque groupe aux différents niveaux du modèle.
Dans notre exemple sur la performance scolaire, notre variable Y a été modélisée avec une distribution normale. Le modèle assume donc une uniformité de sa variance (homoscédasticité). La figure 9.16 nous montre ainsi que, qu’elle que soit la classe, la dispersion des points (notes des élèves) semble bien respecter la variance attendue par le modèle (représentée par les lignes noires).
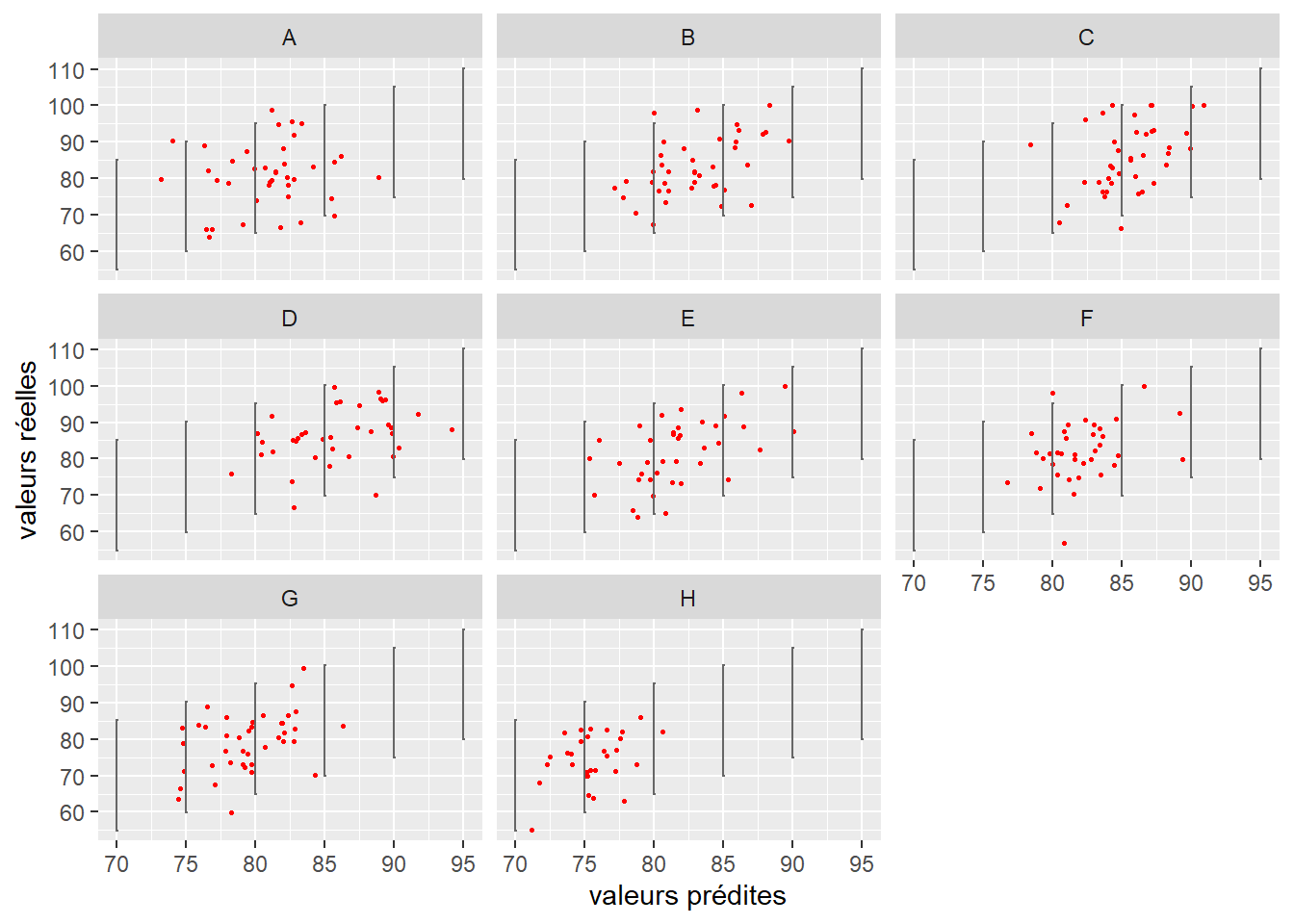
Figure 9.16: Homogénéité de la variance pour les différents groupes d’un modèle GLMM gaussien