3.2 Principaux graphiques
Puisque vous avez désormais une certaine connaissance des bases de la grammaire des graphiques implémentées par ggplot2, vous apprendrez dans les sous-sections suivantes à construire les principaux graphiques que vous utiliserez régulièrement ou que vous présenterez dans un article scientifique.
3.2.1 Histogramme
L’histogramme permet de décrire graphiquement la forme de la distribution d’une variable. Pour le réaliser, nous utilisons la fonction geom_histogram. Le paramètre le plus important est le nombre de barres (bins) qui composent l’histogramme. Plus ce nombre est grand, plus l’histogramme est précis et, à l’inverse, plus il est petit, plus l’histogramme est simplifié. En revanche, il faut éviter d’utiliser un nombre de barres trop élevé comparativement au nombre d’observations disponibles dans le jeu de données, sinon l’histogramme risque d’avoir plein de trous.
3.2.1.1 Histogramme simple
Générons quatre variables ayant respectivement une distribution gaussienne, Student, Gamma et bêta, puis réalisons un histogramme pour chacune de ces variables et combinons-les avec la fonction ggarrange (figure 3.21).
distribs <- data.frame(
gaussien = rnorm(1000, mean = 5, sd = 1.5),
gamma = rgamma(1000, shape = 2, rate = 12),
beta = rbeta(1000,shape1 = 5, shape2 = 1, ncp = 2),
student = rt(1000,ncp = 20, df = 5)
)
plot1 <- ggplot(data = distribs) +
geom_histogram(aes(x = gaussien), bins = 50, color = "#343a40", fill = "#e63946")+
labs(y="fréquences")+ylim(c(0,130))
plot2 <- ggplot(data = distribs) +
geom_histogram(aes(x = gamma), bins = 50, color = "#343a40", fill = "#f1faee")+
labs(y="fréquences")+ylim(c(0,130))
plot3 <- ggplot(data = distribs) +
geom_histogram(aes(x = beta), bins = 50, color = "#343a40", fill = "#a8dadc")+
labs(y="fréquences")+ylim(c(0,130))
plot4 <- ggplot(data = distribs) +
geom_histogram(aes(x = student), bins = 50, color = "#343a40", fill = "#1d3557")+
labs(y="fréquences")+ylim(c(0,130))
histogrammes <- list(plot1, plot2, plot3, plot4)
ggarrange(plotlist = histogrammes, ncol = 2, nrow = 2)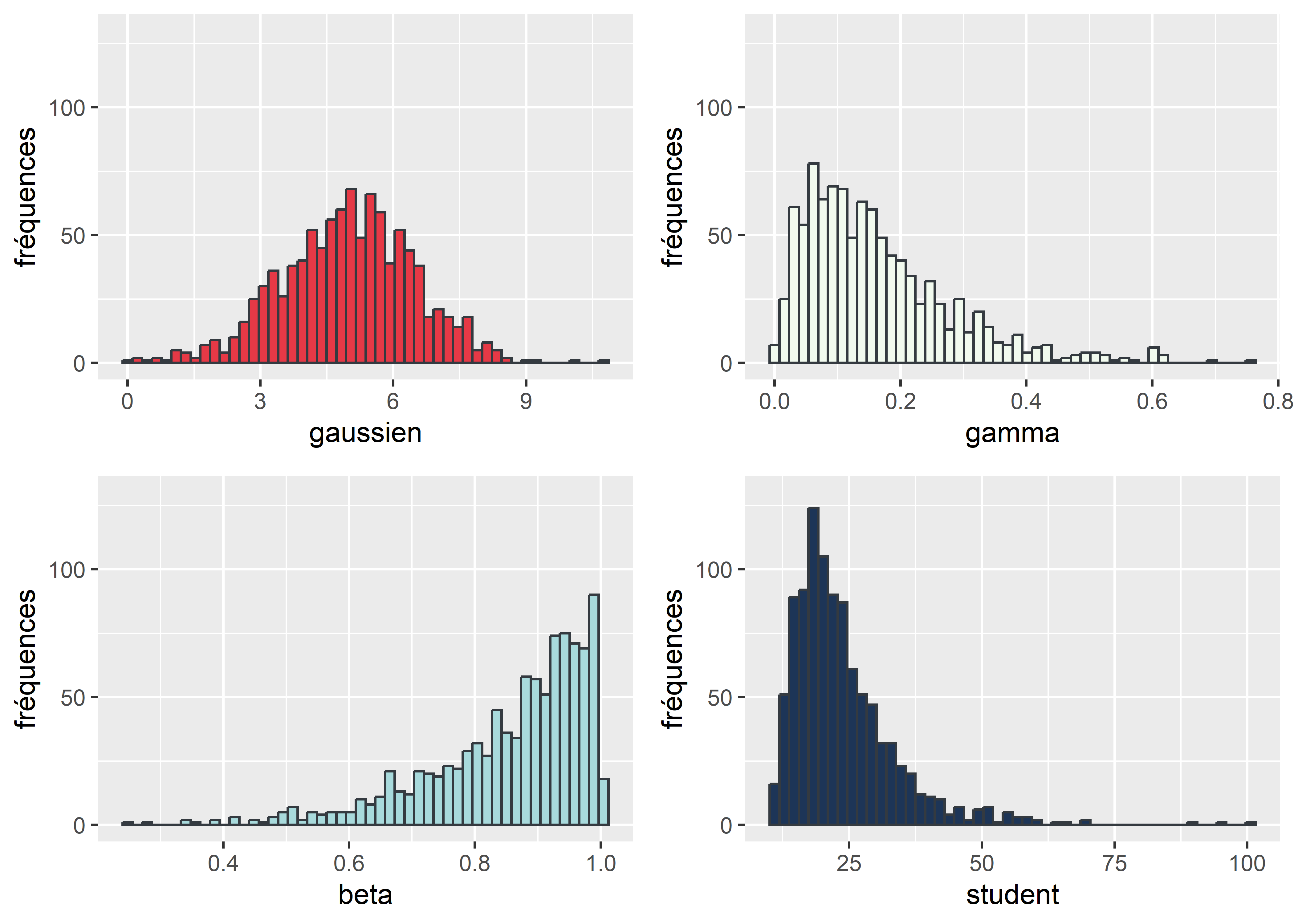
Figure 3.21: Histogrammes
Notez que cette syntaxe est très lourde. Dans le cas présent, il serait plus judicieux d’utiliser la fonction facet_wrap. Pour cela, nous devons au préalable empiler nos données, ce qui signifie changer la forme du DataFrame actuel, qui comprend quatre colonnes (gaussien, Gamma, bêta et student) et 1000 observations, pour qu’il n’ait plus que deux colonnes (la valeur originale et le nom de l’ancienne colonne) et 4000 observations. La figure 3.22 décrit graphiquement ce processus qui peut être effectué avec la fonction melt du package reshape2.
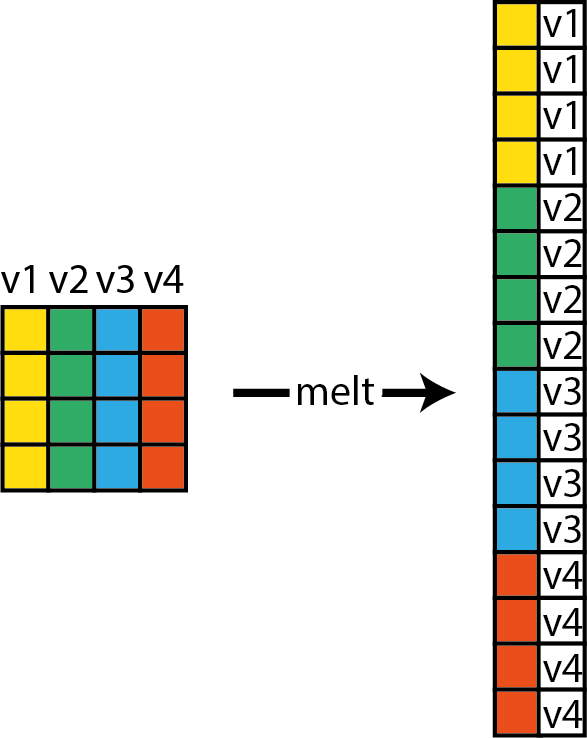
Figure 3.22: Empiler les données d’un DataFrame
library(reshape2)
#faire fondre le jeu de données
melted_distribs <- melt(distribs, measure.vars = c("gaussien", "gamma",
"beta","student"))
#renommer les colonnes du nouveau DataFrame
names(melted_distribs) <- c("distribution", "valeur")
#convertir la variable catégorielle en facteur
melted_distribs$distribution <- as.factor(melted_distribs$distribution)
ggplot(data = melted_distribs)+
geom_histogram(aes(x = valeur, fill = distribution), bins = 50, color = "#343a40") +
ylim(c(0,130)) +
labs(x = "valeur",
y = "fréquences")+
scale_fill_manual(values = c("#e63946","#f1faee","#a8dadc","#1d3557"))+
facet_wrap(vars(distribution), ncol=2, scales = "free")+
theme(legend.position = "none")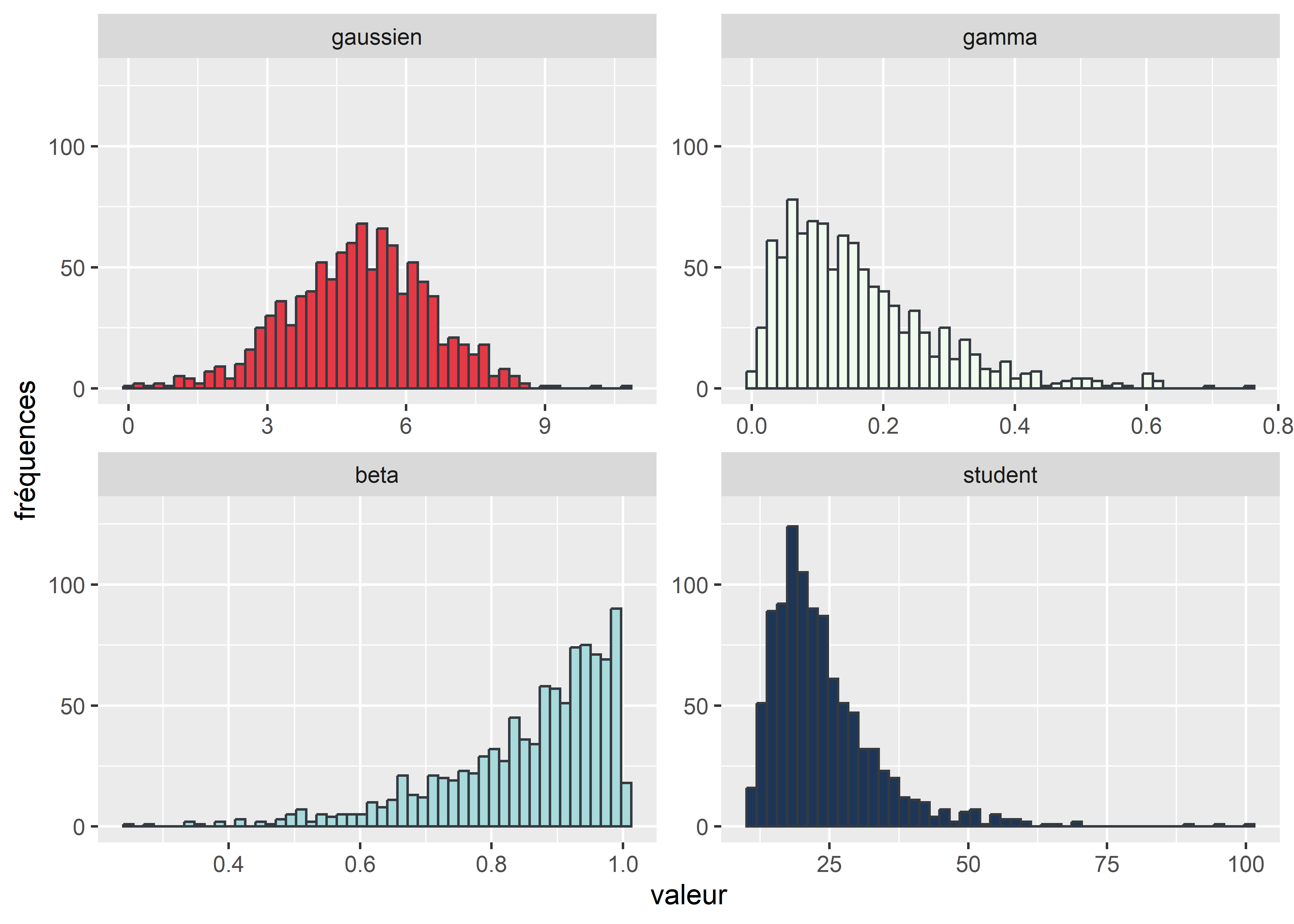
Figure 3.23: Histogrammes à facettes
3.2.1.2 Histogramme de densité
Les histogrammes que nous venons de construire utilisent la fréquence des observations pour délimiter la hauteur des barres. Il est possible de changer ce comportement pour plutôt utiliser la densité. L’intérêt est notamment de se rapprocher encore de la définition d’une distribution puisqu’avec cette configuration, la somme totale de la surface de l’histogramme est égale à 1. La hauteur de chaque barre représente alors la probabilité d’obtenir l’étendue de valeurs représentées par cette barre. Prenons pour exemple la variable avec la distribution normale que nous venons de voir.
plot1 <- ggplot(data = distribs) +
geom_histogram(aes(x = gaussien, y = ..density..),
bins = 30, color = "#343a40", fill = "#1d3557")+
labs(x = "gaussien", y = "densité")
plot2 <- ggplot(data = distribs) +
geom_histogram(aes(x = gaussien, y = ..count..),
bins = 30, color = "#343a40", fill = "#a8dadc")+
labs(x = "gaussien", y = "fréquences")
ggarrange(plotlist = list(plot1, plot2), ncol = 2)
Figure 3.24: Histogrammes de densité
Le graphique de droite (fréquence) nous indique donc que plus de 60 observations ont une valeur d’environ 5 (entre 4,76 et 5,34, compte tenu de la largeur de la barre), ce qui se traduit par une probabilité de presque 30 % d’obtenir cette valeur en tirant une observation au hasard dans le jeu de données.
3.2.1.3 Histogramme avec courbe de distribution
Les histogrammes sont souvent utilisés pour vérifier graphiquement si une distribution empirique s’approche d’une courbe normale. Pour cela, nous ajoutons sur l’histogramme de la variable empirique la forme qu’aurait une distribution normale parfaite en utilisant la moyenne et l’écart type de la distribution empirique. Pour créer cette figure dans ggplot2, il suffit d’utiliser la fonction stat_function pour créer un nouveau calque. Il est aussi possible d’ajouter une ligne verticale (geom_vline) pour indiquer la moyenne de la distribution.
moyenne <- mean(distribs$gaussien)
ecart_type <- sd(distribs$gaussien)
ggplot(data = distribs) +
geom_histogram(aes(x = gaussien, y = ..density..),
bins = 30, color = "#343a40", fill = "#a8dadc") +
labs(x = "gaussien",
y = "densité")+
stat_function(fun = dnorm, args = list(mean = moyenne, sd = ecart_type),
color = "#e63946", size = 1.2, linetype = "dashed") +
geom_vline(xintercept = moyenne, color = 'red', size = 1)+
annotate("text", x = round(moyenne,2)+0.5, y = 0.31, hjust = 'left',
label = paste('moyenne : ',round(moyenne,2),sep=''))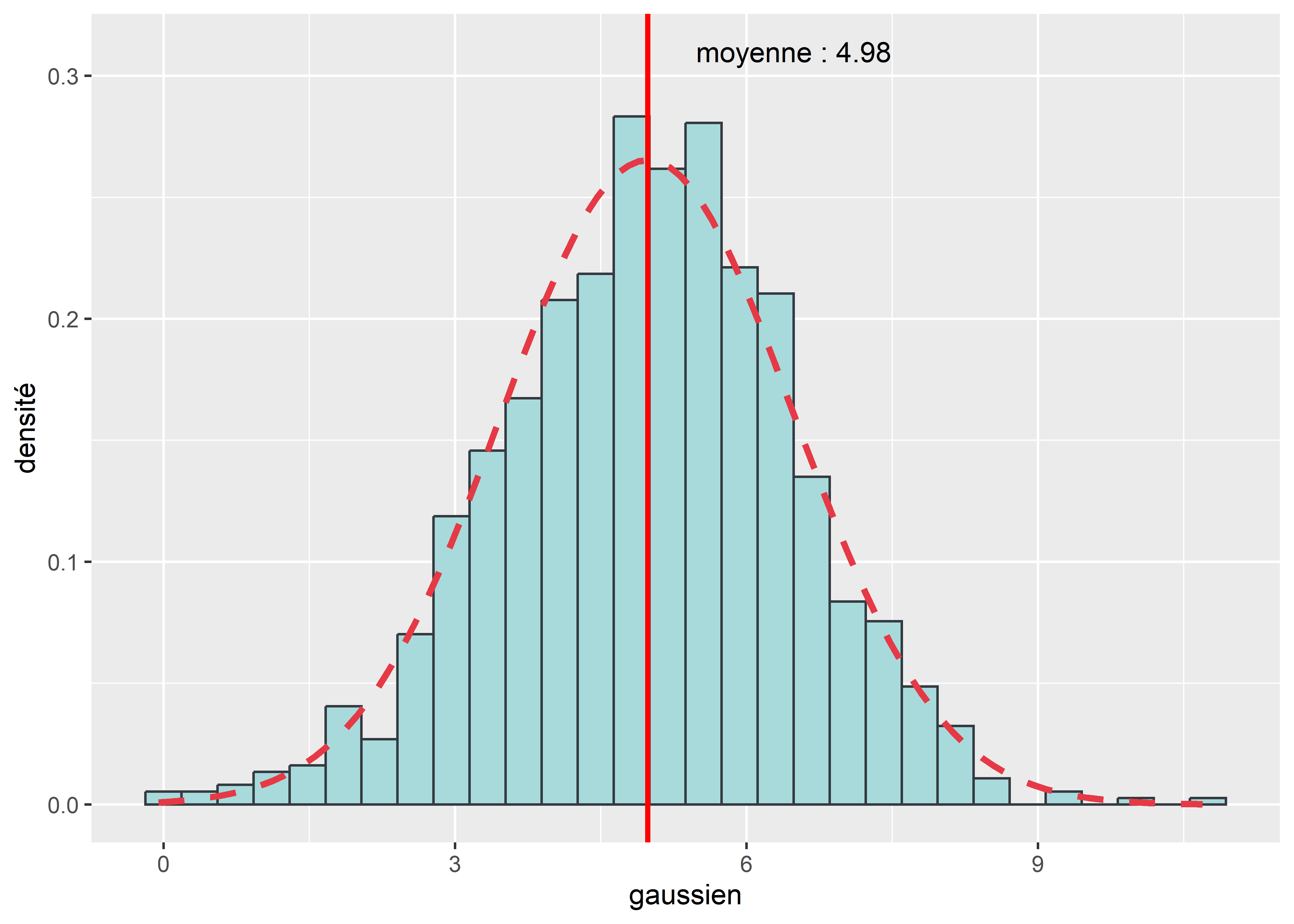
Figure 3.25: Histogramme et courbe normale
Dans notre cas, nous savons que notre variable est normalement distribuée (car produite avec la fonction rnorm), et nous pouvons constater la grande proximité entre l’histogramme et la courbe normale.
3.2.1.4 Histogramme avec coloration des valeurs extrêmes
Il peut être nécessaire d’attirer le regard sur certaines parties de l’histogramme, comme sur des valeurs extrêmes. Si nous reprenons notre distribution de Student, nous pouvons clairement distinguer un ensemble de valeurs fortes à droite de la distribution. Nous pourrions, dans notre cas, considérer que des valeurs au-delà de 50 constituent des cas extrêmes que nous souhaitons représenter dans une autre couleur. Pour cela, nous devons créer une variable catégorielle nous permettant de distinguer ces cas particuliers.
distribs$cas_extreme <- ifelse(distribs$student >=50, "extrême", "normale")
ggplot(data = distribs) +
geom_histogram(aes(x = student, y = ..count.., fill = cas_extreme),
bins = 30, color = "#343a40")+
scale_fill_manual("", values = c("#a8dadc","#e63946"))+
labs(title = 'Distribution de Student',x = "valeur", y = "fréquence")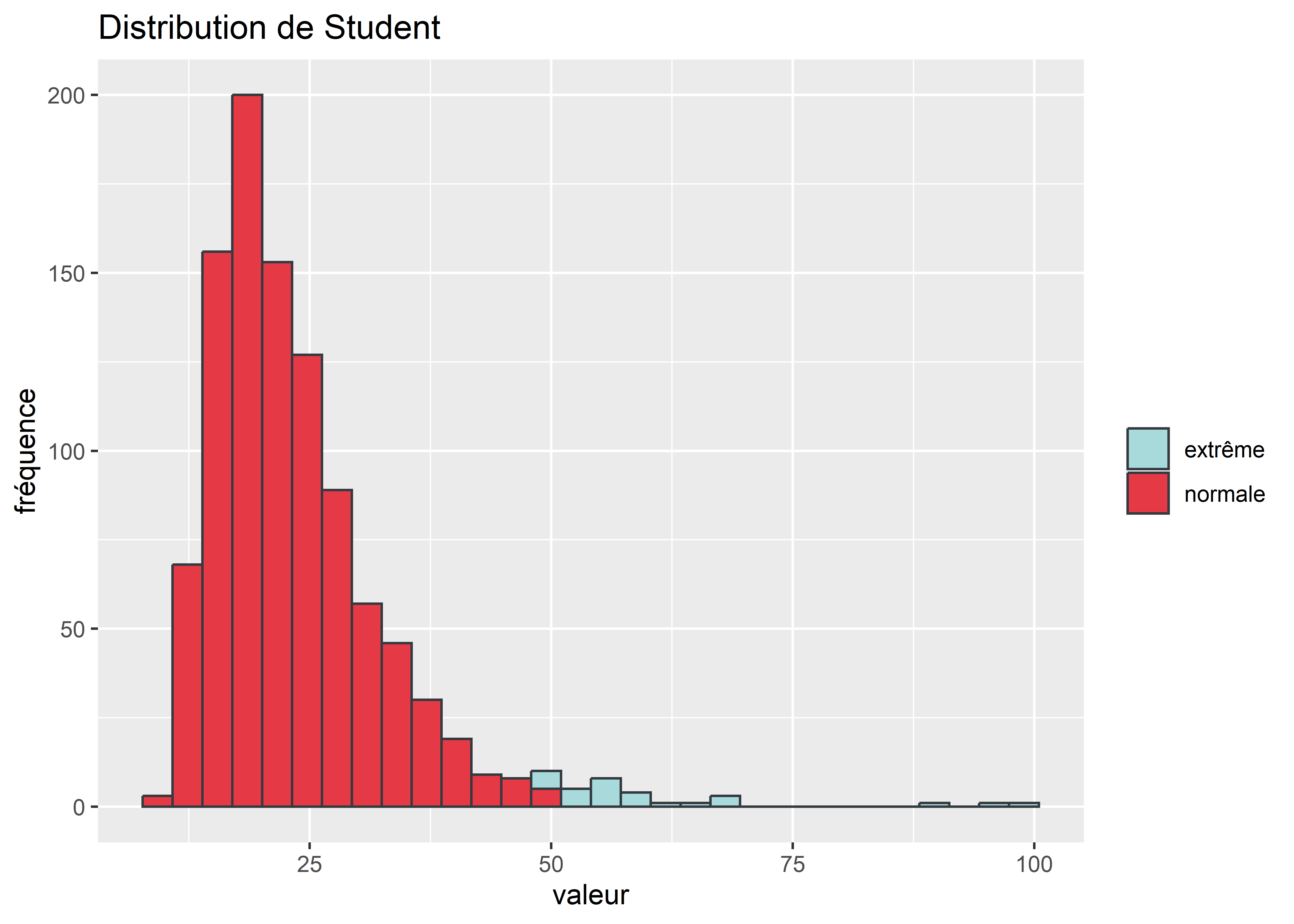
Figure 3.26: Histogramme coloré
3.2.2 Graphique de densité
L’histogramme est utilisé pour approximer graphiquement la distribution d’une variable. Sa principale limite est de représenter la variable de façon discontinue. Une option intéressante est d’utiliser une version lissée de l’histogramme, soit le graphique de densité. Cette opération de lissage est réalisée le plus souvent à partir de fonctions kernel. Reconstruisons notre figure avec les quatre distributions, mais en utilisant cette fois-ci des graphiques de densité.
ggplot(data = melted_distribs)+
geom_density(aes(x = valeur, fill = distribution), color = "#343a40") +
scale_fill_manual(values = c("#e63946","#f1faee","#a8dadc","#1d3557"))+
facet_wrap(vars(distribution), ncol=2, scales = "free")+
theme(legend.position = "none")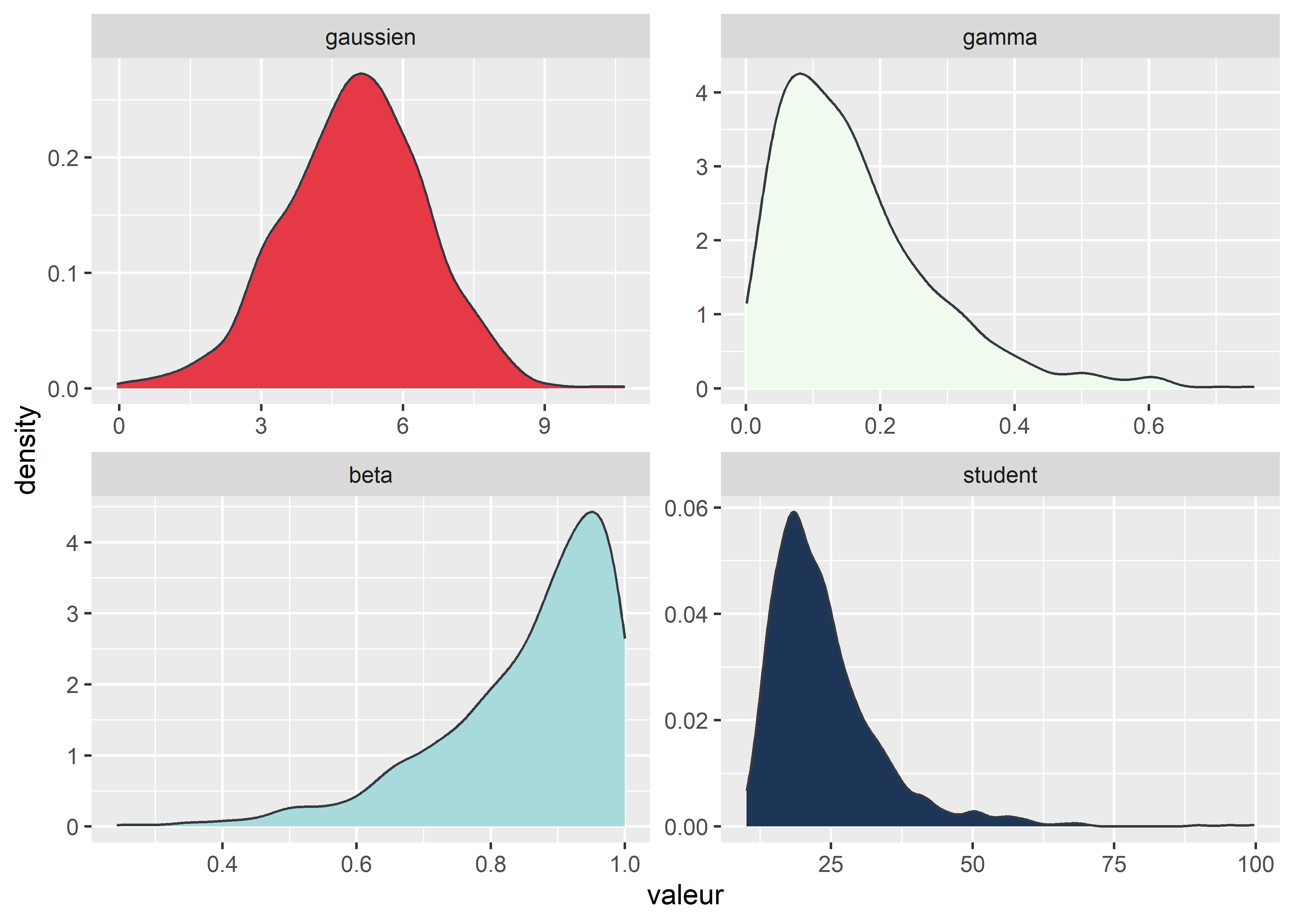
Figure 3.27: Graphiques de densité à facette
Les graphiques de densité sont souvent utilisés pour comparer la distribution d’une variable pour plusieurs sous-groupes d’une population. Si nous reprenons le jeu de données iris, nous pouvons comparer les longueurs de sépales en fonction des espèces. Nous constatons ainsi que les setosas ont une nette tendance à avoir des sépales plus courts et qu’à l’inverse, les virginicas ont les sépales généralement les plus longs.
ggplot(data = iris)+
geom_density(aes(x = Sepal.Length, fill = Species),
color = "#343a40", alpha = 0.4)+
labs(x = 'Longueur de sépales',
y = '',
fill = 'Espèce')
Figure 3.28: Graphiques de densité superposés
3.2.3 Nuage de points
Un nuage de points est un outil très intéressant pour visualiser la relation existante entre deux variables. Prenons un exemple concret et analysons le volume de CO2 produit annuellement par habitant en comparaison avec le niveau d’urbanisation dans l’ensemble des pays à travers le monde. Nous avons extrait ces données sur le site web de la Banque mondiale, puis nous les avons structurés dans un fichier csv.
data_co2 <- read.csv("data/graphique/world_urb_co2.csv", encoding = "UTF-8")
names(data_co2)## [1] "country_code" "year" "Population" "Urbanisation" "CO2_kt" "Country.Name"
## [7] "CO2t_hab" "region7" "region23"3.2.3.1 Nuage de points simple
Commençons par un nuage de points simple avec l’ensemble des données.
ggplot(data = data_co2)+
geom_point(aes(x = Urbanisation, y = CO2t_hab))+
labs(x = "Niveau d'urbanisation (%)",
y = 'Tonnes de CO2 annuelle / habitant',
title = 'Relation entre urbanisation et production de CO2 par habitant')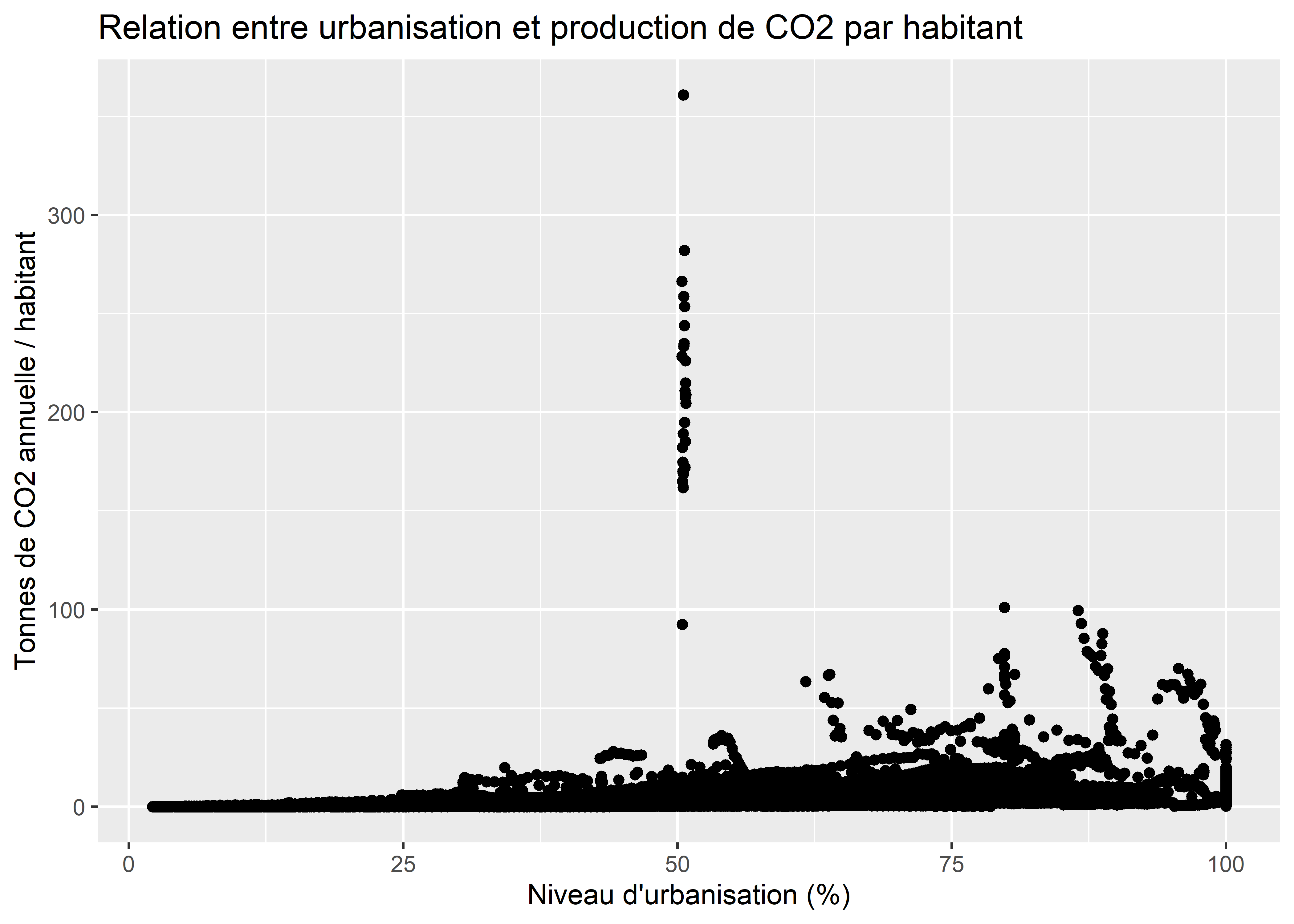
Figure 3.29: Nuage de points simple
À la première lecture de ce graphique, nous observons immédiatement un ensemble de points étranges dont le volume de CO2 par habitant annuel est au-dessus de 150 tonnes et dont le niveau d’urbanisation est proche de 50 %. Isolons ces données pour observer de quoi il s’agit.
cas_etrange <- subset(data_co2, data_co2$CO2t_hab >= 150)
print(cas_etrange$Country.Name)## [1] "Aruba" "Aruba" "Aruba" "Aruba" "Aruba" "Aruba" "Aruba" "Aruba" "Aruba" "Aruba" "Aruba" "Aruba"
## [13] "Aruba" "Aruba" "Aruba" "Aruba" "Aruba" "Aruba" "Aruba" "Aruba" "Aruba" "Aruba" "Aruba" "Aruba"
## [25] "Aruba"Il s’agit d’une petite île néerlandaise des Caraïbes nommée Aruba disposant d’une faible population, mais avec des activités très polluantes (raffinerie et extraction d’or). Nous faisons ici le choix de retirer ces observations puisqu’elles sont assez peu représentatives de la tendance mondiale. Cette démarche si simple relève ainsi de l’analyse exploratoire des données! Sans ce graphique, nous n’aurions probablement jamais identifié ces cas problématiques.
data_co2 <- subset(data_co2, data_co2$CO2t_hab <= 150)Reconstruisons le nuage de points maintenant que ces données aberrantes ont été retirées.
graphique <- ggplot(data = data_co2)+
geom_point(aes(x = Urbanisation, y = CO2t_hab))+
labs(x = "Niveau d'urbanisation (%)",
y = 'Tonnes de CO2 annuelle / habitant',
title = 'Relation entre urbanisation et production de CO2 par habitant')Voilà qui est mieux! Cependant, le grand nombre de points restant rend la lecture du graphique assez difficile puisqu’ils se superposent. Une première option à envisager, dans ce cas, est à la fois d’ajouter de la transparence aux points et de réduire leur taille :
ggplot(data = data_co2)+
geom_point(aes(x = Urbanisation, y = CO2t_hab), alpha = 0.2, size = 0.5)+
labs(x = "Niveau d'urbanisation (%)",
y = 'Tonnes de CO2 annuelle / habitant',
title = 'Relation entre urbanisation et production de CO2 par habitant')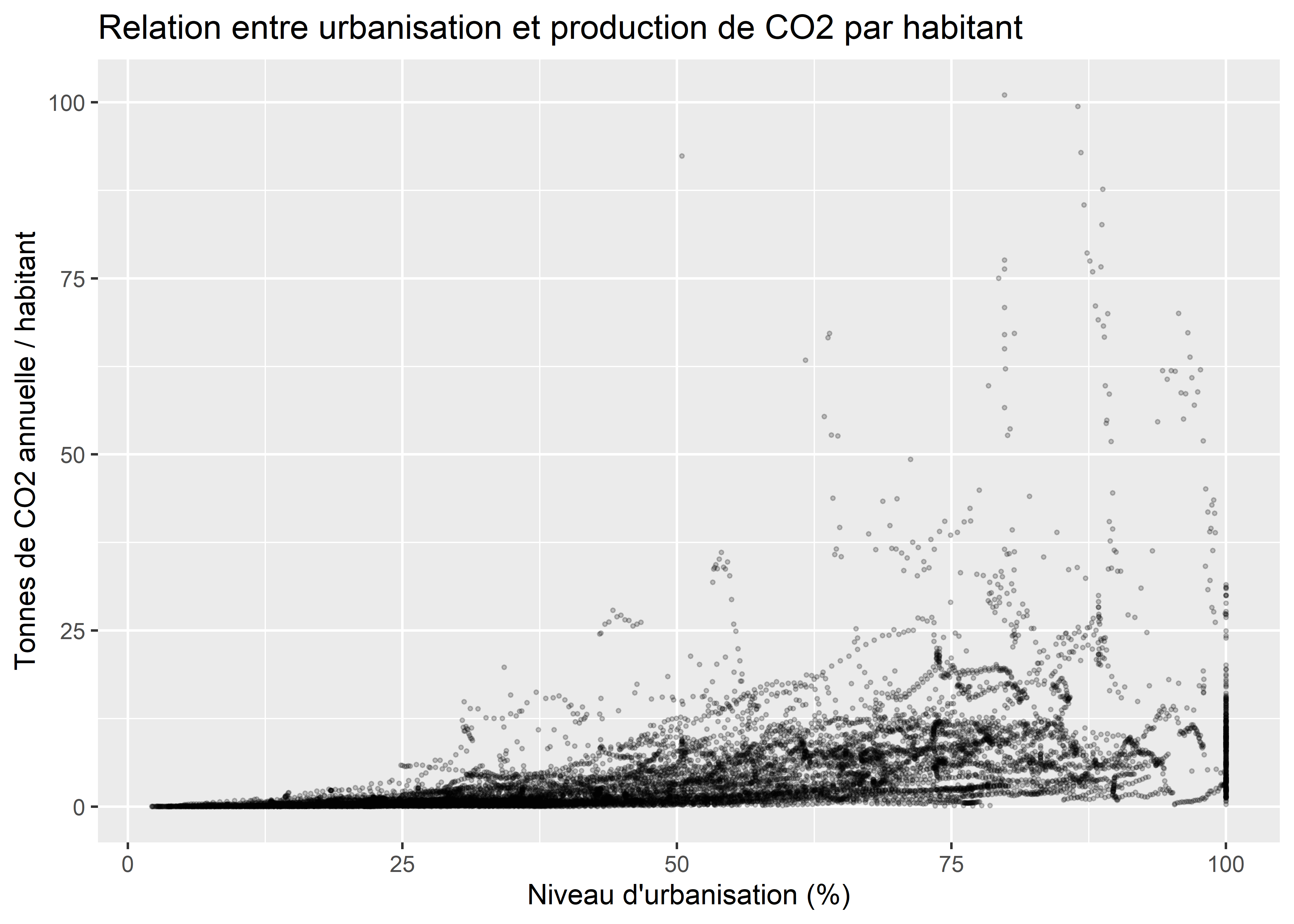
Figure 3.30: Nuage de points simple avec transparence
3.2.3.2 Nuage de points avec densité
Bien que la transparence nous aide un peu à distinguer les secteurs du graphique avec le plus de points, il serait plus efficace d’abandonner la géométrie des points pour la remplacer par une géométrie de densité en deux dimensions. Une première approche consiste à diviser l’espace du graphique en petits carrés et à compter le nombre de points tombant dans chaque carré (en somme, un histogramme en deux dimensions).
ggplot(data = data_co2)+
geom_bin2d(aes(x = Urbanisation, y = CO2t_hab), bins = 50) +
scale_fill_continuous(type = "viridis") +
labs(x = "Niveau d'urbanisation (%)",
y = 'Tonnes de CO2 annuelle / habitant',
fill = "Effectif",
title = 'Relation entre urbanisation et production de CO2 par habitant')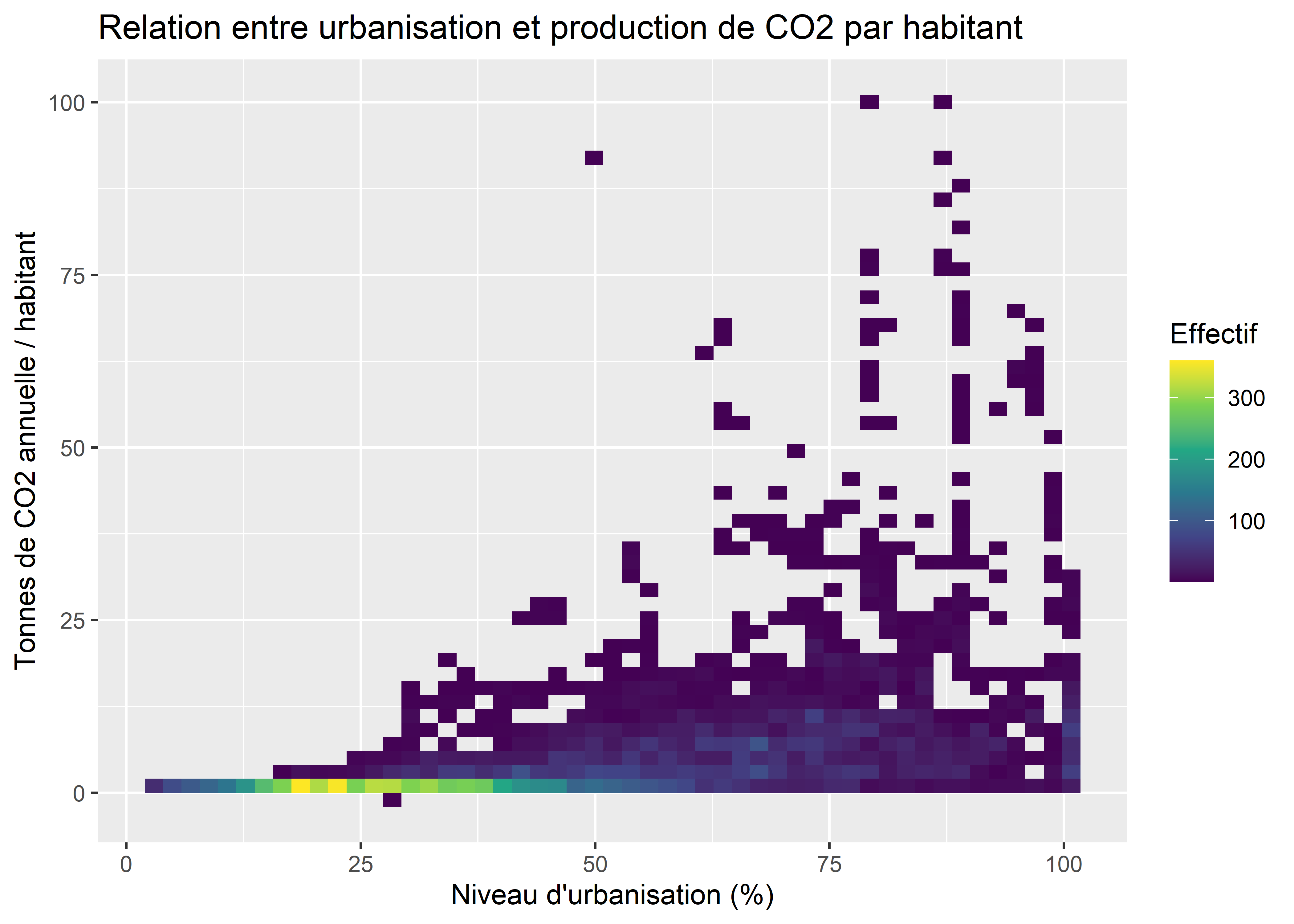
Figure 3.31: Nuage de points simple
Nous observons ainsi une forte concentration dans le bas du graphique; les pays avec des rejets annuels de CO2 supérieurs à 15 tonnes par habitant sont relativement rares. Pour les personnes préférant les représentations plus élaborées, il est aussi possible de diviser l’espace du graphique avec des hexagones en utilisant le package hexbin.
ggplot(data = data_co2)+
geom_hex(aes(x = Urbanisation, y = CO2t_hab), bins = 50) +
scale_fill_continuous(type = "viridis") +
labs(x = "Niveau d'urbanisation (%)",
y = 'Tonnes de CO2 annuelle / habitant',
fill = "Effectif",
title = 'Relation entre urbanisation et production de CO2 par habitant')
Figure 3.32: Densité en deux dimensions par hexagones
Enfin, il est aussi possible de réaliser une version lissée de ces graphiques avec une fonction kernel en deux dimensions (stat_density_2d) :
ggplot(data = data_co2)+
stat_density_2d(aes(x = Urbanisation, y = CO2t_hab, fill = ..density..),
geom = "raster", n = 50, contour = FALSE) +
scale_fill_continuous(type = "viridis") +
labs(x = "Niveau d'urbanisation (%)",
y = 'Tonnes de CO2 annuelle / habitant',
fill = "densité",
title = 'Relation entre urbanisation et production de CO2 par habitant')+
ylim(0,25)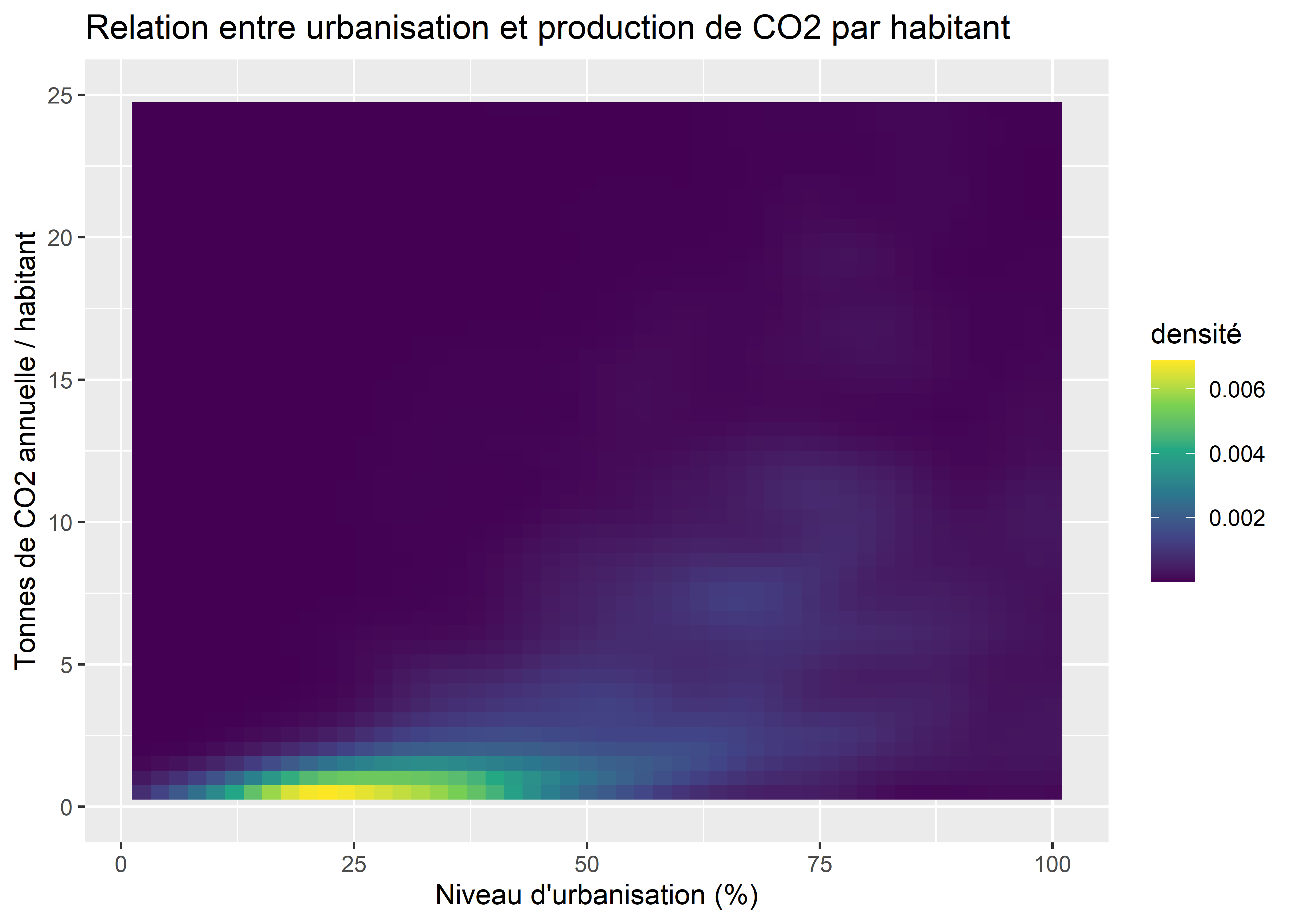
Figure 3.33: Densité lissée en deux dimensions
3.2.3.3 Nuage de points et droite de régression
Afin de faire ressortir une éventuelle relation entre les variables représentées sur les deux axes, il est possible d’afficher la droite de régression sur le graphique entre X et Y. Cette opération s’effectue avec la fonction geom_smooth.
graphique <- ggplot(data = data_co2)+
geom_point(aes(x = Urbanisation, y = CO2t_hab), alpha = 0.2, size = 0.5)+
geom_smooth(aes(x = Urbanisation, y = CO2t_hab), method = lm, color = "red")+
labs(x = "Niveau d'urbanisation (%)",
y = 'Tonnes de CO2 annuelle / habitant',
title = 'Relation entre urbanisation et production de CO2 par habitant')Notez que l’argument method = lm permet d’indiquer que nous souhaitons utiliser une régression linéaire (linear model) pour tracer la géométrie (une droite de régression). La droite semble bien indiquer une relation positive entre les deux variables : une augmentation de l’urbanisation serait associée à une augmentation de la production annuelle de CO2 par habitant. Nous pourrions également vérifier si une relation non linéaire serait plus adaptée au jeu de données. Dans notre cas, une relation quadratique pourrait produire un meilleur ajustement.
ggplot(data = data_co2)+
geom_point(aes(x = Urbanisation, y = CO2t_hab), alpha = 0.2, size = 0.7)+
geom_smooth(aes(x = Urbanisation, y = CO2t_hab), method = lm,
color = "red", formula = y ~ I(x**2))+
labs(x = "Niveau d'urbanisation (%)",
y = 'Tonnes de CO2 annuelle / habitant',
title = 'Relation entre urbanisation et production de CO2 par habitant')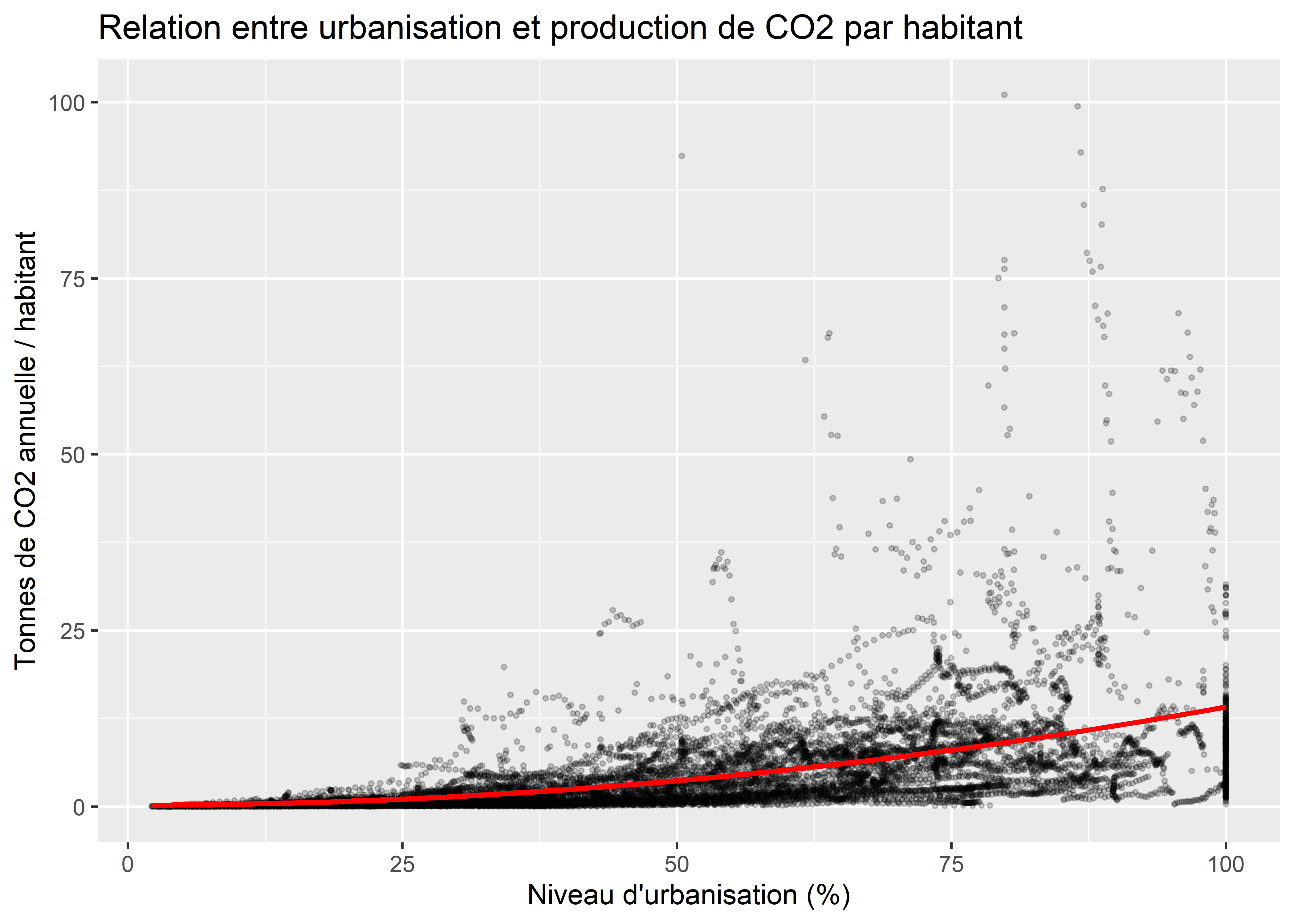
Figure 3.34: Nuage de points avec droite de régression quadratique
La régression quadratique (avec x au carré) nous indique ainsi que l’impact du niveau d’urbanisation est plus important à mesure que ce niveau augmente. Vous pouvez également constater que la courbe ne prédit pas de valeurs négatives comparativement à la droite précédente. Il est également possible d’ajuster une courbe sans choisir au préalable sa forme (dans le cas précédent \(x^2\)) en utilisant une méthode d’ajustement local appelée loess.
graphique <- ggplot(data = data_co2)+
geom_point(aes(x = Urbanisation, y = CO2t_hab), alpha = 0.2, size = 0.5)+
geom_smooth(aes(x = Urbanisation, y = CO2t_hab), method = loess,
color = "red")+
labs(x = "Niveau d'urbanisation (%)",
y = 'Tonnes de CO2 annuelle / habitant',
title = 'Relation entre urbanisation et production de CO2 par habitant')La relation non linéaire révèle davantage d’informations : l’augmentation de l’urbanisation est associée à une augmentation de l’émission de CO2 par habitant uniquement jusqu’à 75 % d’urbanisation; au-delà de ce seuil, la relation ne tient plus. Ces résultats semblent cohérents avec l’évolution classique de l’économie d’un pays passant progressivement d’une économie agricole, à une économie industrialisée et finalement une économie de services.
3.2.4 Graphique en ligne
Un graphique en ligne permet de représenter l’évolution d’une variable, généralement dans le temps. Dans le jeu de données précédent, nous disposons des émissions de CO2 par habitant de nombreux pays sur plusieurs années. Nous pouvons ainsi représenter l’évolution des émissions pour chaque pays avec un graphique en ligne. Pour éviter de le surcharger, cet exercice est réalisé uniquement sur les pays de l’Europe de l’Ouest.
# conversion de la variable year textuelle en variable numérique
data_co2$an <- as.numeric(data_co2$year)
# extraction des données d'Europe de l'Ouest
data_europe <- subset(data_co2, data_co2$region23 == "Europe de l'Ouest")
# choix des valeurs pour l'axe des x
x_ticks <- seq(1960,2020,10)
ggplot(data = data_europe)+
geom_path(aes(x = an, y = CO2t_hab, color = Country.Name))+
labs(x = "Années",
y = 'Tonnes de CO2 annuelle / habitant',
color = "Pays",
title = 'Évolution de la production de CO2 par habitant') +
scale_x_continuous(breaks = x_ticks, labels = x_ticks)+
theme_tufte()
Figure 3.35: Graphique en ligne
Nous remarquons notamment qu’aucune donnée, avant 2005, n’est disponible pour le Liechtenstein.
3.2.4.1 Barre d’erreur et en bande
Sur un graphique, il est souvent pertinent de représenter l’incertitude que nous avons sur nos données. Cela peut être fait à l’aide de barres d’erreur ou à l’aide de polygones délimitant les marges d’incertitude. En guise d’exemple, admettons que les données précédentes sont fiables à plus ou moins 10 %. En d’autres termes, la valeur d’émission de CO2 annuelle serait relativement incertaine et pourrait se situer dans un intervalle de 10 % autour de la valeur fournie par la Banque mondiale. Nous obtenons ainsi une borne inférieure (valeur donnée - 10 %) et une borne supérieure (valeur donnée + 10 %). Nous pouvons facilement calculer ces bornes et les faire apparaître dans notre graphique précédent.
data_europe$borne_basse <- data_europe$CO2t_hab - 0.1 * data_europe$CO2t_hab
data_europe$borne_haute <- data_europe$CO2t_hab + 0.1 * data_europe$CO2t_hab
ggplot(data = data_europe)+
geom_point(aes(x = an, y = CO2t_hab, color = Country.Name), size = 0.7)+
geom_errorbar(aes(x = an, ymin = borne_basse, ymax = borne_haute, color = Country.Name))+
labs(x = "Années",
y = 'Tonnes de CO2 annuelle / habitant',
color = "Pays",
title = 'Évolution de la production de CO2 par habitant') +
scale_x_continuous(breaks = x_ticks, labels = x_ticks)+
theme_tufte()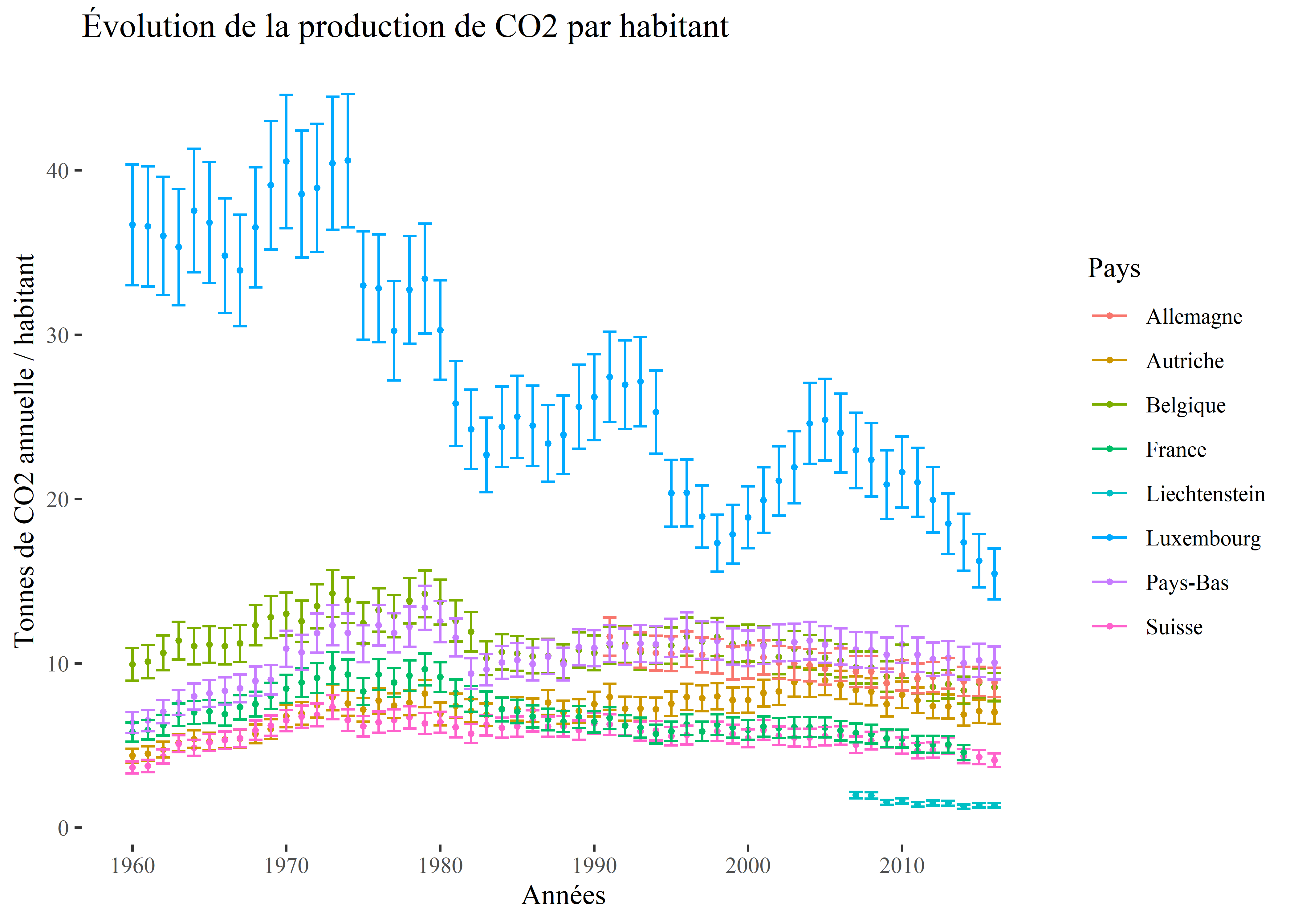
Figure 3.36: Graphique en ligne avec barres d’erreur
Ces barres d’erreurs indiquent notamment qu’il n’y a finalement aucun écart significatif entre la Belgique, les Pays-Bas et l’Allemagne à partir des années 1990. Une autre option de représentation est d’utiliser des polygones avec la fonction geom_ribbon.
ggplot(data = data_europe)+
geom_path(aes(x = an, y = CO2t_hab, color = Country.Name), size = 0.7)+
geom_ribbon(aes(x = an, ymin = borne_basse, ymax = borne_haute,
fill = Country.Name), alpha = 0.4)+
labs(x = "Années",
y = 'Tonnes de CO2 annuelle / habitant',
color = "Pays",
title = 'Évolution de la production de CO2 par habitant') +
scale_x_continuous(breaks = x_ticks, labels = x_ticks)+
theme_tufte()+
guides( fill = FALSE)## Warning: The `<scale>` argument of `guides()` cannot be `FALSE`. Use "none" instead as of ggplot2
## 3.3.4.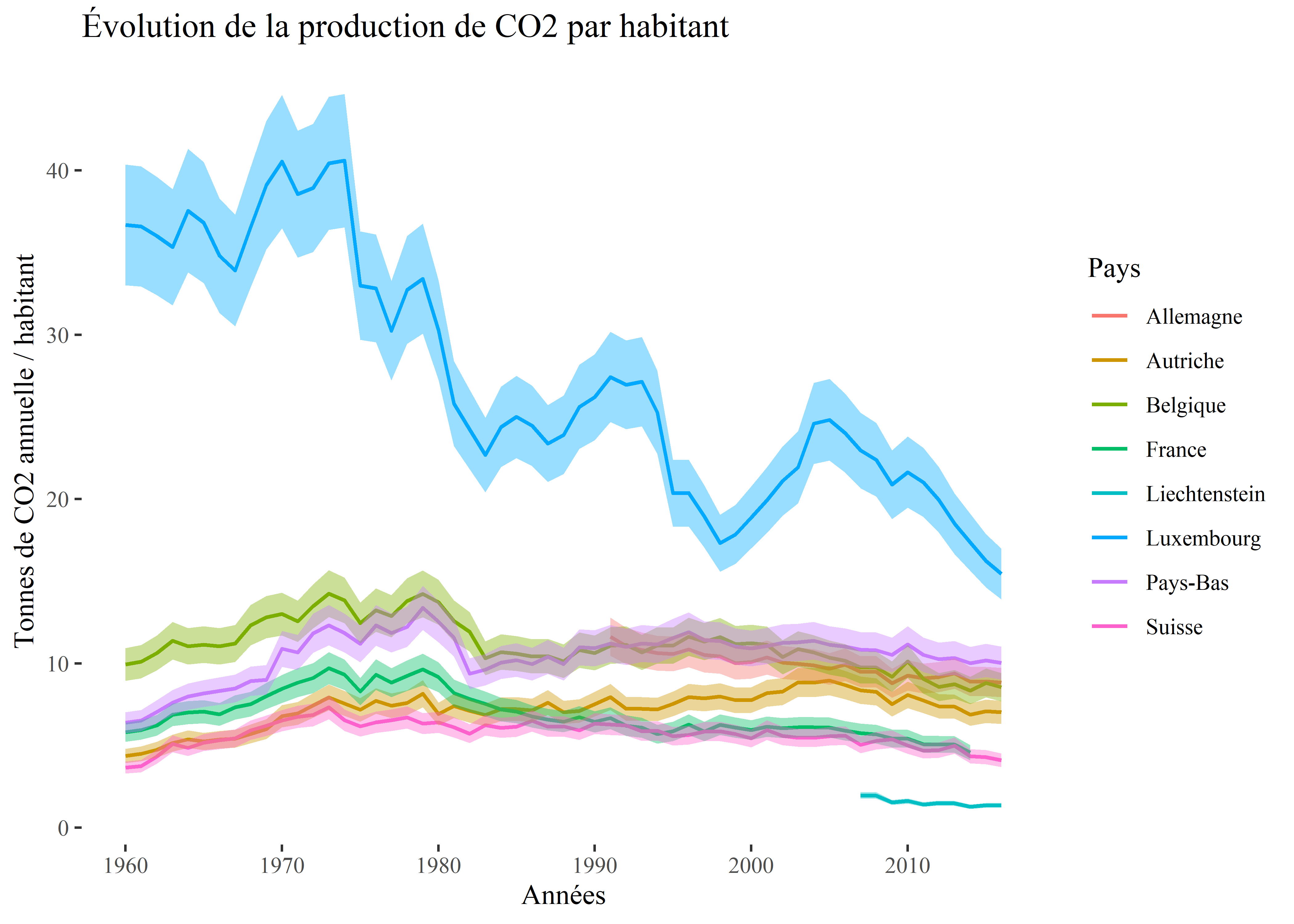
Figure 3.37: Graphique en ligne avec marge d’erreur
Le message du graphique est le même. Notez que nous avons utilisé ici la fonction guides pour retirer de la légende les couleurs associées au remplissage des marges d’erreur. Ces couleurs sont les mêmes que celles des lignes et il n’est pas utile de dédoubler la légende. De nombreuses méthodes statistiques produisent des résultats accompagnés d’une mesure de l’incertitude associée à ces résultats. Représenter cette incertitude est crucial pour que le lecteur puisse délimiter la portée des conclusions de vos analyses.
3.2.5 Boîte à moustaches
Les boîtes à moustaches (box plot en anglais) sont des graphiques permettant de comparer les moyennes et les intervalles interquartiles d’une variable continue selon plusieurs groupes d’une population. Si nous reprenons notre exemple précédent, nous pourrions comparer, en fonction de la région du monde, la moyenne de production annuelle de CO2 par habitant. Pour cela, il suffit d’utiliser la fonction geom_boxplot.
#retirer les observations n'étant pas associées à une région
data_co2_comp <- subset(data_co2, is.na(data_co2$region7) == F)
ggplot(data = data_co2_comp)+
geom_boxplot(aes(y = region7, x = CO2t_hab))+
labs(x="Tonnes de CO2 par an et habitant", y="Région")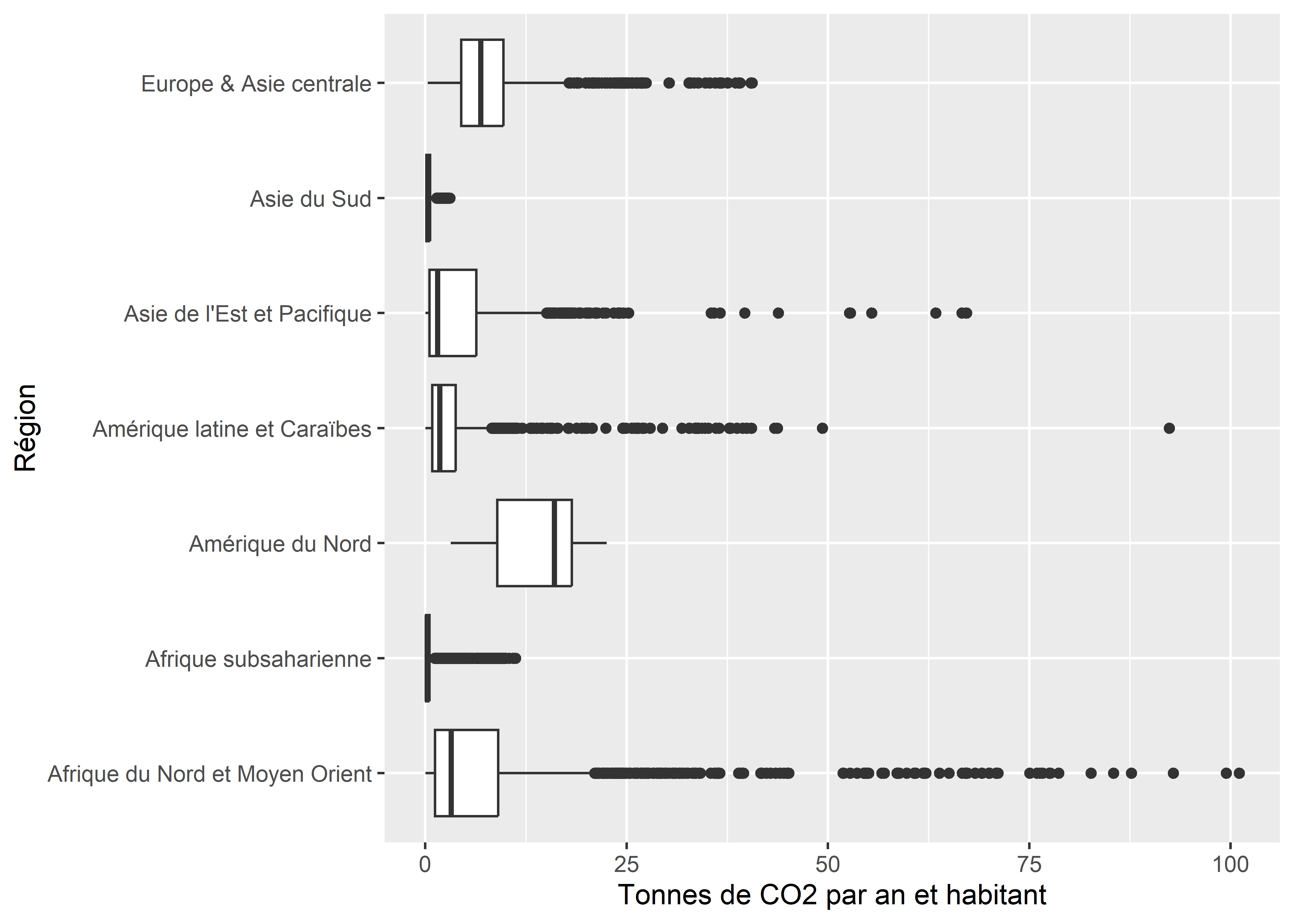
Figure 3.38: Boîtes à moustaches
La barre centrale d’une boîte représente la moyenne. Les extrémités de la boîte représentent le premier et le troisième quartile. Plus une boîte est allongée, plus les situations sont diversifiées pour les observations appartenant au groupe représenté par la boîte. Au contraire, une boîte étroite indique un groupe homogène. Notez qu’en inversant les variables dans les axes X et Y, nous obtiendrions des boîtes à moustaches verticales. Cependant, les noms des régions étant assez longs, cela nécessiterait d’avoir un graphique très large. Améliorons quelque peu le rendu de ce graphique en ajoutant des titres.
ggplot(data = data_co2_comp)+
geom_boxplot(aes(y = region7, x = CO2t_hab))+
xlim(c(0,50))+
labs(x = "Tonnes de CO2 par an et habitant",
y = 'Région')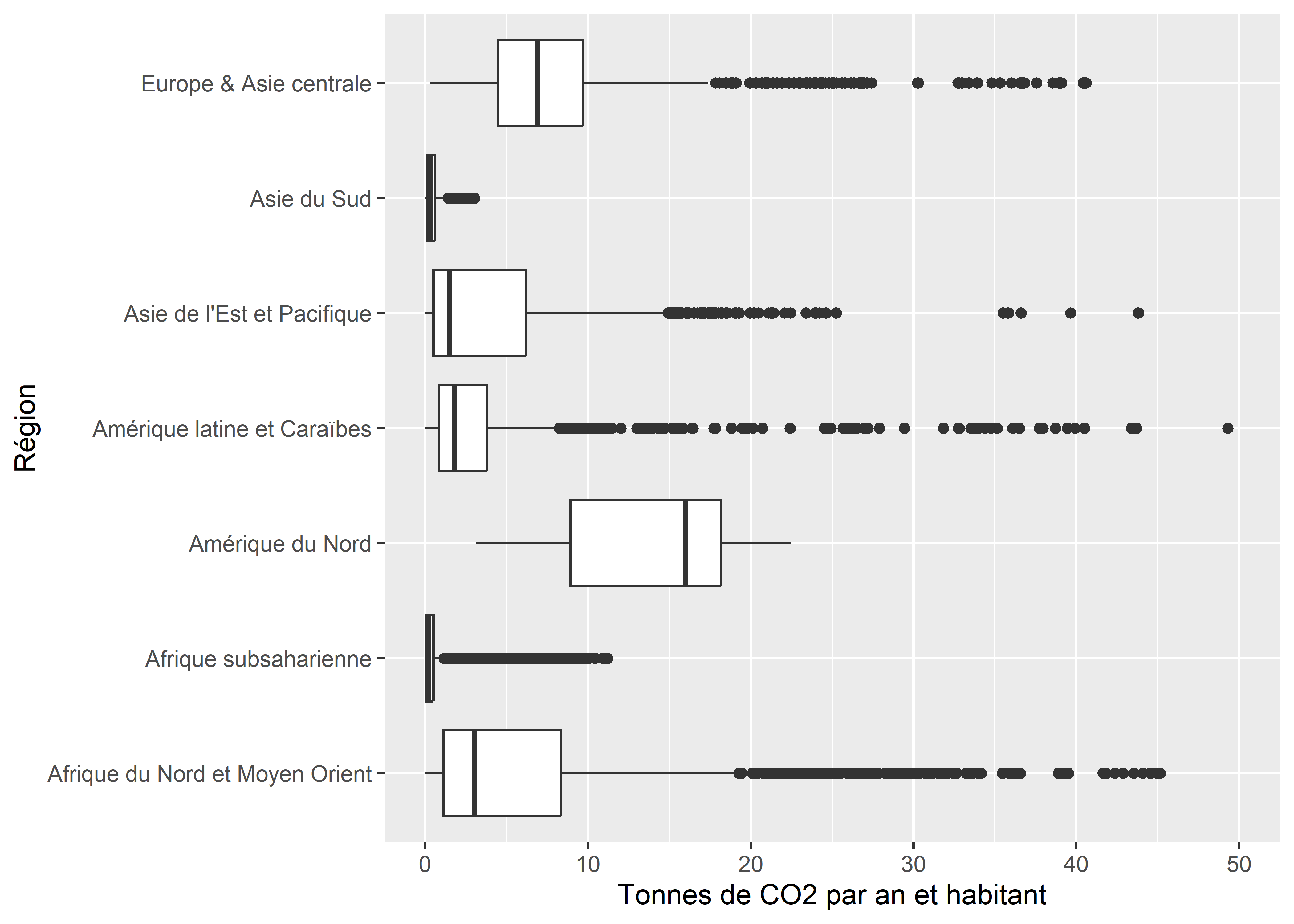
Figure 3.39: Boîtes à moustaches améliorées
Les points noirs sur le graphique représentent des valeurs extrêmes, soit des observations situées à plus de 1,5 intervalle interquartile d’une extrémité de la boîte. Pour mieux rendre compte de la densité d’observations le long de chaque boîte à moustaches, il est possible de les représenter directement avec la fonction geom_jitter.
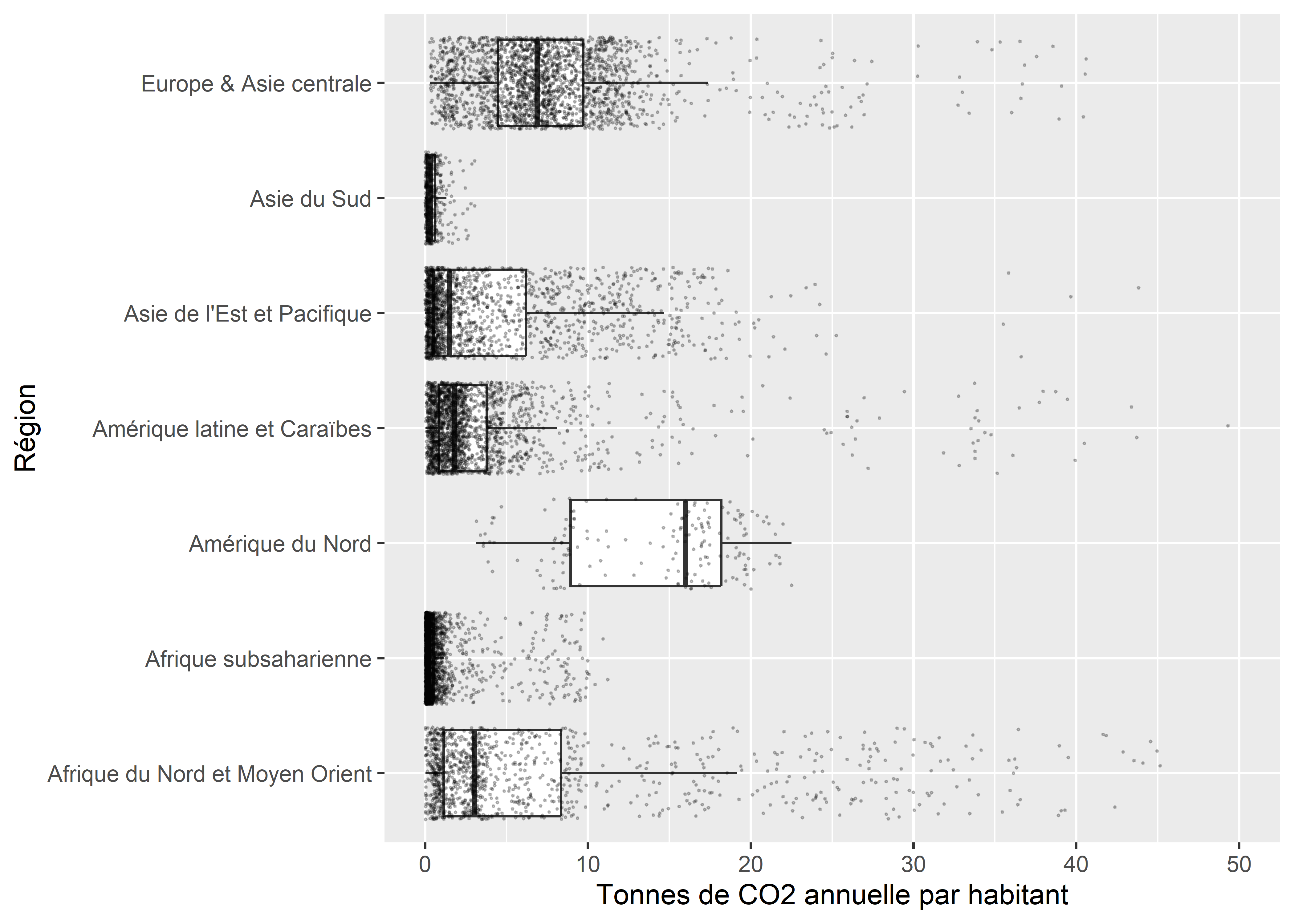
Figure 3.40: Boîtes à moustaches avec observations
Notez que pour éviter que les valeurs extrêmes identifiées par la fonction geom_boxplot se superposent avec les points représentant les observations, nous les avons supprimées avec l’argument outlier.shape = NA.
3.2.6 Graphique en violon
Les boîtes à moustaches donnent des informations pertinentes sur le centre et la dispersion d’une variable en fonction de sous groupes de la population. Cependant, une grande partie de l’information reste masquée par la représentation sous forme de boîte. Une solution est de remplacer la simple boîte par la distribution de la variable étudiée. Nous obtenons ainsi des graphiques en violon (geom_violin). Considérant les très grands écarts que nous avons observés entre les régions avec les boîtes à moustaches, il est préférable de tracer les graphiques en violon en excluant les régions Afrique Sub-Saharienne et Asie du Sud.
# retirons les observations de régions que nous ne souhaitons par garder
data_co2_comp <- subset(data_co2, (! data_co2$region7 %in%
c("Sub-Saharan Africa", "South Asia"))
& is.na(data_co2$region7)==FALSE)
ggplot(data = data_co2_comp)+
geom_violin(aes(y = region7,x = CO2t_hab))+
xlim(c(0,50))+
labs(x = "Tonnes de CO2 annuelle / habitant",
y = '')+
geom_vline(xintercept = 12, linetype = 'dashed', color = 'blue')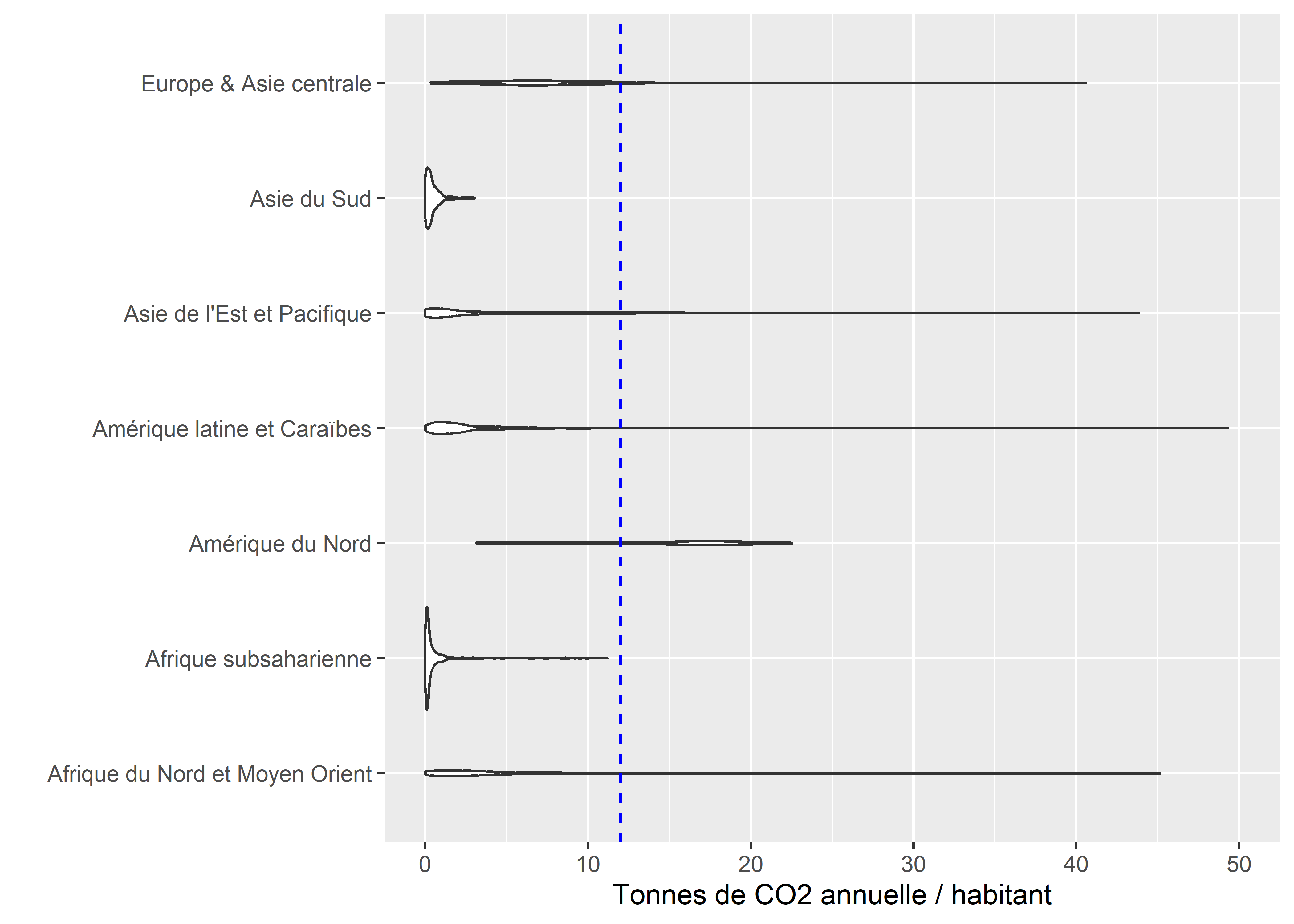
Figure 3.41: Graphiques en violon
Ces distributions permettent notamment de souligner que deux groupes distincts se retrouvent en Amérique du Nord. L’un dont les émissions annuelles de CO2 par habitant sont inférieures à 12 tonnes (ligne bleue) et l’autre pour lequel elles sont supérieures. En explorant les données, nous constatons que les Bermudes appartiennent au groupe Amérique du Nord, mais ont des niveaux d’émission inférieurs à ceux du Canada et des États-Unis, ce qui explique cette distribution bimodale. Cette information était masquée avec les boîtes à moustaches. Finalement, il est aussi possible de superposer un graphique en violon et une boîte à moustaches pour bénéficier des avantages des deux.
ggplot(data = data_co2_comp)+
geom_violin(aes(y = region7,x = CO2t_hab))+
geom_boxplot(aes(y = region7,x = CO2t_hab), width = 0.15)+
xlim(c(0,50))+
labs(x = "Tonnes de CO2 annuelle / habitant",
y = '')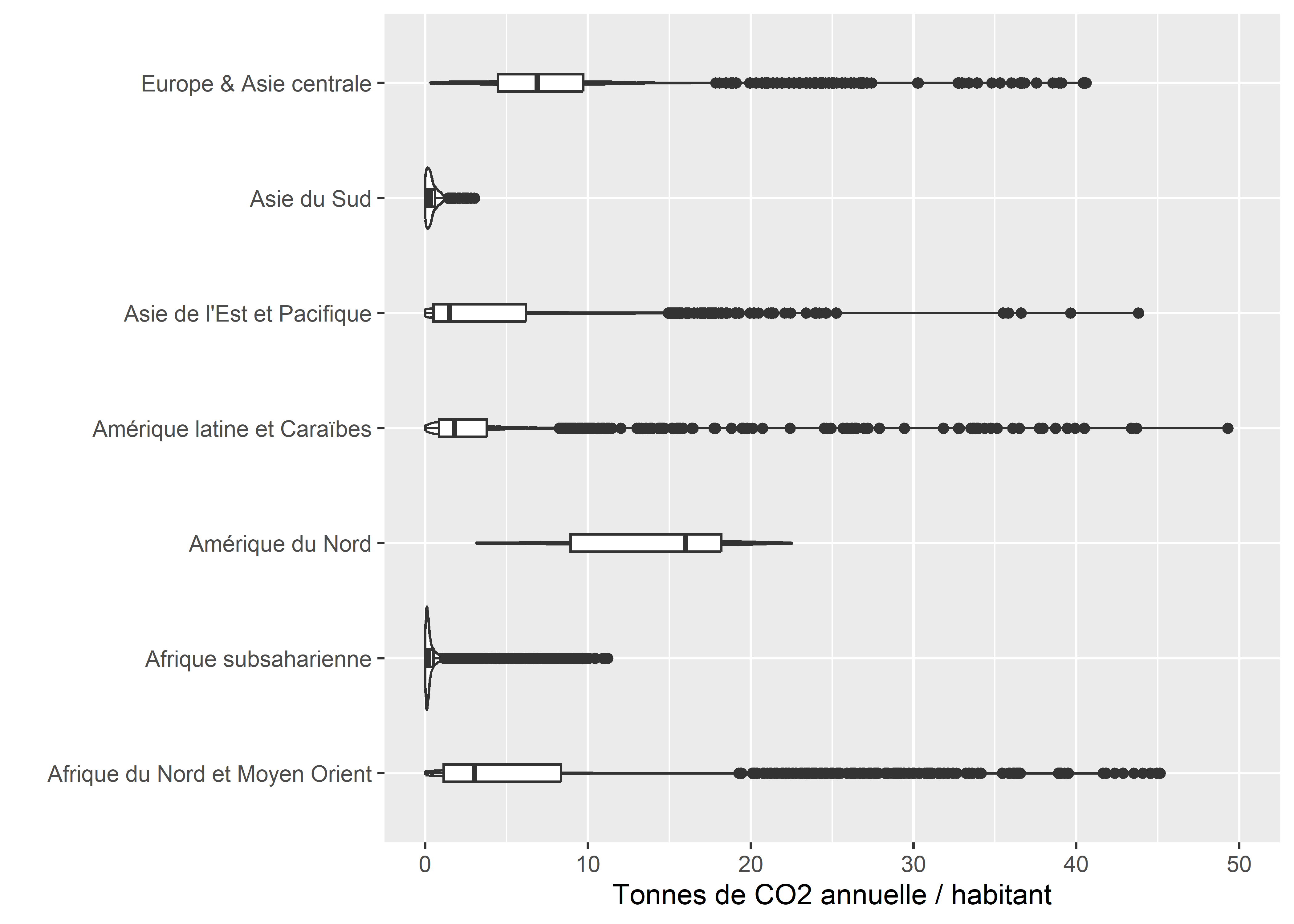
Figure 3.42: Graphiques en violon et boîtes à moustaches
3.2.7 Graphique en barre
Les graphiques en barre permettent de représenter des quantités (hauteur des barres) réparties dans des catégories (une barre par catégorie). Nous proposons ici un exemple avec des données de déplacements issues de l’Enquête origine-destination 2017 - Région Québec-Lévis, au niveau des grands secteurs. La figure 3.42, tirée du rapport intitulé La mobilité des personnes dans la région de Québec-Lévis (Volet Enquête-ménages : faits saillants) délimite ces grands secteurs.

Figure 3.43: Grands secteurs de Québec
Nous représentons pour chaque secteur le nombre moyen de déplacements entrant et sortant un jour de semaine en heures de pointe. Les données sont présentées sous forme d’une matrice carrée (avec autant de lignes que de colonnes). L’intersection de la ligne A et de la colonne C indique le nombre de personnes partant du secteur A pour se rendre au secteur C. À l’inverse, l’intersection de la ligne C et de la colonne A indique le nombre de personnes partant du secteur C pour se rendre au secteur A. En sommant les valeurs de chaque ligne, nous obtienons le nombre total de départs par secteur tandis que le nombre d’arrivées est la somme de chaque colonne. Ces opérations peuvent simplement être effectuées avec les fonctions rowSums et colSums.
# Chargement des donneées
matriceOD <- read.csv('data/graphique/Quebec_2017_OD_MJ.csv',
header = FALSE, sep = ';') # fichier csv sans entête
# Calcul des sommes en lignes et en colonnes
tot_depart <- rowSums(matriceOD)
tot_arrivee <- colSums(matriceOD)
# Création d'un DataFrame avec les valeurs et les noms des secteurs
df <- data.frame(depart = tot_depart,
arrivee = tot_arrivee,
secteur = c('Arr. de Beauport (Québec)',
'Arr. de Charlesbourg (Québec)',
'Arr. des Rivières (Québec)',
'Arr. de la Cité-Limoilou (Québec)',
'Arr. de la Haute-Saint-Charles (Québec)',
'Arr. de Sainte-Foy-Sillery-Cap-Rouge (Québec)',
'Arr.de Desjardins (Lévis)',
'Arr. des Chutes–de-la-Chaudière-Est (Lévis)',
'Arr. des Chutes de la Chaudière-Ouest (Lévis)',
'Ceinture Nord',
'Ceinture Sud',
'Hors Territoire'),
code = c('A','B','C','D','E','F','G','H','I','J','K','X'))
# Création des deux graphiques en barre
plot1 <- ggplot(data = df)+
geom_bar(aes(x = code, weight = depart))+
labs(subtitle = 'Départs',
x = 'total',
y = '')
plot2 <- ggplot(data = df)+
geom_bar(aes(x = code, weight = arrivee))+
labs(subtitle = 'Arrivées',
x = 'total',
y = '')
# Stocker les graphiques dans une liste et composer une figure
list_plot <- list(plot1, plot2)
tot_plot <- ggarrange(plotlist = list_plot, ncol = 1)
# Création d'une légende pour associer le code de chaque secteur
# à son nom. Pour cela nous concaténons en premier les lettres et les noms.
# Nous fusionons ensuite le tout en les séparant par le symbole \n représentant
# un saut de ligne.
nom_secteurs <- paste(df$code, df$secteur, sep= ' : ')
string_names <- paste(nom_secteurs, collapse = '\n')
titre <- "Déplacements journaliers moyens en heures de pointe"
# Production finale de la figure
annotate_figure(tot_plot,
top = text_grob(titre, face = "bold", size = 11, just = "left"),
right = text_grob(string_names, face = "italic", size = 8,
just = "left", x = 0.05) # position du texte
)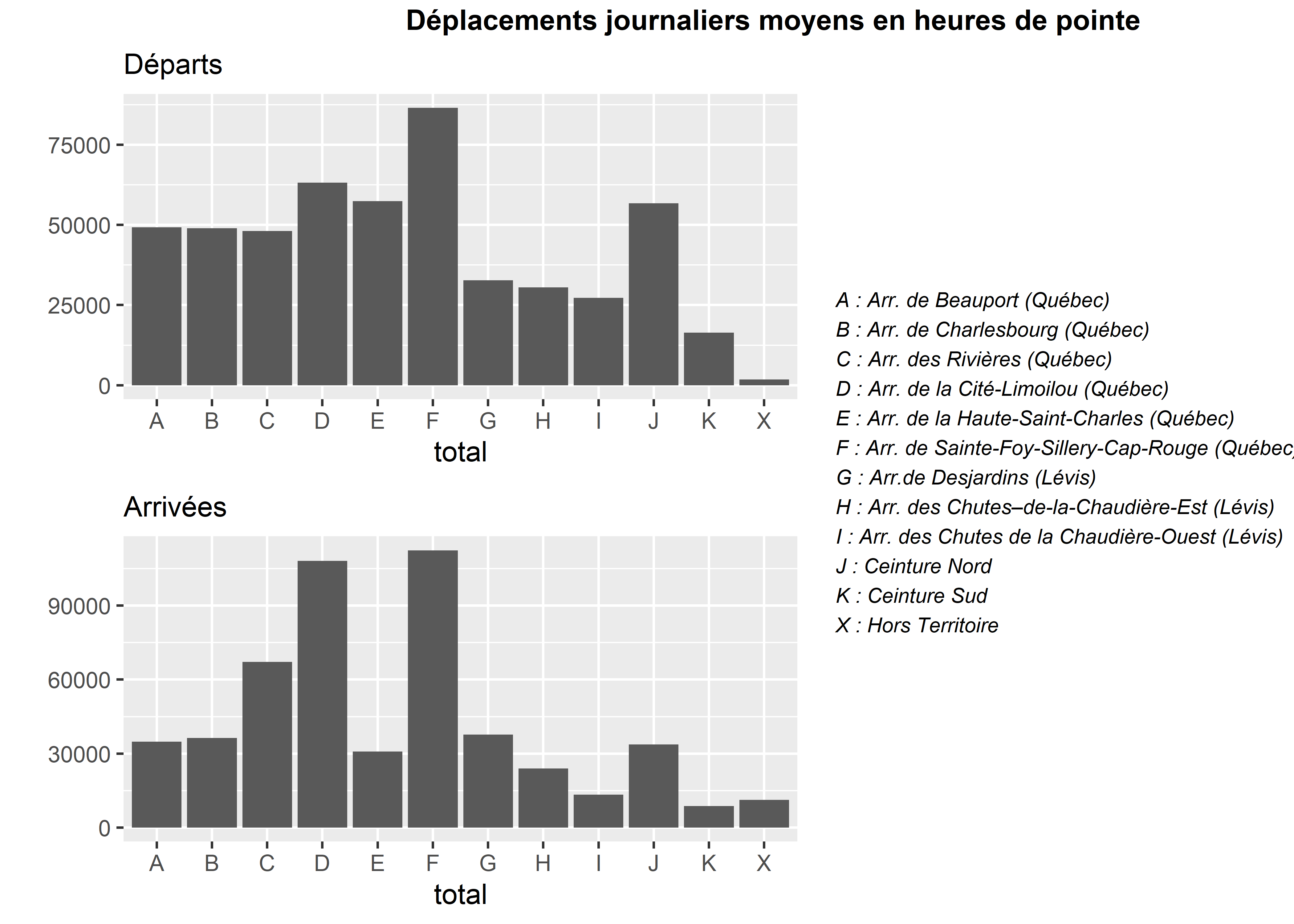
Figure 3.44: Graphiques en barre simples
Plutôt que de représenter les arrivées et les départs dans deux graphiques séparés, il est possible de les empiler dans un même graphique en barre. Nous devons au préalable « faire fondre nos données » avec la fonction melt.
# Faire fondre le jeu de données (empiler les colonnes depart et arrivee)
melted_df <- melt(df, id.vars = c('code'), measure.vars = c('depart','arrivee'))
names(melted_df) <- c('code','deplacement','effectif')
# Ajouter les accents dans la colonne déplacement
melted_df$deplacement <- ifelse(melted_df$deplacement == 'depart', 'départs', 'arrivées')
# Comparaison du format original et du format "fondu"
head(df)## depart arrivee secteur code
## V1 49241 34777 Arr. de Beauport (Québec) A
## V2 48909 36344 Arr. de Charlesbourg (Québec) B
## V3 48044 67198 Arr. des Rivières (Québec) C
## V4 63132 108138 Arr. de la Cité-Limoilou (Québec) D
## V5 57367 30859 Arr. de la Haute-Saint-Charles (Québec) E
## V6 86504 112379 Arr. de Sainte-Foy-Sillery-Cap-Rouge (Québec) Fhead(melted_df)## code deplacement effectif
## 1 A départs 49241
## 2 B départs 48909
## 3 C départs 48044
## 4 D départs 63132
## 5 E départs 57367
## 6 F départs 86504# Réalisation du graphique
plot1 <- ggplot(data = melted_df)+
geom_bar(aes(x = code,weight = effectif, fill = deplacement),color = '#e3e3e3')+
scale_fill_manual(values = c("#e63946","#1d3557"))+
labs(title = titre,
y = 'Effectifs',
x = '',
fill = 'Déplacements')
annotate_figure(plot1,right = text_grob(string_names, face = "italic", size = 7,
just = "left", x = 0.05)) # position du texte)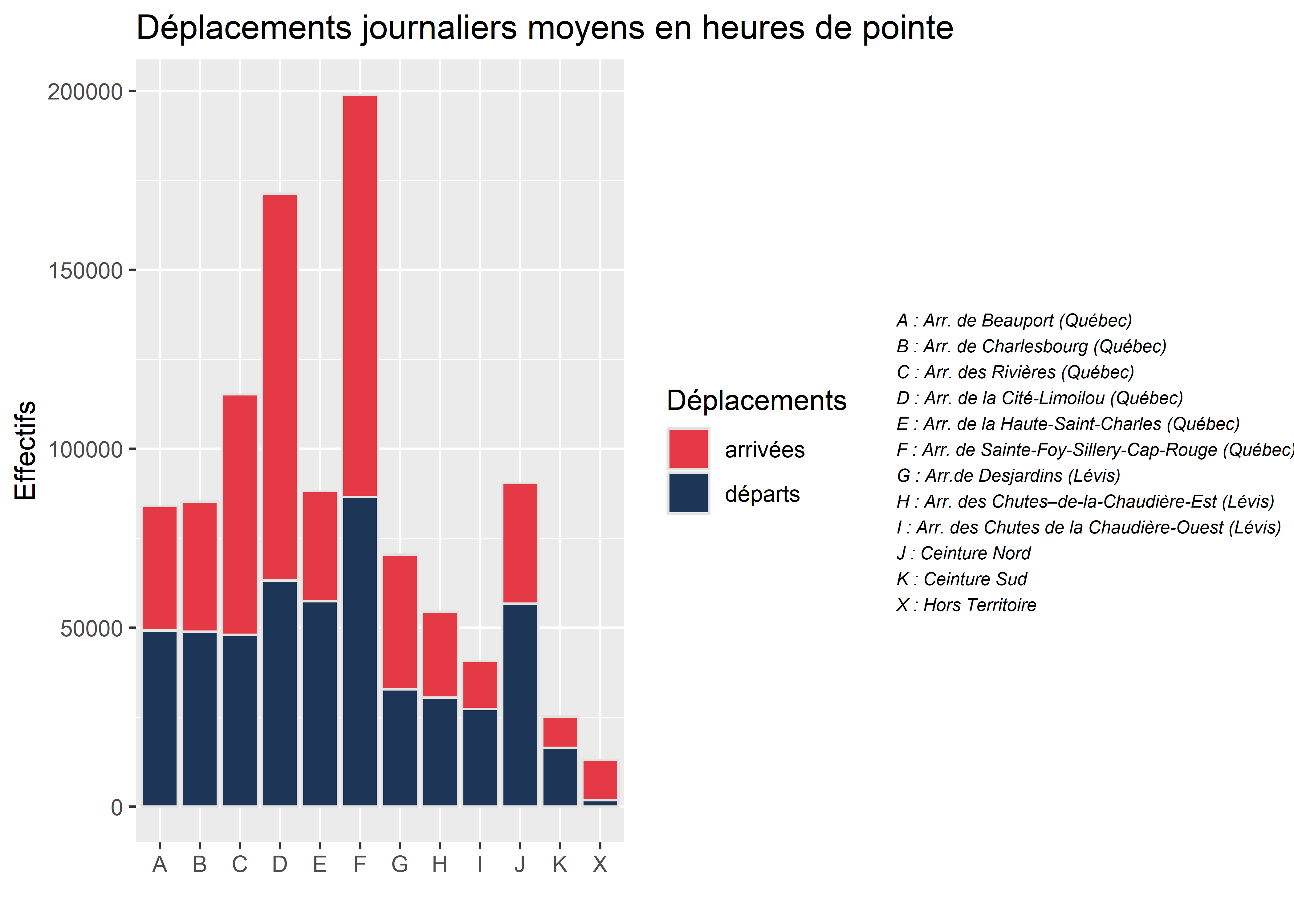
Figure 3.45: Graphique en barre empilée
3.2.8 Graphique circulaire
Une option directe au graphique en barre est le graphique ou diagramme circulaire, appelé aussi graphique en tarte (pour les personnes à la dent sucrée) ou en camembert (pour celles amatrices de fromage). Il est suffissamment connu et utilisé pour qu’aucune présentation ne s’impose. Pour être exact, un graphique en tarte n’est rien d’autre qu’un graphique en barre dont le système de coordonnées a été modifié. Cela impose cependant de calculer à l’avance la position des étiquettes que nous souhaitons ajouter sur le graphique. Reprenons les données de production mondiale de CO2 et calculons les productions totales par région géographique en 2015.
library(dplyr)
# Extraire les données de 2018 pour lesquelles nous connaissons la région
data_co2_2015 <- subset(data_co2,data_co2$year == "2015" & ! is.na(data_co2$region7))
# Effectuer la somme du CO2 par région
co2_2015 <- data_co2_2015 %>%
group_by(region7) %>%
summarise(total_co2 = sum(CO2_kt,na.rm = TRUE))
# Attribuer un code à chaque région pour faciliter la lecture
co2_2015$code <- c("A","B","C","D","E","F","G")
# Modifier l'ordre des données, calculer les proportions et la position des labels
df <- co2_2015 %>%
arrange(desc(code)) %>%
mutate(prop = total_co2 / sum(co2_2015$total_co2) *100) %>%
mutate(ypos = cumsum(prop)- 0.5*prop )
# Préparer la légende (pourcentages et vrais noms)
nom_region <- rev(paste(df$code, " : ", df$region7, "(", round(df$prop,1),"%)"))
string_region <- paste(nom_region, collapse = '\n')
# Construire le graphique
plot1 <- ggplot(df, aes(x="", y=prop, fill=code)) +
geom_bar(stat="identity", width=1, color="white") +
coord_polar("y", start=0) +
theme_void() +
theme(legend.position="none") +
geom_text(aes(y = ypos, label = code), color = "white", size=3) +
scale_fill_grey()+
labs(title = "Proportion du CO2 émis en 2015")
# Ajouter la légende
annotate_figure(plot1,right = text_grob(string_region, face = "italic", size = 9,
just = "left", x = 0.05)) # position du texte)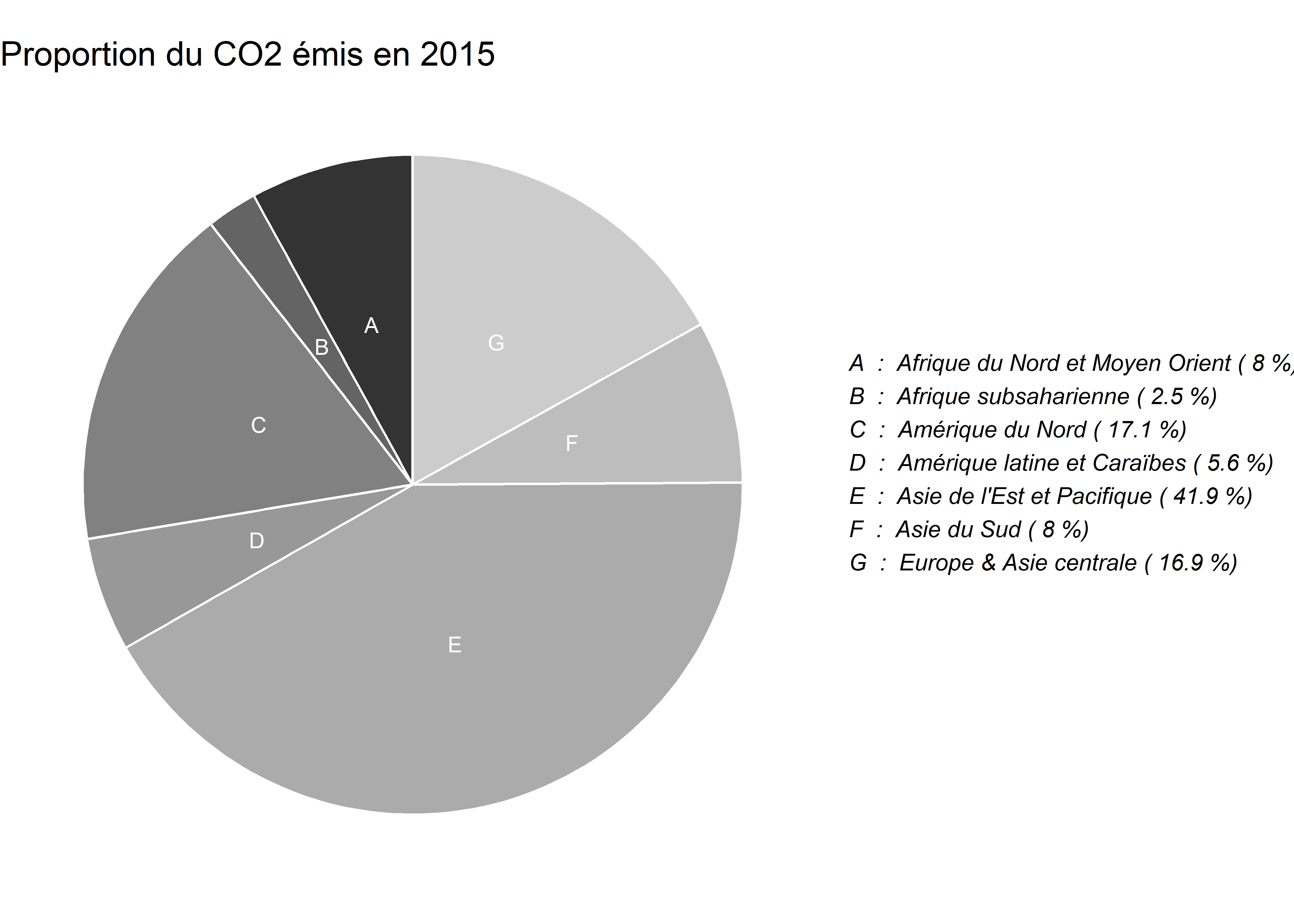
Figure 3.46: Graphique en tarte
Si à la place de la géométrie geom_bar, vous utilisez geom_rect, vous pouvez convertir votre graphique en tarte en graphique en anneau (ou en beigne, pour les personnes à la dent sucrée) :
# Calculer la limite inférieure et supérieure du beigne
df$ymax <- cumsum(df$prop)
df$ymin <- c(0, head(df$ymax, n=-1))
# Construire le graphique
plot1 <- ggplot(df, aes(ymax=ymax, ymin=ymin,
xmax=4, xmin=3,
y=prop, fill=code)) +
geom_rect(stat="identity", color="white") +
coord_polar("y", start=0) +
theme_void() +
theme(legend.position="none") +
geom_text(aes(x = 3.5,y = ypos, label = code), color = "white", size=3) +
scale_fill_grey()+
xlim(c(2,4))+
labs(title = "Proportion du CO2 émis en 2015")
# Ajouter la légende
annotate_figure(plot1,right = text_grob(string_region, face = "italic", size = 8,
just = "left", x = 0.05)) # position du texte)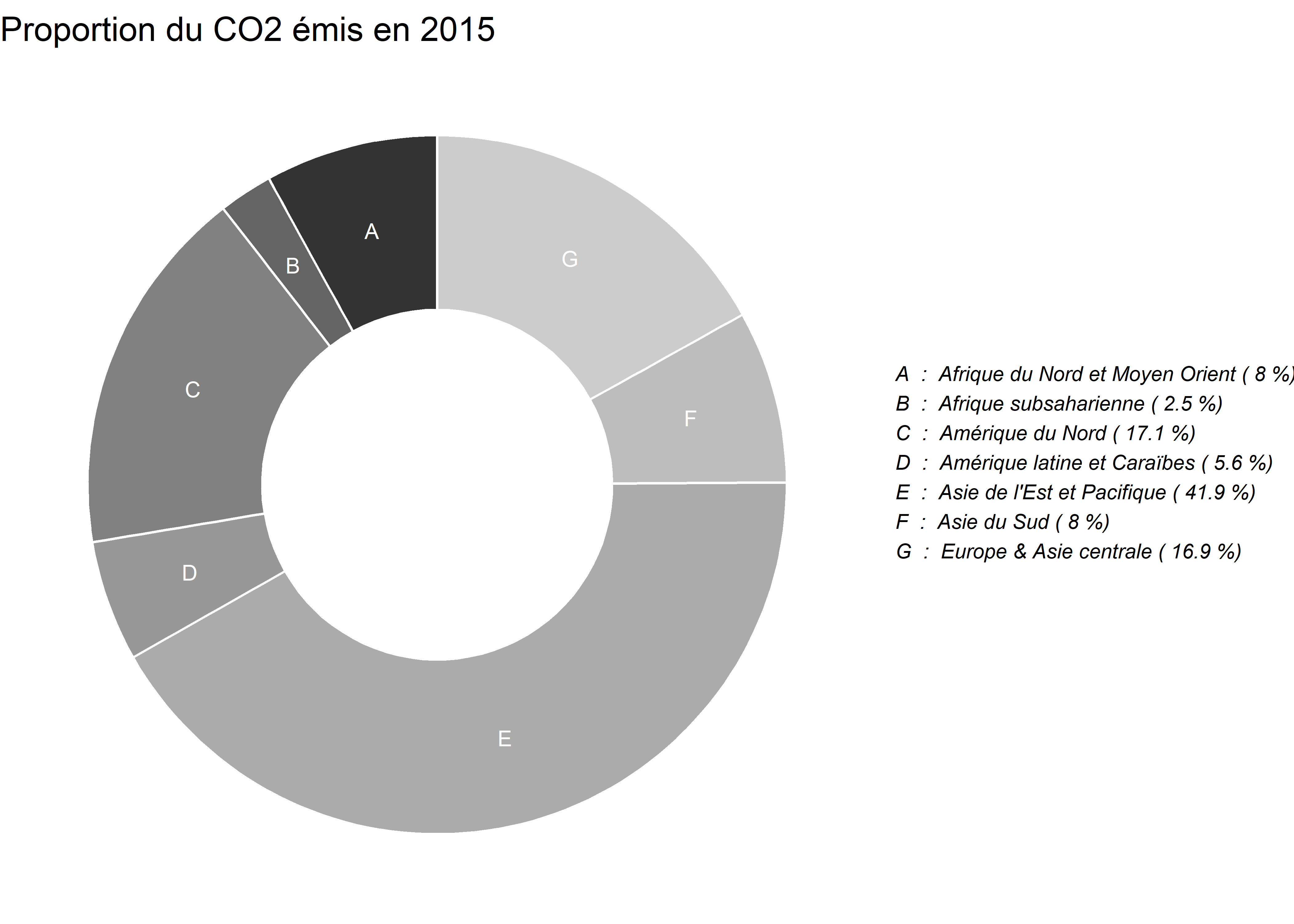
Figure 3.47: Graphique en anneau