13.2 Notions essentielles en classification
Avant de décrire différentes méthodes de classification non supervisées, il convient de définir deux notions centrales, soit la distance et l’inertie.
13.2.1 Distance
La distance en analyse de données est définie comme une fonction (d) permettant de déterminer à quel point deux observations sont semblables ou différentes l’une de l’autre. Elle doit respecter les conditions suivantes :
- la non-négativité : la distance minimale entre deux objets est égale à 0; \(d(x,y) \geq 0\).
- le principe d’identité des indiscernables : la distance entre deux objets \(x\) et \(y\) est égale à 0, si \(x = y\); \(d(x,y)=0\text{ si et seulement si }x=y\).
- la symétrie : la distance entre \(x\) et \(y\) est la même qu’entre \(y\) et \(x\); \(d(x,y) = d(y,x)\).
- le triangle d’inégalité : passer d’un point \(x\) à un point \(z\) est toujours plus court ou égal que de passer par \(y\) entre \(x\) et \(z\); \(d(x,z)\leq d(x,y)+d(y,z)\).
Il existe un grand nombre de types de distance qui peuvent être utilisés pour déterminer le degré de similarité entre les observations. Nous présentons ici les six types les plus fréquemment utilisés en sciences sociales, mais retenez qu’il en existe bien d’autres.
13.2.1.1 Distance euclidienne
Il s’agit vraisemblablement de la distance la plus couramment utilisée, soit la longueur de la ligne droite la plus courte entre les deux objets considérés. Pour la représenter, admettons que nous nous intéressons à trois classes d’étudiants et d’étudiantes A, B et C pour lesquelles nous avons calculé la moyenne de leurs notes dans les cours de méthodes quantitatives et qualitatives. Ces deux variables sont mesurées dans la même unité et varient de 0 à 100. Le nuage de points à la figure 13.4 illustre cette situation avec des données fictives.
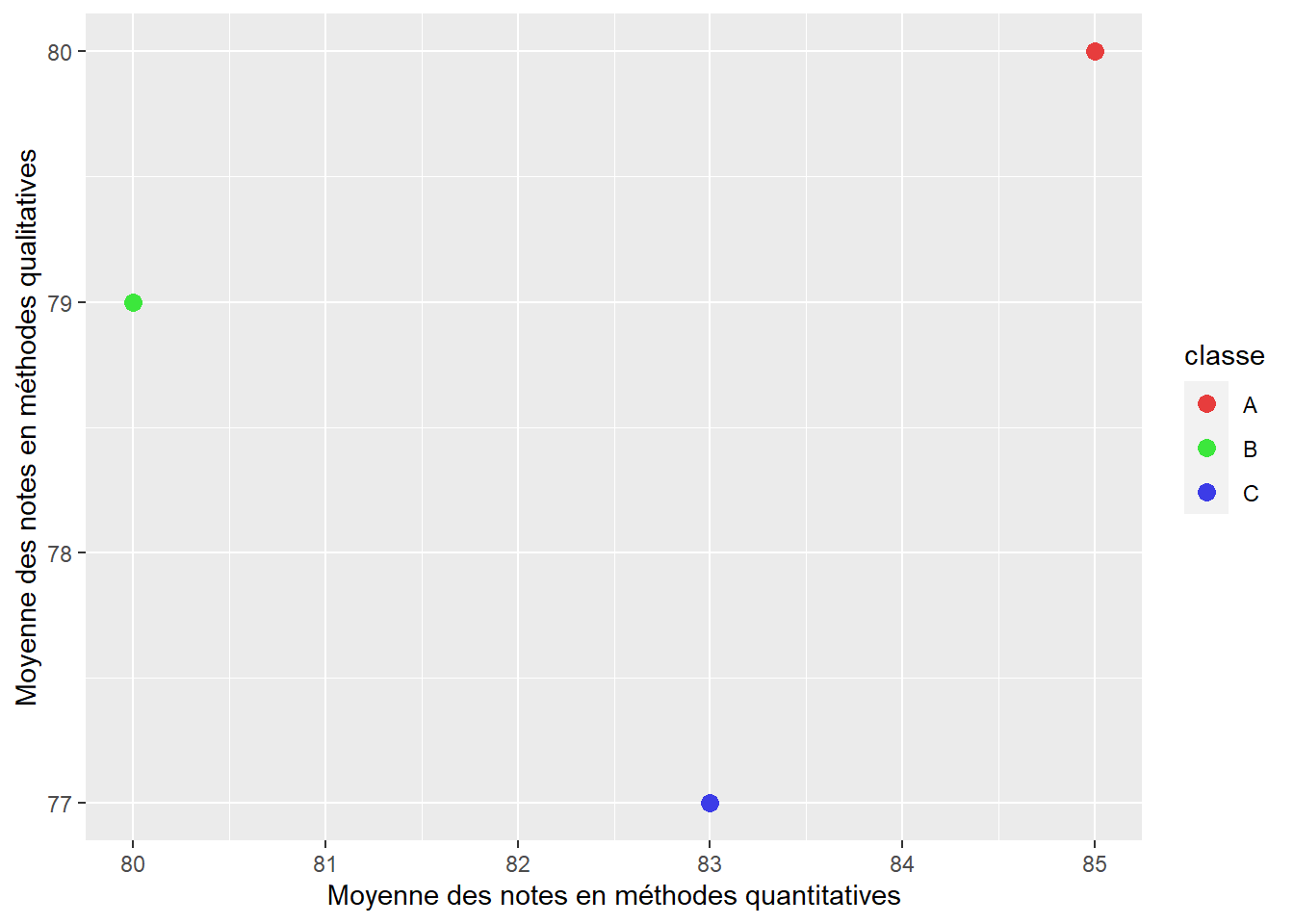
Figure 13.4: Situation de base pour le calcul de distance
Les distances euclidiennes entre les classes B et C et les classes C et A sont représentées par les lignes noires à la figure 13.5. Nous pouvons constater que la distance entre les classes C et B est plus petite que celle entre les classes A et C, ce qui signale que les deux premières se ressemblent davantage.
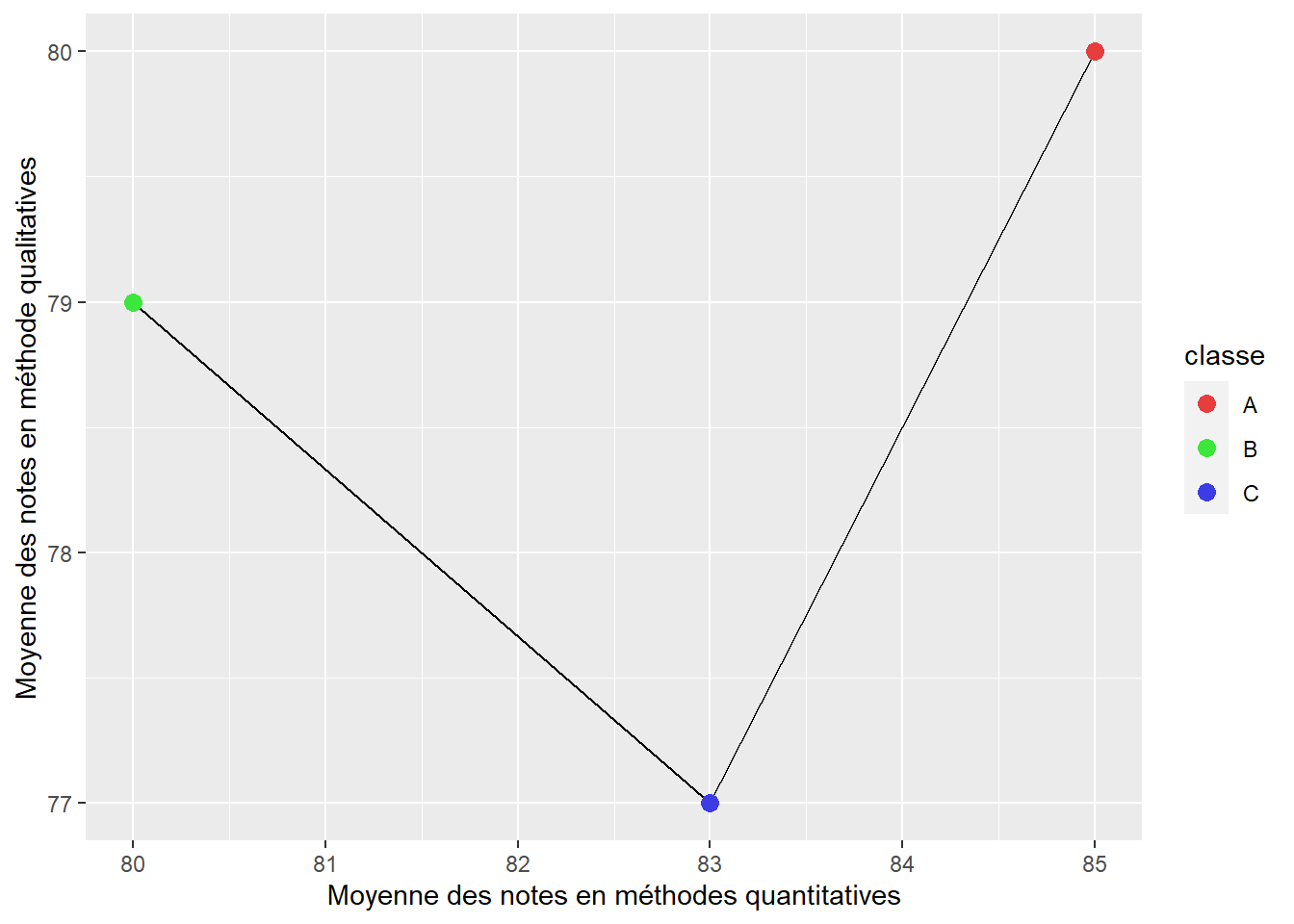
Figure 13.5: Représentation de la distance euclidienne
La formule de la distance euclidienne (équation (13.1)) est simplement la racine carrée de la somme des écarts au carré pour chacune des variables décrivant les observations a et b.
\[\begin{equation} d(a,b) = \sqrt{\sum{}^v_{i=1}(a_i-b_i)^2} \tag{13.1} \end{equation}\]
avec v le nombre de variables décrivant les observations a et b.
Nous pouvons facilement calculer la distance euclidienne pour notre jeu de données :
- \(d(A,B)=\sqrt{(\mbox{85}-\mbox{80})^2+(\mbox{80}-\mbox{77})^2} = \mbox{5,83}\)
- \(d(B,C)=\sqrt{(\mbox{80}-\mbox{83})^2+(\mbox{79}-\mbox{77})^2} = \mbox{3,60}\)
Distance et unité de mesure
Il est très important de garder à l’esprit que la distance entre deux observations dépend directement des unités de mesure utilisées. Cela est très souvent problématique, car il est rare que toutes les variables utilisées pour décrire des observations soient mesurées dans la même unité. Ainsi, une variable dont les valeurs numériques sont plus grandes risque de déséquilibrer les calculs de distance. À titre d’exemple, une variable mesurée en mètres plutôt qu’en kilomètres produit des distances euclidiennes 1000 fois plus grandes.
Il est donc nécessaire de standardiser les variables utilisées avant de calculer des distances. Cette opération permet de transformer les variables originales vers une échelle commune. Plusieurs types de transformations peuvent être utilisés tels que décrits à la section 2.5.5.2 :
- Le centrage et la réduction qui consistent à soustraire de chaque valeur sa moyenne, puis à la diviser par son écart-type. La nouvelle variable obtenue s’exprime alors en écart-type (appelé aussi score-z). La formule de la transformation est \(f(x) = \frac{x - \bar{x}}{\sigma_x}\), avec \(\bar{x}\) la moyenne de \(x\) et \(\sigma_x\) l’écart-type de \(x\).
- La transformation sur une mise à l’échelle de 0 à 1 qui permet de modifier l’étendue d’une variable afin que sa valeur maximale soit de 1 et sa valeur minimale soit de 0. La formule de cette transformation est \(f(x) = \frac{x-min(x)}{max(x)-min(x)}\).
- La transformation en rang qui consiste à remplacer les valeurs d’une variable par leur rang. La valeur la plus faible est remplacée par 1, et la plus forte par n (nombre d’observations). Notez que cette transformation modifie la distribution de la variable originale contrairement aux deux transformations précédentes. Cette propriété peut être désirable si les écarts absolus entre les valeurs ont peu d’importance, si la variable n’a pas été mesurée avec précision ou encore si des valeurs extrêmes sont présentes.
- La transformation en percentile qui consiste à remplacer les valeurs d’une variable par leur percentile correspondant. Elle peut être vue comme une standardisation de la transformation en rang, car elle ne dépend pas du nombre d’observations.
La figure 13.6 montre l’effet de ces transformations sur l’histogramme d’une variable.
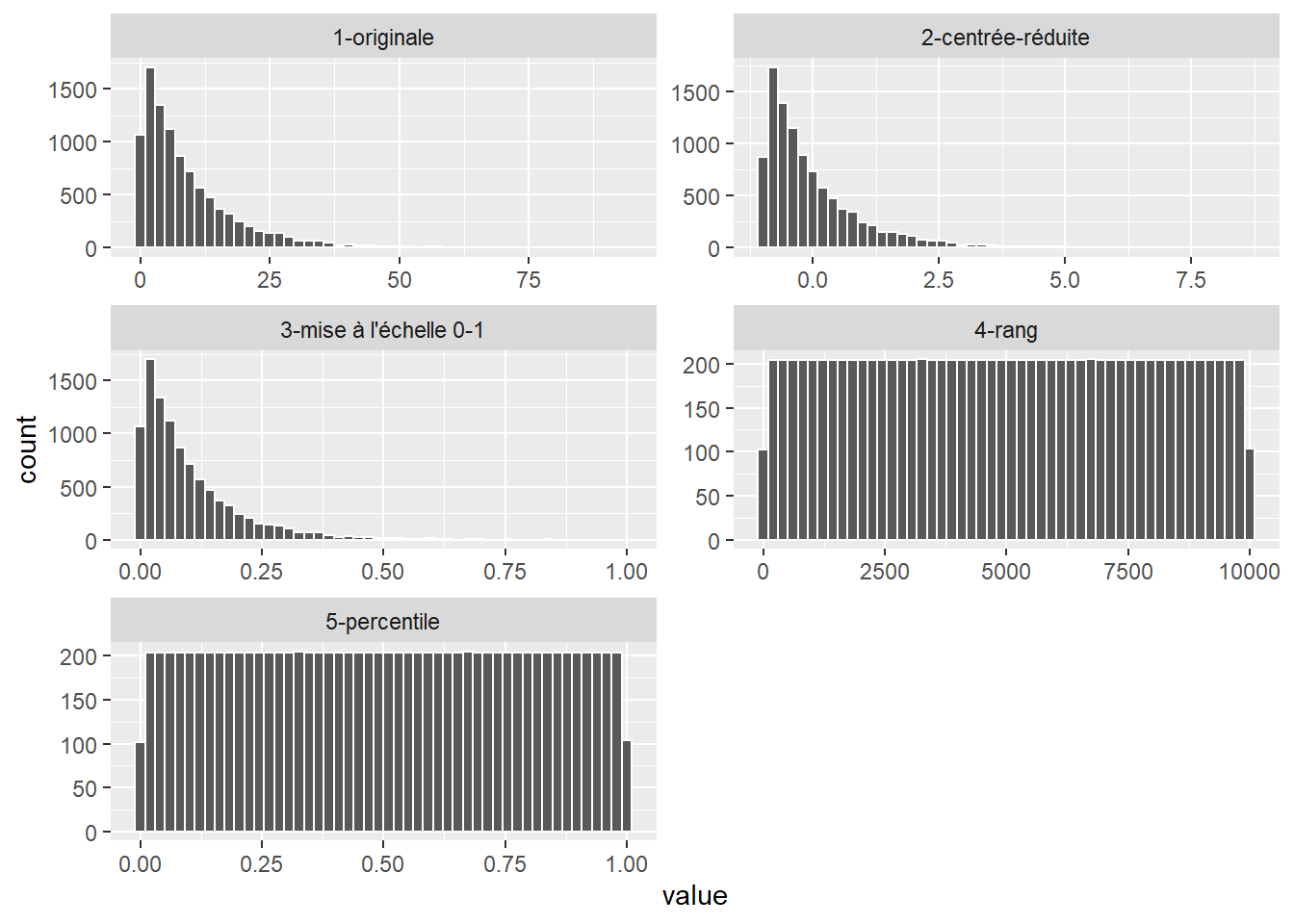
Figure 13.6: Effets de différentes transformations sur la distribution d’une variable
13.2.1.2 Distance de Manhattan
Cette seconde distance est également couramment utilisée. Elle doit son nom au réseau de rue de l’île de Manhattan qui suit un plan quadrillé. La distance de Manhattan correspond à la somme des écarts absolus entre les valeurs des différentes variables décrivant les observations (équation (13.2)). La figure 13.7 illustre que la distance Manhattan (lignes noires) représente les deux côtés opposés de l’hypoténuse d’un triangle rectangle; l’hypoténuse représentant quant à elle la distance euclidienne.
\[\begin{equation} d(a,b) = \sum{}^v_{i=1}(|a_i-b_i|) \tag{13.2} \end{equation}\]
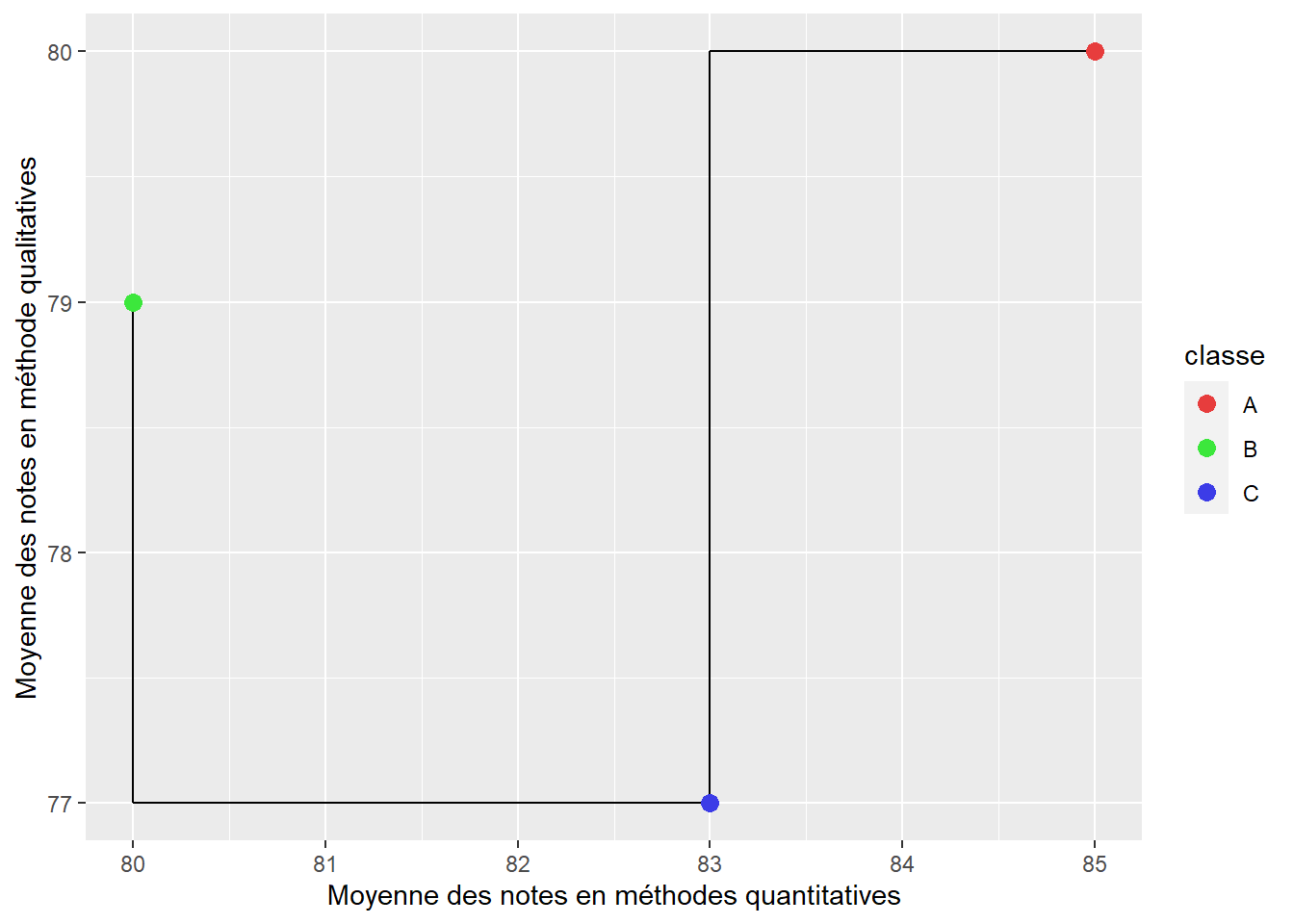
Figure 13.7: Représentation de la distance de Manhattan
La distance de Manhattan doit être privilégiée à la distance euclidienne lorsque les données considérées ont un très grand nombre de dimensions (variables). En effet, lorsque le nombre de variables est important (supérieur à 30), la distance euclidienne tend à être grande pour toutes les paires d’observations et à moins bien discriminer les observations proches et lointaines les unes des autres. Du fait de sa nature additive, la distance de Manhattan est moins sujette à ce problème (Aggarwal, Hinneburg et Keim 2001).
Calculons la distance de Manhattan pour nos deux paires d’observations :
- \(d(A,B)=|85-80|+|80-77| = 8\)
- \(d(B,C)=|80-83|+|79-77| = 5\)
13.2.1.3 Distance du khi-deux
La distance du khi-deux est basée sur le test du khi-deux (chapitre 5) et est généralement utilisée pour calculer la distance entre deux histogrammes, deux images ou deux ensembles de mots. Plus précisément, elle permet de mesure la distance entre deux observations A et B, pour lesquelles nous disposons d’un ensemble de variables étant toutes des variables de comptage.
Prenons un exemple concret en générant trois histogrammes A, B et C sur l’intervalle [0,50] à partir des distributions normale, log-normale et Gamma, puis comptons le nombre de valeurs de chaque unité (1, 2, 3, 4, etc.). Ces histogrammes sont représentés à la figure 13.8.
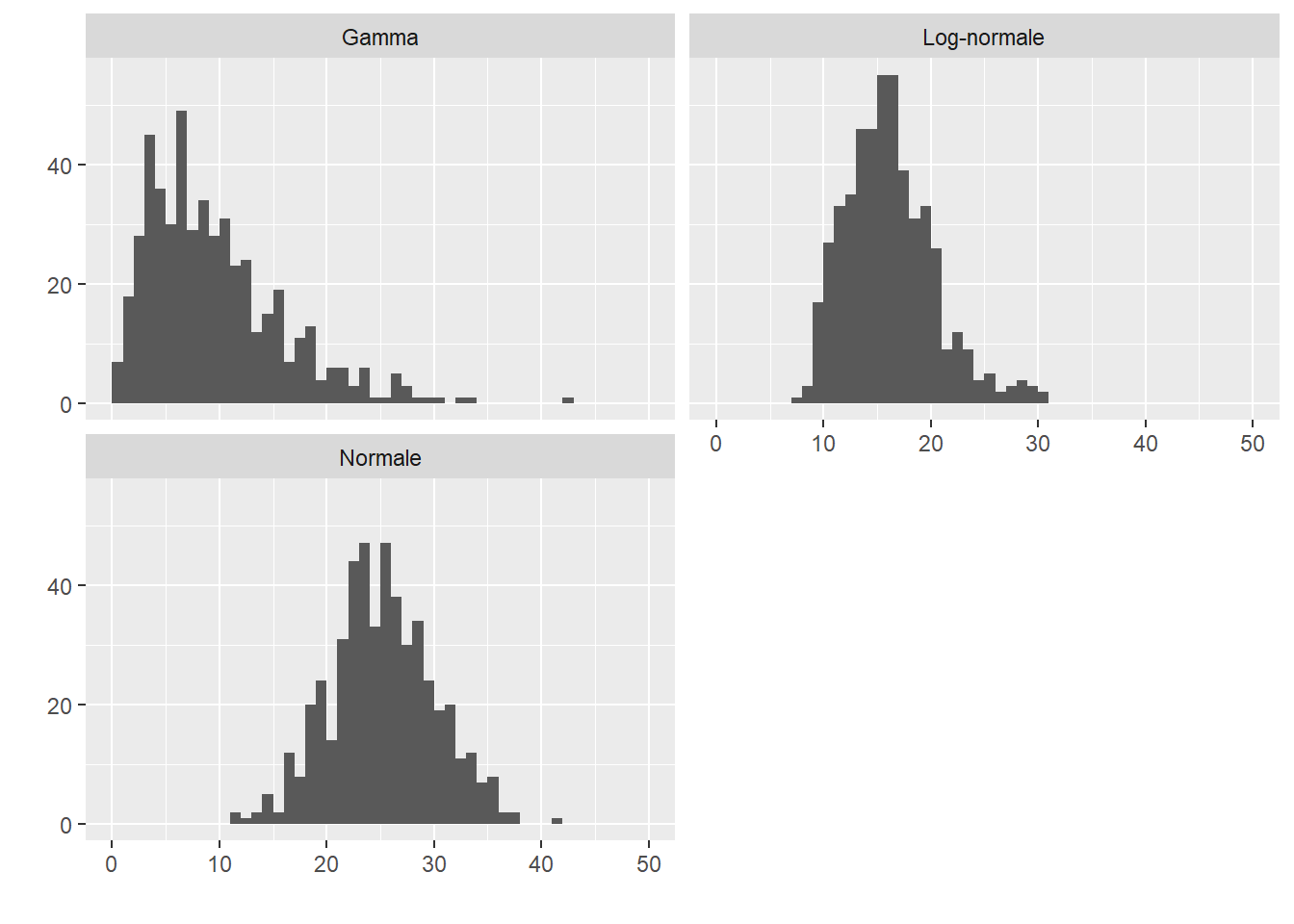
Figure 13.8: Trois histogrammes pour illustrer le calcul de la distance du khi-deux
Nous pouvons calculer les distances du khi-deux entre les paires d’histogrammes (tableau 13.1). Nous constatons ainsi que les histogrammes B et C sont les plus semblables.
| Histogrammes | Distance du khi-deux |
|---|---|
| A-B | 284,8375 |
| A-C | 376,7862 |
| B-C | 219,5133 |
La formule de cette distance est la suivante :
\[\begin{equation} d_{\chi^2}(a,b) = \frac{1}{2}\sum^n_{i=1}\frac{(a_i-b_i)^2}{(a_i+b_i)} \tag{13.3} \end{equation}\]
avec \(a_i\) et \(b_i\) les comptages pour les histogrammes. Notez que si \(a_i\) et \(b_i\) valent tous les deux 0, il faut retirer ces valeurs avant le calcul, car cela provoquerait une division par 0.
À première vue, cette distance peut paraître moins utile que les deux précédentes. Pourtant, de nombreuses données sont collectées comme des histogrammes. Un premier exemple serait des images que nous pouvons représenter sous forme de trois histogrammes, un pour chaque canal de couleur (rouge, vert et bleu). Un second exemple serait des données sonores, souvent synthétisées sous forme d’histogrammes des fréquences sonores enregistrées (octaves ou tiers d’octaves). Un dernier exemple pourrait être le nombre d’accidents de la route enregistré à diverses intersections d’une ville chaque heure. Dans ce contexte, un histogramme serait formé par l’intersection avec les heures de la journée comme limites des bandes et le nombre d’accidents comme hauteur des bandes.
13.2.1.4 Distance de Mahalanobis
Proposée dans les années 1930 par le statisticien indien Prasanta Chandra Mahalanobis (1936), cette distance se base sur la matrice de covariance des variables analysées. Plus spécifiquement, elle est utilisée pour calculer la distance entre un point et une distribution normale multivariée. Elle permet notamment de tenir compte du fait que certaines variables sont corrélées et ainsi d’éviter de surestimer les distances entre des observations dans des jeux de données comprenant des variables corrélées entre elles.
La formule permettant de calculer cette distance est la suivante :
\[\begin{equation} d(a,b) = \sqrt{(a-b)^TS^{-1}(a-b)} \tag{13.4} \end{equation}\]
avec S étant la matrice de covariance.
13.2.1.5 Distance de Hamming
Cette distance est utilisée quand les écarts entre les variables de deux observations sont uniquement binaires. Un bon exemple serait un jeu de données ne comprenant que des variables qualitatives pouvant avoir une valeur identique pour deux observations (distance = 0) ou différente (distance = 1). La distance de Hamming est la simple addition de ces écarts.
Prenons un exemple très simple en prenant trois maisons pour lesquelles nous connaissons cinq caractéristiques 13.2).
| couleur | jardin | garage | cheminée | sous-sol |
|---|---|---|---|---|
| blanc | non | oui | oui | non |
| blanc | non | non | oui | non |
| rouge | oui | oui | non | oui |
Nous pouvons utiliser la distance de Hamming pour estimer le niveau de dissimilarité entre ces différentes maisons et l’organiser dans une matrice de distances. À la lecture du tableau 13.3), les maisons 2 et 3 sont les plus dissimilaires (distance de Hamming = 5), et les maisons 1 et 2 les plus similaires (distance de Hamming = 1).
| maison 1 | maison 2 | maison 3 | |
|---|---|---|---|
| maison 1 | 0 | 1 | 4 |
| maison 2 | 1 | 0 | 5 |
| maison 3 | 4 | 5 | 0 |
13.2.1.6 Distance de Gower
La distance de Gower (1971) peut être utilisée pour mesurer la distance entre deux observations lorsque les données sont à la fois qualitatives et quantitatives. Cette distance est comprise dans un intervalle de 0 à 1, 0 signifiant que les deux observations sont identiques et 1, que les observations sont radicalement différentes.
Elle se calcule de la façon suivante :
\[\begin{equation} \begin{aligned} &d(a,b) = 1-\frac{1}{p}\sum^p_{j=1}s_{12j}\\ &\left\{\begin{array}{c} s_{xyj} = 1 \text{ si } x_j = y_j \text{, 0 autrement pour une variable qualitative} \\ s_{xyj} = 1 - \frac{|x_j-y_j|}{max(j)-min(j)} \text{ pour une variable quantitative} \end{array}\right. \end{aligned} \tag{13.5} \end{equation}\]
avec p le nombre de variables, x et y deux observations et j une variable.
Autrement dit, si la valeur d’une variable qualitative diffère entre deux observations, la distance entre ces deux observations augmente de \(1/p\). Pour une variable quantitative, la distance augmente selon la différence absolue entre les valeurs de la variable divisée par l’étendue totale de la variable, le tout à nouveau divisé par p.
Si cette mesure semble intéressante puisqu’elle permet de combiner des variables quantitatives et qualitatives, elle souffre de deux limites importantes :
- Elle ne prend pas en compte le fait que certaines modalités des variables qualitatives sont moins fréquentes ni que certaines combinaisons sont également moins fréquentes.
- Les variables qualitatives tendent à affecter bien plus la distance que les variables quantitatives. En effet, pour obtenir un écart de 1 sur une variable quantitative, il faut que les deux valeurs soient respectivement le maximum et le minimum de cette variable.
D’autres distances pour des données mixtes
Il existe bien d’autres distances qui peuvent être utilisées dans le cas de données mixtes. Le package kmed en implémente cinq (auxquelles s’ajoute la distance de Gower) dans sa fonction distmix : les distances de Wishart, de Podani, d’Huang, d’Harikumar et d’Ahmad. Ces différentes distances ont toutes leurs avantages et leurs défauts respectifs; pour plus d’information, référez-vous à la documentation de la fonction distmix.
13.2.1.7 Distance du Phi2
La distance du \(\Phi^2\) (Phi2) est une variante de la distance du \(\chi^2\). Il s’agit donc d’une distance à utiliser lorsque les données à analyser sont uniquement qualitatives. Elle calcule la distance entre deux observations en additionnant les différences entre les valeurs de chaque variable (1 si différentes, 0 si identiques, pour chaque variable), divisées respectivement par la fréquence totale d’occurrences de chaque modalité dans le jeu de données. En d’autres termes, cette distance tient compte du fait que certaines valeurs pour des variables qualitatives peuvent être observées plus fréquemment que d’autres et qu’une distance plus grande devrait être obtenue entre deux observations si l’une des deux présente des modalités rares comparativement au reste du jeu de données.
Elle peut être calculée de la façon suivante :
\[\begin{equation} d_{\Phi^2}(i,j) = \frac{1}{Q}\sum_k\frac{(\delta_{ik} - \delta_{jk})^2}{f_k} \tag{13.6} \end{equation}\]
avec i et j deux observations, k une modalité d’une variable qualitative, Q le nombre total de modalités des variables qualitatives, \(\delta_{ik} = 1\) si l’observation i a la modalité k, 0 sinon et \(f_k\) la fréquence de la modalité k dans le jeu de données.
La distance du \(\Phi^2\) est très utile pour analyser les résultats de questionnaires.
13.2.2 Inertie
Une notion importante à saisir dans le cadre des méthodes de classification non supervisée est celui celle l’inertie d’un jeu de données. Elle est proche de la notion de variance qui a été présentée dans le chapitre sur la statistique univariée (section 2.5.3).
L’inertie est une quantité permettant de décrire la dispersion des observations d’un jeu de données. Cette mesure dépend à la fois des données (nombres d’observations et de variables, échelle des variables) et de la mesure de distance retenue entre deux observations. Plus spécifiquement, l’inertie correspond à la somme des distances entre chaque observation et le centre du jeu de données.
\[\begin{equation} inertie= \sum{}^n_{i=1} d(c,x_i) \tag{13.7} \end{equation}\]
avec c le centre du jeu de données, n le nombre d’observations, x une observation et d la fonction calculant la distance entre deux observations.
L’enjeu est de définir c dans un contexte où la distance euclidienne est utilisée. Il s’agit simplement d’une observation fictive dont les coordonnées sont les moyennes des différentes variables du jeu de données. Dans le cas d’autres distances, il peut s’agir de l’observation minimisant la distance à toutes les autres observations.
Pour bien visualiser la notion d’inertie, prenons une fois encore le jeu de données IRIS comme exemple. Admettons que nous ne nous intéressons qu’à deux variables de ce jeu de données : sepal.Length et sepal.Width. Nous pouvons représenter l’inertie totale du jeu de données à la figure 13.9.
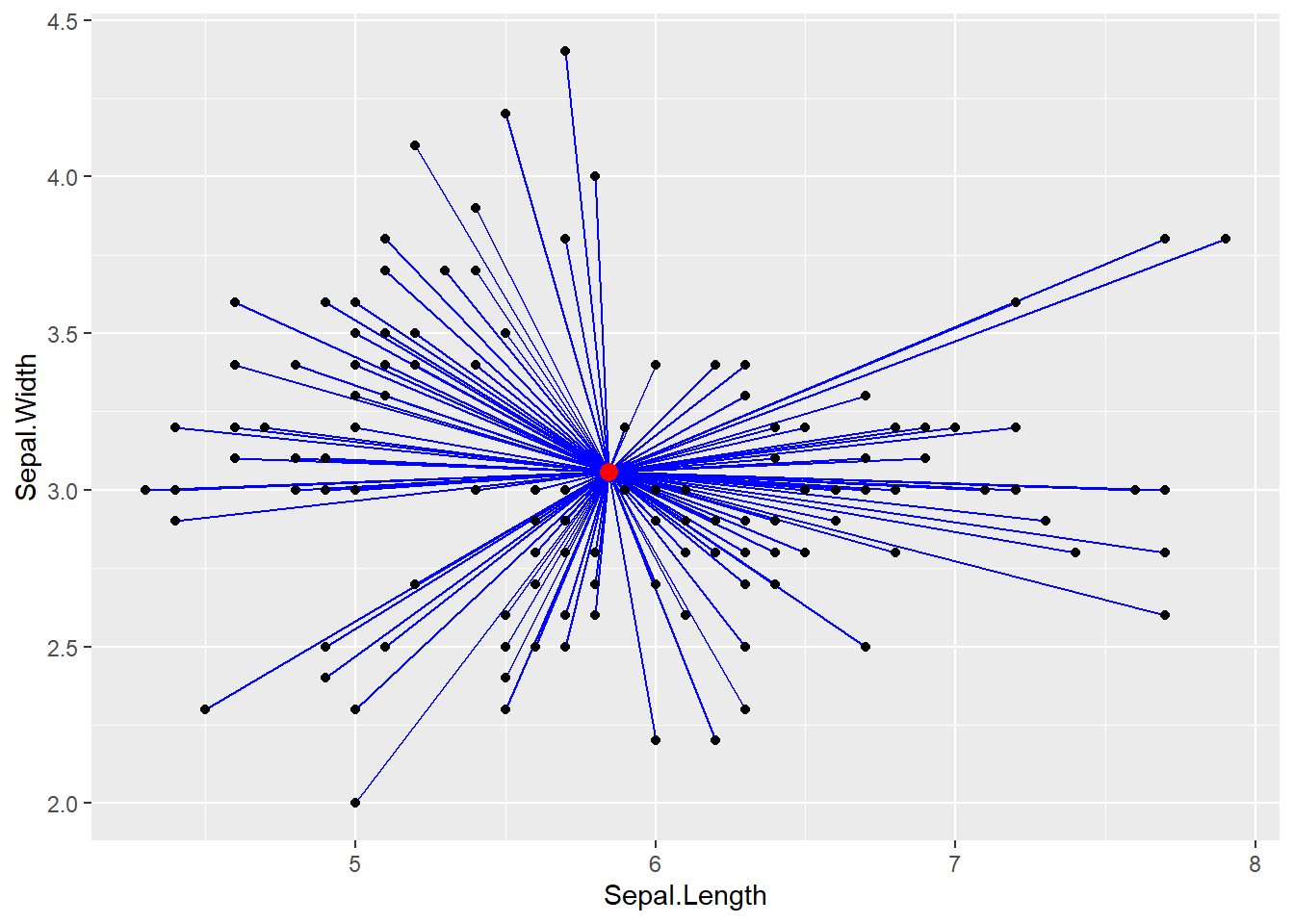
Figure 13.9: Représentation de l’inertie du jeu de données IRIS
Chaque ligne bleue représente la contribution de chaque point à l’inertie totale du jeu de données. Pour chaque iris, nous connaissons son espèce (Setosa, Versicolor ou Virginica). Nous pouvons donc attribuer chaque point de ce jeu de données à un groupe (une espèce dans notre cas). Il devient alors possible de calculer l’inertie de chacun des sous-groupes de notre jeu de données. Pour cela, nous devons calculer le centre de chaque groupe (généralement les moyennes des variables des observations au sein d’un groupe) et ensuite calculer l’inertie entre chaque observation et le centre de son groupe. Nous représentons cette situation à la figure 13.10.
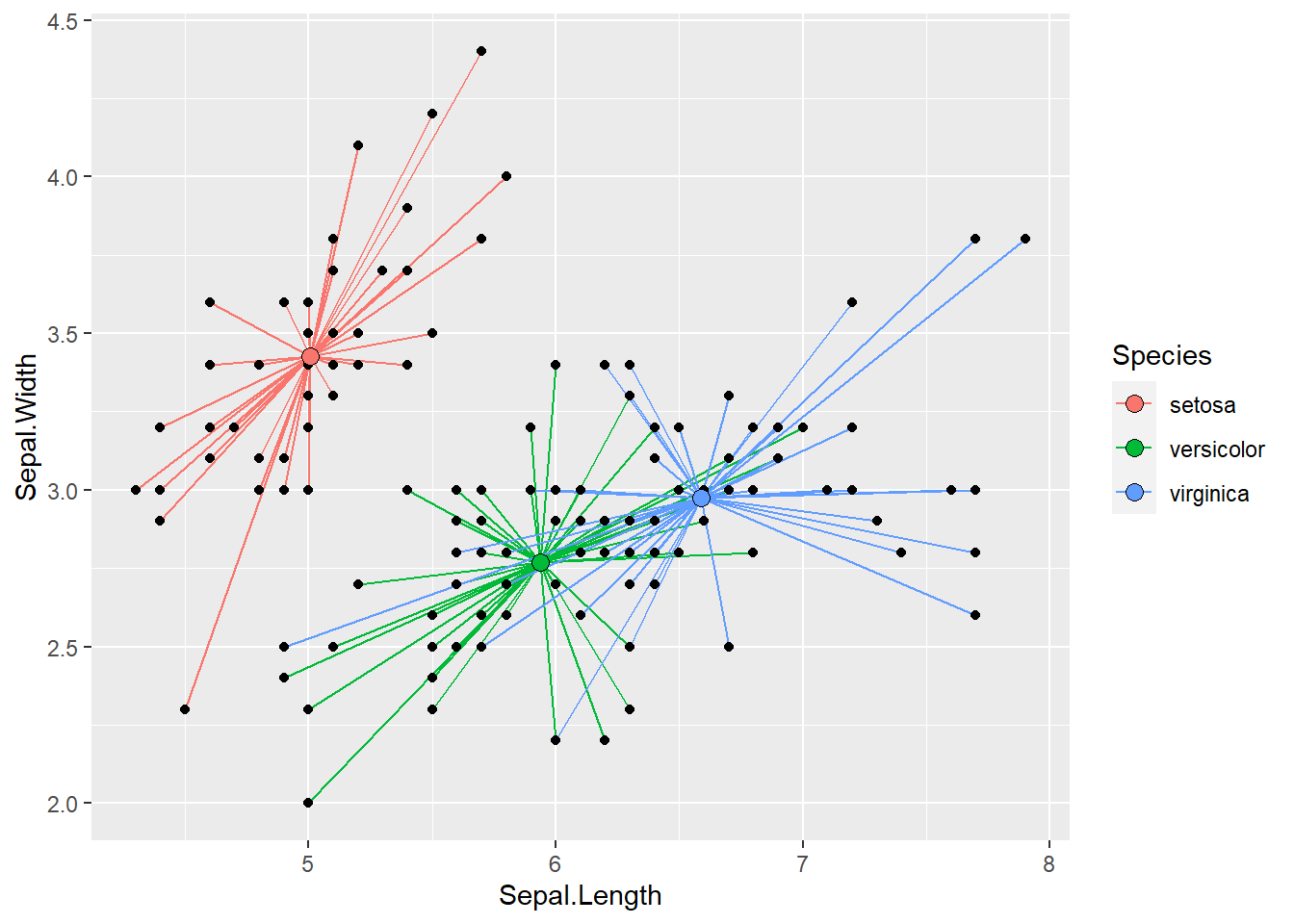
Figure 13.10: Représentation de l’inertie par groupe pour le jeu de données IRIS
Cette inertie propre aux groupes est toujours inférieure ou égale à l’inertie totale du jeu de données. Il s’agit en réalité de l’inertie que la structure de groupe n’est pas en mesure d’expliquer. En utilisant ces concepts, il est possible de calculer la part de l’inertie totale expliquée par les groupes (équation (13.8)) :
\[\begin{equation} \text{inertie expliquée} = 1-\frac{\text{inertie totale}}{\text{inertie restante}} \tag{13.8} \end{equation}\]
Cette valeur nous renseigne sur la capacité d’une classification à bien réduire l’inertie totale d’un jeu de données. Elle est comprise entre 0 et 1. Si l’inertie expliquée est à 0, c’est que la classification n’explique absolument aucune part de l’inertie totale. Si l’inertie expliquée est à 1, la classification utilisée explique l’intégralité de l’inertie, ce qui en pratique n’est atteignable que si le nombre de groupes de la classification est égal au nombre d’observations. En d’autres termes, chaque observation est attribuée à un groupe dont elle est la seule représentante. Un telle situation n’a aucun intérêt puisque l’objectif d’une classification est bien de réduire la complexité d’un jeu de données en regroupant les observations.