3.3 Graphiques spéciaux

Dans cette dernière section, nous abordons des graphiques plus rarement utilisés. Ils sont toutefois très utiles dans certains contextes du fait de leur capacité à synthétiser des informations complexes.

3.3.1 Graphique en radar

Les graphiques en radar (ou en toile d’araignée) sont utilisés pour comparer une série de variables continues pour plusieurs observations ou groupes d’observations. Chaque variable est associée à un axe et chaque observation est représentée avec un polygone. Prenons l’exemple de données relatives aux logements par secteur de recensement dans la région métropolitaine de Montréal en 2016. Nous pourrions souhaiter comparer la moyenne des pourcentages des différents types de logements pour les régions des Laurentides, de la Montérégie, de Laval, de Longueuil et de Montréal. Malheureusement, ggplot2 ne permet pas de dessiner des graphiques en radar satisfaisants, nous devons donc utiliser le package fmsb.

library(fmsb)

data <- read.csv('data/bivariee/sr_rmr_mtl_2016.csv', header = T, encoding = 'UTF-8')

# Agréger les données au niveau des régions en calculant la moyenne des pourcentages
variables <- c("MaisonIndi","App5Plus","MaisRangee","AppDuplex","Proprio","Locataire")

data_region <- data[c("Region",variables)] %>% 
  group_by(Region) %>%
  summarise_all(.funs = list(mean))

# Gérer le nom des colonnes pour ajuster les données aux besoins de 
# la fonction radachart
new_names <- c("Region",paste(variables,"_mean",sep=""))
names(data_region) <- new_names
data_region <- data.frame(data_region)
rownames(data_region) <- data_region$Region
data_region$Region <- NULL

# Ajouter deux lignes aux données avec les valeurs maximales et minimales 
# de chaque colonne. Ces informations aideront la fonction radachart à
# dessiner chacun des axes du radar
data_chart <- rbind(apply(data_region,MARGIN = 2, FUN = max),
                    apply(data_region,MARGIN = 2, FUN = min),
                    data_region
                    )

# Choisir les couleurs pour l'intérieur des polygones (avec transparence)
couleurs <- c(
  rgb(0.94, 0.28, 0.44, 0.25),
  rgb(1.00, 0.82, 0.40, 0.25),
  rgb(0.02, 0.84, 0.63, 0.25),
  rgb(0.07, 0.54, 0.70, 0.25),
  rgb(0.03, 0.23, 0.30, 0.25)
)

# Choisir les couleurs pour l'intérieur des polygones (sans transparence)
couleurs_contour <- c(
  rgb(0.94, 0.28, 0.44),
  rgb(1.00, 0.82, 0.40),
  rgb(0.02, 0.84, 0.63),
  rgb(0.07, 0.54, 0.70),
  rgb(0.03, 0.23, 0.30)
)

# Dessiner du graphique
radarchart(data_chart,
           title = "Comparaison des types de logements dans la RMR",
           pcol = couleurs_contour, pfcol = couleurs,
           plwd = 2, plty=1,
           cglcol="grey", cglty=1, axislabcol="grey", cglwd=0.8,
           vlcex=0.8,
           vlabels = c("maison individuelle", "immeuble d'appartements",
                       "maison \nen rangée", "duplex",
                       "propriétaire", "locataire")
           )

# Ajouter une légende
legend(x=1.3, y=1, legend = rownames(data_chart[-c(1,2),]), bty = "n", 
       pch=20 , col=couleurs , text.col = "black", cex=0.9, pt.cex=1.5)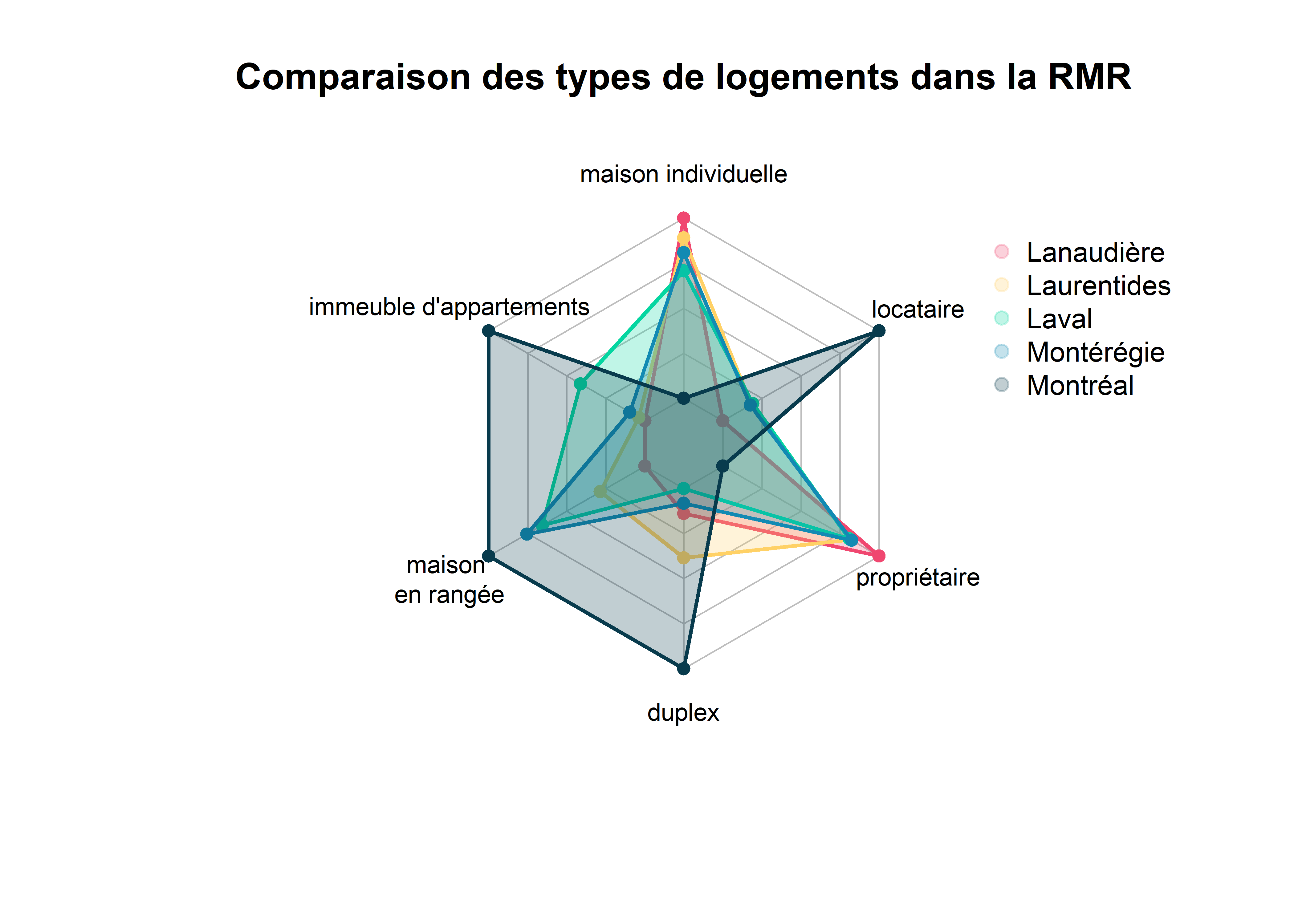
Graphique en anneau

Figure 3.48: Graphique en anneau

À la lecture du graphique, nous constatons rapidement que l’île de Montréal a une situation très différente des trois autres régions. Laval se distingue également avec une part importante de logements dans des immeubles d’appartements. Ce type de graphique a pour objectif d’orienter le regard sur de potentielles différences dans un contexte multidimensionnel, mais il présente quelques inconvénients :

  • Les échelles de chaque axe sont différentes. Il est donc essentiel de se rapporter aux valeurs exactes pour estimer si les écarts sont importants en termes absolus.
  • La superposition de plusieurs polygones peut rendre la lecture difficile. Une solution envisageable est de réaliser un graphique par polygone, mais cela prend beaucoup de place dans un document.
  • L’utilisation de polygones donne parfois de fausses impressions d’écarts. Dans le précédent graphique, l’œil est attiré en bas à gauche par le polygone de Montréal qui est très différent des autres. Cependant, les écarts sur l’axe maison en rangée sont relativement petits comparativement à l’axe locataire situé à l’opposé.

3.3.2 Diagramme d’accord

Les diagrammes d’accord (chord diagram en anglais) sont utilisés pour représenter des échanges ou des connexions entre des entités. Il peut s’agir par exemple de marchandises importées / exportées entre pays, des messages envoyés entre personnes via un réseau social, de flux de population, etc. Reprenons nos données de l’Enquête origine-destination 2017 - Région Québec-Lévis pour illustrer le tout. Nous utilisons le package chorddiag, très facile d’utilisation et produisant des graphiques interactifs, pour faciliter grandement la lecture de ce type de graphique. Cependant, ce package ne fait pas partie du répertoire CRAN, nous devons l’installer directement depuis github avec la fonction devtools::install_github.

devtools::install_github('mattflor/chorddiag')
library(chorddiag)

# Chargement des données
matriceOD <- read.csv('data/graphique/Quebec_2017_OD_MJ.csv',
                 header = FALSE, sep = ';') # fichier csv sans entête

# Transformation du DataFrame en matrice
matriceOD <- as.matrix(matriceOD)
codes <- c('A','B','C','D','E','F','G','H','I','J','K','X')
secteurs <- c('Arr. de Beauport',
            'Arr. de Charlesbourg',
            'Arr. des Rivières',
            'Arr. de la Cité-Limoilou',
            'Arr. de la Haute-St-Charles',
            'Arr. de Sainte-Foy-Sillery-Cap-Rouge',
            'Arr.de Desjardins',
            'Arr. des Chutes–de-la-Chaudière-Est',
            'Arr. Les Chutes de la-Chaudière-Ouest',
            'Ceinture Nord',
            'Ceinture Sud',
            'Hors Territoire')

# Ajout de noms aux colonnes et aux lignes de la matrice
rownames(matriceOD) <- secteurs
colnames(matriceOD) <- secteurs

# Nous supprimons les trois secteurs Ceinture Nord, Sud et Hors territoire 
# qui comprennent de toute façon peu de déplacements
mat <- matriceOD[1:8,1:8]

# Choix aléatoire de couleurs pour les lignes
# col <- sample(colors(),nrow(mat),replace = F)

# Choix de couleurs 
col <- c("#a491d3", "#818aa3", "#C5DCA0", "#F5F2B8",
         "#F9DAD0", "#F45B69", "#22181C", "#5A0001")

# Réalisation du graphique : sortie HTLM
if(knitr::is_html_output()){
  chorddiag(mat, groupColors = col, showTicks = F,
        type = 'bipartite', chordedgeColor = 'white',
        groupnameFontsize = 12, groupnamePadding = 5)
}

Figure 3.49: Diagramme d’accord 

# Pour la sortie PDF
if(knitr::is_latex_output()){
  knitr::include_graphics('images/magie_graphiques/chord_diagramme.png', dpi = NA)
}

Le graphique permet de remarquer que la plupart des flux s’effectuent au sein d’un même secteur. La majorité des déplacements se font au sein du secteur Sainte-Foy (segment rouge central). Nous pouvons cependant constater que les secteurs des Rivières, de la Cité-Limoilou et de la Haute-Saint-Charles attirent une plus grande quantité et diversité de flux. Si vous lisez ce livre dans un navigateur web (et pas au format pdf), le graphique est interactif! En plaçant votre souris sur un lien, vous verrez s’afficher le nombre de déplacements qu’il représente.

3.3.3 Nuage de mots

Un nuage de mots est un graphique utilisé en analyse de texte pour représenter les mots les plus importants d’un document. Mesurer l’importance des termes dans un document est une discipline à part entière (Natural Language Processing). Nous proposons un simple exemple ici avec la méthode TextRank (basée sur la théorie des graphes) proposée par Mihalcea et Tarau (2004) et implémentée dans le package textrank. Nous avons également besoin des packages udpipe (fournissant des dictionnaires linguistiques), RColorBrewer (pour sélectionner une palette de couleurs) et wordcloud2 (pour générer le graphique). En guise d’exemple, nous avons choisi d’extraire les textes de deux schémas d’aménagement et de développement (SAD), ceux des agglomérations de Québec et de Montréal en vigueur en 2020. Il s’agit de deux documents de planification définissant les lignes directrices de l’organisation physique du territoire des municipalités régionales de comté (MRC) ou des agglomérations. Pour ces deux documents, nous nous concentrons sur le chapitre portant sur les grandes orientations d’aménagement et de développement, soit les pages 30 à 135 pour Québec et 30 à 97 pour Montréal. Pour extraire les textes des fichiers pdf, nous utilisons le package pdftools.

Nous devons donc réaliser les étapes suivantes pour produire le nuage de mots :

  1. Extraire les sections qui nous intéressent des fichiers pdf.
  2. Extraire le texte de ces sections.
  3. Retirer les caractères représentant les sauts de lignes et les sauts de paragraphes (\n et \r).
  4. Concaténer tout le texte en une seule longue chaîne de caractère.
  5. Utiliser un dictionnaire pour déterminer la nature des mots du texte (nom, adjectif, verbe, etc.).
  6. Utiliser l’algorithme TextRank pour identifier les mots clefs.
  7. Nettoyer les erreurs potentielles parmi les mots clefs.
  8. Construire le nuage de mots.

Notez que toutes ces étapes de nettoyage ne seraient pas nécessaires si nous utilisions un simple fichier texte comme point de départ. Cependant, comme il est plus courant de rencontrer des fichiers pdf, cet exercice est donc davantage révélateur de la difficulté réelle de la réalisation d’un nuage de mots.

library(wordcloud2)
library(udpipe)
library(RColorBrewer)
library(pdftools)
library(textrank)

# Étape 1 : extraire les sections pertinentes des fichiers pdf
extrait_qc <- pdf_subset("data/graphique/SAD_quebec.pdf", pages = c(30:135),
                         output = "data/graphique/SAD_quebec_ext.pdf")
extrait_mtl <- pdf_subset("data/graphique/SAD_montreal.pdf", pages = c(30:97),
                          output = "data/graphique/SAD_montral_ext.pdf")

# Étape 2 : extraire le texte des fichiers pdf sous forme de vecteur de texte
file_qc <- pdf_text(extrait_qc)
file_mtl <- pdf_text(extrait_mtl)

# Étape 3 : retirer les sauts de lignes et les paragraphes
file_qc <- gsub("\r","",x = file_qc)
file_qc <- gsub("\n","",x = file_qc)

file_mtl <- gsub("\r","",x = file_mtl)
file_mtl <- gsub("\n","",x = file_mtl)

# Étape 4 : créer une seule longue chaîne de caractères
# à partir des vecteurs de texte
text_qc <- paste(file_qc, collapse = " ")
text_mtl <- paste(file_mtl, collapse = " ")

# charger le modèle linguistique français
model <- udpipe_load_model('data/graphique/french-sequoia-ud-2.4-190531.udpipe')

# pour télécharger le modèle si ce n'est pas encore fait : 
# model <- udpipe_download_model("french-sequoia")
# model <- udpipe_load_model(model)

# Étape 5 : analyse de la nature des mots du texte avec le dictionnaire fr
# Nous obtenons des DataFrames décrivant les mots des textes
annote_qc <- udpipe_annotate(model, text_qc)
df_qc <- data.frame(annote_qc)

annote_mtl <- udpipe_annotate(model, text_mtl)
df_mtl <- data.frame(annote_mtl)

# Étape 6 : utilisation de la méthode TextRank
stats_qc <- textrank_keywords(df_qc$lemma,
                  relevant = df_qc$upos %in% c("NOUN", "ADJ"), ngram_max=2)

stats_mtl <- textrank_keywords(df_mtl$lemma,
                  relevant = df_mtl$upos %in% c("NOUN","ADJ"), ngram_max=2)

# Étape 7 : nettoyer les coquilles dans les mots clefs 
# Note : nous faisons ici le choix de garder des mots clefs uniques (ngram == 1)
# Il serait aussi possible de garder des associations de plusieurs mots
dfstats_qc <- subset(stats_qc$keywords, stats_qc$keywords$ngram == 1 &
                       nchar(stats_qc$keywords$keyword)>2)
dfstats_qc$keyword <- gsub("d’","",dfstats_qc$keyword,fixed = T)
dfstats_qc$keyword <- gsub("l’","",dfstats_qc$keyword,fixed = T)

dfstats_mtl <- subset(stats_mtl$keywords, stats_mtl$keywords$ngram == 1 &
                        nchar(stats_mtl$keywords$keyword)>2)
dfstats_mtl$keyword <- gsub("d’","",dfstats_mtl$keyword,fixed = T)
dfstats_mtl$keyword <- gsub("l’","",dfstats_mtl$keyword,fixed = T)

# Étape 8 : réaliser les nuages de mots
couleurs <- sample(brewer.pal(12, "Paired")) # mise en désordre des couleurs

wordcloud2(data = dfstats_mtl[c("keyword", "freq")],
           color = couleurs, size = 0.5, shuffle = F)

wordcloud2(data = dfstats_qc[c("keyword", "freq")],
           color = couleurs, size = 0.6, shuffle = F)
Nuage de mots pour le SAD de Montréal

Figure 3.50: Nuage de mots pour le SAD de Montréal

Nuage de mots pour le SAD de Québec

Figure 3.51: Nuage de mots pour le SAD de Québec

Notez qu’à chaque génération du nuage de mots, vous obtiendrez une disposition différente. N’hésitez pas à en essayer plusieurs jusqu’à ce que vous trouviez celle qui vous semble optimale.

3.3.4 Carte proportionnelle

Une carte proportionnelle ou carte à cases (treemap en anglais) est un graphique permettant de représenter une quantité partagée entre plusieurs observations structurées dans une hiérarchie de groupe. Le jeu de données portant sur les émissions de CO2 se prête tout à fait à une représentation par treemap. La variable de quantité est bien sûr les émissions de CO2 par pays; ces pays sont regroupés dans un premier ensemble de régions (découpage en 23 régions), qui elles-mêmes sont regroupées dans des régions plus larges (découpage en sept régions). Pour construire un treemap, nous allons utilisons le package treemap.

library(treemap)
library(RColorBrewer)

# extraire les données de CO2 en 2015
data_co2_2015 <- subset(data_co2,data_co2$year == "2015" & ! is.na(data_co2$region7))

# construire le treemap

treemap(data_co2_2015, index=c("region7","region23"),
    vSize="CO2_kt", type="index",
    title = "CO2 rejetés par pays en 2015",
    fontsize.labels=c(12,8), # taille des étiquettes              
    fontcolor.labels=c("white","black"), # couleur des étiquettes
    fontface.labels=c(2,1), # style des polices
    bg.labels = 0, # arrière-plan des étiquettes
    align.labels=list(
        c("center", "center"), 
        c("right", "bottom")
        ),  # localisation des étiquettes dans les boîtes
    overlap.labels=0.5, # tolérance de superposition
    inflate.labels=F, # agrandir la taille des étiquettes ou non
    palette = brewer.pal(7,'Paired')
)
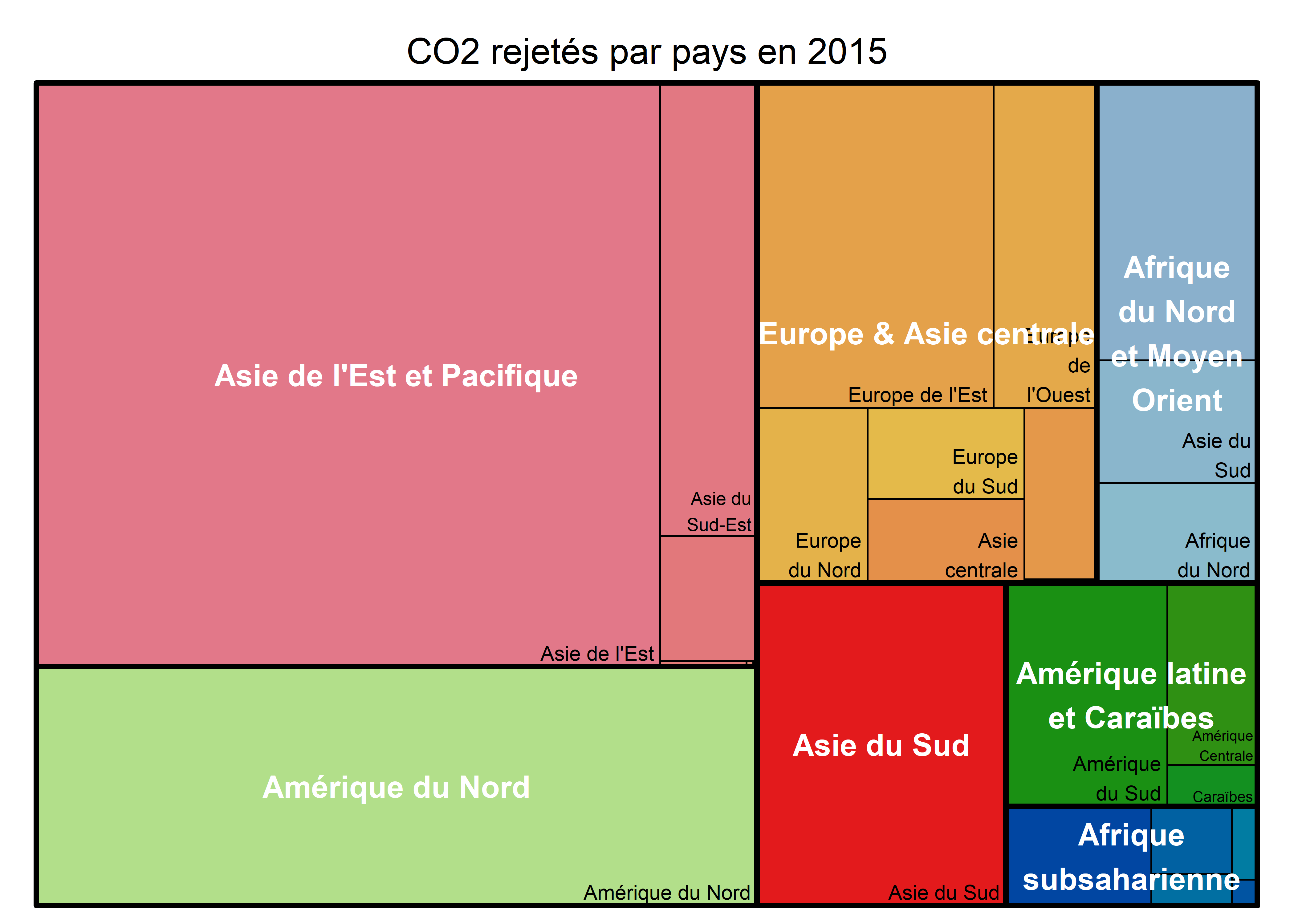
Treemap

Figure 3.52: Treemap

Références

Mihalcea, Rada et Paul Tarau. 2004. « Textrank: Bringing order into text. » In Proceedings of the 2004 conference on empirical methods in natural language processing, 404‑411. s.n.