7.1 Objectifs de la régression linéaire multiple et construction d’un modèle de régression
Selon Barbara G. Tabachnich et Linda S. Fidell (2007), un modèle de régression permet de répondre à deux objectifs principaux relevant chacun d’une approche de modélisation particulière.
La première approche a pour objectif d’identifier les relations entre une variable dépendante (VD) et plusieurs variables indépendantes (VI). Il s’agit alors de déterminer si ces relations sont positives ou négatives, significatives ou non et d’évaluer leur ampleur. La construction du modèle de régression repose alors sur un cadre théorique et la formulation d’hypothèses, sur les relations entre chacune des VI et la VD.
La seconde approche est exploratoire et très utilisée en forage ou en fouille de données (data mining en anglais). Parmi un grand ensemble de variables disponibles dans un jeu de données, elle vise à identifier la ou les variables permettant de prédire le plus efficacement (précisément) une variable dépendante. Parfois, ce type de démarche ne repose ni sur un cadre théorique ni sur la formulation d’hypothèses entre les VI et la VD. Dans des cas extrêmes, on s’intéresse uniquement à la capacité de prédiction du modèle, et ce, sans analyser les associations entre les VI et la VD. L’objectif étant d’obtenir le modèle le plus efficace possible afin de prédire à l’avenir la valeur de la variable dépendante pour des observations pour lesquelles elle est inconnue. Pour ce faire, nous avons recours à des régressions séquentielles (stepwise regressions) dans lesquelles les variables peuvent être ajoutées une à une au modèle ou retirées de celui-ci; nous conserverons dans le modèle final uniquement celles qui ont un apport explicatif significatif. Signalons d’emblée que dans le reste du chapitre, comme du livre, nous ne nous étendons pas plus sur cette approche de modélisation, et ce, pour deux raisons. D’une part, cette approche met souvent en évidence des relations significatives entre des variables sans qu’il y ait une relation de causalité entre elles. D’autre part, en sciences sociales, un modèle de régression doit être basé sur un cadre théorique et conceptuel élaboré à la suite à d’une revue de littérature rigoureuse.
Cadre conceptuel et élaboration d’un modèle de régression
Pour bien construire un modèle de régression, il convient de définir un cadre conceptuel élaboré à la suite à une revue de littérature sur le sujet de recherche. Ce cadre conceptuel permet d’identifier les dimensions et les concepts clefs permettant d’expliquer le phénomène à l’étude. Par la suite, pour chacun de ces concepts ou les dimensions, il est alors possible 1) d’identifier les différentes variables indépendantes qui sont introduites dans le modèle et 2) de formuler une hypothèse pour chacune d’elles. Par exemple, pour telle ou telle variable explicative, on s’attendra à ce qu’elle fasse augmenter ou diminuer significativement la variable dépendante. De nouveau, la formulation de cette hypothèse doit s’appuyer sur une interprétation théorique de la relation entre la VI et la VD.
Prenons en guise d’exemple une étude récente portant sur la multiexposition des cyclistes au bruit et à la pollution atmosphérique (Gelb et Apparicio 2020). Dans cet article, les auteurs s’intéressent aux caractéristiques de l’environnement urbain qui contribuent à augmenter ou réduire l’exposition des cyclistes à la pollution de l’air et au bruit routier. Pour ce faire, une collecte de données primaires a été réalisée avec trois cyclistes dans les rues de Paris du 4 au 7 septembre 2017. Au total, 64 heures et 964 kilomètres ont ainsi été parcourus à vélo afin de maximiser la couverture de la ville de Paris et les types d’environnements urbains traversés.
Leur cadre conceptuel est schématisé à la figure 7.1. Les deux variables indépendantes (à expliquer) sont l’exposition au dioxyde d’azote (NO2) et l’exposition au bruit (mesurée en décibel dB(A)). Avant d’identifier les caractéristiques de l’environnement urbain affectant ces deux expositions, plusieurs facteurs, dits variables de contrôle, sont considérés. Par exemple, la concentration de NO2 varie en fonction des conditions météorologiques (vent, température et humidité) et de la pollution d’arrière-plan (variant selon le moment de la journée, le jour de la semaine et la localisation géographique au sein de la ville). Ces dimensions ne sont pas le centre d’intérêt direct de l’étude. En effet, les auteurs s’intéressent aux impacts des caractéristiques locales de l’environnement urbain. Pour pouvoir les identifier sans biais, il est nécessaire de contrôler (filtrer) l’ensemble de ces autres facteurs.
Dans leur cadre conceptuel, les auteurs regroupent les caractéristiques locales de l’environnement urbain en trois grandes dimensions : les caractéristiques du segment (type de rues ou de voies cyclables empruntés, intersections traversées, pente et vitesse), celles de la forme urbaine (densité résidentielle, végétation, ouverture de la rue et occupations du sol) et celles du trafic (nombre et types de véhicules croisés, congestion et zones 30 km/h). Une fois ce cadre conceptuel construit, il reste alors à identifier les variables qui permettent d’opérationnaliser chacun de concepts retenus.
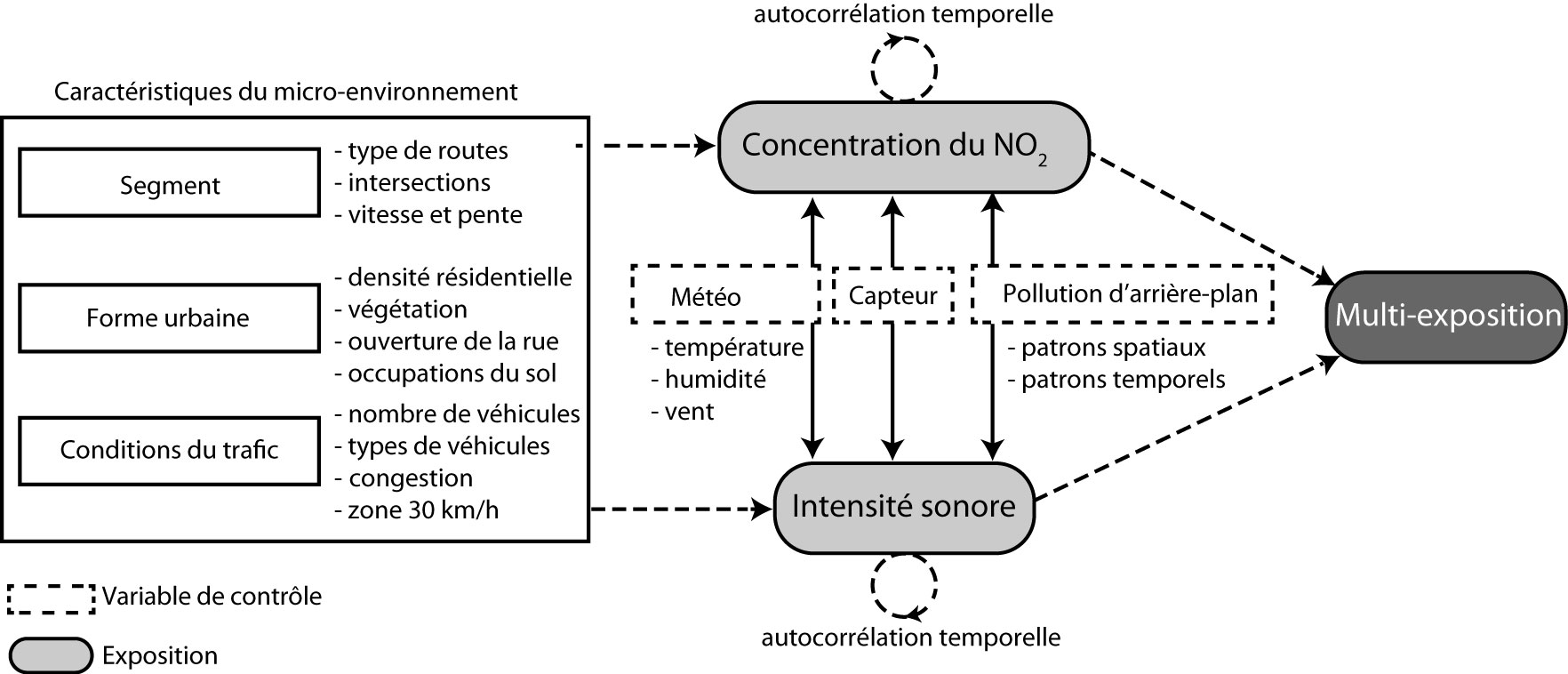
Figure 7.1: Exemple de cadre conceptuel
Notion de variables de contrôle versus variables explicatives
Dans un modèle de régression, nous distinguons habituellement trois types de variables : la variable dépendante (Y) que nous souhaitons prédire ou expliquer et les variables indépendantes (X) qui peuvent être soit des variables de contrôle (covariates en anglais), soit des variables explicatives. Les premières sont des facteurs qu’il faut prendre en compte (contrôler) avant d’évaluer nos variables d’intérêt (explicatives).
Dans l’exemple précédent, les chercheurs voulaient évaluer l’impact des caractéristiques de l’environnement urbain (variables explicatives) sur les expositions des cyclistes au dioxyde d’azote et au bruit, et ce, une fois contrôlés les effets de facteurs reconnus comme ayant un impact significatif sur la concentration de ces polluants (conditions météorologiques et la pollution d’arrière-plan). Autrement dit, si les variables de contrôle n’avaient pas été prises en compte, l’étude des variables d’intérêt serait biaisée par les effets de ces facteurs qui n’auraient pas été contrôlés. À titre d’exemple, il est possible que les zones de circulation limitées à 30 km/h soient concentrées dans les quartiers centraux et denses de Paris. Dans ces quartiers, la pollution d’arrière-plan a tendance à être supérieure. Si nous tenons pas compte de cette pollution d’arrière-plan, nous pourrions arriver à la conclusion que les zones de 30 km/h sont des milieux dans lesquels les cyclistes sont plus exposés à la pollution atmosphérique.
Construction de modèles de régression imbriqués, incrémentiels
En lien avec le cadre conceptuel du modèle, il est fréquent de construire plusieurs modèles emboîtés. Par exemple, à partir du cadre conceptuel (figure 7.1), les auteurs auraient très bien pu construire quatre modèles :
- un premier avec uniquement les variables de contrôle (modèle A);
- un second incluant les variables de contrôle et les variables explicatives de la dimension des caractéristiques du segment (modèle B);
- un troisième reprenant les variables du modèle B dans lequel sont introduites les variables explicatives relatives à la forme urbaine (modèle C);
- un dernier modèle dans lequel sont ajoutées les variables explicatives relatives aux conditions du trafic (modèle D).
L’intérêt d’une telle approche est qu’elle permet d’évaluer successivement l’apport explicatif de chacune des dimensions du modèle; nous y reviendrons dans la section 5.3.
Nous disons alors que deux modèles sont imbriqués lorsque le modèle avec le plus de variables comprend également toutes les variables du modèle avec le moins de variables.