9.2 Principes de base des GLMM

Un GLMM est donc un modèle GLM introduisant à la fois des effets fixes et des effets aléatoires. Si nous ne considérons que les effets de groupes, un GLMM peut avoir trois formes : constantes aléatoires, pentes aléatoires et constantes et pentes aléatoires. Nous présentons ici ces trois formes en reprenant l’exemple ci-dessus avec des élèves intégré(e)s dans des classes et pour lesquel(le)s le niveau de performance à l’examen ministériel de mathématique nous intéresse.

9.2.1 GLMM avec constantes aléatoires

Il s’agit de la forme la plus simple d’un GLMM. Plus spécifiquement, elle autorise le modèle à avoir une constante différente pour chaque catégorie d’une variable multinomiale. En d’autres termes, si nous reprenons l’exemple des élèves dans leurs classes, nous tentons d’ajouter dans le modèle l’idée que chaque classe a une moyenne différente en termes de performance à l’examen de mathématique. Il est assez facile de visualiser ce que cela signifie à l’aide d’un graphique. Admettons que nous modélisons la note obtenue par des élèves du secondaire à l’examen ministériel de mathématique à partir d’une autre variable continue représentant le temps de travail moyen par semaine en dehors des heures de classe et d’une variable catégorielle représentant dans quelle classe se trouve chaque élève. Notez qu’il ne s’agit pas ici de vraies données, mais de simples simulations utilisées à titre d’illustration. Si nous ne tenons pas compte des classes, nous pouvons ajuster une régression linéaire simple entre nos deux variables continues comme le propose la figure 9.2.

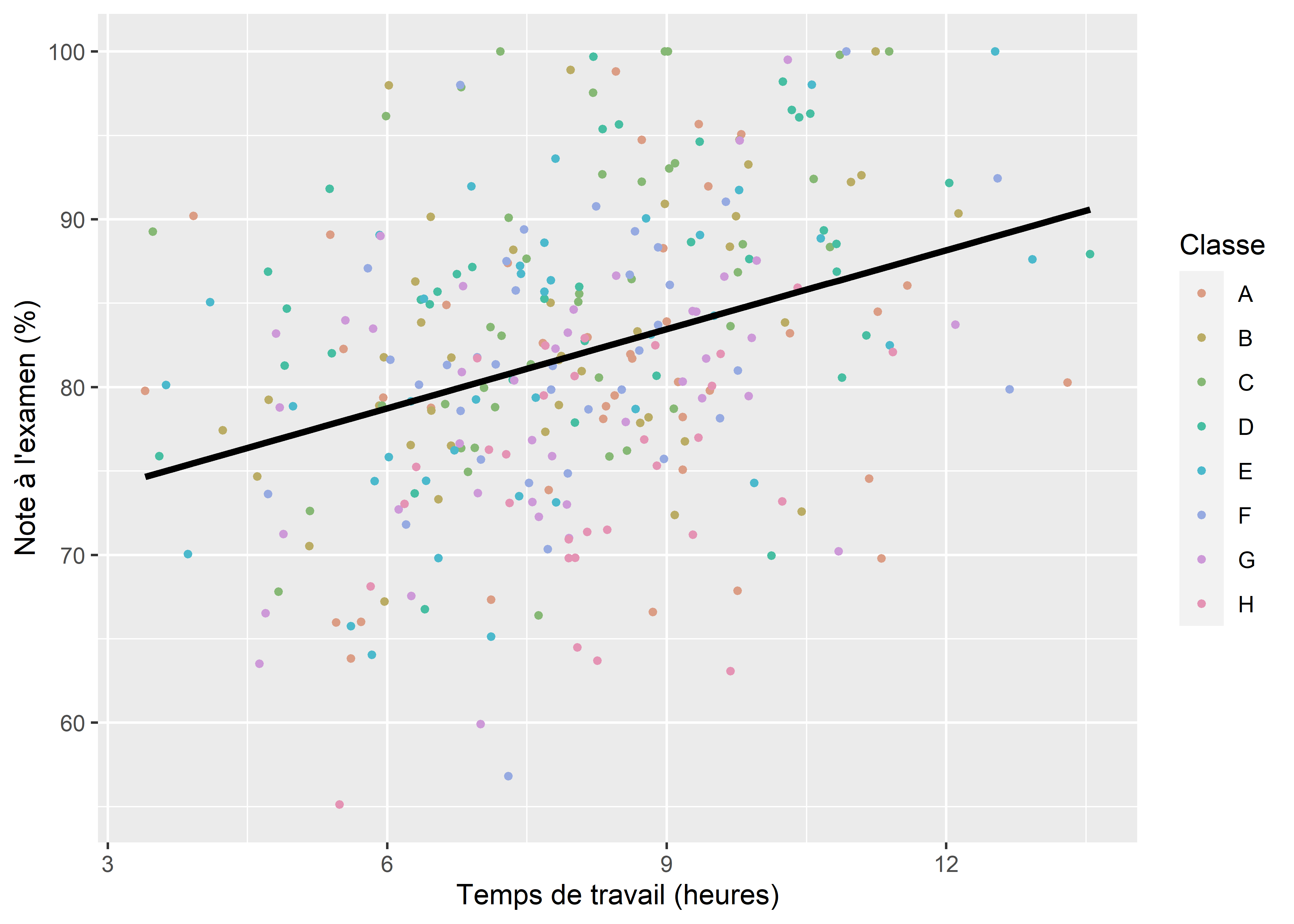
Figure 9.2: Influence du temps de travail sur la performance scolaire d’élèves

Nous constatons que notre modèle semble bien identifier la relation positive entre le temps de travail et le niveau de performance, mais la droite de régression est très éloignée de chaque point; nous avons ainsi énormément d’erreurs de prédiction, et donc des résidus importants. Jusqu’ici, nous avons vu que nous pouvons ajouter un prédicteur et intégrer l’effet des classes comme un effet fixe (figure 9.3).

Figure 9.3: Influence du temps de travail sur la performance scolaire d’élèves en tenant compte de l’effet de leur classe (effet fixe)

Cet ajustement constitue une nette amélioration du modèle. Prenons un instant pour reformuler clairement notre modèle à effets fixes :

\[\begin{equation} \begin{aligned} &Y \sim Normal(\mu,\sigma)\\ &g(\mu) = \beta_0 + \beta_1 x_1 + \sum^k_{j=1}{\beta_j x_{2j}}\\ &g(x) = x \end{aligned} \tag{9.1} \end{equation}\]

avec \(x_1\) le temps de travail et \(x_2\) la classe ayant k-1 modalités (puisqu’une modalité est la référence). Nous ajustons ainsi un coefficient pour chaque classe, ce qui a pour effet de tirer vers le haut ou vers le bas la prédiction du modèle en fonction de la classe. Cet effet est pour l’instant fixe, mais nous avons déterminé dans les sections précédentes qu’il serait conceptuellement plus approprié de le traiter comme un effet aléatoire.

Passons à présent à la reformulation de ce modèle en transformant l’effet fixe de la classe en effet aléatoire.

\[\begin{equation} \begin{aligned} &Y \sim Normal(\mu,\sigma_e)\\ &g(\mu) = \beta_0 + \beta_1 x_1 + \upsilon \\ &\upsilon \sim Normal(0, \sigma_{\upsilon}) \\ &g(x) = x \end{aligned} \tag{9.2} \end{equation}\]

Remarquez que l’effet fixe de la classe \(\sum^k_{j=1}{\beta_j x_{2j}}\) a été remplacé par \(\upsilon\) qui est un terme aléatoire propre aux classes et qui suit une distribution normale centrée sur 0 (\(\upsilon \sim Normal(0, \sigma_{\upsilon})\)). En d’autres termes, cela signifie que l’effet des classes sur la performance des élèves suit une distribution normale et que si nous moyennons l’effet de toutes les classes, cet effet serait de 0. Nous ne modélisons donc plus l’effet moyen de chaque classe comme dans le modèle à effets fixes, mais la variabilité de l’effet des classes, soit \(\sigma_{\upsilon}\). Notre modèle a donc deux variances, une au niveau des élèves (\(\sigma_e\)) et une au niveau des classes (\(\sigma_{\upsilon}\)). Cette particularité explique souvent pourquoi ce type de modèle est appelé un modèle hiérarchique ou un modèle de partition de la variance. Cette information est particulièrement intéressante, car elle permet de calculer la part de la variance présente au niveau des élèves et celle au niveau des classes.

Selon cette formulation, les constantes propres à chaque classe sont issues d’une distribution normale (nous reviendrons d’ailleurs sur ce choix plus tard), mais elles n’apparaissent pas directement dans le modèle. Ces paramètres ne sont plus estimés directement dans le modèle, mais a posteriori à partir des prédictions du modèle, et sont appelés Best Linear Unbiased Predictor (BLUP). Ces dernières précisions devraient d’ailleurs mieux vous aider à comprendre l’origine des définitions 1, 2 et 4 que nous avons mentionnées précédemment.

Figure 9.4: Influence du temps de travail sur la performance scolaire d’élèves en tenant compte de l’effet de leur classe (effet aléatoire)

En comparant les figures 9.3 et 9.4, la différence ne saute pas aux yeux; vous pourriez alors légitimement vous demander pourquoi tous ces efforts et cette complexité théorique pour une différence d’ajustement minime? Trois arguments permettent de justifier l’utilisation de constantes aléatoires plutôt que d’effets fixes dans notre cas.

9.2.1.1 Resserrement (shrinkage) et mutualisation (partial pooling)

Le premier intérêt d’utiliser un effet aléatoire réside dans sa méthode d’estimation qui diffère largement d’un effet fixe. Il est assez facile de se représenter intuitivement la différence entre les deux. Dans le cas de nos élèves et de nos classes, lorsque l’effet des classes est estimé avec un effet fixe, l’effet de chaque classe est déterminé de façon totalement indépendante des autres classes. En d’autres termes, il n’est possible d’en apprendre plus sur une classe qu’en collectant des données dans cette classe (separate pooling). Si l’effet des classes est estimé comme un effet aléatoire, alors l’information entre les classes est mutualisée (partial pooling). L’idée étant que l’information que nous apprenons sur des élèves dans une classe est au moins en partie valide dans les autres classes. Cette méthode d’estimation est particulièrement intéressante si nous ne disposons que de peu d’observations dans certaines classes, puisque nous pouvons apprendre au moins une partie de l’effet de cette classe à partir des données des autres classes. Cela n’est pas possible dans le cas d’un effet fixe où l’on traite chaque classe en silo. McElreath (2020) écrit à ce sujet qu’un effet fixe « n’a pas de mémoire » et qu’il oublie tout ce qu’il a appris sur les classes lorsqu’il passe à une nouvelle classe. La conséquence de cette mutualisation de l’information est un resserrement (shrinkage) des effets des classes autour de leur moyenne. Cela signifie que les tailles des effets de chaque classe sont plus petites dans le cas d’un effet aléatoire que d’un effet fixe. Utiliser des effets aléatoires conduit donc à une estimation plus conservatrice de l’effet des classes. Nous pouvons le visualiser en comparant les effets de classes dans le modèle à effets mixtes et le modèle à effets fixes. La figure 9.5 montre clairement que les effets aléatoires tendent à se rapprocher (resserrement) de leur moyenne (ligne noire), et donc à identifier des effets moins extrêmes pour chaque classe. Cette explication est directement en lien avec la définition 5 d’un effet aléatoire vu précédemment.

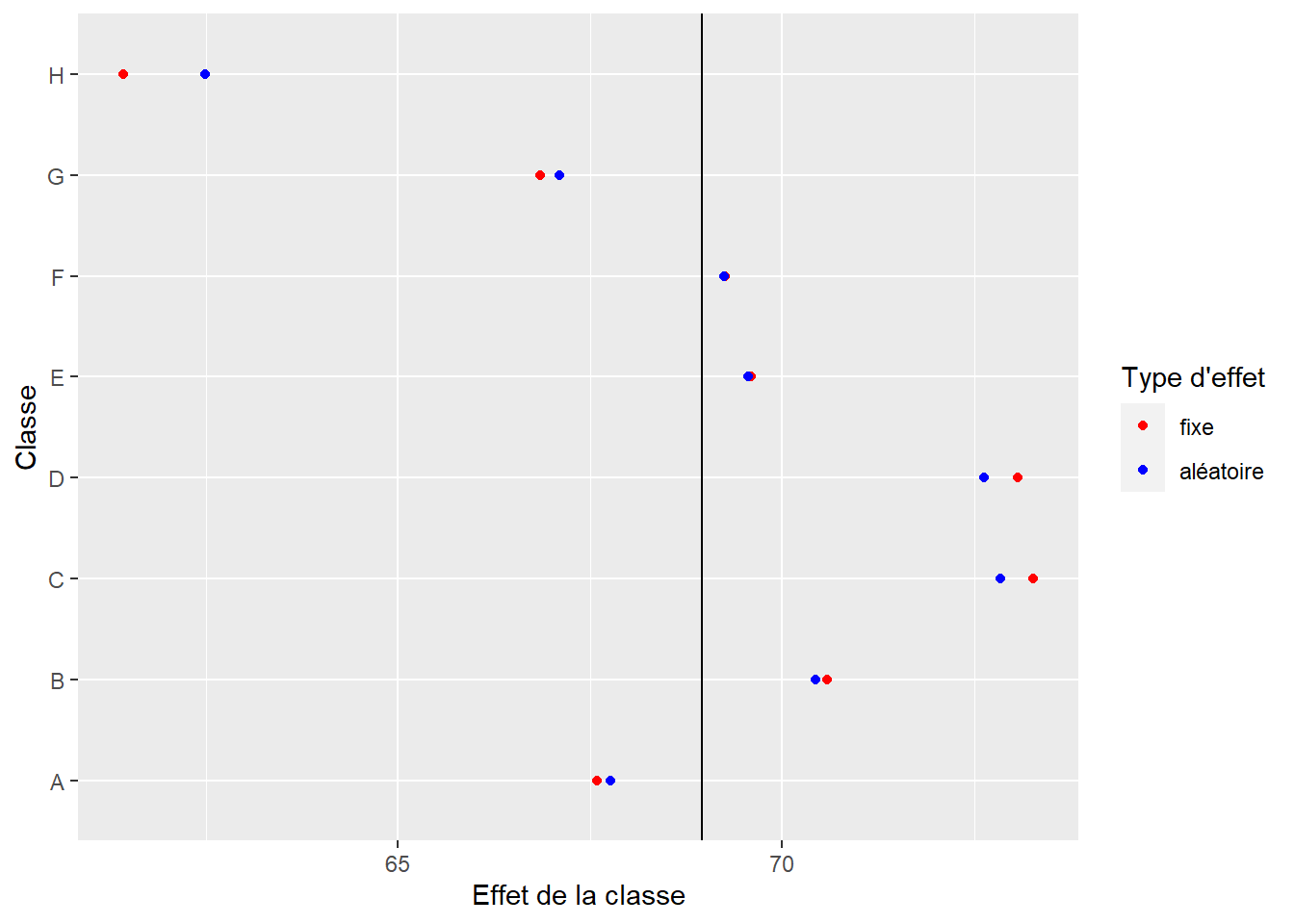
Figure 9.5: Comparaison des effets des classes pour le modèle à effets fixes versus le modèle à effets aléatoires

9.2.1.2 Prédiction pour de nouveaux groupes

Une autre retombée directe de la mutualisation de l’information est la capacité du modèle à envisager les effets plausibles pour de nouvelles classes. En effet, puisque nous avons approximé l’effet des classes sous forme d’une distribution normale dont nous connaissons la moyenne (0) et l’écart-type (\(\sigma_{\upsilon}\)), nous pouvons simuler des données pour de nouvelles classes, ce que ne permet pas un effet fixe. Ce constat est d’ailleurs directement lié à la définition 3 des effets aléatoires vue précédemment. Dans notre cas, \(\sigma_{\upsilon}\) = 3,542, ce qui nous permet d’affirmer que dans 95 % des classes, l’effet de la classe sur la performance scolaire doit se trouver entre -1,96 \(\times\) 3,542 et +1,96 \(\times\) 3,542, soit l’intervalle [-6,942, 6,942].

9.2.1.3 Partition de la variance

Un autre avantage net de l’effet aléatoire est l’estimation du paramètre \(\sigma_{\upsilon}\), soit la variance au niveau des écoles. Ce dernier permet de calculer un indicateur très intéressant, soit le coefficient de corrélation intraclasse (ICC) :

\[\begin{equation} ICC = \frac{\sigma_{\upsilon}}{\sigma_{\upsilon} + \sigma_{e}} \tag{9.3} \end{equation}\]

Il s’agit donc du pourcentage de la variance présente au niveau des classes, qui peut être interprétée comme le niveau de corrélation (de ressemblance) entre les élèves d’une même classe.

Dans notre cas, l’écart-type est de 3,542 au niveau des classes et de 7,734 au niveau des élèves. Nous pouvons donc calculer l’ICC au niveau des classes avec la formule précédente : 3,542 / (3,542 + 7,734) = 0,314. Cela signifie que le niveau de corrélation entre deux élèves d’une même classe est de 0,314 ou encore que 31,4 % de la variance de Y se situe au niveau des classes, ce qui est conséquent. Une telle information ne peut être extraite d’un modèle avec uniquement des effets fixes. Notez ici que l’ICC peut être calculé pour chaque niveau d’un modèle à effet mixte. Dans notre exemple, nous n’avons qu’un seul niveau au-dessus des élèves, soit les classes, mais nous pourrions étendre cette logique à des écoles, par exemple. Notez également que cette formule de l’ICC n’est valide que pour un modèle pour lequel la distribution de la variable Y est normale. Des développements apparaissent pour proposer d’autres formulations adaptées à d’autres distributions, mais il est également possible d’estimer l’ICC à partir des simulations issues du modèle (Nakagawa, Johnson et Schielzeth 2017; Aly et al. 2014; Stryhn et al. 2006; Wu, Crespi et Wong 2012). L’idée générale reste d’expliquer la partition de la variance dans le modèle.

En plus de l’ICC, il est également possible de calculer les R² marginal et conditionnel du modèle. Le premier représente la variance expliquée par le modèle si seulement les effets fixes sont pris en compte, et le second si les effets fixes et aléatoires sont pris en compte. Distinguer les deux sources d’information permet de mieux cerner l’importance du rôle des écoles dans la performance des élèves. Dans notre cas, nous obtenons un R² marginal de 0,115 et un R² conditionnel de 0,269, ce qui nous confirme à nouveau que le rôle joué par la classe dans le niveau de performance est loin d’être négligeable.

9.2.2 GLMM avec pentes aléatoires

Dans cette seconde version du GLMM, nous n’envisageons plus de faire varier une constante en fonction des classes, mais un coefficient en fonction des classes. Admettons que nous voulons tester ici si l’effet du temps de travail (\(x_1\)) sur la performance scolaire (Y) n’est pas constant partout. En d’autres termes, nous supposons que, dans certaines classes, le temps de travail hebdomadaire en dehors de l’école est plus ou moins efficace que d’autres classes. L’idée sous-jacente est que nous n’observons pas de différence en termes de moyenne entre deux classes, mais en termes d’effet pour notre variable \(x_1\). À nouveau, nous pouvons nous contenter d’un effet fixe pour intégrer cette idée dans notre modèle. Pour cela, nous avons simplement à ajouter une interaction entre notre variable quantitative temps de travail et notre variable qualitative classe. Nous obtenons le résultat décrit par la figure 9.6. Notez ici que la constante est bien la même pour chaque classe (les lignes s’intersectent à 0 sur l’axe des x), et que seule la pente change.

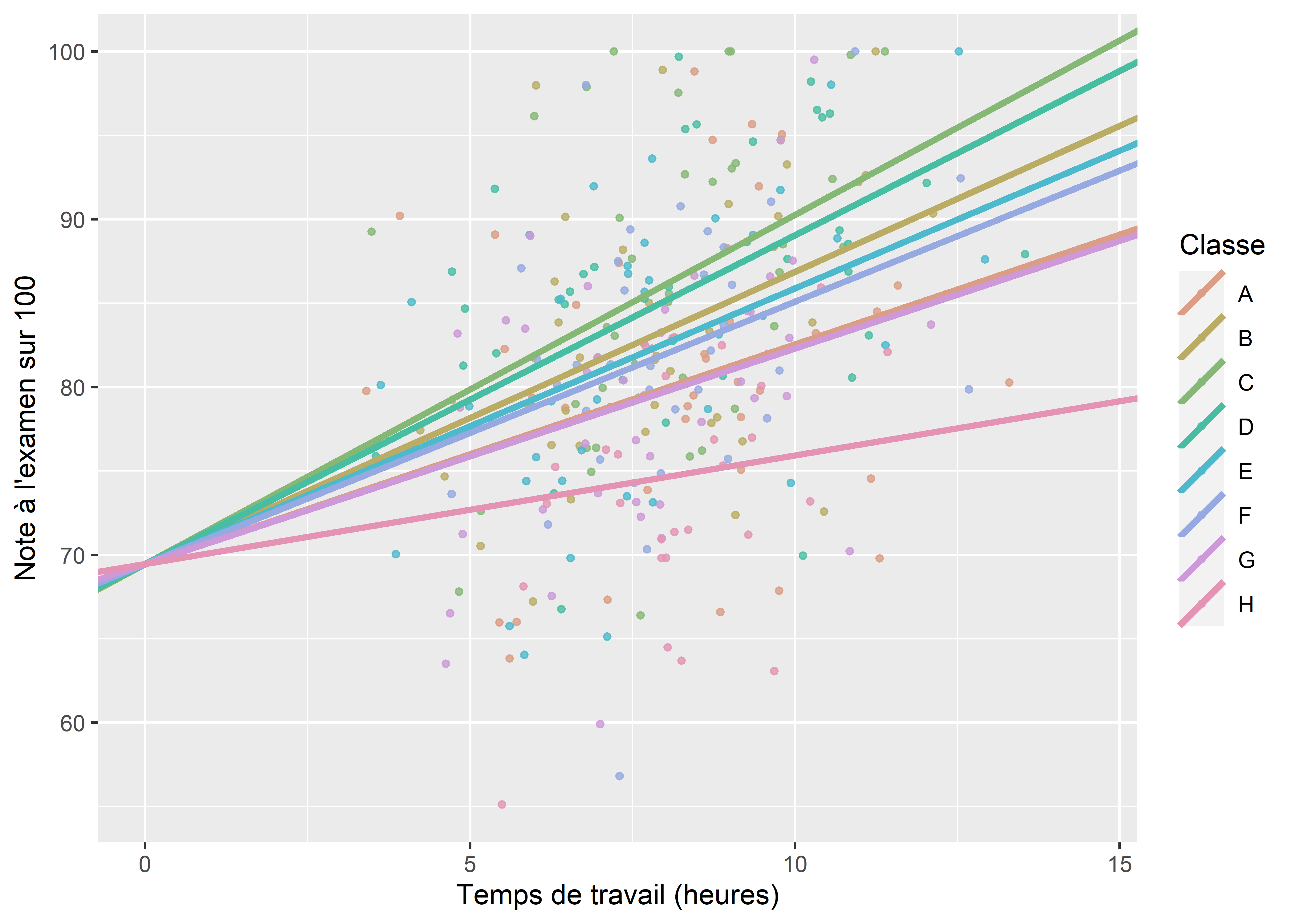
Figure 9.6: Influence du temps de travail sur la performance scolaire d’élèves en interraction avec la classe (effet fixe)

La formulation de ce modèle à effets fixes seulement est la suivante :

\[\begin{equation} \begin{aligned} &Y \sim Normal(\mu,\sigma)\\ &g(\mu) = \beta_0 + \beta_1 x_1 + \sum^k_{j=1}{\beta_j x_{2j} x_1}\\ &g(x) = x \end{aligned} \tag{9.4} \end{equation}\]

Nous constatons donc que nous avons un effet principal \(\beta_1\) décrivant le lien entre le temps de travail et la note obtenue à l’examen pour l’ensemble des élèves, ainsi qu’un bonus ou un malus sur cet effet \(\beta_j\) s’appliquant en fonction de la classe. Nous pouvons reformuler ce modèle pour inclure cet effet spécifique par classe comme un effet aléatoire :

\[\begin{equation} \begin{aligned} &Y \sim Normal(\mu,\sigma_e)\\ &g(\mu) = \beta_0 + \beta_1 x_1 + \upsilon x_1 \\ &\upsilon \sim Normal(0,\sigma_{\upsilon})\\ &g(x) = x \end{aligned} \tag{9.5} \end{equation}\]

Nous formulons ici un modèle dans lequel la classe modifie l’effet de la variable temps d’étude sur la variable note à l’examen. L’effet moyen de \(x_1\) (propre aux individus) est capté par le coefficient \(\beta_1\), les bonus ou malus ajoutés à cet effet par la classe sont issus d’une distribution normale centrée sur 0 avec un écart-type, soit \(\sigma_{\upsilon}\). À nouveau, l’idée est que si nous moyennons l’effet de toutes les classes, nous obtenons 0. Aussi, le fait de modéliser cet effet comme un effet aléatoire nous permet de partitionner la variance, de mutualiser l’information entre les classes et de resserrer l’estimation des effets des classes.

Les résultats pour ce second modèle sont présentés à la figure 9.7, et une comparaison entre les estimations des effets fixes et des effets aléatoires est présentée à la figure 9.8. Nous pouvons ainsi constater à nouveau l’effet de resserrement provoqué par l’effet aléatoire.

Figure 9.7: Influence du temps de travail sur la réussite scolaire d’élèves en interraction avec la classe (effet aléatoire)

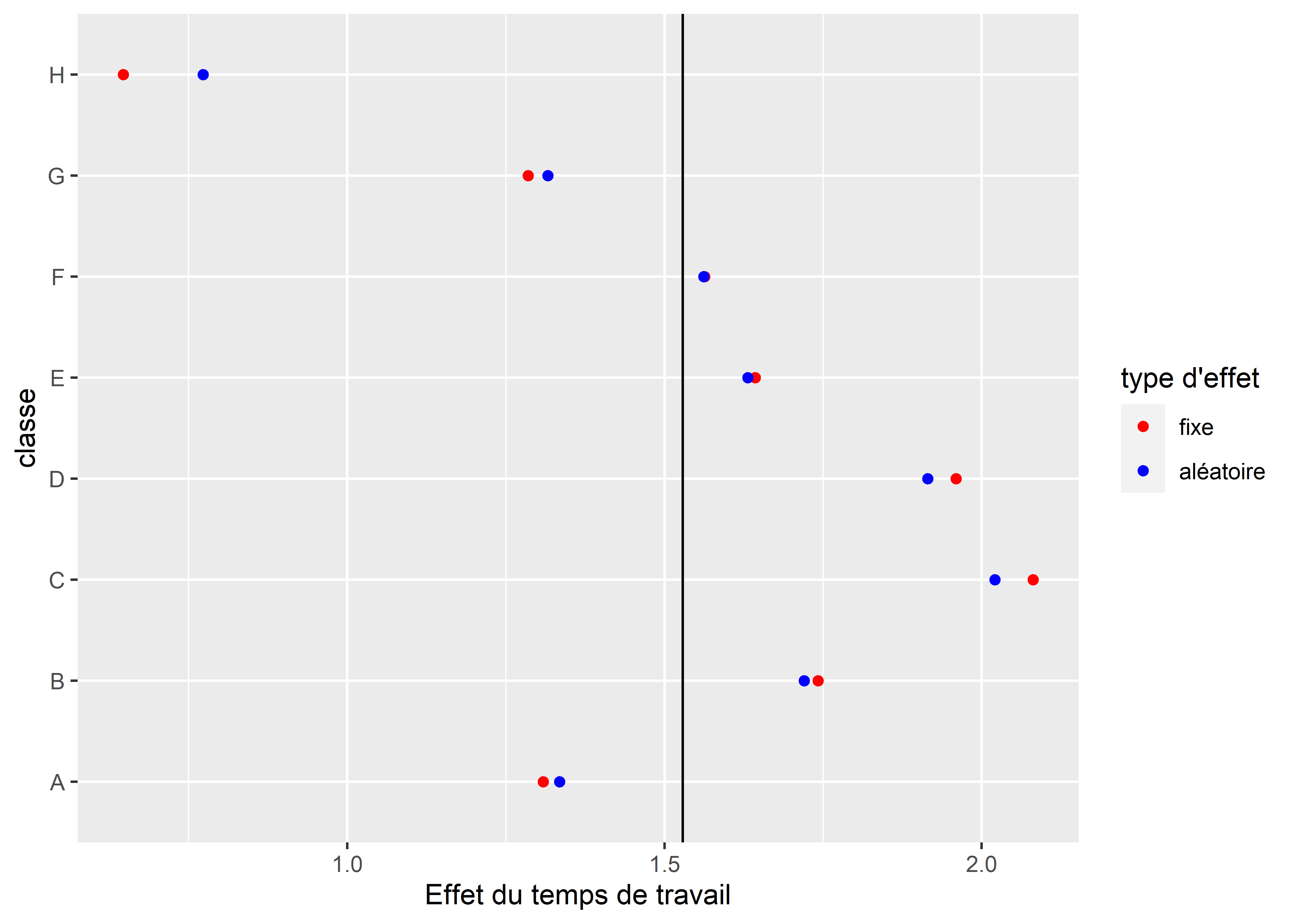
Figure 9.8: Influence du temps de travail sur la réussite scolaire d’élèves en interraction avec la classe (effet aléatoire)

Lorsque nous intègrons des pentes aléatoires dans un modèle, nous faisons face au problème suivant : la variance associée aux pentes aléatoires n’est pas fixe, mais proportionnelle à la variable X autorisée à varier. Si nous comparons la figure 9.4 (constantes aléatoires) et la figure 9.7 (pentes aléatoires), nous constatons bien que la dispersion des prédictions du modèle (représentées par les lignes) augmente dans le cas de pentes aléatoires et reste identique dans le cas des constantes aléatoires. La conséquence pratique est qu’il existe un nombre infini de valeurs possibles pour l’ICC. Dans ce contexte, il est préférable de laisser de côté cet indicateur et de ne reporter que les R² marginal et conditionnel. Dans notre cas, nous obtenons les valeurs 0,109 et 0,258, ce qui confirme une fois encore que le rôle joué par la classe est loin d’être négligeable.

9.2.3 GLMM avec constantes et pentes aléatoires

Vous l’aurez certainement deviné en lisant le titre de cette section : il est tout à fait possible de combiner à la fois des constantes et des pentes aléatoires dans un modèle. Cela augmente bien sûr la complexité du modèle et introduit quelques subtilités comme la notion de distribution normale multivariée, mais chaque chose en son temps.

Si nous reprenons notre exemple avec nos élèves et nos classes, combiner à la fois des constantes et des pentes aléatoires revient à formuler l’hypothèse que chaque classe a un effet sur la moyenne de la performance de ses élèves, mais également un effet sur l’efficacité du temps de travail. Il est possible de créer un modèle avec uniquement des effets fixes tenant compte de ces deux aspects en ajoutant dans le modèle la variable multinomiale classe ainsi que son interaction avec la variable temps de travail. La formulation de ce modèle à effets fixes est la suivante :

\[\begin{equation} \begin{aligned} &Y \sim Normal(\mu,\sigma)\\ &g(\mu) = \beta_0 + \beta_1 x_1 + \sum^k_{j=1}{\beta_{2j} x_{2j} + \beta_{3j} x_{2j} x_1}\\ &g(x) = x \end{aligned} \tag{9.6} \end{equation}\]

Nous pouvons représenter les résultats de ce modèle avec la figure 9.9.

Figure 9.9: Influence du temps de travail sur la performance scolaire d’élèves en tenant compte de l’effet de leur classe et de l’effet de la classe sur l’efficacité du temps de travail (effet fixe)

Nous reformulons à présent ce modèle pour intégrer l’effet moyen de chaque classe (constante) et l’effet des classes sur l’efficacité du temps de travail (pente) comme deux effets aléatoires :

\[\begin{equation} \begin{aligned} &Y \sim Normal(\mu,\sigma)\\ &g(\mu) = \beta_0 + \upsilon_1 + (\beta_1 + \upsilon_2) x_1\\ &\left(\begin{array}{l} \upsilon_{1} \\ \upsilon_{2} \end{array}\right) \sim \mathcal{N}\left(\left(\begin{array}{l} 0 \\ 0 \end{array}\right),\left(\begin{array}{cc} \sigma_{\upsilon_1} & \sigma_{\upsilon_1\upsilon_2} \\ \sigma_{\upsilon_1\upsilon_2} & \sigma_{\upsilon_1} \end{array}\right)\right) \\ &g(x) = x \end{aligned} \tag{9.7} \end{equation}\]

Pas de panique! Cette écriture peut être interprétée de la façon suivante :

Le modèle a deux effets aléatoires, l’un faisant varier la constante en fonction de la classe (\(\upsilon_1\)) et l’autre l’effet de la classe sur l’efficacité du temps de travail (\(\upsilon_2\)). Ces deux effets sont issus d’une distribution normale bivariée (une dimension par effet aléatoire). Cette distribution normale bivariée a donc deux moyennes et ces deux moyennes sont à 0 (les effets s’annulent si nous considérons toutes les classes ensemble). Elle dispose également d’une variance par effet aléatoire (\(\sigma_{\upsilon_1}\) et \(\sigma_{\upsilon_2}\)) et d’une covariance entre les deux effets aléatoires (\(\sigma_{\upsilon_1\upsilon_2}\)). Cette covariance permet de tenir compte du fait que, potentiellement, les classes avec une constante plus élevée pourraient systématiquement avoir une efficacité du temps de travail plus faible ou plus élevée. Cette formulation implique donc d’ajuster trois paramètres de variance : \(\sigma_{\upsilon_1}\), \(\sigma_{\upsilon_2}\) et \(\sigma_{\upsilon_1\upsilon_2}\). Il peut arriver que nous n’ayons pas assez de données pour estimer ces trois paramètres, ou que nous décidions, pour des raisons théoriques, qu’aucune corrélation ne soit attendue entre \(\sigma_{\upsilon_1}\) et \(\sigma_{\upsilon_2}\). Dans ce cas, il est possible de fixer \(\sigma_{\upsilon_1\upsilon_2}\) à 0, ce qui revient à indiquer au modèle que \(\upsilon_1\) et \(\upsilon_2\) proviennent de deux distributions normales distinctes, nous pouvons donc écrire :

\[\begin{equation} \begin{aligned} &Y \sim Normal(\mu,\sigma)\\ &g(\mu) = \beta_0 + \upsilon_1 + (\beta_1 + \upsilon_2) x_1\\ &\left(\begin{array}{l} \upsilon_{1} \\ \upsilon_{2} \end{array}\right) \sim \mathcal{N}\left(\left(\begin{array}{l} 0 \\ 0 \end{array}\right),\left(\begin{array}{cc} \sigma_{\upsilon_1} & 0 \\ 0 & \sigma_{\upsilon_1} \end{array}\right)\right) \\ &g(x) = x \end{aligned} \tag{9.8} \end{equation}\]

Ce qui est identique à :

\[\begin{equation} \begin{aligned} &Y \sim Normal(\mu,\sigma)\\ &g(\mu) = \beta_0 + \upsilon_1 + (\beta_1 + \upsilon_2) x_1\\ &\upsilon_{1} \sim Normal(0,\sigma_{\upsilon_1}) \\ &\upsilon_{2} \sim Normal(0,\sigma_{\upsilon_2}) \\ &g(x) = x \end{aligned} \tag{9.9} \end{equation}\]

Nous avons déjà abordé la notion de covariance dans la section 4.2. Pour rappel, la covariance dépend de l’unité de base des deux variables sur laquelle elle est calculée. Ici, il s’agit d’un coefficient et d’une constante. Il est donc préférable de la standardiser pour obtenir la corrélation entre les deux effets :

\[\begin{equation} corr(\upsilon_1;\upsilon_2) = \frac{\sigma_{\upsilon_1\upsilon_2}}{\sqrt{\sigma_{\upsilon_1}}\sqrt{\sigma_{\upsilon_2}}} \tag{9.10} \end{equation}\]

Si cette corrélation est positive, cela signifie que les classes ayant tendance à avoir un effet positif sur la performance scolaire ont également tendance à influencer positivement l’efficacité du temps de travail. À l’inverse, une corrélation négative signifie que l’efficacité du temps de travail a tendance à être plus faible dans les classes où la performance scolaire moyenne est élevée. Si la corrélation n’est pas significative, c’est que les deux effets sont indépendants l’un de l’autre.

Pour cet exemple, nous conservons la première formulation afin de montrer comment interpréter \(\sigma_{\upsilon_1\upsilon_2}\), mais nous ne disposons probablement pas de suffisamment de classes différentes pour estimer correctement ces trois paramètres. Les résultats de ce modèle sont représentés à la figure 9.10.

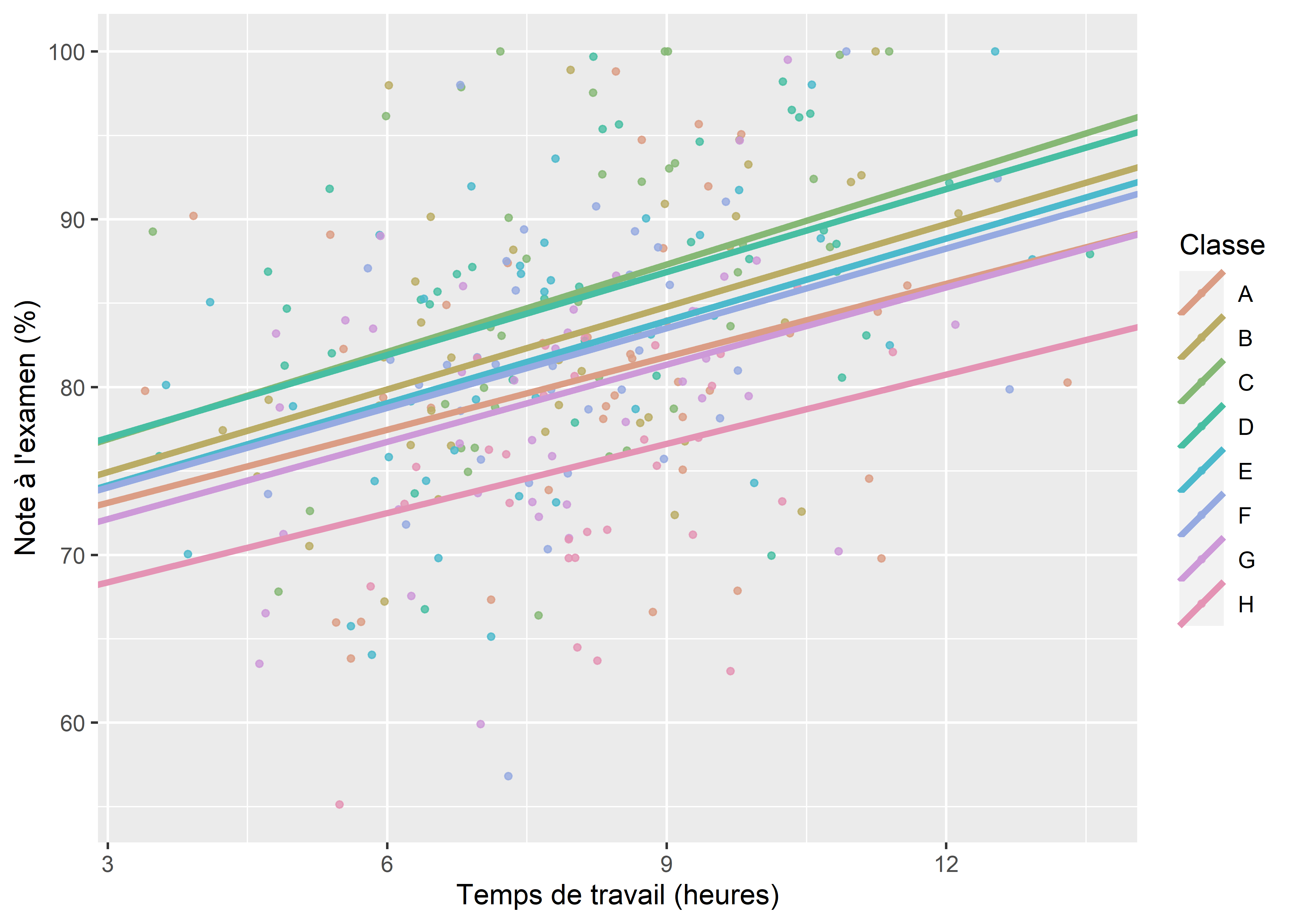
Figure 9.10: Influence du temps de travail sur la performance scolaire d’élèves en tenant compte de l’effet de leur classe et de l’effet de la classe sur l’efficacité du temps de travail (effet aléatoire)

Nous pouvons ainsi constater que pour ce troisième modèle, l’effet de resserrement est bien plus prononcé que pour les modèles précédents (figure 9.11). Si nous nous fions au modèle à effets fixes (figure 9.9), alors l’effet de l’école sur l’efficacité du temps de travail est très important. En revanche, le modèle à effet aléatoire identifie que la différence de moyenne entre les écoles est importante, mais la différence en termes d’efficacité du temps de travail est beaucoup plus anecdotique.

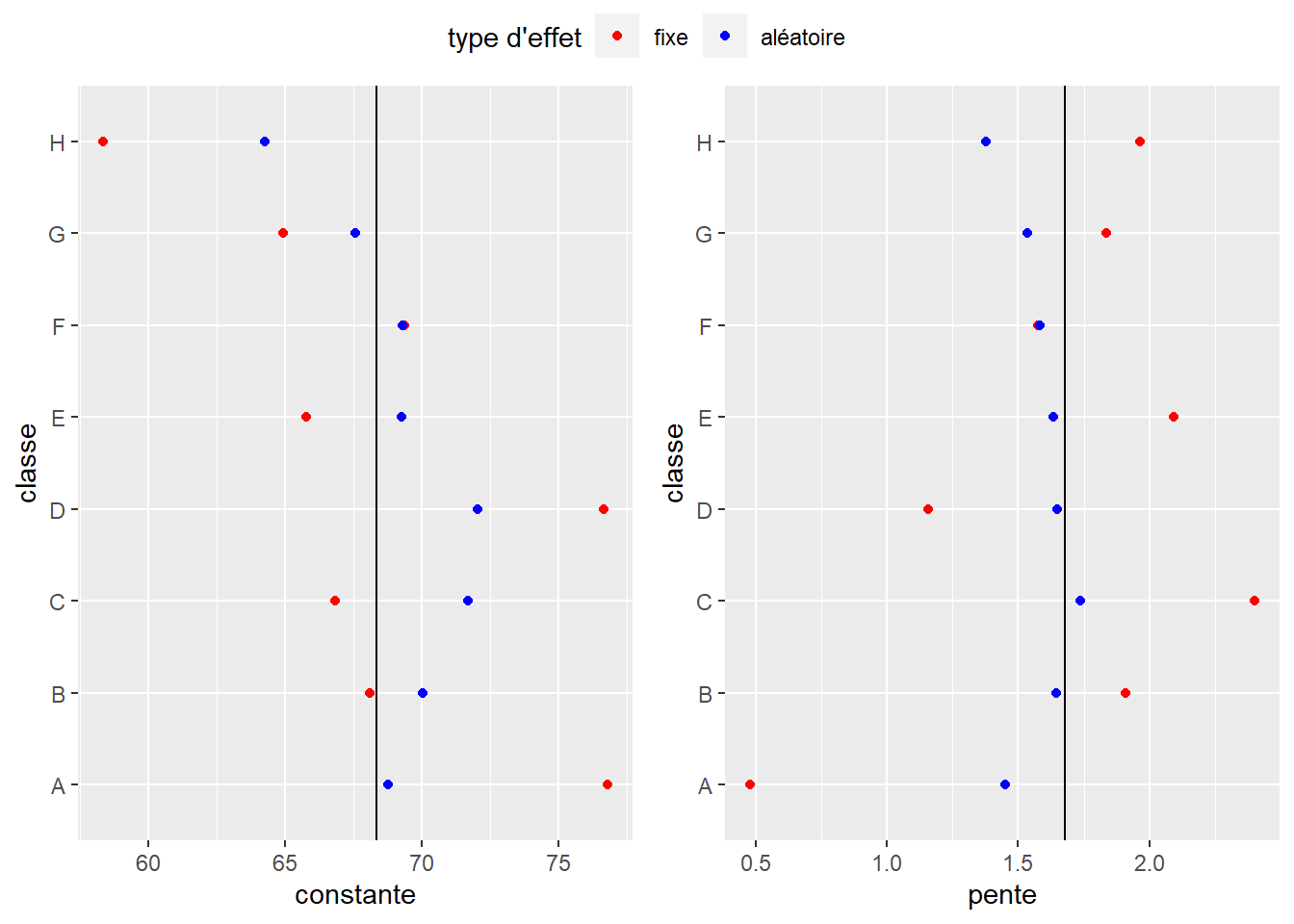
Figure 9.11: Comparaison des effets fixes et aléatoires pour le modèle intégrant l’effet des classes et l’interaction entre les classes et le temps de travail

Notre modèle estime les valeurs de \(\sigma_{\upsilon_1}\) à 8,563, de \(\sigma_{\upsilon_2}\) à 0,042 et de \(\sigma_{\upsilon_1\upsilon_2}\) à 0,073. La corrélation entre les deux effets est donc de 0,122, ce qui est relativement faible (pour l’anecdote, notez que la valeur originale de corrélation entre ces deux effets était de 0,1 lorsque nous avons simulé ces données, notre modèle a donc bien été capable de retrouver le paramètre original). À nouveau, puisque nous avons des pentes aléatoires dans ce modèle, nous ne pouvons pas calculer l’ICC; nous pouvons cependant rapporter les R² marginal et conditionnel. Leurs valeurs respectives sont 0,115 et 0,269, ce qui nous confirme une nouvelle fois que l’ajout d’effets aléatoires contribue à expliquer une partie importante de la variance de la performance scolaire.

Pour terminer cette section, comparons brièvement les trois modèles (constantes aléatoires, pentes aléatoires, constantes et pentes aléatoires) pour déterminer lequel est le mieux ajusté à nos données. Nous ajoutons également un quatrième modèle dans lequel les deux effets aléatoires sont présents, mais non corrélés (\(\sigma_{\upsilon_1\upsilon_2}=0\)). Le tableau 9.1 nous permet de constater que l’ajout des constantes aléatoires joue un rôle essentiel dans le premier modèle : le R² conditionnel est plus que deux fois supérieur au R² marginal. Cependant, l’ajout des pentes aléatoires dans les trois autres modèles apporte finalement très peu d’information, nous laissant penser que l’effet de la classe sur le temps de travail est faible, voire inexistant.

Tableau 9.1: Comparaison des trois modèles à effets aléatoires

modèle	AIC	R2 marginal	R2 conditionnel
Constantes aléatoires	2 100,9	0,12	0,27
Pentes aléatoires	2 101,6	0,11	0,26
Pentes et constantes aléatoires corrélées	2 104,7	0,11	0,27
Pentes et constantes aléatoires non-corrélées	2 102,7	0,11	0,27

Modèles à effets mixtes avec des structures croisées

Jusqu’à présent, nous avons abordé des modèles GLMM comprenant des structures imbriquées (nested en anglais), c’est-à-dire qu’une observation d’un niveau 1 est incluse dans un et un seul groupe du niveau 2. Comme structure imbriquée à trois niveaux, nous avons vu comme exemple des élèves intégrés dans des classes elles-mêmes intégrées dans des écoles (figure 9.1) : un ou une élève appartient à une et une seule classe qui est elle-même localisée dans une et une seule école (élève / classe / école).

Notez qu’il est aussi possible d’avoir des structures des données croisées (crossed).

Admettons à présent que nous ne nous intéressons pas à la classe dans laquelle se situe l’élève, mais plutôt à la personne qui enseigne. Admettons également que ces personnes peuvent donner des cours dans plusieurs écoles. Nous nous retrouvons dans un cas de figure où une personne qui enseigne peut se situer dans plusieurs écoles, ce qui diffère du cas précédent où chaque classe appartient à une seule école. Dans ce second cas, on parle d’une structure croisée plutôt qu’imbriquée.

Si les personnes enseignent dans toutes les écoles, il est possible de dire que le design d’étude est croisé complet ou croisé partiel si elles n’enseignent que dans certaines écoles. La figure 9.12 résume ces trois situations.

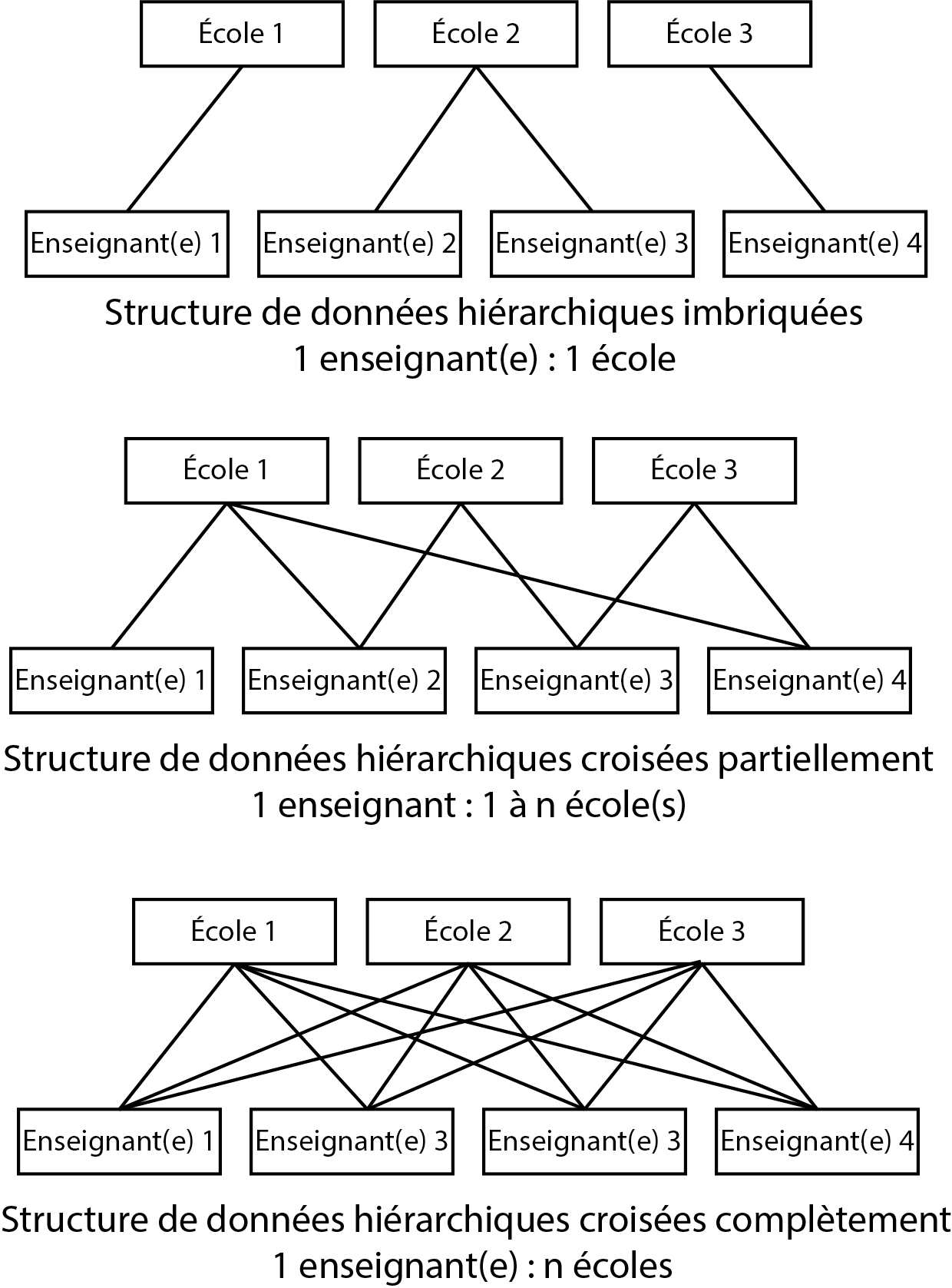
Figure 9.12: Différentes structures de données hiérarchiques (imbriquée versus croisée)

Il est important de bien saisir la structure de son jeu de données, car l’estimation d’un modèle avec effets imbriqués ou croisés peut donner des résultats parfois significativement différents. De plus, un modèle imbriqué est généralement moins difficile à ajuster qu’un modèle croisé. En effet, dans un modèle imbriqué, deux personnes étudiant dans deux écoles différentes sont jugées indépendantes. Dans un modèle croisé, deux élèves provenant de deux écoles différentes peuvent tout de même partager une dépendance du fait qu’ils ou elles ont pu avoir le même professeur ou la même professeure. La structure de dépendance (et donc de la matrice de covariance des effets aléatoires) est ainsi plus complexe pour un modèle croisé.

Références

Aly, Sharif S, Jianyang Zhao, Ben Li et Jiming Jiang. 2014. « Reliability of environmental sampling culture results using the negative binomial intraclass correlation coefficient. » SpringerPlus 3 (1): 40. https://doi.org/10.1186/2193-1801-3-40.

McElreath, Richard. 2020. Statistical rethinking: A Bayesian course with examples in R and Stan. CRC press.

Nakagawa, Shinichi, Paul C. D. Johnson et Holger Schielzeth. 2017. « The coefficient of determination R2 and intra-class correlation coefficient from generalized linear mixed-effects models revisited and expanded. » Journal of The Royal Society Interface 14 (134): 20170213. https://doi.org/10.1098/rsif.2017.0213.

Stryhn, H, J Sanchez, P Morley, C Booker et IR Dohoo. 2006. « Interpretation of variance parameters in multilevel Poisson regression models. » In Proceedings of the 11th International Symposium on Veterinary Epidemiology and Economics. Vol. 702. s.n.

Wu, Sheng, Catherine M Crespi et Weng Kee Wong. 2012. « Comparison of methods for estimating the intraclass correlation coefficient for binary responses in cancer prevention cluster randomized trials. » Contemporary clinical trials 33 (5): 869‑880. https://doi.org/10.1016/j.cct.2012.05.004.