2.5 Statistiques descriptives sur des variables quantitatives
2.5.1 Paramètres de tendance centrale
Trois mesures de tendance centrale permettent de résumer rapidement une variable quantitative :
- la moyenne arithmétique est simplement la somme des données d’une variable divisée par le nombre d’observations (n), soit \(\frac{\sum_{i=1}^n x_i}{n}\) notée \(\mu\) (prononcé mu) pour des données pour une population et \(\bar{x}\) (prononcé x barre) pour un échantillon.
- la médiane est la valeur qui coupe la distribution d’une variable d’une population ou d’un échantillon en deux parties égales. Autrement dit, 50 % des valeurs des observations lui sont supérieures et 50 % lui sont inférieures.
- le mode est la valeur la plus fréquente parmi un ensemble d’observations pour une variable. Il s’applique ainsi à des variables discrètes (avec un nombre fini de valeurs discrètes dans un intervalle donné) et non à des variables continues (avec un nombre infini de valeurs réelles dans un intervalle donné). Prenons deux variables : l’une discrète relative au nombre d’accidents par intersection (avec \(X \in \left[0,20\right]\)) et l’autre continue relative à la distance de dépassement (en mètres) d’un personne à vélo par un personne conduisant un véhicule motorisé (avec \(X \in \left[0,5\right]\)). Pour la première, le mode – la valeur la plus fréquente – est certainement 0. Pour la seconde, identifier le mode n’est pas pertinent puisqu’il peut y avoir un nombre infini de valeurs entre 0 et 5 mètres.
Il convient de ne pas confondre moyenne et médiane! Dans le tableau 2.1, nous avons reporté les valeurs moyennes et médianes des revenus des ménages pour les municipalités de l’île de Montréal en 2015. Par exemple, les 8685 ménages résidant à Wesmount disposaient en moyenne d’un revenu de 295 099 $; la moitié de ces 8685 ménages avaient un revenu inférieur à 100 153 $ et l’autre moitié un revenu supérieur à cette valeur (médiane). Cela démontre clairement que la moyenne peut être grandement affectée par des valeurs extrêmes (faibles ou fortes). Autrement dit, plus l’écart entre les valeurs de la moyenne et la médiane est important, plus les données de la variable sont inégalement réparties. À Westmount, soit la municipalité la plus nantie de l’île de Montréal, les valeurs extrêmes sont des ménages avec des revenus très élevés tirant fortement la moyenne vers le haut. À l’inverse, le faible écart entre les valeurs moyenne et médiane dans la municipalité de Montréal-Est (58 594 $ versus 50 318 $) souligne que les revenus des ménages sont plus également répartis. Cela explique que pour comparer les revenus totaux ou d’emploi entre différents groupes (selon le sexe, le groupe d’âge, le niveau d’éducation, la municipalité ou région métropolitaine, etc.), nous privilégions habituellement l’utilisation des revenus médians.
| Municipalité | Nombre de ménages | Revenu moyen | Revenu médian |
|---|---|---|---|
|
Baie-D’Urf |
1 330 | 171 390 | 118 784 |
| Beaconsfield | 6 660 | 187 173 | 123 392 |
|
C |
13 490 | 94 570 | 58 935 |
| Dollard-Des Ormeaux | 17 210 | 102 104 | 78 981 |
| Dorval | 8 390 | 89 952 | 64 689 |
| Hampstead | 2 470 | 250 497 | 122 496 |
| Kirkland | 6 685 | 144 676 | 115 381 |
|
Montr |
779 805 | 69 047 | 50 227 |
|
Montr |
1 730 | 58 594 | 50 318 |
|
Montr |
1 850 | 159 374 | 115 029 |
| Mont-Royal | 7 370 | 205 309 | 109 540 |
| Pointe-Claire | 12 380 | 100 294 | 80 242 |
| Sainte-Anne-de-Bellevue | 1 960 | 102 969 | 67 200 |
| Senneville | 345 | 203 790 | 116 224 |
| Westmount | 8 685 | 295 099 | 100 153 |
2.5.2 Paramètres de position
Les paramètres de position permettent de diviser une distribution en n parties égales.
- Les quartiles qui divisent une distribution en quatre parties (25 %) :
- Q1 (25 %), soit le quartile inférieur ou premier quartile;
- Q2 (50 %), soit la médiane;
- Q3 (75 %), soit le quartile supérieur ou troisième quartile.
- Les quintiles qui divisent une distribution en cinq parties égales (20 %).
- Les déciles (de D1 à D9) qui divisent une distribution en dix parties égales (10 %).
- Les centiles (de C1 à C99) qui divisent une distribution en cent parties égales (1 %).
En cartographie, les quartiles et les quintiles sont souvent utilisés pour discrétiser une variable quantitative (continue ou discrète) en quatre ou cinq classes et plus rarement, en dix classes (déciles). Avec les quartiles, les bornes des classes qui comprennent chacune 25 % des unités spatiales sont définies comme suit : [Min à Q1], [Q1 à Q2], [Q2 à Q3] et [Q3 à Max]. La méthode de discrétisation selon les quartiles ou quintiles permet de repérer, en un coup d’œil, à quelle tranche de 25 % ou de 20 % des données appartient chacune des unités spatiales. Cette méthode de discrétisation est aussi utile pour comparer plusieurs cartes et vérifier si deux phénomènes sont ou non colocalisés (Pumain et Béguin 1994). En guise d’exemple, les pourcentages de personnes à faible revenu et de locataires par secteur de recensement ont clairement des distributions spatiales très semblables dans la région métropolitaine de Montréal en 2016 (figure 2.24).
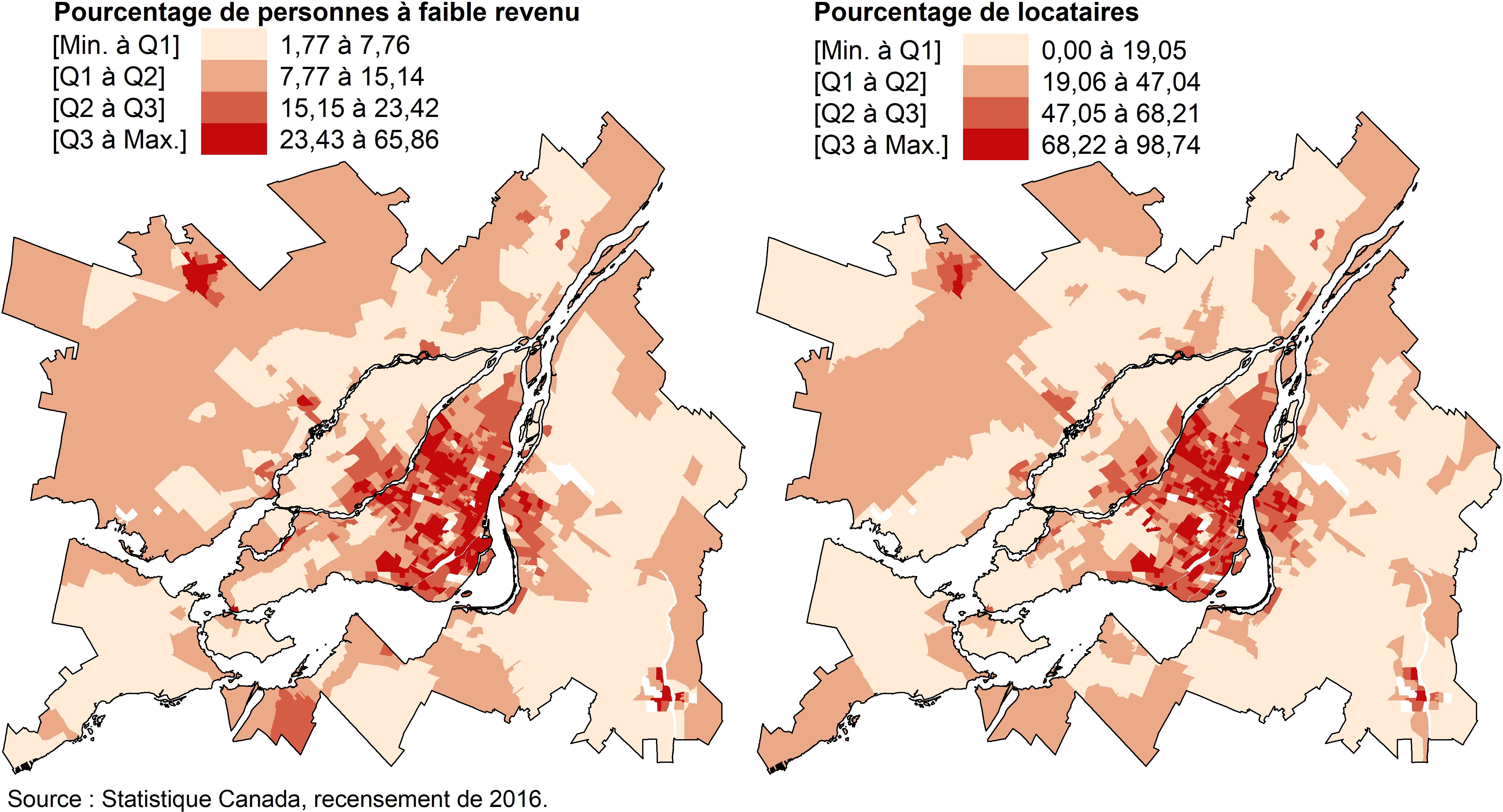
Figure 2.24: Exemples de cartographie avec une discrétisation selon les quantiles
Une lecture attentive des valeurs des centiles permet de repérer la présence de valeurs extrêmes, voire aberrantes, dans un jeu de données. Il n’est donc pas rare de les voir reportées dans un tableau de statistiques descriptives d’un article scientifique, et ce, afin de décrire succinctement les variables à l’étude. Par exemple, dans une étude récente comparant les niveaux d’exposition au bruit des cyclistes dans trois villes (Apparicio et Gelb 2020), les auteurs reportent à la fois les valeurs moyennes et celles de plusieurs centiles. Globalement, la lecture des valeurs moyennes permet de constater que, sur la base des données collectées, les cyclistes sont plus exposés au bruit à Paris qu’à Montréal et Copenhague (73,4 dB(A) contre 70,7 et 68,4, tableau 2.2). Compte tenu de l’échelle logarithmique du bruit, la différence de 5 dB(A) entre les valeurs moyennes du bruit de Copenhague et de Paris peut être considérée comme une multiplication de l’énergie sonore par plus de 3. Pour Paris, l’analyse des quartiles montre que durant 25 % du temps des trajets à vélo (plus de 63 heures de collecte), les participantes et participants ont été exposés à des niveaux de bruit soit inférieurs à 69,1 dB(A) (premier quartile), soit supérieurs à 74 dB(A) (troisième quartile). Quant à l’analyse des centiles, elle permet de constater que durant 5 % et 10 % du temps, les participantes et participants étaient exposés à des niveaux de bruit très élevés, dépassant 75 dB(A) (C90 = 76 et C90 = 77,2).
| Statistiques | Copenhague | Montréal | Paris |
|---|---|---|---|
| N | 6 212,0 | 4 723,0 | 3 793,0 |
| Moyenne de bruit | 68,4 | 70,7 | 73,4 |
| Centiles | |||
| 1 | 57,5 | 59,2 | 62,3 |
| 5 | 59,1 | 61,1 | 65,0 |
| 10 | 60,3 | 62,3 | 66,5 |
| 25 (premier quartile) | 62,7 | 64,5 | 69,1 |
| 50 (médiane) | 66,0 | 67,7 | 71,6 |
| 75 (troisième quartile) | 69,2 | 71,0 | 74,0 |
| 90 | 71,9 | 73,7 | 76,0 |
| 95 | 73,3 | 75,2 | 77,2 |
| 99 | 76,5 | 78,9 | 81,0 |
2.5.3 Paramètres de dispersion
Cinq principales mesures de dispersion permettent d’évaluer la variabilité des valeurs d’une variable quantitative : l’étendue, l’écart interquartile, la variance, l’écart-type et le coefficient de variation. Notez d’emblée que cette dernière mesure ne s’applique pas à des variables d’intervalle (section 2.1.2.2).
L’étendue est la différence entre les valeurs minimale et maximale d’une variable, soit l’intervalle des valeurs dans lequel elle a été mesurée. Il convient d’analyser avec prudence cette mesure puisqu’elle inclut dans son calcul des valeurs potentiellement extrêmes, voire aberrantes (faibles ou fortes).
L’intervalle ou écart interquartile est la différence entre les troisième et premier quartiles (Q3 − Q1). Il représente ainsi une mesure de la dispersion des valeurs de 50 % des observations centrales de la distribution. Plus la valeur de l’écart interquartile est élevée, plus la dispersion des 50 % des observations centrales est forte. Contrairement à l’étendue, cette mesure élimine l’influence des valeurs extrêmes puisqu’elle ne tient pas compte des 25 % des observations les plus faibles [Min à Q1] et des 25 % des observations les plus fortes [Q3 à Max]. Graphiquement, l’intervalle interquartile est représenté à l’aide d’une boîte à moustaches (boxplot en anglais) : plus l’intervalle interquartile est grand, plus la boîte est allongée (figure 2.25)
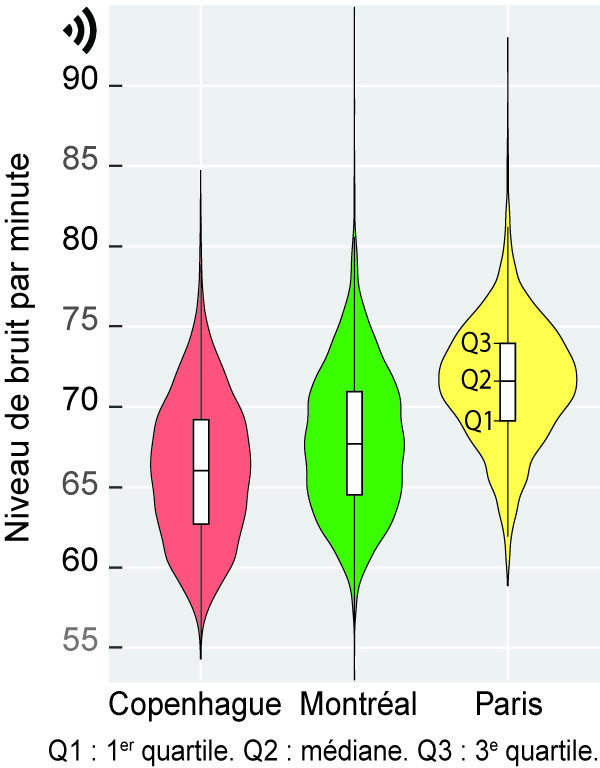
Figure 2.25: Graphique en violon, boîte à moustaches et intervalle interquartile
- La variance est la somme des déviations à la moyenne au carré (numérateur) divisée par le nombre d’observations pour une population (\(\sigma^2\)) ou divisée par le nombre d’observations moins une (\(s^2\)) pour un échantillon (équation (2.20)). Puisque les déviations à la moyenne sont mises au carré, la valeur de la variance (tout comme celle de l’écart-type) est toujours positive. Plus sa valeur est élevée, plus les observations sont dispersées autour de la moyenne. La variance représente ainsi l’écart au carré moyen des observations à la moyenne.
\[\begin{equation} \sigma^2=\frac{\sum_{i=1}^n (x_{i}-\mu)^2}{n} \text{ ou } s^2=\frac{\sum_{i=1}^n (x_{i}-\bar{x})^2}{n-1} \tag{2.20} \end{equation}\]
- L’écart-type est la racine carrée de la variance (équation (2.21)). Rappelez-vous que la variance est calculée à partir des déviations à la moyenne mises au carré. Étant donné que l’écart-type est la racine carrée de la variance, il est donc évalué dans la même unité que la variable, contrairement à la variance. Bien entendu, comme pour la variance, plus la valeur de l’écart-type est élevée, plus la distribution des observations autour de la moyenne est dispersée.
\[\begin{equation} \sigma=\sqrt{\sigma^2}=\sqrt{\frac{\sum_{i=1}^n (x_{i}-\mu)^2}{n}} \text{ ou } s=\sqrt{s^2}=\sqrt{\frac{\sum_{i=1}^n (x_{i}-\bar{x})^2}{n-1}} \tag{2.21} \end{equation}\]
Les formules des variances et des écarts-types pour une population et un échantillon sont très similaires : seul le dénominateur change avec \(n\) versus \(n-1\) observations. Par conséquent, plus le nombre d’observations de votre jeu de données est important, plus l’écart entre ces deux mesures de dispersion pour une population et un échantillon est minime.
Comme dans la plupart des logiciels de statistique, les fonctions de base var et sd de R calculent la variance et l’écart-type pour un échantillon (\(n-1\) au dénominateur). Si vous souhaitez les calculer pour une population, adaptez la syntaxe ci-dessous dans laquelle df$var1 représente la variable intitulée var1 présente dans un DataFrame nommé df.
var.p <- mean((df$var1 - mean(df$var1))^2)
sd.p <- sqrt(mean((df$var1 - mean(df$var1))^2))
- Le coefficient de variation (CV) est le rapport entre l’écart-type et la moyenne, représentant ainsi une standardisation de l’écart-type ou, en d’autres termes, une mesure de dispersion relative (équation (2.22)). L’écart-type étant exprimé dans l’unité de mesure de la variable, il ne peut pas être utilisé pour comparer les dispersions de variables exprimées des unités de mesure différentes (par exemple, en pourcentage, en kilomètres, en dollars, etc.). Pour y remédier, nous utilisons le coefficient de variation : une variable est plus dispersée qu’une autre si la valeur de son CV est plus élevée. Certaines personnes préfèrent multiplier la valeur du CV par 100 : l’écart-type est alors exprimé en pourcentage de la moyenne.
\[\begin{equation} CV=\frac{\sigma}{\mu} \text{ ou } CV=\frac{s^2}{\bar{x}} \tag{2.22} \end{equation}\]
Illustrons comment calculer les cinq mesures de dispersion précédemment décrites à partir de valeurs fictives pour huit observations (colonne intitulée \(x_i\) au tableau 2.3). Les différentes statistiques reportées dans ce tableau sont calculées comme suit :
La moyenne est la somme divisée par le nombre d’observations, soit \(\mbox{248/8}=\mbox{31}\).
L’étendue est la différence entre les valeurs maximale et minimale, soit \(\mbox{40}-\mbox{22}=\mbox{30}\).
Les quartiles coupent la distribution en quatre parties égales. Avec huit observations triées par ordre croissant, le premier quartile est égal à la valeur de la deuxième observation (soit 25), la médiane à celle de la quatrième (30), le troisième quartile à celle de la sixième (35).
L’écart interquartile est la différence entre Q3 et Q1, soit \(\mbox{35}-\mbox{25}=\mbox{10}\).
La seconde colonne du tableau est l’écart à la moyenne (\(x_i-\bar{x}\)), soit \(\mbox{22} - \mbox{31} = -\mbox{9}\) pour l’observation 1; la somme de ces écarts est toujours égale à 0. La troisième colonne est cette déviation mise au carré (\((x_i-\bar{x})^2\)), soit \(-\mbox{9}^2 = \mbox{81}\), toujours pour l’observation 1. La somme de ces déviations à la moyenne au carré (268) représente le numérateur de la variance (équation (2.20)). En divisant cette somme par le nombre d’observations, nous obtenons la variance pour une population (\(\mbox{268}/\mbox{8}=\mbox{33,5}\)) tandis que la variance d’un échantillon est égale à \(\mbox{268}/(\mbox{8}-\mbox{1})=\mbox{38,29}\).
L’écart-type est la racine carrée de la variance (équation (2.21)), soit \(\sigma=\sqrt{\mbox{33,5}}=\mbox{5,79}\) et \(s=\sqrt{\mbox{38,29}}=\mbox{6,19}\).
Finalement, les valeurs des coefficients de variation (équation (2.22)) sont de \(\mbox{5,79}/\mbox{31}=\mbox{0,19}\) pour une population et \(\mbox{6,19}/\mbox{31}=\mbox{0,20}\) pour un échantillon.
| Observation | \(x_i\) | \(x_i-\bar{x}\) | \((x_i-\bar{x})^2\) |
|---|---|---|---|
| 1 | 22,00 | -9 | 81,0 |
| 2 | 25,00 | -6 | 36,0 |
| 3 | 27,00 | -4 | 16,0 |
| 4 | 30,00 | -1 | 1,0 |
| 5 | 32,00 | 1 | 1,0 |
| 6 | 35,00 | 4 | 16,0 |
| 7 | 37,00 | 6 | 36,0 |
| 8 | 40,00 | 9 | 81,0 |
| Statistique | |||
| N | 8,00 | ||
| Somme | 248,00 | 0 | 268,0 |
| Moyenne (\(\bar{x}\) ou \(\mu\)) | 31,00 | 0 | 33,5 |
| Étendue | 18,00 | ||
| Premier quartile | 25,00 | ||
| Troisième quartile | 35,00 | ||
| Intervalle interquartile | 10,00 | ||
| Variance (population, \(\sigma^2\)) | 33,50 | ||
| Écart-type (population, \(\sigma\)) | 5,79 | ||
| Variance (échantillon, \(s^2\)) | 38,29 | ||
| Écart-type (échantillon, \(s\)) | 6,19 | ||
| Coefficient de variation (\(\sigma / \mu\)) | 0,19 | ||
| Coefficient de variation (\(s / \bar{x}\)) | 0,20 |
Le tableau 2.4 vise à démontrer, à partir de trois variables, comment certaines mesures de dispersion sont sensibles à l’unité de mesure et/ou aux valeurs extrêmes.
Concernant l’unité de mesure, nous avons créé deux variables A et B, où B étant simplement A multipliée par 10. Pour A, les valeurs de la moyenne, de l’étendue et de l’intervalle interquartile sont respectivement 31, 18 et 10. Sans surprise, celles de B sont multipliées par 10 (310, 180, 100). La variance étant la moyenne des déviations à la moyenne au carré, elle est égale à 33,50 pour A et donc à \(\mbox{33,50}\times10^2=\mbox{3350}\) pour B; l’écart-type de B est égal à celui de A multiplié par 10. Cela démontre que l’étendue, l’intervalle interquartile, la variance et l’écart-type sont des mesures de dispersion dépendantes de l’unité de mesure. Par contre, étant donné que le coefficient de variation (CV) est le rapport de l’écart-type avec la moyenne, il a la même valeur pour A et B, ce qui démontre que le CV est bien une mesure de dispersion relative permettant de comparer des variables exprimées dans des unités de mesure différentes.
Concernant la sensibilité aux valeurs extrêmes, nous avons créé la variable C pour laquelle seule la huitième observation a une valeur différente (40 pour A et 105 pour B). Cette valeur de 105 pourrait être soit une valeur extrême positive mesurée, soit une valeur aberrante (par exemple, si l’unité de mesure était un pourcentage variant de 0 à 100 %). Cette valeur a un impact important sur la moyenne (31 contre 39,12) et l’étendue (18 contre 83) et corollairement sur la variance (33,50 contre 641,86), l’écart-type (5,79 contre 25,33) et le coefficient de variation (0,19 contre 0,65). Par contre, comme l’intervalle interquartile est calculé sur 50 % des observations centrales (\(\mbox{Q3}-\mbox{Q1}\)), il n’est pas affecté par cette valeur extrême.
| Observation | A | B | C |
|---|---|---|---|
| 1 | 22,00 | 220,00 | 22,00 |
| 2 | 25,00 | 250,00 | 25,00 |
| 3 | 27,00 | 270,00 | 27,00 |
| 4 | 30,00 | 300,00 | 30,00 |
| 5 | 32,00 | 320,00 | 32,00 |
| 6 | 35,00 | 350,00 | 35,00 |
| 7 | 37,00 | 370,00 | 37,00 |
| 8 | 40,00 | 400,00 | 105,00 |
| Statistique | |||
| Moyenne (\(\mu\)) | 31,00 | 310,00 | 39,12 |
| Étendue | 18,00 | 180,00 | 83,00 |
| Intervalle interquartile | 10,00 | 100,00 | 10,00 |
| Variance (population, \(\sigma^2\)) | 33,50 | 3 350,00 | 641,86 |
| Écart-type (population, \(\sigma\)) | 5,79 | 57,88 | 25,33 |
| Coefficient de variation (\(\sigma / \mu\)) | 0,19 | 0,19 | 0,65 |
| Statistique | Unité de mesure | Valeurs extrêmes |
|---|---|---|
| Moyenne | X | X |
| Étendue | X | X |
| Intervalle interquartile | X | |
| Variance | X | X |
| Écart-type | X | X |
| Coefficient de variation | X |
2.5.4 Paramètres de forme
2.5.4.1 Vérification de la normalité d’une variable quantitative
De nombreuses méthodes statistiques qui sont abordées dans les chapitres suivants – entre autres, la corrélation de Pearson, les test t et l’analyse de variance, les régressions simple et multiple – requièrent que la variable quantitative suive une distribution normale (nommée aussi distribution gaussienne).
Dans cette sous-section, nous décrivons trois démarches pour vérifier si la distribution d’une variable est normale : les coefficients d’asymétrie et d’aplatissement (skewness et kurtosis en anglais), les graphiques (histogramme avec courbe normale et diagramme quantile-quantile), les tests de normalité (tests de Shapiro-Wilk, de Kolmogorov-Smirnov, de Lilliefors, d’Anderson-Darling et de Jarque-Bera).
Il est vivement recommandé de réaliser les trois démarches!
Une distribution est normale quand elle est symétrique et mésokurtique (figure 2.26).
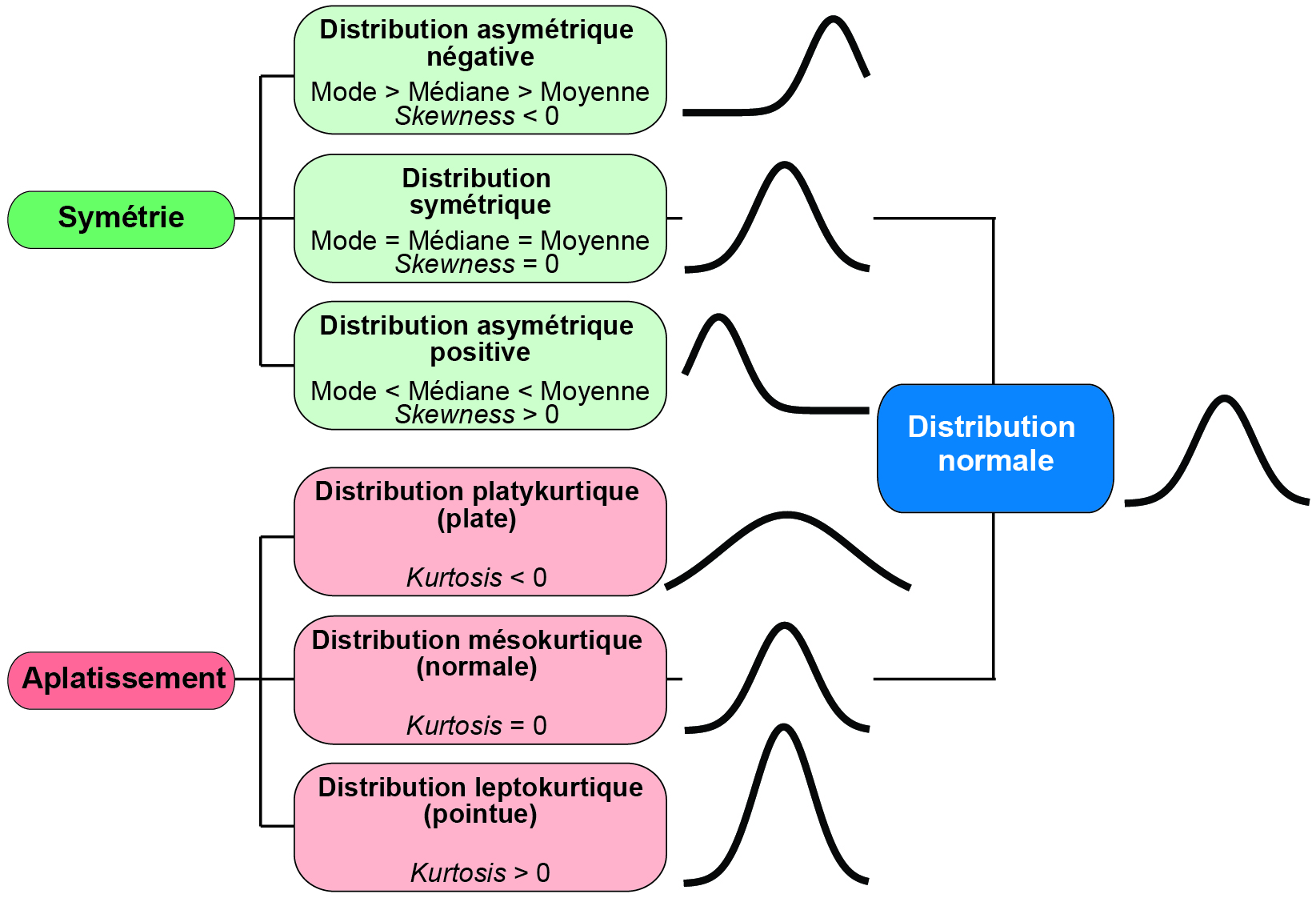
Figure 2.26: Formes d’une distribution et coefficients d’asymétrie et d’aplatissement
2.5.4.1.1 Vérification de la normalité avec les coefficients d’asymétrie et d’aplatissement
Une distribution est dite symétrique quand la moyenne arithmétique est au centre de la distribution, c’est-à-dire que les observations sont bien réparties de part et d’autre de la moyenne qui est alors égale à la médiane et au mode (nous utilisons uniquement le mode pour une variable discrète et non pour une variable continue). Pour évaluer l’asymétrie, nous utilisons habituellement le coefficient d’asymétrie (skewness en anglais).
Sachez toutefois qu’il existe trois façons (formules) pour le calculer (Joanes et Gill 1998) : \(g_1\) est la formule classique (équation (2.23)), disponible dans R avec la fonction skewness du package moments), \(G_1\) est une version ajustée (équation (2.24)), utilisée dans les logiciels SAS et SPSS notamment) et \(b_1\) est une autre version ajustée (équation (2.25)), utilisée par les logiciels MINITAB et BMDP). Nous verrons qu’avec les packages DescTools ou e1071, il est possible de calculer ces trois méthodes. Aussi, pour des grands échantillons (\(n>100\)), il y a très peu de différences entre les résultats produits par ces trois formules (Joanes et Gill 1998). Quelle que soit la formule utilisée, le coefficient d’asymétrie s’interprète comme suit (figure 2.27) :
- Quand la valeur du skewness est négative, la distribution est asymétrique négative. La distribution est alors tirée à gauche par des valeurs extrêmes faibles, mais peu nombreuses. Nous employons souvent l’expression la queue de distribution est étirée vers la gauche. La moyenne est alors inférieure à la médiane.
- Quand la valeur du skewness est égale à 0, la distribution est symétrique (la médiane est égale à la moyenne). Pour une variable discrète, les valeurs du mode, de la moyenne et de la médiane sont égales.
- Quand la valeur du skewness est positive, la distribution est symétrique positive. La distribution est alors tirée à droite par des valeurs extrêmes fortes, mais peu nombreuses. La queue de distribution est alors étirée vers la droite et la moyenne est supérieure à la médiane. En sciences sociales, les variables de revenu (totaux ou d’emploi, des individus ou des ménages) ont souvent des distributions asymétriques positives : la moyenne est affectée par quelques observations avec des valeurs de revenu très élevées et est ainsi supérieure à la médiane. En études urbaines, la densité de la population pour des unités géographiques d’une métropole donnée (secteur de recensement par exemple) a aussi souvent une distribution asymétrique positive : quelques secteurs de recensement au centre de la métropole sont caractérisés par des valeurs de densité très élevées qui tirent la distribution vers la droite.
\[\begin{equation} g_1=\frac{ \frac{1}{n} \sum_{i=1}^n(x_i-\bar{x})^3} { \left[\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2\right] ^\frac{3}{2}} \tag{2.23} \end{equation}\]
\[\begin{equation} G_1= \frac{\sqrt{n(n-1)}}{n-2} g_1 \tag{2.24} \end{equation}\]
\[\begin{equation} b_1= \left( \frac{n-1}{n} \right) ^\frac{3}{2} g_1 \tag{2.25} \end{equation}\]
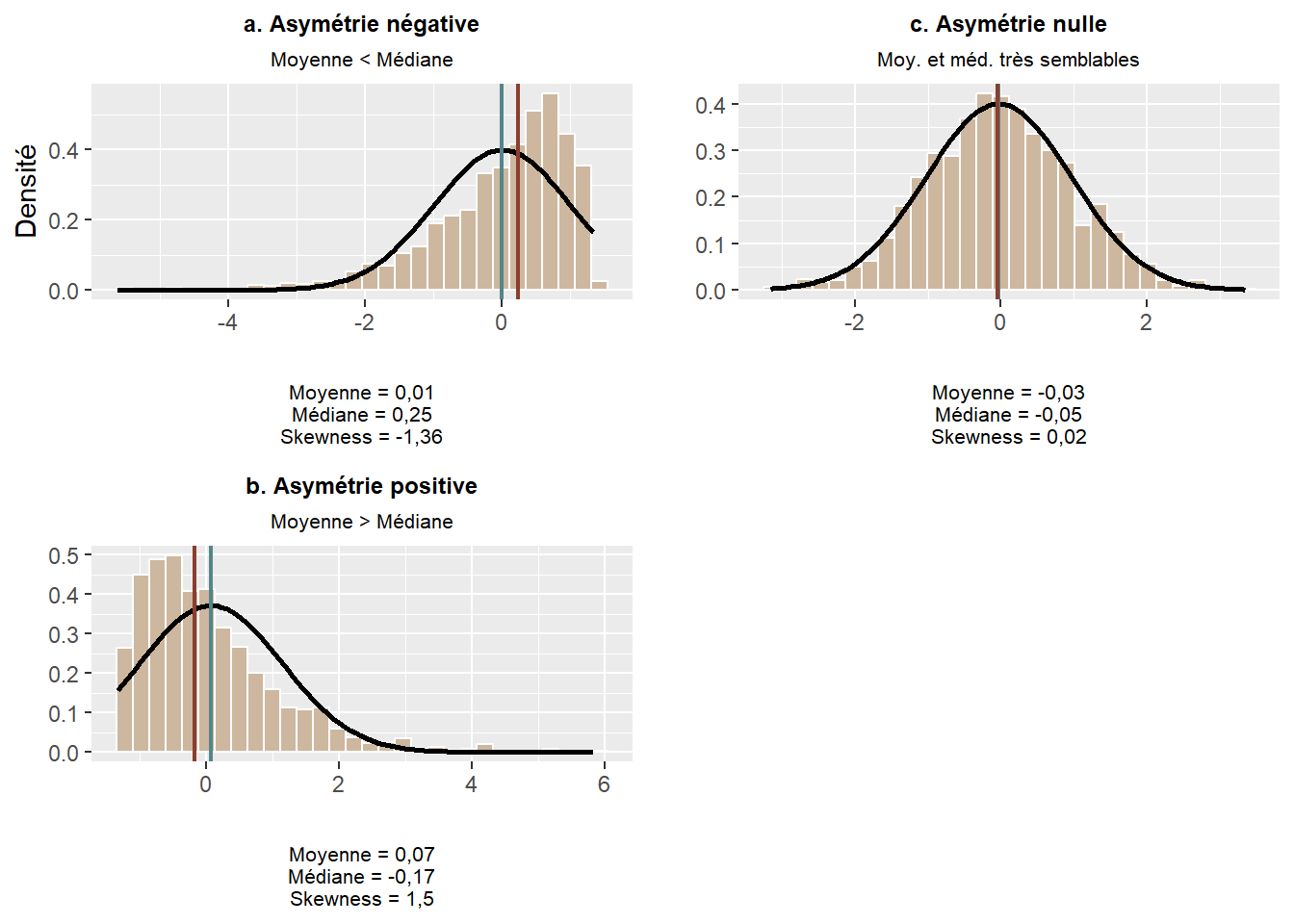
Figure 2.27: Asymétrie d’une distribution
Pour évaluer l’aplatissement d’une distribution, nous utilisons le coefficient d’aplatissement (kurtosis en anglais). Là encore, il existe trois formules pour le calculer (équation (2.26), (2.27), (2.28)) qui renvoient des valeurs très semblables pour de grands échantillons (Joanes et Gill 1998). Cette mesure s’interprète comme suit (figure 2.27) :
- Quand la valeur du kurtosis est négative, la distribution est platikurtique. La distribution est dite plate, c’est-à-dire que la valeur de l’écart-type est importante (comparativement à une distribution normale), signalant une grande dispersion des valeurs de part et d’autre la moyenne.
- Quand la valeur du kurtosis est égale à 0, la distribution est mésokurtique, ce qui est typique d’une distribution normale.
- Quand la valeur du kurtosis est positive, la distribution est leptokurtique, signalant que l’écart-type (la dispersion des valeurs) est plutôt faible. Autrement dit, la dispersion des valeurs autour de la moyenne est faible.
\[\begin{equation} g_2=\frac{\frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^4} {\left( \frac{1}{n}\sum_{i=1}^n(x_i-\bar{x})^2\right)^2}-3 \tag{2.26} \end{equation}\]
\[\begin{equation} G_2 = \frac{n-1}{(n-2)(n-3)} \{(n+1) g_2 + 6\} \tag{2.27} \end{equation}\]
\[\begin{equation} b_2 = (g_2 + 3) (1 - 1/n)^2 - 3 \tag{2.28} \end{equation}\]
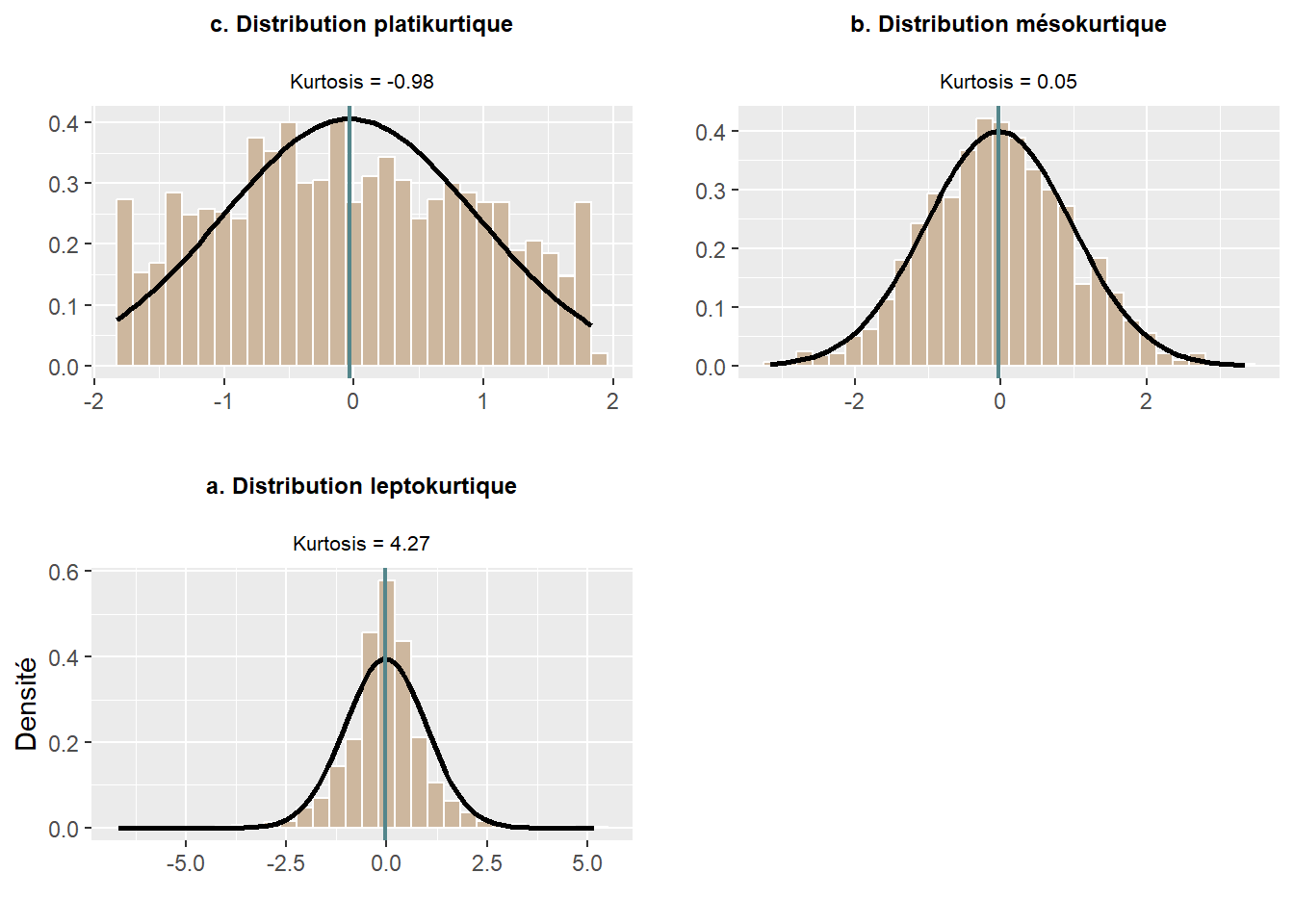
Figure 2.28: Applatissement d’une distribution
Regardez attentivement les équations (2.26), (2.27), (2.28); vous remarquez que pour \(g_2\) et \(b_2\), il y a une soustraction de 3 et une addition 6 pour \(G_2\). Nous parlons alors de kurtosis normalisé (excess kurtosis en anglais). Pour une distribution normale, il prend la valeur de 0, comparativement à la valeur de 3 pour un kurtosis non normalisé. Par conséquent, avant de calculer le kurtosis, il convient de s’assurer que la fonction que vous utilisez implémente une méthode de calcul normalisée (donnant une valeur de 0 pour une distribution normale). Par exemple, la fonction Kurt du package DescTools calcule les trois formules normalisées tandis que la fonction kurtosis du package moments renvoie un kurtosis non normalisé.
library(DescTools)
library(moments)
# Générer une variable normalement distribuée avec 1000 observations
Normale <- rnorm(1500,0,1)
round(DescTools::Kurt(Normale),3)## [1] 0.185round(moments::kurtosis(Normale),3)## [1] 3.192.5.4.1.2 Vérification de la normalité avec des graphiques
Les graphiques sont un excellent moyen de vérifier visuellement si une distribution est normale ou pas. Bien entendu, les histogrammes, que nous avons déjà largement utilisés, sont un incontournable. À titre de rappel, ils permettent de représenter la forme de la distribution des données (figure 2.29). Un autre type de graphique intéressant est le diagramme quantile-quantile (Q-Q plot en anglais), qui permet de comparer la distribution d’une variable avec une distribution gaussienne (normale). Trois éléments composent ce graphique comme qu’illustré à la figure 2.30 :
- les points, représentant les observations de la variable;
- la distribution gaussienne (normale), représentée par une ligne;
- l’intervalle de confiance à 95 % de la distribution normale (en marron sur la figure).
Quand la variable est normalement distribuée, les points sont situés le long de la ligne. Plus les points localisés en dehors de l’intervalle de confiance (bande marron) sont nombreux, plus la variable est alors anormalement distribuée.
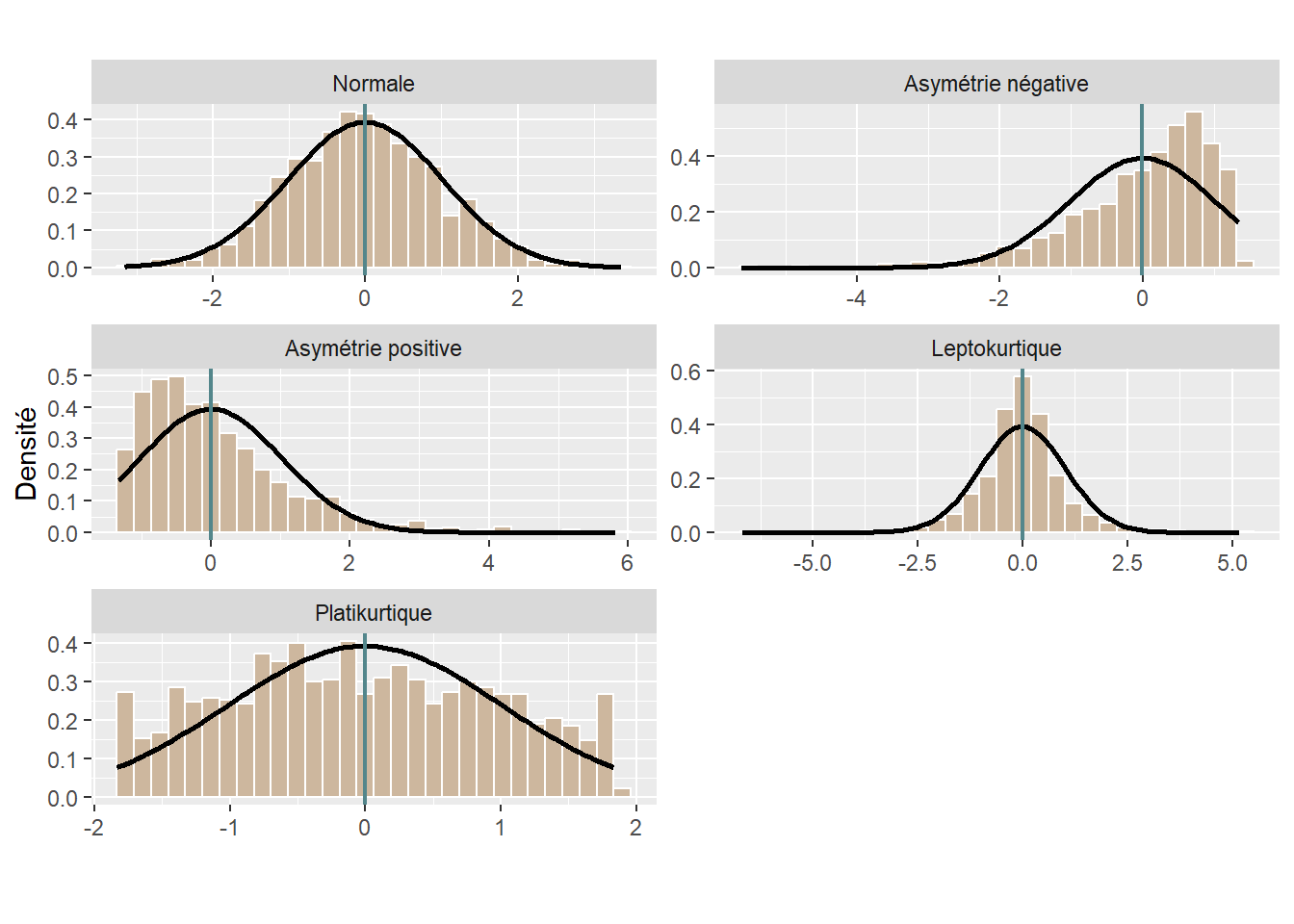
Figure 2.29: Histogrammes et courbe normale
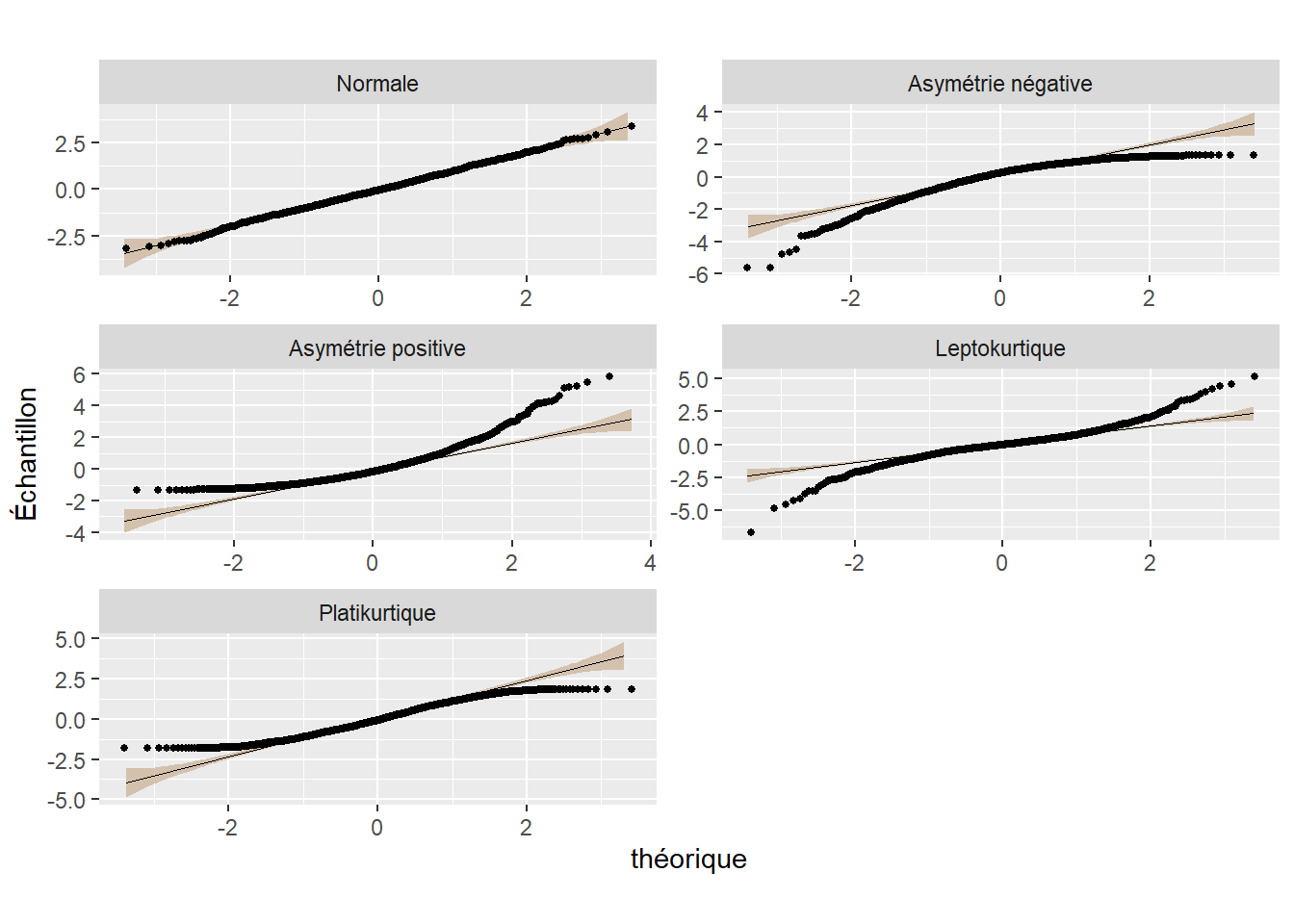
Figure 2.30: Diagrammes quantile-quantile
2.5.4.1.3 Vérification de la normalité avec des tests de normalité
Cinq principaux tests d’hypothèse permettent de vérifier la normalité d’une variable : les tests de Kolmogorov-Smirnov (KS), de Lilliefors (LF), de Shapiro-Wilk (SW), d’Anderson-Darling et de Jarque-Bera (JB). Sachez toutefois qu’il y en a d’autres non discutés ici (tests de d’Agostino–Pearson, de Cramer–von Mises, de Ryan-Joiner, de Shapiro–Francia, etc.). Pour les formules et une description détaillée de ces tests, vous pouvez consulter Razali et al. (2011) ou Yap et Sim (2011). Quel test choisir? Plusieurs auteur(e)s ont comparé ces différents tests à partir de plusieurs échantillons, et ce, en faisant varier la forme de la distribution et le nombre d’observations (Razali et Wah 2011; Yap et Sim 2011). Selon Razali et al. (2011), le meilleur test semble être celui de Shapiro-Wilk, puis ceux d’Anderson-Darling, de Lilliefors et de Kolmogorov-Smirnov. Yap et Sim (2011) concluent aussi que le Shapiro-Wilk semble être le plus performant.
Quoi qu’il en soit, ces cinq tests postulent que la variable suit une distribution gaussienne (hypothèse nulle, H0).
Cela signifie que si la valeur de p associée à la valeur de chacun des tests est inférieure ou égale au seuil alpha choisi (habituellement \(\alpha=\mbox{0,05}\)), la distribution est anormale. À l’inverse, si \(p>\mbox{0,05}\), la distribution est normale.
| Test | Propriétés et interprétation | Fonction R |
|---|---|---|
| Kolmogorov-Smirnov | Plus sa valeur est proche de zéro, plus la distribution est normale. L’avantage de ce test est qu’il peut être utilisé pour vérifier si une variable suit la distribution de n’importe quelle loi (autre que la loi normale). |
ks.test du package stats
|
| Lilliefors | Ce test est une adaptation du test de Kolmogorov-Smirnov. Plus sa valeur est proche de zéro, plus la distribution est normale. |
lillie.test du package nortest
|
| Shapiro-Wilk | Si la valeur de la statistique de Shapiro-Wilk est proche de 1, alors la distribution est normale; anormale quand elle est inférieure à 1. |
shapiro.test du package stats
|
| Anderson-Darling | Ce test est une modification du test de Cramer-von Mises (CVM). Il peut être aussi utilisé pour tester d’autres distributions (uniforme, log-normale, exponentielle, Weibull, distribution de pareto généralisée, logistique, etc.). |
ad.test du package stats
|
| Jarque-Bera | Basé sur un test du type multiplicateur de Lagrange, ce test utilise dans son calcul les valeurs du Skewness et du Kurtosis. Plus sa valeur s’approche de 0, plus la distribution est normale. Ce test est surtout utilisé pour vérifier si les résidus d’un modèle de régression linéaire sont normalement distribués; nous y reviendrons dans le chapitre sur la régression multiple. Il s’écrit \(JB=\frac{1}{6} \left({g_1}^2+\frac{{g_1}^2}{4} \right)\) avec \(g_1\) et \(g_2\) qui sont respectivement les valeurs du skewness et du kurtosis de la variable (voir les équations (2.23) et (2.26)). |
JarqueBeraTest du package DescTools
|
Dans le tableau 2.7 sont reportées les valeurs des différents tests pour les cinq types de distribution générés à la figure 2.29. Sans surprise, pour l’ensemble des tests, la valeur de p est inférieure à 0,05 pour la distribution normale.
| Normale | Asymétrie négative | Asymétrie positive | Leptokurtique | Platikurtique | |
|---|---|---|---|---|---|
| Skewness | 0,007 | 1,398 | -1,450 | -0,750 | -0,017 |
| Kurtosis | 0,167 | 2,323 | 3,215 | 9,690 | -1,023 |
| Kolmogorov-Smirnov (KS) | 0,026 | 0,121 | 0,108 | 0,088 | 0,044 |
| Lilliefors (LF) | 0,026 | 0,121 | 0,108 | 0,088 | 0,044 |
| Shapiro-Wilk (SW) | 0,998 | 0,891 | 0,898 | 0,913 | 0,968 |
| Anderson-Darling (AD) | 0,306 | 13,374 | 11,676 | 7,217 | 2,988 |
| Jarque-Bera (JB) | 0,632 | 441,316 | 559,918 | 3 570,539 | 15,770 |
| KS (valeur p) | 0,879 | 0,000 | 0,000 | 0,001 | 0,280 |
| LF (valeur p) | 0,546 | 0,000 | 0,000 | 0,000 | 0,020 |
| SW (valeur p) | 0,791 | 0,000 | 0,000 | 0,000 | 0,000 |
| AD (valeur p) | 0,565 | 0,000 | 0,000 | 0,000 | 0,000 |
| JB (valeur p) | 0,729 | 0,000 | 0,000 | 0,000 | 0,000 |
La plupart des auteurs s’entendent sur le fait que ces tests sont très restrictifs : plus la taille de votre échantillon est importante, plus les tests risquent de vous signaler que vos distributions sont anormales (à la lecture des valeurs de p).
Certains conseillent même de ne pas les utiliser quand \(n>200\) et de vous fier uniquement aux graphiques (histogramme et diagramme Q-Q)!
Bref, vérifier la normalité d’une variable n’est pas une tâche si simple. De nouveau, nous vous conseillons vivement de :
- Construire les graphiques pour analyser visuellement la forme de la distribution (histogramme avec courbe normale et diagramme Q-Q).
- Calculer le skewness et le kurtosis.
- Calculer plusieurs tests (minimalement Shapiro-Wilk et Kolmogorov-Smirnov).
- Accorder une importance particulière aux graphiques lorsque vous traitez de grands échantillons (\(n>200\)).
2.5.4.2 Tests pour d’autres formes de distribution
Comme nous l’avons vu, la distribution normale n’est que l’une des multiples distributions existantes. Dans de nombreuses situations, elle ne sera pas adaptée pour décrire vos variables. La démarche à adopter pour trouver une distribution adaptée est la suivante :
- Définissez la nature de votre variable : identifier si elle est discrète ou continue et l’intervalle dans lequel elle est définie. Une variable dont les valeurs sont positives ou négatives ne peut pas être décrite avec une distribution Gamma par exemple (à moins de la décaler).
- Explorez votre variable : affichez son histogramme et son graphique de densité pour avoir une vue générale de sa morphologie.
- Présélectionnez un ensemble de distributions candidates en tenant compte des observations précédentes. Vous pouvez également vous reporter à la littérature existante sur votre sujet d’étude pour inclure d’autres distributions. Soyez flexible! Une variable strictement positive pourrait tout de même avoir une forme normale. De même, une variable décrivant des comptages suffisamment grands pourrait être mieux décrite par une distribution normale qu’une distribution de Poisson.
- Tentez d’ajuster chacune des distributions retenues à vos données et comparez les qualités d’ajustements pour retenir la plus adaptée.
Pour ajuster une distribution à un jeu de données, il faut trouver les valeurs des paramètres de cette distribution qui lui permettent d’adopter une forme la plus proche possible des données. Nous appelons cette opération ajuster un modèle, puisque la distribution théorique est utilisée pour modéliser les données. L’ajustement des paramètres est un problème d’optimisation que plusieurs algorithmes sont capables de résoudre (gradient descent, Newton-Raphson method, Fisher scoring, etc.). Dans R, le package fitdistrplus permet d’ajuster pratiquement n’importe quelle distribution à des données en offrant plusieurs stratégies d’optimisation grâce à la fonction fitdist. Il suffit de disposer d’une fonction représentant la distribution de densité ou de masse de la distribution en question, généralement noté dnomdeladistribution (dnorm, dgamma, dpoisson, etc.) dans R. Notez que certains packages comme VGAM ou gamlss.dist ajoutent un grand nombre de fonctions de densité et de masse à celles déjà disponibles de base dans R.
Pour comparer l’ajustement de plusieurs distributions théoriques à des données, trois approches doivent être combinées :
- Observer graphiquement l’ajustement de la courbe théorique à l’histogramme des données. Cela permet d’éliminer au premier coup d’œil les distributions qui ne correspondent pas.
- Comparer les loglikelihood. Le loglikelihood est un score d’ajustement des distributions aux données. Pour faire simple, plus le loglikelihood est grand, plus la distribution théorique est proche des données. Référez-vous à l’encadré suivant pour une description plus en profondeur du loglikelihood.
- Utiliser le test de Kolmogorov-Smirnov pour déterminer si une distribution particulière est mieux ajustée pour les données.
Qu’est-ce-que le loglikelihood?
Le loglikelihood est une mesure de l’ajustement d’un modèle à des données. Il est utilisé à peu près partout en statistique. Comprendre sa signification est donc un exercice important pour développer une meilleure intuition du fonctionnement général de nombreuses méthodes. Si les concepts de fonction de densité et de fonction de masse vous semblent encore flous, reportez-vous à la section 2.4 sur les distributions dans un premier temps.
Admettons que nous disposons d’une variable continue v que nous tentons de modéliser avec une distribution d (il peut s’agir de n’importe quelle distribution). d a une fonction de densité avec laquelle il est possible de calculer, pour chacune des valeurs de v, la probabilité d’être observée selon le modèle d.
Prenons un exemple concret dans R. Admettons que nous avons une variable comprenant 10 valeurs (oui, c’est un petit échantillon, mais c’est pour faire un exemple simple).
v <- c(5,8,7,8,10,4,7,6,9,7)
moyenne <- mean(v)
ecart_type <- sd(v)En calculant la moyenne et l’écart-type de la variable, nous obtenons les paramètres d’une distribution normale que nous pouvons utiliser pour représenter les données observées. En utilisant la fonction dnorm (la fonction de densité de la distribution normale), nous pouvons calculer la probabilité d’observer chacune des valeurs de v selon cette distribution normale.
probas <- dnorm(v, moyenne, ecart_type)
df <- data.frame(valeur = v,
proba = probas)
print(df)## valeur proba
## 1 5 0.11203710
## 2 8 0.19624888
## 3 7 0.22228296
## 4 8 0.19624888
## 5 10 0.06009897
## 6 4 0.04985613
## 7 7 0.22228296
## 8 6 0.18439864
## 9 9 0.12689976
## 10 7 0.22228296Nous observons ainsi que les valeurs 7 et 8 sont très probables selon le modèle alors que les valeurs 4 et 10 sont très improbables.
Le likelihood est simplement le produit de toutes ces probabilités. Il s’agit donc de la probabilité conjointe d’avoir observé toutes les valeurs de v sous l’hypothèse que d est la distribution produisant ces valeurs. Si d décrit efficacement v, alors le likelihood est plus grand que si d ne décrit pas efficacement v. Il s’agit d’une forme de raisonnement par l’absurde : après avoir observé v, nous calculons la probabilité d’avoir observé v (likelihood) si notre modèle d était vrai. Si cette probabilité est très basse, alors c’est que notre modèle est mauvais puisqu’on a bien observé v.
likelihood_norm <- prod(probas)
print(likelihood_norm)## [1] 3.322759e-09Cependant, multiplier un grand nombre de valeurs inférieures à zéro tend à produire des chiffres infiniment petits et donc à complexifier grandement le calcul. Nous préférons donc utiliser le loglikelihood : l’idée étant transformer les probabilités obtenues avec la fonction log puis d’additionner leurs résultats, puisque \(log(xy) = log(x)+log(y)\).
loglikelihood_norm <- sum(log(probas))
print(loglikelihood_norm)## [1] -19.52247Comparons ce loglikelihood à celui d’un second modèle dans lequel nous utilisons toujours la distribution normale, mais avec une moyenne différente (faussée en ajoutant +3) :
probas2 <- dnorm(v, moyenne+3, ecart_type)
loglikelihood_norm2 <- sum(log(probas2))
print(loglikelihood_norm2)## [1] -33.53631Ce second loglikehood est plus faible, indiquant clairement que le premier modèle est plus adapté aux données.
Passons à la pratique avec deux exemples.
2.5.4.2.1 Temps de retard des bus de la ville de Toronto
Analysons les temps de retard pris par les bus de la ville de Toronto lorsqu’un évènement perturbe la circulation. Ce jeu de données est disponible sur le site des données ouvertes de la Ville de Toronto. Compte tenu de la grande quantité d’observations, nous avons fait le choix de nous concentrer sur les évènements ayant eu lieu durant le mois de janvier 2019. Puisque la variable étudiée est une durée exprimée en minutes, elle est strictement positive (supérieure à 0), car un bus avec zéro minute de retard est à l’heure! Nous considérons également qu’un bus ayant plus de 150 minutes de retard (2 heures 30) n’est tout simplement pas passé (personne ne risque d’attendre 2 heures 30 pour prendre son bus). Commençons par charger les données et observer leur distribution empirique.
library(ggplot2)
# charger le jeu de données
data_trt_bus <- read.csv('data/univariee/bus-delay-2019_janv.csv', sep =';')
# retirer les observations aberrantes
data_trt_bus <- subset(data_trt_bus, data_trt_bus$Min.Delay > 0 &
data_trt_bus$Min.Delay < 150)
# représenter la distribution empirique du jeu de données
ggplot(data = data_trt_bus) +
geom_histogram(aes(x=Min.Delay, y = ..density..), bins = 40)+
geom_density(aes(x=Min.Delay), color = 'blue', bw = 2, size = 0.8)+
labs(x = 'temps de retard (en minutes)',
y = '')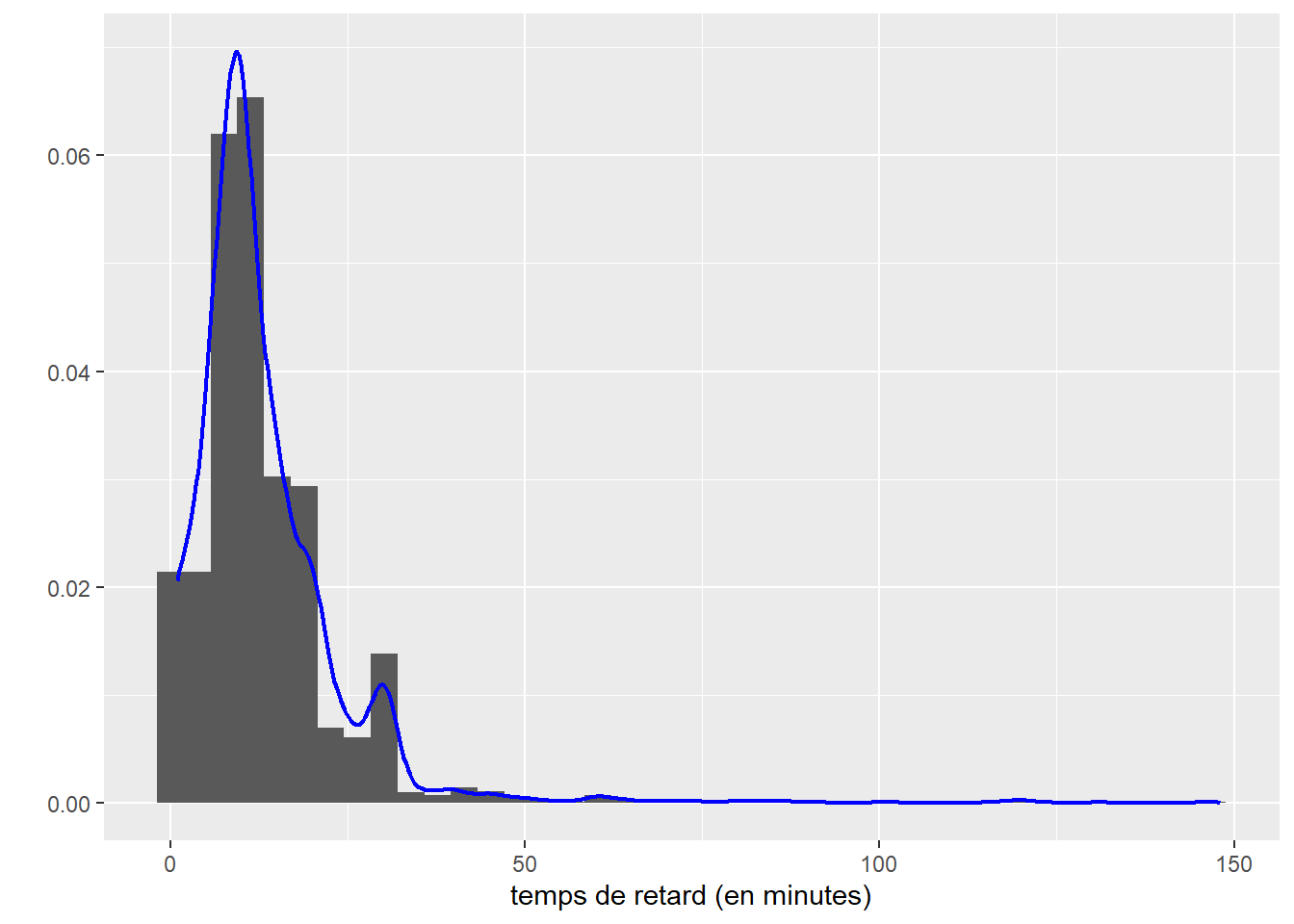
Figure 2.31: Distribution empirique des temps de retard des bus à Toronto en janvier 2019
Compte tenu de la forme de la distribution empirique et de sa nature, quatre distributions sont envisageables :
- La distribution Gamma, strictement positive et asymétrique, est aussi une généralisation de la distribution exponentielle utilisée pour modéliser des temps d’attente. Pour des raisons similaires, nous pouvons aussi retenir la distribution de Weibull et la distribution log-normale. Nous écartons ici la distribution normale asymétrique puisque le jeu de données n’a clairement pas une forme normale au départ.
- La distribution de Pareto, strictement positive et permettant de représenter ici le fait que la plupart des retards durent moins de 10 minutes, mais que quelques retards sont également beaucoup plus longs.
Commençons par ajuster les quatre distributions avec la fonction fitdist du package fitdistrplus et représentons-les graphiquement pour éliminer les moins bons candidats. Nous utilisons également le package actuar pour la fonction de densité de Pareto (dpareto).
library(fitdistrplus)
library(actuar)
library(ggpubr)
# ajustement des modèles
model_gamma <- fitdist(data_trt_bus$Min.Delay, distr = "gamma")
model_weibull <- fitdist(data_trt_bus$Min.Delay, distr = "weibull")
model_lognorm <- fitdist(data_trt_bus$Min.Delay, distr = "lnorm")
model_pareto <- fitdist(data_trt_bus$Min.Delay, distr = "pareto",
start = list(shape = 1, scale = 1),
method = "mse") # différentes méthodes d'optimisations
# réalisation des graphiques
plot1 <- ggplot(data = data_trt_bus) +
geom_histogram(aes(x=Min.Delay, y = ..density..), bins = 40)+
stat_function(fun = dgamma, color = 'red', size = 0.8,
args = as.list(model_gamma$estimate))+
labs(x = 'temps de retard (en minutes)',
y = '',
subtitle = "Modèle Gamma")
plot2 <- ggplot(data = data_trt_bus) +
geom_histogram(aes(x=Min.Delay, y = ..density..), bins = 40)+
stat_function(fun = dweibull, color = 'red', size = 0.8,
args = as.list(model_weibull$estimate))+
labs(x = 'temps de retard (en minutes)',
y = '',
subtitle = "Modèle Weibull")
plot3 <- ggplot(data = data_trt_bus) +
geom_histogram(aes(x=Min.Delay, y = ..density..), bins = 40)+
stat_function(fun = dlnorm, color = 'red', size = 0.8,
args = as.list(model_lognorm$estimate))+
labs(x = 'temps de retard (en minutes)',
y = '',
subtitle = "Modèle log-normal")
plot4 <- ggplot(data = data_trt_bus) +
geom_histogram(aes(x=Min.Delay, y = ..density..), bins = 40)+
stat_function(fun = dpareto, color = 'red', size = 0.8,
args = as.list(model_pareto$estimate))+
labs(x = 'temps de retard (en minutes)',
y = '',
subtitle = "Modèle Pareto")
ggarrange(plotlist = list(plot1, plot2, plot3, plot4),
ncol = 2, nrow = 2)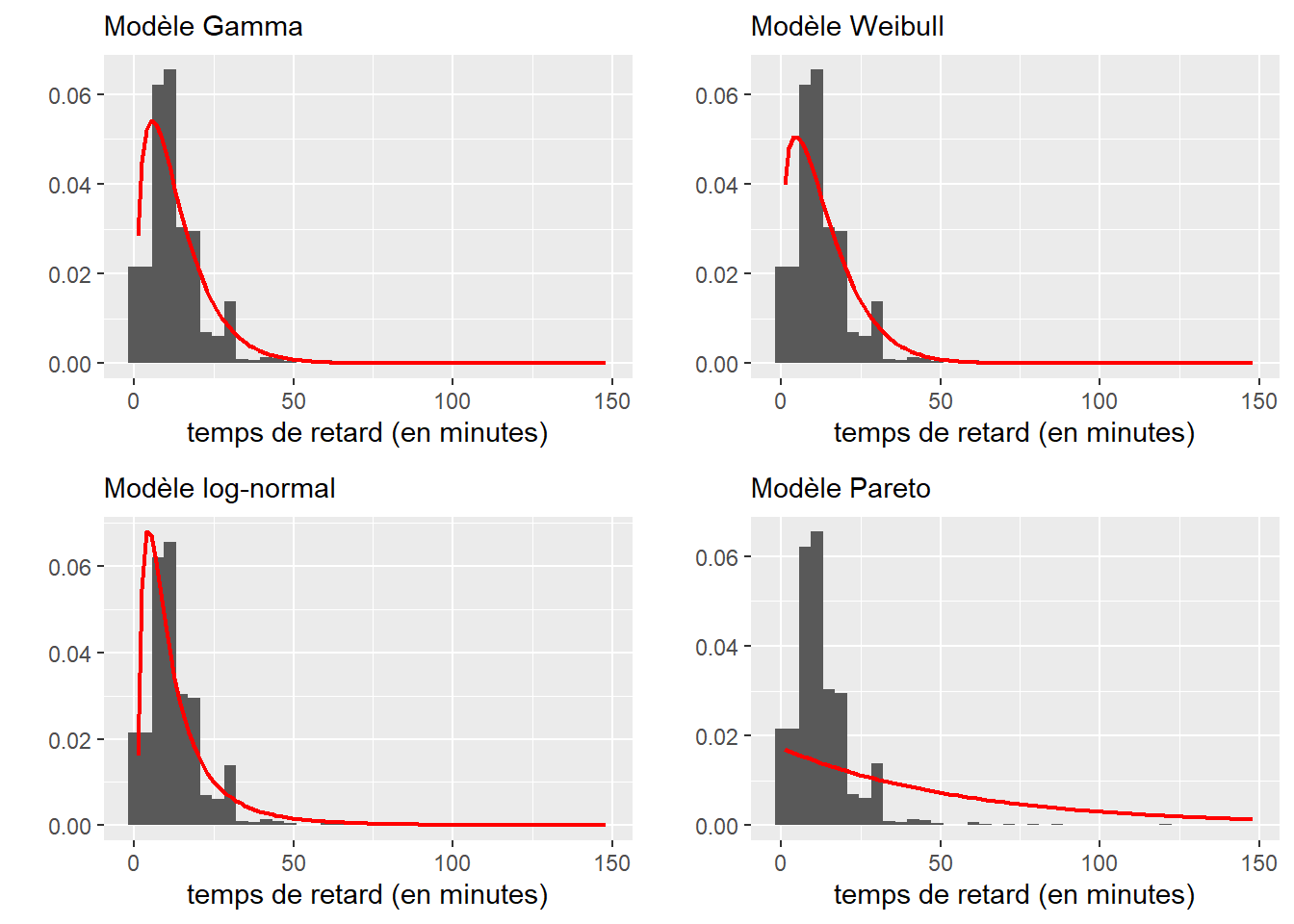
Figure 2.32: Comparaison des distributions ajustées aux données de retard des bus
Visuellement, nous constatons que la distribution de Pareto est un mauvais choix. Pour les trois autres distributions, la comparaison des valeurs de loglikelihood s’impose (tableau 2.8).
df <- data.frame(model = c("Gamma","Weibull",
"log-normal"),
loglikelihood = c(model_gamma$loglik,
model_weibull$loglik,
model_lognorm$loglik))
show_table(df,
col.names = c("Distribution","LogLikelihood"),
caption = 'Comparaison des LogLikelihood des trois distributions',
align= c("l", "r")
)| Distribution | LogLikelihood |
|---|---|
| Gamma | -23 062,56 |
| Weibull | -23 195,54 |
| log-normal | -23 375,74 |
Le plus grand logLikelihood est obtenu par la distribution Gamma qui s’ajuste donc le mieux à nos données. Pour finir, nous pouvons tester formellement, avec le test de Kolmogorov-Smirnov, si les données proviennent bien de cette distribution Gamma.
params <- as.list(model_gamma$estimate)
ks.test(data_trt_bus$Min.Delay,
y = pgamma, shape = params$shape, rate = params$rate)##
## Asymptotic one-sample Kolmogorov-Smirnov test
##
## data: data_trt_bus$Min.Delay
## D = 0.099912, p-value < 2.2e-16
## alternative hypothesis: two-sidedComme la valeur de p est inférieure à 0,05, nous ne pouvons pas accepter l’hypothèse que notre jeu de données suit effectivement un loi de Gamma. Considérant le nombre d’observations et le fait que de nombreux temps d’attente sont identiques (ce à quoi le test est très sensible), ce résultat n’est pas surprenant. La distribution Gamma reste cependant la distribution qui représente le mieux nos données. Nous pouvons estimer grâce, à cette distribution, la probabilité qu’un bus ait un retard de plus de 10 minutes de la façon suivante :
pgamma(10, shape = params$shape, rate = params$rate, lower.tail = F)## [1] 0.5409424ce qui correspond à 54 % de chance.
Pour moins de 10 minutes :
pgamma(10, shape = params$shape, rate = params$rate, lower.tail = T)## [1] 0.4590576soit 46 %.
Un dernier exemple avec la probabilité qu’un retard dépasse 45 minutes :
pgamma(45, shape = params$shape, rate = params$rate, lower.tail = F)## [1] 0.01348194Soit seulement 1,3 %.
Par conséquent, si un matin à Toronto votre bus a plus de 45 minutes de retard, bravo, vous êtes tombé sur une des très rares occasions où un tel retard se produit!
2.5.4.2.2 Accidents de vélo à Montréal
Le second jeu de données représente le nombre d’accidents de la route impliquant un vélo sur les intersections dans les quartiers centraux de Montréal (2.33). Le jeu de données complet est disponible sur le site des données ouvertes de la Ville de Montréal. Puisque ces données correspondent à des comptages, la première distribution à envisager est la distribution de Poisson. Cependant, puisque nous aurons également un grand nombre d’intersections sans accident, il serait judicieux de tester la distribution de Poisson avec excès de zéro.
library(ggplot2)
# charger le jeu de données
data_accidents <- read.csv('data/univariee/accidents_mtl.csv', sep =',')
counts <- data.frame(table(data_accidents$nb_accident))
names(counts) <- c("nb_accident",'frequence')
counts$nb_accident <- as.numeric(as.character(counts$nb_accident))
counts$prop <- counts$frequence / sum(counts$frequence)
# représenter la distribution empirique du jeu de donnée
ggplot(data = counts) +
geom_bar(aes(x=nb_accident, weight = frequence), width = 0.5)+
labs(x = "nombre d'accidents",
y = 'fréquence')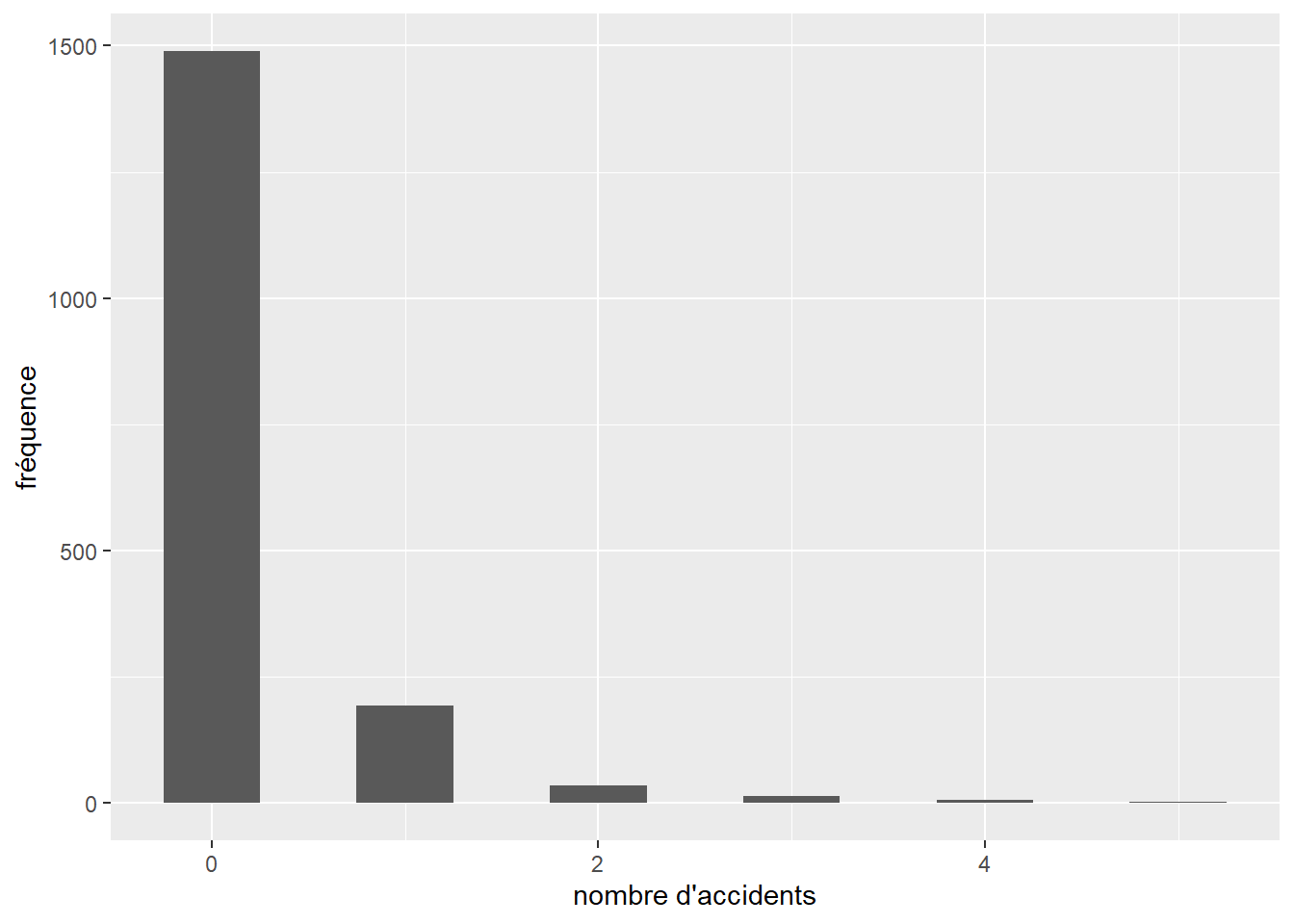
Figure 2.33: Distribution empirique du nombre d’accidents par intersection impliquant un ou une cycliste à Montréal en 2017 dans les quartiers centraux
Nous avons effectivement de nombreux zéros, alors essayons d’ajuster nos deux distributions à ce jeu de données. Dans la figure 2.34, les barres grises représentent la distribution empirique du jeu de données et les barres rouges, les distributions théoriques ajustées. Nous utilisons ici le package gamlss.dist pour avoir la fonction de masse d’une distribution de Poisson avec excès de zéros.
library(gamlss.dist)
#ajuster le modèle de poisson
model_poisson <- fitdist(data_accidents$nb_accident, distr = "pois")
#ajuster le modèle de poisson avec excès de zéros
model_poissonzi <- fitdist(data_accidents$nb_accident, "ZIP",
start = list(mu = 4, sigma = 0.15), # valeurs pour faciliter la convergence
optim.method = "L-BFGS-B", # méthode d'optimisation recommandée dans la documentation
lower = c(0.00001, 0.00001), # valeurs minimales des deux paramètres
upper = c(Inf, 1)# valeurs maximales des deux paramètres
)
dfpoisson <- data.frame(x=c(0:10),
y=dpois(0:10, model_poisson$estimate)
)
plot1 <- ggplot() +
geom_bar(aes(x=nb_accident, weight = prop), width = 0.6, data = counts)+
geom_bar(aes(x=x, weight = y), width = 0.15, data = dfpoisson, fill = "red")+
scale_x_continuous(limits = c(-0.5,7), breaks = c(0:7))+
labs(subtitle = "Modèle de Poisson",
x = "nombre d'accidents",
y = "")
dfpoissonzi <- data.frame(x=c(0:10),
y=dZIP(0:10, model_poissonzi$estimate[[1]],
model_poissonzi$estimate[[2]])
)
plot2 <- ggplot() +
geom_bar(aes(x=nb_accident, weight = prop), width = 0.6, data = counts)+
geom_bar(aes(x=x, weight = y), width = 0.15, data = dfpoissonzi, fill = "red")+
scale_x_continuous(limits = c(-0.5,7), breaks = c(0:7))+
labs(subtitle = "Modèle de Poisson avec excès de zéro",
x = "nombre d'accident",
y = "")
ggarrange(plotlist = list(plot1,plot2), ncol = 2)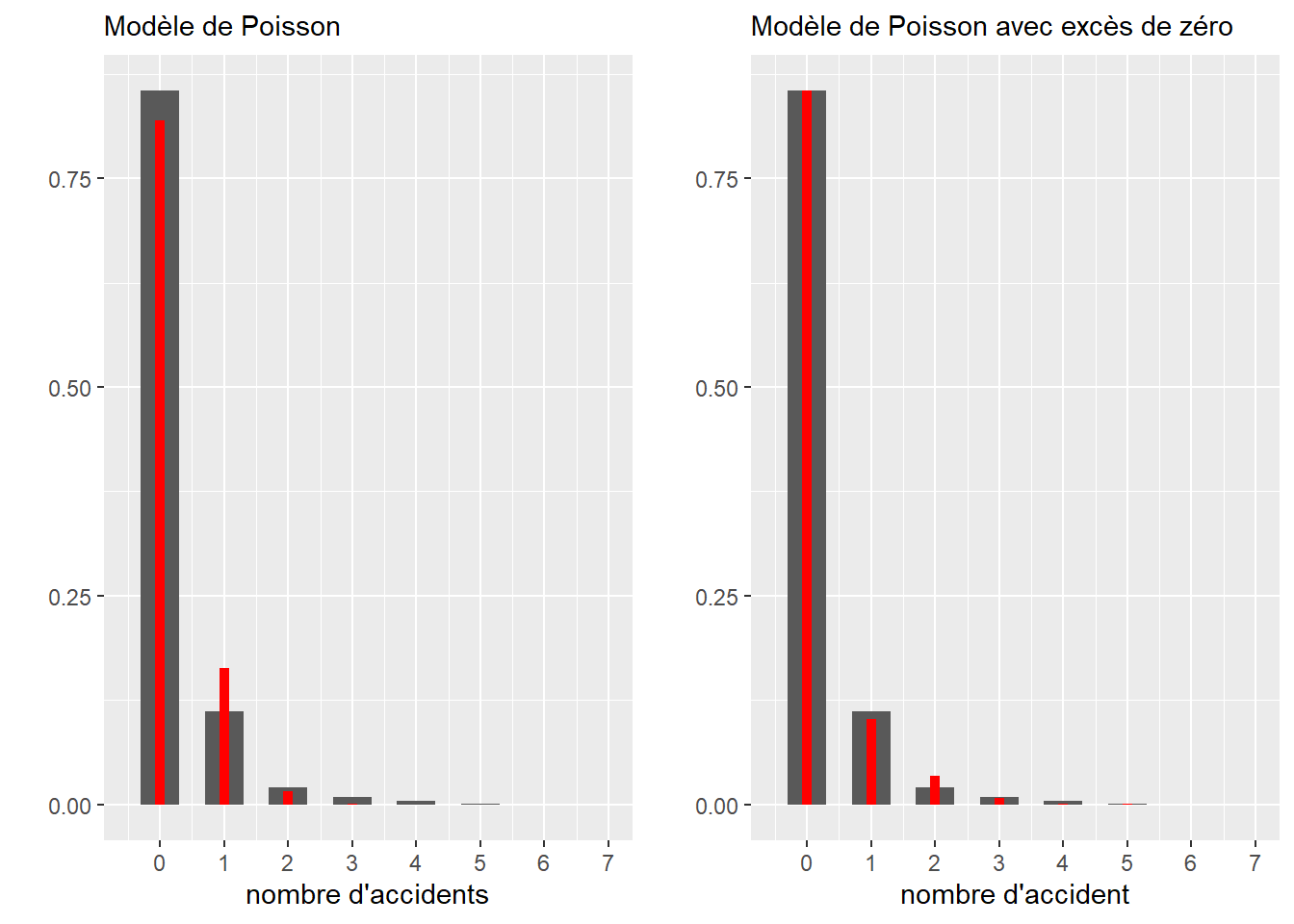
Figure 2.34: Ajustement des distributions de Poisson et Poisson avec excès de zéros
Visuellement, comme nous pouvons l’observer à la figure 2.34, le modèle avec excès de zéro semble s’imposer. Nous pouvons vérifier cette impression avec la comparaison des loglikelihood.
print(model_poisson$loglik)## [1] -989.83print(model_poissonzi$loglik)## [1] -931.8778#afficher les paramètres ajustés
model_poisson$estimate## lambda
## 0.1991963model_poissonzi$estimate## mu sigma
## 0.6690301 0.7022605Nous avons donc la confirmation que le modèle de Poisson avec excès de zéros est mieux ajusté. Nous apprenons donc que 70 % (sigma = 0,70) des intersections sont en fait exclues du phénomène étudié (probablement parce que très peu de cyclistes les utilisent ou parce qu’elles sont très peu accidentogènes) et que pour les autres, le taux d’accidents par année en 2017 était de 0,67 (mu = 0,669, mu signifiant \(\lambda\) pour le package gamlss). À nouveau, nous pouvons effectuer un test formel avec le fonction ks.test.
params <- as.list(model_poissonzi$estimate)
ks.test(data_accidents$nb_accident,
y = pZIP, mu = params$mu, sigma = params$sigma)##
## Asymptotic one-sample Kolmogorov-Smirnov test
##
## data: data_accidents$nb_accident
## D = 0.85476, p-value < 2.2e-16
## alternative hypothesis: two-sidedEncore une fois, nous devons rejeter l’hypothèse selon laquelle le test suit une distribution de Poisson avec excès de zéros. Ces deux exemples montrent à quel point ce test est restrictif.
2.5.5 Transformation des variables
2.5.5.1 Transformations visant à atteindre la normalité
Comme énoncé au début de cette section, plusieurs méthodes statistiques nécessitent que la variable quantitative soit normalement distribuée. C’est notamment le cas de l’analyse de variance et des tests t (abordés dans les chapitres suivants) qui fournissent des résultats plus robustes lorsque la variable est normalement distribuée. Plusieurs transformations sont possibles, les plus courantes étant la racine carrée, le logarithme et l’inverse de la variable. Selon plusieurs auteur(e)s (notamment, les statisticiennes Barbara G. Tabacknick et Linda S. Fidell (2007, 89)), en fonction du type (positive ou négative) et du degré d’asymétrie, les transformations suivantes sont possibles afin d’améliorer la normalité de la variable :
- Asymétrie positive modérée : la racine carrée de la variable X avec la fonction
sqrt(df$x). - Asymétrie positive importante : le logarithme de la variable avec
log10(df$x). - Asymétrie positive sévère : l’inverse de la variable avec
1/(df$x).
Pour une valeur égale ou inférieure à 0, nous ne pouvons pas calculer une racine carrée ou un logarithme. Par conséquent, il convient de décaler simplement la distribution vers la droite afin de s’assurer qu’il n’y ait plus de valeurs négatives ou égales à 0 :
sqrt(df$x - min(df$x+1))pour une asymétrie positive avec des valeurs négatives ou égales à 0log(df$x - min(df$x+1))pour une asymétrie positive avec des valeurs négatives ou égales à 0
Par exemple, si la valeur minimale de la variable est égale à -10, la valeur minimale de variable décalée sera ainsi de 11.
- Asymétrie négative modérée :
sqrt(max(df$x+1) - df$x) - Asymétrie négative importante :
log(max(df$x+1) - df$x) - Asymétrie négative sévère :
1/(max(df$x+1) - df$x)
Transformation des variables pour atteindre la normalité : ce n’est pas toujours la panacée!
La transformation des données fait et fera encore longtemps débat à la fois parmi les statisticien(ne)s, et les personnes utilisatrices débutantes ou avancées des méthodes quantitatives. Field et al. (2012, 193) résument le tout avec humour : « to transform or not transform, that is the question ».
Avantages de la transformation
- L’obtention de résultats plus robustes.
- Dans une régression linéaire multiple, la transformation de la variable dépendante peut remédier au non-respect des hypothèses de base liées à la régression (linéarité et homoscédasticité des erreurs, absence de valeurs aberrantes, etc.).
Inconvénients de la transformation
Une variable transformée est plus difficile à interpréter puisque cela change l’unité de mesure de la variable. Prenons un exemple concret : vous souhaitez comparer les moyennes de revenu de deux groupes A et B. Vous obtenez une différence de 15 000 $, soit une valeur facile à interpréter. Par contre, si la variable a été préalablement transformée en logarithme, il est possible que vous obteniez une différence de 9, ce qui est beaucoup moins parlant. Aussi, en transformant la variable en log, vous ne comparez plus les moyennes arithmétiques des deux groupes, mais plutôt leurs moyennes géométriques (Field, Miles et Field 2012, 193).
Pourquoi perdre la forme initiale de la distribution du phénomène à expliquer? Il est possible, pour de nombreuses méthodes de choisir la distribution que nous souhaitons utiliser, il n’est donc pas nécessaire de toujours se limiter à la distribution normale. Par exemple, dans les modèles de régression généralisés (GLM), nous pourrions indiquer que la variable indépendante suit une distribution de Student plutôt que de vouloir à tout prix la rendre normale. De même, certains tests non paramétriques permettent d’analyser des variables ne suivant pas une distribution normale.
Démarche à suivre avant et après la transformation
La transformation est-elle nécessaire? Ne transformez jamais une variable sans avoir analysé rigoureusement sa forme (histogramme avec courbe normale, skewness et kurtosis, tests de normalité).
D’autres options à la transformation d’une variable dépendante (VD) sont-elles envisageables? Identifiez la forme de la distribution de la VD et utilisez au besoin un modèle GLM adapté à cette distribution. Autrement dit, ne transformez pas automatiquement votre VD simplement pour l’introduire dans une régression linéaire multiple.
La transformation a-t-elle un apport significatif? Premièrement, vérifiez si la transformation utilisée (logarithme, racine carrée, inverse, etc.) améliore la normalité de la variable. Ce n’est pas toujours le cas, parfois c’est pire! Prenez soin de comparer les histogrammes, les valeurs de skewness, de kurtosis et des différents tests de normalité avant et après la transformation. Deuxièmement, comparez les résultats de vos analyses statistiques sans et avec transformation, et ce, dans une démarche coût-avantage. Vos résultats sont-ils bien plus robustes? Par exemple, un R2 qui passe de 0,597 à 0,602 (avant et après la transformation des variables) avec des associations significatives similaires, mais qui sont plus difficiles à interpréter (du fait des transformations), n’est pas forcément un gain significatif. La modélisation en sciences sociales ne vise pas à prédire la trajectoire d’un satellite ou l’atterrissage d’un engin sur Mars! La précision à la quatrième décimale n’est pas une condition! Par conséquent, un modèle un peu moins robuste, mais plus facile à interpréter est parfois préférable.
2.5.5.2 Autres types de transformations
Les trois transformations les plus couramment utilisées sont :
- La côte \(z\) (z score en anglais) qui consiste à soustraire à chaque valeur sa moyenne (soit un centrage), puis à la diviser par son écart-type (soit une réduction) (équation (2.29)). Par conséquent, nous parlons aussi de variable centrée réduite qui a comme propriétés intéressantes une moyenne égale à 0 et un écart-type égal à 1 (la variance est aussi égale à 1 puisque 12 = 1). Nous verrons que cette transformation est largement utilisée dans les méthodes de classification (chapitre 13) et les méthodes factorielles (chapitre 12).
\[\begin{equation} z= \frac{x_i-\mu}{\sigma} \tag{2.29} \end{equation}\]
La transformation en rang qui consiste simplement à trier une variable en ordre croissant, puis à affecter le rang de chaque observation de 1 à \(n\). Cette transformation est très utilisée quand la variable est très anormalement distribuée, notamment pour calculer le coefficient de corrélation de Spearman (section 4.3.3) et certains tests non paramétriques (sections 6.1.2 et 6.2.2).
La transformation sur une échelle de 0 à 1 (ou de 0 à 100) qui consiste à soustraite à chaque observation la valeur minimale et à diviser le tout par l’étendue (équation (2.30)).
\[\begin{equation} X_{\in\lbrack0-1\rbrack}= \frac{x_i-max}{max-min} \text{ ou } X_{\in\lbrack0-100\rbrack}= \frac{x_i-min}{max-min}\times100 \tag{2.30} \end{equation}\]
| Observation | \(x_i\) | Côte \(z\) | Rang | 0 à 1 |
|---|---|---|---|---|
| 1 | 22,00 | -1,45 | 1 | 0,00 |
| 2 | 27,00 | -0,65 | 3 | 0,28 |
| 3 | 25,00 | -0,97 | 2 | 0,17 |
| 4 | 30,00 | -0,16 | 4 | 0,44 |
| 5 | 37,00 | 0,97 | 7 | 0,83 |
| 6 | 32,00 | 0,16 | 5 | 0,56 |
| 7 | 35,00 | 0,65 | 6 | 0,72 |
| 8 | 40,00 | 1,45 | 8 | 1,00 |
| Moyenne | 31,00 | 0,00 | ||
| Écart-type | 6,19 | 1,00 |
Pour un DataFrame, nommé df, comprenant une variable X, la syntaxe ci-dessous illustre comment obtenir quatre transformations (côte \(z\), rang, 0 à 1 et 0 à 100).
df2 <- data.frame(X = c(22,27,25,30,37,32,35,40))
# Transformation centrée réduite : côte Z
df2$zX <- (df2$X-mean(df2$X))/sd(df2$X)
# ou encore avec la fonction scale
df2$zX <- scale(df2$X, center = TRUE, scale = TRUE)
# Transformation en rang avec la fonction rank
df2$rX <- rank(df2$X)
# Transformation de 0 à 1 ou de 0 à 100
df2$X01 <- (df2$X-min(df2$X))/(max(df2$X)-min(df2$X))
df2$X0100 <- (df2$X-min(df2$X))/(max(df2$X)-min(df2$X))*100Ces trois transformations sont parfois utilisées pour générer un indice composite à partir de plusieurs variables ou encore dans une analyse de sensibilité avec les indices de Sobol (1993).
2.5.6 Mise en œuvre dans R
Il existe une multitude de packages dédiés au calcul des statistiques descriptives univariées. Par parcimonie, nous en utiliserons uniquement trois : DescTools, nortest et stats. Libre à vous de faire vos recherches sur Internet pour utiliser d’autres packages au besoin. Les principales fonctions que nous utilisons ici sont :
summary: pour obtenir un résumé sommaire des statistiques descriptives (minimum, Q1, Q2, Q3, maximum)mean: moyennemin: minimummax: maximumrange: minimum et maximumquantile: quartilesquantile((x, probs = seq(.0, 1, by = .2)): quintilesquantile((x, probs = seq(.0, 1, by = .1)): décilesvar: variancesd: écart-typeSkewdu packageDescTools: coefficient d’asymétrieKurtdu packageDescTools: coefficient d’aplatissementks.test(x, "pnorm", mean=mean(x), sd=sd(x))du packagenortest: test de Kolmogorov-Smirnovshapiro.testdu packageDescTools: test de Shapiro-Wilklillie.testdu packageDescTools: du packagenortest: test de Lillieforsad.testdu packageDescTools: test d’Anderson-DarlingJarqueBeraTestdu packageDescTools: test de Jarque-Bera
2.5.6.1 Application à une seule variable
Admettons que vous voulez obtenir des statistiques pour une seule variable présente dans un DataFrame (dataMTL$PctFRev) :
library(DescTools)
library(stats)
library(nortest)
# Importation du fichier csv dans un DataFrame
dataMTL <- read.csv("data/univariee/DataSR2016.csv")
# Tableau sommaire pour la variable PctFRev
summary(dataMTL$PctFRev)## Min. 1st Qu. Median Mean 3rd Qu. Max.
## 1.846 11.242 15.471 16.822 20.229 68.927# PARAMÈTRES DE TENDANCE CENTRALE
mean(dataMTL$PctFRev) # Moyenne## [1] 16.82247median(dataMTL$PctFRev) # Médiane## [1] 15.471# PARAMÈTRES DE POSITION
# Quartiles
quantile(dataMTL$PctFRev)## 0% 25% 50% 75% 100%
## 1.8460 11.2420 15.4710 20.2285 68.9270# Quintiles
quantile(dataMTL$PctFRev, probs = seq(.0, 1, by = .2))## 0% 20% 40% 60% 80% 100%
## 1.846 10.294 13.626 16.918 21.756 68.927# Déciles
quantile(dataMTL$PctFRev, probs = seq(.0, 1, by = .1))## 0% 10% 20% 30% 40% 50% 60% 70% 80% 90% 100%
## 1.846 8.402 10.294 12.172 13.626 15.471 16.918 18.868 21.756 26.854 68.927# Percentiles personnalisés avec apply
quantile(dataMTL$PctFRev, probs = c(0.01,.05,0.10,.25,.50,.75,.90,.95,.99))## 1% 5% 10% 25% 50% 75% 90% 95% 99%
## 5.2290 7.1470 8.4020 11.2420 15.4710 20.2285 26.8540 31.7530 45.6010# PARAMÈTRES DE DISPERSION
range(dataMTL$PctFRev) # Min et Max## [1] 1.846 68.927# Étendue
max(dataMTL$PctFRev)-min(dataMTL$PctFRev)## [1] 67.081# Écart interquartile
quantile(dataMTL$PctFRev)[4]-quantile(dataMTL$PctFRev)[2]## 75%
## 8.9865var(dataMTL$PctFRev) # Variance## [1] 66.62482sd(dataMTL$PctFRev) # Écart-type## [1] 8.162403sd(dataMTL$PctFRev) / mean(dataMTL$PctFRev) # CV## [1] 0.4852083# PARAMÈTRES DE FORME
Skew(dataMTL$PctFRev) # Skewness## [1] 1.67367Kurt(dataMTL$PctFRev) # Kurtosis## [1] 4.858815# TESTS D'HYPOTHÈSE SUR LA NORMALITÉ
# K-Smirnov
ks.test(dataMTL$PctFRev, "pnorm", mean=mean(dataMTL$PctFRev), sd=sd(dataMTL$PctFRev))##
## Asymptotic one-sample Kolmogorov-Smirnov test
##
## data: dataMTL$PctFRev
## D = 0.10487, p-value = 1.646e-09
## alternative hypothesis: two-sidedshapiro.test(dataMTL$PctFRev) ##
## Shapiro-Wilk normality test
##
## data: dataMTL$PctFRev
## W = 0.88748, p-value < 2.2e-16lillie.test(dataMTL$PctFRev) ##
## Lilliefors (Kolmogorov-Smirnov) normality test
##
## data: dataMTL$PctFRev
## D = 0.10487, p-value < 2.2e-16ad.test(dataMTL$PctFRev) ##
## Anderson-Darling normality test
##
## data: dataMTL$PctFRev
## A = 21.072, p-value < 2.2e-16JarqueBeraTest(dataMTL$PctFRev) ##
## Robust Jarque Bera Test
##
## data: dataMTL$PctFRev
## X-squared = 2173.1, df = 2, p-value < 2.2e-16Pour construire un histogramme avec la courbe normale, consultez la section 3.2.1.3 ou la syntaxe ci-dessous.
moyenne <- mean(dataMTL$PctFRev)
ecart_type <- sd(dataMTL$PctFRev)
ggplot(data = dataMTL) +
geom_histogram(aes(x = PctFRev, y = ..density..),
bins = 30, color = "#343a40", fill = "#a8dadc") +
labs(x="personnes à faible revenu (%)", y = "densité")+
stat_function(fun = dnorm, args = list(mean = moyenne, sd = ecart_type),
color = "#e63946", size = 1.2, linetype = "dashed")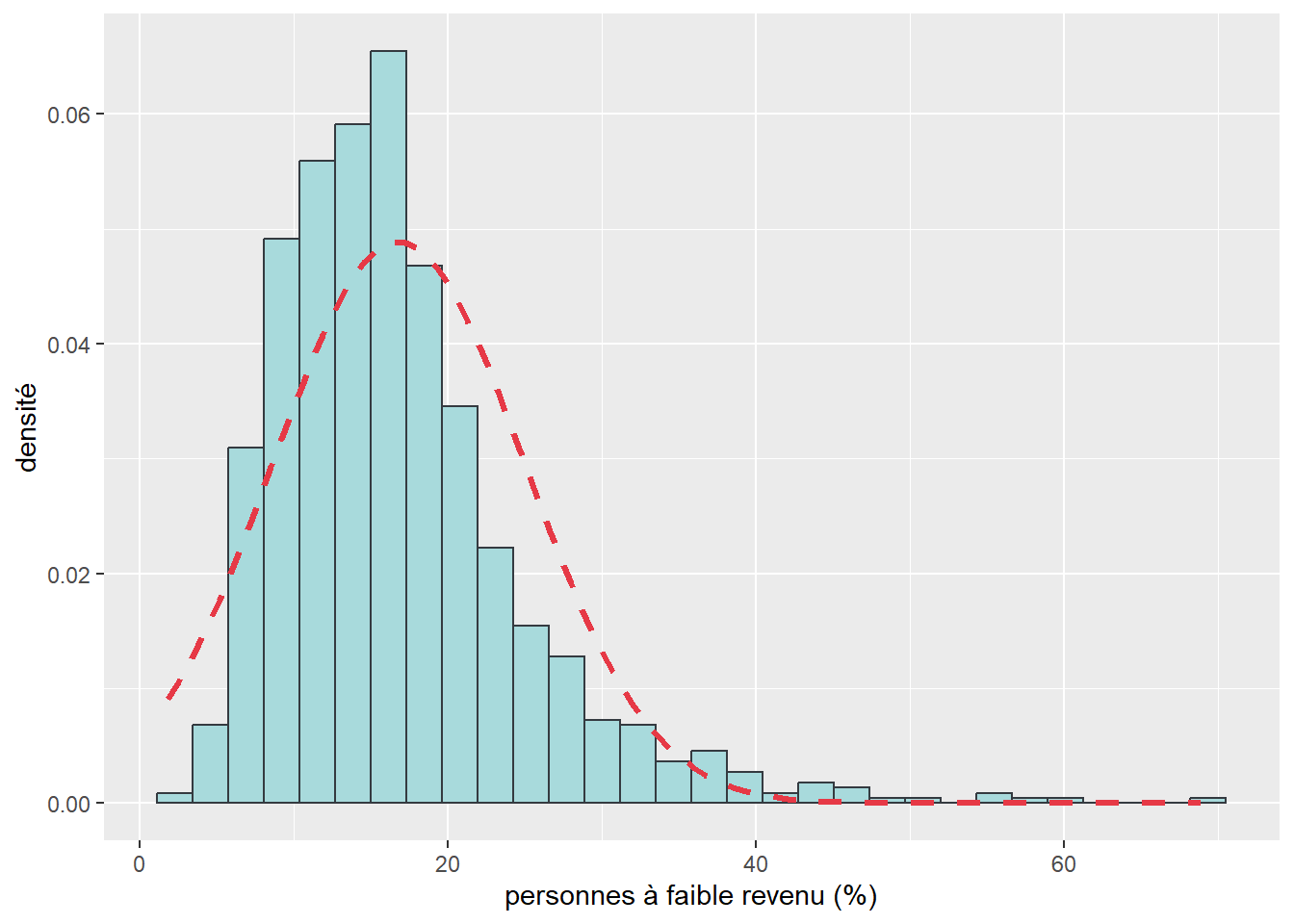
Figure 2.35: Histogramme avec courbe normale
2.5.6.2 Application à plusieurs variables
Pour obtenir des sorties de statistiques descriptives pour plusieurs variables, nous vous conseillons :
- de créer un vecteur avec les noms des variables (VarsSelect dans la syntaxe ci-dessous);
- d’utiliser ensuite les fonctions
sapplyetapply.
# Noms des variables du DataFrame
names(dataMTL)## [1] "CTNAME" "PopTotal" "HabKm2" "PctFRev"
## [5] "TxChomage" "PctImmigrant" "PctImgRecent" "PctMenage1pers"
## [9] "PctFamilleMono" "PctLangueMaternelleFR" "PctLangueMaternelleAN" "PctLangueMaternelleAU"# Vecteur pour trois variables
VarsSelect <- c("HabKm2", "TxChomage", "PctFRev" )
# Tableau sommaire pour les 3 variables
summary(dataMTL[VarsSelect])## HabKm2 TxChomage PctFRev
## Min. : 18 Min. : 1.942 Min. : 1.846
## 1st Qu.: 1980 1st Qu.: 5.482 1st Qu.:11.242
## Median : 3773 Median : 7.130 Median :15.471
## Mean : 5513 Mean : 7.743 Mean :16.822
## 3rd Qu.: 7916 3rd Qu.: 9.391 3rd Qu.:20.229
## Max. :50282 Max. :26.882 Max. :68.927# PARAMÈTRES DE TENDANCE CENTRALE
sapply(dataMTL[VarsSelect], mean) # Moyenne## HabKm2 TxChomage PctFRev
## 5512.830705 7.743329 16.822470sapply(dataMTL[VarsSelect], median) # Médiane## HabKm2 TxChomage PctFRev
## 3773.000 7.130 15.471# PARAMÈTRES DE POSITION
# Quartiles
sapply(dataMTL[VarsSelect], quantile)## HabKm2 TxChomage PctFRev
## 0% 18.0 1.9420 1.8460
## 25% 1980.5 5.4825 11.2420
## 50% 3773.0 7.1300 15.4710
## 75% 7915.5 9.3910 20.2285
## 100% 50282.0 26.8820 68.9270# Quintiles
apply(dataMTL[VarsSelect], 2, function(x) quantile(x, probs = seq(.0, 1, by = .2)))## HabKm2 TxChomage PctFRev
## 0% 18 1.942 1.846
## 20% 1525 5.116 10.294
## 40% 2953 6.422 13.626
## 60% 4971 7.973 16.918
## 80% 9509 10.000 21.756
## 100% 50282 26.882 68.927# Déciles
apply(dataMTL[VarsSelect], 2, function(x) quantile(x, probs = seq(.0, 1, by = .1)))## HabKm2 TxChomage PctFRev
## 0% 18 1.942 1.846
## 10% 455 4.369 8.402
## 20% 1525 5.116 10.294
## 30% 2298 5.780 12.172
## 40% 2953 6.422 13.626
## 50% 3773 7.130 15.471
## 60% 4971 7.973 16.918
## 70% 6918 8.909 18.868
## 80% 9509 10.000 21.756
## 90% 13055 11.749 26.854
## 100% 50282 26.882 68.927# Percentiles personnalisés avec apply
apply(dataMTL[VarsSelect], 2,
function(x) quantile(x, probs = c(0.01,.05,0.10,.25,.50,.75,.90,.95,.99)))## HabKm2 TxChomage PctFRev
## 1% 58.5 2.9665 5.2290
## 5% 178.0 3.8980 7.1470
## 10% 455.0 4.3690 8.4020
## 25% 1980.5 5.4825 11.2420
## 50% 3773.0 7.1300 15.4710
## 75% 7915.5 9.3910 20.2285
## 90% 13055.0 11.7490 26.8540
## 95% 15355.0 13.8400 31.7530
## 99% 18578.5 17.1920 45.6010# PARAMÈTRES DE DISPERSION
sapply(dataMTL[VarsSelect], range) # Min et Max## HabKm2 TxChomage PctFRev
## [1,] 18 1.942 1.846
## [2,] 50282 26.882 68.927# Étendue
sapply(dataMTL[VarsSelect], max) - sapply(dataMTL[VarsSelect], min)## HabKm2 TxChomage PctFRev
## 50264.000 24.940 67.081# Écart interquartile
sapply(dataMTL[VarsSelect], quantile)[4,] - sapply(dataMTL[VarsSelect], quantile)[2,]## HabKm2 TxChomage PctFRev
## 5935.0000 3.9085 8.9865sapply(dataMTL[VarsSelect], var) # Variance## HabKm2 TxChomage PctFRev
## 2.633462e+07 9.880932e+00 6.662482e+01sapply(dataMTL[VarsSelect], sd) # Écart-type## HabKm2 TxChomage PctFRev
## 5131.726785 3.143395 8.162403# Coefficient de variation
sapply(dataMTL[VarsSelect], sd) / sapply(dataMTL[VarsSelect], mean)## HabKm2 TxChomage PctFRev
## 0.9308696 0.4059488 0.4852083# PARAMÈTRES DE FORME
sapply(dataMTL[VarsSelect], Skew) # Skewness## HabKm2 TxChomage PctFRev
## 1.967468 1.280216 1.673670sapply(dataMTL[VarsSelect], Kurt) # Kurtosis## HabKm2 TxChomage PctFRev
## 8.546403 2.892443 4.858815# TESTS D'HYPOTHÈSE POUR LA NORMALITÉ
# K-Smirnov
apply(dataMTL[VarsSelect], 2, function(x) ks.test(x, "pnorm", mean=mean(x), sd=sd(x)))## $HabKm2
##
## Asymptotic one-sample Kolmogorov-Smirnov test
##
## data: x
## D = 0.14899, p-value < 2.2e-16
## alternative hypothesis: two-sided
##
##
## $TxChomage
##
## Asymptotic one-sample Kolmogorov-Smirnov test
##
## data: x
## D = 0.080183, p-value = 9.778e-06
## alternative hypothesis: two-sided
##
##
## $PctFRev
##
## Asymptotic one-sample Kolmogorov-Smirnov test
##
## data: x
## D = 0.10487, p-value = 1.646e-09
## alternative hypothesis: two-sidedsapply(dataMTL[VarsSelect], shapiro.test) # Shapiro-Wilk## HabKm2 TxChomage PctFRev
## statistic 0.8385086 0.9235146 0.8874803
## p.value 5.648795e-30 1.451222e-21 1.00278e-25
## method "Shapiro-Wilk normality test" "Shapiro-Wilk normality test" "Shapiro-Wilk normality test"
## data.name "X[[i]]" "X[[i]]" "X[[i]]"sapply(dataMTL[VarsSelect], lillie.test) # Lilliefors## HabKm2
## statistic 0.148988
## p.value 5.689619e-58
## method "Lilliefors (Kolmogorov-Smirnov) normality test"
## data.name "X[[i]]"
## TxChomage
## statistic 0.0801829
## p.value 7.758887e-16
## method "Lilliefors (Kolmogorov-Smirnov) normality test"
## data.name "X[[i]]"
## PctFRev
## statistic 0.1048704
## p.value 7.43257e-28
## method "Lilliefors (Kolmogorov-Smirnov) normality test"
## data.name "X[[i]]"sapply(dataMTL[VarsSelect], ad.test) # Anderson-Darling## HabKm2 TxChomage
## statistic 36.40276 14.9237
## p.value 3.7e-24 3.7e-24
## method "Anderson-Darling normality test" "Anderson-Darling normality test"
## data.name "X[[i]]" "X[[i]]"
## PctFRev
## statistic 21.07194
## p.value 3.7e-24
## method "Anderson-Darling normality test"
## data.name "X[[i]]"sapply(dataMTL[VarsSelect], JarqueBeraTest) # Jarque-Bera## HabKm2 TxChomage PctFRev
## statistic 4270.113 639.2741 2173.082
## parameter 2 2 2
## p.value 0 0 0
## method "Robust Jarque Bera Test" "Robust Jarque Bera Test" "Robust Jarque Bera Test"
## data.name "X[[i]]" "X[[i]]" "X[[i]]"2.5.6.3 Transformation d’une variable dans R
La syntaxe ci-dessous illustre trois exemples de transformation (logarithme, racine carrée et inverse de la variable). Rappelez-vous qu’il faut comparer les valeurs de skewness et de kurtosis et des tests de Shapiro-Wilk avant et après les transformations pour identifier celle qui est la plus efficace.
library(ggpubr)
# Importation du fichier csv dans un DataFrame
dataMTL <- read.csv("data/univariee/DataSR2016.csv")
# Noms des variables du DataFrame
names(dataMTL)## [1] "CTNAME" "PopTotal" "HabKm2" "PctFRev"
## [5] "TxChomage" "PctImmigrant" "PctImgRecent" "PctMenage1pers"
## [9] "PctFamilleMono" "PctLangueMaternelleFR" "PctLangueMaternelleAN" "PctLangueMaternelleAU"# Transformations
dataMTL$HabKm2_log <- log10(dataMTL$HabKm2)
dataMTL$HabKm2_sqrt <- sqrt(dataMTL$HabKm2)
dataMTL$HabKm2_inv <- 1/dataMTL$HabKm2
# Vecteur pour la variable et les trois transformations
VarsSelect <- c("HabKm2", "HabKm2_log", "HabKm2_sqrt", "HabKm2_inv")
# paramètres de forme
sapply(dataMTL[VarsSelect], Skew) # Skewness## HabKm2 HabKm2_log HabKm2_sqrt HabKm2_inv
## 1.9674683 -1.2071326 0.4179037 8.2536901sapply(dataMTL[VarsSelect], Kurt) # Kurtosis## HabKm2 HabKm2_log HabKm2_sqrt HabKm2_inv
## 8.54640302 1.55670769 0.04563433 82.85604898# TESTS D'HYPOTHÈSE SUR LA NORMALITÉ
sapply(dataMTL[VarsSelect], shapiro.test) ## HabKm2 HabKm2_log HabKm2_sqrt
## statistic 0.8385086 0.9113234 0.9771699
## p.value 5.648795e-30 4.11156e-23 4.638049e-11
## method "Shapiro-Wilk normality test" "Shapiro-Wilk normality test" "Shapiro-Wilk normality test"
## data.name "X[[i]]" "X[[i]]" "X[[i]]"
## HabKm2_inv
## statistic 0.2530266
## p.value 8.324983e-52
## method "Shapiro-Wilk normality test"
## data.name "X[[i]]"# Histogrammes avec courbe normale
Graph1 <- ggplot(data = dataMTL) +
geom_histogram(aes(x = HabKm2, y = ..density..),
bins = 30, color = "#343a40", fill = "#a8dadc") +
labs(x=expression("Habitants au km"^2),
y = "densité")+
stat_function(fun = dnorm,
args = list(mean = mean(dataMTL$HabKm2),
sd = sd(dataMTL$HabKm2)),
color = "#e63946", size = 1.2)
Graph2 <- ggplot(data = dataMTL) +
geom_histogram(aes(x = HabKm2_log, y = ..density..),
bins = 30, color = "#343a40", fill = "#a8dadc") +
labs(x=expression("Logarithme d'habitants au km"^2),
y = "densité")+
stat_function(fun = dnorm,
args = list(mean = mean(dataMTL$HabKm2_log),
sd = sd(dataMTL$HabKm2_log)),
color = "#e63946", size = 1.2)
Graph3 <- ggplot(data = dataMTL) +
geom_histogram(aes(x = HabKm2_sqrt, y = ..density..),
bins = 30, color = "#343a40", fill = "#a8dadc") +
labs(x=expression("Racine carrée d'habitants au km"^2),
y = "densité")+
stat_function(fun = dnorm,
args = list(mean = mean(dataMTL$HabKm2_sqrt),
sd = sd(dataMTL$HabKm2_sqrt)),
color = "#e63946", size = 1.2)
Graph4 <- ggplot(data = dataMTL) +
geom_histogram(aes(x = HabKm2_inv, y = ..density..),
bins = 30, color = "#343a40", fill = "#a8dadc") +
labs(x=expression("Inverse d'habitants au km"^2),
y = "densité")+
stat_function(fun = dnorm,
args = list(mean = mean(dataMTL$HabKm2_inv),
sd = sd(dataMTL$HabKm2_inv)),
color = "#e63946", size = 1.2)
ggarrange(plotlist = list(Graph1, Graph2, Graph3, Graph4), ncol = 2, nrow=2)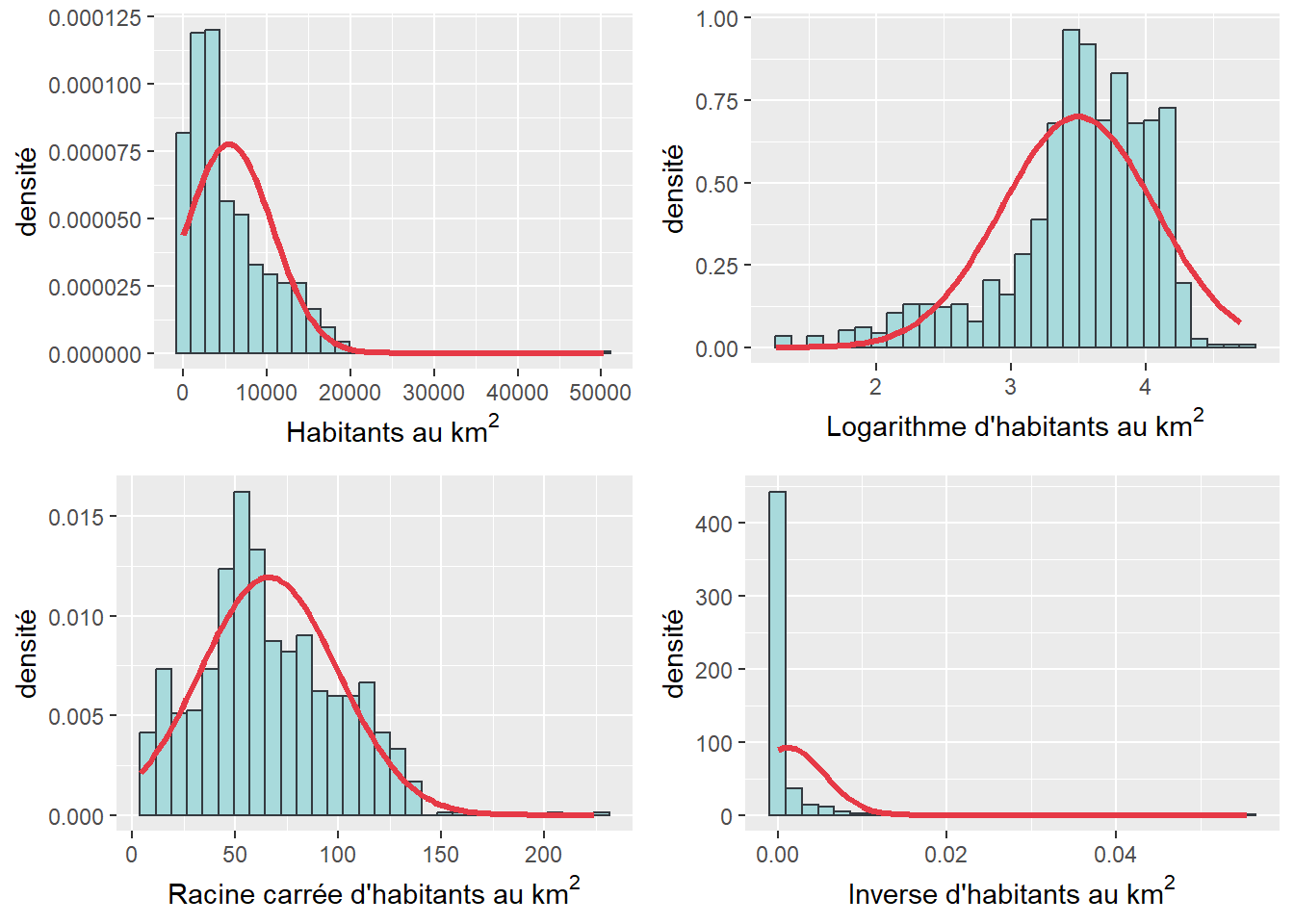
Figure 2.36: Histogramme des transformations
La variable HabKm2 est asymétrique positive et leptokurtique. Les valeurs des statistiques de forme et du test de Shapiro-Wilk ainsi que les histogrammes semblent démontrer que la transformation la plus efficace est la racine carrée. Si la variable originale est asymétrique positive, sa transformation logarithme est par contre asymétrique négative. Cela démontre que la transformation logarithmique n’est pas toujours la panacée.