7.7 Mise en œuvre dans R
7.7.1 Fonctions lm, summary() et confint()
Les fonctions de base lm, summary() et confint() permettent respectivement 1) de construire un modèle, 2) d’afficher ces résultats et 3) d’obtenir les intervalles de confiance des coefficients de régression :
monModele <- lm(Y ~X1+X2+..+Xk)avec Y étant la variable dépendante et les variables indépendantes (X1 à Xk) étant séparées par le signe +.summary(monModele)confint(monModele, level=.95).
Dans la syntaxe ci-dessous, vous retrouverez les différents modèles abordés dans les sections précédentes; remarquez que toutes que les lignes summary sont mises en commentaires afin de ne pas afficher les résultats des modèles.
# Chargement des données
load("data/lm/DataVegetation.RData")
# 1er modèle de régression
modele1 <- lm(VegPct ~ HABHA+AgeMedian+Pct_014+Pct_65P+Pct_MV+Pct_FR,
data = DataFinal)
# summary(Modele1)
# 2e modèle de régression : fonction polynomiale d'ordre 2 (poly(AgeMedian,2))
modele2 <- lm(VegPct ~ HABHA+poly(AgeMedian,2)+Pct_014+Pct_65P+Pct_MV+Pct_FR,
data = DataFinal)
# summary(Modele2)
# 3e modèle de régression : forme logarithmique (log(HABHA))
modele3 <- lm(VegPct ~ log(HABHA)+poly(AgeMedian,2)+Pct_014+Pct_65P+Pct_MV+Pct_FR,
data = DataFinal)
# summary(Modele3)
# 4e modèle de régression : VI dichotomique
# création de la variable dichotomique (VilleMtl)
DataFinal$VilleMtl <- ifelse(DataFinal$SDRNOM == "Montréal", 1, 0)
modele4 <- lm(VegPct ~ log(HABHA)+poly(AgeMedian,2)+Pct_014+Pct_65P+Pct_MV+Pct_FR+
VilleMtl, # variable dichotomique
data = DataFinal)
# summary(Modele4)
# 5e modèle de régression : VI polytomique
# création de la variable polytomique (Munic)
DataFinal$Munic <- relevel(DataFinal$SDRNOM, ref="Montréal")
modele5 <- lm(VegPct ~ log(HABHA)+poly(AgeMedian,2)+Pct_014+Pct_65P+Pct_MV+Pct_FR+
Munic, data = DataFinal)
# summary(Modele5)
# 6e modèle de régression : interaction entre deux VI continues,
# soit DistCBDkm*Pct_014
modele6 <- lm(VegPct ~ log(HABHA)+poly(AgeMedian,2)+Pct_014+Pct_65P+Pct_MV+Pct_FR+
DistCBDkm+DistCBDkm*Pct_014,
data = DataFinal)
# summary(Modele6)
# 7e modèle de régression : interaction entre une VI continue et une VI dichotomique,
# soit VilleMtl*Pct_FR
modele8 <- lm(VegPct ~ log(HABHA)+poly(AgeMedian,2)+Pct_014+Pct_65P+Pct_MV+Pct_FR+
VilleMtl*Pct_FR,
data = DataFinal)
# summary(Modele7)À la figure 7.12, les résultats de la régression linéaire multiple, obtenus avec la summary(monModele), sont présentés en quatre sections distinctes :
- Le rappel de l’équation du modèle.
- Quelques statistiques descriptives sur les résidus du modèle, soit la différence entre les valeurs observées et prédites.
- Un tableau pour les coefficients de régression comprenant plusieurs colonnes, à savoir les coefficients de régression (
Estimate), l’erreur type du coefficient (Std. Error), la valeur de t (t value) et la probabilité associée à la valeur de t (Pr(>|t|)). La première ligne de ce tableau (Estimate) est pour la constante (Intercept en anglais) et celles qui suivent sont pour les variables indépendantes. - Les mesures d’ajustement du modèle, dont le RMSE (
Residual standard error), les R2 classique (Multiple R-squared) et ajusté (Adjusted R-squared), la statistique F avec le nombre de degrés de liberté en lignes (nombre d’observations) et en colonnes (n-k-1) ainsi que la valeur de p qui est lui associée (F-statistic: 1223 on 6 and 10203 DF, p-value: < 2.2e-16).

Figure 7.12: Différentes parties obtenues avec la fonction summary(Modèle)
# Intervalle de confiance des coefficients à 95 %
confint(modele3)## 2.5 % 97.5 %
## (Intercept) 50.8684505 54.79255157
## log(HABHA) -7.1847527 -6.52495353
## poly(AgeMedian, 2)1 -18.5676034 42.53686203
## poly(AgeMedian, 2)2 -313.4726002 -258.81630119
## Pct_014 0.8793672 1.00190861
## Pct_65P 0.2699504 0.34250907
## Pct_MV -0.0557951 -0.01681481
## Pct_FR -0.3659445 -0.322695627.7.2 Comparaison des modèles
Tel que détaillé à la section 7.3.2, pour comparer des modèles imbriqués, il convient d’analyser les valeurs du R2 ajusté et du F incrémentiel, ce qui peut être fait en trois étapes.
Première étape. Il peut être judicieux d’afficher l’équation des différents modèles afin de se remémorer les VI introduites dans chacun d’eux, et ce, avec la fonction MonModèle$call$formula.
# Rappel des équations des huit modèles
print(modele1$call$formula)## VegPct ~ HABHA + AgeMedian + Pct_014 + Pct_65P + Pct_MV + Pct_FRprint(modele2$call$formula)## VegPct ~ HABHA + poly(AgeMedian, 2) + Pct_014 + Pct_65P + Pct_MV +
## Pct_FRprint(modele3$call$formula)## VegPct ~ log(HABHA) + poly(AgeMedian, 2) + Pct_014 + Pct_65P +
## Pct_MV + Pct_FRprint(modele4$call$formula)## VegPct ~ log(HABHA) + poly(AgeMedian, 2) + Pct_014 + Pct_65P +
## Pct_MV + Pct_FR + VilleMtlprint(modele5$call$formula)## VegPct ~ log(HABHA) + poly(AgeMedian, 2) + Pct_014 + Pct_65P +
## Pct_MV + Pct_FR + Municprint(modele6$call$formula)## VegPct ~ log(HABHA) + poly(AgeMedian, 2) + Pct_014 + Pct_65P +
## Pct_MV + Pct_FR + DistCBDkm + DistCBDkm * Pct_014print(modele7$call$formula)## VegPct ~ log(HABHA) + poly(AgeMedian, 2) + Pct_014 + Pct_65P +
## Pct_MV + Pct_FR + VilleMtl + VilleMtlX_Pct_FRDeuxième étape. La syntaxe ci-dessous vous permet de comparer les R2 ajustés des différents modèles. Nous constatons ainsi que :
- La valeur du R2 ajusté du modèle 2 est supérieure à celle du modèle 1 (0,4378 versus 0,4179), signalant que la forme polynomiale d’ordre 2 pour l’âge médian des bâtiments (
poly(AgeMedian, 2)) améliore la prédiction comparativement à la forme originelle de (AgeMedian). - La valeur du R2 ajusté du modèle 3 est supérieure à celle du modèle 2 (0,4653 versus 0,4378), signalant que la forme logarithmique pour la densité de population (
log(HABHA)) améliore la prédiction comparativement à la forme originelle (HABHA). - La valeur du R2 ajusté du modèle 4 est supérieure à celle du modèle 3 (0,4863 versus 0,4653), signalant que l’introduction de la variable dichotomique (
VilleMtl) pour la municipalité apporte un gain de variance expliquée non négligeable. - La valeur du R2 ajusté du modèle 5 est supérieure à celle du modèle 4 (0,5064 versus 0,4863), signalant que l’introduction de la variable polytomique pour les municipalités de l’île de Montréal (
Muni) améliore la prédiction du modèle comparativement à la variable dichotomique (VilleMtl). - La valeur du R2 ajusté du modèle 6 est supérieure à celle du modèle 2 (0,4953 versus 0,4378), signalant que l’introduction d’une variable d’interaction entre deux variables continues (
DistCBDkm + DistCBDkm * Pct_014) apporte également un gain substantiel comparativement au modèle 2, ne comprenant pas cette variable d’interaction. - La valeur du R2 ajusté du modèle 7 est supérieure à celle du modèle 2 (0,4877 versus 0,4378), signalant que l’introduction d’une variable d’interaction entre une variable continue et la variable dichotomique (
DistCBDkm + DistCBDkm * Pct_014) apporte également un gain substantiel comparativement au modèle 2, ne comprenant pas cette variable d’interaction.
cat("\nComparaison des R2 ajustés :",
"\nModèle 1.", round(summary(modele1)$adj.r.squared,4),
"\nModèle 2.", round(summary(modele2)$adj.r.squared,4),
"\nModèle 3.", round(summary(modele3)$adj.r.squared,4),
"\nModèle 4.", round(summary(modele4)$adj.r.squared,4),
"\nModèle 5.", round(summary(modele5)$adj.r.squared,4),
"\nModèle 6.", round(summary(modele6)$adj.r.squared,4),
"\nModèle 7.", round(summary(modele7)$adj.r.squared,4)
)##
## Comparaison des R2 ajustés :
## Modèle 1. 0.4179
## Modèle 2. 0.4378
## Modèle 3. 0.4653
## Modèle 4. 0.4863
## Modèle 5. 0.5064
## Modèle 6. 0.4953
## Modèle 7. 0.4877Troisième étape. La syntaxe ci-dessous permet d’obtenir le F incrémentiel pour des modèles ne comprenant pas le même nombre de variables dépendantes, et ce, en utilisant la fonction anova(modele1, modele2, ..., modelen).
Par exemple, la syntaxe anova(modele1, modele2) permet de comparer les deux modèles et signale que le gain de variance expliquée entre les deux modèles (R2 de 0,4179 et de 0,4378) est significatif (F incrémentiel = 362,64; p < 0,001).
# Comparaison des deux modèles uniquement (modèles 1 et 2)
anova(modele1, modele2)## Analysis of Variance Table
##
## Model 1: VegPct ~ HABHA + AgeMedian + Pct_014 + Pct_65P + Pct_MV + Pct_FR
## Model 2: VegPct ~ HABHA + poly(AgeMedian, 2) + Pct_014 + Pct_65P + Pct_MV +
## Pct_FR
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 10203 2046427
## 2 10202 1976182 1 70245 362.64 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Il est aussi possible de comparer plusieurs modèles simultanément. Notez que dans la syntaxe ci-dessous, le troisième modèle n’est pas inclus, car il comprend le même nombre de variables indépendantes que le second modèle; il en va de même pour le sixième modèle comparativement au cinquième. Ici aussi, l’analyse des valeurs de F et de p vous permettent de vérifier si les modèles, et donc leurs R2 ajustés, sont significativement différents (quand p < 0,05).
# Comparaison de plusieurs modèles
anova(modele1, modele2, modele4, modele5, modele7)## Analysis of Variance Table
##
## Model 1: VegPct ~ HABHA + AgeMedian + Pct_014 + Pct_65P + Pct_MV + Pct_FR
## Model 2: VegPct ~ HABHA + poly(AgeMedian, 2) + Pct_014 + Pct_65P + Pct_MV +
## Pct_FR
## Model 3: VegPct ~ log(HABHA) + poly(AgeMedian, 2) + Pct_014 + Pct_65P +
## Pct_MV + Pct_FR + VilleMtl
## Model 4: VegPct ~ log(HABHA) + poly(AgeMedian, 2) + Pct_014 + Pct_65P +
## Pct_MV + Pct_FR + Munic
## Model 5: VegPct ~ log(HABHA) + poly(AgeMedian, 2) + Pct_014 + Pct_65P +
## Pct_MV + Pct_FR + VilleMtl + VilleMtlX_Pct_FR
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 10203 2046427
## 2 10202 1976182 1 70245 412.995 < 2.2e-16 ***
## 3 10201 1805547 1 170636 1003.224 < 2.2e-16 ***
## 4 10188 1732849 13 72698 32.878 < 2.2e-16 ***
## 5 10200 1800664 -12 -67815 33.226 < 2.2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1Quel modèle choisir?
Nous avons déjà évoqué le principe de parcimonie. À titre de rappel, l’ajout de variables indépendantes qui s’avèrent significatives fait inévitablement augmenter la variance expliquée et ainsi la valeur R2 ajusté. Par contre, elle peut rendre le modèle plus complexe à analyser, voire entraîner un surajustement du modèle. Nous avons vu que l’introduction des variables ditchtomique, polytomique et d’interaction avait pour effet d’augmenter la capacité de prédiction du modèle. Quoi qu’il en soit, le gain de variance expliquée s’élève à environ 4nbsp;% entre le troisième modèle versus le cinquième et le sixième :
- Modèle 3 (R2=0,465).
VegPct ~ log(HABHA) + poly(AgeMedian, 2) + Pct_014 + Pct_65P + Pct_MV + Pct_FR - Modèle 5 (R2=0,506).
VegPct ~ log(HABHA) + poly(AgeMedian, 2) + Pct_014 + Pct_65P + Muni - Modèle 6 (R2=0,495).
VegPct ~ log(HABHA) + poly(AgeMedian, 2) + Pct_014 + Pct_65P + Pct_MV + Pct_FR + DistCBDkm + DistCBDkm * Pct_014
Par conséquent, il est légitime de se questionner sur le bien-fondé de conserver ces variables indépendantes additionnelles : Muni pour le modèle 5 et DistCBDkm + DistCBDkm * Pct_014 pour le modèle 6. Trois options sont alors envisageables :
- Bien entendu, conservez l’une ou l’autre de ces variables additionnelles si elles sont initialement reliées à votre cadre théorique.
- Conservez l’une ou l’autre de ces variables additionnelles si elles permettent de répondre à une question spécifique (non prévue initialement) et si les associations ainsi révélées méritent, selon vous, discussion.
- Supprimez-les si leur apport est limité et ne fait que complexifier le modèle.
7.7.3 Diagnostic sur un modèle
7.7.3.1 Vérification le nombre d’observations
La syntaxe suivante permet de vérifier si le nombre d’observations est suffisant pour tester le R2 et chacune des variables indépendantes.
modele3 <- lm(VegPct ~ log(HABHA)+poly(AgeMedian,2)+
Pct_014+Pct_65P+Pct_MV+Pct_FR, data = DataFinal)
# Nombre d'observation
nobs <- length(modele3$fitted.values)
# Nombre de variables indépendantes (coefficients moins la constante)
k <- length(modele3$coefficients)-1
# Première règle de pouce
if(nobs >= 50+(8*k)){
cat("\nNombre d'observations suffisant pour tester le R2")
}else{
cat("\nAttention! Nombre d'observations insuffisant pour tester le R2")
}##
## Nombre d'observations suffisant pour tester le R2# Deuxième règle de pouce
if(nobs >= 104+k){
cat("\nNombre d'observations suffisant pour tester individuellement chaque VI")
}else{
cat("\nAttention! Nombre d'observations insuffisant",
"\npour tester individuellement chaque VI")
}##
## Nombre d'observations suffisant pour tester individuellement chaque VI7.7.3.2 Vérification la normalité des résidus
La syntaxe suivante permet de vérifier la normalité des résidus selon les trois démarches classiques : 1) coefficients d’asymétrie et d’aplatissement, 2) test de normalité de Jarque-Bera (fonction JarqueBeraTest du package DescTools) et 3) les graphiques (histogramme avec courbe normale et diagramme quantile-quantile).
library(DescTools)
library(stats)
library(ggplot2)
library(ggpubr)
# Vecteur pour les résidus du modèle
residus <- modele3$residuals
# 1. coefficients d’asymétrie et d’aplatissement
c(Skewness= round(DescTools::Skew(residus),3),
Kurtosis = round(DescTools::Kurt(residus),3))## Skewness Kurtosis
## -0.263 1.149# 2. Test de normalité de Jarque-Bera
JarqueBeraTest(residus)##
## Robust Jarque Bera Test
##
## data: residus
## X-squared = 528.51, df = 2, p-value < 2.2e-16# 3. Graphiques
Ghisto <- ggplot() +
geom_histogram(aes(x = residus, y = ..density..),
bins = 30, color = "#343a40", fill = "#a8dadc") +
stat_function(fun = dnorm,
args = list(mean = mean(residus),
sd = sd(residus)),
color = "#e63946", size = 1.2, linetype = "dashed")+
labs(title="Histogramme et courbe normale",
y = "densité", "Résidus du modèle")
Gqqplot <- qplot(sample = residus)+
geom_qq_line(line.p = c(0.25, 0.75),
color = "#e63946", size=1.2)+
labs(title="Diagramme quantile-quantile",
x="Valeurs théoriques",
y = "Résidus")
ggarrange(Ghisto, Gqqplot, ncol=2, nrow=1)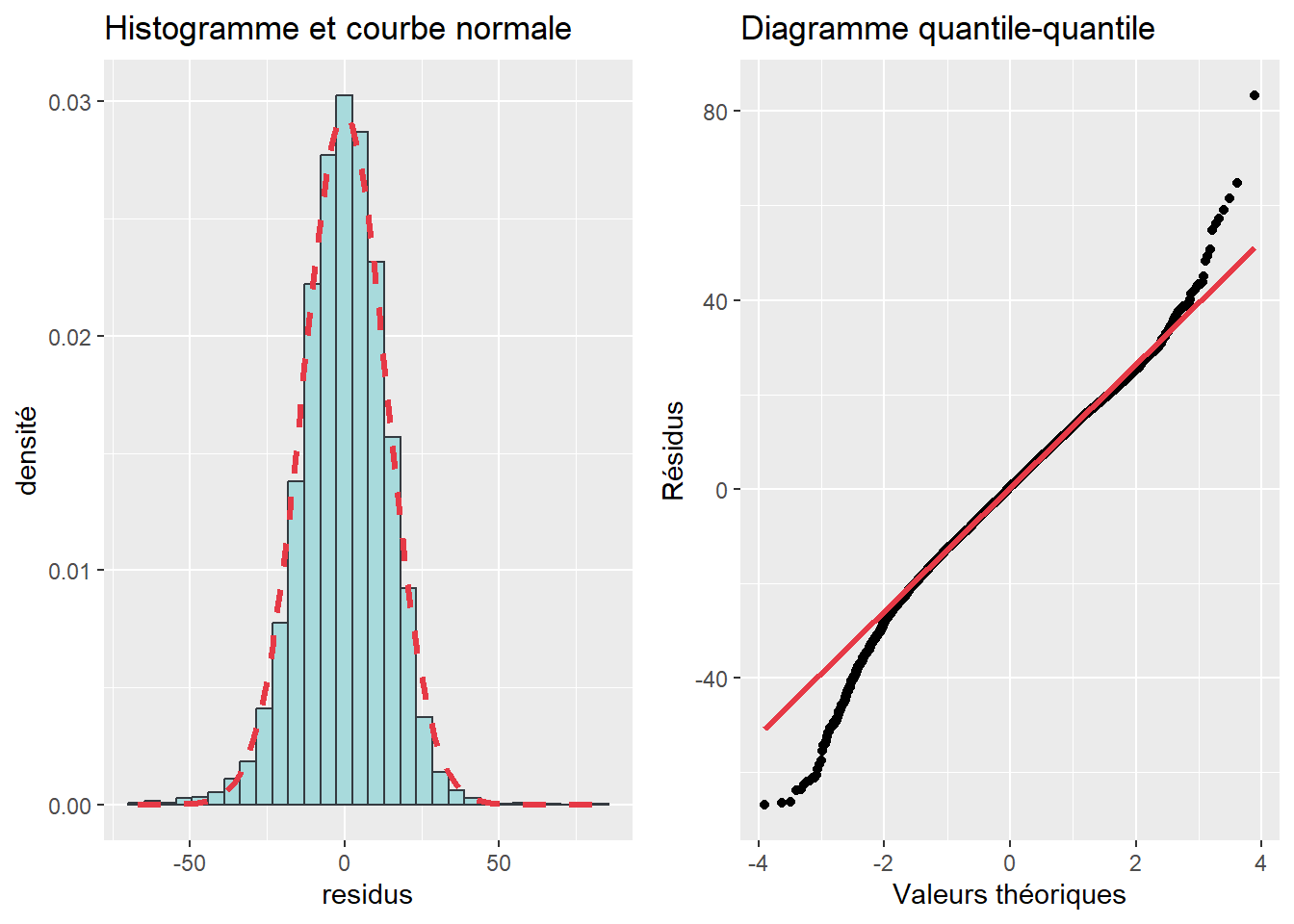
Figure 7.13: Diagnostic : la normalité des résidus
7.7.3.3 Évaluation de la linéarité et l’homoscédasticité des résidus
La syntaxe suivante permet de vérifier si l’hypothèse d’homoscédasticité des résidus est respectée avec : 1) un nuage de points entre les valeurs prédites et des résidus, 3) les graphiques (histogramme avec courbe normale et diagramme quantile-quantile) et 2) le test de Breusch-Pagan (fonction bptest du package lmtest).
# 1. Test de Breusch-Pagan pour vérifier l'homoscédasticité
library(lmtest)
bptest(modele3)##
## studentized Breusch-Pagan test
##
## data: modele3
## BP = 1651.5, df = 7, p-value < 2.2e-16if(bptest(modele3)$p.value < 0.05){
cat("\nAttention : problème d'hétéroscédasticité des résidus")
}else{
cat("\nParfait : homoscédasticité des résidus")
}##
## Attention : problème d'hétéroscédasticité des résidus# 2. Graphique entre les valeurs prédites et les résidus
residus <- modele3$residuals
ypredits <- modele3$fitted.values
ggplot() +
geom_point(aes(x = ypredits, y = residus),
color = "#343a40", fill = "#a8dadc",
alpha = 0.2, size = 0.8) +
geom_smooth(aes(x = ypredits, y = residus),
method = lm, color = "red")+
labs(x="Valeurs prédites", y = "Résidus")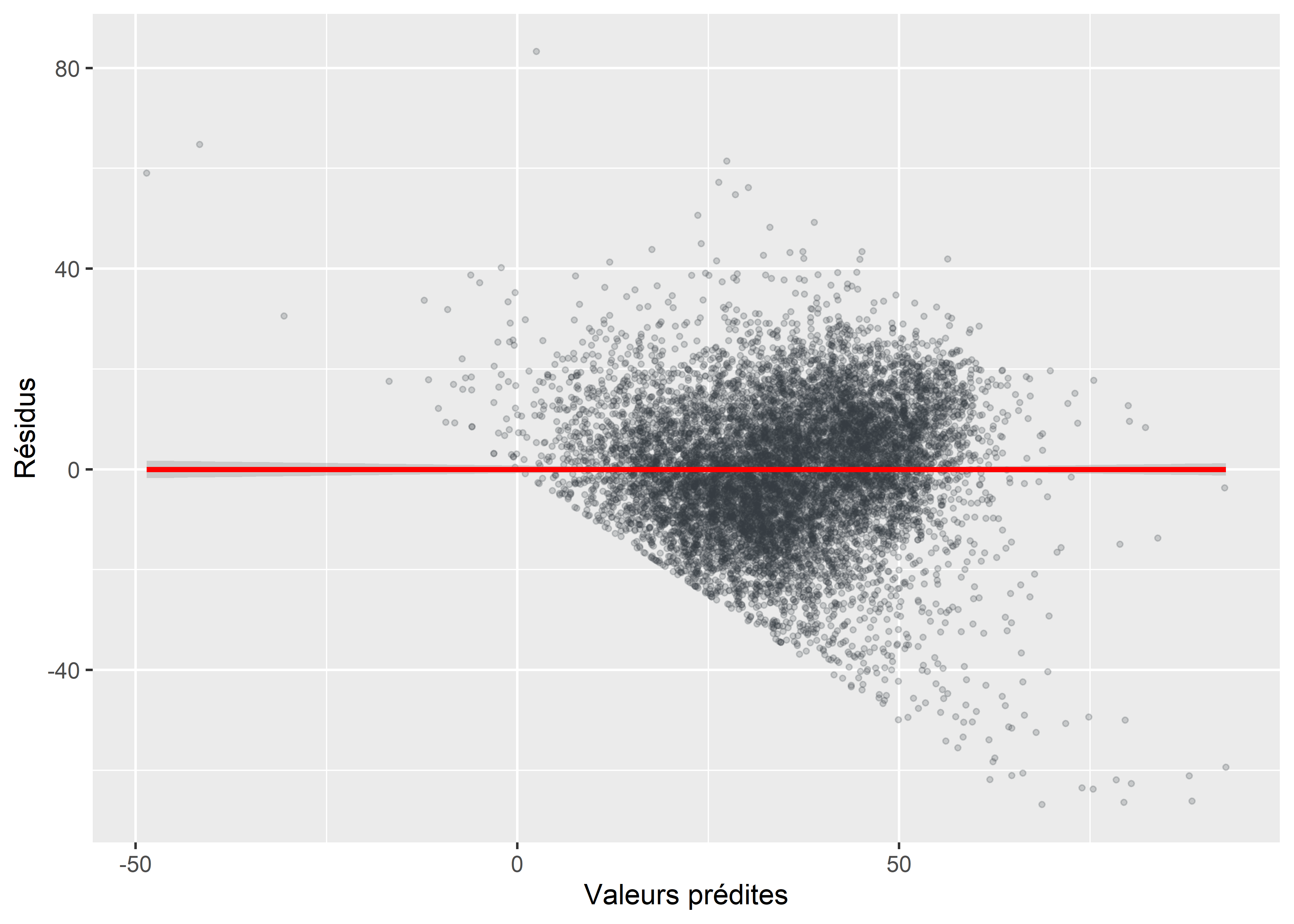
Figure 7.14: Distribution des résidus en fonction des valeurs prédites
7.7.3.4 Vérification la multicolinéarité excessive
Pour vérifier la présence ou l’absence de multicolinéarité excessive, nous utilisons habituellement la fonction vif du package car.
library(car)
# facteur d'inflation de la variance
round(car::vif(modele3),3)## GVIF Df GVIF^(1/(2*Df))
## log(HABHA) 1.289 1 1.136
## poly(AgeMedian, 2) 1.387 2 1.085
## Pct_014 1.518 1 1.232
## Pct_65P 1.304 1 1.142
## Pct_MV 1.480 1 1.217
## Pct_FR 1.730 1 1.315# problème de multicolinéarité (VIF > 10)?
car::vif(modele3) > 10## GVIF Df GVIF^(1/(2*Df))
## log(HABHA) FALSE FALSE FALSE
## poly(AgeMedian, 2) FALSE FALSE FALSE
## Pct_014 FALSE FALSE FALSE
## Pct_65P FALSE FALSE FALSE
## Pct_MV FALSE FALSE FALSE
## Pct_FR FALSE FALSE FALSE# problème de multicolinéarité (VIF > 5)?
car::vif(modele3) > 5 ## GVIF Df GVIF^(1/(2*Df))
## log(HABHA) FALSE FALSE FALSE
## poly(AgeMedian, 2) FALSE FALSE FALSE
## Pct_014 FALSE FALSE FALSE
## Pct_65P FALSE FALSE FALSE
## Pct_MV FALSE FALSE FALSE
## Pct_FR FALSE FALSE FALSE7.7.3.5 Répérage des valeurs très influentes du modèle
La syntaxe suivante permet d’évaluer le nombre de valeurs très influentes dans le modèle avec les critères de \(\mbox{4/n}\), \(\mbox{8/n}\) et \(\mbox{16/n}\) pour la distance de Cook.
nobs <- length(modele3$fitted.values)
DistanceCook <- cooks.distance(modele3)
n4 <- length(DistanceCook[DistanceCook > 4/nobs])
n8 <- length(DistanceCook[DistanceCook > 8/nobs])
n16 <- length(DistanceCook[DistanceCook > 16/nobs])
cat("Nombre d'observations =", nobs, "(100 %)",
"\n 4/n =", round(4/nobs,5),
"\n 8/n =", round(8/nobs,5),
"\n 16/n =", round(16/nobs,5),
"\nObservations avec une valeur supérieure ou égale aux différents seuils",
"\n 4/n =", n4, "soit", round(n4/nobs*100,2)," %",
"\n 8/n =", n8, "soit", round(n8/nobs*100,2)," %",
"\n 16/n =", n16, "soit", round(n16/nobs*100,2), " %"
)## Nombre d'observations = 10210 (100 %)
## 4/n = 0.00039
## 8/n = 0.00078
## 16/n = 0.00157
## Observations avec une valeur supérieure ou égale aux différents seuils
## 4/n = 604 soit 5.92 %
## 8/n = 285 soit 2.79 %
## 16/n = 132 soit 1.29 %Vous pouvez également construire un nuage de points avec la distance de Cook et l’effet de levier (leverage value) pour repérer visuellement les observations très influentes.
library(car)
library(ggpubr)
DistanceCook <- cooks.distance(modele3)
LeverageValue <- hatvalues(modele3)
G1 <- ggplot()+
geom_point(aes(x = LeverageValue, y = DistanceCook),
alpha = 0.2, size = 2, col="black", fill="red")+
labs(x = "Effet levier",
y = 'Distance de Cook',
title = 'Repérer les valeurs influentes',
subtitle = '(toutes les observations)')
G2 <- ggplot()+
geom_point(aes(x = LeverageValue, y = DistanceCook),
alpha = 0.2, size = 2, col="black", fill="red")+
ylim(0,0.01)+
xlim(0,0.01)+
labs(x = "Effet levier",
y = 'Distance de Cook',
title = 'Repérer les valeurs influentes',
subtitle = '(agrandissement)')
ggarrange(G1,G2, nrow=1, ncol=2)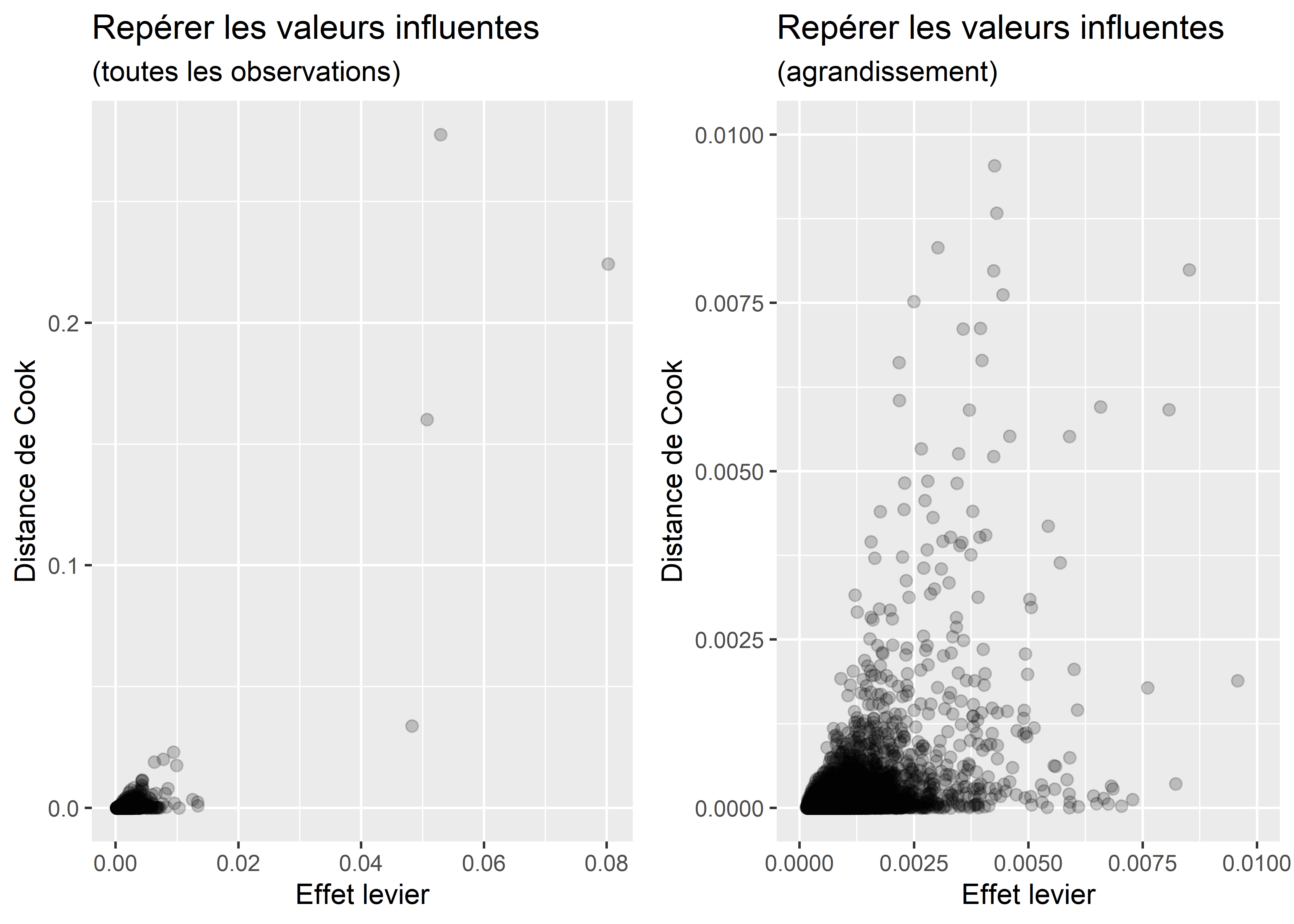
Figure 7.15: Repérage graphique des valeurs influentes du modèle
7.7.3.6 Construction d’un nouveau modèle en supprimant les observations très influentes du modèle
Dans un premier temps, il convient de construire un nouveau modèle sans les valeurs influentes du modèle de départ.
# Nombre d'observation dans le modèle 3
nobs <-length(modele3$fitted.values)
# Distance de Cook
cook <- cooks.distance(modele3)
# Les observations très influentes avec le critère de 16/n
DataSansOutliers <- cbind(DataFinal, cook)
DataSansOutliers <- DataSansOutliers[DataSansOutliers$cook < 8/nobs, ]
modele3b <- lm(VegPct ~ log(HABHA)+poly(AgeMedian,2)+Pct_014+Pct_65P+Pct_MV+Pct_FR,
data = DataSansOutliers)
nobsb <-length(modele3b$fitted.values)Comparez les valeurs du R2 ajusté des deux modèles. Habituellement, la suppression des valeurs très influentes s’accompagne d’une augmentation du R2 ajusté. C’est notamment le cas ici puisque sa valeur grimpe de 0,4653 à 0,5684, signalant ainsi un gain important pour la variance expliquée.
# Comparaison des mesures d'ajustement
cat("\nComparaison des R2 ajustés :",
"\nModèle de départ (n=", nobs, "), ",
round(summary(modele3)$adj.r.squared,4),
"\nModèle sans les observations très influentes (n=", nobsb, "), ",
round(summary(modele3b)$adj.r.squared,4),
sep=""
)##
## Comparaison des R2 ajustés :
## Modèle de départ (n=10210), 0.4653
## Modèle sans les observations très influentes (n=9925), 0.5684Pour le modèle, il convient alors de refaire le diagnostic de la régression et de vérifier si la suppression des observations très influentes a amélioré : 1) la normalité, la linéarité et l’homoscédasticité des résidus, 2) la multicolinéarité excessive et 3) l’absence de valeurs trop influentes.
La normalité des résidus s’est-elle ou non améliorée?
Pour ce faire, comparez les valeurs d’asymétrie,d’aplatissement et du test de Jarque-Bera et les graphiques de normalité. À la lecture des valeurs :
- l’asymétrie est très similaire (-0,260 à -0,265);
- l’aplatissement s’est amélioré (1,183 à 0,164);
- le test de Jarque-Bera signale toujours un problème de normalité (p < 0,001), mais sa valeur a nettement diminué (548,7 à 131,24);
- les graphiques démontrent une nette amélioration de la normalité des résidus.
# 1. coefficients d’asymétrie et d’aplatissement
resmodele3 <- rstudent(modele3)
resmodele3b <- rstudent(modele3b)
c(Skewness= round(Skew(resmodele3),3),
Kurtosis = round(Kurt(resmodele3),3))## Skewness1 Skewness2 Skewness3 Skewness4 Kurtosis1 Kurtosis2 Kurtosis3 Kurtosis4
## -0.260 0.024 -10.739 0.000 1.185 0.048 24.448 0.000c(Skewness= round(Skew(resmodele3b),3),
Kurtosis = round(Kurt(resmodele3b),3))## Skewness1 Skewness2 Skewness3 Skewness4 Kurtosis1 Kurtosis2 Kurtosis3 Kurtosis4
## -0.265 0.025 -10.790 0.000 0.165 0.049 3.360 0.000# 2. Test de normalité de Jarque-Bera
JarqueBeraTest(resmodele3)##
## Robust Jarque Bera Test
##
## data: resmodele3
## X-squared = 548.7, df = 2, p-value < 2.2e-16JarqueBeraTest(resmodele3b)##
## Robust Jarque Bera Test
##
## data: resmodele3b
## X-squared = 131.24, df = 2, p-value < 2.2e-16# 3. Graphiques
Ghisto1 <- ggplot() +
geom_histogram(aes(x = resmodele3, y = ..density..),
bins = 30, color = "#343a40", fill = "#a8dadc") +
stat_function(fun = dnorm, args = list(mean = mean(resmodele3),
sd = sd(resmodele3)),
color = "#e63946", size = 1.2, linetype = "dashed")+
labs(title="Modèle de départ", y = "densité", x="Résidus studentisés")
Gqqplot1 <- qplot(sample = residus)+
geom_qq_line(line.p = c(0.25, 0.75), color = "#e63946", size=1.2)+
labs(title="Modèle de départ", x="Valeurs théoriques", y = "Résidus studentisés")
Ghisto2 <- ggplot() +
geom_histogram(aes(x = resmodele3b, y = ..density..),
bins = 30, color = "#343a40", fill = "#a8dadc") +
stat_function(fun = dnorm, args = list(mean = mean(resmodele3b),
sd = sd(resmodele3b)),
color = "#e63946", size = 1.2, linetype = "dashed")+
labs(title="Modèle après suppression", x="Valeurs théoriques", y="Résidus studentisés")
Gqqplot2 <- qplot(sample = resmodele3b)+
geom_qq_line(line.p = c(0.25, 0.75), color = "#e63946", size=1.2)+
labs(title="Modèle après suppression",x="Valeurs théoriques", y = "Résidus studentisés")
library(ggpubr)
ggarrange(Ghisto1, Ghisto2, Gqqplot1, Gqqplot2, ncol=2, nrow=2)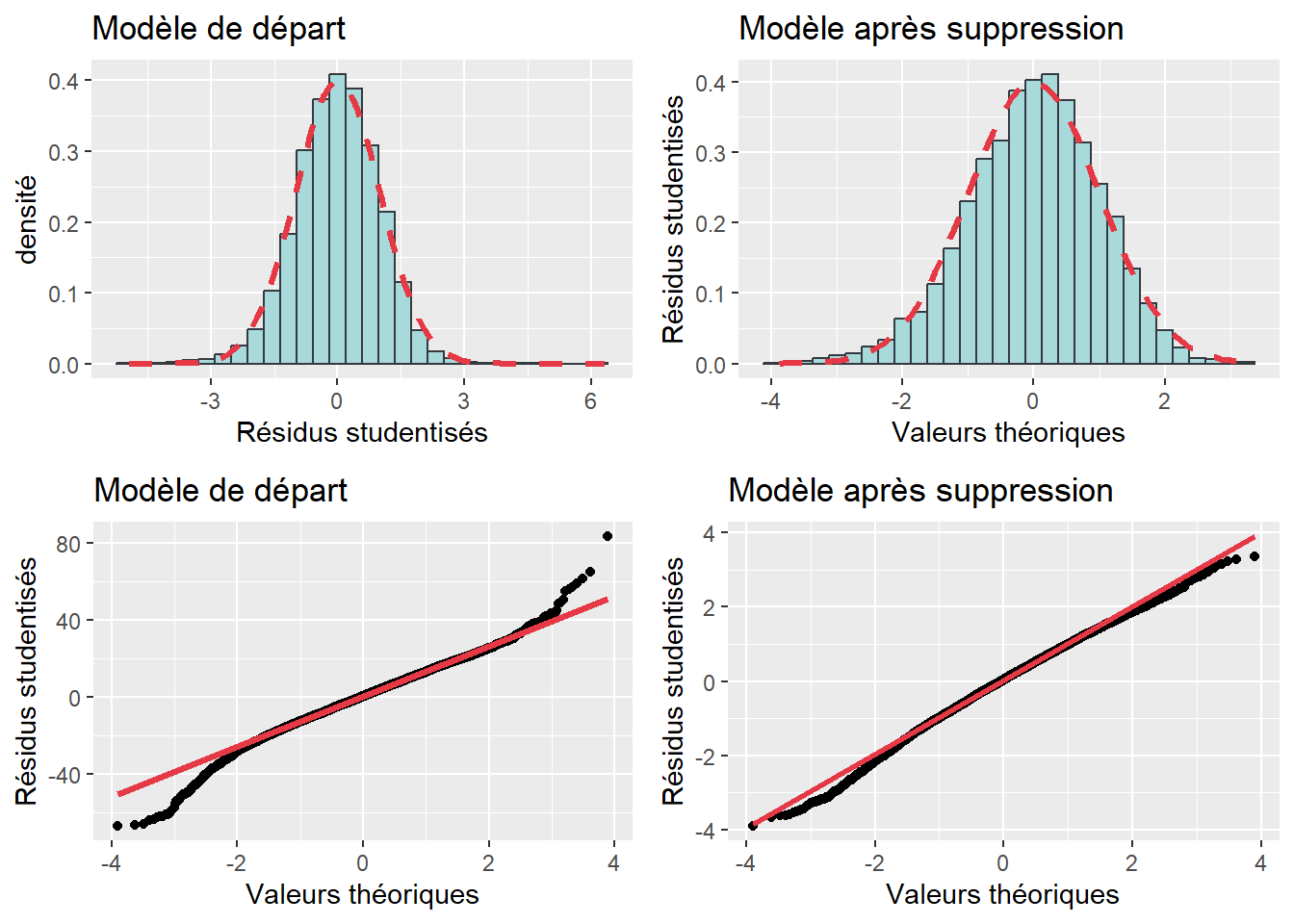
Figure 7.16: Normalité des résidus avant et après la suppression des valeurs influentes
Le problème d’hétéroscédasticité est-il corrigé?
- la valeur du test de Breusch-Pagan est beaucoup plus faible, mais il semble persister un problème d’hétéroscédasticité.
# homoscédasticité des résidus améliorée ou non?
library(lmtest)
library(ggpubr)
bptest(modele3)##
## studentized Breusch-Pagan test
##
## data: modele3
## BP = 1651.5, df = 7, p-value < 2.2e-16bptest(modele3b)##
## studentized Breusch-Pagan test
##
## data: modele3b
## BP = 640.53, df = 7, p-value < 2.2e-16resmodele3 <- residuals(modele3)
resmodele3b <- residuals(modele3b)
ypredits3 <- modele3$fitted.values
ypredits3b <- modele3b$fitted.values
G1 <- ggplot() +
geom_point(aes(x = ypredits3, y = resmodele3),
color = "#343a40", fill = "#a8dadc", alpha = 0.2, size = 0.8) +
geom_smooth(aes(x = ypredits3, y = resmodele3), method = lm, color = "red")+
labs(title="Modèle de départ",x="Valeurs prédites", y = "Résidus studentisés")
G2 <- ggplot() +
geom_point(aes(x = ypredits3b, y = resmodele3b),
color = "#343a40", fill = "#a8dadc", alpha = 0.2, size = 0.8) +
geom_smooth(aes(x = ypredits3b, y = resmodele3b), method = lm, color = "red")+
labs(title="Modèle après suppression",x="Valeurs prédites", y = "Résidus studentisés")
ggarrange(G1, G2, ncol=2, nrow=1)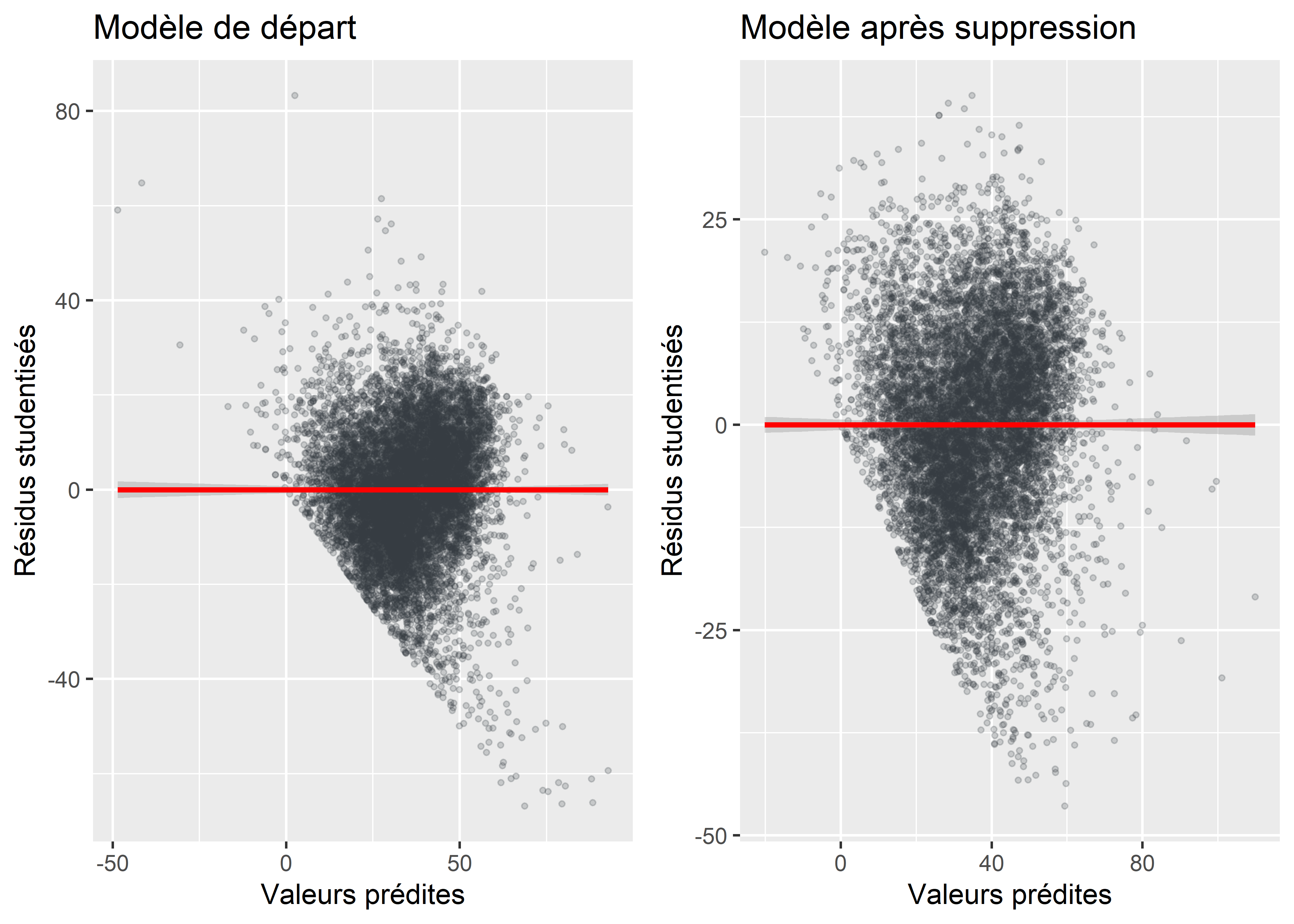
Figure 7.17: Amélioration de l’homoscédasticité des résidus
Finalement, il convient de comparer les coefficients de régression.
# Comparaison des coefficients
summary(modele3)##
## Call:
## lm(formula = VegPct ~ log(HABHA) + poly(AgeMedian, 2) + Pct_014 +
## Pct_65P + Pct_MV + Pct_FR, data = DataFinal)
##
## Residuals:
## Min 1Q Median 3Q Max
## -66.848 -8.660 0.381 8.961 83.269
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.283e+01 1.001e+00 52.781 < 2e-16 ***
## log(HABHA) -6.855e+00 1.683e-01 -40.730 < 2e-16 ***
## poly(AgeMedian, 2)1 1.198e+01 1.559e+01 0.769 0.441958
## poly(AgeMedian, 2)2 -2.861e+02 1.394e+01 -20.525 < 2e-16 ***
## Pct_014 9.406e-01 3.126e-02 30.093 < 2e-16 ***
## Pct_65P 3.062e-01 1.851e-02 16.546 < 2e-16 ***
## Pct_MV -3.630e-02 9.943e-03 -3.651 0.000262 ***
## Pct_FR -3.443e-01 1.103e-02 -31.212 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 13.57 on 10202 degrees of freedom
## Multiple R-squared: 0.4657, Adjusted R-squared: 0.4653
## F-statistic: 1270 on 7 and 10202 DF, p-value: < 2.2e-16summary(modele3b)##
## Call:
## lm(formula = VegPct ~ log(HABHA) + poly(AgeMedian, 2) + Pct_014 +
## Pct_65P + Pct_MV + Pct_FR, data = DataSansOutliers)
##
## Residuals:
## Min 1Q Median 3Q Max
## -46.417 -7.734 0.456 8.290 40.085
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 6.748e+01 9.869e-01 68.370 < 2e-16 ***
## log(HABHA) -1.000e+01 1.720e-01 -58.167 < 2e-16 ***
## poly(AgeMedian, 2)1 4.357e+01 1.387e+01 3.142 0.00168 **
## poly(AgeMedian, 2)2 -3.564e+02 1.250e+01 -28.510 < 2e-16 ***
## Pct_014 8.351e-01 2.870e-02 29.101 < 2e-16 ***
## Pct_65P 2.271e-01 1.807e-02 12.566 < 2e-16 ***
## Pct_MV -8.517e-03 9.109e-03 -0.935 0.34976
## Pct_FR -2.924e-01 1.028e-02 -28.440 < 2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 11.96 on 9917 degrees of freedom
## Multiple R-squared: 0.5687, Adjusted R-squared: 0.5684
## F-statistic: 1868 on 7 and 9917 DF, p-value: < 2.2e-167.7.4 Graphiques pour les effets marginaux
Tel que signalé ultérieurement, il est courant de représenter l’effet marginal d’une VI sur une VD, une fois contrôlées les autres VI. Pour ce faire, il est possible d’utiliser les packages ggplot2 et ggeffects.
7.7.4.1 Effet marginal pour une variable continue
La syntaxe ci-dessous illustre comment obtenir un graphique pour nos quatre variables explicatives. Bien entendu, si le coefficient de régression est positif (comme pour les pourcentages de jeunes de moins de 15 ans et les personnes âgées), la pente est alors montante, et inversement descendante pour des coefficients négatifs (comme pour les personnes ayant déclaré appartenir à une minorité visible et les personnes à faible revenu). En outre, plus la valeur absolue du coefficient est forte, plus la pente est prononcée.
library(ggplot2)
library(ggeffects)
library(ggpubr)
# Création d'un DataFrame pour les valeurs prédites pour chaque VI continue
fitV1 <- ggpredict(modele3, terms = "Pct_014")
fitV2 <- ggpredict(modele3, terms = "Pct_65P")
fitV3 <- ggpredict(modele3, terms = "Pct_MV")
fitV4 <- ggpredict(modele3, terms = "Pct_FR")
# Construction des graphiques
G1 <-ggplot(fitV1, aes(x, predicted)) +
# ligne de régression
geom_line(color = 'red', size = 1) +
# intervalle de confiance à 95 %
geom_ribbon(aes(ymin = conf.low, ymax = conf.high), alpha = .3)+
# Titres
labs(y="valeur prédite Y", x = "Moins de 15 ans (%)")
G2 <-ggplot(fitV2, aes(x, predicted)) +
geom_line(color = 'red', size = 1) +
geom_ribbon(aes(ymin = conf.low, ymax = conf.high), alpha = .3)+
labs(y="valeur prédite Y", x = "65 ans et plus (%)")
G3 <-ggplot(fitV3, aes(x, predicted)) +
geom_line(color = 'blue', size = 1) +
geom_ribbon(aes(ymin = conf.low, ymax = conf.high), alpha = .3)+
labs(y="valeur prédite Y", x = "Minorités visibles (%)")
G4 <-ggplot(fitV4, aes(x, predicted)) +
geom_line(color = 'blue', size = 1) +
geom_ribbon(aes(ymin = conf.low, ymax = conf.high), alpha = .3)+
labs(y="valeur prédite Y", x = "Personne à faible revenu (%)")
# Assemblage des graphiques
ggarrange(G1, G2, G3, G4, ncol =2, nrow =2)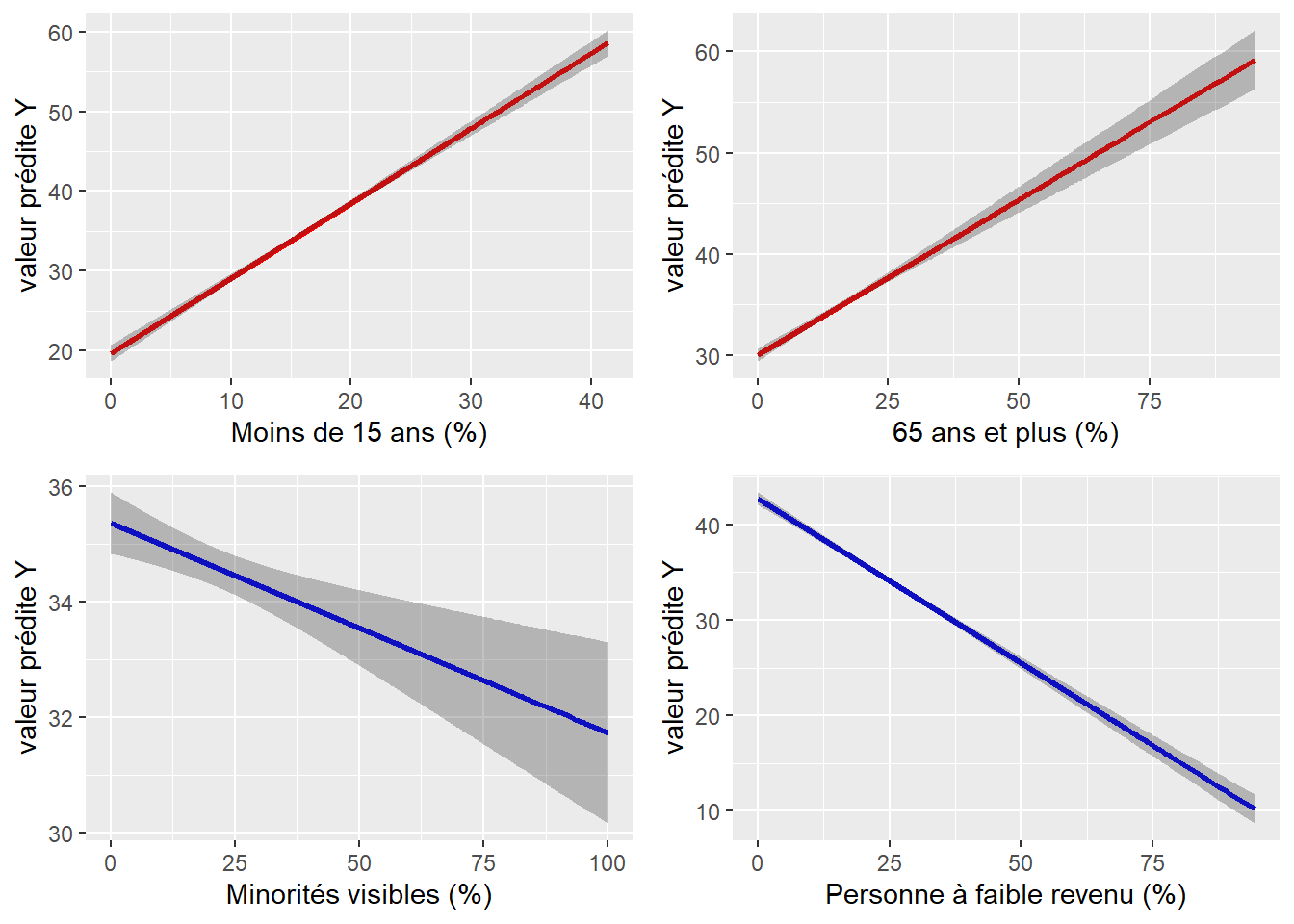
Figure 7.18: Effets marginaux pour des variables continues
7.7.4.2 Effet marginal pour une variable avec une fonction polynomiale d’ordre 2
library(ggplot2)
library(ggeffects)
library(ggpubr)
fitAgeMedian <- ggpredict(modele3, terms = "AgeMedian")
ggplot(fitAgeMedian, aes(x, predicted)) +
geom_line(color = 'green', size = 1) +
geom_ribbon(aes(ymin = conf.low, ymax = conf.high), alpha = .3)+
labs(title="Variable sous forme polynomiale (ordre 2)",
y="VD: valeur prédite", x = "Âge médian des bâtiments")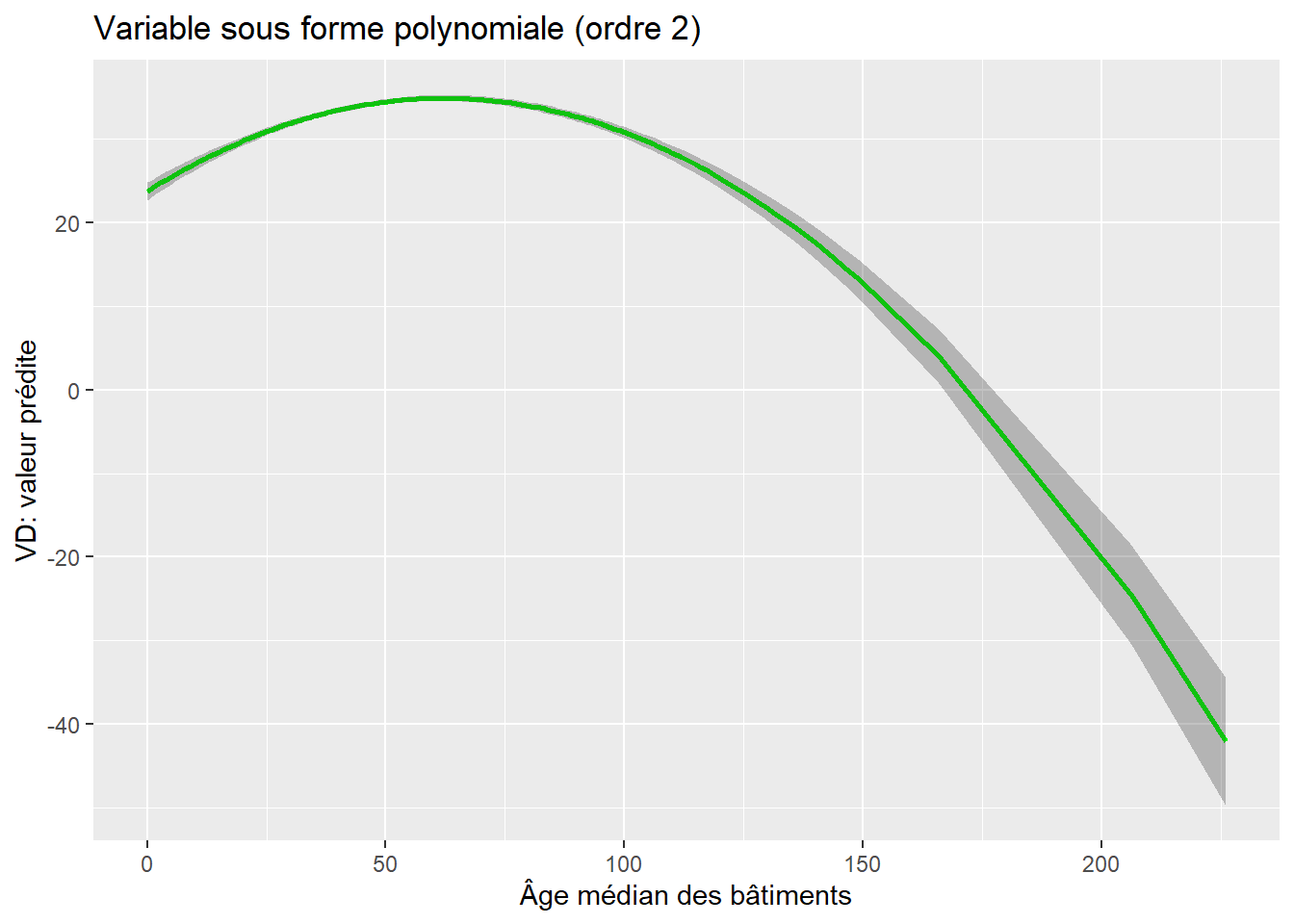
Figure 7.19: Effet marginal d’une variable avec un fonction polynomiale d’ordre 2
7.7.4.3 Effet marginal pour une variable transformée en logarithme
fitHabHa <- ggpredict(modele3, terms = "HABHA")
ggplot(fitHabHa, aes(x, predicted)) +
geom_line(color = 'blue', size = 1) +
geom_ribbon(aes(ymin = conf.low, ymax = conf.high), alpha = .3)+
labs(y="VD: valeur prédite", x = "Habitants km2")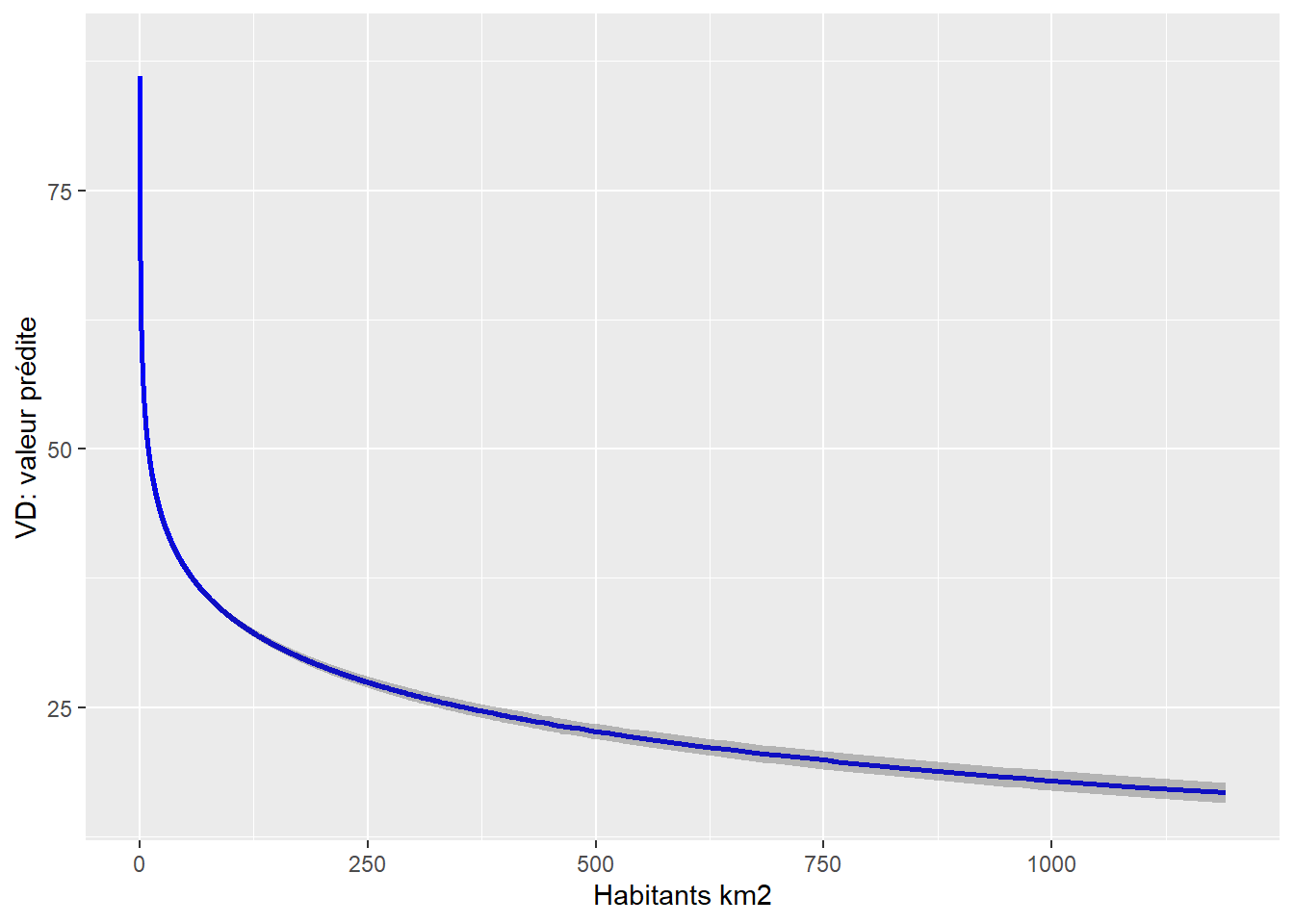
Figure 7.20: Effet du logarithme de la densité
7.7.4.4 Effet marginal pour une variable dichotomique
# Valeurs prédites selon le modèle avec la variable dichotomique
fitVilleMtl <- ggpredict(modele4, terms = "VilleMtl")
# Graphique
ggplot(fitVilleMtl, aes(x=x, y=predicted)) +
geom_bar(stat = "identity", position = position_dodge(), fill="wheat") +
geom_errorbar(aes(ymin = conf.low, ymax = conf.high), alpha = .9,position = position_dodge())+
labs(title="Effet marginal de la ville de Montréal sur la végétation",
x="Municipalités de la région de Montréal",
y="Couverture végétation de l'îlot (%)")+
scale_x_continuous(breaks=c(0,1),
labels = c("Autre municipalité", "Ville de Montréal"))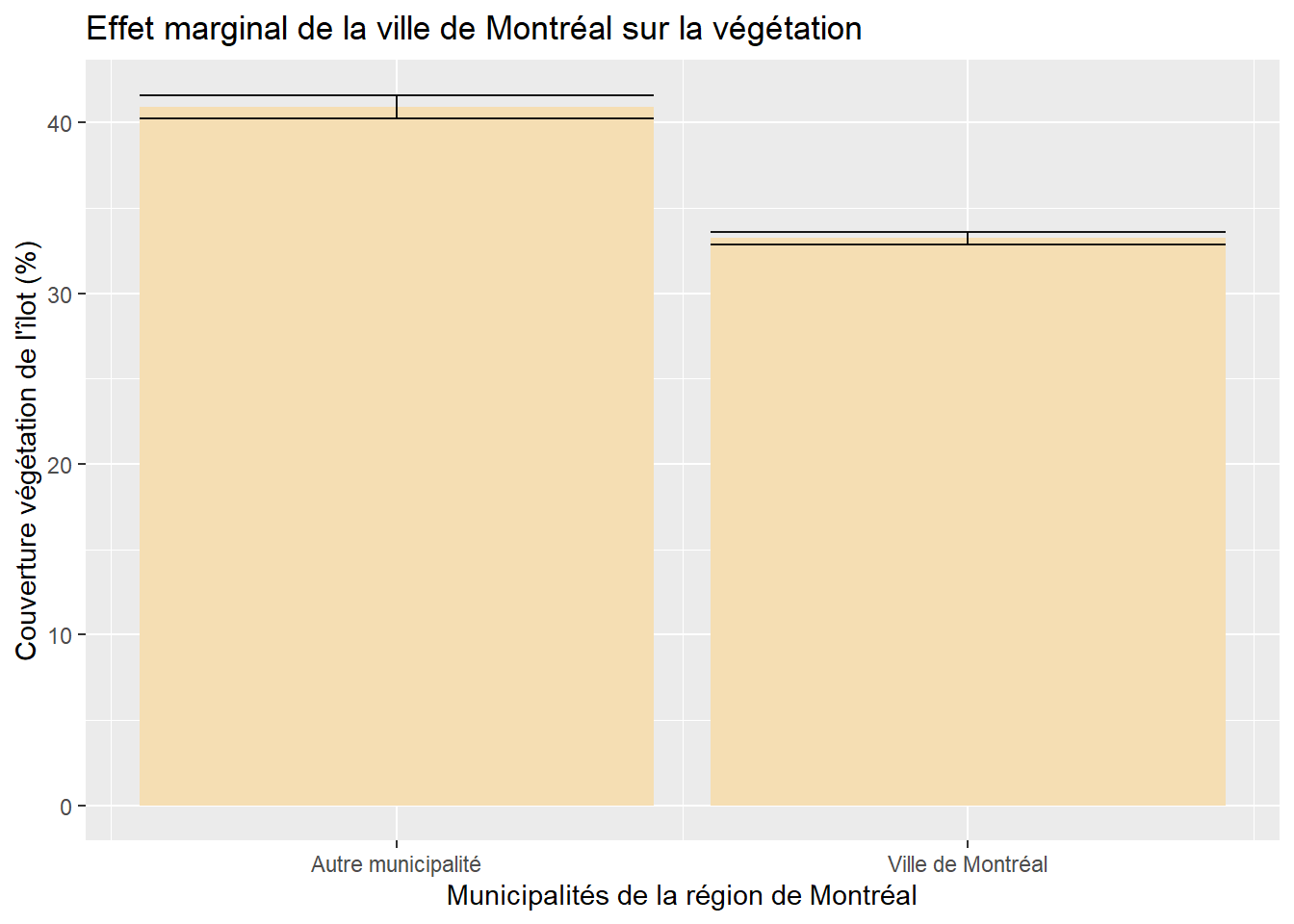
Figure 7.21: Effet marginal d’une variable dichotomique
7.7.4.5 Effet marginal pour une variable polytomique
# Valeurs prédites selon le modèle avec la variable polytomique
fitVilles <- ggpredict(modele5, terms = "Munic")
# Graphique
Graphique <- ggplot(fitVilles, aes(x=x, y=predicted)) +
geom_bar(stat = "identity", position = position_dodge(), fill="wheat") +
geom_errorbar(aes(ymin = conf.low, ymax = conf.high), alpha = .9,position = position_dodge())+
labs(title="Effet marginal de la ville de Montréal sur la végétation",
x="Municipalités de la région de Montréal",
y="Couverture végétation de l'îlot (%)")
# Rotation du graphique
Graphique + coord_flip()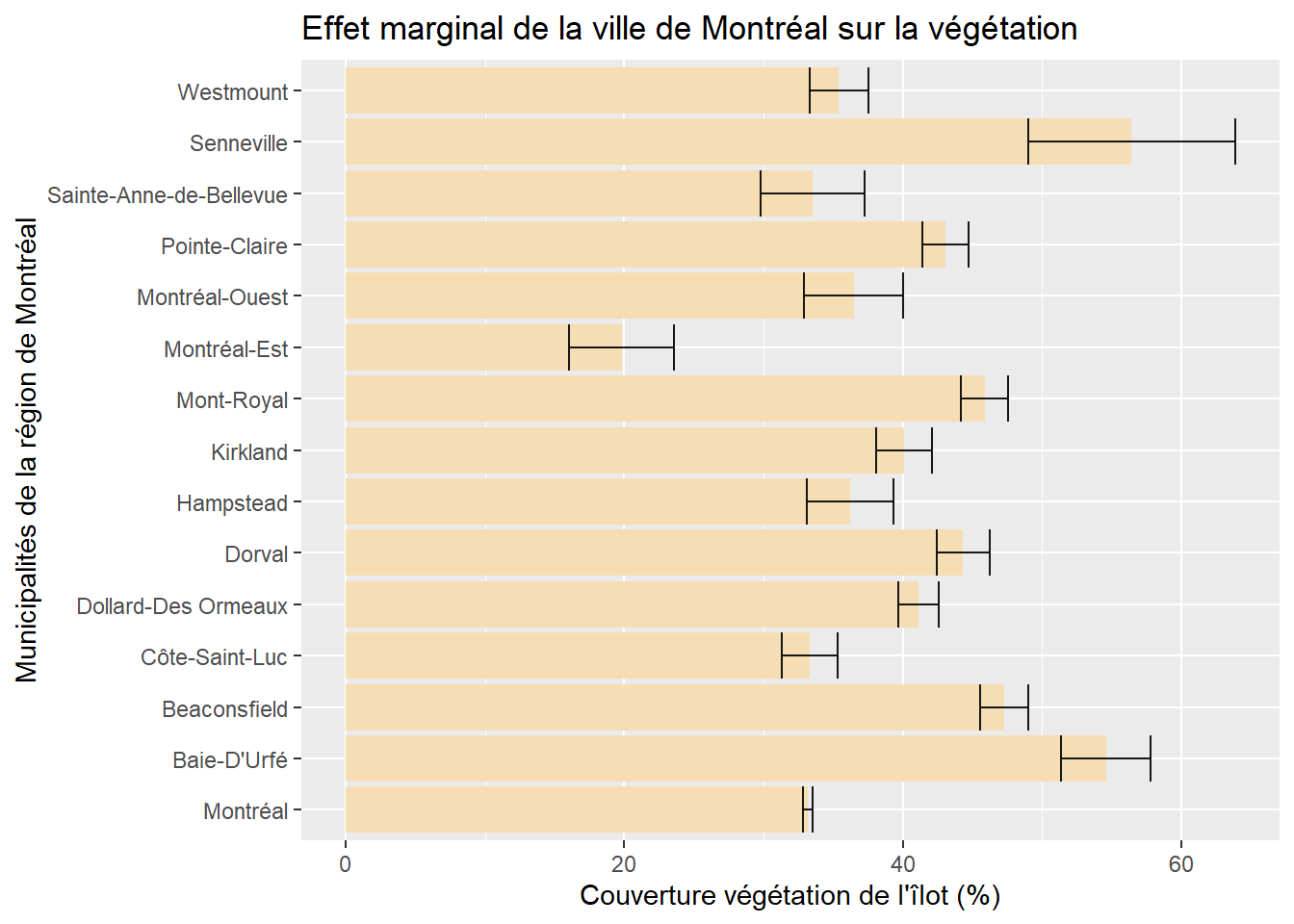
Figure 7.22: Effet marginal d’une variable polytomique
7.7.4.6 Effet marginal pour une variable d’interaction (deux VI continues)
library(metR) # pour ajouter des labels aux contours
df <- expand.grid(
DistCBDkm = seq(0,33,0.1),
Pct_FR = seq(0,95,1),
HABHA = mean(DataFinal$HABHA),
AgeMedian = mean(DataFinal$AgeMedian),
Pct_014 = mean(DataFinal$Pct_014),
Pct_65P = mean(DataFinal$Pct_65P),
Pct_MV = mean(DataFinal$Pct_MV)
)
df$DistCBDkmX_Pct_FR <- df$DistCBDkm * df$Pct_FR
pred <- predict(modele6, newdata = df, se = T)
df$pred <- pred$fit
df$pred_se <- pred$se.fit
df$lower <- df$pred - 1.96 * df$pred_se
df$upper <- df$pred + 1.96 * df$pred_se
P1 <- ggplot(data = df) +
geom_tile(aes(x = DistCBDkm, y = Pct_FR, fill = pred)) +
stat_contour(aes(x = DistCBDkm, y = Pct_FR, z = pred),
color = "black", linetype = "dashed") +
geom_text_contour(aes(x = DistCBDkm, y = Pct_FR, z = pred), )+
scale_fill_viridis(discrete=FALSE) +
labs(x = "Distance au centre-ville",
y = "Pers à faible revenu (%)",
fill = "",
subtitle = "Prédiction")
P2 <- ggplot(data = df) +
geom_tile(aes(x = DistCBDkm, y = Pct_FR, fill = lower)) +
stat_contour(aes(x = DistCBDkm, y = Pct_FR, z = lower),
color = "black", linetype = "dashed") +
geom_text_contour(aes(x = DistCBDkm, y = Pct_FR, z = lower), )+
scale_fill_viridis(discrete=FALSE)+
labs(x = "Distance au centre-ville",
y = "Pers à faible revenu (%)",
fill = "",
subtitle = "IC 2,5 %")
P3 <- ggplot(data = df) +
geom_tile(aes(x = DistCBDkm, y = Pct_FR, fill = upper)) +
stat_contour(aes(x = DistCBDkm, y = Pct_FR, z = upper),
color = "black", linetype = "dashed") +
geom_text_contour(aes(x = DistCBDkm, y = Pct_FR, z = upper), )+
scale_fill_viridis(discrete=FALSE)+
labs(x = "Distance au centre-ville",
y = "Pers à faible revenu (%)",
fill = "",
subtitle = "IC 97,5 %")
ggarrange(P1,P2,P3,common.legend = F, ncol = 2, nrow = 2)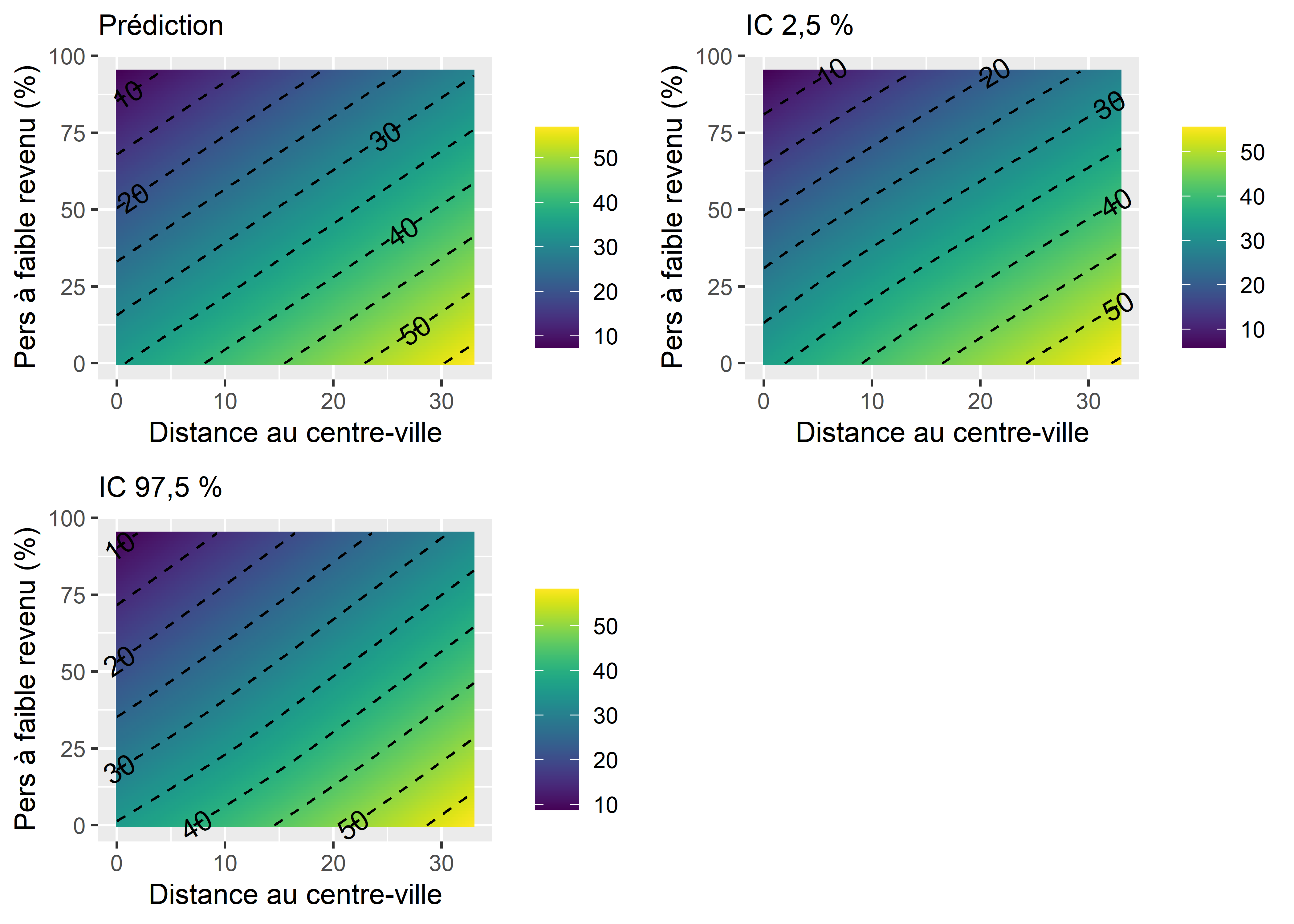
Figure 7.23: Effet marginal de l’interaction entre deux variables continues
7.7.4.7 Effet marginal pour une variable d’interaction (une VI continue et une VI dichotomique)
df <- expand.grid(
VilleMtl = c(0,1),
Pct_FR = seq(0,95,1),
HABHA = mean(DataFinal$HABHA),
AgeMedian = mean(DataFinal$AgeMedian),
Pct_014 = mean(DataFinal$Pct_014),
Pct_65P = mean(DataFinal$Pct_65P),
Pct_MV = mean(DataFinal$Pct_MV)
)
df$VilleMtlX_Pct_FR <- df$VilleMtl * df$Pct_FR
head(df, n=5)## VilleMtl Pct_FR HABHA AgeMedian Pct_014 Pct_65P Pct_MV VilleMtlX_Pct_FR
## 1 0 0 87.7694 52.11494 15.89268 14.86761 20.96675 0
## 2 1 0 87.7694 52.11494 15.89268 14.86761 20.96675 0
## 3 0 1 87.7694 52.11494 15.89268 14.86761 20.96675 0
## 4 1 1 87.7694 52.11494 15.89268 14.86761 20.96675 1
## 5 0 2 87.7694 52.11494 15.89268 14.86761 20.96675 0pred <- predict(modele7, se = T, newdata = df)
df$pred <- pred$fit
df$upper <- df$pred + 1.96*pred$se.fit
df$lower <- df$pred - 1.96*pred$se.fit
df$VilleMtl_str <- ifelse(df$VilleMtl==0,"Autre municipalité","Ville de Montréal")
DataFinal$VilleMtl_str <- ifelse(DataFinal$VilleMtl==0,"Autre municipalité","Ville de Montréal")
cols <- c("Autre municipalité" ="#1d3557" ,"Ville de Montréal"="#e63946")
ggplot(data = df) +
geom_point(data = DataFinal, mapping = aes(x = Pct_FR, y = VegPct, color = VilleMtl_str),
size = 0.2, alpha = 0.2)+
geom_ribbon(aes(x = Pct_FR, ymin = lower, ymax = upper, group = VilleMtl_str),
fill = rgb(0.1,0.1,0.1,0.4))+
geom_path(aes(x = Pct_FR, y = pred, color = VilleMtl_str), size = 1) +
scale_colour_manual(values = cols)+
labs(x = "Personnes à faible revenu (%)",
y = "Densité de végétation prédite (%)",
color = "")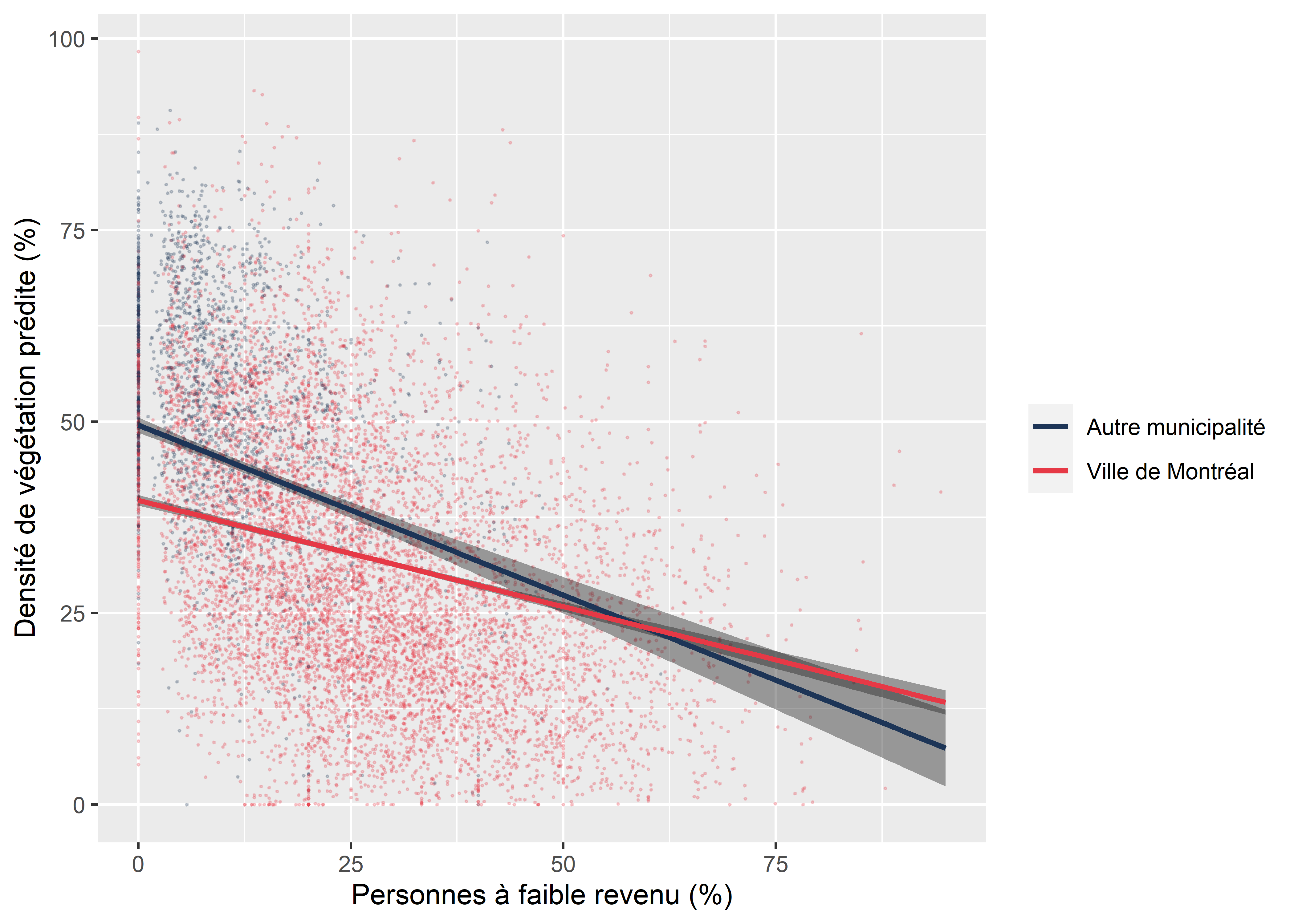
Figure 7.24: Graphique de l’effet marginal de l’interaction entre une variable quantitative et qualitative