12.3 Analyse factorielle des correspondances (AFC)
Pour bien comprendre l’AFC, il est essentiel de bien maîtriser les notions de tableau de contingence (marges du tableau, fréquences observées et théoriques, pourcentages en ligne et en colonne, contributions au khi-deux) et de distance du khi-deux. Si ce n’est pas le cas, il est conseillé de (re)lire le chapitre 5.
Dans le chapitre 5, nous avons vu comment construire un tableau de contingence (figure 12.23) à partir de deux variables qualitatives comprenant plusieurs modalités, puis comment vérifier s’il y a dépendance entre les deux variables qualitatives avec le test du khi-deux. Or, s’il y a bien dépendance, il est peut-être judicieux de résumer l’information que contient le tableau de contingence en quelques nouvelles variables synthétiques, objectif auquel répond l’analyse factorielle des correspondances (AFC).
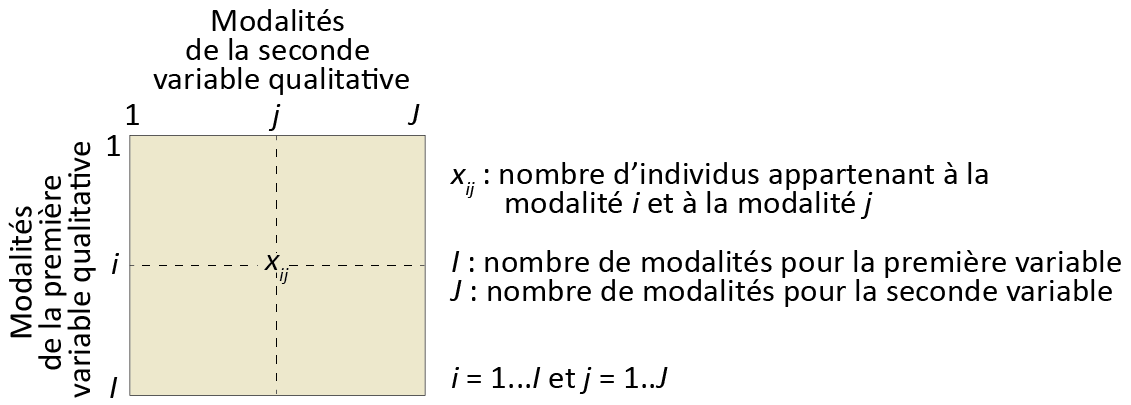
Figure 12.23: Tableau de contingence pour une AFC
À titre de rappel (section 12.1.2), l’AFC a été développée par le statisticien français Jean-Paul Benzécri (1973). Cela explique qu’elle est souvent enseignée et utilisée en sciences sociales dans les universités francophones, mais plus rarement dans les universités anglophones. Pourtant, les applications de l’AFC sont nombreuses dans différentes disciplines des sciences sociales comme illustrées avec les exemples suivants :
- En géographie, les modalités de la première variable du tableau de contingence sont souvent des entités spatiales (régions, municipalités, quartiers, etc.) croisées avec les modalités d’une autre variable qualitative (catégories socioprofessionnelles, modes de transport, tranches de revenu des ménages ou des individus, etc.).
- En économie régionale, nous pourrions vouloir explorer un tableau de contingence croisant des entités spatiales (par exemple, MRC au Québec, départements en France) et les effectifs d’emplois pour différents secteurs d’activité.
- En sciences politiques, le recours à l’AFC peut être intéressant pour explorer les résultats d’une élection. Les deux variables qualitatives pourraient être les circonscriptions électorales et les partis politiques. Le croisement des lignes et des colonnes du tableau de contingence représenterait le nombre de votes obtenus par un parti politique j dans la circonscription électorale i. Appliquer une AFC sur un tel tableau de contingence permettrait de révéler les ressemblances entre les différents partis politiques et celles entre les circonscriptions électorales.
Application d’une ACP sur un tableau de contingence transformé en un tableau avec les pourcentages en ligne : un bien mauvais calcul…
Il pourrait être tentant de transformer le tableau de contingence initial (tableau 12.7) en un tableau avec les pourcentages en ligne (tableau 12.8) afin de lui appliquer une analyse en composantes principales. Une telle démarche a deux inconvénients majeurs : chacune des modalités de la première variable qualitative (I) aurait alors le même poids; chacune des modalités de la deuxième variable (J) aurait aussi le même poids. Or, à la lecture des marges en ligne et en colonne au tableau 12.7, il est clair que les modalités j1 et i1 comprennent bien plus d’individus que les autres modalités respectives.
Si nous reprenons le dernier exemple applicatif, cela signifierait que le même poids est accordé à chaque parti puisque les variables sont centrées réduites en ACP (moyenne = 0 et variance = 1). Autrement dit, les grands partis traditionnels seraient ainsi sur le pied d’égalité que les autres partis. Aussi, chaque circonscription électorale aurait le même poids bien que certaines comprennent bien plus d’électeurs et d’électrices que d’autres.
| j1 | j2 | j3 | j4 | j5 | Marge (ligne) | |
|---|---|---|---|---|---|---|
| i1 | 357 060 | 22 010 | 276 625 | 65 000 | 29 415 | 750 110 |
| i2 | 427 530 | 26 400 | 295 860 | 69 410 | 30 645 | 849 845 |
| i3 | 147 500 | 6 545 | 34 545 | 4 415 | 1 040 | 194 045 |
| i4 | 128 520 | 6 405 | 42 925 | 6 565 | 2 670 | 187 085 |
| Marge (colonne) | 1 060 610 | 61 360 | 649 955 | 145 390 | 63 770 | 1 981 085 |
| V1 | V2 | V3 | V4 | V5 | |
|---|---|---|---|---|---|
| i1 | 47,6 | 2,9 | 36,9 | 8,7 | 3,9 |
| i2 | 50,3 | 3,1 | 34,8 | 8,2 | 3,6 |
| i3 | 76,0 | 3,4 | 17,8 | 2,3 | 0,5 |
| i4 | 68,7 | 3,4 | 22,9 | 3,5 | 1,4 |
12.3.1 Recherche d’une simplification basée sur la distance du khi-deux
Sur le plan mathématique et des objectifs visés, l’AFC est similaire à l’ACP puisqu’elle permet d’explorer un tableau de trois façons : 1) en montrant les ressemblances entre un ensemble d’individus (I), 2) en révélant les liaisons entre les variables (J) et 3) en résumant le tout avec des variables synthétiques. Toutefois, avec l’AFC, les ensembles I et J sont les modalités de deux variables qualitatives (dont le croisement forme un tableau de contingence) et elle est basée sur la distance du khi-deux (et non sur la distance euclidienne comme en ACP).
Ainsi, avec la distance du khi-deux, la proximité (ressemblance) entre deux lignes (i et l) et deux colonnes (j et k) est mesurée comme suit :
\[\begin{equation} d_{\chi_{il}^2} = \sum_j \frac{1}{f_{.j}}(\frac{f_{ij}}{f_{i.}}-\frac{f_{lj}}{f_{l.}})^2 \tag{12.5} \end{equation}\]
\[\begin{equation} d_{\chi_{jk}^2} = \sum_i \frac{1}{f_{i.}}(\frac{f_{ij}}{f_{.j}}-\frac{f_{ik}}{f_{.k}})^2 \tag{12.6} \end{equation}\]
Prenons un exemple fictif pour calculer ces deux distances. Le tableau 12.9 comprend trois modalités en ligne (I) et trois autres en colonne (J). Le total des effectifs de ce tableau de contingence est égal à 1 665.
À partir des données brutes, il est facile de construire deux tableaux : le profil des lignes et le profil des colonnes (tableau 12.10), c’est-à-dire les proportions en ligne et en colonne.
| j1 | j2 | j3 | Total (ligne) | |
|---|---|---|---|---|
| i1 | 360 | 65 | 275 | 700 |
| i2 | 420 | 70 | 290 | 780 |
| i3 | 145 | 5 | 35 | 185 |
| Total (colonne) | 925 | 140 | 600 | 1 665 |
| j1 | j2 | j3 | Total | |
|---|---|---|---|---|
| Profil des lignes | ||||
| i1 | 0,514 | 0,093 | 0,393 | 1 |
| i2 | 0,538 | 0,090 | 0,372 | 1 |
| i3 | 0,784 | 0,027 | 0,189 | 1 |
| Profils des colonnes | ||||
| i1 | 0,389 | 0,464 | 0,458 | |
| i2 | 0,454 | 0,500 | 0,483 | |
| i3 | 0,157 | 0,036 | 0,058 | |
| Total | 1,000 | 1,000 | 1,000 | |
En divisant les valeurs du tableau 12.9 par le grand total (1 665), nous obtenons tous les termes utilisés dans les équations (12.5) et (12.6) au tableau 12.11 :
- Les fréquences relatives dénommées \(f_{ij}\).
- La marge \(fi.\) est égale à la somme des fréquences relatives en ligne.
- La marge \(f.j\) est égale à la somme des fréquences relatives en colonne.
- La somme de toutes les fréquences relatives est donc égale à 1, soit \(\sum{f_{i.}}\) ou \(\sum{f_{.j}}\).
| j1 | j2 | j3 | Total (fi.) | |
|---|---|---|---|---|
| i1 | 0,216 | 0,039 | 0,165 | 0,420 |
| i2 | 0,252 | 0,042 | 0,174 | 0,468 |
| i3 | 0,087 | 0,003 | 0,021 | 0,111 |
| Total (f.j) | 0,556 | 0,084 | 0,360 | 1,000 |
Il est possible de calculer les distances entre les différentes modalités de I en appliquant l’équation (12.5); par exemple, la distance entre les observations i1 et i2 est égale à :
\[d_{(i1,i2)}=\frac{\mbox{1}}{\mbox{0,556}}(\mbox{0,216}-\mbox{0,252})^2+\frac{\mbox{1}}{\mbox{0,084}}(\mbox{0,039}-\mbox{0,042})^2+ \frac{\mbox{1}}{\mbox{0,360}}(\mbox{0,165}-\mbox{0,174})^2=\mbox{0,003}\]
Avec l’équation (12.6), la distance entre les modalités j1 et j2 de J est égale à :
\[d_{(j1,j2)}=\frac{\mbox{1}}{\mbox{0,420}}(\mbox{0,216}-\mbox{0,039})^2+ \frac{\mbox{1}}{\mbox{0,468}}(\mbox{0,252}-\mbox{0,042})^2 + \frac{\mbox{1}}{\mbox{0,111}}(\mbox{0,087}-\mbox{0,003})^2=\mbox{0,233}\]
À la lecture du tableau 12.12, les modalités les plus semblables sont
i1 et i2 (0,003) pour I et j1 et j3 (0,058) pour J.
| Ind. | i1 | i2 | i3 | Col. | j1 | j2 | j3 |
|---|---|---|---|---|---|---|---|
| i1 | 0,000 | 0,003 | 0,103 | j1 | 0,000 | 0,233 | 0,058 |
| i2 | 0,003 | 0,000 | 0,132 | j2 | 0,233 | 0,000 | 0,078 |
| i3 | 0,103 | 0,132 | 0,000 | j3 | 0,058 | 0,078 | 0,000 |
Finalement, l’approche pour déterminer les axes factoriels de l’AFC est similaire à celle de l’ACP : les axes factoriels sont les droites orthogonales qui minimisent les distances aux points du profil des lignes, excepté que la métrique pour mesurer ces distances est celle du khi-deux (et non celle la distance euclidienne comme pour l’ACP). Pour plus détails sur le calcul de ces axes (notamment les formulations matricielles), consultez notamment Benzécri (1973), Escofier et Pagès (1998) et Lebart et al. (1995).
12.3.2 Aides à l’interprétation
Pour illustrer les aides à l’interprétation de l’AFC, nous utilisons un jeu de données spatiales extrait du profil du recensement de 2016 de Statistique Canada pour les secteurs de recensement de l’île de Montréal. La liste des modalités des variables qu’il comprend est reportée au tableau 12.13. L’AFC est calculée sur un tableau de contingence croisant les secteurs de recensement (lignes) et les modalités d’une variable relative au mode de transport utilisé pour les déplacements domicile-travail (colonnes). Ces modalités sont cartographiées à la figure 12.24.
| Nom | Intitulé | Somme |
|---|---|---|
| Modalités de la variable utilisée dans l’AFC (mode de transport) | ||
| VehCond | Véhicule motorisé (conducteur·trice) | 427 560 |
| VehPass | Véhicule motorisé (passager·ère) | 26 490 |
| TranspC | Transport en commun | 295 800 |
| Apied | À pied | 69 330 |
| Velo | Bicyclette | 30 615 |
| AutreMoyen | Autre moyen | 7 750 |
| Modalités de la variable supplémentaire (durée du trajet) | ||
| T15min | Moins de 15 minutes | 130 435 |
| T1529min | 15 à 29 minutes | 287 500 |
| T3044min | 30 à 44 minutes | 244 425 |
| T4559min | 45 à 59 minutes | 107 065 |
| T60plus | 60 minutes et plus | 88 050 |
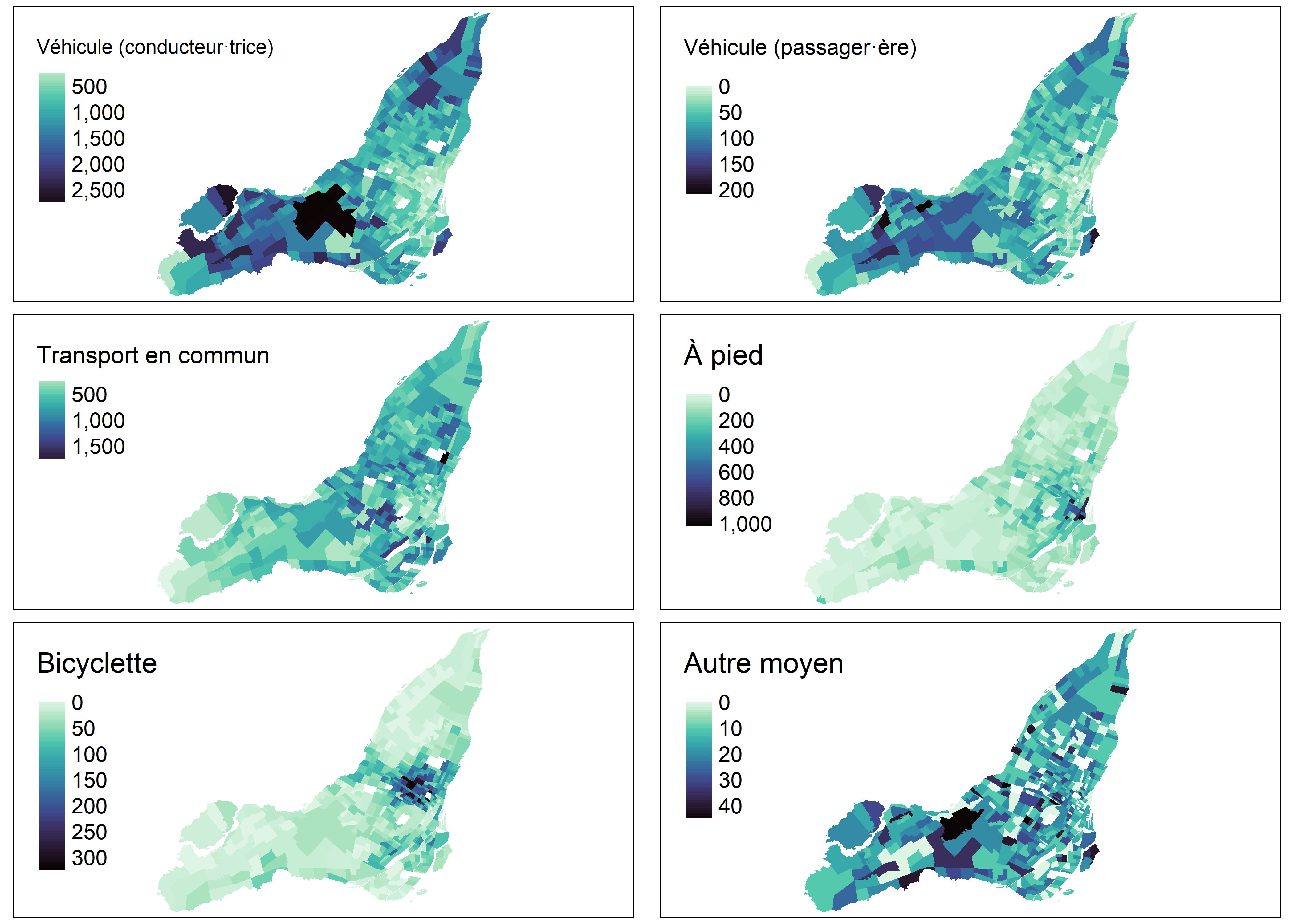
Figure 12.24: Cartographie des modalités de la variable mode de transport utilisée pour l’AFC
12.3.2.1 Résultats de l’AFC pour les valeurs propres
Avant de calculer l’AFC, il convient de vérifier s’il y a bien une dépendance entre les modalités des deux variables qualitatives. En effet, si les deux variables sont indépendantes, il n’est pas nécessaire de résumer le tableau de contingence avec une AFC. Pour ce faire, nous utilisons le test du khi-deux largement décrit à la section 5.2. Les résultats de ce test signalent qu’il existe des associations entre les modalités des deux variables (\(\chi\) = 203 971, p < 0,001, tableau 12.14). Nous pouvons donc appliquer une AFC sur ce tableau de contingence.
| Mesure | Valeur |
|---|---|
| Modalités I (secteurs de recensement) | 521,00 |
| Modalités J (variable mode de transport) | 6,00 |
| Somme des données brutes (\(n_{ij}\)) | 857 545,00 |
| Khi-deux (\(\chi^2\)) | 207 129,27 |
| Degrés de liberté, soit \((c-1)\times(l-1)\) | 2 600,00 |
| Valeur de p | 0,00 |
| Coefficient Phi au carré (\(\phi^2=\chi^2 / n_{ij})\) | 0,24 |
Nous avons vu qu’en ACP normée (section 12.2.2.1), la somme des valeurs propres est égale au nombre de variables puisqu’elles sont centrées réduites. Par contre, en AFC, cette somme est égale à l’inertie totale du tableau de contingence, c’est-à-dire à la valeur du khi-deux divisée par le nombre total des effectifs bruts (soit le coefficient phi au carré, \(\phi^2\)) (section 5.2). Le tableau 12.15 permet de vérifier que la somme des valeurs propres est bien égale au coefficient phi au carré :
\[\mbox{0,156}+\mbox{0,046}+\mbox{0,031}+\mbox{0,004}+\mbox{0,004} = \mbox{0,24}\]
\[\phi^2 = \chi^2 / n_{ij}=\mbox{203 971}/ \mbox{849 795} = \mbox{0,24}\]| Axe factoriel | Valeur propre | Pourcentage | Pourc. cumulé |
|---|---|---|---|
| 1 | 0,156 | 64,590 | 64,590 |
| 2 | 0,046 | 19,250 | 83,840 |
| 3 | 0,031 | 12,995 | 96,835 |
| 4 | 0,004 | 1,683 | 98,518 |
| 5 | 0,004 | 1,482 | 100,000 |
Combien d’axes d’une AFC faut-il retenir?
Approche statistique. Mike Bendixen (1995), cité dans l’excellent site STHDA, propose deux critères pour sélectionner les premiers axes d’une AFC : \(c_1= 1 / (l-1) \times 100\) et \(c_2= 1 / (c-1) \times 100\) avec l et c étant respectivement les nombres de modalités en ligne et en colonne. Autrement dit, lorsque les données sont distribuées aléatoirement, la valeur propre en pourcentage devrait être égale à \(c_1\) et celle de l’axe factoriel moyen à \(c_2\). Par conséquent, nous pourrions retenir uniquement les axes dont les valeurs propres en pourcentage excèdent : \(c_1 = \mbox{1}/(\mbox{521}-\mbox{1})\times \mbox{100}=\mbox{0,19 }%\) et \(c_2=\mbox{1}/(\mbox{6}-\mbox{1})\times \mbox{100}=\mbox{20 }%\). En appliquant ces deux critères, seul le premier axe factoriel qui résume 65,6 % mérite d’être retenu.
Approche empirique basée sur la lecture des pourcentages et des pourcentages cumulés. Nous retenons uniquement les deux premières composantes qui résument 85 % de la variance totale. Pour faciliter le choix du nombre d’axes avec cette approche empirique, il est fortement conseillé de construire un histogramme à partir des valeurs propres, soit brutes, soit en pourcentage, soit en pourcentage cumulé (figure 12.25).
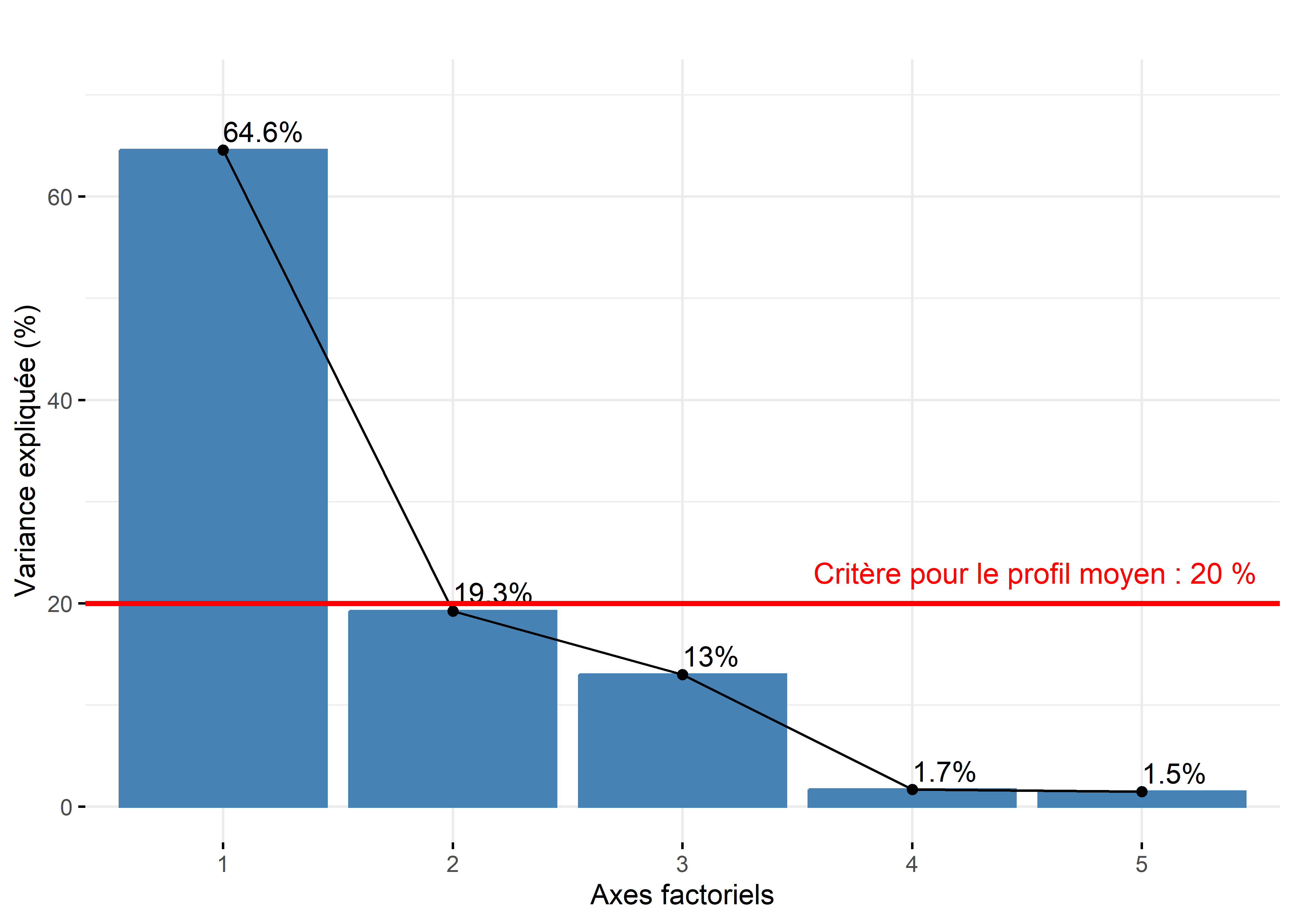
Figure 12.25: Histogramme des valeurs propres de l’AFC
12.3.2.2 Résultats de l’AFC pour les variables et les individus
Comme pour l’ACP, nous retrouvons les trois mêmes mesures pour les variables et les individus : 1) les coordonnées factorielles, 2) les contributions et 3) les cosinus carrés.
Compréhension des axes factoriels de l’AFC : une étape essentielle, incontournable…
Comme en ACP, l’analyse des trois mesures (coordonnées, contributions et cosinus carrés) pour les variables et les individus doit vous permettre de comprendre la signification des axes factoriels retenus de l’AFC. Cette étape d’interprétation est essentielle afin de qualifier les variables latentes (axes factoriels, variables synthétiques) produites par l’AFC.
- Les coordonnées factorielles sont simplement les projections des points-lignes et des points-colonnes sur les axes de l’AFC. Tant pour les lignes que pour les colonnes, ces coordonnées bénéficient de deux propriétés intéressantes. Premièrement, pour chaque axe factoriel k, la somme du produit des marges des variables (\(f.j\), colonnes) ou des individus (\(fi.\), lignes) avec leurs coordonnées respectives (\(C^k_j\) et \(C^k_i\)) est égale à 0 (équation (12.7)). Deuxièmement, pour chaque axe factoriel k, la somme des produits entre les marges (en ligne et en colonne) et les coordonnées au carré (en ligne et en colonne) est égale à la valeur propre de l’axe (équation (12.8)).
\[\begin{equation} \sum{f.j (C^k_j)}= 0 \text{ et} \sum{fi. (C^k_i)}= 0 \tag{12.7} \end{equation}\]
\[\begin{equation} \sum{fi. (C^k_i)^2}= \mu_k \text{ et} \sum{f.j (C^k_j)^2}= \mu_k \tag{12.8} \end{equation}\]
En guise d’exemple, le tableau 12.16 permet de vérifier les deux propriétés des coordonnées pour les variables. Les sommes de \({f.j (C^k_j)}\) pour les axes 1 et 2 sont bien égales à 0; et les sommes de \({f.j (C^k_j)^2}\) pour les axes 1 et 2 sont bien égales aux valeurs propres de ces deux axes, soit 0,156 et 0,046 (comparez ces valeurs avec celles reportées au tableau 12.15 plus haut).
| Modalité | f.j | 1 | 2 | 1 | 2 | 1 | 2 |
|---|---|---|---|---|---|---|---|
| VehCond | 0,499 | -0,329 | 0,077 | -0,164 | 0,038 | 0,054 | 0,003 |
| VehPass | 0,031 | -0,255 | 0,081 | -0,008 | 0,003 | 0,002 | 0,000 |
| TranspC | 0,345 | 0,208 | -0,229 | 0,072 | -0,079 | 0,015 | 0,018 |
| Apied | 0,081 | 0,813 | 0,545 | 0,066 | 0,044 | 0,053 | 0,024 |
| Velo | 0,036 | 0,938 | -0,187 | 0,033 | -0,007 | 0,031 | 0,001 |
| AutreMoyen | 0,009 | 0,142 | 0,078 | 0,001 | 0,001 | 0,000 | 0,000 |
| Somme | 1,000 | 0,000 | 0,000 | 0,156 | 0,046 |
Contrairement à l’ACP, les coordonnées factorielles pour les variables en AFC ne sont pas les coefficients de corrélation de Pearson des variables sur les axes!
- Les contributions des colonnes ou des lignes en AFC permettent des repérer celles qui contribuent le plus à la formation des axes factoriels (de manière analogue à l’ACP). Pour un axe donné, leur sommation est égale à 100 %. Elles s’obtiennent en multipliant la coordonnée au carré avec la marge et en divisant le tout par la valeur propre de l’axe (équations (12.9) et (12.10)).
\[\begin{equation} \mbox{Ctr}_j^k =\frac{f.j(C^k_j)^2}{\mu_{k}}\times 100 \tag{12.9} \end{equation}\]
\[\begin{equation} \mbox{Ctr}_i^k =\frac{fi.(C^k_i)^2}{\mu_{k}}\times 100 \tag{12.10} \end{equation}\]
- Les cosinus carrés (Cos2) (appelés aussi les qualités de représentation sur un axe) permettent de repérer le ou les axes qui concourent le plus à donner un sens aux colonnes (variables) et aux lignes (individus), de manière analogue à l’ACP. Pour une variable ou un individu, la sommation des Cos2 pour tous les axes de l’AFC est aussi égale à 1.
Interprétation des résultats pour les colonnes (variables)
Maintenant, analysons ces trois statistiques pour les variables pour les deux premiers axes de l’AFC (tableau 12.17 et figure 12.26).
Pour l’axe 1, résumant 65 % de la variance, trois modalités concourent à sa formation : VehCond (34,69 %), Apied (34,25 %) et Velo (20,13 %). À la lecture des coordonnées factorielles sur cet axe, les modes de transport relatifs aux véhicules motorisés (VehCond = -0,33 et VehPass = -0,25) s’opposent clairement aux modes actifs (Apied = 0,81 et Velo = 0,94), constat qu’il est possible de confirmer visuellement avec la figure 12.26. La modalité VehCond a d’ailleurs la plus forte valeur de Cos2 sur cet axe (0,92), ce qui signale, sans l’ombre d’un doute, que l’axe 1 est celui qui donne le plus de sens à cette modalité.
Puisque l’axe 2 résume une partie beaucoup plus limitée de la variance du tableau (19,25 %), il n’est pas étonnant qu’un nombre plus limité de modalités concourent à sa formation : seules les contributions de la modalité Apied (51,68 %) et secondairement de VehPass (38,81 %) sont importantes. Leurs coordonnées factorielles s’opposent d’ailleurs sur cet axe (respectivement 0,81 et 0,21).
| Modalité | 1 | 2 | 1 | 2 | 1 | 2 |
|---|---|---|---|---|---|---|
| VehCond | -0,33 | 0,08 | 0,92 | 0,05 | 34,69 | 6,33 |
| VehPass | -0,25 | 0,08 | 0,34 | 0,03 | 1,28 | 0,44 |
| TranspC | 0,21 | -0,23 | 0,39 | 0,47 | 9,53 | 38,81 |
| Apied | 0,81 | 0,54 | 0,67 | 0,30 | 34,25 | 51,61 |
| Velo | 0,94 | -0,19 | 0,56 | 0,02 | 20,13 | 2,69 |
| AutreMoyen | 0,14 | 0,08 | 0,05 | 0,01 | 0,12 | 0,12 |
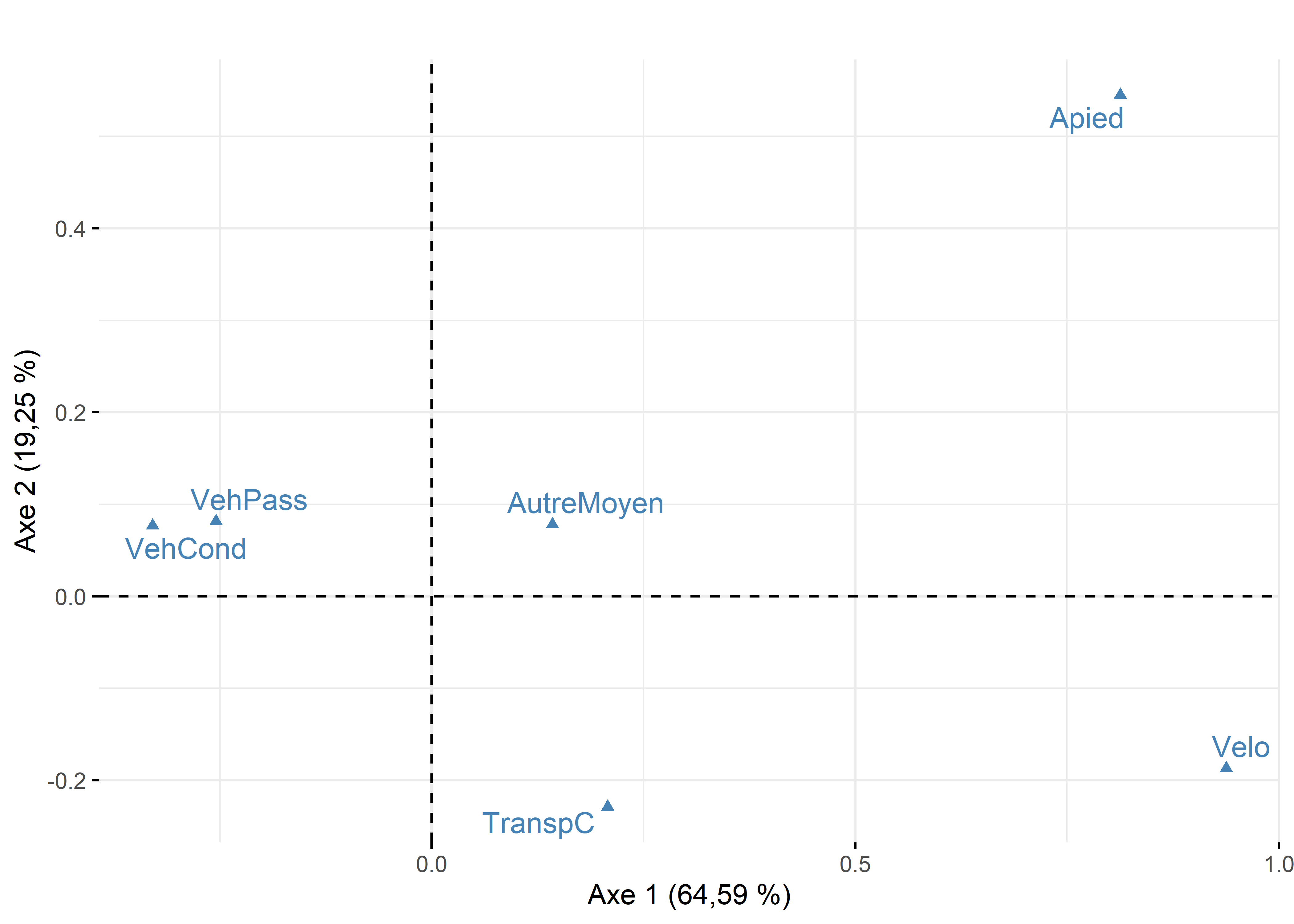
Figure 12.26: Premier plan factoriel de l’AFC pour les variables
Interprétation des résultats pour les individus
Premier plan factoriel pour les variables et les individus
Lorsque le jeu de données comprend à la fois peu de modalités en ligne et en colonne, il est judicieux de les représenter simultanément sur le premier plan factoriel (axes 1 et 2). Pour ce faire, vous pouvez utiliser la fonction fviz_ca_biplot du package factoextra.
Étant donné que notre jeu de données comprend 521 secteurs de recensement, nous proposons ici de cartographier les coordonnées factorielles des individus pour les deux premiers axes de l’AFC (figure 12.27). Pour l’axe 1, les secteurs de recensement à l’est et l’ouest de l’île de Montréal présentent les coordonnées les plus fortement négatives (en rouge); dans ces zones, l’usage des véhicules motorisés pour des déplacements domicile-travail est certainement surreprésenté, comparativement aux modes actifs. À l’inverse, dans les secteurs de recensement du centre de l’île présentant de fortes valeurs positives (en rouge), le recours aux modes de transports actifs (marche et vélo) est bien plus important, toutes proportions gardées. Quant à la cartographie des coordonnées pour l’axe 2, elle permet surtout de repérer quelques secteurs de recensement autour du centre-ville (très fortes valeurs positives en vert foncé) où les déplacements domicile-travail à pied sont plus fréquents, toutes proportions gardées.
En résumé, suite à l’analyse des coordonnées factorielles des variables et des individus, nous pouvons conclure que le premier axe est certainement le plus intéressant puisqu’il permet d’opposer l’usage des modes de transports motorisés versus les modes de transports actifs pour les déplacements domicile-travail sur l’île de Montréal. Cette nouvelle variable synthétique (variable latente) pourrait ainsi être introduite dans des analyses subséquentes (par exemple, dans un modèle de régression). Cela démontre qu’au même titre que l’ACP, l’AFC est une méthode de réduction de données puisque nous sommes passés d’un tableau comprenant 512 secteurs de recensement et six modalités à un tableau comprenant une seule variable synthétique (axe 1).
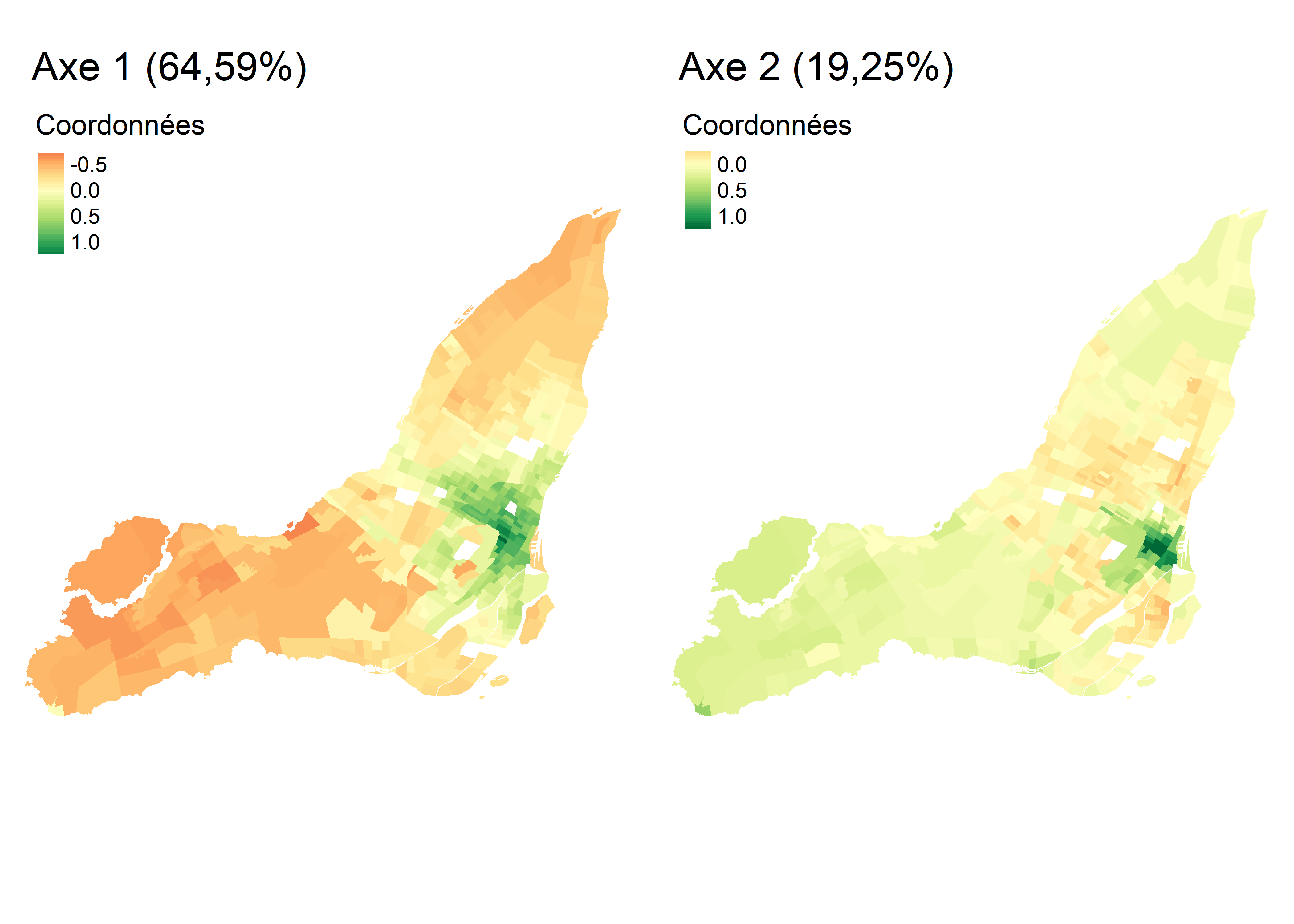
Figure 12.27: Cartographie de coordonnées factorielles des individus pour l’AFC
Ajout de modalités supplémentaires dans une analyse des correspondances (AFC)
Comme pour l’ACP, il est possible d’ajouter des variables et des individus supplémentaires une fois l’AFC calculée. En guise d’illustration, nous avons ajouté à l’AFC précédemment analysée des modalités relatives à la durée des temps de déplacements : moins de 15 minutes, 15 à 29, 30 à 44, 45 à 59, 60 minutes et plus. Sans surprise, sur le premier plan factoriel à la figure 12.27, cette dernière modalité, représentant les trajets les plus longs, est la plus proche des modalités relatives à l’usage des véhicules motorisés (VehCond et VehPass).
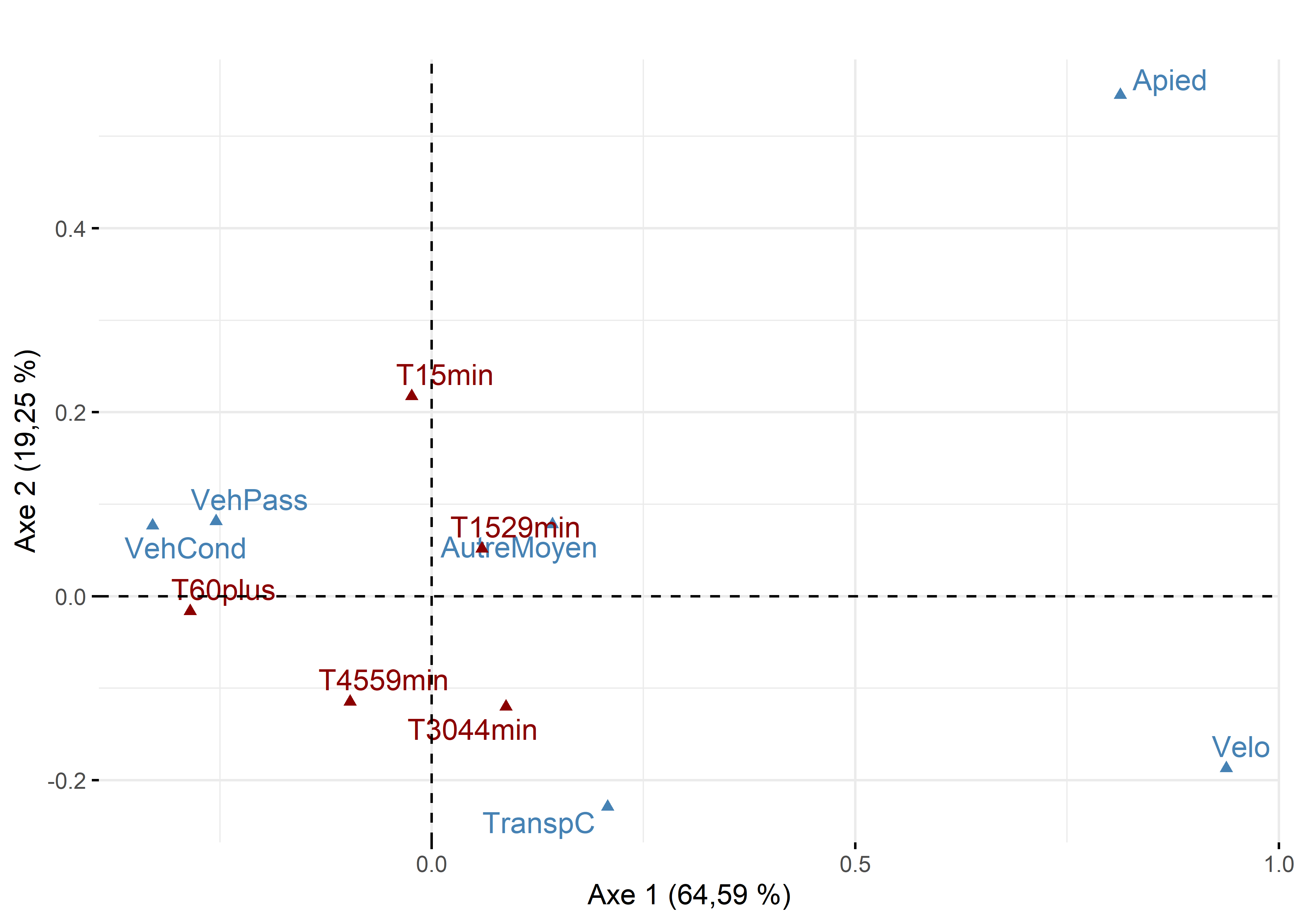
Figure 12.28: Ajout de modalités supplémentaires sur le premier plan factoriel de l’AFC
12.3.3 Mise en œuvre dans R
12.3.3.1 Calcul d’une AFC avec FactoMineR
Plusieurs packages permettent de calculer une AFC dans R, notamment ca (fonction ca), MASS (fonction corresp), ade4 (fonction dudi.coa) et FactoMineR (fonction CA). De nouveau, nous utilisons FactoMineR couplé au package factoextra pour réaliser rapidement des graphiques avec les résultats pour les variables et les coordonnées.
Pour calculer l’AFC, il suffit d’utiliser la fonction CA de FactoMineR, puis la fonction summary(res.afc), qui renvoie les résultats de l’AFC pour :
- Les valeurs propres (section
Eigenvalues) pour les axes factoriels (Dim.1àDim.n) avec leur variance expliquée brute (Variance), en pourcentage (% of var.) et en pourcentage cumulé (Cumulative % of var.). - Les dix premières observations (section
Rows) avec les coordonnées factorielles (Dim.1àDim.n), les contributions (ctr) et les cosinus carrés (cos2). Pour accéder aux résultats pour toutes les observations, utilisez les fonctionsres.afc$rowou encoreres.afc$row$coord(uniquement les coordonnées factorielles),res.afc$row$contrib(uniquement les contributions) etres.afc$row$cos2(uniquement les cosinus carrés). - Les colonnes (section
Columns) avec les coordonnées factorielles (Dim.1àDim.n), les contributions (ctr) et les cosinus carrés (cos2).
# Chargement des packages
library(FactoMineR)
library(factoextra)
# Chargement des données
load("data/analysesfactorielles/DonneesAFC.Rdata")
# Avant de calculer l'AFC, il convient de vérifier si les deux variables
# qualitatives sont dépendantes avec le test du khi-deux
khideux <- chisq.test(dfDonneesAFC[,1:6])
print(khideux)##
## Pearson's Chi-squared test
##
## data: dfDonneesAFC[, 1:6]
## X-squared = 207129, df = 2600, p-value < 2.2e-16if(khideux$p.value <=0.05){
cat("La valeur de p < 0,05. Les variables sont dépendantes. Calculer l'AFC.")
}else {
cat("La valeur de p > 0,05. Les variables sont indépendantes. Inutile de calculer l'AFC")
}## La valeur de p < 0,05. Les variables sont dépendantes. Calculer l'AFC.# Calcul de l'analyse des correspondances sur les six premières variables
res.afc <- CA(dfDonneesAFC[,1:6], graph=F)
# Affichage des résultats de la fonction CA
print(res.afc)## **Results of the Correspondence Analysis (CA)**
## The row variable has 521 categories; the column variable has 6 categories
## The chi square of independence between the two variables is equal to 207129.3 (p-value = 0 ).
## *The results are available in the following objects:
##
## name description
## 1 "$eig" "eigenvalues"
## 2 "$col" "results for the columns"
## 3 "$col$coord" "coord. for the columns"
## 4 "$col$cos2" "cos2 for the columns"
## 5 "$col$contrib" "contributions of the columns"
## 6 "$row" "results for the rows"
## 7 "$row$coord" "coord. for the rows"
## 8 "$row$cos2" "cos2 for the rows"
## 9 "$row$contrib" "contributions of the rows"
## 10 "$call" "summary called parameters"
## 11 "$call$marge.col" "weights of the columns"
## 12 "$call$marge.row" "weights of the rows"# Visualisation des marges en colonne
round(res.afc$call$marge.col,4)## VehCond VehPass TranspC Apied Velo AutreMoyen
## 0.4986 0.0309 0.3449 0.0808 0.0357 0.0090# Visualisation des marges en ligne. Étant donnée que nous avons 521 individus,
# la ligne ci-dessous est en commentaire
# round(res.afc$call$marge.row,4)
# Sommaire des résultats de l'AFC
# Remarquez que la première ligne de ce sommaire est le résultat du khi-deux
summary(res.afc)##
## Call:
## CA(X = dfDonneesAFC[, 1:6], graph = F)
##
## The chi square of independence between the two variables is equal to 207129.3 (p-value = 0 ).
##
## Eigenvalues
## Dim.1 Dim.2 Dim.3 Dim.4 Dim.5
## Variance 0.156 0.046 0.031 0.004 0.004
## % of var. 64.590 19.250 12.995 1.683 1.482
## Cumulative % of var. 64.590 83.840 96.835 98.518 100.000
##
## Rows (the 10 first)
## Iner*1000 Dim.1 ctr cos2 Dim.2 ctr cos2 Dim.3 ctr cos2
## 1 | 0.155 | -0.304 0.095 0.961 | -0.023 0.002 0.006 | 0.048 0.012 0.024 |
## 2 | 0.123 | -0.232 0.067 0.850 | 0.028 0.003 0.012 | -0.021 0.003 0.007 |
## 3 | 0.268 | -0.246 0.127 0.737 | -0.002 0.000 0.000 | -0.046 0.022 0.026 |
## 4 | 0.102 | -0.168 0.034 0.513 | -0.111 0.049 0.222 | -0.117 0.080 0.246 |
## 5 | 0.118 | -0.251 0.067 0.883 | 0.004 0.000 0.000 | -0.007 0.000 0.001 |
## 6 | 0.120 | -0.130 0.024 0.313 | -0.103 0.051 0.196 | -0.144 0.146 0.380 |
## 7 | 0.124 | -0.029 0.002 0.022 | -0.158 0.167 0.626 | -0.079 0.061 0.155 |
## 8 | 0.073 | -0.157 0.028 0.598 | -0.090 0.031 0.195 | -0.006 0.000 0.001 |
## 9 | 0.014 | -0.060 0.005 0.506 | -0.033 0.005 0.150 | -0.018 0.002 0.048 |
## 10 | 0.040 | 0.004 0.000 0.000 | -0.204 0.073 0.838 | 0.053 0.007 0.056 |
##
## Columns
## Iner*1000 Dim.1 ctr cos2 Dim.2 ctr cos2 Dim.3 ctr cos2
## VehCond | 58.559 | -0.329 34.687 0.924 | 0.077 6.331 0.050 | 0.051 4.141 0.022 |
## VehPass | 5.923 | -0.255 1.283 0.338 | 0.081 0.440 0.035 | 0.001 0.000 0.000 |
## TranspC | 38.261 | 0.208 9.534 0.389 | -0.229 38.812 0.472 | -0.124 16.995 0.139 |
## Apied | 79.193 | 0.813 34.252 0.675 | 0.545 51.610 0.303 | -0.147 5.543 0.022 |
## Velo | 55.633 | 0.938 20.126 0.564 | -0.187 2.688 0.022 | 0.802 73.180 0.413 |
## AutreMoyen | 3.969 | 0.142 0.117 0.046 | 0.078 0.119 0.014 | 0.070 0.140 0.011 |12.3.3.2 Exploration graphique des résultats de l’AFC avec factoextra
Comme pour l’ACP, factoextra dispose de plusieurs fonctions très intéressantes pour construire rapidement des graphiques avec les résultats de l’AFC. Premièrement, la syntaxe ci-dessous (avec la fonction fviz_screeplot) renvoie deux graphiques pour analyser les résultats des valeurs propres de l’AFC (figure 12.29).
library(factoextra)
library(ggplot2)
library(ggpubr)
# Nombre de modalités en ligne et en colonne
ModalitesLig <- nrow(dfDonneesAFC)
ModalitesCol <- ncol(dfDonneesAFC[,1:6])
# Critère statistique du profil moyen
critere2 <- round(1/(ModalitesCol-1)*100,2)
texte <- paste0("Critère pour le profil moyen : ", as.character(critere2), " %")
# Graphique avec les valeurs propres
G1 <- fviz_screeplot(res.afc, choice="eigenvalue",
ylab="Valeurs propres",
xlab="Axes factoriels",
main="Valeurs propres")
G2 <- fviz_screeplot(res.afc, choice="variance", addlabels = TRUE, ylim = c(0, 70),
ylab="Variance expliquée (%)",
xlab="Axes factoriels",
main="Valeurs propres (%)")+
geom_hline(yintercept = c2, linetype = 1, color = "red", size=1)+
annotate(geom="text", x = ModalitesCol-.5,
y= critere2+3, label=texte,
color="red", hjust = 1, size = 4)
ggarrange(G1, G2)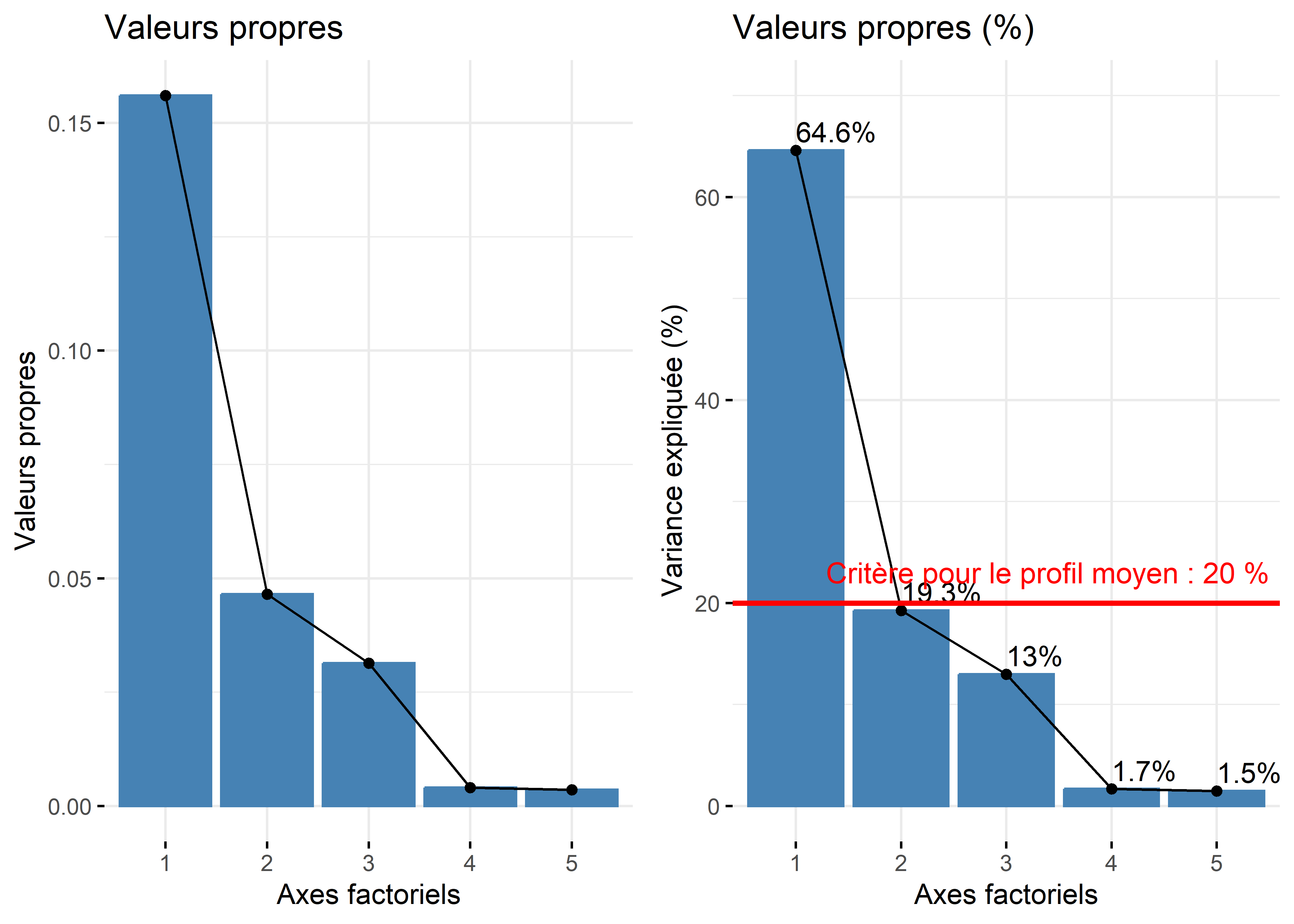
Figure 12.29: Graphiques pour les valeurs propres de l’AFC avec factoextra
Avec les fonctions fviz_contrib et fviz_cos2, il est très facile de réaliser des histogrammes pour les contributions et les cosinus carrés pour les variables (colonnes) ou les individus (lignes), et ce, avec le paramètre choice = c("row", "col") (figure 12.30).
library(factoextra)
library(ggplot2)
library(ggpubr)
VP1pct <- round(res.afc$eig[1,2],2)
VP2pct <- round(res.afc$eig[2,2],2)
G1 <- fviz_contrib (res.afc, choice = "col", axes = 1, title="Axe 1")
G2 <- fviz_contrib (res.afc, choice = "col", axes = 2, title="Axe 2")
ggarrange(G1, G2, ncol = 2, nrow = 1)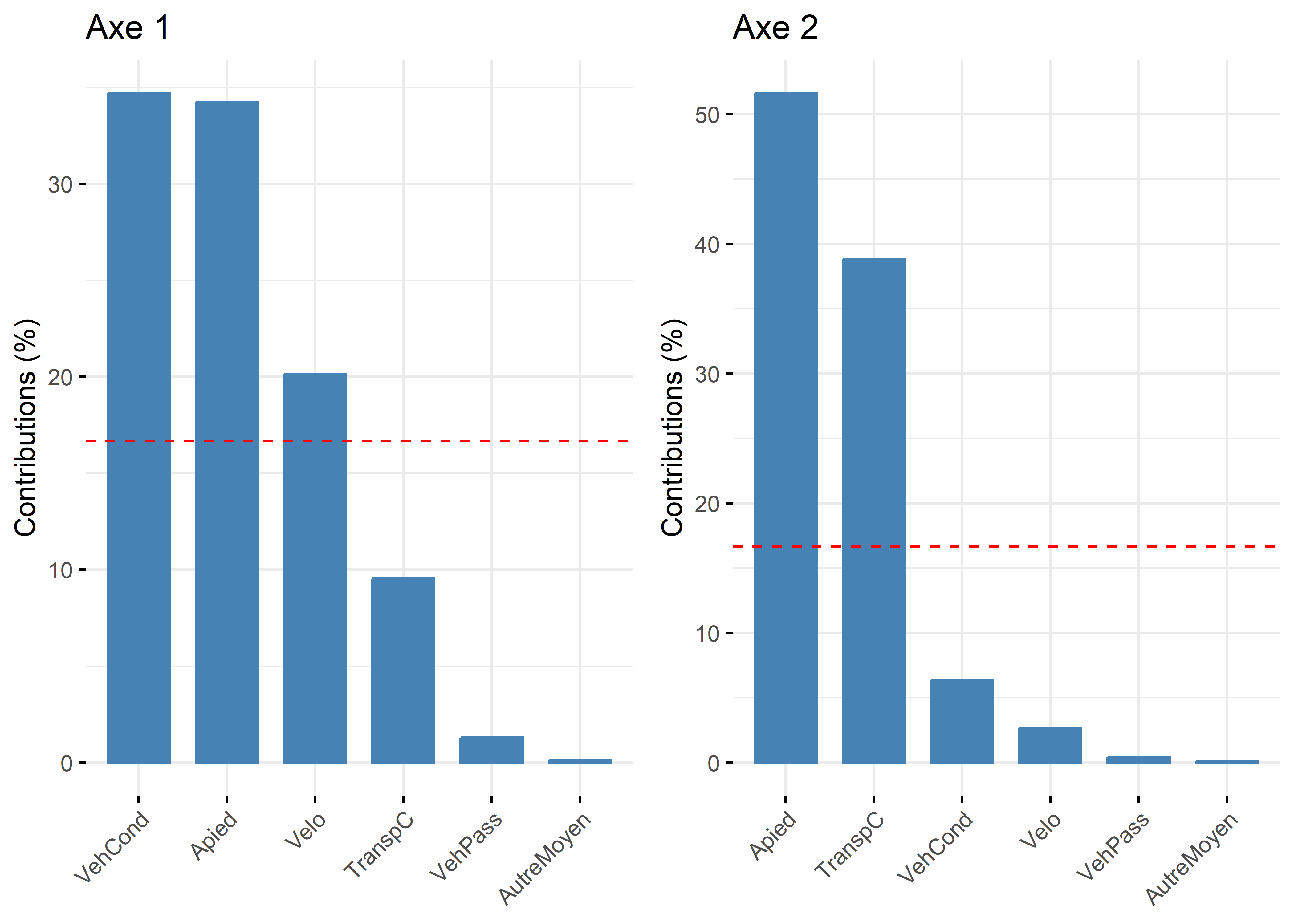
Figure 12.30: Contributions des variables avec factoextra
Quant aux fonctions fviz_ca_col et fviz_ca_row, elles permettent rapidement de construire le premier plan factoriel pour les colonnes (variables) et les lignes (individus) (figure 12.31). Aussi, la fonction fviz_ca_biplot permet de construire un plan factoriel, mais avec les lignes et les colonnes simultanément.
G3 <- fviz_ca_col(res.afc,
repel = TRUE,
geom= c("text","point"),
col.col = "steelblue",
title = "Mode de transport",
xlab=paste0("Axe 1 (", VP1pct, " %)"),
ylab=paste0("Axe 2 (", VP2pct, " %)"))
G4 <- fviz_ca_row(res.afc,
repel = TRUE,
geom= c("point"),
col.row = "steelblue",
title = "Secteurs de recensement",
xlab=paste0("Axe 1 (", VP1pct, " %)"),
ylab=paste0("Axe 2 (", VP2pct, " %)"))
ggarrange(G3, G4, ncol = 2, nrow = 1)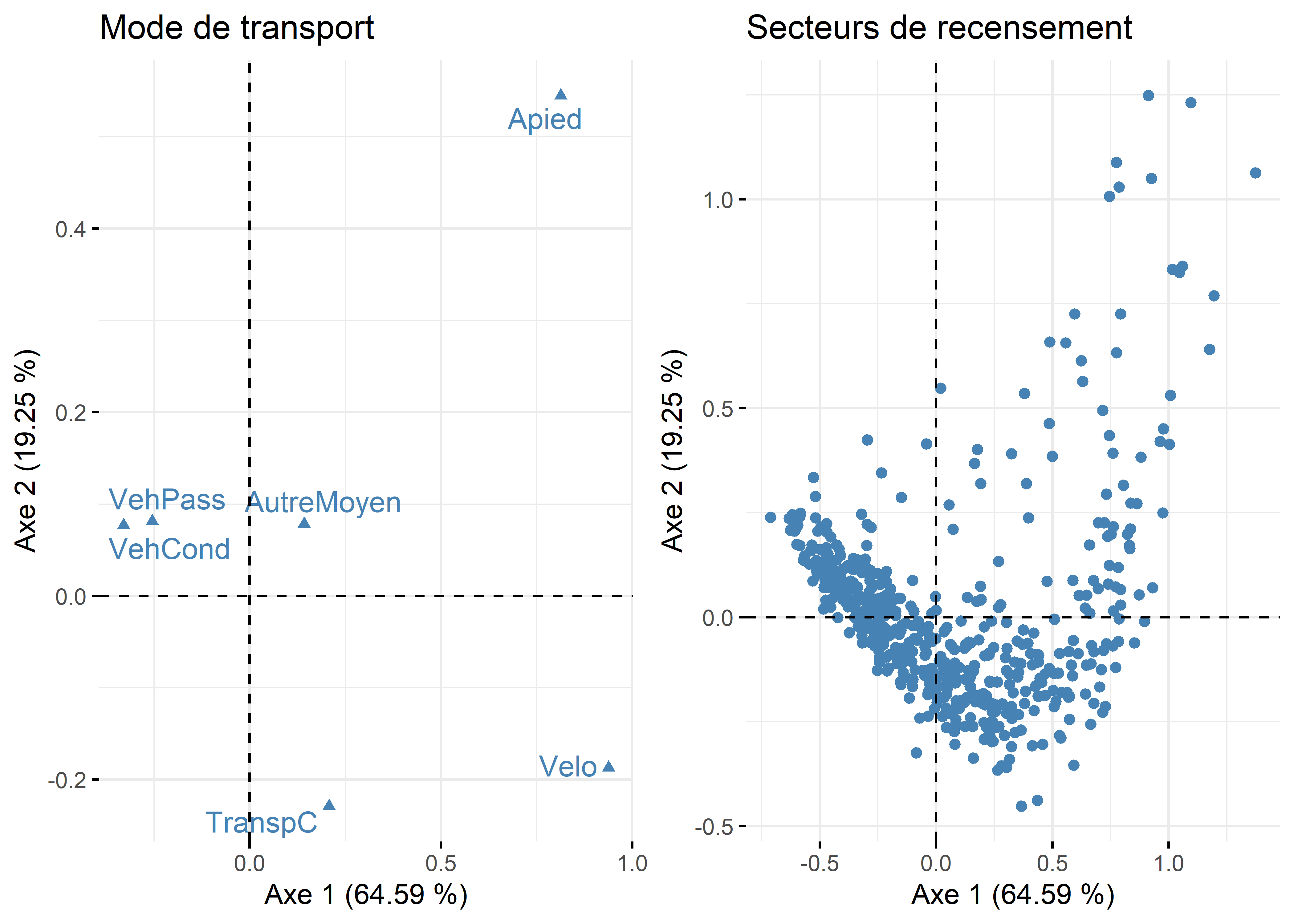
Figure 12.31: Premier plan factoriel de l’AFC pour les variables et les individus avec factoextra
La syntaxe ci-dessous permet d’ajouter des modalités supplémentaires dans l’AFC et de constuire le graphique du premier plan factoriel (figure 12.32).
# Les colonnes 7 à 11 sont mises comme des variables supplémentaires dans l'AFC
res.afc2 <- CA(dfDonneesAFC, col.sup = 7:11, graph = FALSE)
VP1pct <- round(res.afc2$eig[1,2],2)
VP2pct <- round(res.afc2$eig[2,2],2)
fviz_ca_col(res.afc2,
repel = TRUE,
geom= c("text","point"),
col.col = "steelblue",
title = "",
xlab=paste0("Axe 1 (", VP1pct, " %)"),
ylab=paste0("Axe 2 (", VP2pct, " %)"))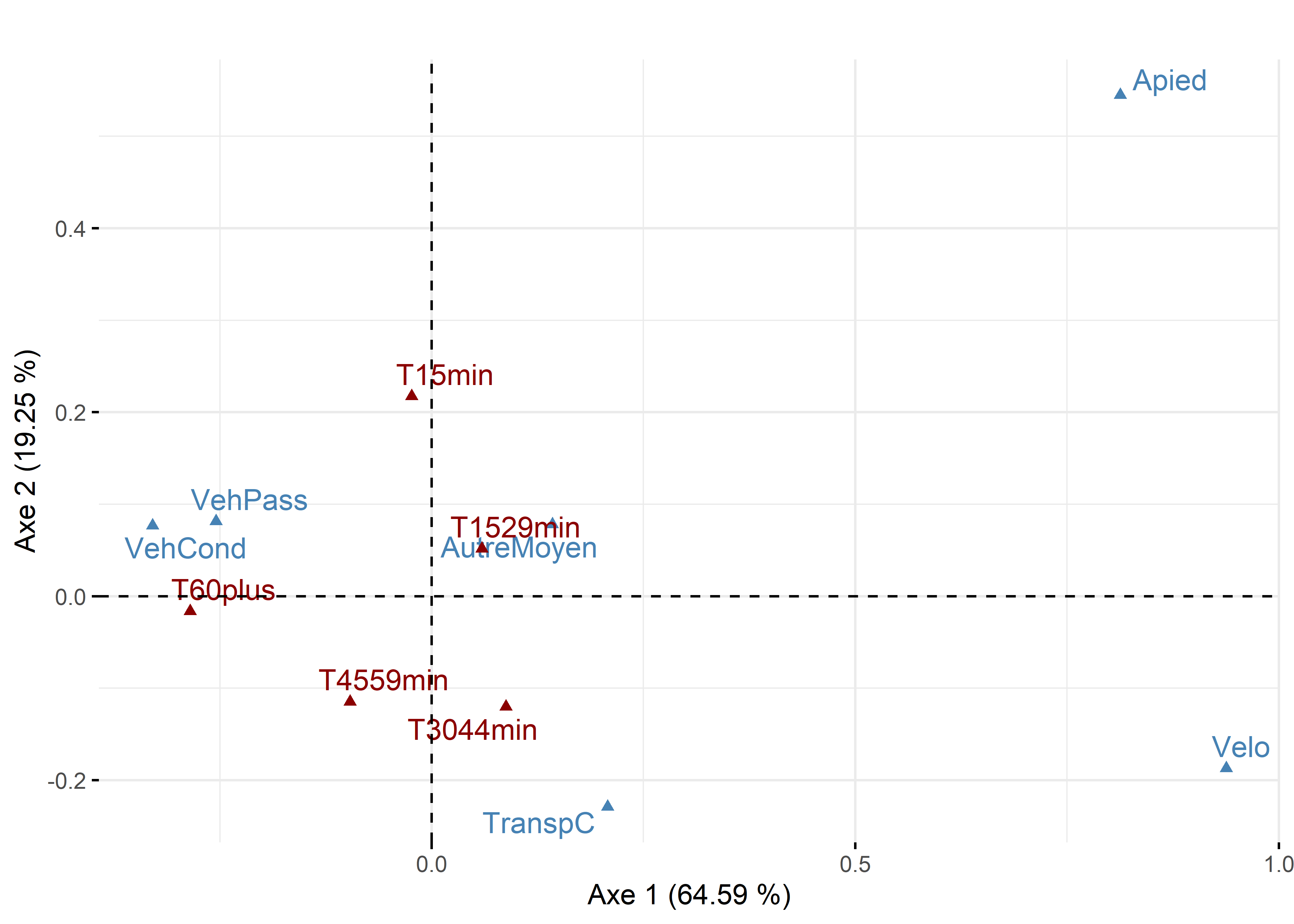
Figure 12.32: Ajout de modalités supplémentaires sur le premier plan factoriel l’AFC avec factoextra
Finalement, la syntaxe ci-dessous permet de cartographier les coordonnées factorielles des individus de l’AFC avec le package tmap (figure 12.33).
library(tmap)
library(stringr)
dfAFCInd <- data.frame(Coord = res.afc$row$coord,
Cos2 = res.afc$row$cos2,
Ctr = res.afc$row$contrib)
names(dfAFCInd) <- str_replace(names(dfAFCInd), ".Dim.", "Comp")
CartoAFC <- cbind(sfDonneesAFC, dfAFCInd)
VP1pct <- tofr(round(res.afc$eig[1,2],2))
VP2pct <- tofr(round(res.afc$eig[2,2],2))
Carte1 <- tm_shape(CartoAFC) +
tm_fill(col = "CoordComp1", style = "cont", midpoint = 0, title = 'Coordonnées')+
tm_layout(title = paste0("Axe 1 (", VP1pct,"%)"), attr.outside = TRUE, frame = FALSE)
Carte2 <- tm_shape(CartoAFC) +
tm_fill(col = "CoordComp2", style = "cont", midpoint = 0, title = 'Coordonnées')+
tm_layout(title = paste0("Axe 2 (", VP2pct,"%)"), attr.outside = TRUE, frame = FALSE)
tmap_arrange(Carte1, Carte2, nrow = 1)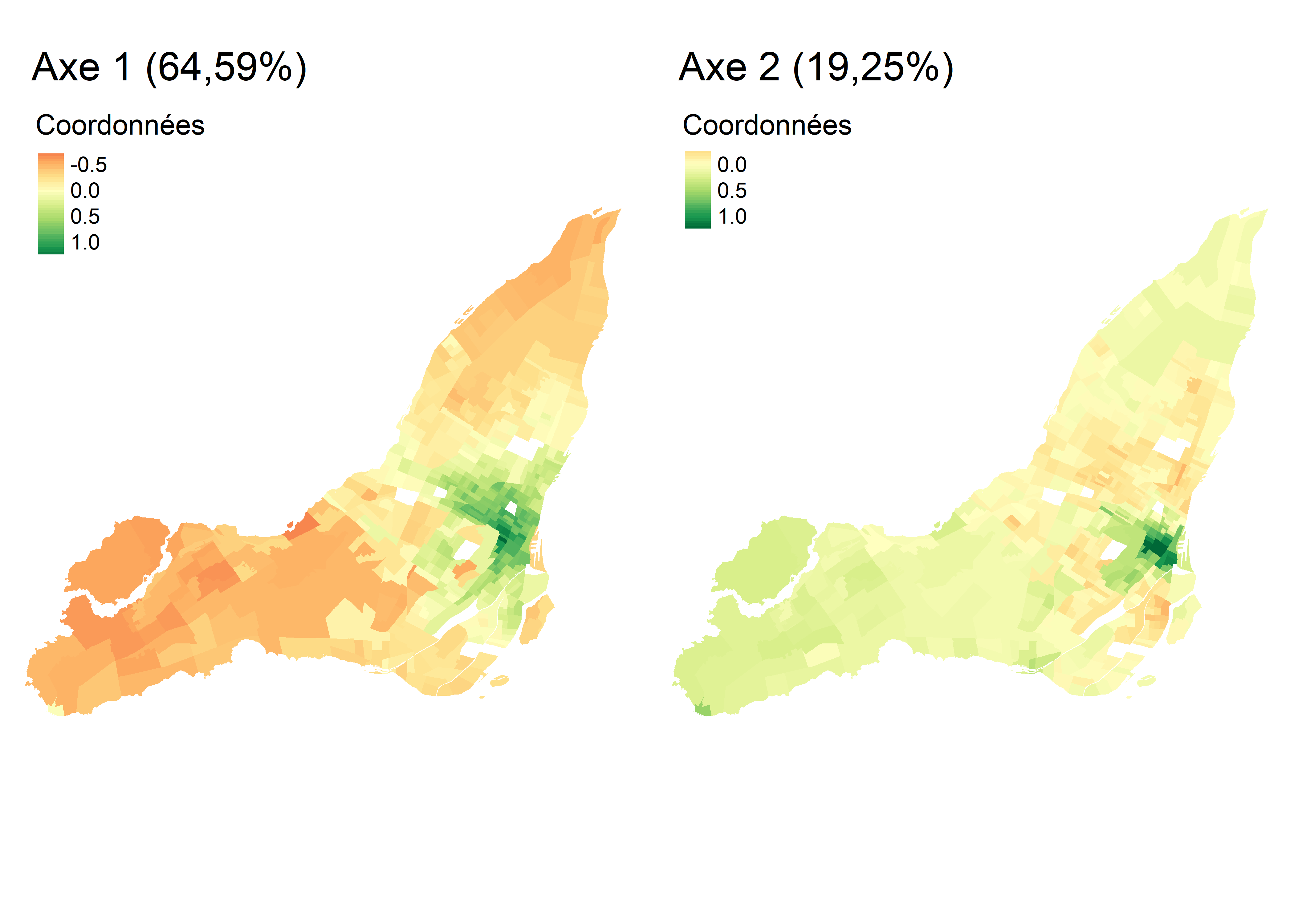
Figure 12.33: Cartographie de coordonnées factorielles des individus pour l’AFC