2.4 Notion de distribution

Dans cette section, nous abordons un concept central de la statistique : les distributions. Prenez le temps de lire cette section à tête reposée et assurez-vous de bien comprendre chaque idée avant de passer à la suivante. N’hésitez pas à y revenir plusieurs fois si nécessaire, car la compréhension de ces concepts est essentielle pour utiliser adéquatement les méthodes que nous abordons dans ce livre.

2.4.1 Définition générale

En probabilité, nous nous intéressons aux résultats d’expériences. Du point de vue de la théorie des probabilités, lancer un dé, mesurer la pollution atmosphérique, compter le nombre de collisions à une intersection, et demander à une personne d’évaluer son sentiment de sécurité sur une échelle de 1 à 10 sont autant d’expériences pouvant produire des résultats.

Une distribution est un modèle mathématique permettant d’associer pour chaque résultat possible d’une expérience la probabilité d’obtenir ce résultat. D’un point de vue pratique, si nous disposons de la distribution régissant l’expérience : « mesurer la concentration d’ozone à Montréal à 13 h en été », nous pouvons calculer la probabilité de mesurer une valeur inférieure à 15 μg/m³.

Loi de probabilité et distribution

L’utilisation que nous faisons ici du terme « distribution » est un anglicisme (éhonté diront certaines personnes). En effet, en français, la définition précédente est plus proche du terme « loi de probabilité ». Cependant, la quasi-totalité de la documentation sur R est en anglais et, dans la pratique, ces deux termes ont tendance à se confondre. Nous avons donc fait le choix de poursuivre avec ce terme dans le reste du livre.

Une distribution est toujours définie dans un intervalle en dehors duquel elle n’est définie; les valeurs dans cet intervalle sont appelées l’espace d’échantillonnage. Il s’agit donc des valeurs possibles que peut produire l’expérience. La somme des probabilités de l’ensemble des valeurs de l’espace d’échantillonnage est 1 (100 %). Intuitivement, cela signifie que si nous réalisons l’expérience, nous obtenons nécessairement un résultat, et que la somme des probabilités est répartie entre tous les résultats possibles de l’expérience. En langage mathématique, nous disons que l’intégrale de la fonction de densité d’une distribution est 1 dans son intervalle de définition.

Prenons un exemple concret avec l’expérience suivante : tirer à pile ou face avec une pièce de monnaie non truquée. Si l’on souhaite décrire la probabilité d’obtenir pile ou face, nous pouvons utiliser une distribution qui aura comme espace d’échantillonnage [pile; face] et ces deux valeurs auront chacune comme probabilité 0,5. Il est facile d’étendre cet exemple au cas d’un dé à six faces. La distribution de probabilité décrivant l’expérience « lancer le dé » a pour espace d’échantillonnage [1,2,3,4,5,6], chacune de ces valeurs étant associée à la probabilité de 1/6.

Chacune des deux expériences précédentes est régie par une distribution appartenant à la famille des distributions discrètes. Elles servent à représenter des expériences dont le nombre de valeurs possibles est fini. Par opposition, la seconde famille de distributions regroupe les distributions continues, décrivant des expériences dont le nombre de résultats possibles est en principe infini. Par exemple, mesurer la taille d’une personne adulte sélectionnée au hasard peut produire en principe un nombre infini de valeurs. Les distributions sont utiles pour décrire les résultats potentiels d’une expérience. Reprenons notre exemple du dé. Nous savons que chaque face a une chance sur six d’être tirée au hasard. Nous pouvons représenter cette distribution avec un graphique (figure 2.3).

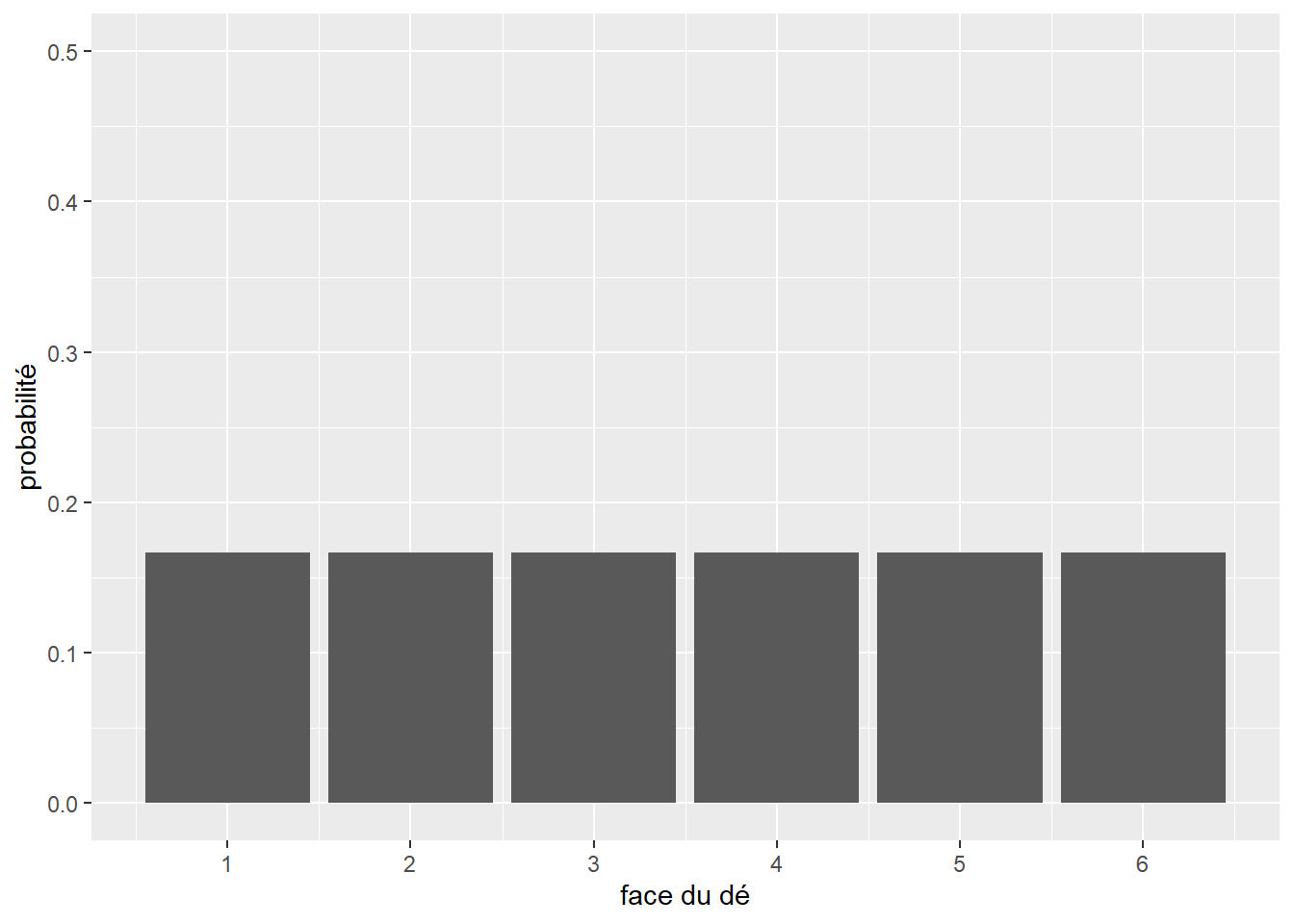
Figure 2.3: Distribution théorique d’un lancer de dé

Nous avons donc sous les yeux un modèle statistique décrivant le comportement attendu d’un dé, soit sa distribution théorique. Cependant, si nous effectuons dix fois l’expérience (nous collectons donc un échantillon), nous obtiendrons une distribution différente de cette distribution théorique (figure 2.4).

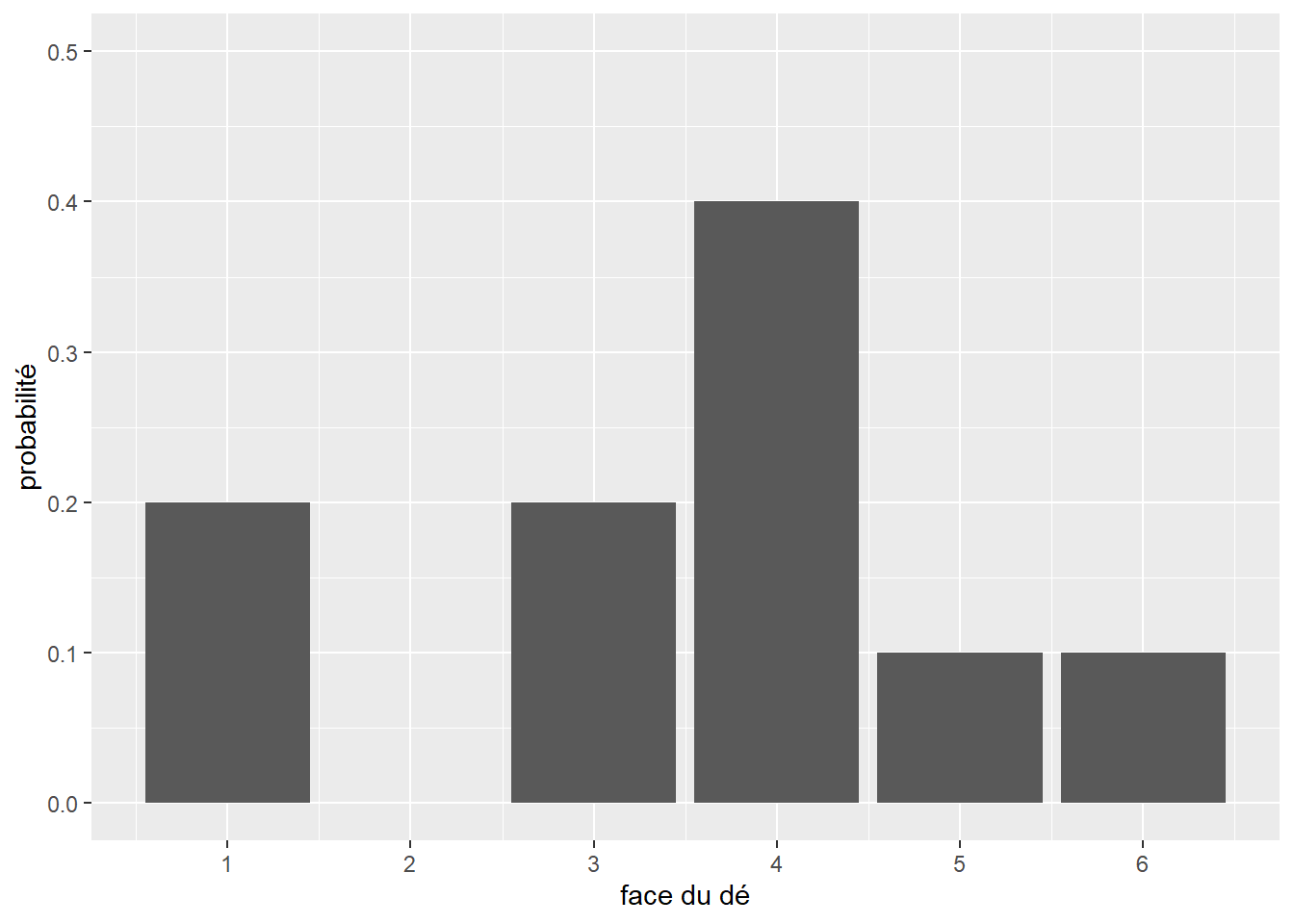
Figure 2.4: Distribution empirique d’un lancer de dé (n=10)

Il s’agit de la distribution empirique. Chaque échantillon aura sa propre distribution empirique. Cependant, comme le prédit la loi des grands nombres : si une expérience est répétée un grand nombre de fois, la probabilité empirique d’un résultat se rapproche de la probabilité théorique à mesure que le nombre de répétitions augmente. Du point de vue de la théorie des probabilités, chaque échantillon correspond à un ensemble de tirages aléatoires effectués à partir de la distribution théorique du phénomène étudié.

Pour nous en convaincre, collectons trois échantillons de lancer de dé de respectivement 30, 100 et 1000 observations (figure 2.5). Comme le montre la figure 2.4, nous connaissons la distribution théorique qui régit cette expérience.

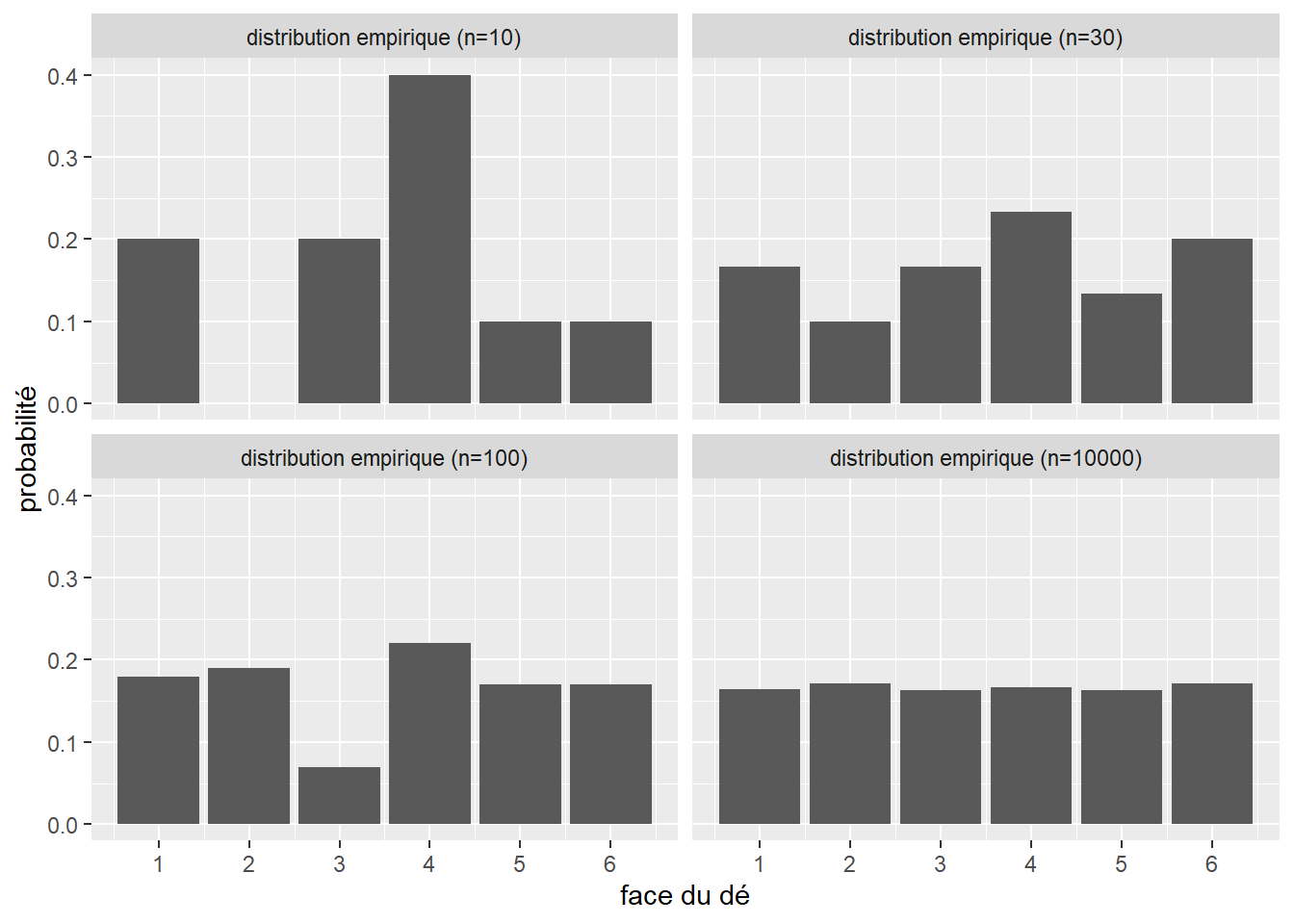
Figure 2.5: Distribution empirique d’un lancer de dé

Nous constatons bien qu’au fur et à mesure que la taille de l’échantillon augmente, nous tendons vers la distribution théorique.

Cette relation a été étudiée pour la première fois au XVIII^e siècle par le mathématicien Daniel Bernoulli, qui a montré que la probabilité que la moyenne d’une distribution empirique soit éloignée de la moyenne de la distribution théorique dont elle est tirée diminuait lorsque nous augmentons le nombre des tirages et donc la taille de l’échantillon. Un autre mathématicien, Siméon-Denis Poisson, a fait connaître cette relation sous le nom de « loi des grands nombres ».

Les distributions théoriques sont utilisées pour modéliser des phénomènes réels et sont à la base de presque tous les tests statistiques d’inférence fréquentiste ou bayésienne. En pratique, la question que nous nous posons le plus souvent est : quelle distribution théorique peut le mieux décrire le phénomène empirique à l’étude? Pour répondre à cette question, deux approches sont possibles :

Considérant la littérature existante sur le sujet, les connaissances accumulées et la nature de la variable étudiée, sélectionner des distributions théoriques pouvant vraisemblablement correspondre au phénomène mesuré.
Comparer visuellement ou à l’aide de tests statistiques la distribution empirique de la variable et diverses distributions théoriques pour trouver la plus adaptée.

Idéalement, le choix d’une distribution théorique devrait reposer sur ces deux méthodes combinées.

2.4.2 Anatomie d’une distribution

Une distribution (ou loi de probabilité) est une fonction. Il est possible de la représenter à l’aide d’une formule mathématique (appelée fonction de masse pour les distributions discrètes et fonction de densité pour les distributions continues) associant chaque résultat possible de l’expérience régie par la distribution à la probabilité d’observer ce résultat. Prenons un premier exemple concret avec la distribution théorique associée au lancer de pièce de monnaie : la distribution de Bernoulli. Sa formule est la suivante :

\[\begin{equation} f(x ; p)=\left\{\begin{array}{ll} q=1-p & \text { si } x=0 \\ p & \text { si } x=1 \end{array}\right. \tag{2.1} \end{equation}\]

avec p la probabilité d’obtenir $x = 1$ (pile), et $1 – p$ la probabilité d’avoir $x = 0$ (face). La distribution de Bernoulli ne dépend que d’un paramètre : p. Avec différentes valeurs de p, nous pouvons obtenir différentes formes pour la distribution de Bernoulli. Si p = 1/2, la distribution de Bernoulli décrit parfaitement l’expérience : obtenir pile à un lancer de pièce de monnaie. Si p = 1/6, elle décrit alors l’expérience : obtenir 4 (tout comme n’importe quelle valeur de 1 à 6) à un lancer de dé. Pour un exemple plus appliqué, la distribution de Bernoulli est utilisée en analyse spatiale pour étudier la concentration d’accidents de la route ou de crimes en milieu urbain. À chaque endroit du territoire, il est possible de calculer la probabilité qu’un tel évènement ait lieu ou non en modélisant les données observées au moyen de la loi de Bernoulli. La distribution continue la plus simple à décrire est certainement la distribution uniforme. Il s’agit d’une distribution un peu spéciale puisqu’elle attribue la même probabilité à toutes ses valeurs dans son espace d’échantillonnage. Elle est définie sur l’intervalle $[-\infty; +\infty]$ et a la fonction de densité suivante :

\[\begin{equation} f(x ; \mathrm{a} ; \mathrm{b})=\left\{\begin{array}{cc} \frac{1}{a-b} & \text { si } a \geq x \geq b \\ 0 & \text { sinon } \end{array}\right. \tag{2.2} \end{equation}\]

La fonction de densité de la distribution uniforme a donc deux paramètres, a et b, représentant respectivement les valeurs maximale et minimale au-delà desquelles les valeurs ont une probabilité 0 d’être obtenues. Pour avoir une meilleure intuition de ce que décrit une fonction de densité, il est intéressant de la représenter avec un graphique (figure 2.6). Notez que sur ce graphique, l’axe des ordonnées n’indique pas précisément la probabilité associée à chaque valeur, car celle-ci est infinitésimale. Il sert uniquement à représenter la valeur de la fonction de densité de la distribution pour chaque valeur de x.

## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.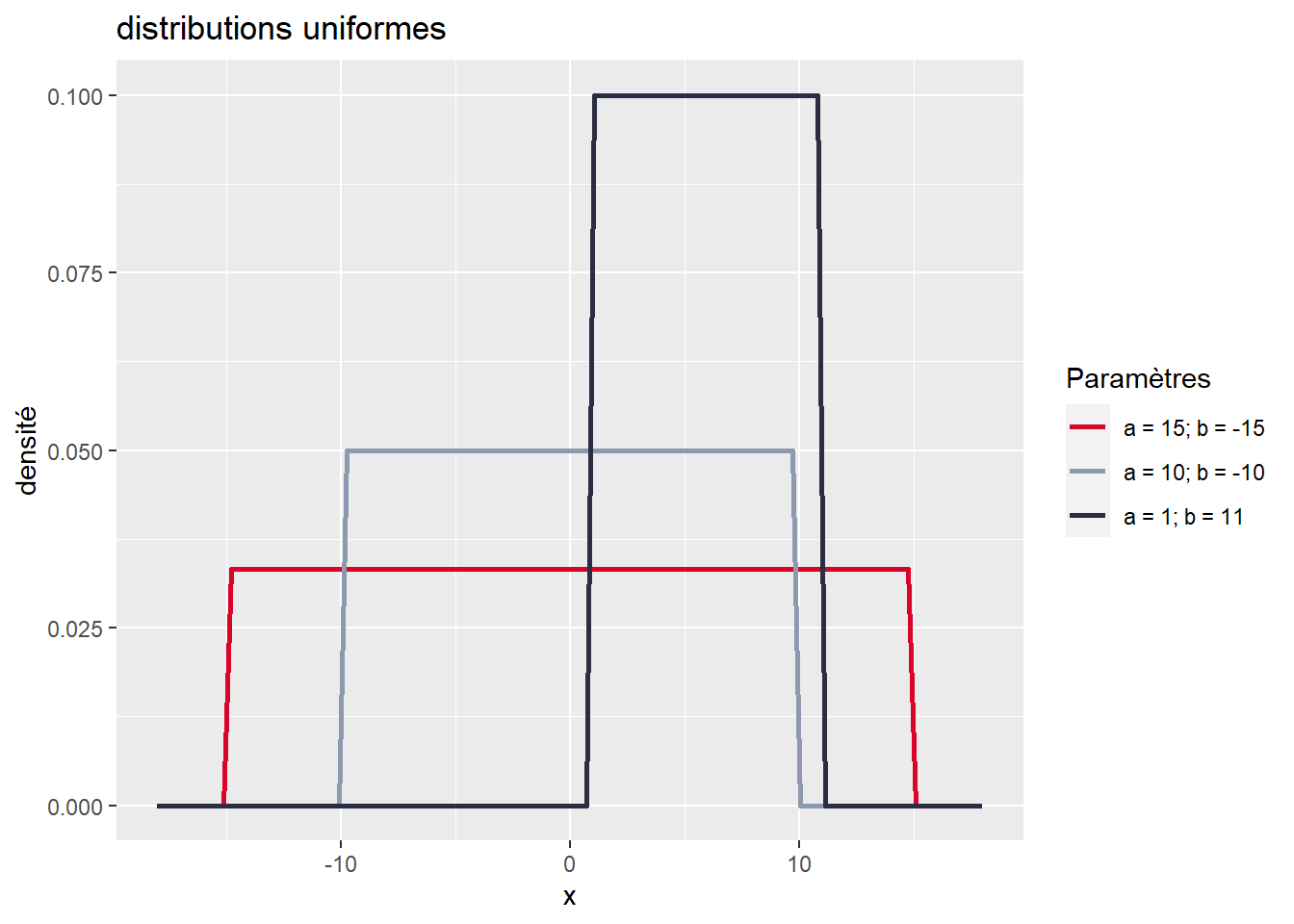

Figure 2.6: Distributions uniformes continues

Nous observons clairement que toutes les valeurs de x entre a et b ont la même probabilité pour chacune de trois distributions uniformes présentées dans le graphique. Plus l’étendue est grande ($a-b$), plus l’espace d’échantillonnage est grand et plus la probabilité totale est répartie dans cet espace. Cette distribution est donc idéale pour décrire un phénomène pour lequel chaque valeur a autant de chance de se produire qu’une autre. Prenons pour exemple un cas fictif avec un jeu de hasard qui vous proposerait la situation suivante : en tirant sur la manette d’une machine à sous, un nombre est tiré aléatoirement entre -60 et +50. Si le nombre est négatif, vous perdez de l’argent et inversement si le nombre est positif. Nous pouvons représenter cette situation avec une distribution uniforme continue et l’utiliser pour calculer quelques informations essentielles :

Selon cette distribution, quelle est la probabilité de gagner de l’argent lors d’un tirage (x > 0)?
Quelle est la probabilité de perdre de l’argent (x < 0)?
Si je perds moins de 30 $ au premier tirage, quelle est la probabilité que j’ai de récupérer au moins ma mise au second tirage (x > 30)?

Il est assez facile de calculer ces probabilités en utilisant la fonction punif dans R. Concrètement, cela permet de calculer l’intégrale de la fonction de masse sur un intervalle donné.

# Probabilité d'obtenir une valeur supérieure ou égale à 0
punif(0,min = -60, max = 50)

## [1] 0.5454545

# Probabilité d'obtenir une valeur inférieure à 0
punif(0,min = -60, max = 50, lower.tail = F)

## [1] 0.4545455

# Probabilité d'obtenir une valeur supérieure à 30
punif(30, min = -60, max = 50,lower.tail = F)

## [1] 0.1818182

Les paramètres permettent donc d’ajuster la fonction de masse ou de densité d’une distribution afin de lui permettre de prendre des formes différentes. Certains paramètres changent la localisation de la distribution (la déplacer vers la droite ou la gauche de l’axe des X), d’autres changent son degré de dispersion (distribution pointue ou aplatie) ou encore sa forme (symétrie). Les différents paramètres d’une distribution correspondent donc à sa carte d’identité et donnent une idée précise sur sa nature.

Fonction de répartition, de survie et d’intensité

Si les fonctions de densité ou de masse d’une distribution sont le plus souvent utilisée pour décrire une distribution, d’autres types de fonctions peuvent également être employées et disposent de propriétés intéressantes.

La fonction de répartition : il s’agit d’une fonction décrivant le cumul de probabilités d’une distribution. Cette fonction a un minimum de zéro qui est obtenu pour la plus petite valeur de l’espace d’échantillonnage de la distribution, et un maximum d’un pour la plus grande valeur de ce même espace. Formellement, la fonction de répartition ($F$) est l’intégrale de la fonction de densité ($f$).

\[F(x) = \int_{-\infty}^{x}f(u)du\] 2. La fonction de survie : soit l’inverse additif de la fonction de répartition ($R$)

\[R(x) = 1-F(x)\] 3. La fonction de d’intensité, soit le quotient de la fonction de densité et de la fonction de survie ($D$). \[D(x) = \frac{f(x)}{D(x)}\] Ces fonctions jouent notamment un rôle central dans la modélisation des phénomènes qui régissent la survenue des événements, par exemple la mort, les accidents de la route ou les bris d’équipement.

2.4.3 Principales distributions

Il existe un très grand nombre de distributions théoriques et parmi elles, de nombreuses sont en fait des cas spéciaux d’autres distributions. Pour un petit aperçu du « bestiaire », vous pouvez faire un saut à la page Univariate Distribution Relationships, qui liste près de 80 distributions.

Nous nous concentrons ici sur une sélection de dix-huit distributions très répandues en sciences sociales. La figure 2.7 présente graphiquement leurs fonctions de masse et de densité présentées dans cette section. Notez que ces graphiques correspondent tous à une forme possible de chaque distribution. En modifiant leurs paramètres, il est possible de produire une figure très différente. Les distributions discrètes sont représentées avec des graphiques en barre, et les distributions continues avec des graphiques de densité.

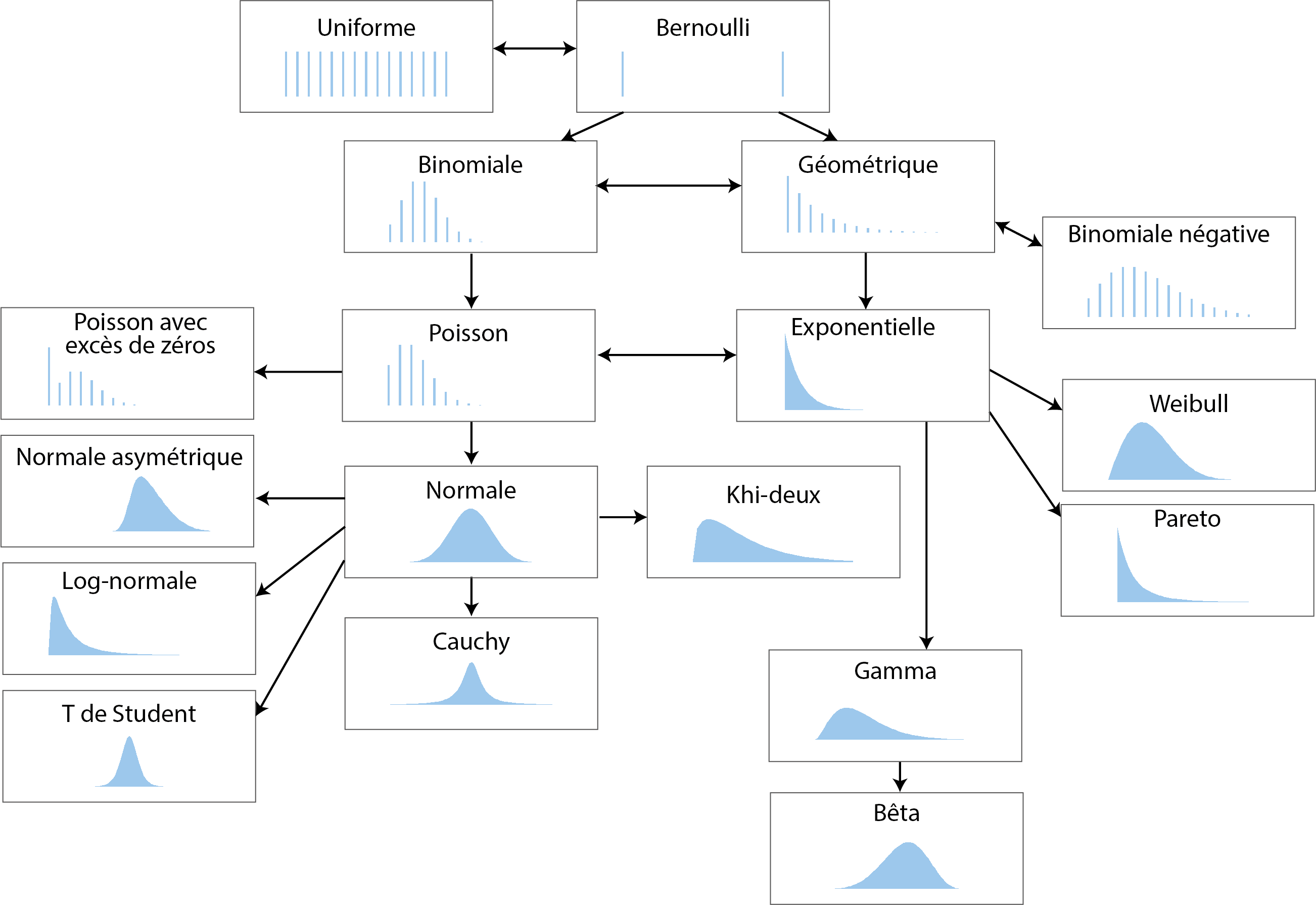
Figure 2.7: Dix-huit distributions essentielles, figure inspirée de Sean (2018)

2.4.3.1 Distribution uniforme discrète

Nous avons déjà abordé cette distribution dans les exemples précédents. Elle permet de décrire un phénomène dont tous les résultats possibles ont exactement la même probabilité de se produire. L’exemple classique est bien sûr un lancer de dé.

2.4.3.2 Distribution de Bernoulli

La distribution de Bernoulli permet de décrire une expérience pour laquelle deux résultats sont possibles. Son espace d’échantillonnage est donc $[0; 1]$. Sa fonction de masse est la suivante :

\[\begin{equation} f(x ; p)=\left\{\begin{array}{ll} q=1-p & \text { si } x=0 \\ p & \text { si } x=1 \end{array}\right. \tag{2.3} \end{equation}\]

avec p la probabilité d’obtenir $x = 1$ (réussite) et donc $1 – p$ la probabilité d’avoir $x = 0$ (échec). La distribution de Bernoulli ne dépend que d’un paramètre : p, contrôlant la probabilité de réussite de l’expérience. Notez que si $p = 1/2$, alors la distribution de Bernoulli est également une distribution uniforme. Un exemple d’application de la distribution de Bernoulli en études urbaines est la modélisation de la survie d’un ou d’une cycliste (1 pour survie, 0 pour décès) lors d’une collision avec un véhicule motorisé, selon une vitesse donnée.

2.4.3.3 Distribution binomiale

La distribution binomiale est utilisée pour caractériser la somme de variables aléatoires (expériences) suivant chacune une distribution de Bernoulli. Un exemple simple est l’accumulation des lancers d’une pièce de monnaie. Si nous comptons le nombre de fois où nous obtenons pile, cette expérience est décrite par une distribution binomiale. Son espace d’échantillonnage est donc $[0; +\infty[$ (limité aux nombres entiers). Sa fonction de masse est la suivante :

\[\begin{equation} f(x ; n )=\binom{n}{x}p^x(1-p)^{n-x} \tag{2.4} \end{equation}\]

avec x le nombre de tirages réussis sur n essais avec une probabilité p de réussite à chaque tirage (figure 2.8). Pour reprendre l’exemple précédent concernant les accidents de la route, une distribution binomiale permettrait de représenter la distribution du nombre de cyclistes ayant survécu sur dix personnes à vélo impliquées dans un accident avec une voiture à une intersection.

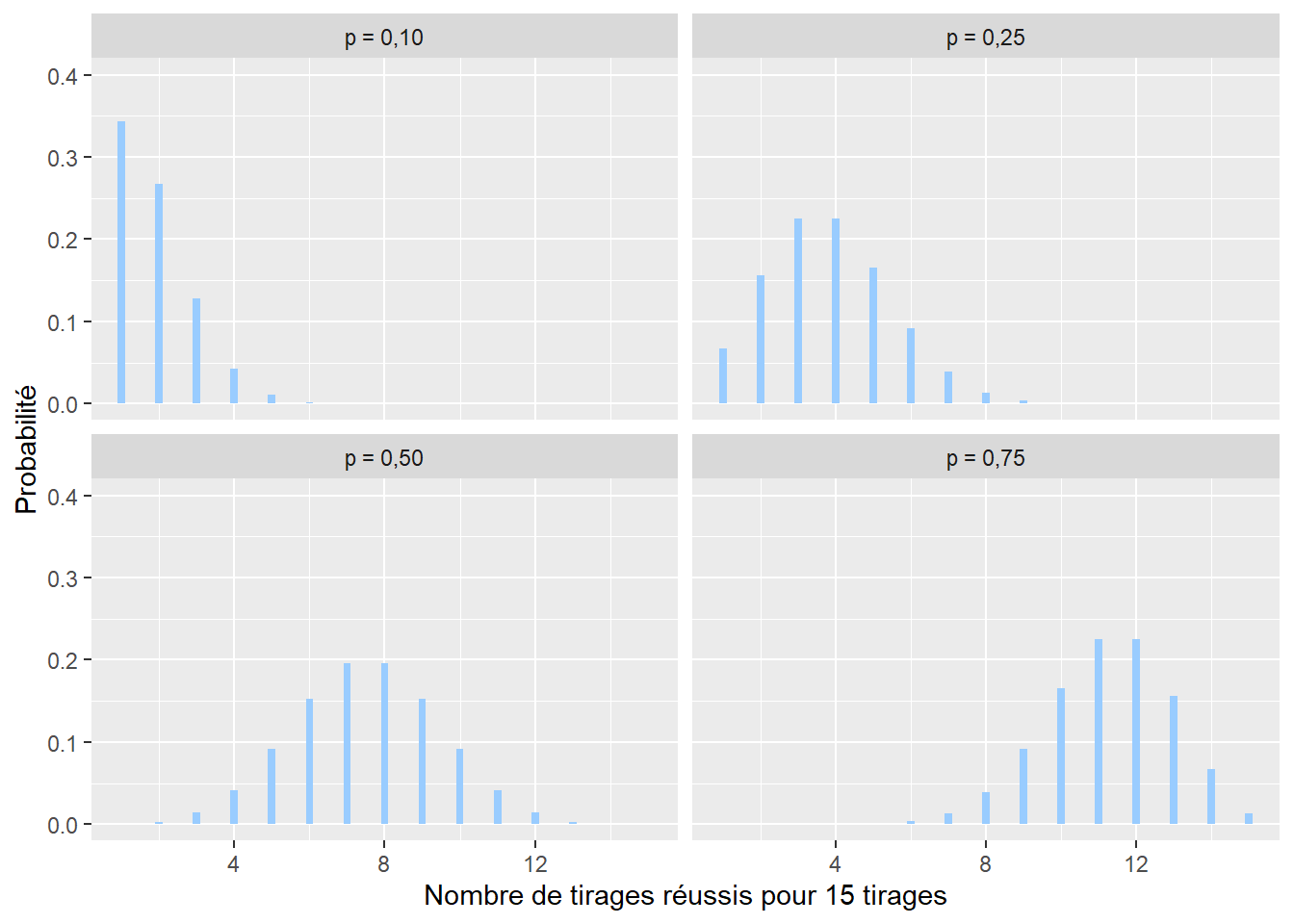
Figure 2.8: Distribution binomiale

2.4.3.4 Distribution géométrique

La distribution géométrique permet de représenter le nombre de tirages qu’il faut faire avec une distribution de Bernoulli avant d’obtenir une réussite. Par exemple, avec un lancer de dé, l’idée serait de compter le nombre de lancers nécessaires avant de tomber sur un 6. Son espace d’échantillonnage est donc $[1; +\infty[$ (limité aux nombres entiers). Sa distribution de masse est la suivante :

\[\begin{equation} f(x; p)= (1-p)^xp \tag{2.5} \end{equation}\]

avec x le nombre de tentatives avant d’obtenir une réussite, $f(x)$ la probabilité que le premier succès n’arrive qu’après x tentatives et p la probabilité de réussite à chaque tentative (figure 2.9). Cette distribution est notamment utilisée en marketing pour modéliser le nombre d’appels nécessaires avant de réussir une vente.

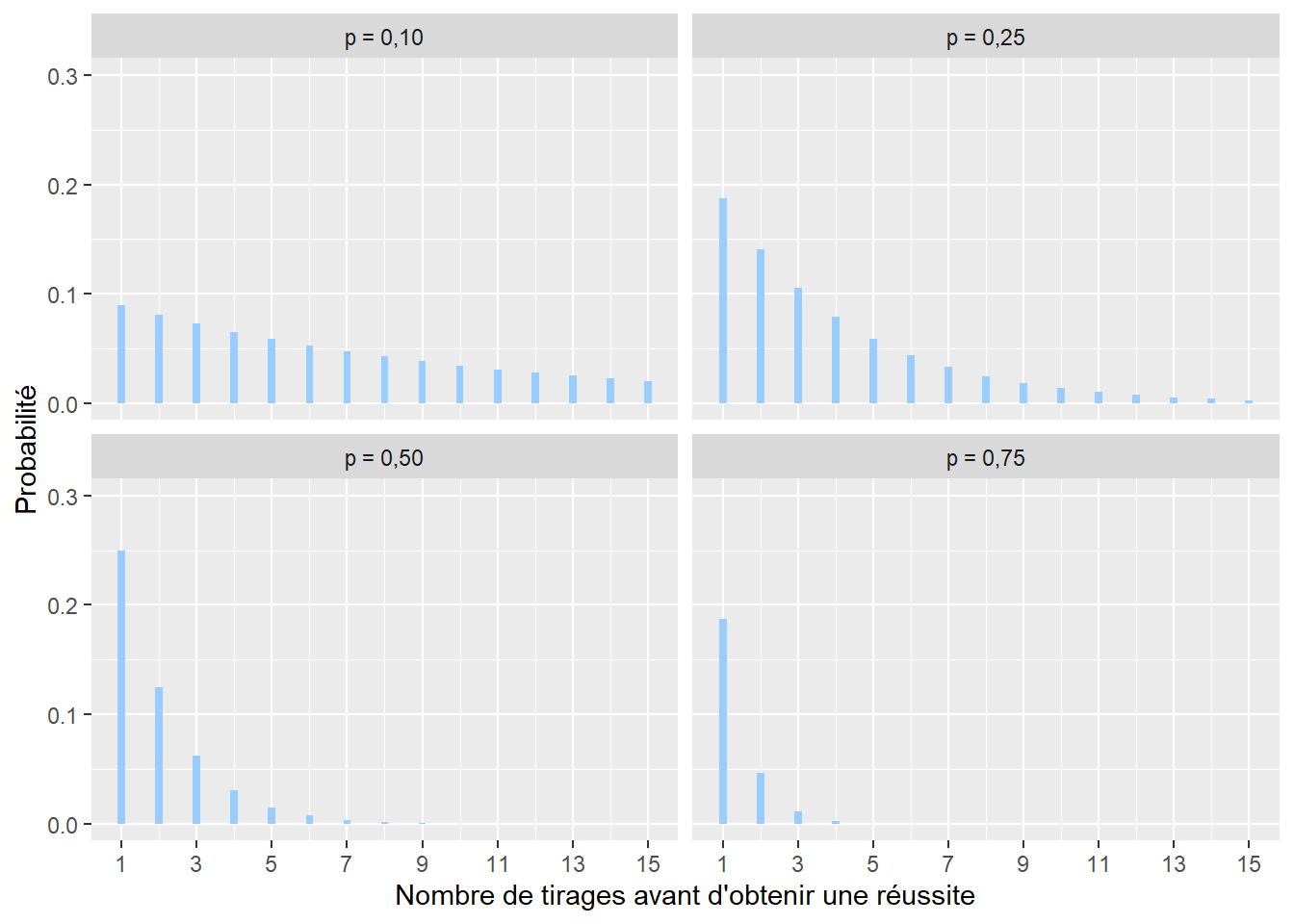
Figure 2.9: Distribution géométrique

2.4.3.5 Distribution binomiale négative

La distribution binomiale négative est proche de la distribution géométrique. Elle permet de représenter le nombre de tentatives nécessaires afin d’obtenir un nombre n de réussites $[1; +\infty[$ (limité aux nombres entiers positifs). Sa formule est la suivante :

\[\begin{equation} f(x; n; p)=\left(\begin{array}{c} x+n-1 \\ n \end{array}\right) p^{n}(1-p)^{x} \tag{2.6} \end{equation}\]

avec x le nombre de tentatives avant d’obtenir n réussites et p la probabilité d’obtenir une réussite à chaque tentative (figure 2.10). Cette distribution pourrait être utilisée pour modéliser le nombre de questionnaires x à envoyer pour une enquête pour obtenir au moins n réponses, sachant que la probabilité d’une réponse est p.

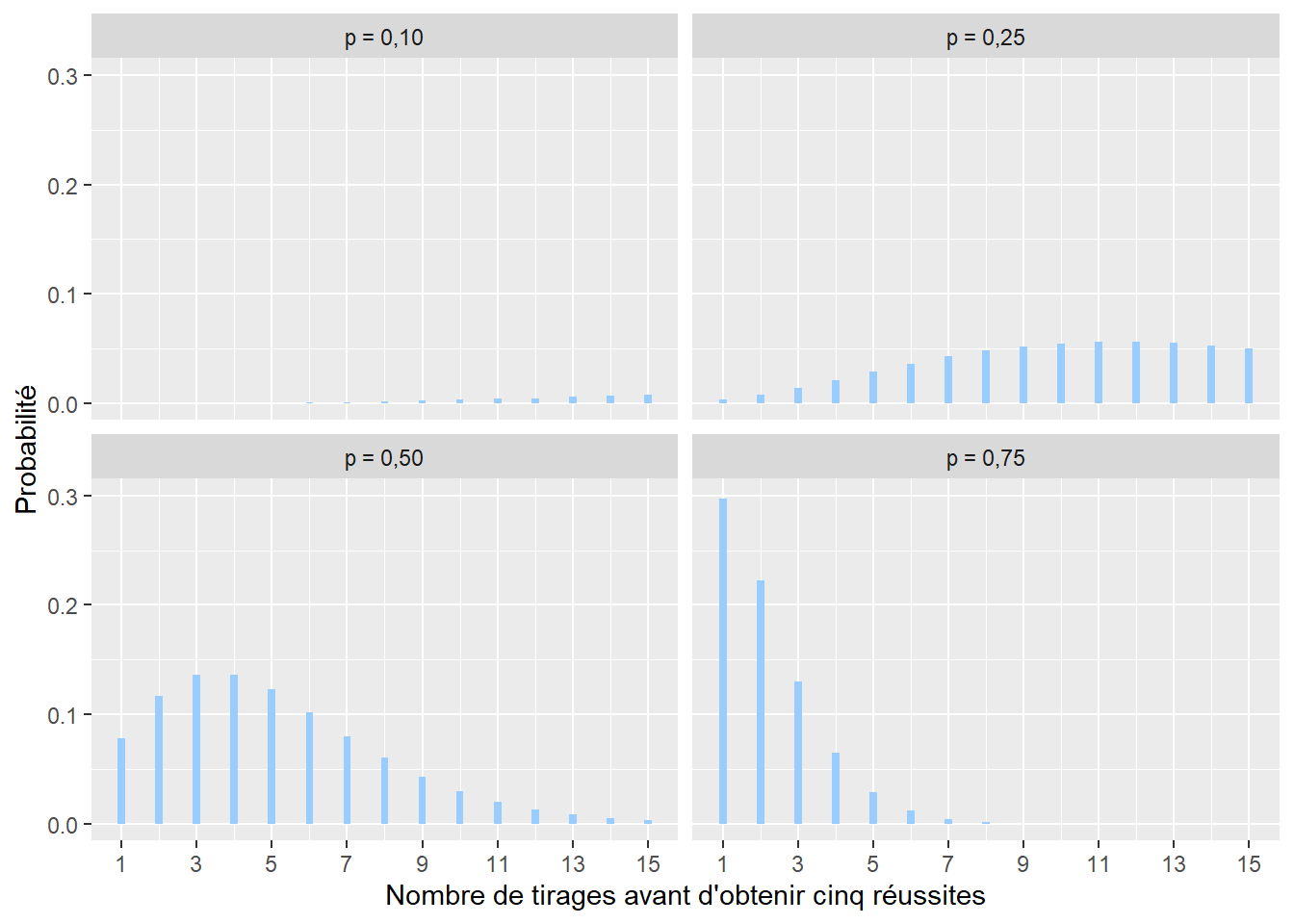
Figure 2.10: Distribution binomiale négative

2.4.3.6 Distribution de Poisson

La distribution de Poisson est utilisée pour modéliser des comptages. Son espace d’échantillonnage est donc $[0; +\infty[$ (limité aux nombres entiers positifs). Par exemple, il est possible de compter à une intersection le nombre de collisions entre des automobilistes et des cyclistes sur une période donnée. Cet exemple devrait vous faire penser à la distribution binomiale vue plus haut. En effet, il est possible de noter chaque rencontre entre une voiture et un ou une cycliste et de considérer que leur collision est une « réussite » (0 : pas d’accidents, 1 : accident). Cependant, ce type de données est fastidieux à collecter comparativement au simple comptage des accidents. La distribution de Poisson a une fonction de densité avec un seul paramètre généralement noté $\lambda$ (lambda) et est décrite par la formule suivante :

\[\begin{equation} f(x; \lambda)=\frac{\lambda^{x}}{x !} e^{-\lambda} \tag{2.7} \end{equation}\]

avec x le nombre de cas, f(x) la probabilité d’obtenir x sachant $\lambda$. $\lambda$ peut être vu comme le taux moyen d’occurrences (nombre d’évènements divisé par la durée totale de l’expérience). Il permet à la fois de caractériser le centre et la dispersion de la distribution. Notez également que plus le paramètre $\lambda$ augmente, plus la distribution de Poisson tend vers une distribution normale.

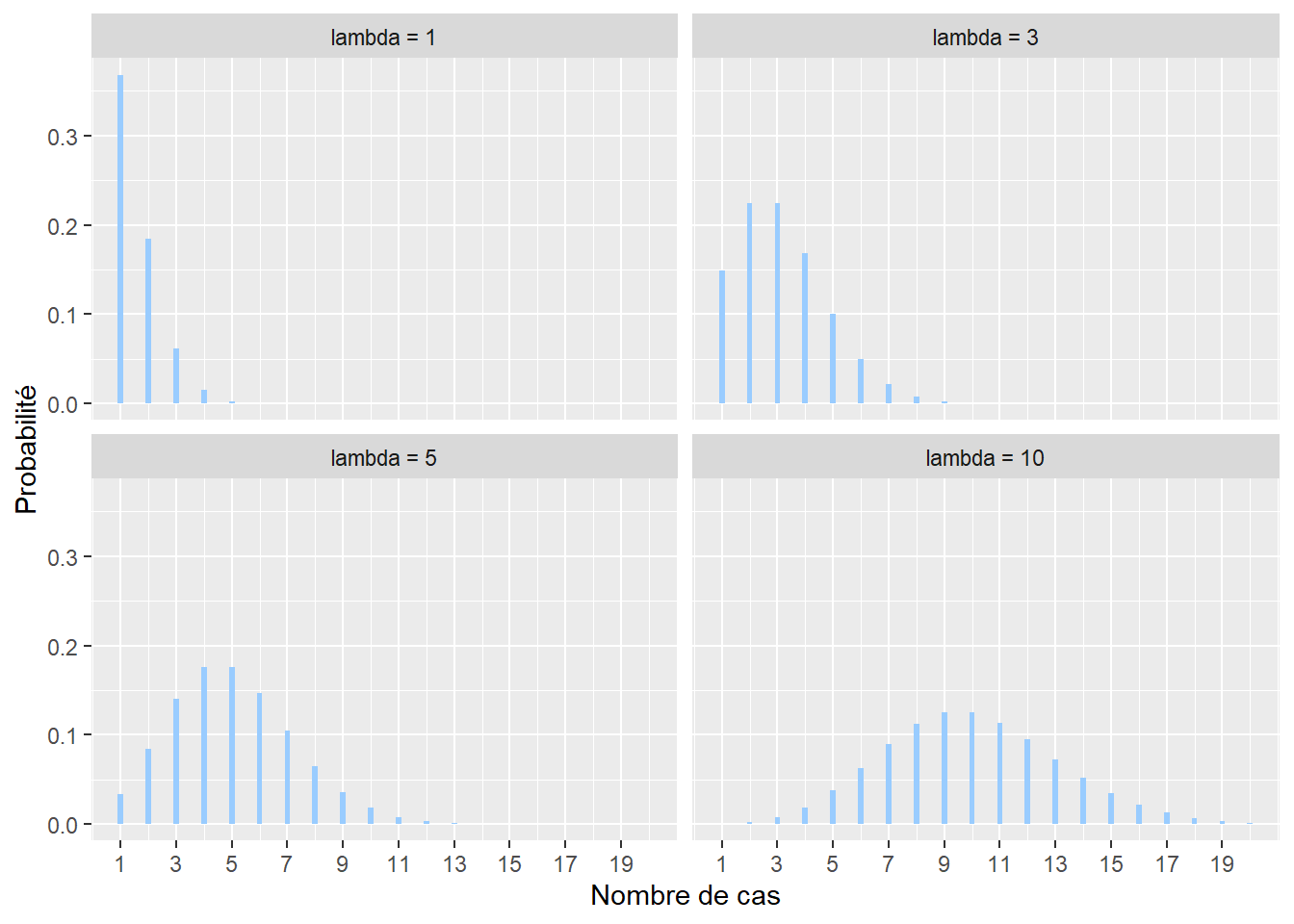
Figure 2.11: Distribution de Poisson

2.4.3.7 Distribution de Poisson avec excès de zéros

Il arrive régulièrement qu’une variable de comptage mesurée produise un très grand nombre de zéros. Prenons pour exemple le nombre de seringues de drogue injectable par tronçon de rue ramassées sur une période d’un mois. À l’échelle de toute une ville, un très grand nombre de tronçons n’auront tout simplement aucune seringue et dans ce contexte, la distribution classique de Poisson n’est pas adaptée. Nous lui préfèrons alors une autre distribution : la distribution de Poisson avec excès de zéros (ou distribution de Pólya) qui inclut un paramètre contrôlant la forte présence de zéros. Sa fonction de densité est la suivante :

\[\begin{equation} f(x; \lambda; p)=(1-p)\frac{\lambda^{x}}{x !} e^{-\lambda} \tag{2.8} \end{equation}\]

Plus exactement, la distribution de Poisson avec excès de zéro (zero-inflated en anglais) est une combinaison de deux processus générant des zéros. En effet, un zéro peut être produit par la distribution de Poisson proprement dite (aussi appelé vrai zéro) ou alors par le processus générant les zéros excédentaires dans le jeu de données, capturé par la probabilité p (faux zéro). p est donc le paramètre contrôlant la probabilité d’obtenir un zéro, indépendamment du phénomène étudié.

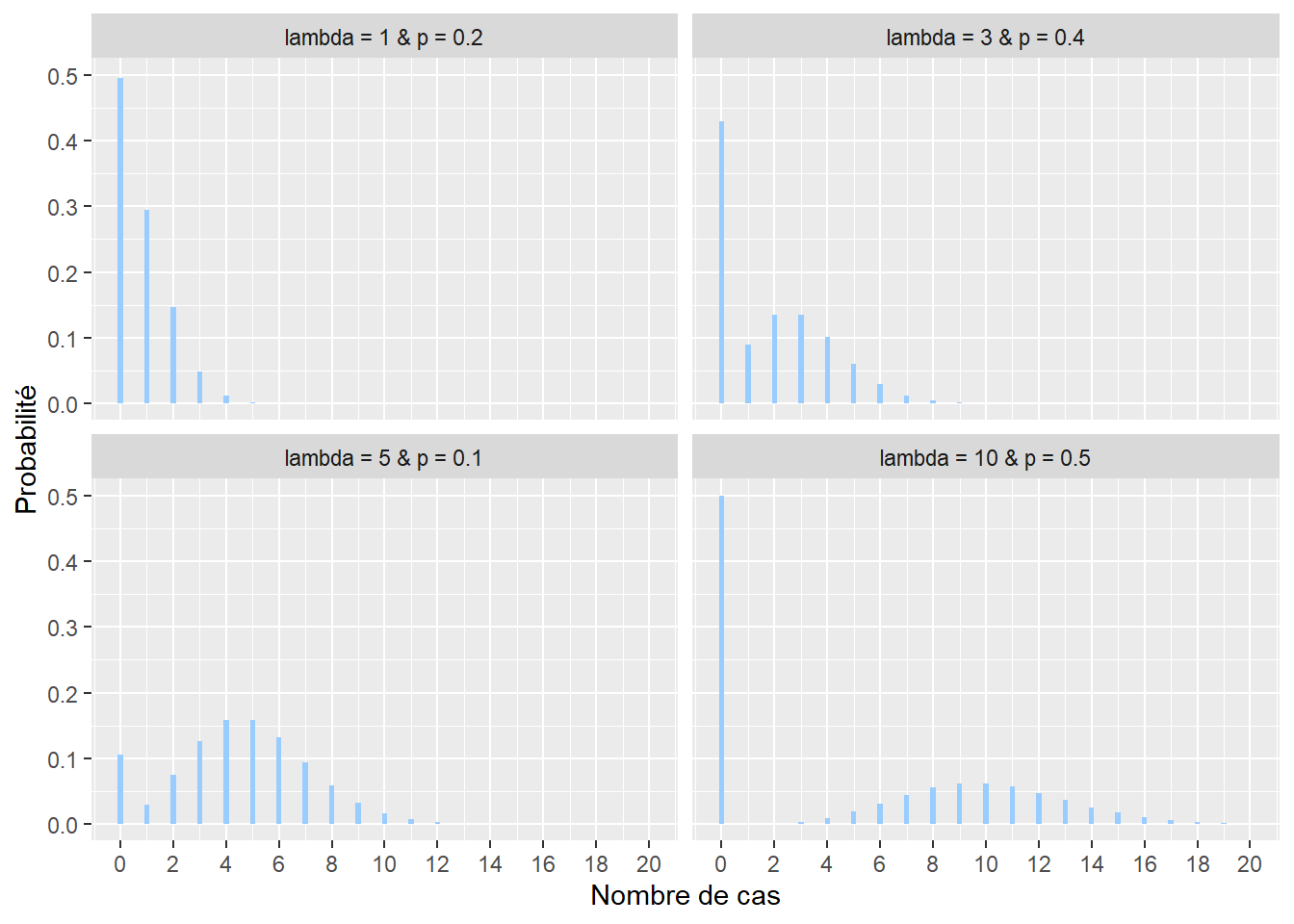
Figure 2.12: Distribution de Poisson avec excès de zéros

2.4.3.8 Distribution gaussienne

Plus communément appelée la distribution normale, la distribution gaussienne est utilisée pour représenter des variables continues centrées sur leur moyenne. Son espace d’échantillonnage est $]-\infty; +\infty[$. Cette distribution joue un rôle central en statistique. Selon la formule consacrée, cette distribution résulte de la superposition d’un très grand nombre de petits effets fortuits indépendants. C’est ce qu’exprime formellement le théorème central limite qui montre que la somme d’un grand nombre de variables aléatoires tend généralement vers une distribution normale. Autrement dit, lorsque nous répétons une même expérience et que nous conservons les résultats de ces expériences, la distribution du résultat de ces expériences tend vers la normalité. Cela s’explique par le fait qu’en moyenne, chaque répétition de l’expérience produit le même résultat, mais qu’un ensemble de petits facteurs aléatoires viennent ajouter de la variabilité dans les données collectées. Prenons un exemple concret : si nous plantons une centaine d’arbres simultanément dans un parc avec un degré d’ensoleillement identique et que nous leur apportons les mêmes soins pendant dix ans, la distribution de leurs tailles suivra une distribution normale. Un ensemble de facteurs aléatoires (composition du sol, exposition au vent, aléas génétiques, passage de nuages, etc.) auront affecté différemment chaque arbre, ajoutant ainsi un peu de hasard dans leur taille finale. Cette dernière est cependant davantage affectée par des paramètres majeurs (comme l’espèce, l’ensoleillement, l’arrosage, etc.), et est donc centrée autour d’une moyenne. La fonction de densité de la distribution normale est la suivante :

\[\begin{equation} f(x ; \mu ; \sigma)=\frac{1}{\sigma \sqrt{2 \pi}} e^{-\frac{1}{2}\left(\frac{x-\mu}{\sigma}\right)^{2}} \tag{2.9} \end{equation}\]

avec x une valeur dont nous souhaitons connaître la probabilité, f(x) sa probabilité, $\mu$ (mu) la moyenne de la distribution normale (paramètre de localisation) et $\sigma$ (sigma) son écart-type (paramètre de dispersion). Cette fonction suit une courbe normale ayant une forme de cloche. Notez que :

68,2 % de la masse de la distribution normale est comprise dans l’intervalle $[\mu- \sigma≤x≤ \mu+ \sigma]$
95,4 % dans l’intervalle $[\mu- 2\sigma≤x≤ \mu+ 2\sigma]$
99,7 % dans l’intervalle $[\mu- 3\sigma≤x≤ \mu+ 3\sigma]$

Autrement dit, dans le cas d’une distribution normale, il est très invraisemblable d’observer des données situées à plus de trois écarts types de la moyenne. Ces différentes égalités sont vraies quelles ques soient les valeurs de la moyenne et de l’écart-type. Notez ici que lorsque $\mu = 0$ et $\sigma = 1$, nous obtenons la loi normale générale (ou centrée réduite) (section 2.5.5.2).

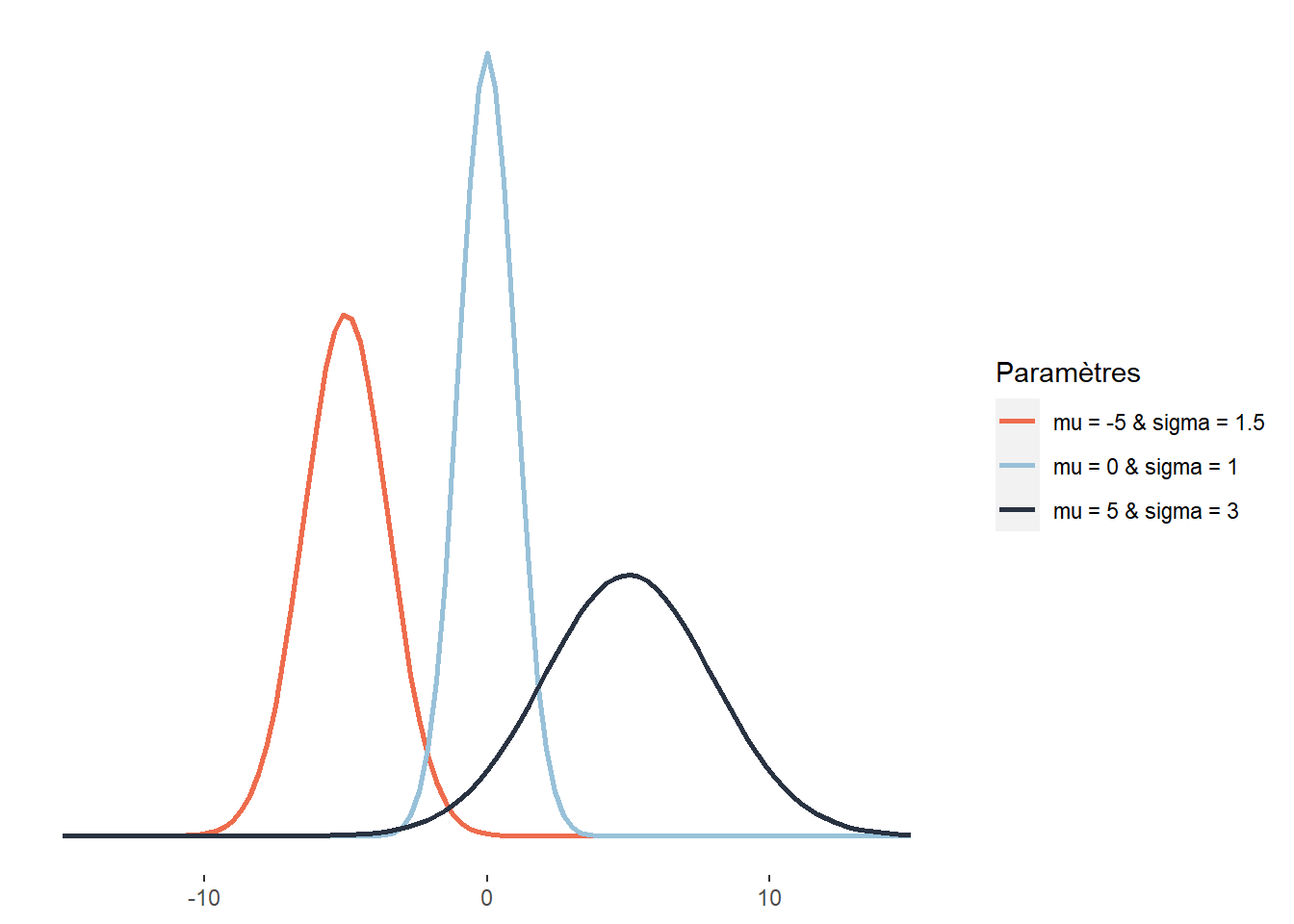
Figure 2.13: Distribution gaussienne

2.4.3.9 Distribution gaussienne asymétrique

La distribution normale asymétrique (skew-normal) est une extension de la distribution gaussienne permettant de lever la contrainte de symétrie de la simple distribution gaussienne. Son espace d’échantillonnage est donc $]-\infty; +\infty[$. Sa fonction de densité est la suivante :

\[\begin{equation} f(x;\xi;\omega;\alpha) = \frac{2}{\omega \sqrt{2 \pi}} e^{-\frac{(x-\xi)^{2}}{2 \omega^{2}}} \int_{-\infty}^{\alpha\left(\frac{x-\xi}{\omega}\right)} \frac{1}{\sqrt{2 \pi}} e^{-\frac{t^{2}}{2}} d t \tag{2.10} \end{equation}\]

avec $\xi$ (xi) le paramètre de localisation, $\omega$ (omega) le paramètre de dispersion (ou d’échelle) et $\alpha$ (alpha) le paramètre de forme (contrôlant le degré de symétrie). Si $\alpha = 0$, alors la distribution normale asymétrique est une distribution normale ordinaire. Ce type de distribution est très utile lorsque nous souhaitons modéliser une variable pour laquelle nous savons que des valeurs plus extrêmes s’observeront d’un côté ou de l’autre de la distribution. Les revenus totaux annuels des personnes ou des ménages sont de très bons exemples puisqu’ils sont distribués généralement avec une asymétrie positive : bien qu’une moyenne existe, il y a généralement plus de personnes ou de ménages avec des revenus très faibles que de personnes ou de ménages avec des revenus très élevés.

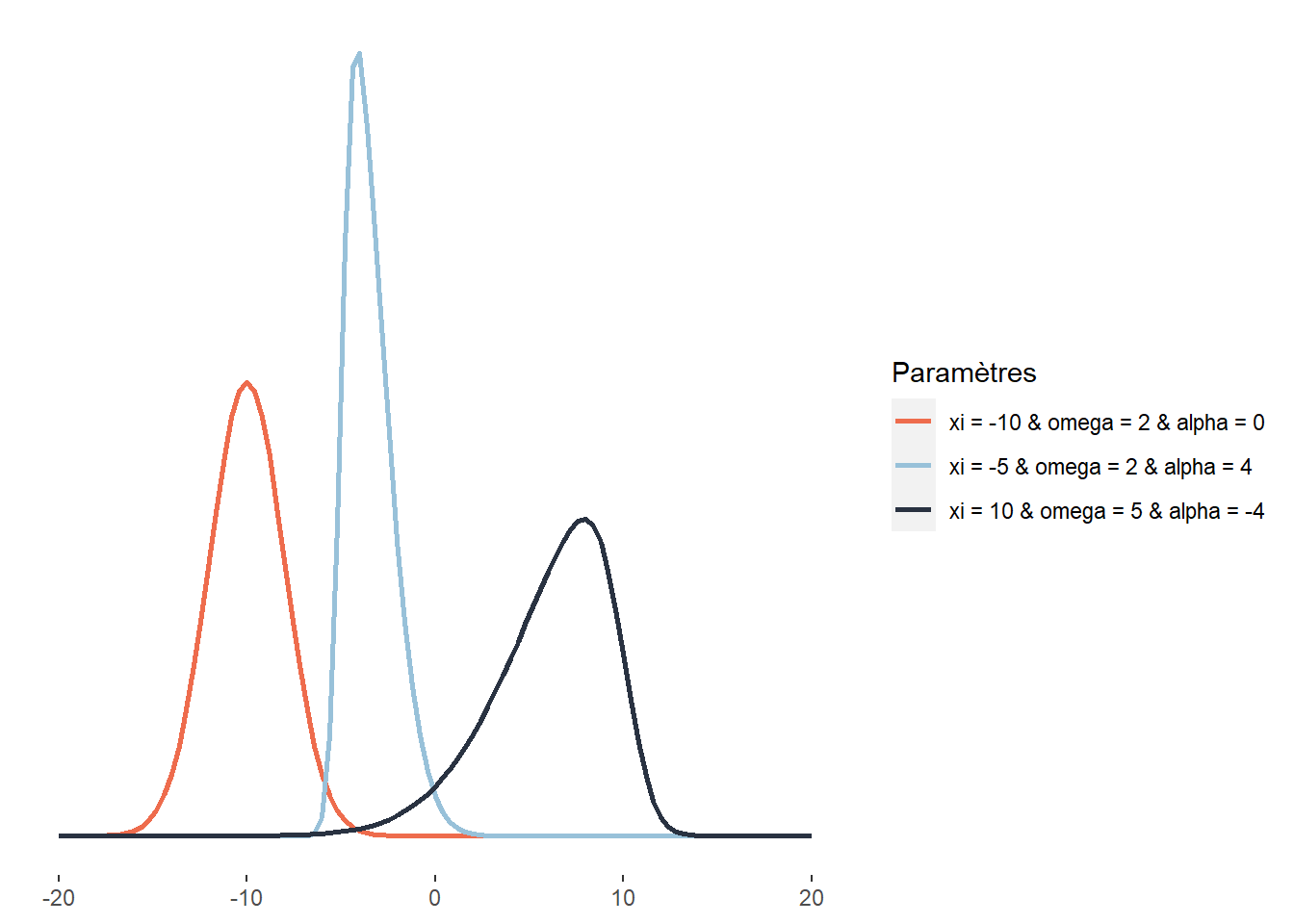
Figure 2.14: Distribution gaussienne asymétrique

2.4.3.10 Distribution log-normale

Au même titre que la distribution normale asymétrique, la distribution log-normale est une version asymétrique de la distribution normale. Son espace d’échantillonnage est $]0; +\infty[$. Cela signifie que cette distribution ne peut décrire que des données continues et positives. Sa fonction de densité est la suivante : \[\begin{equation} f(x ; \mu ; \sigma)=\frac{1}{x \sigma \sqrt{2 \pi}} e^{-\left(\frac{(\ln x-\mu)^{2}}{2 \sigma^{2}}\right)} \tag{2.11} \end{equation}\]

À la différence la distribution skew-normal, la distribution log-normale ne peut avoir qu’une asymétrie positive (étirée vers la droite). Elle est cependant intéressante puisqu’elle ne compte que deux paramètres ($\mu$ et $\sigma$), ce qui la rend plus facile à ajuster. À nouveau, une distribution log-normale peut être utilisée pour décrire les revenus totaux annuels des individus ou des ménages ou les revenus d’emploi. Elle est aussi utilisée en économie sur les marchés financiers pour représenter les cours des actions et des biens (ces derniers ne pouvant pas être inférieurs à 0).

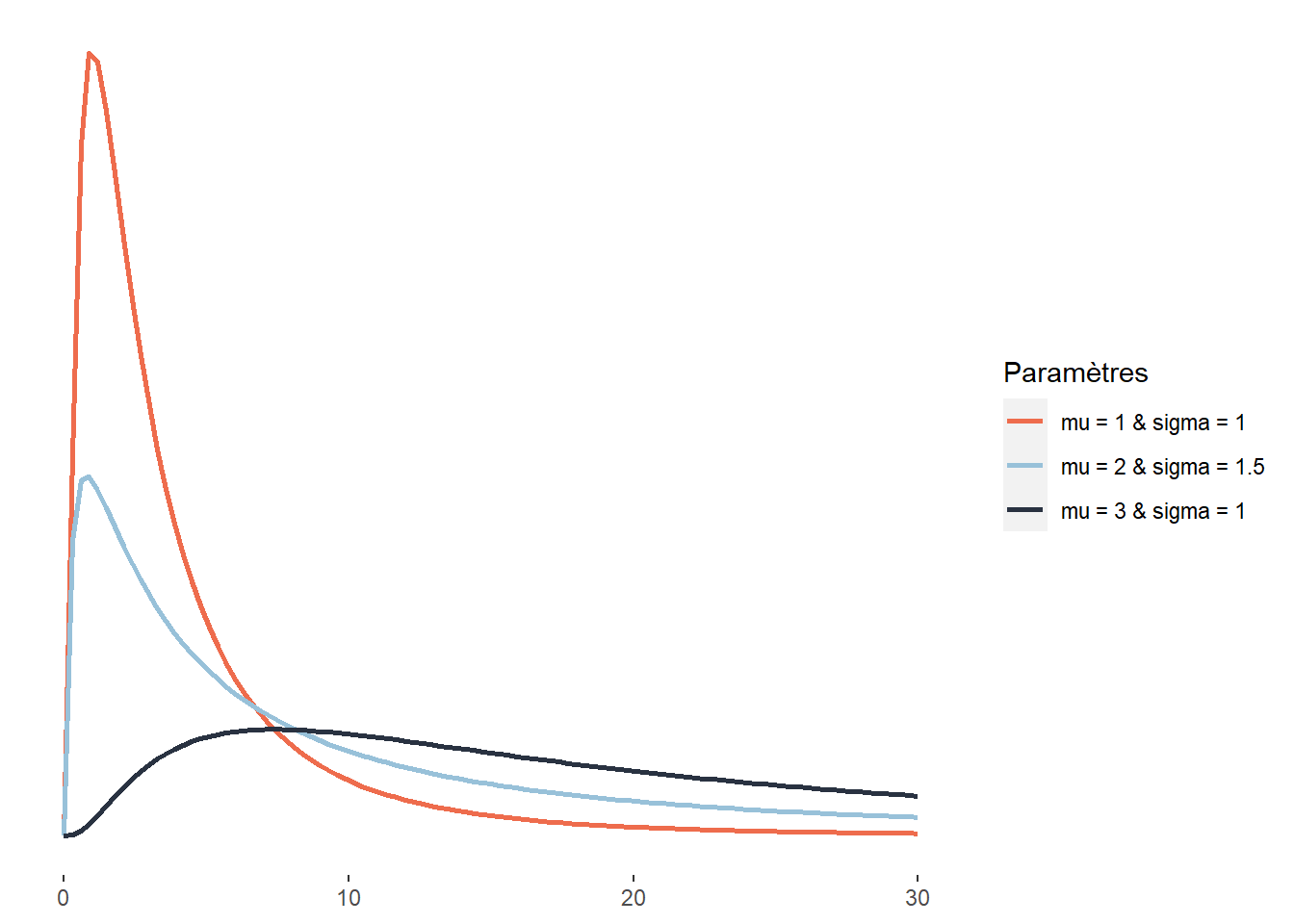
Figure 2.15: Distribution log-gaussienne

Plus spécifiquement, la distribution log-normale est une transformation de la distribution normale. Comme son nom l’indique, elle permet de décrire le logarithme d’une variable aléatoire suivant une distribution normale.

2.4.3.11 Distribution de Student

La distribution de Student joue un rôle important en statistique. Elle est par exemple utilisée lors du test t pour calculer le degré de significativité du test. Comme la distribution gaussienne, la distribution de Student a une forme de cloche, est centrée sur sa moyenne et définie sur $]-\infty; +\infty[$. Elle se distingue de la distribution normale principalement par le rôle que joue son troisième paramètre, $\nu$ : le nombre de degrés de liberté, contrôlant le poids des queues de la distribution. Une petite valeur de $\nu$ signifie que la distribution a des « queues plus lourdes » (heavy tails en anglais). Entendez par-là que les valeurs extrêmes ont une plus grande probabilité d’occurrence :

\[\begin{equation} p(x ; \nu ; \hat{\mu} ; \hat{\sigma})=\frac{\Gamma\left(\frac{\nu+1}{2}\right)}{\Gamma\left(\frac{\nu}{2}\right) \sqrt{\pi \nu} \hat{\sigma}}\left(1+\frac{1}{\nu}\left(\frac{x-\hat{\mu}}{\hat{\sigma}}\right)^{2}\right)^{-\frac{\nu+1}{2}} \tag{2.12} \end{equation}\]

avec $\mu$ le paramètre de localisation, $\sigma$ le paramètre de dispersion (qui n’est cependant pas un écart-type comme pour la distribution normale) et $\nu$ le nombre de degrés de liberté. Plus $\nu$ est grand, plus la distribution de Student tend vers une distribution normale. Ici, la lettre grecque $\Gamma$ représente la fonction mathématique gamma (à ne pas confondre avec la distribution Gamma). Un exemple d’application en études urbaines est l’exposition au bruit environnemental de cyclistes. Cette distribution s’approcherait certainement d’une distribution normale, mais les cyclistes croisent régulièrement des secteurs peu bruyants (parcs, rues résidentielles, etc.) et des secteurs très bruyants (artères majeures, zones industrielles, etc.), plus souvent que ce que prévoit une distribution normale, justifiant le choix d’une distribution de Student.

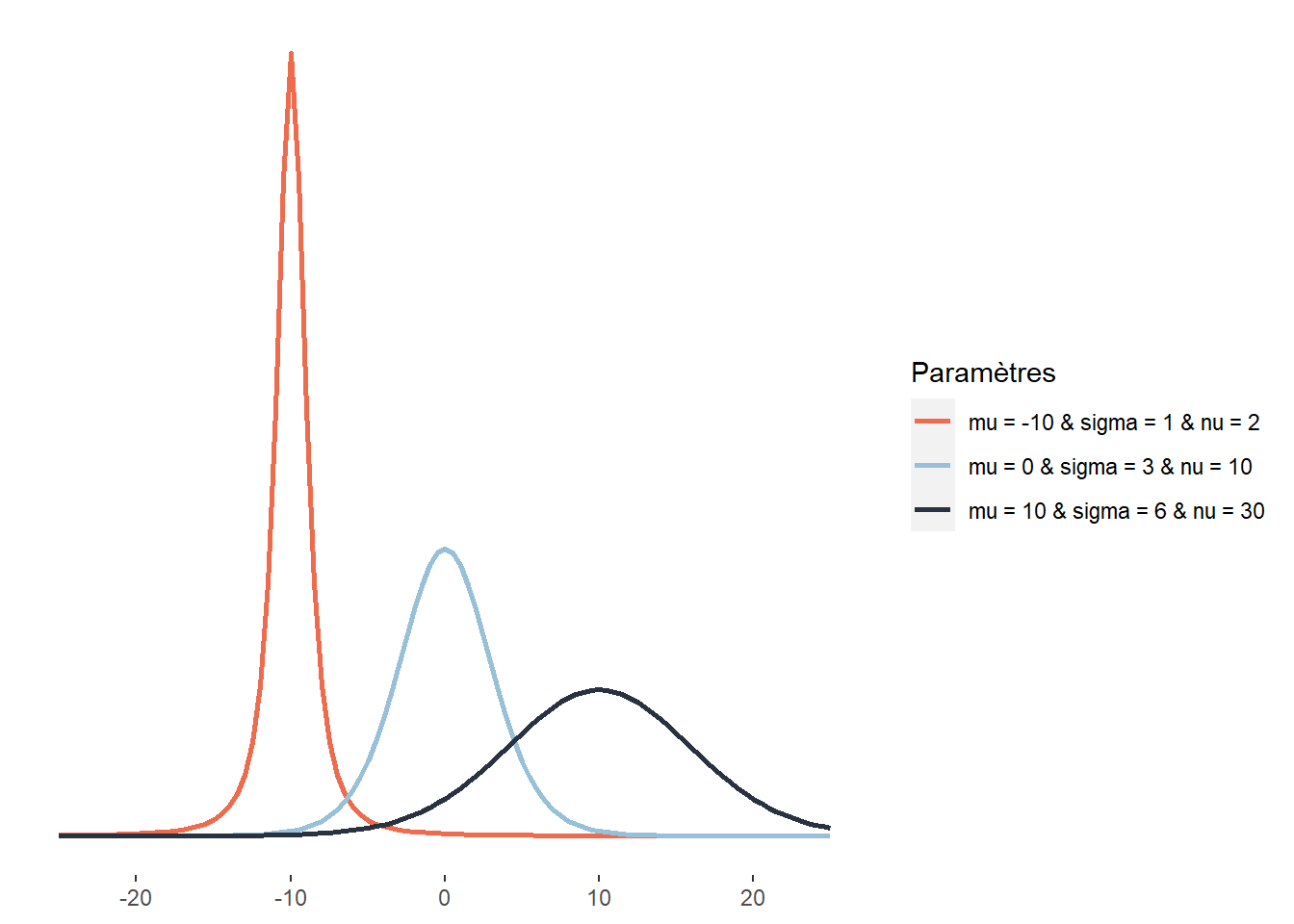
Figure 2.16: Distribution de Student

2.4.3.12 Distribution de Cauchy

La distribution de Cauchy est également une distribution symétrique définie sur l’intervalle $]-\infty; +\infty[$. Elle a comme particularité d’être plus aplatie que la distribution de Student (d’avoir des queues potentiellement plus lourdes). Elle est notamment utilisée pour modéliser des phénomènes extrêmes comme les précipitations maximales annuelles, les niveaux d’inondations maximaux annuels ou les seuils critiques de perte pour les portefeuilles financiers. Il est également intéressant de noter que le quotient de deux variables indépendantes normalement distribuées suit une distribution de Cauchy. Sa fonction de densité est la suivante :

\[\begin{equation} \frac{1}{\pi \gamma}\left[\frac{\gamma^{2}}{\left(x-x_{0}\right)^{2}+\gamma^{2}}\right] \tag{2.13} \end{equation}\]

Elle dépend donc de deux paramètres : $x_0$, le paramètre de localisation indiquant le pic de la distribution et $\gamma$, un paramètre de dispersion.

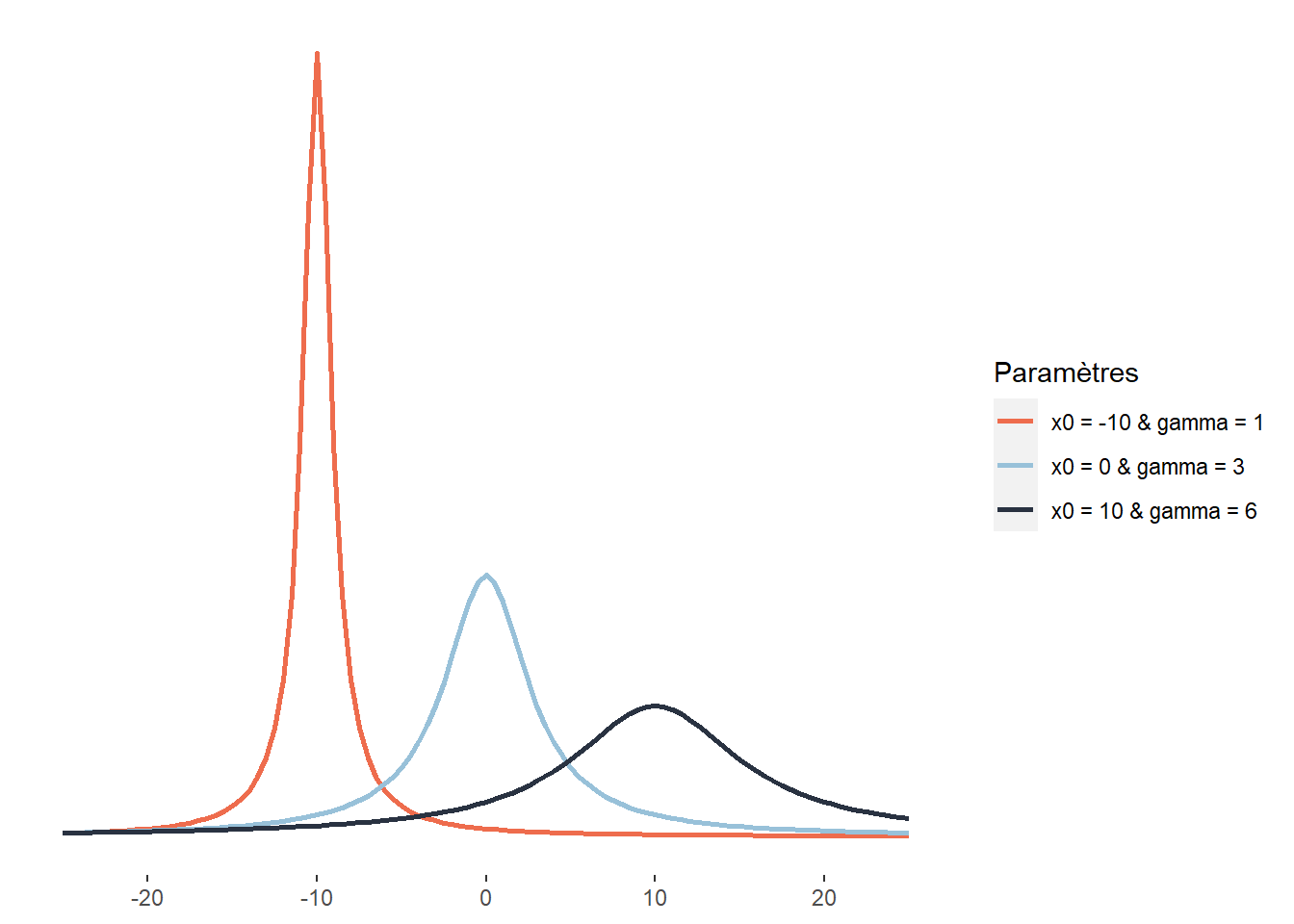
Figure 2.17: Distribution de Cauchy

2.4.3.13 Distribution du khi-deux

La distribution du khi-deux est utilisée dans de nombreux tests statistiques. Par exemple, le test du khi-deux de Pearson est utilisé pour comparer les écarts au carré entre des fréquences attendues et observées de deux variables qualitatives. La distribution du khi-deux décrit plus généralement la somme des carrés d’un nombre k de variables indépendantes normalement distribuées. Il est assez rare de modéliser un phénomène à l’aide d’une distribution du khi-deux, mais son omniprésence dans les tests statistiques justifie qu’elle soit mentionnée ici. Cette distribution est définie sur l’intervalle $[0; +\infty[$ et a pour fonction de densité :

\[\begin{equation} f(x;k) = \frac{1}{2^{k / 2} \Gamma(k / 2)} x^{k / 2-1} e^{-x / 2} \tag{2.14} \end{equation}\]

La distribution du khi-deux n’a qu’un paramètre k, représentant donc le nombre de variables mises au carré et dont nous faisons la somme pour obtenir la distribution du khi-deux.

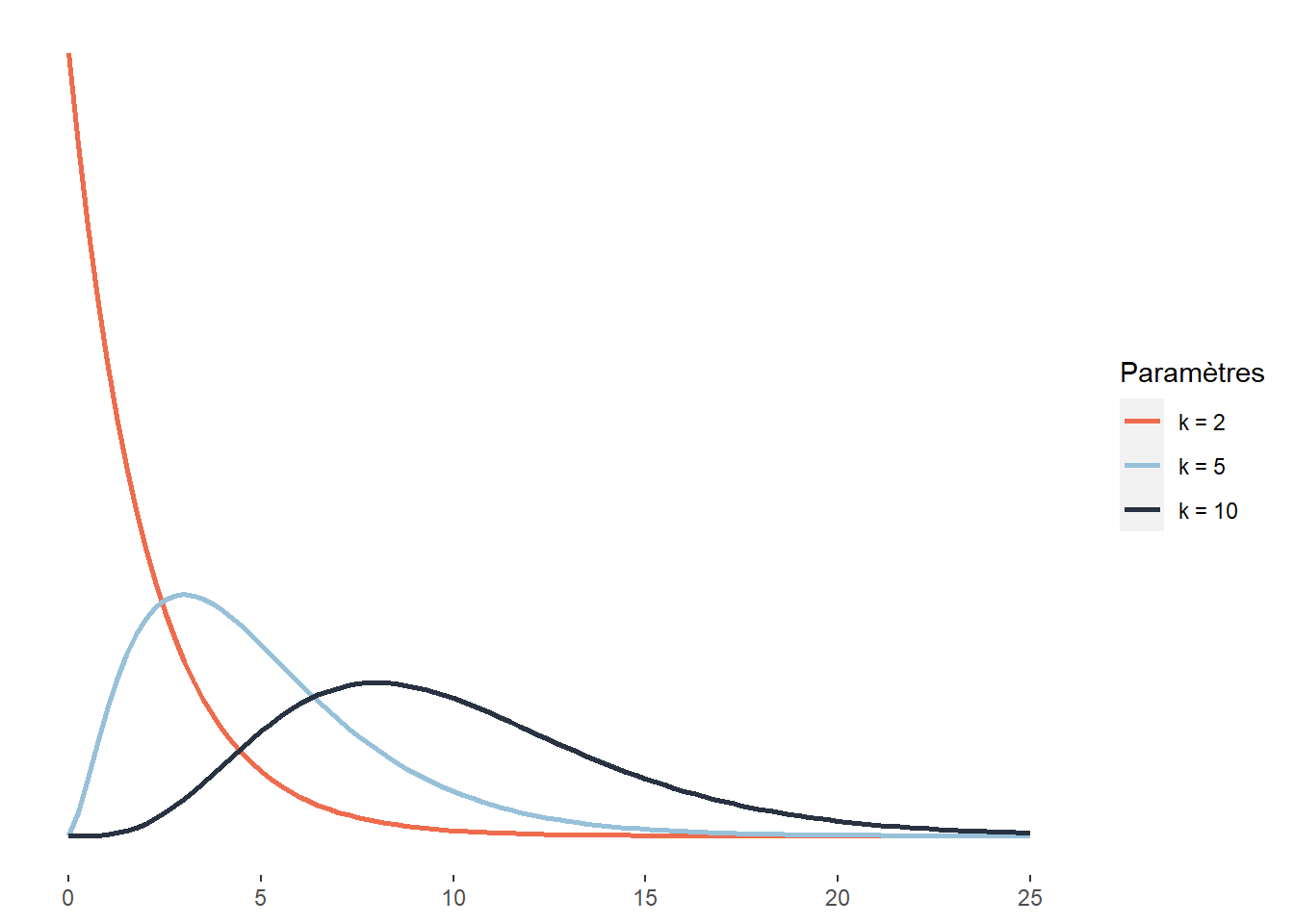
Figure 2.18: Distribution du khi-deux

2.4.3.14 Distribution exponentielle

La distribution exponentielle est une version continue de la distribution géométrique. Pour cette dernière, nous nous intéressons au nombre de tentatives nécessaires pour obtenir un résultat positif, soit une dimension discrète. Pour la distribution exponentielle, cette dimension discrète est remplacée par une dimension continue. L’exemple le plus intuitif est sûrement le cas du temps. Dans ce cas, la distribution exponentielle sert à modéliser le temps d’attente nécessaire pour qu’un évènement se produise. Il peut aussi s’agir d’une force que nous appliquons jusqu’à ce qu’un matériau cède. Cette distribution est donc définie sur l’intervalle [0; +$\infty$[ et a pour fonction de densité :

\[\begin{equation} f(x;\lambda) = \lambda e^{-\lambda x} \tag{2.15} \end{equation}\]

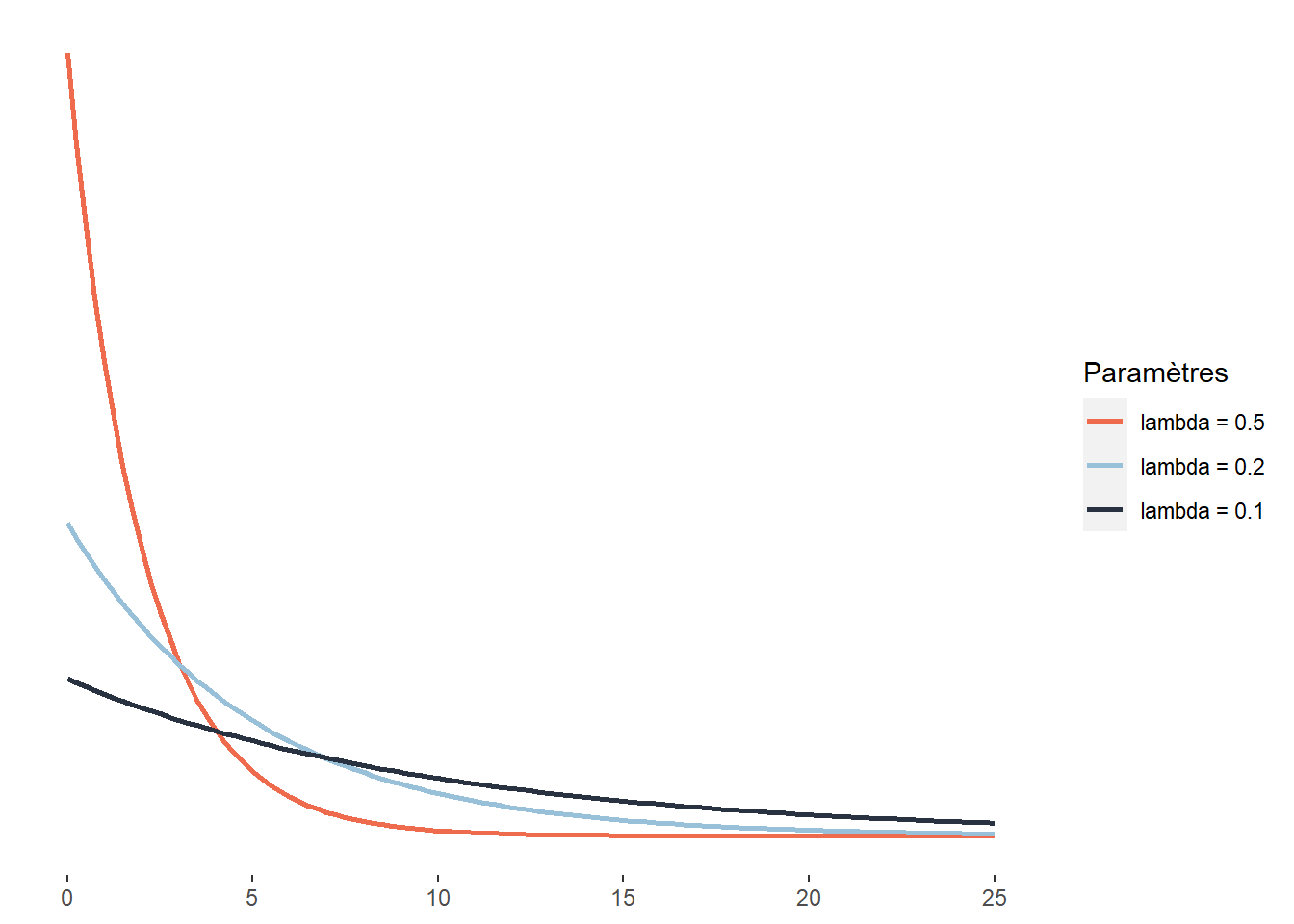
Figure 2.19: Distribution exponentielle

La distribution exponentielle est conceptuellement proche de la distribution de Poisson. La distribution de Poisson régit le nombre des événements qui surviennent au cours d’un laps de temps donné. La distribution exponentielle peur servir à modéliser le temps qui s’écoule entre deux événements.

2.4.3.15 Distribution Gamma

La distribution Gamma peut être vue comme la généralisation d’un grand nombre de distributions. Ainsi, la distribution exponentielle et du khi-deux peuvent être vues comme des cas particuliers de la distribution Gamma. Cette distribution est définie sur l’intervalle ]0; +$\infty$[ (notez que le 0 est exclu) et sa fonction de densité est la suivante :

\[\begin{equation} f(x ; \alpha; \beta)=\frac{\beta^{\alpha} x^{\alpha-1} e^{-\beta x}}{\Gamma(\alpha)} \tag{2.16} \end{equation}\]

Elle comprend donc deux paramètres : $\alpha$ et $\beta$. Le premier est le paramètre de forme et le second un paramètre d’échelle (à l’inverse d’un paramètre de dispersion, plus sa valeur est petite, plus la distribution est dispersée). Notez que cette distribution ne dispose pas d’un paramètre de localisation. Du fait de sa flexibilité, cette distribution est largement utilisée, que ce soit dans la modélisation des temps d’attente avant un évènement, de la taille des réclamations d’assurance, des quantités de précipitations, etc.

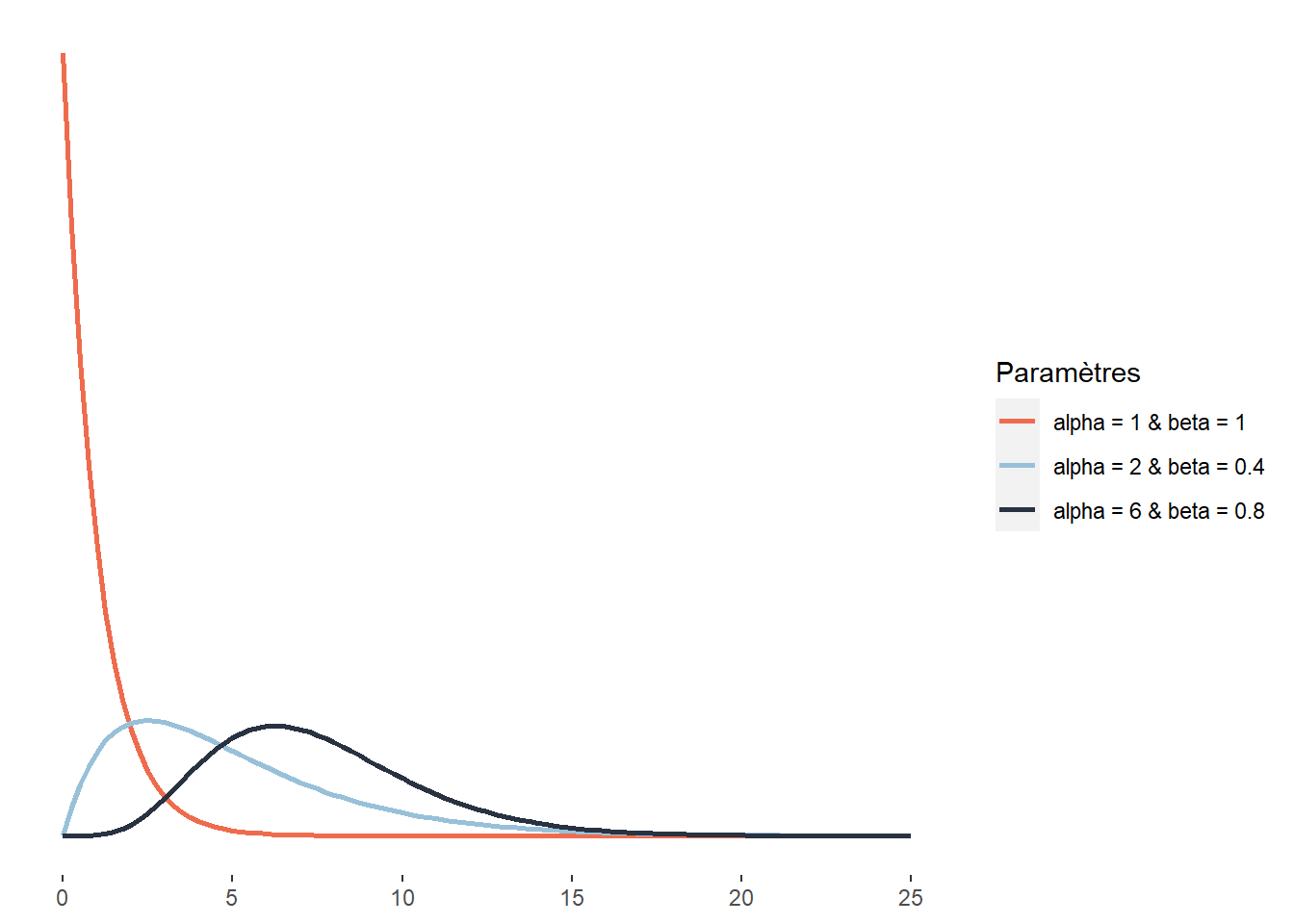
Figure 2.20: Distribution Gamma

2.4.3.16 Distribution bêta

La distribution bêta est définie sur l’intervalle [0; 1], elle est donc énormément utilisée pour modéliser des variables étant des proportions ou des probabilités.

La distribution bêta a été élaborée pour modéliser la superposition d’un très grand nombre de petits effets fortuits qui ne sont pas indépendants et notamment pour étudier l’effet de la réalisation d’un événement aléatoire sur la probabilité des tirages subséquents. Elle a aussi une utilité pratique en statistique, car elle peut être combinée avec d’autres distributions (distribution bêta-binomiale, bêta-negative-binomiale, etc.). Un autre usage plus rare mais intéressant est la modélisation de la fraction du temps représentée par une tâche dans le temps nécessaire à la réalisation de deux tâches de façon séquentielle. Cela est dû au fait que la distribution d’une distribution Gamma g1 divisée par la somme de g1 et d’une autre distribution Gamma g2 suit une distribution bêta. Un exemple concret est, par exemple, la fraction du temps effectué à pied dans un déplacement multimodal. La distribution de bêta a la fonction de densité suivante :

\[\begin{equation} f(x;\alpha;\beta) = \frac{1}{\mathrm{B}(\alpha, \beta)} x^{\alpha-1}(1-x)^{\beta-1} \tag{2.17} \end{equation}\]

Elle a donc deux paramètres $\alpha$ et $\beta$ contrôlant tous les deux la forme de la distribution. Cette caractéristique lui permet d’avoir une très grande flexibilité et même d’adopter des formes bimodales. $B$ correspond à la fonction mathématique Beta : ne pas la confondre avec la distribution Beta et le paramètre Beta ($\beta$) de cette même distribution.

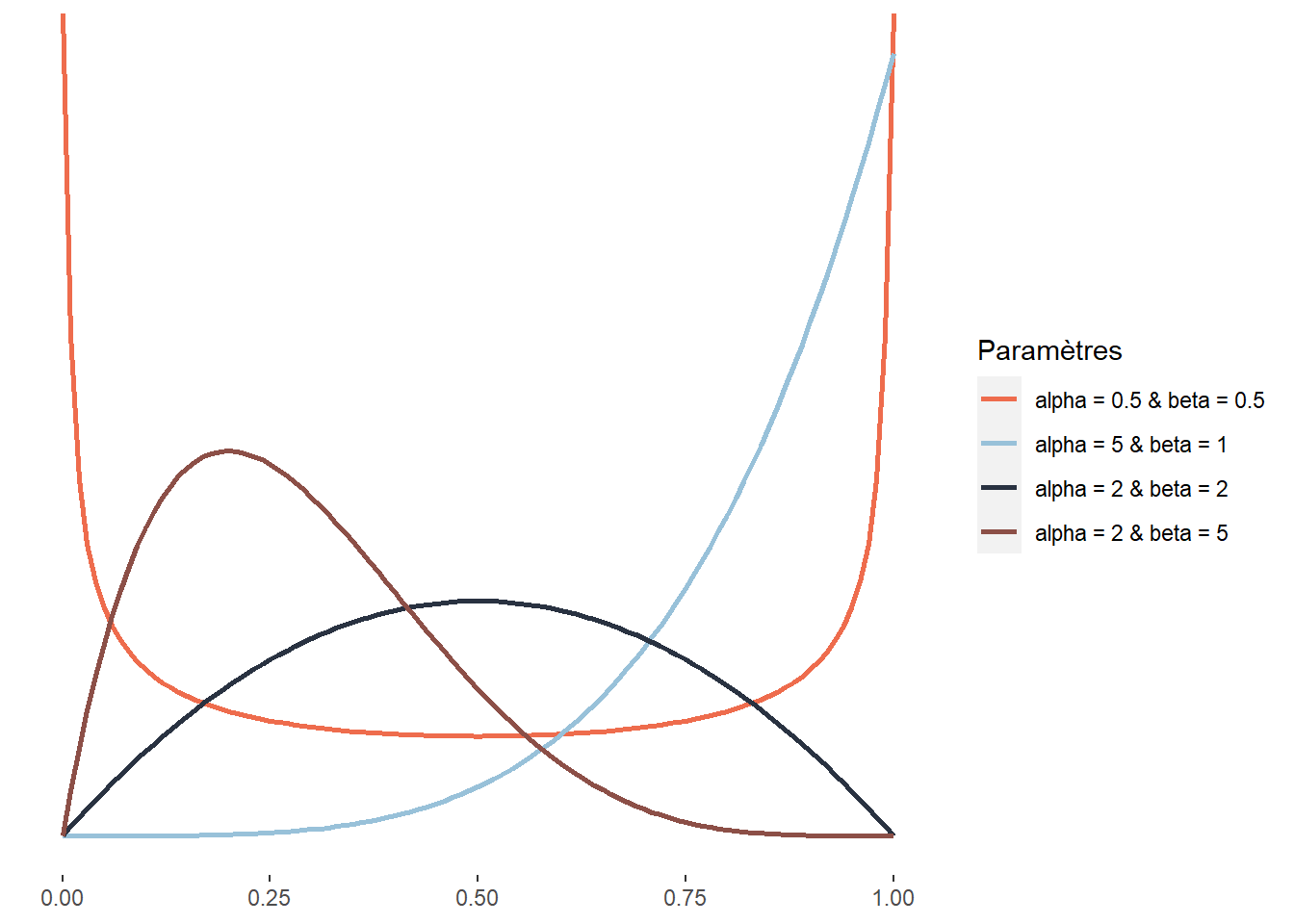
Figure 2.21: Distribution bêta

2.4.3.17 Distribution de Weibull

La distribution de Weibull est directement liée à la distribution exponentielle, cette dernière étant en fait un cas particulier de distribution Weibull. Elle sert donc souvent à modéliser une quantité x (souvent le temps) à accumuler pour qu’un évènement se produise. La distribution de Weibull est définie sur l’intervalle [0; +$\infty$[ et a la fonction de densité suivante :

\[\begin{equation} f(x;\lambda) = \frac{k}{\lambda} (\frac{x}{\lambda})^{k-1} e^{-(\frac{x}{\lambda})^k} \tag{2.18} \end{equation}\]

$\lambda$ est le paramètre de dispersion (analogue à celui d’une distribution exponentielle classique) et k le paramètre de forme. Pour bien comprendre le rôle de k, prenons un exemple : la propagation d’un champignon d’un arbre à son voisin. Si $k<1$, le risque instantané que l’évènement modélisé se produise diminue avec le temps (en d’autres termes, plus le temps passe, plus petite devient la probabilité d’être contaminé). Si $k=1$, alors le risque instantané que l’évènement se produise reste identique dans le temps (la loi de Weibull se résume alors à une loi exponentielle). Si $k > 1$, alors le risque instantané que l’évènement se produise augmente avec le temps (la probabilité pour un arbre d’être contaminé s’il ne l’a pas déjà été — pas seulement le risque cumulé — augmente en fonction du temps). La distribution de Weibull est très utilisée en analyse de survie, en météorologie, en ingénierie des matériaux et dans la théorie des valeurs extrêmes.

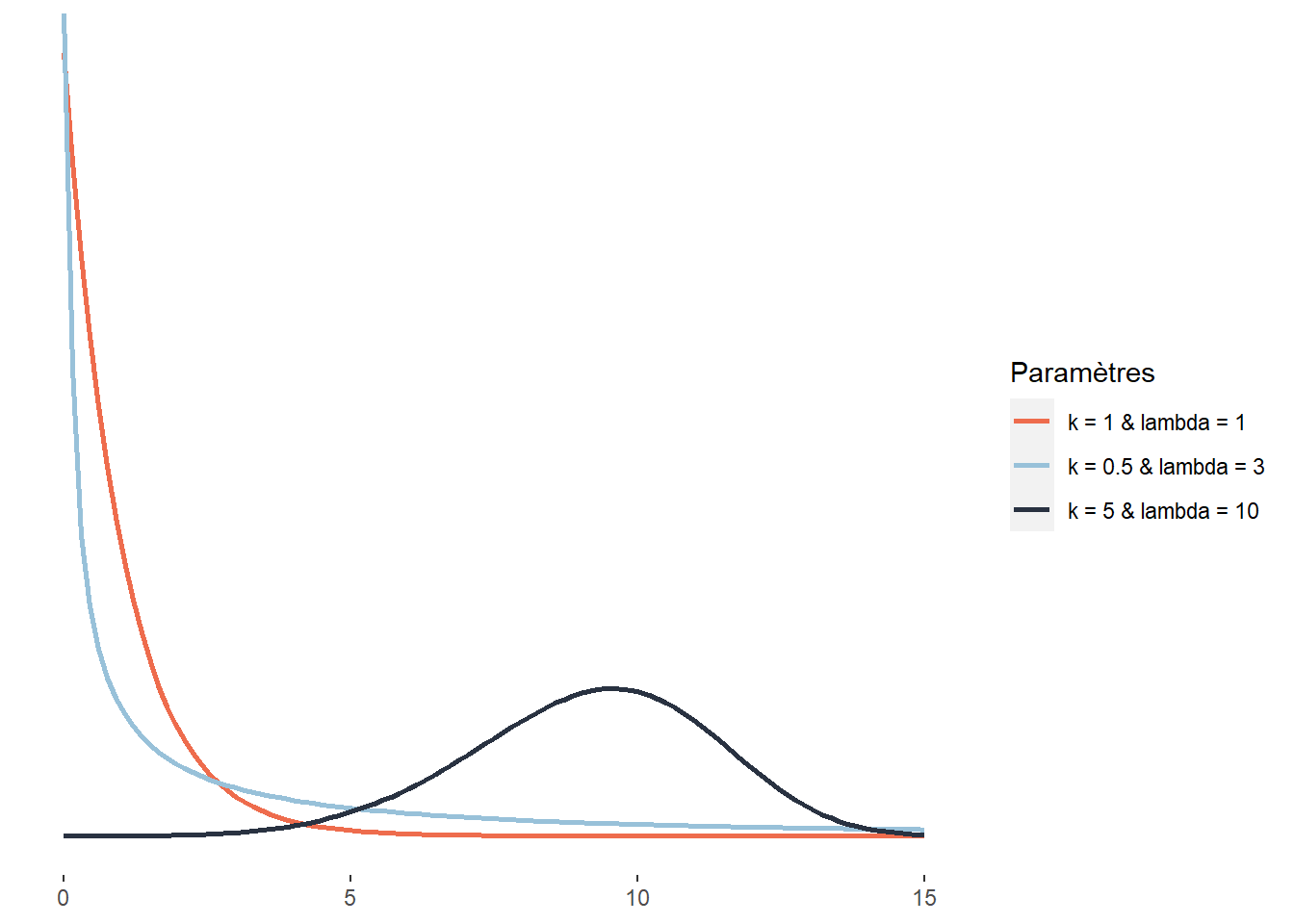
Figure 2.22: Distribution de Weibull

2.4.3.18 Distribution Pareto

Cette distribution a été élaborée par Vilfredo Pareto pour donner une forme mathématique à ce qui porte aujourd’hui le nom de principe de Pareto et que nous exprimons souvent de manière imagée — dans une société donnée, 20 % des individus possèdent 80 % de la richesse —, mais qui est plus justement exprimée en écrivant que, de manière générale, dans toute société, la plus grande partie du capital est détenue par une petite fraction de la population. Elle est définie sur l’intervalle $[x_m; +\infty[$ avec la fonction de densité suivante :

\[\begin{equation} f(x;x_m;k) = (\frac{x_m}{x})^k \tag{2.19} \end{equation}\]

Elle comprend donc deux paramètres, $x_m$ étant un paramètre de localisation (décalant la distribution vers la droite ou vers la gauche) et $k$ un paramètre de forme. Plus $k$ augmente, plus la probabilité prédite par la distribution décroît rapidement.

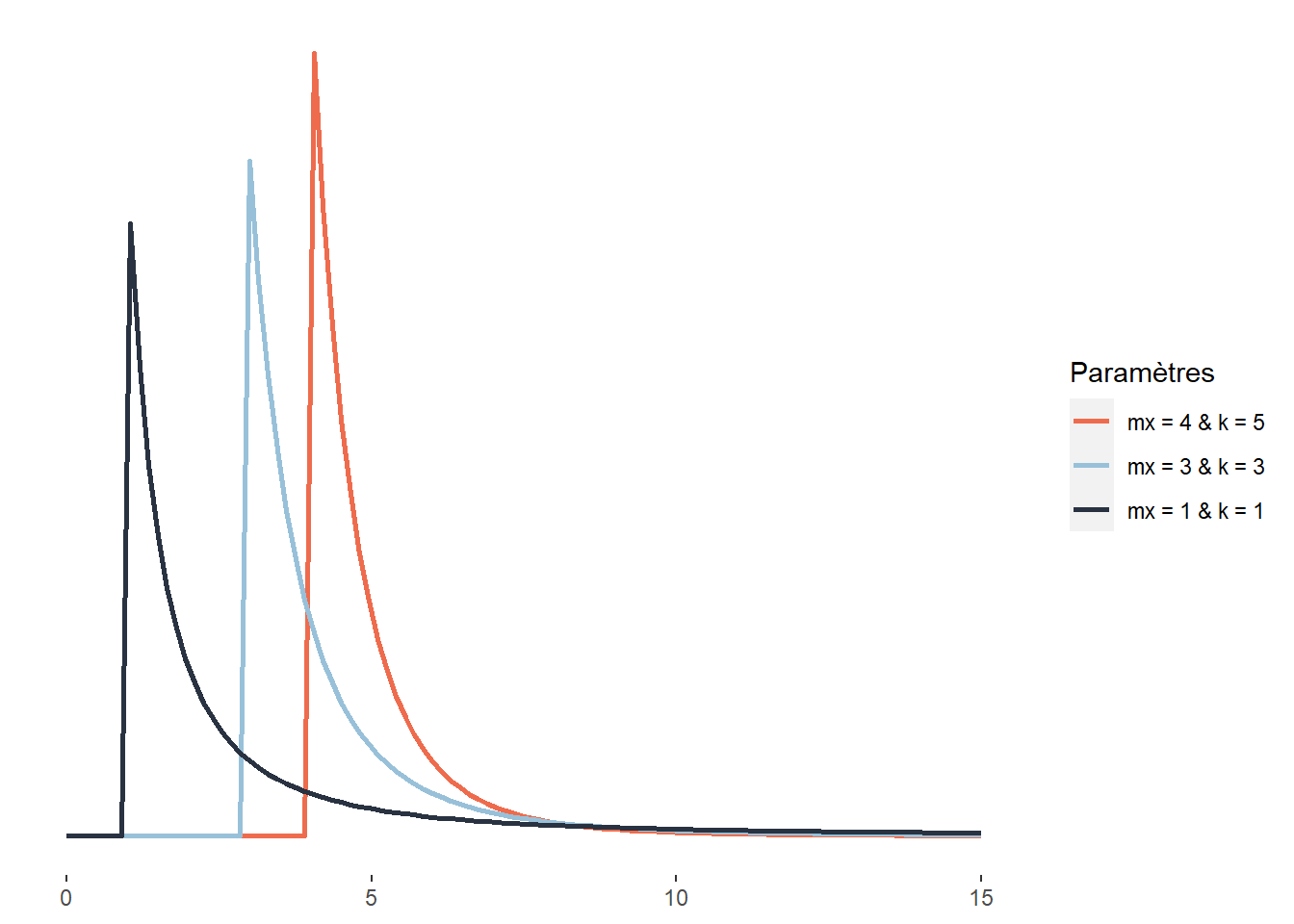
Figure 2.23: Distribution de Pareto

Au-delà de la question de la répartition de la richesse, la distribution de Pareto peut également être utilisée pour décrire la répartition de la taille des villes (Reed 2002), la popularité des hommes sur Tinder ou la taille des fichiers échangés sur Internet (Reed et Jorgensen 2004). Pour ces trois exemples, nous avons les situations suivantes : de nombreuses petites villes, profils peu attractifs, petits fichiers échangés et à l’inverse très peu de grandes villes, profils très attractifs, gros fichiers échangés.

La loi de Pareto est liée à la loi exponentielle. Si une variable aléatoire suit une loi de Pareto, le logarithme du quotient de cette variable et de son paramètre de localisation est une variable aléatoire qui suit une loi exponentielle.

2.4.3.19 Cas particuliers

Sachez également qu’il existe des distributions « plus exotiques » que nous n’abordons pas ici, mais auxquelles vous pourriez être confrontés un jour :

Les distributions sphériques, servant à décrire des données dont le 0 est équivalent à la valeur maximale. Par exemple, des angles puisque 0 et 360 degrés sont identiques.
Les distributions composées (mixture distributions), permettant de modéliser des phénomènes issus de la superposition de plusieurs distributions. Par exemple, la distribution de la taille de l’ensemble des êtres humains est en réalité une superposition de deux distributions gaussiennes, une pour chaque sexe, puisque ces deux distributions n’ont pas la même moyenne ni le même écart-type.
Les distributions multivariées permettant de décrire des phénomènes multidimensionnels. Par exemple, la réussite des élèves en français et en mathématique pourrait être modélisée par une distribution gaussienne bivariée plutôt que deux distributions distinctes. Ce choix serait pertinent si nous présumons que ces deux variables sont corrélées plutôt qu’indépendantes.
Les distributions censurées décrivant des variables pour lesquelles les données sont issues d’un tirage « censuré ». En d’autres termes, la variable étudiée varie sur une certaine étendue, mais du fait du processus de tirage (collecte des données), les valeurs au-delà de certaines limites sont censurées. Un bon exemple est la mesure de la pollution sonore avec un capteur incapable de détecter des niveaux sonores en dessous de 55 décibels. Il arrive parfois en ville que les niveaux sonores descendent plus bas que ce seuil, mais les données collectées ne le montrent pas. Dans ce contexte, il est important d’utiliser des versions censurées des distributions présentées précédemment. Les observations au-delà de la limite sont conservées dans l’analyse, mais nous ne disposons que d’une information partielle à leur égard (elles sont au-delà de la limite).
Les distributions tronquées, souvent confondues avec les distributions censurées, décrivent des situations où des données au-delà d’une certaine limite sont impossibles à collecter et retirées simplement de l’analyse.

2.4.4 Conclusion sur les distributions

Voilà qui conclut cette exploration des principales distributions à connaître. L’idée n’est bien sûr pas de toutes les retenir par cœur (et encore moins les formules mathématiques), mais plutôt de se rappeler dans quels contextes elles peuvent être utiles. Vous aurez certainement besoin de le relire cette section avant d’aborder le chapitre 8 portant sur les modèles linéaires généralisés (GLM). Wikipédia dispose d’informations très détaillées sur chaque distribution si vous avez besoin d’informations complémentaires. Pour un tour d’horizon plus exhaustif des distributions, vous pouvez aussi faire un tour sur les projets ProbOnto et the ultimate probability distribution explorer.

Références

Reed, William J. 2002. « On the rank-Size distribution for human settlements. » Journal of Regional Science 42 (1): 1‑17. https://onlinelibrary.wiley.com/doi/abs/10.1111/1467-9787.00247.

Reed, William J. et Murray Jorgensen. 2004. « The souble Pareto-Lognormal sistribution: A new parametric model for size distributions. » Communications in Statistics - Theory and Methods 33 (8). Taylor & Francis: 1733‑1753. https://doi.org/10.1081/STA-120037438.

Sean, Owen. 2018. « Common probability distributions. » https://medium.com/@srowen/common-probability-distributions-347e6b945ce4.