11.2 Spline de régression et spline de lissage
Dans les exemples précédents, nous avons vu que la construction d’une spline nécessite d’effectuer deux choix importants : le nombre de nœuds et leur localisation. Un trop grand nombre de nœuds conduit à un surajustement du modèle alors qu’un trop faible nombre de nœuds conduit à un sous-ajustement. Lorsque ces choix sont effectués par l’utilisateur et que les bases sont ajoutées manuellement dans le modèle tel que décrit précédemment, nous parlons alors de splines de régression (Regression Spline en anglais).
Une approche a été proposée pour faciliter le choix du nombre de nœuds, il s’agit de splines de lissage (smoothing spline en anglais). L’idée derrière cette approche est d’introduire dans le modèle une pénalisation associée avec le nombre de nœuds (ou degré de liberté) de la spline, dans un souci de parcimonie : chaque noeud supplémentaire doit suffisamment contribuer au modèle pour être conservé. Il n’est pas nécessaire ici de rentrer dans le détail mathématique de cette pénalisation qui est un peu complexe. Retenez simplement qu’elle dépend d’un paramètre appelé \(\lambda\) :
- plus \(\lambda\) tend vers 0, plus la pénalisation est faible et plus la spline de lissage devient une simple spline de régression;
- à l’inverse, plus elle est forte, plus la pénalité est importante, au point que la spline peut se résumer à une simple ligne droite.
Cela est illustré à la figure 11.12 comprenant trois splines avec 20 nœuds et des valeurs \(\lambda\) différentes contrôlant la force de la pénalité.
Bien évidemment, nous constatons qu’avec la spline de régression (non pénalisée), 20 nœuds conduisent à un fort surajustement du modèle. En revanche, les splines de lissage (pénalisées) permettent de corriger ce problème de surajustement. Toutefois, une valeur trop importante de \(\lambda\) conduit à un sous-ajustement du modèle (ici \(\lambda = 3\) et \(\lambda = 100\), lignes verte et bleue).
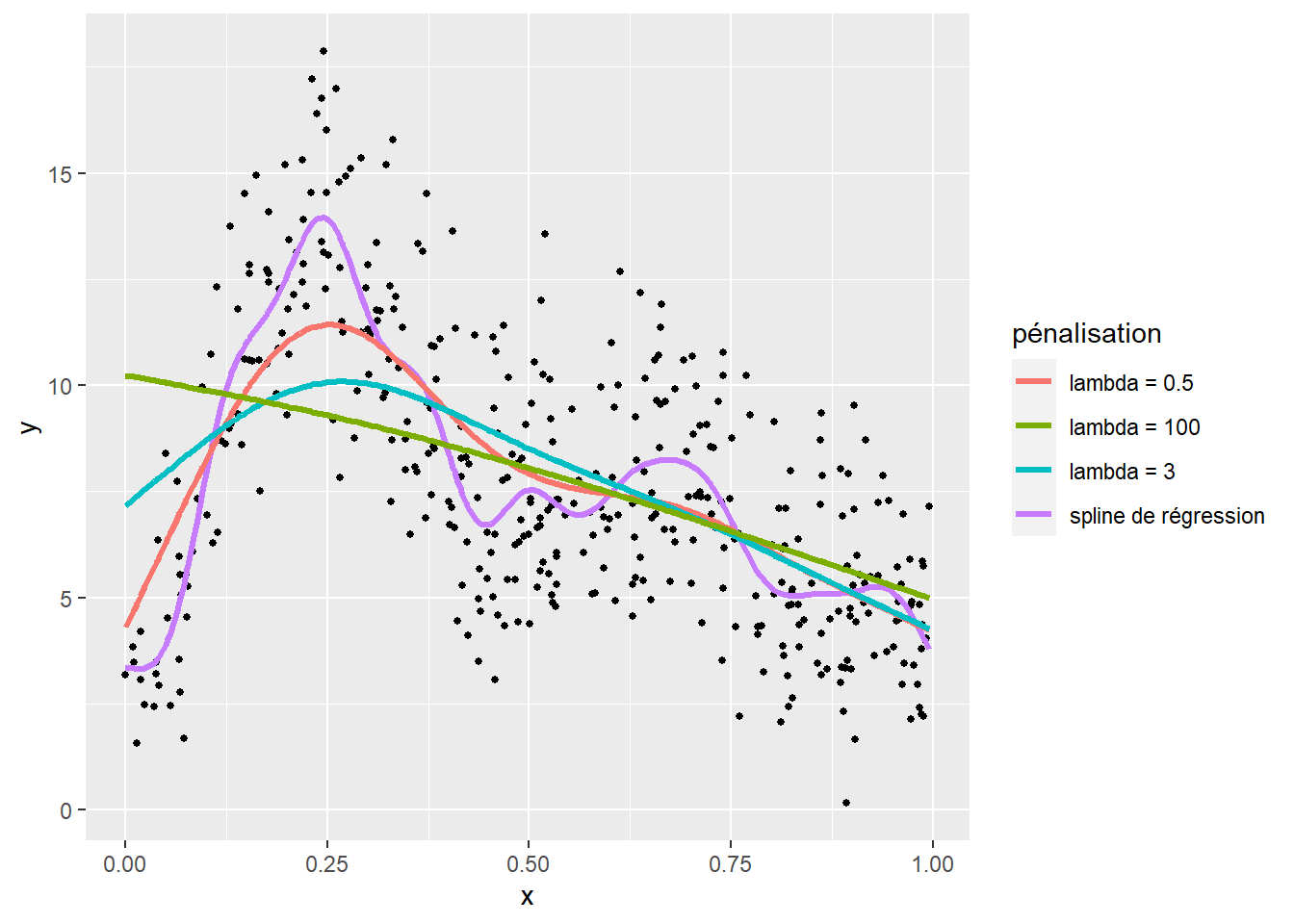
Figure 11.12: Pénalisation des splines
Avec les splines de lissage, l’enjeu est de sélectionner une valeur optimale de \(\lambda\). Le plus souvent, les packages R estiment eux-mêmes ce paramètre à partir des données utilisées dans le modèle. Toutefois, gardez en mémoire que vous pouvez modifier ce paramètre. Mentionnons également que les splines de lissage peuvent être reparamétrées dans un modèle pour être intégrées comme des effets aléatoires. Dans ce cas-ci, \(\lambda\) est remplacé par un simple paramètre de variance directement estimé dans le modèle (Wood 2004).