11.6 Mise en oeuvre dans R

Il est possible d’ajuster des splines de régression dans n’importe quel package permettant d’ajuster des coefficients pour un modèle de régression. Il suffit de construire les bases des splines en amont à l’aide du package splines2 et de les ajouter directement dans l’équation de régression. En revanche, il est nécessaire d’utiliser des packages spécialisés pour ajuster des splines de lissage. Parmi ceux-ci, mgcv est probablement le plus populaire du fait de sa (très) grande flexibilité, suivi des packages gamlss, gam et VGAM. Nous comparons ici les deux approches, puis nous tentons d’améliorer le modèle que nous avons ajusté pour prédire le pourcentage de surface couverte par des îlots de chaleur dans les aires de diffusion de Montréal, dans une perspective d’équité environnementale. Pour rappel, la variable dépendante est exprimée en pourcentage et nous utilisons une distribution bêta pour la modéliser.

library(mgcv)
# Chargement des données
dataset <- read.csv("data/gam/data_chaleur.csv",fileEncoding = "utf8")
# Ajustement du modèle de base
refmodel <- gam(hot ~
          A65Pct + A014Pct + PopFRPct + PopMVPct +
          poly(prt_veg, degree = 2)  + Arrond,
        data = dataset, family = betar(link = "logit"))

Dans notre première analyse de ces données, nous avons ajusté une polynomiale d’ordre 2 pour représenter un potentiel effet non linéaire de la végétation sur les îlots de chaleur. Nous remplaçons à présent ce terme par une spline de régression en sélectionnant quatre nœuds.

library(splines2)
# Création des bases de la spline
basis <- bSpline(x = dataset$prt_veg, df =4, intercept = FALSE)
# Ajouter les bases au DataFrame
basisdf <- as.data.frame(basis)
names(basisdf) <- paste('spline',1:ncol(basisdf),sep='')
dataset <- cbind(dataset, basisdf)
# Ajuster le modèle
model0 <- gam(hot ~
          A65Pct + A014Pct + PopFRPct + PopMVPct +
          spline1 + spline2 + spline3 + spline4 + Arrond,
        data = dataset, family = betar(link = "logit"))

Nous pouvons à présent ajuster une spline de lissage et laisser mgcv déterminer son niveau de complexité.

# Ajustement du modèle avec une spline simple
model1 <- gam(hot ~
          A65Pct + A014Pct + PopFRPct + PopMVPct +
          s(prt_veg)  + Arrond,
        data = dataset, family = betar(link = "logit"))

Notez ici que la syntaxe à employer est très simple, il suffit de spécifier s(prt_veg) pour indiquer à la fonction gam que vous souhaitez ajuster une spline pour la variable prt_veg. Nous pouvons à présent comparer l’ajustement des deux modèles en utilisant la mesure de l’AIC.

# Comparaison des AIC
AIC(refmodel, model0, model1)

##                df       AIC
## refmodel 40.00000 -6399.784
## model0   42.00000 -6419.630
## model1   44.61065 -6417.562

Nous constatons que la valeur de l’AIC du second modèle est plus réduite, indiquant un meilleur ajustement du modèle avec une spline de régression. Notons cependant que la différence avec la spline de lissage est anecdotique (deux points de l’AIC) et que nous connaissions a priori le bon nombre de nœuds à utiliser. Pour des relations plus complexes, les splines de lissage ont tendance à nettement mieux performer. Voyons à présent comment représenter ces trois termes non linéaires.

# Création d'un DataFrame de prédiction dans lequel seule
# la variable prt_veg varie.
dfpred <- data.frame(
  prt_veg = seq(min(dataset$prt_veg), max(dataset$prt_veg), 0.5),
  A65Pct = mean(dataset$A65Pct),
  A014Pct = mean(dataset$A014Pct),
  PopFRPct = mean(dataset$PopFRPct),
  PopMVPct = mean(dataset$PopMVPct),
  Arrond = "Verdun"
)

# Recréation des bases de la spline de régression
# pour les nouvelles observations
nvl_bases <- data.frame(predict(basis,newx = dfpred$prt_veg))
names(nvl_bases) <- paste('spline',1:ncol(basisdf),sep='')
dfpred <- cbind(dfpred, nvl_bases)

# Définition de la fonction inv.logit, soit l'inverse de la fonction 
# de lien du modèle pour retrouver les prédictions dans l'échelle 
# originales des données
inv.logit <- function(x){exp(x)/(1+exp(x))}

# Utilisation des deux modèles pour effectuer les prédictions
predref <- predict(refmodel, newdata = dfpred, type = 'link', se.fit = T)
predmod0 <- predict(model0, newdata = dfpred, type = 'link', se.fit = T)
predmod1 <- predict(model1, newdata = dfpred, type = 'link', se.fit = T)

# Calcul de la valeur prédite et construction des intervalles de confiance
dfpred$polypred <- inv.logit(predref$fit)
dfpred$poly025 <- inv.logit(predref$fit - 1.96 * predref$se.fit)
dfpred$poly975 <- inv.logit(predref$fit + 1.96 * predref$se.fit)

dfpred$regsplinepred <- inv.logit(predmod0$fit)
dfpred$regspline025 <- inv.logit(predmod0$fit - 1.96 * predmod0$se.fit)
dfpred$regspline975 <- inv.logit(predmod0$fit + 1.96 * predmod0$se.fit)

dfpred$splinepred <- inv.logit(predmod1$fit)
dfpred$spline025 <- inv.logit(predmod1$fit - 1.96 * predmod1$se.fit)
dfpred$spline975 <- inv.logit(predmod1$fit + 1.96 * predmod1$se.fit)

# Créer un graphique pour afficher les résultats
ggplot(dfpred) + 
  geom_ribbon(aes(x = prt_veg, ymin = poly025, ymax = poly975),
              alpha = 0.4, color = 'grey') +
  geom_ribbon(aes(x = prt_veg, ymin = spline025, ymax = spline975),
              alpha = 0.4, color = 'grey') +
  geom_ribbon(aes(x = prt_veg, ymin = regspline025, ymax = regspline975),
              alpha = 0.4, color = 'grey') +
  geom_line(aes(y = polypred, x = prt_veg, color = 'polynomiale'),
            size = 1) + 
  geom_line(aes(y = regsplinepred, x = prt_veg, color = 'spline de régression'),
            size = 1)+
  geom_line(aes(y = splinepred, x = prt_veg, color = 'spline de lissage'),
            size = 1)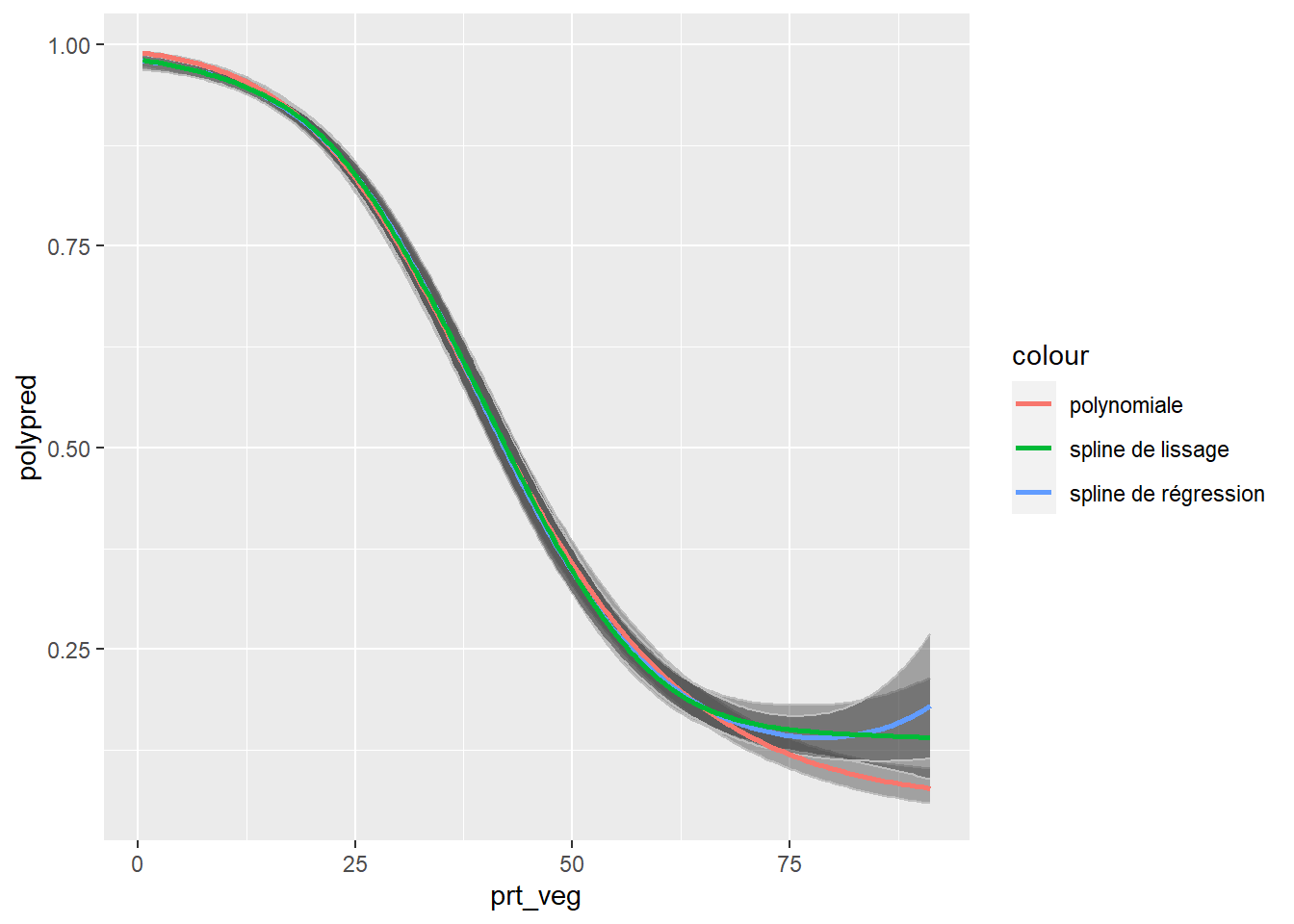

Figure 11.16: Comparaison d’une spline et d’une polynomiale

Nous constatons que les trois termes renvoient des prédictions très similaires et qu’une légère différence n’est observable que pour les secteurs avec les plus hauts niveaux de végétation (supérieurs à 75 %).

Jusqu’ici, nous utilisons l’arrondissement dans lequel est comprise chaque aire de diffusion comme une variable nominale afin de capturer la dimension spatiale du jeu de données. Puisque nous avons abordé la notion de splines bivariées, il serait certainement plus efficace d’en construire une à partir des coordonnées géographiques (x,y) des centroïdes des aires de diffusion. En effet, il est plus probable que la distribution des îlots de chaleur suive un patron spatial continu sur le territoire plutôt que les délimitations arbitraires des arrondissements.

# Ajustement du modèle avec une spline bivariée pour l'espace
model2 <- gam(hot ~
          A65Pct + A014Pct + PopFRPct + PopMVPct +
          s(prt_veg)  + s(X,Y),
        data = dataset, family = betar(link = "logit"))

Notez ici que l’expression s(X,Y) permet de créer une spline bivariée à partir des coordonnées (x,y), soit deux colonnes présentes dans le jeu de données. Ces coordonnées sont exprimées toutes deux en mètres et n’interagissent pas ensemble au sens strict, nous devons donc ajuster une spline bivariée. Si vous avez besoin d’ajuster une spline d’interaction (notamment quand les variables sont dans des unités différentes), il est nécessaire d’utiliser une autre syntaxe te(X,Y) ou t2(X,Y) faisant appel à une structure mathématique légèrement différente, soit des tensor product smooths.

Puisque notre modèle intègre deux splines, nous devons nous assurer que nous n’avons pas de problème de concurvité, ce que nous pouvons faire avec la fonction concurvity du package mgcv.

values <- concurvity(model2, full = FALSE)

# Worst, estimation pessimiste de la concurvité
round(values$worst,3)

##            para s(prt_veg) s(X,Y)
## para          1      0.000  0.000
## s(prt_veg)    0      1.000  0.458
## s(X,Y)        0      0.458  1.000

# Observed, estimation optimiste de la concurvité
round(values$observed,3)

##            para s(prt_veg) s(X,Y)
## para          1      0.000  0.000
## s(prt_veg)    0      1.000  0.154
## s(X,Y)        0      0.403  1.000

# Estimate, estimation entre deux de la concurvité
round(values$estimate,3)

##            para s(prt_veg) s(X,Y)
## para          1      0.000  0.000
## s(prt_veg)    0      1.000  0.142
## s(X,Y)        0      0.358  1.000

Nous pouvons ainsi constater des niveaux de concurvité tout à fait acceptables dans notre modèle. Des valeurs supérieures à 0,8 devraient être considérées comme alarmantes, surtout si elles sont reportées pour observed et estimate.

Voyons désormais, le résumé d’un modèle GAM tel que présenté dans R.

summary(model2)

## 
## Family: Beta regression(15.469) 
## Link function: logit 
## 
## Formula:
## hot ~ A65Pct + A014Pct + PopFRPct + PopMVPct + s(prt_veg) + s(X, 
##     Y)
## 
## Parametric coefficients:
##               Estimate Std. Error z value Pr(>|z|)    
## (Intercept) -0.6050031  0.0645191  -9.377  < 2e-16 ***
## A65Pct       0.0027671  0.0014072   1.966   0.0493 *  
## A014Pct     -0.0019040  0.0027674  -0.688   0.4914    
## PopFRPct     0.0095992  0.0014323   6.702 2.06e-11 ***
## PopMVPct     0.0010113  0.0008159   1.239   0.2152    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Approximate significance of smooth terms:
##              edf Ref.df Chi.sq p-value    
## s(prt_veg)  6.38  7.565   6731  <2e-16 ***
## s(X,Y)     27.10 28.764   1349  <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## R-sq.(adj) =  0.891   Deviance explained = 90.8%
## -REML = -3234.3  Scale est. = 1         n = 3157

La première partie du résumé comprend les résultats pour les effets fixes et linéaires du modèle. Ils s’interprètent comme pour ceux d’un GLM classique. La seconde partie présente les résultats pour les termes non linéaires. La valeur de p permet de déterminer si la spline a ou non un effet différent de 0. Une valeur non significative indique que la spline ne contribue pas au modèle. Les colonnes edf et Ref.df indiquent la complexité de la spline et peuvent être considérées comme une approximation du nombre de nœuds. Dans notre cas, la spline spatiale (s(X,Y)) est environ 5 fois plus complexe que la spline ajustée pour la végétation (s(prt_veg)). Cela n’est pas surprenant puisque la dimension spatiale (spline bivariée) du phénomène est certainement plus complexe que l’effet de la végétation. Notez ici que des valeurs edf et Ref.df proches de 1 signaleraient que l’effet d’un prédicteur est essentiellement linéaire et qu’il n’est pas nécessaire de recourir à une spline pour cette variable.

La dernière partie du résumé comprend deux indicateurs de qualité d’ajustement, soit le R² ajusté et la part de la déviance expliquée.

AIC(refmodel, model1, model2)

##                df       AIC
## refmodel 40.00000 -6399.784
## model1   44.61065 -6417.562
## model2   40.06053 -6596.884

Nous pouvons constater que le fait d’introduire la spline spatiale dans le modèle contribue à réduire encore la valeur de l’AIC, et donc à améliorer le modèle. À ce stade, nous pourrions tenter de forcer la spline à être plus complexe en augmentant le nombre de nœuds.

# Augmentation de la complexité de la spline spatiale
model3 <- gam(hot ~
          A65Pct + A014Pct + PopFRPct + PopMVPct +
          s(prt_veg)  + s(X,Y,k = 40),
        data = dataset, family = betar(link = "logit"))

AIC(refmodel, model1, model2, model3)

##                df       AIC
## refmodel 40.00000 -6399.784
## model1   44.61065 -6417.562
## model2   40.06053 -6596.884
## model3   48.28633 -6639.955

Cela a pour effet d’améliorer de nouveau le modèle. Pour vérifier si l’augmentation du nombre nœuds est judicieuse, il est possible de représenter le résultat des deux splines précédentes. Pour ce faire, nous proposons de calculer les valeurs prédites de la spline pour chaque localisation dans notre terrain d’étude, en le découpant préalablement en pixels de 100 de côté. Pour cette prédiction, nous maintenons toutes les autres variables à leur moyenne respective afin d’évaluer uniquement l’effet de la spline spatiale.

library(viridis)
library(metR) # pour placer des étiquettes sur les isolignes

# Création d'un DataFrame fictif pour les prédictions
dfpred <- expand.grid(
  prt_veg =mean(dataset$prt_veg),
  A65Pct = mean(dataset$A65Pct),
  A014Pct = mean(dataset$A014Pct),
  PopFRPct = mean(dataset$PopFRPct),
  PopMVPct = mean(dataset$PopMVPct),
  X = seq(min(dataset$X),max(dataset$X),100),
  Y = seq(min(dataset$Y),max(dataset$Y),100)
)

dfpred$predicted1 <- predict(model2, newdata = dfpred, type = 'response')
dfpred$predicted2 <- predict(model3, newdata = dfpred, type = 'response')

# Centrage des prédictions
dfpred$predicted1 <- dfpred$predicted1 - mean(dfpred$predicted1)
dfpred$predicted2 <- dfpred$predicted2 - mean(dfpred$predicted2)

# Représentation des splines
plot1 <- ggplot(dfpred) + 
  geom_raster(aes(x = X, y = Y, fill = predicted1)) + 
  geom_point(aes(x = X, y = Y),
             size = 0.2, alpha = 0.4,
             color = 'black', data = dataset)+
  geom_contour(aes(x = X, y = Y, z = predicted1),binwidth = 0.1, 
               color = 'white', linetype = 'dashed') + 
  geom_text_contour(aes(x = X, y = Y, z = predicted1), 
                    color = 'white', binwidth = 0.1)+
  scale_fill_viridis() +
  coord_cartesian() + 
  theme(axis.title= element_blank(),
        axis.text = element_blank(),
        axis.ticks =  element_blank()
        ) + 
  labs(subtitle = 'spline de base', fill = "prédictions")

plot2 <- ggplot(dfpred) + 
  geom_raster(aes(x = X, y = Y, fill = predicted2)) + 
  geom_point(aes(x = X, y = Y),
             size = 0.2, alpha = 0.4,
             color = 'black', data = dataset)+
  geom_contour(aes(x = X, y = Y, z = predicted2),
               binwidth = 0.1, color = 'white', linetype = 'dashed') + 
  geom_text_contour(aes(x = X, y = Y, z = predicted2), color = 'white', binwidth = 0.1)+
  scale_fill_viridis() +
  coord_cartesian()+ 
  theme(axis.title= element_blank(),
        axis.text = element_blank(),
        axis.ticks =  element_blank()
        ) + 
  labs(subtitle = 'spline plus complexe', fill = "prédictions")

ggarrange(plot1, plot2, nrow = 1, ncol = 2, common.legend = TRUE, legend = 'bottom')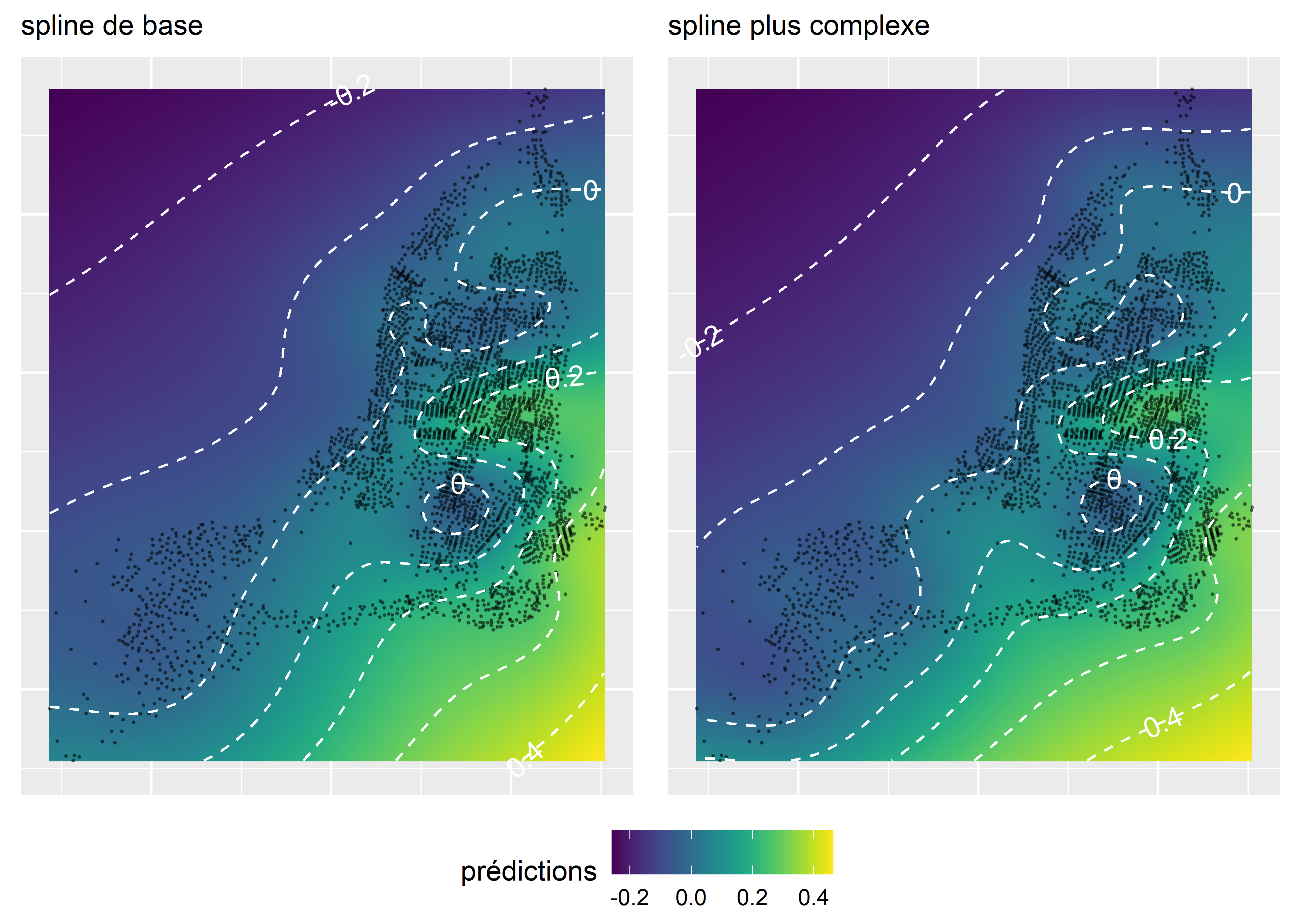

Figure 11.17: Comparaison de deux splines spatiales

Or, il s’avère que les deux splines spatiales sont très similaires (figures 11.17). Par conséquent, il est vraisemblablement plus pertinent de conserver la plus simple des deux. Notez que le Mont-Royal, compris dans le cercle central avec une isoligne à 0, est caractérisé par des valeurs plus faibles d’îlots de chaleur, alors que les quartiers centraux situés un peu plus au nord sont au contraire marqués par des pourcentages d’îlots de chaleur supérieurs de 20 points de pourcentage en moyenne.