9.1 Introduction
9.1.1 Indépendance des observations et effets de groupes
Nous avons vu dans les précédents chapitres que l’indépendance des observations est une condition d’application commune à l’ensemble des modèles de régression. Cette condition implique ainsi que chaque unité d’observation de notre jeu de données est indépendante des autres; en d’autres termes, qu’elle ne soit associée à aucune autre observation par un lien de dépendance. Prenons un exemple concret pour illustrer cette notion. Admettons que nous nous intéressons à la performance scolaire d’élèves du secondaire à Montréal. Pour cela, nous collectons la moyenne des résultats aux examens du Ministère de tous les élèves des différentes commissions scolaires de l’île de Montréal. Chaque élève appartient à une classe spécifique, et chaque classe se situe dans une école spécifique. Les classes constituent des environnements particuliers, la performance des élèves y est influencée par un ensemble de facteurs comme la personne qui enseigne et les relations entre les élèves d’une même classe. Deux élèves provenant d’une même classe sont donc lié(e)s par une forme de structure propre à leur classe et ne peuvent pas être considéré(e)s comme indépendant(e)s. De même, l’école constitue un environnement particulier pouvant influencer la performance des élèves du fait de moyens financiers plus importants, de la mise en place de programmes spéciaux, de la qualité des infrastructures (bâtiment, gymnase, cour d’école) ou d’une localisation minimisant certaines nuisances à l’apprentissage comme le bruit. À nouveau, deux élèves provenant d’une même école partagent une forme de structure qui, cette fois-ci, est propre à leur école. Si nous collectons des données pour l’ensemble du Canada, nous pourrions étendre ce raisonnement aux villes dans lesquelles les écoles se situent et aux provinces.
Dans cet exemple, la dépendance entre les données est provoquée par un effet de groupe : il est possible de rassembler les observations dans des ensembles (classes et écoles) influençant vraisemblablement la variable étudiée (performance scolaire). Les effets des classes et des écoles ne sont cependant pas intrinsèques aux élèves. En effet, il est possible de changer un ou une élève de classe ou d’école, mais pas de changer son âge ou sa situation familiale. Il est ainsi possible de distinguer la population des élèves, la population des classes, et la population des écoles (figure 9.1). Ces effets de groupes sont plus la règle que l’exception dans l’analyse de données en sciences sociales, ce qui met à mal l’hypothèse d’indépendance des observations. Notez que les effets de groupes ne sont pas les seules formes de structures remettant en cause l’indépendance des observations. Il existe également des structures temporelles (deux observations proches dans le temps ont plus de chances de se ressembler) et spatiales (deux observations proches dans l’espace ont plus de chances de se ressembler); cependant, les cas de la dépendance temporelle et spatiale ne sont pas couverts dans ce livre, car ils sont complexes et méritent un ouvrage dédié.
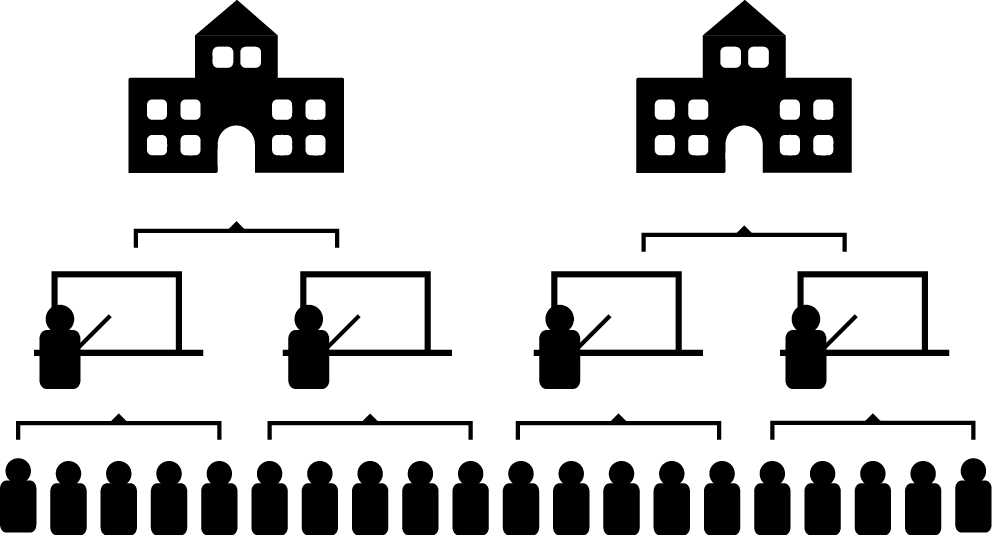
Figure 9.1: Structure hiérarchique entre élèves, classes et écoles
La notion de pseudo-réplication
Les effets de dépendance causés par des structures de groupe, temporelles ou spatiales, sont regroupés sous le terme de pseudo-réplication. Il est intéressant de se pencher sur la signification de ce mot pour comprendre le problème intrinsèque causé par la dépendance entre les observations et son influence sur l’inférence.
Reprenons l’exemple des élèves et de la performance scolaire et admettons que nous souhaitons estimer la moyenne générale de l’ensemble des élèves sur l’île de Montréal, mais que nous ne disposons pas du jeu de données complet. Nous devons donc collecter un échantillon suffisamment grand pour estimer la moyenne pour l’ensemble de cette population. Raisonnons en termes de quantité d’informations. Si nous ne disposons d’aucune observation (nous n’avons pas encore interrogé d’élèves), cette quantité est de 0. Si nous interrogeons un premier ou une première élève, nous obtenons une donnée supplémentaire, et donc un point d’information supplémentaire (+1). Admettons maintenant que nous collectons 30 observations dans une école, 10 dans une seconde et 5 dans une troisième. A priori, nous pourrions dire que nous avons ajouté 45 points d’information à notre total de connaissance. Ce serait le cas si les observations étaient indépendantes les unes des autres. Dans un tel contexte, chaque observation ajoute la même quantité d’information. Cependant, puisque les personnes étudiant dans la même école ont plus de chance de se ressembler, interroger les élèves d’une même école apporte moins d’information. Notez que plus la ressemblance entre les élèves d’une même école est forte, plus la quantité d’information est réduite. Nous sommes donc loin de disposer d’une quantité d’information égale à 45. Chaque réplication de l’expérience (demander à un ou une élève sa moyenne annuelle) n’apporte pas autant d’information qu’attendu si les observations étaient indépendantes, c’est pourquoi on parle de pseudo-réplication.
La pseudo-réplication influence directement l’inférence statistique puisque le calcul des différents tests statistiques assume que chaque observation apporte autant d’information que les autres. En cas de présence de pseudo-réplication, la quantité d’information présente dans l’échantillon est plus petite qu’attendu. Il est possible de voir cela comme une forme de surestimation de la taille de l’échantillon. En cas de pseudo-réplication, nous disposons en réalité de moins de données que ce que l’on attendrait d’un échantillon de cette taille, si les observations étaient indépendantes. La conséquence est la sous-estimation de la variabilité réelle des données et l’augmentation des risques de trouver des effets significatifs dans l’échantillon alors qu’ils ne le sont pas pour l’ensemble de la population.
9.1.2 Terminologie: effets fixes et effets aléatoires
Puisque les effets des classes et des écoles ne sont pas propres aux élèves, il convient de les introduire différemment dans les modèles de régression. Nous appelons un effet fixe, un effet qui est propre aux observations que nous étudions et un effet aléatoire, un effet provoqué par une structure externe (effet de groupe, effet temporel et/ou effet spatial). Un modèle combinant à la fois des effets fixes et des effets aléatoires est appelé un modèle à effets mixtes, ou GLMM pour Generalized Linear Mixed Model. Tous les modèles que nous avons ajustés dans les sections précédentes ne comprenaient que des effets fixes alors qu’à plusieurs reprises, des effets aléatoires induits par l’existence de structure de groupe auraient pu (dû) être utilisés. Prenons pour exemple le modèle logistique binomial visant à prédire la probabilité d’utiliser le vélo comme mode de transport pour son trajet le plus fréquent. La variable multinomiale Pays, représentant le pays dans lequel les personnes interrogées résident, a été introduite comme un effet fixe. Cependant, l’effet du pays ne constitue pas une caractéristique propre aux individus; il s’agit plutôt d’un agrégat complexe mêlant culture, météorologie, politiques publiques et formes urbaines. À l’inverse, le sexe ou l’âge sont bien des caractéristiques intrinsèques des individus et peuvent être considérés comme des effets fixes.
Notez que l’utilisation du terme effet aléatoire peut porter à confusion, car il est utilisé différemment en fonction du champ d’études. Parmi les différentes définitions relevées par Gelman (2005) d’un effet aléatoire, citons les suivantes :
Les effets fixes sont identiques pour tous les individus, alors que les effets aléatoires varient (définition 1).
Les effets sont fixes s’ils sont intéressants en eux-mêmes, et les effets sont aléatoires si nous nous intéressons à la population dont ils sont issus (définition 2).
Lorsqu’un échantillon couvre une grande part de la population, la variable correspondante est un effet fixe. Si l’échantillon couvre une faible part de la population, l’effet est aléatoire (définition 3).
Si l’effet est censé provenir d’une variable aléatoire, alors il s’agit d’un effet aléatoire (définition 4).
Les effets fixes sont estimés par la méthode des moindres carrés ou par le maximum de vraisemblance, alors que les effets aléatoires sont estimés avec régularisation (shrinkage) (définition 5).
Il est ainsi possible de se retrouver dans des cas où un effet serait classé comme fixe selon une définition et aléatoire selon une autre. La deuxième définition suppose même qu’un effet peut être aléatoire ou fixe selon l’objectif de l’étude. La dernière définition a l’avantage d’être mathématique, mais ne permet pas de décider si un effet doit être traité comme aléatoire ou fixe. Nous ne proposons pas ici de clore le débat, mais plutôt de donner quelques pistes de réflexion pour décider si un effet doit être modélisé comme fixe ou aléatoire:
- Est-ce que l’effet en question est propre aux individus étudiés ou est externe aux individus? S’il est propre aux individus, il s’agit plus certainement d’un effet fixe. À titre d’exemple, il n’est pas possible de changer l’âge d’une personne, mais il est certainement possible changer sa ville de résidence.
- Existe-t-il un nombre bien arrêté de catégories possibles pour l’effet en question? Si oui, il s’agit plus certainement d’un effet fixe. Il y a un nombre bien arrêté de catégories pour la variable sexe, mais pour la variable pays, de nombreuses autres valeurs peuvent être ajoutées. Il est également possible de se demander s’il semble cohérent d’effectuer un échantillonnage sur les catégories en question. Dans le cas des pays, nous pourrions mener une étude à l’échelle des pays et collecter des données sur un échantillon de l’ensemble des pays. Il existe donc une population de pays, ce que nous ne pouvons pas affirmer pour la variable sexe.
- L’effet en question est direct ou indirect? Dans le second cas, l’effet en question est un agglomérat complexe découlant de plusieurs processus n’ayant pas été mesurés directement, ce qui correspond davantage à un effet aléatoire. Ainsi, l’effet du pays de résidence des individus sur leur probabilité d’utiliser le vélo est bien une agglomération complexe d’effets (culture, météorologie, orientation des politiques publiques, formes urbaines, etc.) n’ayant pas tous été mesurés. À l’inverse, l’âge d’un individu a bien un effet direct sur sa probabilité d’utiliser le vélo.
- L’effet est-il le même pour tous les individus, ou doit-il varier selon le groupe dans lequel l’individu se situe? Si un effet doit varier en fonction d’un groupe, il s’apparente davantage à un effet aléatoire. Pour reprendre l’exemple de l’âge, nous pourrions décider que cette caractéristique des individus n’a peut-être pas le même effet en fonction du pays dans lequel vit l’individu et l’ajouter au modèle comme un effet aléatoire.
Vous comprendrez donc qu’une partie non négligeable du choix entre effet fixe ou un effet aléatoire réside dans le cadre théorique à l’origine du modèle. Maintenant que cette distinction conceptuelle a été détaillée, nous pouvons passer à la présentation statistique des modèles GLMM.