12.4 Analyse de correspondances multiples (ACM)

L’analyse des correspondances multiples (ACM) est particulièrement adaptée à l’exploration de données issues d’une enquête par sondage, puisqu’elle permet de résumer/synthétiser l’information d’un tableau comprenant uniquement des variables qualitatives (figure 12.34).

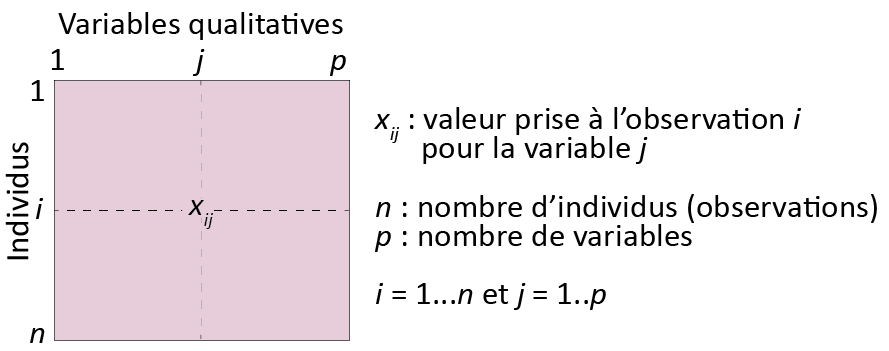
Figure 12.34: Tableau pour une ACM

Par exemple, une enquête sur la mobilité d’une population donnée pourrait comprendre plusieurs variables qualitatives dont celles reportées au tableau 12.18.

Tableau 12.18: Exemple de variables qualitatives issues d’une enquête

Modalités des variables	Codage
Sexe
Homme	1
Femme	2
Groupe d’âge
Moins de 20 ans	1
20 à 39 ans	2
40 à 59 ans	3
60 ans et plus	4
Mode de transport
Automobile	1
Transport en commun	2
Marche	3
Vélo	4

Pour analyser de telles données, il suffit de transformer le tableau condensé (de données brutes) en un tableau disjonctif complet dans lequel chaque modalité des variables qualitatives devient une variable binaire prenant les valeurs de 0 ou 1 (tableaux 12.19 et 12.20). Notez que la somme de chaque ligne est alors égale au nombre de variables qualitatives.

Tableau 12.19: Tableau condensé (données brutes)

	Sexe	Groupe d’âge	Mode de transport
Ind. 1	1	1	2
Ind. 2	1	2	3
Ind. 3	2	3	1
Ind. 4	1	2	1
Ind. 5	2	4	2
Ind. 6	1	4	4

Tableau 12.20: Tableau disjonctif complet

	Sexe		Groupe d’âge				Mode de transport
Individu	Homme	Femme	Moins de 20 ans	20 à 39 ans	40 à 59 ans	60 ans et plus	Auto.	T.C.	Marche	Vélo
Ind. 1	1	0	1	0	0	0	0	1	0	0
Ind. 2	1	0	0	1	0	0	0	0	1	0
Ind. 3	0	1	0	0	1	0	1	0	0	0
Ind. 4	1	0	0	1	0	0	1	0	0	0
Ind. 5	0	1	0	0	0	1	0	1	0	0
Ind. 6	1	0	0	0	0	1	0	0	0	1

ACM versus AFC

Nous avons vu que l’AFC permet d’analyser un tableau de contingence avec deux variables qualitatives. En ACM, les colonnes sont les différentes modalités des variables qualitatives et les lignes sont les observations (par exemple, les individus ayant répondu à une enquête par sondage). En résumé, l’analyse des correspondances multiples (ACM) est simplement une analyse des correspondances (AFC) appliquée sur un tableau disjonctif complet.

L’ACM permet ainsi de révéler les ressemblances entre les différentes modalités des variables qualitatives et les ressemblances entre les différents individus. Par conséquent, elle produit également des variables synthétiques (axes factoriels) résumant l’information contenue dans le tableau initial. L’évaluation de ces ressemblances et la détermination des axes factoriels sont aussi basées sur la distance du khi-deux.

12.4.1 Aides à l’interprétation

Puisque l’ACM est une extension de l’AFC, nous retrouvons les mêmes aides à l’interprétation : les valeurs propres pour les axes, les coordonnées factorielles, les contributions et les cosinus carrés pour les variables et les individus.

Pour présenter l’ACM, nous utilisons des données ouvertes de la Ville de Montréal et, plus particulièrement, celles d’un sondage auprès de la population de l’île de Montréal sur l’agriculture urbaine. Pour ce faire, nous avons conservé uniquement les personnes pratiquant l’agriculture urbaine (n = 352). Les variables qualitatives extraites pour l’ACM sont reportées au tableau 12.21 avec la description des questions, leurs modalités respectives avec les effectifs bruts et en pourcentage. Au final, l’ACM est calculée de la manière suivante :

• Neuf variables qualitatives relatives à la pratique de l’agriculture urbaine sont retenues (q3, q4, q5, q8, q9, q10, q11, q12 et q13).
• Quatre variables relatives au profil socioéconomique des personnes répondantes sont introduites comme variables supplémentaires (q15, q16, q17 et q21).
• Chaque ligne est pondérée avec la variable pond.

L’objectif de cette ACM est double :

1. Montrer les ressemblances entre les différentes modalités relatives à la pratique de l’agriculture urbaine. L’analyse des axes factoriels devrait nous permettre d’identifier différents profils des personnes pratiquant l’agriculture urbaine.
2. Projeter les modalités des variables socioéconomiques afin de vérifier si elles sont ou non associées aux axes factoriels, c’est-à-dire aux différents profils révélés par les axes.

L’analyse du sondage sur l’agriculture urbaine réalisée ici est purement exploratoire : elle vise uniquement à démontrer que l’ACM est un outil particulièrement intéressant pour analyser les données d’un sondage. Par contre, cette analyse n’a aucune prétention scientifique puisque nous ne sommes pas des spécialistes de l’agriculture urbaine. Dans ce champ de recherche très fertile qu’est l’agriculture urbaine (surement pas la meilleure blague du livre…), vous pourrez consulter plusieurs études montréalaises (McClintock 2018; Audate, Cloutier et Lebel 2021; Bhatt et Farah 2016).

Tableau 12.21: Variables qualitatives extraites du sondage sur l’agriculture urbaine de la Ville de Montréal

Modalité	N	%
Q3. Depuis combien de temps cultivez-vous des fruits, des fines herbes ou des légumes?
Q3. Moins de 1 an	35	9,9
Q3. De 1 à 4 ans	101	28,7
Q3. De 5 à 9 ans	66	18,8
Q3. 10 ans ou plus	150	42,6
Q4. Selon vous, quelle proportion des fruits, des fines herbes et des légumes que vous consommez durant l’été provient de votre propre production?
Q4. Moins de 10%	192	54,5
Q4. 10 à 25%	70	19,9
Q4. 26 à 50%	47	13,4
Q4. Plus de 50%	43	12,2
Q5. Utilisez-vous du compost provenant de vos déchets verts ou alimentaires pour faire pousser des fruits, des fines herbes ou des légumes?
Q5. Oui	90	25,6
Q5. Non	262	74,4
Q8. Récupérez-vous l’eau de pluie pour irriguer vos cultures de fruits, de fines herbes ou des légumes ou encore votre jardin?
Q8. Oui	72	20,5
Q8. Non	280	79,5
Q9. Combien de sortes de fruits, de fines herbes ou de légumes cultivez-vous?
Q9. Moins de 5 sortes	170	48,3
Q9. 5 à 9 sortes	124	35,2
Q9. 10 à 14 sortes	42	11,9
Q9. 15 sortes ou plus	16	4,5
Q10. Cultivez-vous suffisamment de fruits, de fines herbes ou de légumes pour partager avec d’autres personnes?
Q10. Oui	143	40,6
Q10. Non	209	59,4
Q11. Échangez-vous vos semis ou vos récoltes de fruits, de fines herbes ou de légumes avec d’autres personnes?
Q11. Oui	90	25,6
Q11. Non	262	74,4
Q12. Selon vous, l’agriculture urbaine contribue-t-elle à améliorer les rapports entre les gens?
Q12. Oui	283	80,4
Q12. Non	46	13,1
Q12. NSP/NRP	23	6,5
Q13. Saviez-vous que la Ville de Montréal encourage et soutient l’agriculture urbaine sur l’île de Montréal?
Q13. Oui	203	57,7
Q13. Non	149	42,3
Q15. À quel groupe d’âge appartenez-vous?
Q15. 18 à 34 ans	54	15,3
Q15. 35 à 49 ans	110	31,2
Q15. 50 à 64 ans	101	28,7
Q15. 65 ans et plus	87	24,7
Q16. Quelle est votre occupation principale?
Q16. Travail temps plein	177	50,3
Q16. Travail. temps partiel	26	7,4
Q16. Étudiant	14	4,0
Q16. Retraité	101	28,7
Q16. Sans emploi	10	2,8
Q16. À la maison	24	6,8
Q17. Quel est le plus haut niveau de scolarité que vous avez complété?
Q17. Aucun certificat ou dipl.	25	7,1
Q17. Dipl. secondaires	80	22,7
Q17. Dipl. collégiales	75	21,3
Q17. Études universitaires	172	48,9
Q21. Êtes-vous propriétaire ou locataire de votre résidence ?
Q21. Propriétaire	250	71,0
Q22. Locataire	102	29,0

12.4.1.1 Résultats de l’ACM pour les valeurs propres

Les résultats pour les valeurs propres sont reportés au tableau 12.22 et à la figure 12.35. En ACM, l’inertie totale du tableau des variables qualitatives est égale au nombre moyen de modalités par variable moins un, soit \(\frac{K}{J}-1\) avec K et J étant respectivement les nombres de modalités et de variables. Aussi, le nombre d’axes produits par l’ACM est égal à \(K - J\). Pour notre tableau, l’inertie est donc égale à \(\mbox{25} / \mbox{9} = \mbox{1,77}\) avec \(\mbox{25}-\mbox{9} = \mbox{16}\) axes. Le nombre d’axes à retenir est souvent plus difficile à déterminer puisque, tel que signalé judicieusement par Jérôme Pagès (2002, 53) : « en pratique, comparée à l’ACP, l’ACM conduit, dans l’ensemble à : des pourcentages d’inertie plus petits; une décroissance de ces pourcentages plus douce ».

L’histogramme des valeurs propres (figure 12.35) révèle plusieurs sauts importants dans les valeurs propres qui pourraient justifier le choix du nombre d’axes factoriels, soit aux axes 1, 2, 3 et 6. Pour l’exercice, nous retenons les trois premiers axes qui résument 30 % de l’inertie du tableau initial.

Tableau 12.22: Résultats de l’ACM pour les valeurs propres

Axe factoriel	Valeur propre	Pourcentage	Pourc. cumulé
1	0,248	13,940	13,940
2	0,156	8,792	22,732
3	0,135	7,620	30,352
4	0,127	7,161	37,513
5	0,126	7,065	44,579
6	0,123	6,916	51,494
7	0,114	6,385	57,879
8	0,107	6,003	63,882
9	0,101	5,671	69,553
10	0,095	5,327	74,880
11	0,093	5,234	80,115
12	0,086	4,822	84,937
13	0,077	4,340	89,277
14	0,071	4,011	93,288
15	0,064	3,619	96,906
16	0,055	3,094	100,000

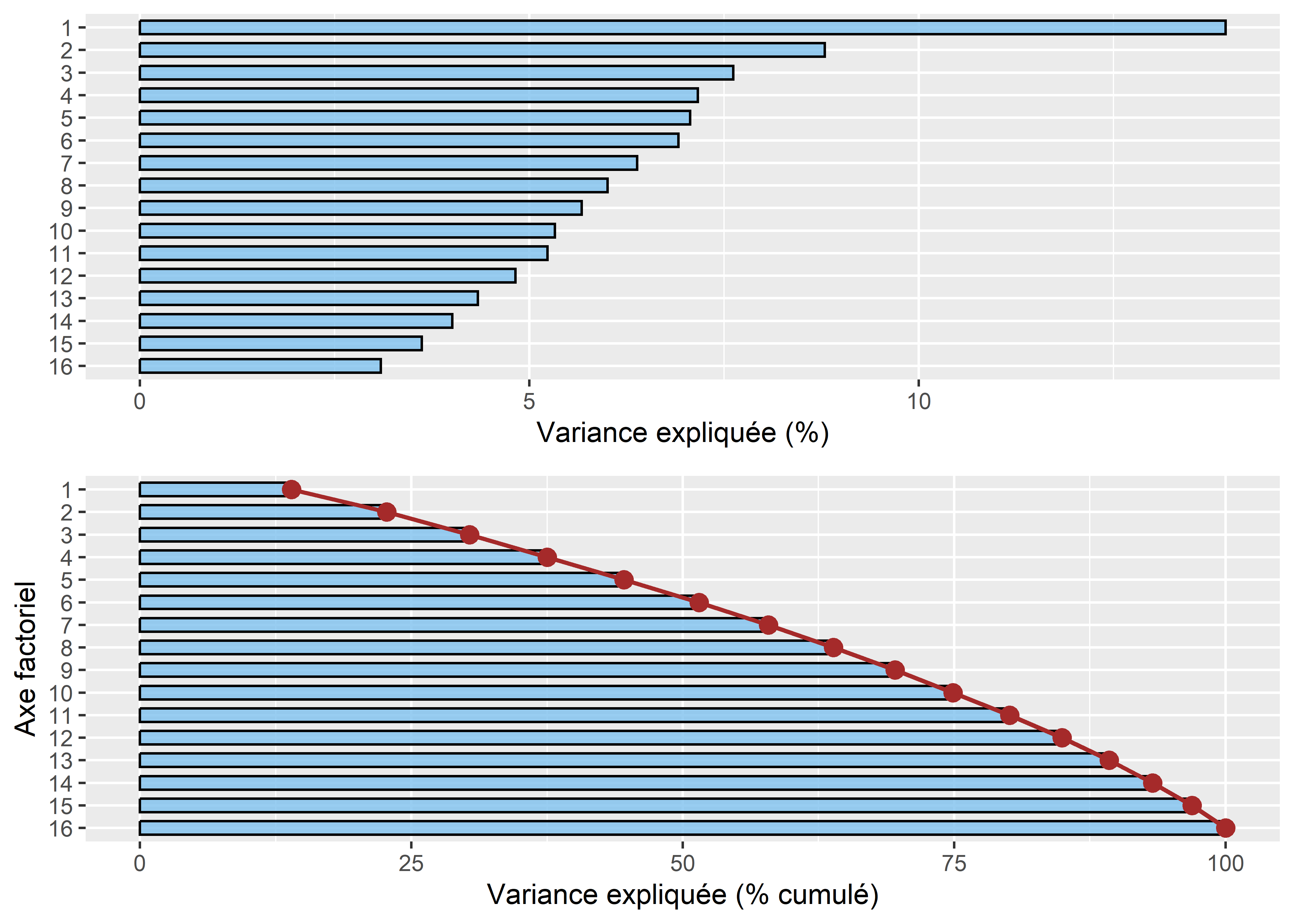
Figure 12.35: Graphiques pour les valeurs propres pour l’ACM

12.4.1.2 Résultats de l’ACM pour les modalités des variables

À titre de rappel, comme pour l’ACP et l’AFC, nous retrouvons les trois mêmes mesures pour les variables et les individus (coordonnées factorielles, contributions et cosinus carrés). Plus les variables qualitatives du jeu données comprennent de modalités, plus la taille du tableau des résultats des modalités est importante et plus il est fastidieux de l’analyser. Il est donc recommandé de construire des histogrammes avec les coordonnées factorielles et les contributions des modalités, mais aussi un nuage de points avec les coordonnées des modalités des variables qualitatives sur le premier, voire le deuxième plan factoriel.

Compréhension des axes factoriels de l’ACM : une étape essentielle, incontournable…

Comme en ACP et en AFC, l’analyse des trois mesures (coordonnées, contributions et cosinus carrés) pour les variables et les individus doit vous permettre de comprendre la signification des axes factoriels retenus de l’ACM. Prenez le temps de bien réaliser cette étape d’interprétation souvent plus fastidieuse qu’en ACP et ACM, en raison du nombre élevé de modalités. Cette étape est en effet essentielle afin de qualifier les variables latentes (axes factoriels, variables synthétiques) produites par l’ACM.

Les résultats pour les variables sont reportés 1) au tableau 12.23, 2) aux figures 12.36, 12.37 et 12.39 pour les coordonnées et les contributions et à la figure 12.38 pour le premier plan factoriel.

Interprétation des résultats de l’axe 1 pour les variables

Sept modalités concourent le plus à la formation de l’axe 1 résumant 13,9 % de la variance : Q9. 10 à 14 sortes (10,35 %), Q10. Oui (9,99 %), Q9. Moins de 5 sortes (9,71 %), Q5. Oui (9,19 %), Q11. Oui (8,20 %), Q4. Moins de 10% (7,87 %) et Q10. Non (7,10 %). Aussi, les modalités suivantes sont aux deux extrémités de cet axe :

• Coordonnées négatives : Q12. Non (-0,84), Q3. Moins de 1 an (-0,73), Q9. Moins de 5 sortes (-0,67), Q4. Moins de 10% (-0,56), Q10. Non (-0,521). Cela signifie que lorsque les coordonnées des individus sont fortement négatives sur cet axe, les personnes pratiquant l’agriculture urbaine :
  • ne pensent pas que l’agriculture urbaine contribue à améliorer les rapports entre les gens (Q12);
  • cultivent des fruits, des fines herbes ou de légumes depuis moins d’un an (Q3);
  • cultivent moins de cinq sortes de fruits, de fines herbes ou de légumes (Q9);
  • moins de 10 % de la proportion des fruits, des fines herbes et des légumes consommés durant l’été provient de leur propre production (Q4);
  • ne cultivent pas suffisamment pour partager avec d’autres personnes (Q10).
• Coordonnées positives : Q9. 15 sortes ou plus (1,36), Q9. 10 à 14 sortes (1,28), Q5. Oui (0,95) et Q11. Oui (0,85). Cela signifie que lorsque les coordonnées des individus sont fortement positives sur cet axe, les personnes pratiquant l’agriculture urbaine :
  • cultivent plus de dix sortes de fruits, de fines herbes ou de légumes (Q9);
  • utilisent du compost provenant de leurs déchets verts ou de leurs déchets alimentaires pour faire pousser des fruits, des fines herbes ou de légumes (Q5);
  • échangent leurs semis ou leurs récoltes de fruits, de fines herbes ou des légumes avec d’autres personnes (Q11).

En résumé, l’axe 1 oppose clairement les néophytes en agriculture versus les personnes expérimentées cultivant des fruits et de légumes variés avec leur propre compost et échangeant leurs semis ou leurs récoltes.

Tableau 12.23: Résultats de l’ACM pour les modalités des variables

	Coordonnées			Cosinus carrés			Contributions (%)
Modalité	1	2	3	1	2	3	1	2	3
Q3. Moins de 1 an	-0,73	0,68	0,63	2,70	3,68	3,64	0,07	0,06	0,05
Q3. De 1 à 4 ans	-0,29	-0,79	0,39	1,26	15,30	4,30	0,04	0,33	0,08
Q3. De 5 à 9 ans	0,12	0,38	-1,11	0,12	2,02	19,43	0,00	0,04	0,29
Q3. 10 ans ou plus	0,45	0,35	0,02	3,19	3,01	0,02	0,11	0,07	0,00
Q4. Moins de 10%	-0,56	0,03	0,07	7,87	0,04	0,22	0,40	0,00	0,01
Q4. 10 à 25%	0,74	-0,76	-0,11	4,92	8,22	0,19	0,14	0,14	0,00
Q4. 26 à 50%	0,78	0,64	0,15	3,82	4,18	0,28	0,10	0,07	0,00
Q4. Plus de 50%	0,53	0,40	-0,37	1,31	1,17	1,19	0,03	0,02	0,02
Q5. Oui	0,95	0,56	-0,13	9,19	5,01	0,29	0,27	0,09	0,00
Q5. Non	-0,28	-0,16	0,04	2,70	1,47	0,09	0,27	0,09	0,00
Q8. Oui	0,55	0,37	1,21	2,58	1,86	23,31	0,07	0,03	0,35
Q8. Non	-0,13	-0,09	-0,29	0,62	0,45	5,60	0,07	0,03	0,35
Q9. Moins de 5 sortes	-0,67	0,01	0,47	9,71	0,00	8,83	0,42	0,00	0,21
Q9. 5 à 9 sortes	0,24	0,11	-0,79	0,89	0,30	17,31	0,03	0,01	0,32
Q9. 10 à 14 sortes	1,28	-0,97	0,07	10,35	9,42	0,06	0,27	0,15	0,00
Q9. 15 sortes ou plus	1,36	2,15	0,65	3,62	14,42	1,50	0,08	0,21	0,02
Q10. Oui	0,73	-0,15	0,07	9,99	0,63	0,18	0,38	0,02	0,00
Q10. Non	-0,52	0,10	-0,05	7,10	0,45	0,13	0,38	0,02	0,00
Q11. Oui	0,85	-0,83	0,32	8,20	12,45	2,11	0,25	0,23	0,03
Q11. Non	-0,29	0,28	-0,11	2,79	4,24	0,72	0,25	0,23	0,03
Q12. Oui	0,16	0,02	0,01	0,97	0,02	0,01	0,11	0,00	0,00
Q12. Non	-0,84	-0,38	0,09	4,12	1,32	0,08	0,11	0,02	0,00
Q12. NSP/NRP	-0,36	0,56	-0,31	0,36	1,39	0,48	0,01	0,02	0,01
Q13. Oui	0,17	0,31	0,31	0,70	3,91	4,37	0,04	0,13	0,12
Q13. Non	-0,22	-0,40	-0,40	0,91	5,05	5,66	0,04	0,13	0,12

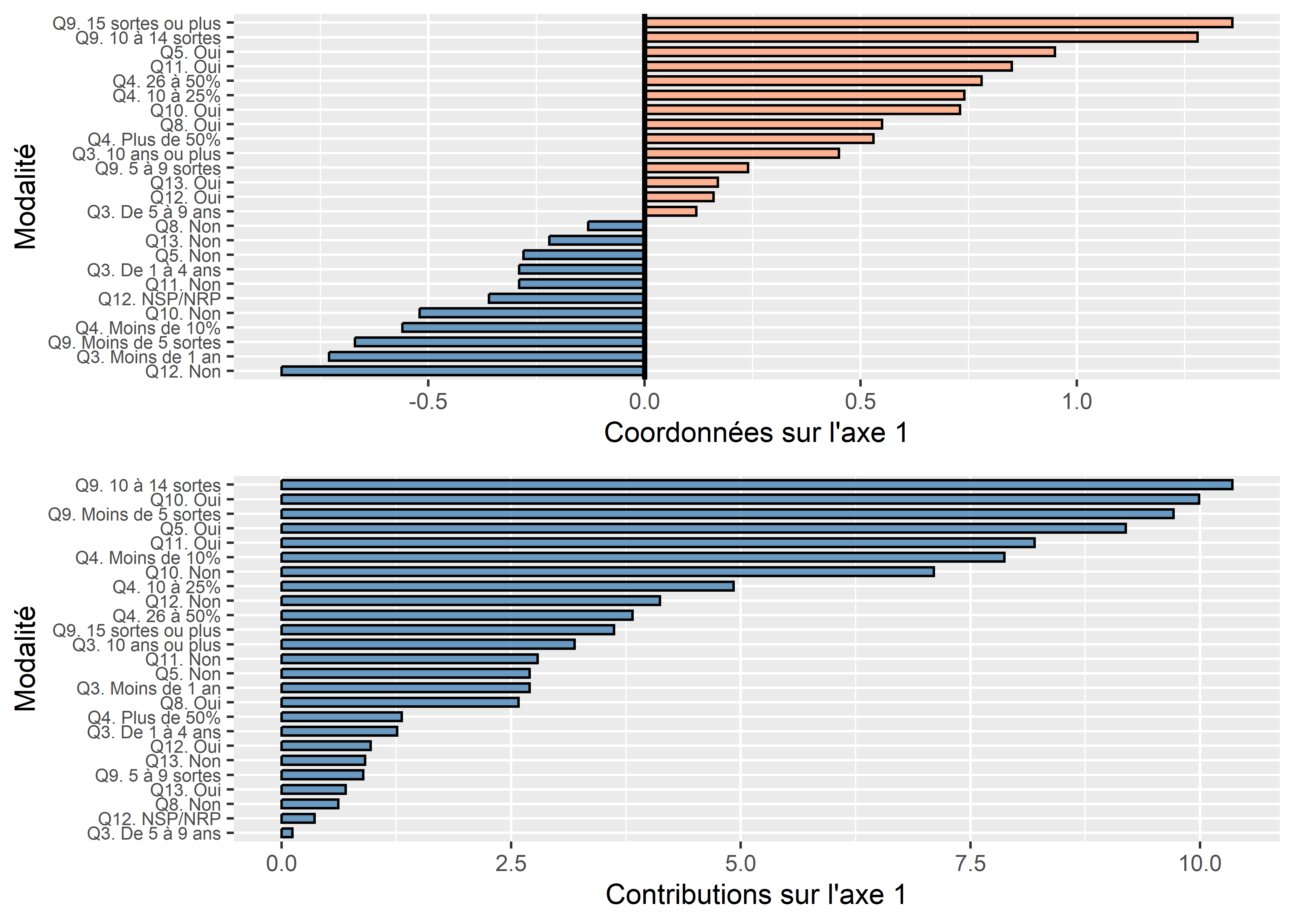
Figure 12.36: Graphiques pour les résultats des modalités de l’axe 1 de l’ACM

Interprétation des résultats de l’axe 2 pour les variables

Quatre modalités concourent le plus à la formation de l’axe 2 résumant 8,8 % de la variance : Q3. De 1 à 4 ans (15,30 %), Q9. 15 sortes ou plus (14,42 %), Q11. Oui (12,45 %) et Q9. 10 à 14 sortes (9,42 %). Les modalités suivantes sont présentes aux deux extrémités de l’axe 2 :

• Coordonnées négatives : Q9. 10 à 14 sortes (-0,97), Q11. Oui (-0,83), Q3. De 1 à 4 ans (-0,79), Q4. 10 à 25% (-0,76). Cela signifie que lorsque les coordonnées des individus sont fortement négatives sur cet axe, les personnes pratiquant l’agriculture urbaine :
  • cultivent de 10 à 14 sortes de fruits, de fines herbes ou de légumes (Q9);
  • échangent leurs semis ou leurs récoltes de fruits, de fines herbes ou de légumes avec d’autres personnes (Q11);
  • cultivent des fruits, des fines herbes ou des légumes depuis 1 à 4 ans (Q3);
  • de 10 à 25 % de la proportion des fruits, des fines herbes et des légumes consommés durant l’été provient de leur propre production (Q4).
• Coordonnées positives : seule la modalité Q9. 15 sortes ou plus (2,15) présente une forte coordonnée positive.

En résumé, l’axe 2 permet surtout d’identifier des personnes pratiquant l’agriculture urbaine depuis quelques années (de 1 à 4 ans), mais cultivant déjà de nombreuses sortes de fruits et légumes et partageant aussi leurs semis ou récoltes.

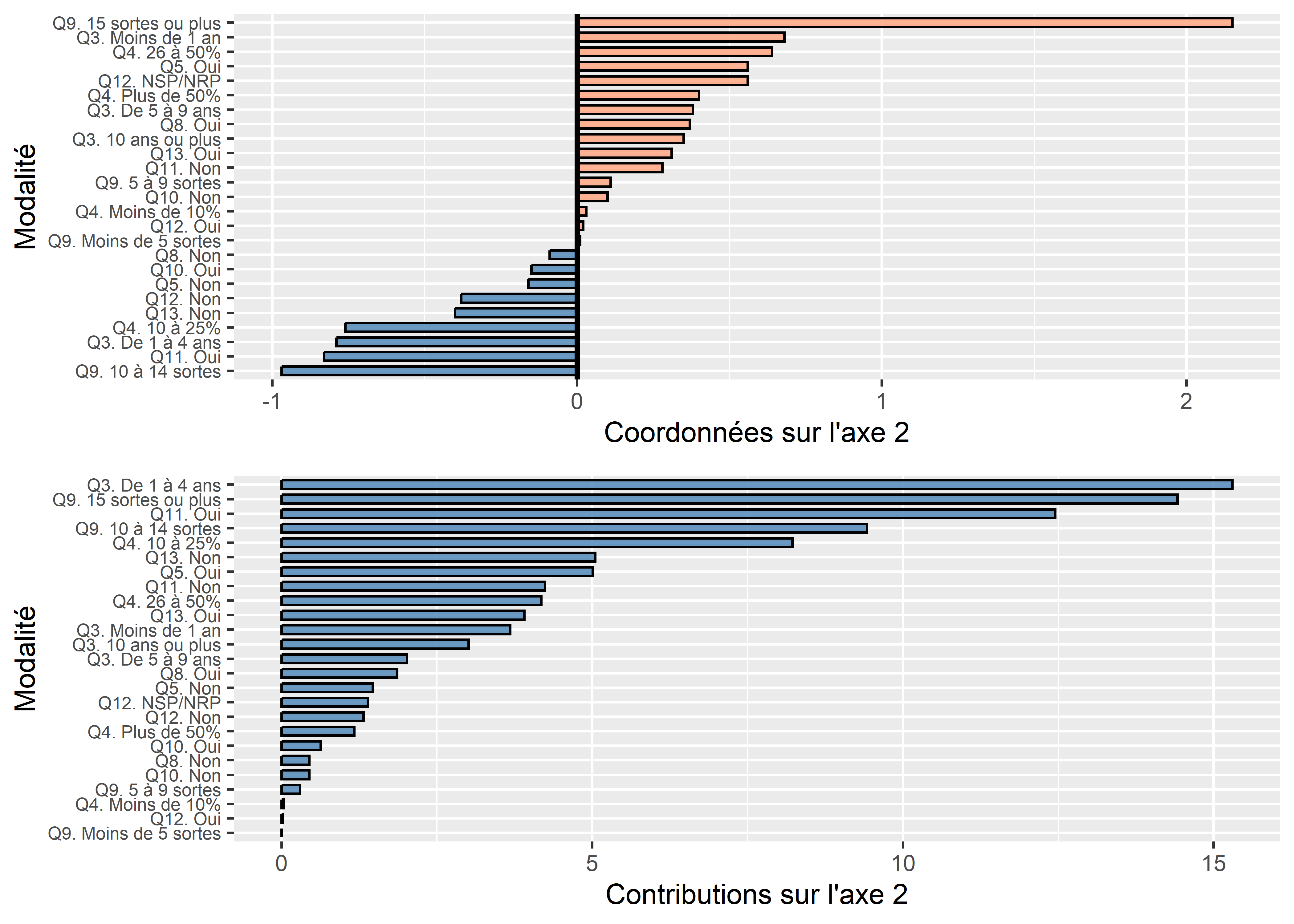
Figure 12.37: Graphiques pour les résultats des modalités de l’axe 2 de l’ACM

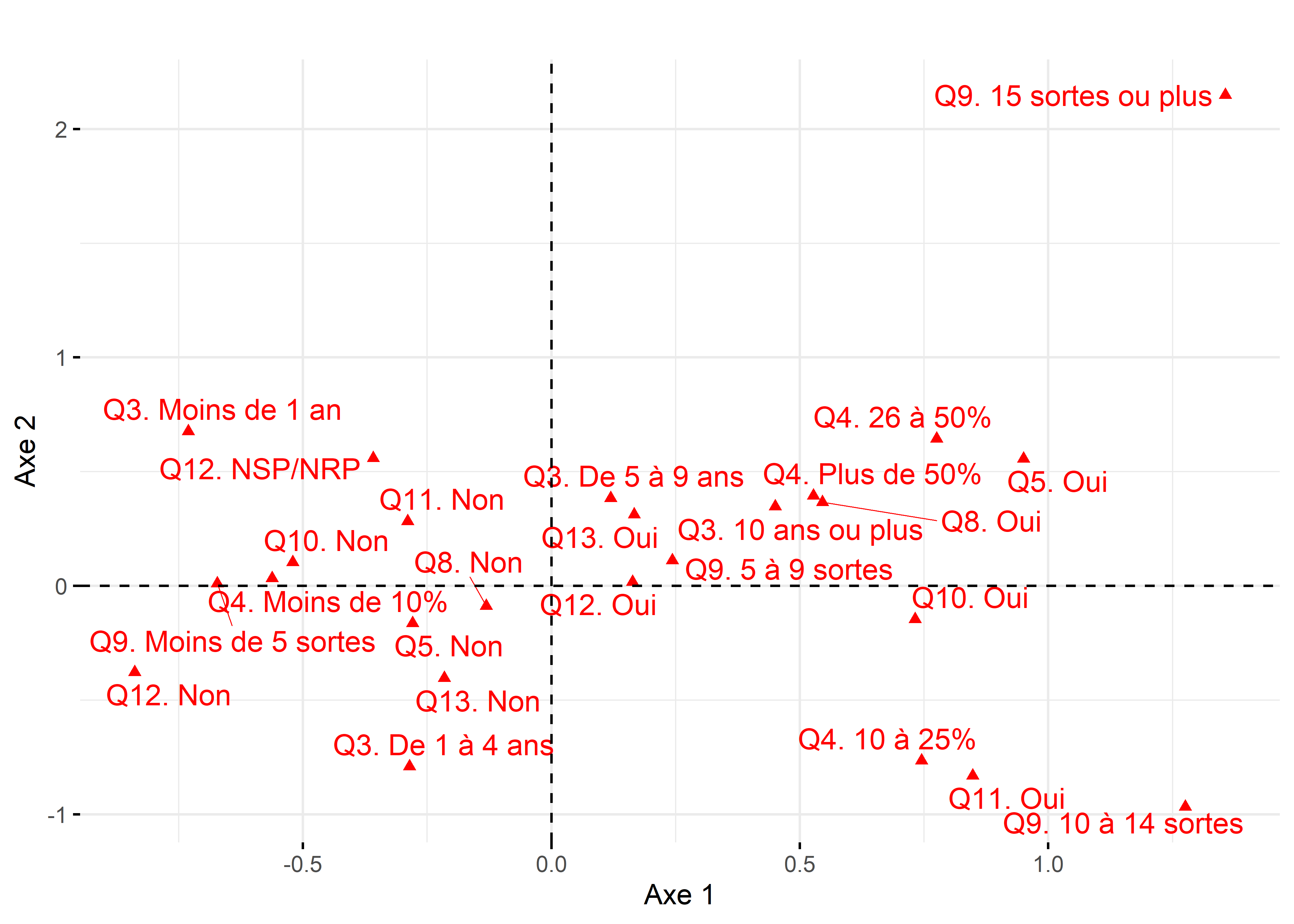
Figure 12.38: Premier plan factoriel de l’ACM pour les modalités

Interprétation des résultats de l’axe 3 pour les variables

Trois modalités concourent le plus à la formation de l’axe 3 résumant 7,6 % de la variance : Q8. Oui (23,31), Q3. De 5 à 9 ans (19,43) et Q9. 5 à 9 sortes (17,31). Les modalités suivantes sont présentes aux deux extrémités de l’axe 3 :

• Coordonnées négatives : Q3. De 5 à 9 ans (-1,11), Q9. 5 à 9 sortes (-0,79).
• Coordonnées positives : seule la modalité Q8. Oui présente une coordonnée fortement positive (1,21).

Par conséquent, cet axe semble plus complexe à analyser et surtout moins intéressant que les deux premiers.

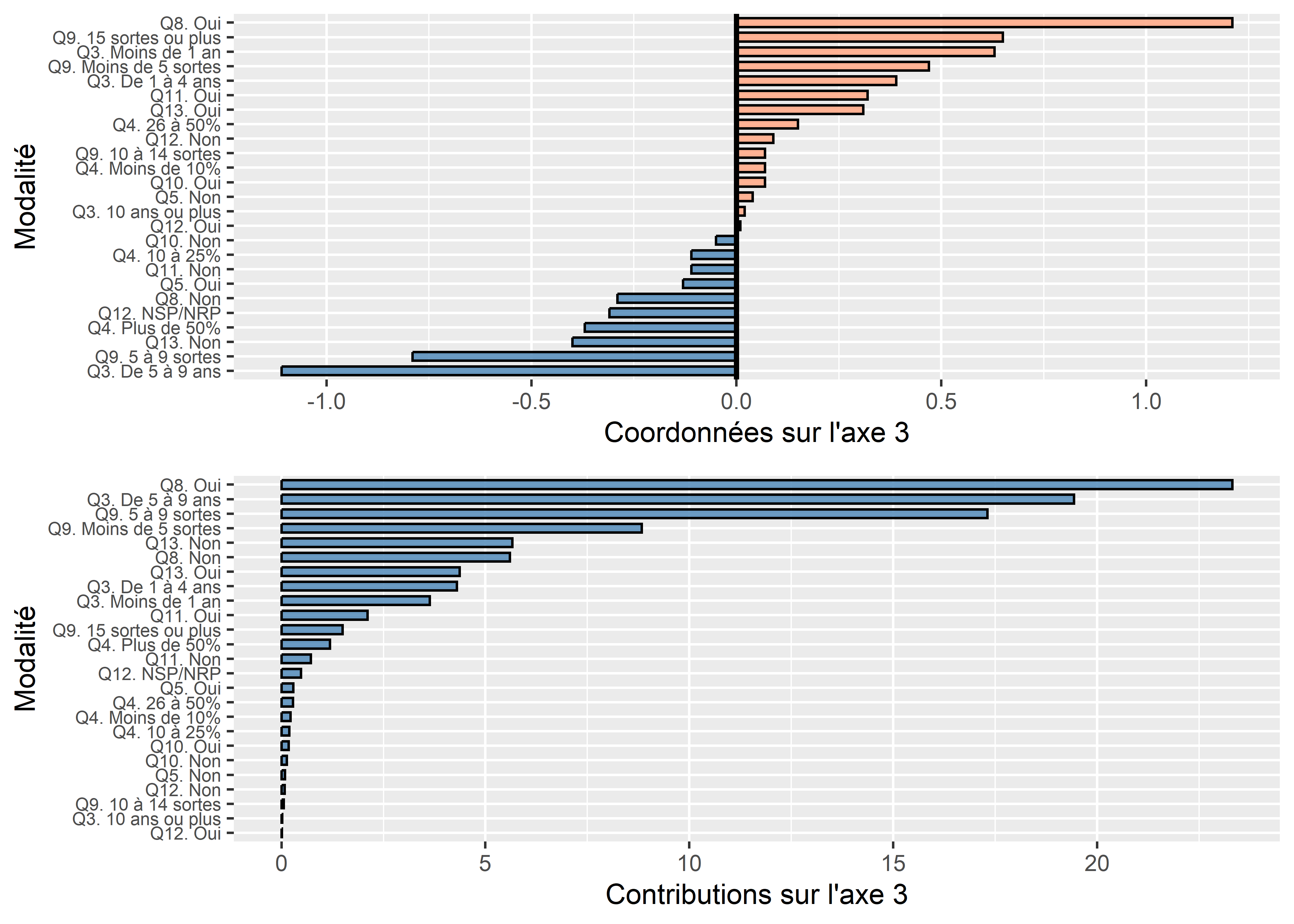
Figure 12.39: Graphiques pour les résultats des modalités de l’axe 3 de l’ACM

Analyse des variables supplémentaires dans l’ACM

Il est ensuite possible de projeter les modalités supplémentaires sur les axes de l’ACM retenus (tableau 12.24 et figure 12.40). Les faibles valeurs des coordonnées factorielles des modalités supplémentaires sur les deux axes semblent indiquer que le profil socioéconomique des personnes pratiquant l’agriculture urbaine ne semble pas (ou peu) relié aux profils identifiés par les axes factoriels.

Tableau 12.24: Résultats de l’ACM pour les modalités des variables supplémentaires

	Coordonnées		Cosinus carrés
Modalité	1	2	1	2
Q15. 18 à 34 ans	-0,09	-0,27	0,00	0,04
Q15. 35 à 49 ans	-0,06	-0,01	0,00	0,00
Q15. 50 à 64 ans	0,14	0,25	0,01	0,02
Q15. 65 ans et plus	0,11	0,25	0,00	0,01
Q16. Travail temps plein	-0,10	-0,06	0,01	0,01
Q16. Travail. temps partiel	0,36	-0,15	0,01	0,00
Q16. Étudiant	-0,14	-0,11	0,00	0,00
Q16. Retraité	0,17	0,25	0,01	0,02
Q16. Sans emploi	0,44	-0,14	0,01	0,00
Q16. À la maison	-0,06	0,18	0,00	0,00
Q17. Aucun certificat ou dipl.	0,28	0,16	0,00	0,00
Q17. Dipl. secondaires	-0,09	0,01	0,00	0,00
Q17. Dipl. collégiales	0,01	0,19	0,00	0,01
Q17. Études universitaires	0,00	-0,10	0,00	0,01
Q21. Propriétaire	0,03	0,02	0,00	0,00
Q22. Locataire	-0,06	-0,03	0,00	0,00

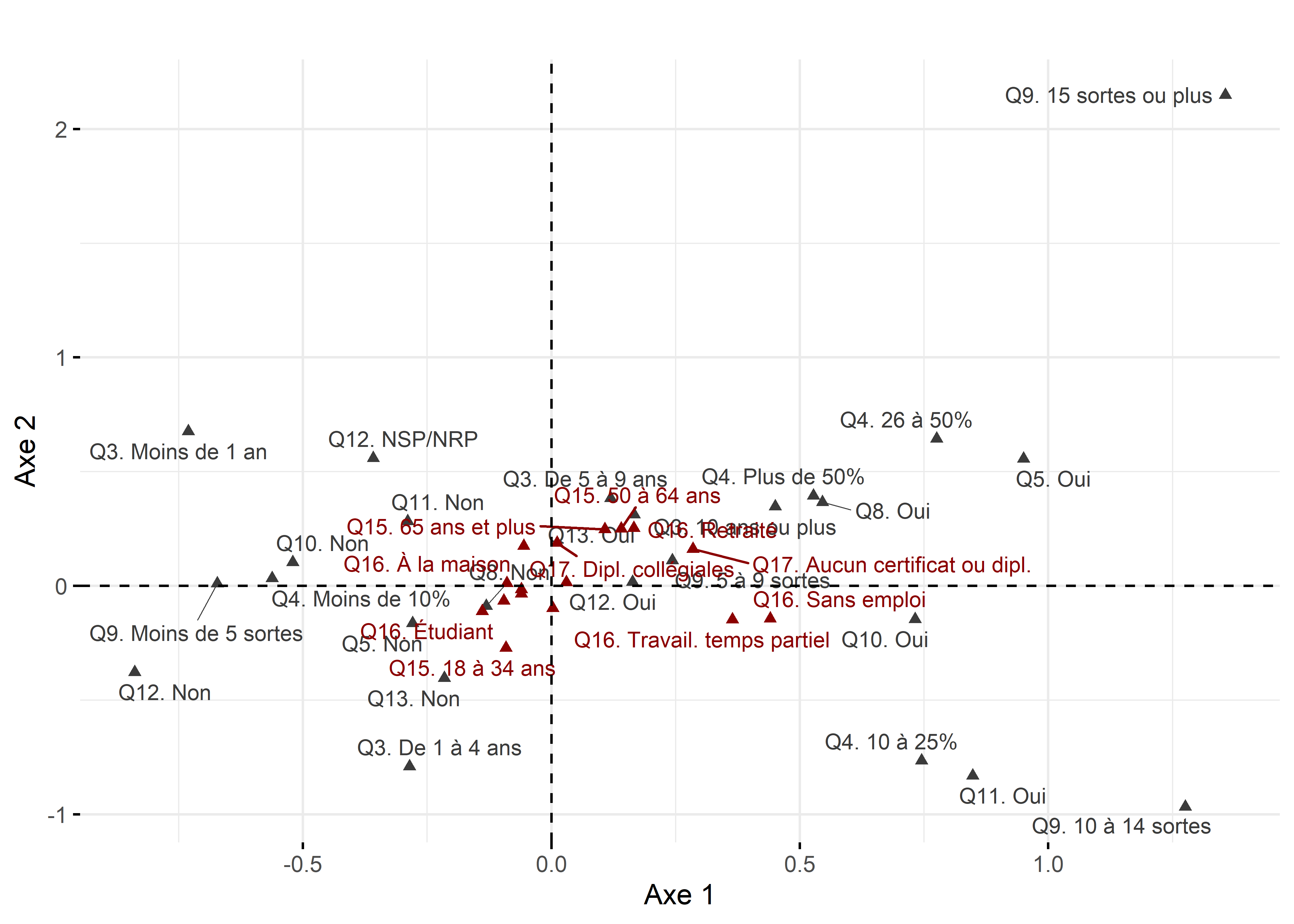
Figure 12.40: Premier plan factoriel de l’ACM avec toutes les modalités incluant celles supplémentaires

Visualisation de variables qualitatives ordinales sur un plan factoriel

Lorsque les variables qualitatives sont ordinales et non nominales, il peut être intéressant de relier les différentes modalités avec une ligne. Cela permet de comprendre en un coup d’œil la trajectoire que suivent les modalités sur les deux axes factoriels. En guise d’exemple, nous réalisons cet exercice pour les variables Q3 et Q9 (figure 12.41).

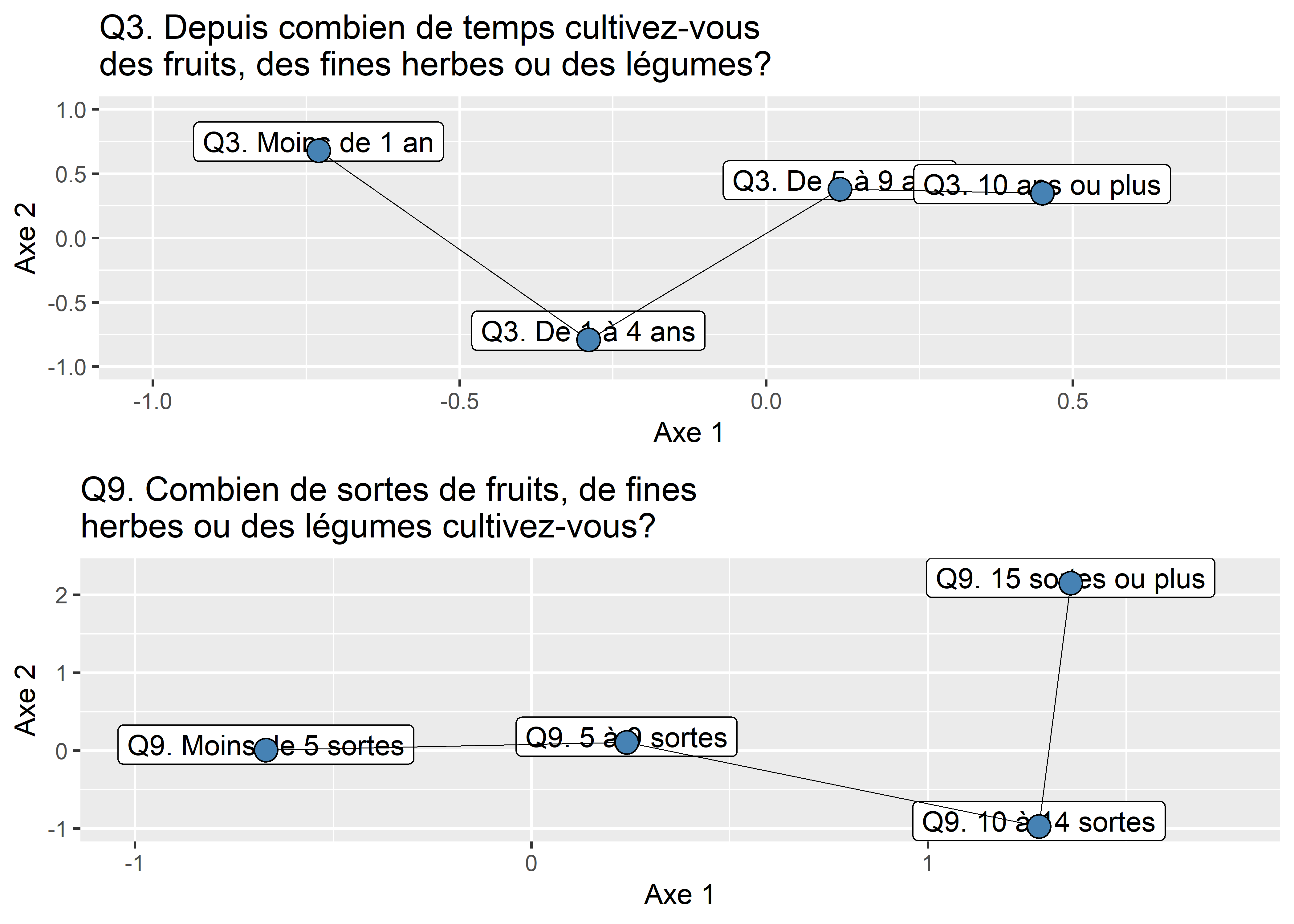
Figure 12.41: Trajectoires des variables ordinales sur le premier plan factoriel de l’ACM

12.4.1.3 Résultats de l’ACM pour les individus

Comme toute méthode factorielle, les coordonnées factorielles, les cosinus carrés et les contributions sont aussi disponibles pour les individus en ACM. Nous proposons ici simplement de réaliser le premier plan factoriel pour les individus en attribuant un dégradé de couleurs avec les cosinus carrés (figure 12.42). Il est aussi possible d’attribuer des couleurs aux différentes modalités d’une variable. Par exemple, sur le premier plan factoriel, nous avons utilisé la variable Q12. Selon vous, l’agriculture urbaine contribue-t-elle à améliorer les rapports entre les gens?. Cela permet de repérer visuellement que les personnes ayant répondu négativement à cette question ont surtout des coordonnées négatives sur l’axe 1.

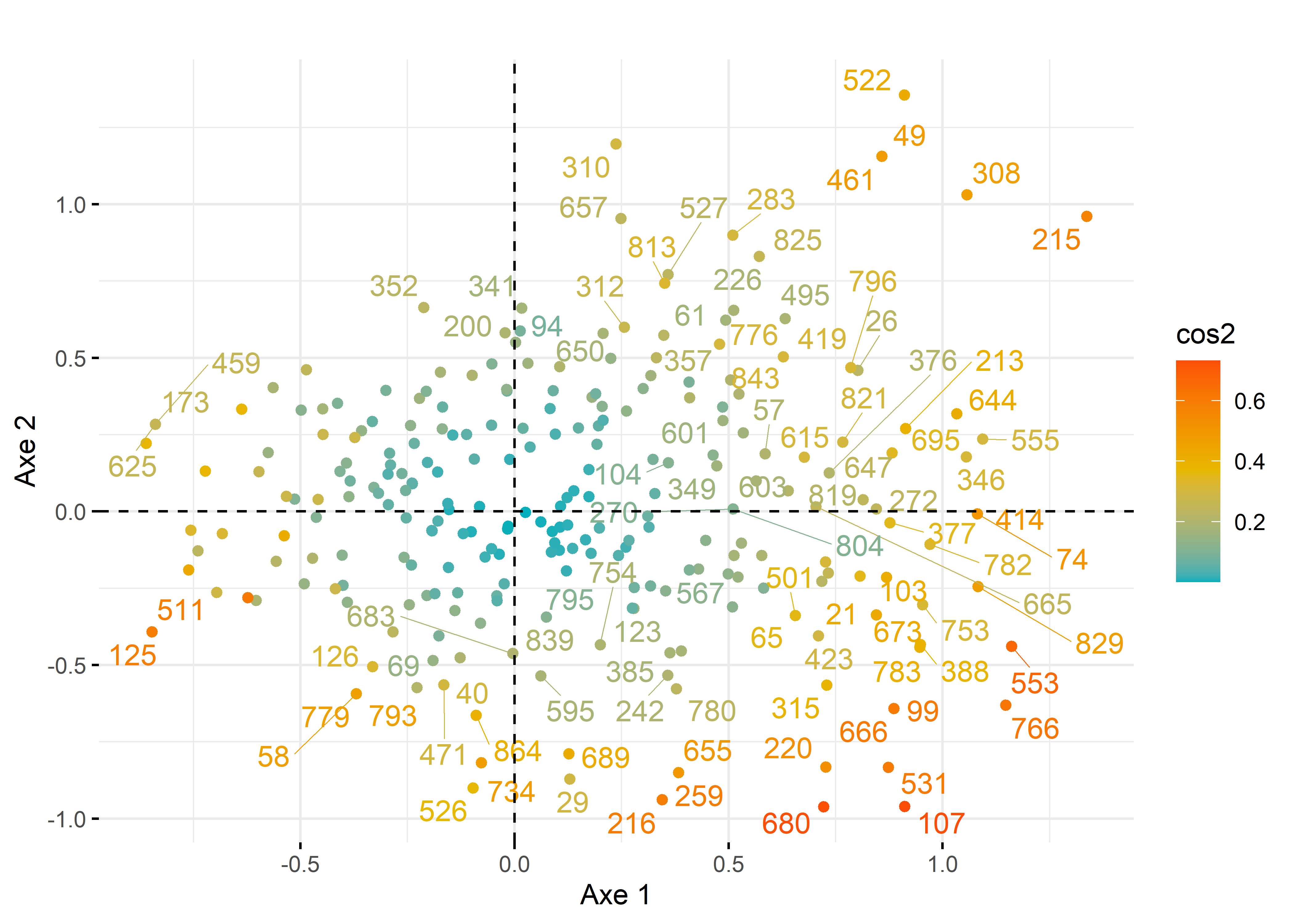
Figure 12.42: Premier plan factoriel de l’ACM pour les individus

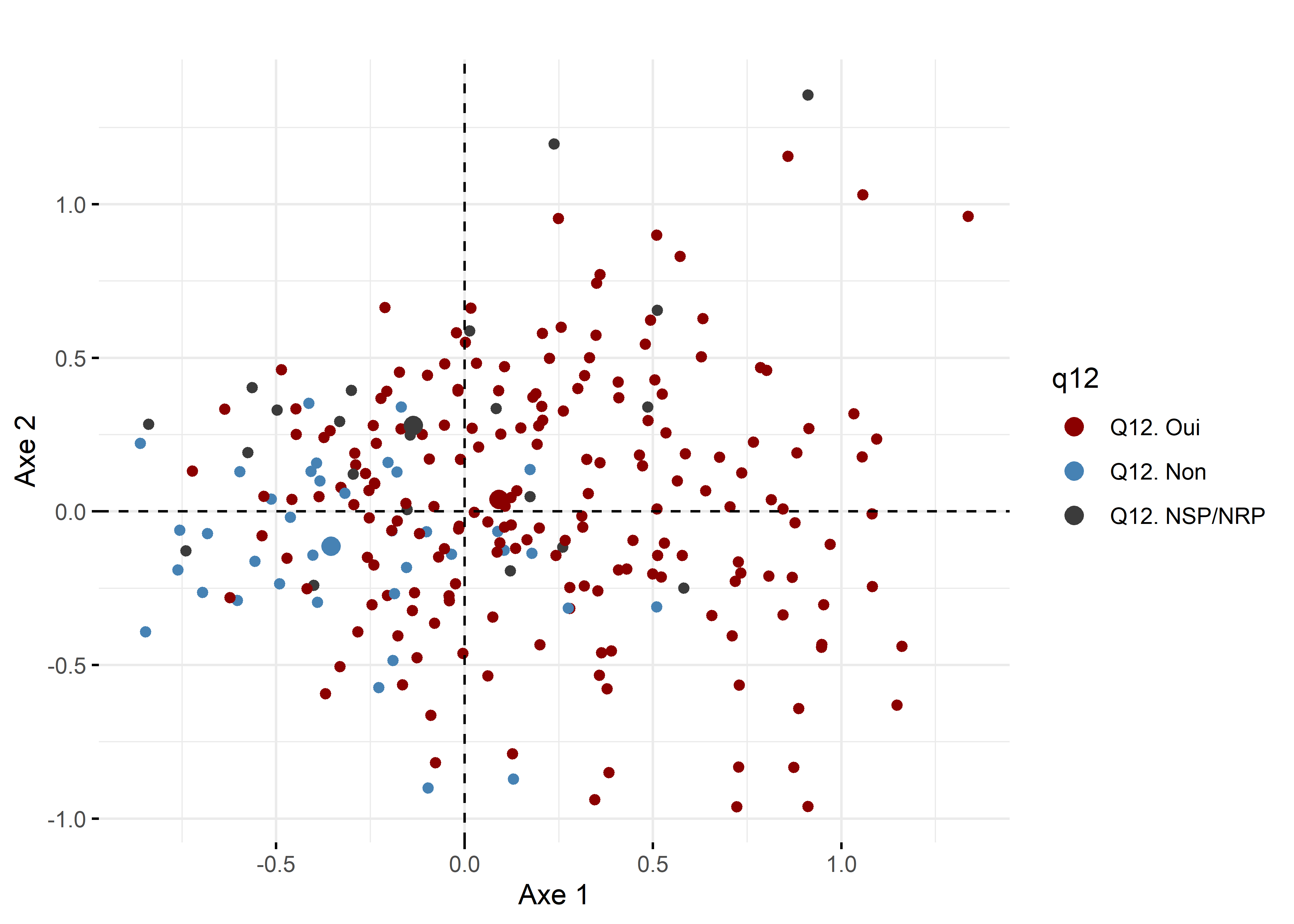
Figure 12.43: Premier plan factoriel de l’ACM pour les individus avec coloration d’une variable

12.4.2 Mise en œuvre dans R

12.4.2.1 Calcul d’une ACM avec FactoMineR

Plusieurs packages permettent de calculer une ACM dans R, notamment ExPosition (fonction epMCA), ade4 (fonction dudi.mca) et FactoMineR (fonction MCA). De nouveau, nous utilisons FactoMineR couplé au package factoextra pour réaliser rapidement des graphiques.

Pour calculer l’ACM, il suffit d’utiliser la fonction MCA de FactoMineR, puis la fonction summary(res.acm) qui renvoie les résultats de l’ACM pour :

• Les valeurs propres (section Eigenvalues) pour les axes factoriels (Dim.1 à Dim.n) avec leur variance expliquée brute (Variance), en pourcentage (% of var.) et en pourcentage cumulé (Cumulative % of var.).
• Les dix premières observations (section Individuals) avec les coordonnées factorielles (Dim.1 à Dim.n), les contributions (ctr) et les cosinus carrés (cos2). Pour accéder aux résultats pour toutes les observations, utilisez les fonctions res.acm$ind ou encore res.acm$ind$coord (uniquement les coordonnées factorielles), res.acm$ind$contrib (uniquement les contributions) et res.acm$ind$cos2 (uniquement les cosinus carrés).
• Les dix premières modalités des variables (section Categories) avec les coordonnées factorielles (Dim.1 à Dim.n), les contributions (ctr) et les cosinus carrés (cos2).

La syntaxe ci-dessous permet, dans un premier temps, de calculer l’ACM, puis de créer un DataFrame pour les résultats des valeurs propres.

library(FactoMineR)
# Calcul de l'AFC
res.acm <-  MCA(dfACM,            # Nom du DataFrame
                ncp = 3,          # Nombre d'axes retenus
                quali.sup=10:13,  # Variables supplémentaires
                graph = FALSE, 
                row.w = dfenquete$pond) # Variables pour la pondération des lignes
# Affichage des résultats
print(res.acm)

## **Results of the Multiple Correspondence Analysis (MCA)**
## The analysis was performed on 352 individuals, described by 13 variables
## *The results are available in the following objects:
## 
##    name                description                                          
## 1  "$eig"              "eigenvalues"                                        
## 2  "$var"              "results for the variables"                          
## 3  "$var$coord"        "coord. of the categories"                           
## 4  "$var$cos2"         "cos2 for the categories"                            
## 5  "$var$contrib"      "contributions of the categories"                    
## 6  "$var$v.test"       "v-test for the categories"                          
## 7  "$ind"              "results for the individuals"                        
## 8  "$ind$coord"        "coord. for the individuals"                         
## 9  "$ind$cos2"         "cos2 for the individuals"                           
## 10 "$ind$contrib"      "contributions of the individuals"                   
## 11 "$quali.sup"        "results for the supplementary categorical variables"
## 12 "$quali.sup$coord"  "coord. for the supplementary categories"            
## 13 "$quali.sup$cos2"   "cos2 for the supplementary categories"              
## 14 "$quali.sup$v.test" "v-test for the supplementary categories"            
## 15 "$call"             "intermediate results"                               
## 16 "$call$marge.col"   "weights of columns"                                 
## 17 "$call$marge.li"    "weights of rows"

summary(res.acm)

## 
## Call:
## MCA(X = dfACM, ncp = 3, quali.sup = 10:13, graph = FALSE, row.w = dfenquete$pond) 
## 
## 
## Eigenvalues
##                        Dim.1   Dim.2   Dim.3   Dim.4   Dim.5   Dim.6   Dim.7   Dim.8   Dim.9  Dim.10  Dim.11  Dim.12  Dim.13
## Variance               0.248   0.156   0.135   0.127   0.126   0.123   0.114   0.107   0.101   0.095   0.093   0.086   0.077
## % of var.             13.940   8.792   7.620   7.161   7.065   6.916   6.385   6.003   5.671   5.327   5.234   4.822   4.340
## Cumulative % of var.  13.940  22.732  30.352  37.513  44.579  51.494  57.879  63.882  69.553  74.880  80.115  84.937  89.277
##                       Dim.14  Dim.15  Dim.16
## Variance               0.071   0.064   0.055
## % of var.              4.011   3.619   3.094
## Cumulative % of var.  93.288  96.906 100.000
## 
## Individuals (the 10 first)
##                                Dim.1    ctr   cos2    Dim.2    ctr   cos2    Dim.3    ctr   cos2  
## 4                           |  0.261  0.063  0.052 |  0.327  0.155  0.081 |  0.251  0.105  0.048 |
## 10                          | -0.533  0.688  0.278 |  0.050  0.010  0.002 | -0.413  0.757  0.167 |
## 11                          |  0.135  0.020  0.014 | -0.120  0.025  0.011 | -0.354  0.252  0.097 |
## 15                          |  0.020  0.000  0.000 |  0.271  0.073  0.061 | -0.503  0.291  0.209 |
## 17                          | -0.133  0.014  0.012 | -0.264  0.088  0.049 |  0.835  1.019  0.486 |
## 18                          |  0.196  0.024  0.018 |  0.279  0.078  0.037 |  0.104  0.012  0.005 |
## 19                          | -0.193  0.041  0.014 | -0.063  0.007  0.002 |  0.159  0.051  0.010 |
## 21                          |  0.845  0.731  0.369 | -0.337  0.184  0.059 | -0.390  0.285  0.079 |
## 23                          | -0.253  0.155  0.058 | -0.020  0.002  0.000 | -0.375  0.624  0.128 |
## 26                          |  0.802  0.552  0.170 |  0.460  0.288  0.056 |  0.098  0.015  0.003 |
## 
## Categories (the 10 first)
##                                 Dim.1     ctr    cos2  v.test     Dim.2     ctr    cos2  v.test     Dim.3     ctr    cos2  v.test
## Q3. Moins de 1 an           |  -0.731   2.704   0.068  -4.940 |   0.677   3.681   0.058   4.578 |   0.627   3.636   0.050   4.236
## Q3. De 1 à 4 ans            |  -0.286   1.259   0.043  -3.921 |  -0.791  15.299   0.328 -10.855 |   0.390   4.304   0.080   5.360
## Q3. De 5 à 9 ans            |   0.119   0.122   0.003   1.102 |   0.385   2.023   0.035   3.556 |  -1.110  19.427   0.293 -10.261
## Q3. 10 ans ou plus          |   0.450   3.189   0.110   6.271 |   0.347   3.006   0.065   4.835 |   0.023   0.016   0.000   0.327
## Q4. Moins de 10%            |  -0.562   7.874   0.395 -11.913 |   0.033   0.044   0.001   0.704 |   0.070   0.221   0.006   1.477
## Q4. 10 à 25%                |   0.745   4.918   0.137   7.006 |  -0.765   8.220   0.144  -7.194 |  -0.109   0.191   0.003  -1.021
## Q4. 26 à 50%                |   0.775   3.815   0.099   5.966 |   0.644   4.176   0.068   4.957 |   0.154   0.276   0.004   1.187
## Q4. Plus de 50%             |   0.527   1.310   0.033   3.424 |   0.395   1.167   0.018   2.566 |  -0.372   1.195   0.016  -2.417
## Q5. Oui                     |   0.950   9.194   0.265   9.760 |   0.557   5.008   0.091   5.720 |  -0.126   0.294   0.005  -1.290
## Q5. Non                     |  -0.279   2.701   0.265  -9.760 |  -0.164   1.471   0.091  -5.720 |   0.037   0.086   0.005   1.290
##                              
## Q3. Moins de 1 an           |
## Q3. De 1 à 4 ans            |
## Q3. De 5 à 9 ans            |
## Q3. 10 ans ou plus          |
## Q4. Moins de 10%            |
## Q4. 10 à 25%                |
## Q4. 26 à 50%                |
## Q4. Plus de 50%             |
## Q5. Oui                     |
## Q5. Non                     |
## 
## Categorical variables (eta2)
##                               Dim.1 Dim.2 Dim.3  
## q3                          | 0.162 0.338 0.334 |
## q4                          | 0.400 0.191 0.023 |
## q5                          | 0.265 0.091 0.005 |
## q8                          | 0.071 0.032 0.352 |
## q9                          | 0.548 0.340 0.338 |
## q10                         | 0.381 0.015 0.004 |
## q11                         | 0.245 0.235 0.034 |
## q12                         | 0.121 0.038 0.007 |
## q13                         | 0.036 0.126 0.122 |
## 
## Supplementary categories (the 10 first)
##                                Dim.1   cos2 v.test    Dim.2   cos2 v.test    Dim.3   cos2 v.test  
## Q15. 18 à 34 ans            | -0.091  0.004 -1.221 | -0.271  0.037 -3.630 |  0.092  0.004  1.232 |
## Q15. 35 à 49 ans            | -0.060  0.001 -0.731 | -0.014  0.000 -0.175 | -0.112  0.005 -1.360 |
## Q15. 50 à 64 ans            |  0.140  0.006  1.419 |  0.251  0.018  2.543 | -0.002  0.000 -0.020 |
## Q15. 65 ans et plus         |  0.107  0.002  0.874 |  0.248  0.011  2.020 |  0.015  0.000  0.122 |
## Q16. Travail temps plein    | -0.096  0.012 -2.084 | -0.065  0.005 -1.404 | -0.025  0.001 -0.540 |
## Q16. Travail. temps partiel |  0.364  0.010  1.875 | -0.147  0.002 -0.757 |  0.291  0.006  1.497 |
## Q16. Étudiant               | -0.139  0.002 -0.774 | -0.111  0.001 -0.617 | -0.088  0.001 -0.488 |
## Q16. Retraité               |  0.166  0.006  1.521 |  0.254  0.015  2.331 |  0.031  0.000  0.284 |
## Q16. Sans emploi            |  0.440  0.006  1.433 | -0.142  0.001 -0.464 | -0.495  0.007 -1.611 |
## Q16. À la maison            | -0.056  0.000 -0.279 |  0.175  0.002  0.878 |  0.144  0.001  0.720 |
## 
## Supplementary categorical variables (eta2)
##                               Dim.1 Dim.2 Dim.3  
## q15                         | 0.010 0.048 0.007 |
## q16                         | 0.027 0.020 0.015 |
## q17                         | 0.006 0.014 0.014 |
## q21                         | 0.002 0.001 0.007 |

# Construction d'un DataFrame pour les valeurs propres
dfACMvp <- data.frame(res.acm$eig)
names(dfACMvp) <- c("VP","VP_pct","VP_pctCumul")
dfACMvp$Axe <- factor(1:nrow(dfACMvp), levels=rev(1:nrow(dfACMvp)))
dfACMvp <- dfACMvp[,c(4,1:3)]

12.4.2.2 Exploration graphique des résultats de l’ACM pour les valeurs propres

Pour créer un histogramme des valeurs propres de l’ACM, vous pouvez utiliser la fonction fviz_screeplot de factoextra.

library(factoextra)
library(ggplot2)

fviz_screeplot(res.acm, addlabels = TRUE,
               x="Composantes", y="Valeur propre", title="")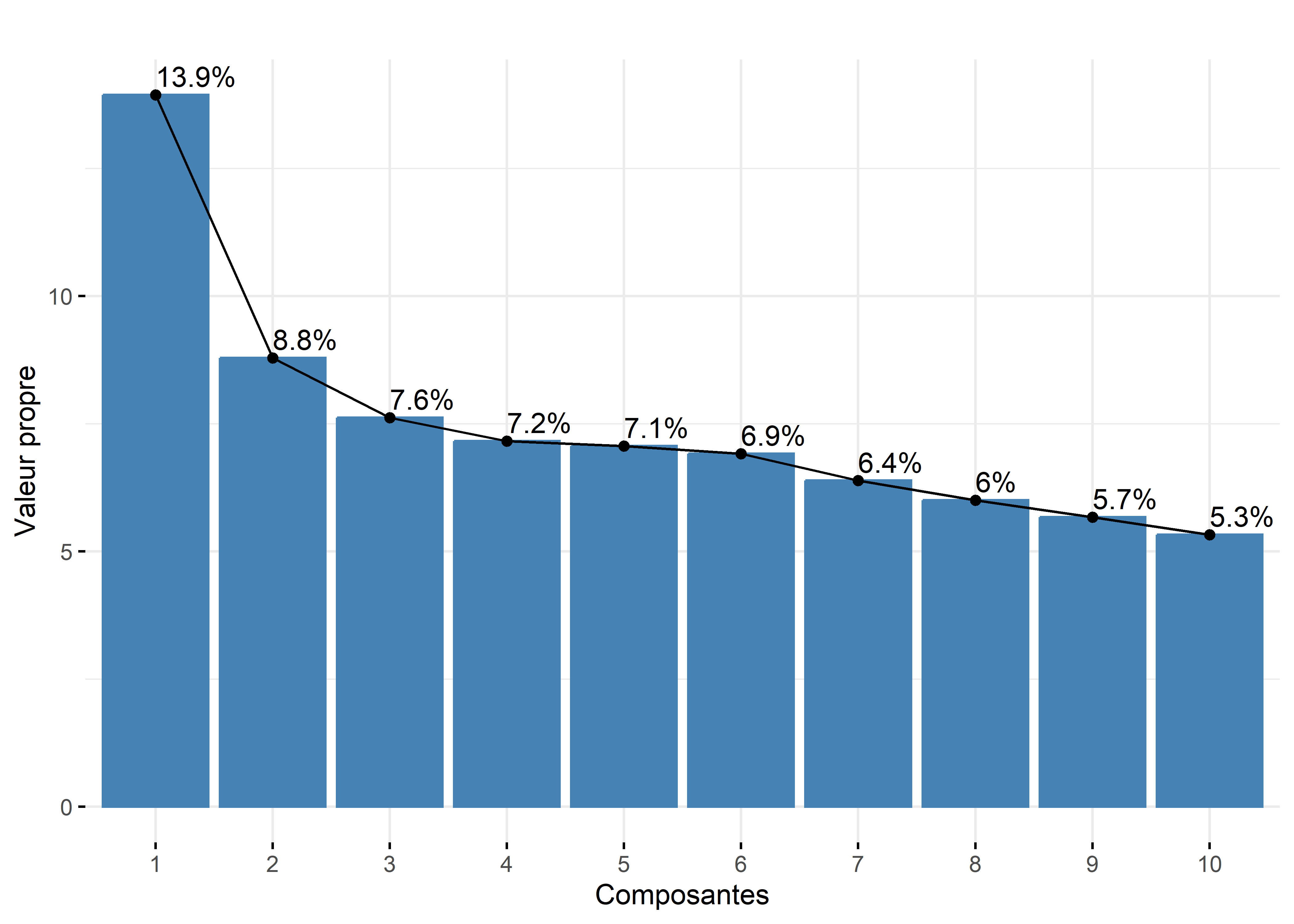

Figure 12.44: Graphique pour les valeurs propres de l’ACM avec factoextra

Avec un peu plus de lignes de code, il est relativement facile d’exploiter le DataFrame des valeurs propres créé précédemment (dfACMvp) pour construire des graphiques plus personnalisés.

library(factoextra)
library(ggplot2)

couleursAxes <- c("steelblue","skyblue2")
g1 <- ggplot(dfACMvp,aes(x=VP, y=Axe))+
  geom_bar(stat="identity", width = .6, alpha=.8, color="black", fill="skyblue2")+
  labs(x="Valeur propre", y="Axe factoriel")
g2 <- ggplot(dfACMvp, aes(x=VP_pct, y=Axe))+
  geom_bar(stat="identity", width = .6, alpha=.8, color="black", fill="skyblue2")+
  theme(legend.position="none")+
  labs(x="Variance expliquée (%)", y="Axe factoriel")
g3 <- ggplot(dfACMvp, aes(x=VP_pctCumul, y=Axe, group=1))+
  geom_bar(stat="identity", width = .6, alpha=.8, color="black", fill="skyblue2")+
  geom_line(colour="brown", linetype="solid", size=.8) +
  geom_point(size=3, shape=21, color="brown", fill="brown")+
  theme(legend.position="none")+
  labs(x="Variance expliquée (% cumulé)", y="Axe factoriel")
ggarrange(g2, g3,  nrow = 2)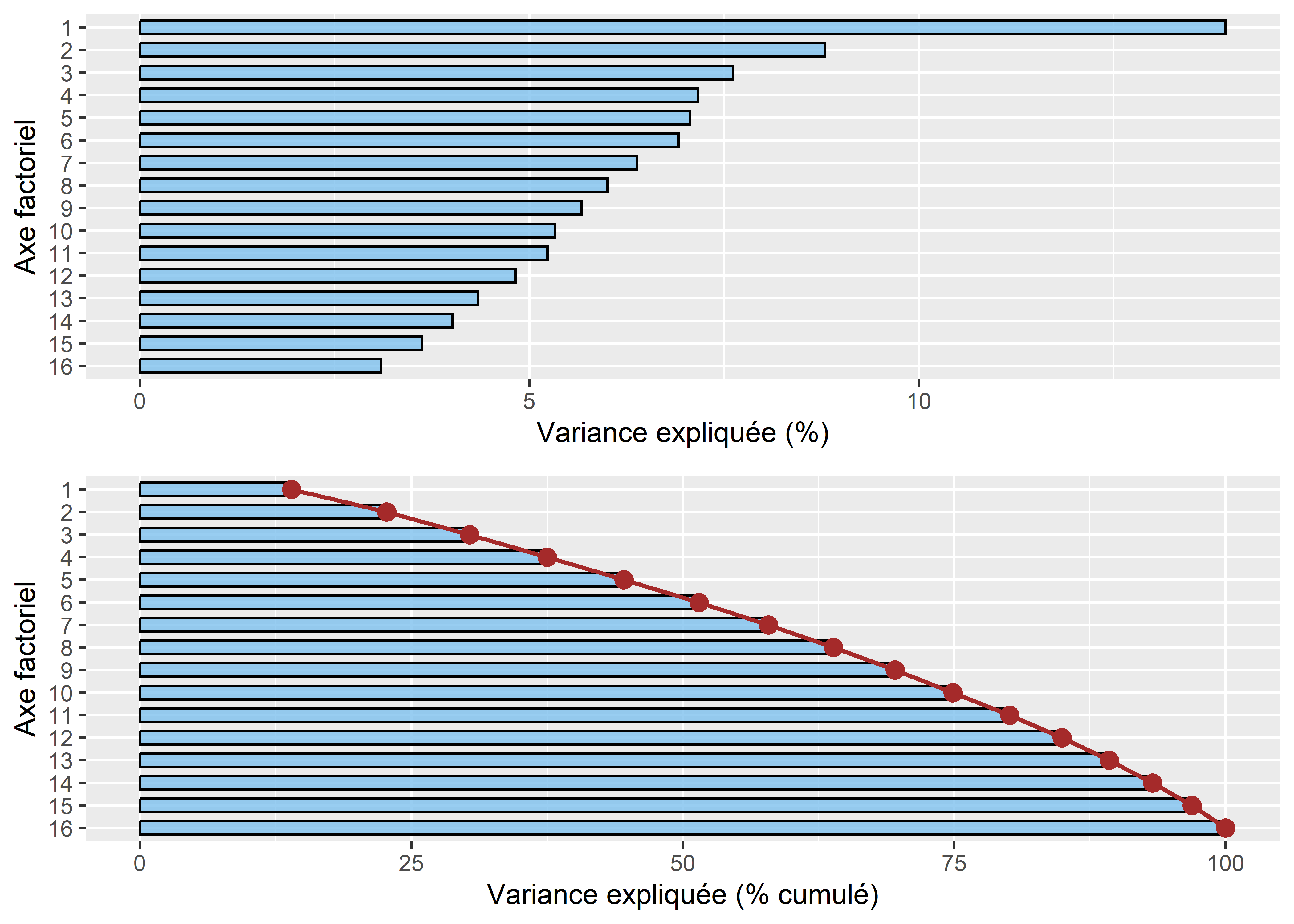

Figure 12.45: Graphiques pour les valeurs propres de l’ACM avec factoextra

La syntaxe ci-dessous permet de construire un tableau avec les coordonnées factorielles, les cosinus carrés et les contributions pour les modalités des variables qualitatives.

library(stringr)
nAxes <- 3
dfmodalites <- data.frame(Modalite =rownames(res.acm$var$coord),
                           Coord = round(res.acm$var$coord[, 1:nAxes],3),
                           Cos2 = round(res.acm$var$cos2[, 1:nAxes],3),
                           ctr = round(res.acm$var$contrib[, 1:nAxes],3))
rownames(dfmodalites) <- 1:nrow(dfmodalites)
names(dfmodalites) <- str_replace(names(dfmodalites), ".Dim.", "F")

12.4.2.3 Exploration graphique des résultats de l’ACM pour les modalités

Avant d’explorer graphiquement les résultats pour les modalités, il est judicieux de construire un DataFrame avec les coordonnées factorielles, les contributions et les cosinus carrés des modalités (voir la syntaxe ci-dessous).

library(kableExtra)
library(stringr)
nAxes <- 3
dfmodalites <- data.frame(Modalite =rownames(res.acm$var$coord),
                           Coord = round(res.acm$var$coord[, 1:nAxes],2),
                           ctr = round(res.acm$var$contrib[, 1:nAxes],2),
                           Cos2 = round(res.acm$var$cos2[, 1:nAxes],2))
rownames(dfmodalites) <- 1:nrow(dfmodalites)
names(dfmodalites) <- str_replace(names(dfmodalites), ".Dim.", "F")

Plusieurs fonctions très faciles à utiliser de factoextra permettent de construire rapidement des graphiques : fviz_mca_var pour un nuage de points d’un plan factoriel, fviz_cos2 et fviz_contrib (en utilisant le paramètre choice=var.cat) pour des histogrammes avec les cosinus carrés et les contributions des modalités. N’hésitez pas à consulter l’aide de ces fonctions ou encore cette section du site de STHDA.

Il est aussi possible de créer vos propres graphiques avec ggplot2 en utilisant le DataFrame créé précédemment avec les modalités. Par exemple, la syntaxe ci-dessous renvoie deux histogrammes pour l’axe 1 : l’un avec les coordonnées, l’autre avec les contributions. Dans la syntaxe, repérez le terme CoordF1. Dupliquez la syntaxe et changez ce terme pour CoordF2 et CoordF3 pour réaliser les graphiques des axes 2 et 3.

# Histogrammes pour les coordonnées des modalités
couleursCoords <- c("lightsalmon","steelblue")
plotCoordF1 <- ggplot(dfmodalites,
                      aes(y = reorder(Modalite, CoordF1),
                          x = CoordF1, fill=CoordF1<0))+
  geom_bar(stat="identity", width = .6, alpha=.8, color="black")+
  geom_vline(xintercept=0, color = "black", size=1)+
  scale_fill_manual(name="Coordonnée",values=couleursCoords,
                    labels = c("Positive","Négative"))+
  labs(x="Coordonnées sur l'axe 1", y="Modalité")+
  theme(legend.position="none", axis.text.y = element_text(size = 7))

plotCtrF1 <- ggplot(dfmodalites, aes(y = reorder(Modalite, ctrF1), x = ctrF1))+
  geom_bar(stat="identity", width = .6, alpha=.8, color="black", fill="steelblue")+
  labs(x="Contributions sur l'axe 1", y="Modalité")+
  theme(legend.position="none", axis.text.y = element_text(size = 7))

ggarrange(plotCoordF1, plotCtrF1, ncol = 1, nrow = 2)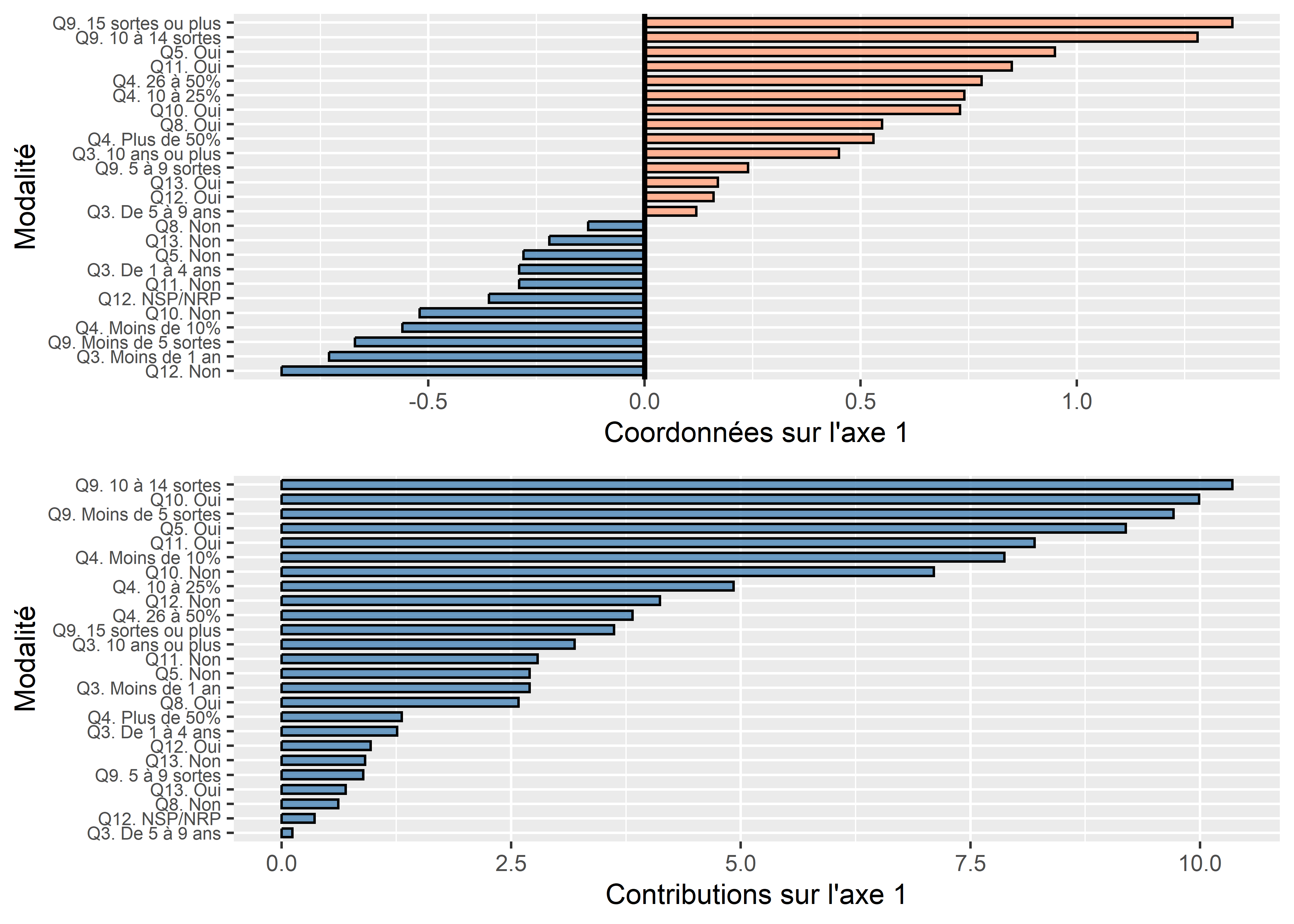

Figure 12.46: Exemple de graphiques pour les résultats des modalités

La syntaxe suivante permet de construire le premier plan factoriel pour les modalités avec la fonction fviz_mca_var de factoextra (figure 12.47).

res.acm2 <-  MCA(dfACM[1:9], ncp = 3, graph = FALSE, row.w = dfenquete$pond)
fviz_mca_var(res.acm2, repel = TRUE,
             choice="var.cat",
             axes = c(1, 2),
             # col.var = "black",
             title="", xlab="Axe 1", ylab="Axe 2",
             ggtheme = theme_minimal ())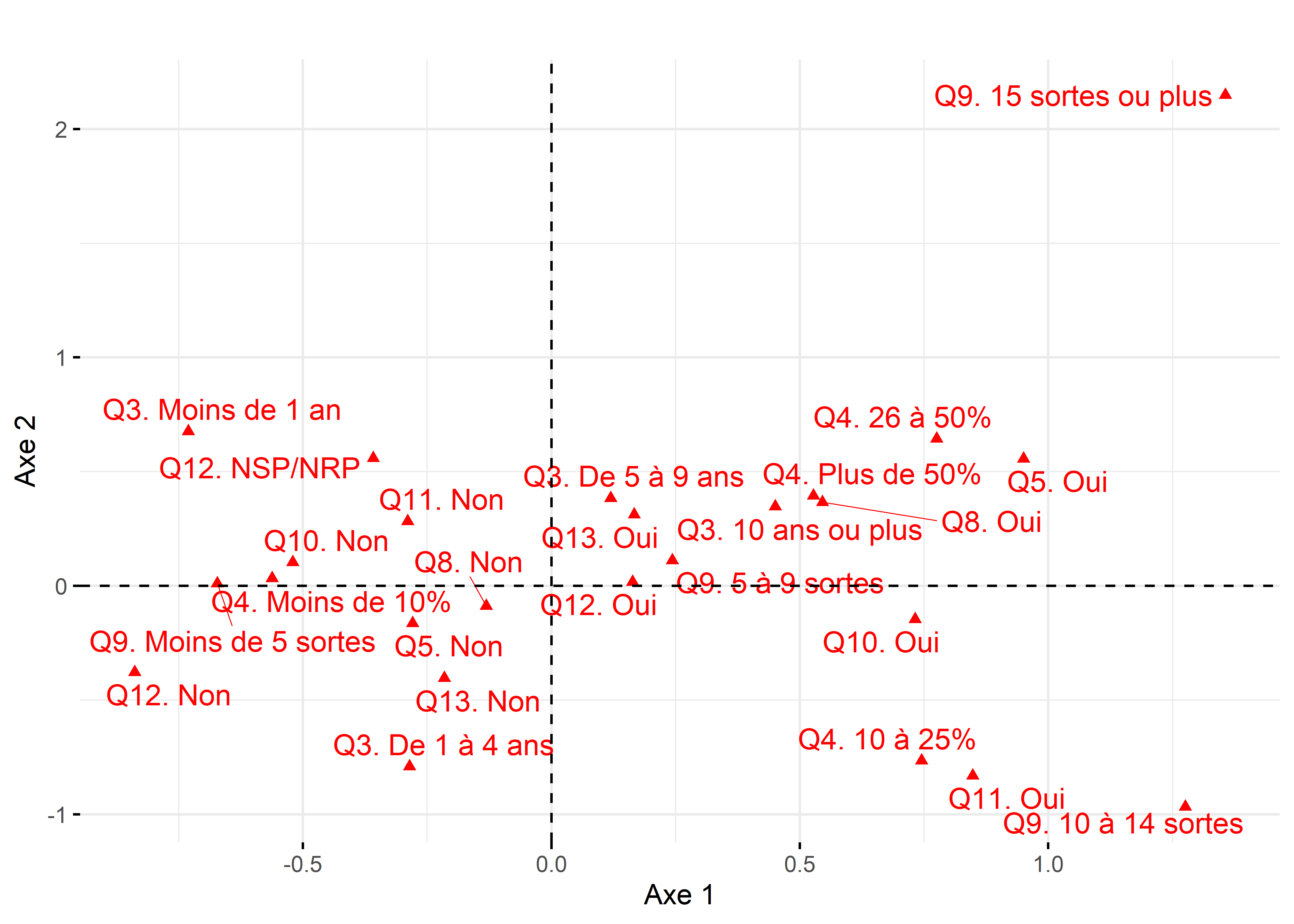

Figure 12.47: Premier plan factoriel de l’ACM pour les modalités

La syntaxe suivante permet de construire le premier plan factoriel pour les modalités supplémentaires avec la fonction fviz_mca_var de factoextra (figure 12.48).

fviz_mca_var(res.acm, repel = TRUE,
             choice="var.cat",
             axes = c(1, 2),
             col.var = "gray23",
             col.quali.sup = "darkred",
             labelsize = 3,
             title="", xlab="Axe 1", ylab="Axe 2", 
             ggtheme = theme_minimal ())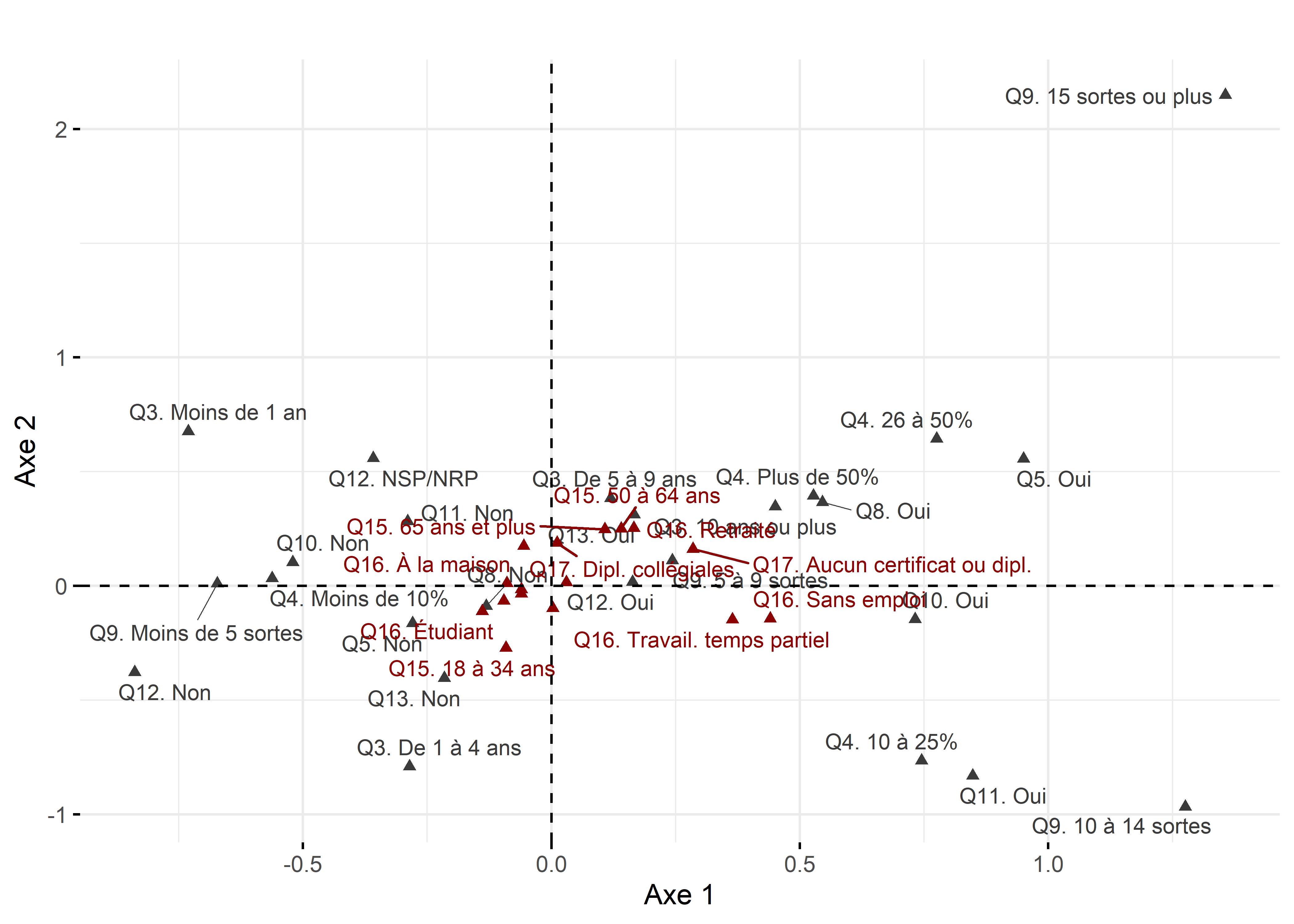

Figure 12.48: Premier plan factoriel de l’ACM pour les modalités supplémentaires

Finalement, la syntaxe ci-dessous renvoie un graphique avec la trajectoire de la variable Q3 (figure 12.49).

library(ggpubr)
Q3 <- dfmodalites[1:4, 1:3]
ggplot(Q3, aes(x=CoordF1, y=CoordF2, label=Modalite))+
  xlim(-1, .75)+ylim(-1, 1)+
  labs(title = "Q3. Depuis combien de temps cultivez-vous \n
        des fruits, des fines herbes ou des légumes?",
       x="Axe 1", y="Axe 2")+
  geom_label(nudge_x=0, nudge_y=0.07) +
  geom_line( color="black", size=.2)+
  geom_point(shape=21, color="black", fill="steelblue", size=4)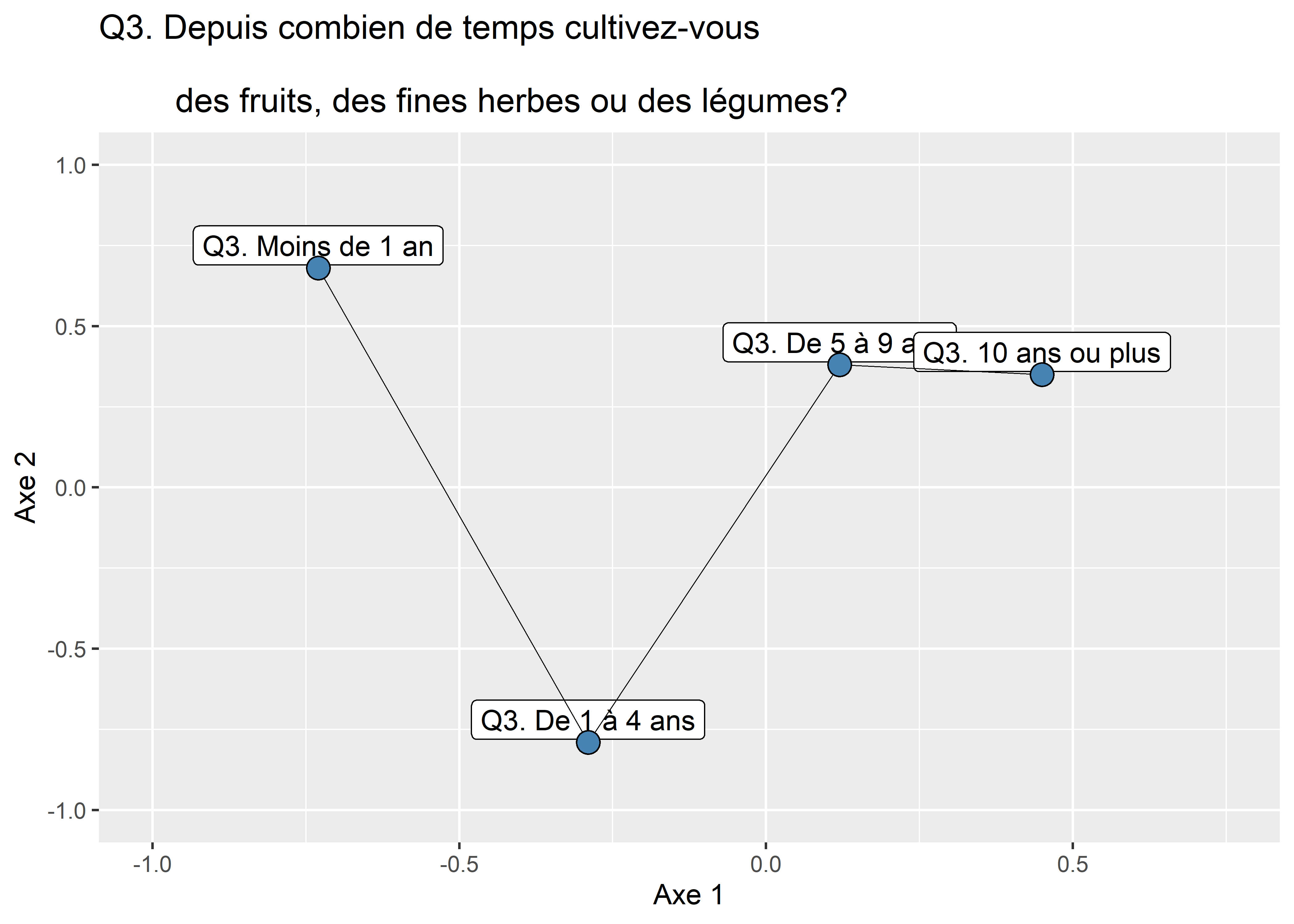

Figure 12.49: Trajectoires des variables ordinales sur le premier plan factoriel de l’ACM

12.4.2.4 Exploration graphique des résultats de l’ACM pour les individus

D’autres fonctions de factoextra produisent rapidement des graphiques pour les individus :

• fviz_cos2 et fviz_contrib (en utilisant le paramètre choice=ind) pour construire des histogrammes pour les cosinus carrés et les contributions des individus.
• fviz_mca_ind pour un nuage de points d’un plan factoriel (axes 1 et 2 habituellement).

La syntaxe ci-dessous produit le premier axe factoriel pour les individus (figure 12.50).

fviz_mca_ind(res.acm, col.ind = "cos2",
             gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
             repel = TRUE,
             xlab="Axe 1", ylab="Axe 2", title="",
             ggtheme = theme_minimal())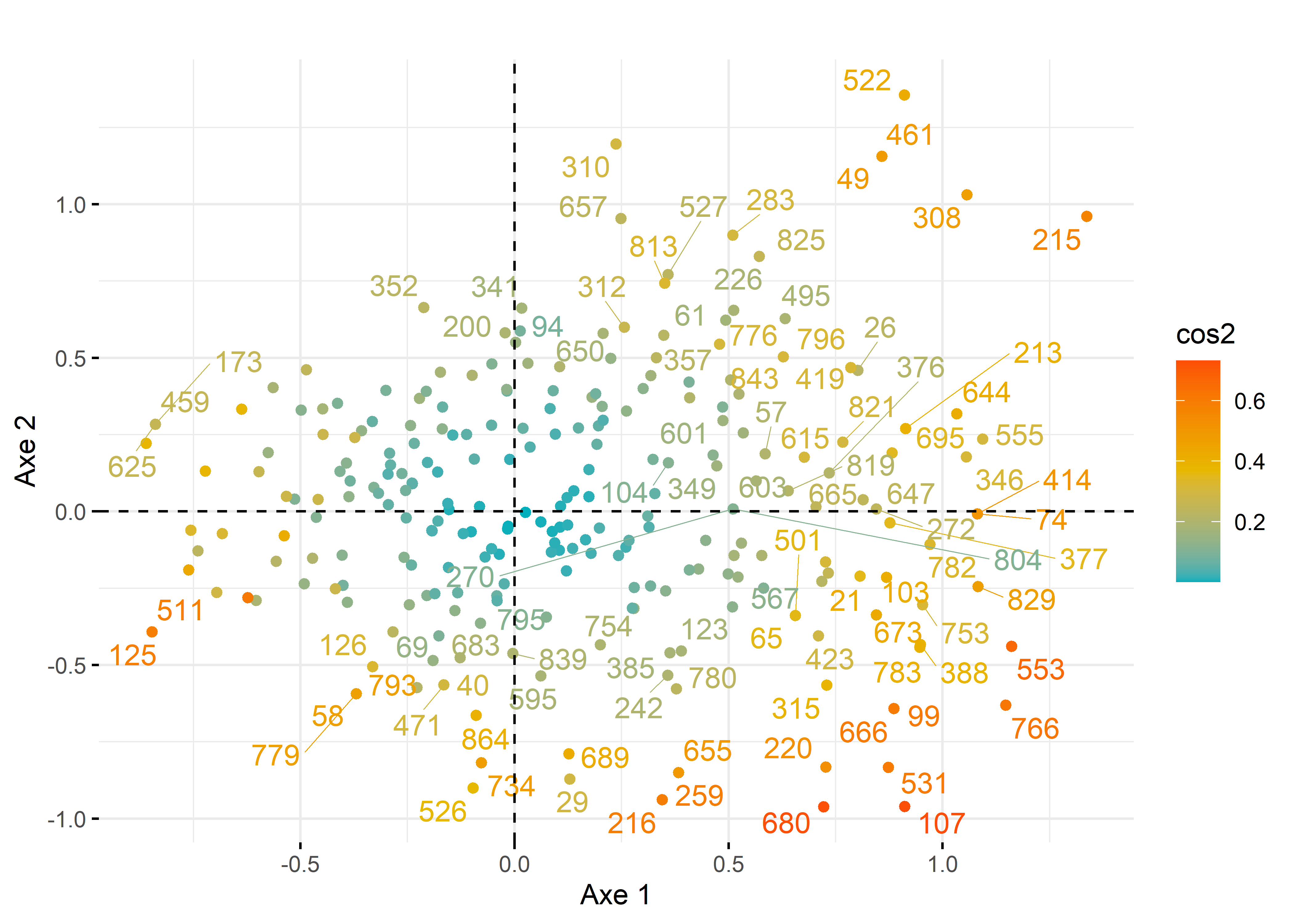

Figure 12.50: Premier plan factoriel de l’ACM pour les individus avec factoextra

La syntaxe ci-dessous produit aussi le premier plan factoriel pour les individus, mais en attribuant une couleur différente aux modalités de la variable q12 (figure 12.51).

fviz_mca_ind (res.acm,
              label = "none",
              habillage = "q12", # colorer par groupes
             xlab="Axe 1", ylab="Axe 2", title="",
              palette = c ("darkred", "steelblue", "gray23"),
              ggtheme = theme_minimal ())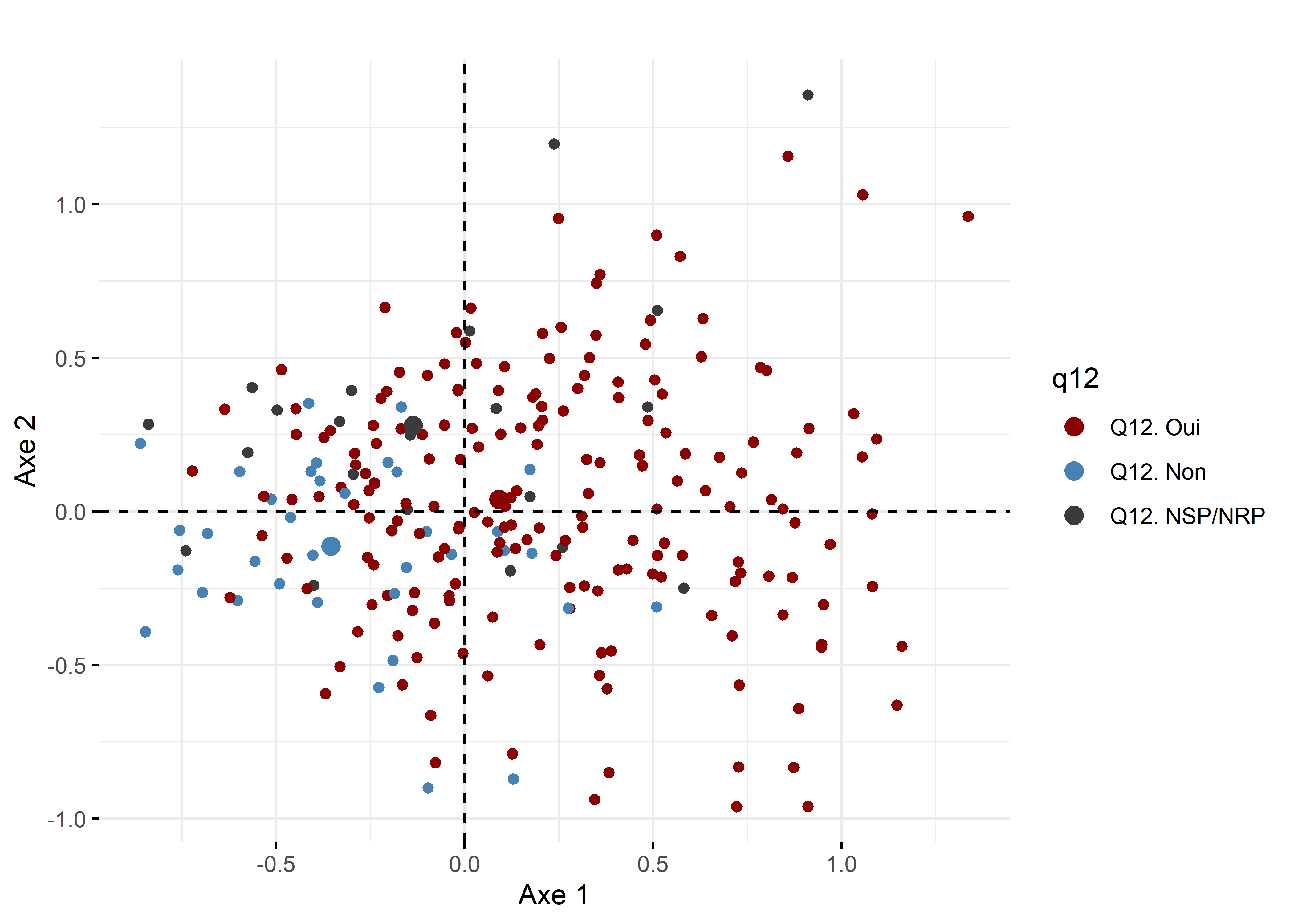

Figure 12.51: Premier plan factoriel de l’ACM pour les individus avec coloration d’une variable avec factoextra

Références

Audate, Pierre Paul, Geneviève Cloutier et Alexandre Lebel. 2021. « The motivations of urban agriculture practitioners in deprived neighborhoods: A comparative study of Montreal and Quito. » Urban Forestry & Urban Greening 62: 127171. https://doi.org/10.1016/j.ufug.2021.127171.

Bhatt, Vikram et Leila Marie Farah. 2016. « Cultivating Montreal: A Brief History of Citizens and Institutions Integrating Urban Agriculture in the City. » Urban Agriculture & Regional Food Systems 1 (1): 1‑12. http://dx.doi.org/10.2134/urbanag2015.01.1511.

McClintock, Nathan. 2018. « Urban agriculture, racial capitalism, and resistance in the settler-colonial city. » Geography Compass 12 (6): 1‑16. https://doi.org/10.1111/gec3.12373.

Pagès, Jérôme. 2002. « Analyse factorielle multiple appliquée aux variables qualitatives et aux données mixtes. » Revue de statistique appliquée 50 (4): 5‑37.