4.3 Corrélation

4.3.1 Formulation

Le coefficient de corrélation de Pearson (\(r\)) est égal à la covariance (numérateur) divisée par le produit des écarts-types des deux variables X et Y (dénominateur). Il représente une standardisation de la covariance. Autrement dit, le coefficient de corrélation repose sur un centrage (moyenne = 0) et une réduction (variance = 1) des deux variables, c’est-à-dire qu’il faut soustraire de chaque valeur sa moyenne correspondante et la diviser par son écart-type. Il correspond ainsi à la moyenne du produit des deux variables centrées réduites. Il s’écrit alors :

\[\begin{equation} r_{xy} = \frac{\sum_{i=1}^n (x_{i}-\bar{x})(y_{i}-\bar{y})}{(n-1)\sqrt{\sum_{i=1}^n(x_i - \bar{x})^2(y_i - \bar{y})^2}}=\sum_{i=1}^n\frac{Zx_iZy_i}{n-1} \tag{4.2} \end{equation}\]

La syntaxe ci-dessous démontre que le coefficient de corrélation de Pearson est bien égal à la moyenne du produit de deux variables centrées réduites.

library("MASS")
N <- 1000     # nombre d'observations
moy_x <- 50   # moyenne de x
moy_y <- 40   # moyenne de y
sd_x <- 10    # écart-type de x
sd_y <- 8     # écart-type de y
rxy <- .80 # corrélation entre X et Y
## création de deux variables fictives normalement distribuées et corrélées entre elles
# Création d'une matrice de covariance
cov <- matrix(c(sd_x^2,  rxy*sd_x*sd_y, rxy*sd_x*sd_y, sd_y^2), nrow=2)
# Création du tableau de données avec deux variables
df1 <- as.data.frame(mvrnorm(N, c(moy_x, moy_y), cov))
# Centrage et réduction des deux variables
df1$zV1 <- scale(df1$V1, center = TRUE, scale = TRUE)
df1$zV2 <- scale(df1$V2, center = TRUE, scale = TRUE)
# Corrélation de Pearson
cor1 <- cor(df1$V1, df1$V2)
cor2 <- sum(df1$zV1*df1$zV2) / (nrow(df1)-1)
cat("Corrélation de Pearson = ",round(cor1,5),
    "\nMoyenne du produit des variables centrées-réduites =", round(cor2,5))
## Corrélation de Pearson =  0.79449 
## Moyenne du produit des variables centrées-réduites = 0.79449

4.3.2 Interprétation

Le coefficient de corrélation \(r\) varie de −1 à 1 avec :

  • 0 quand il n’y a pas de relation linéaire entre les variables X et Y;
  • −1 quand il y a relation linéaire négative parfaite;
  • 1 quand il y a une relation linéaire positive parfaite (figure 4.4).
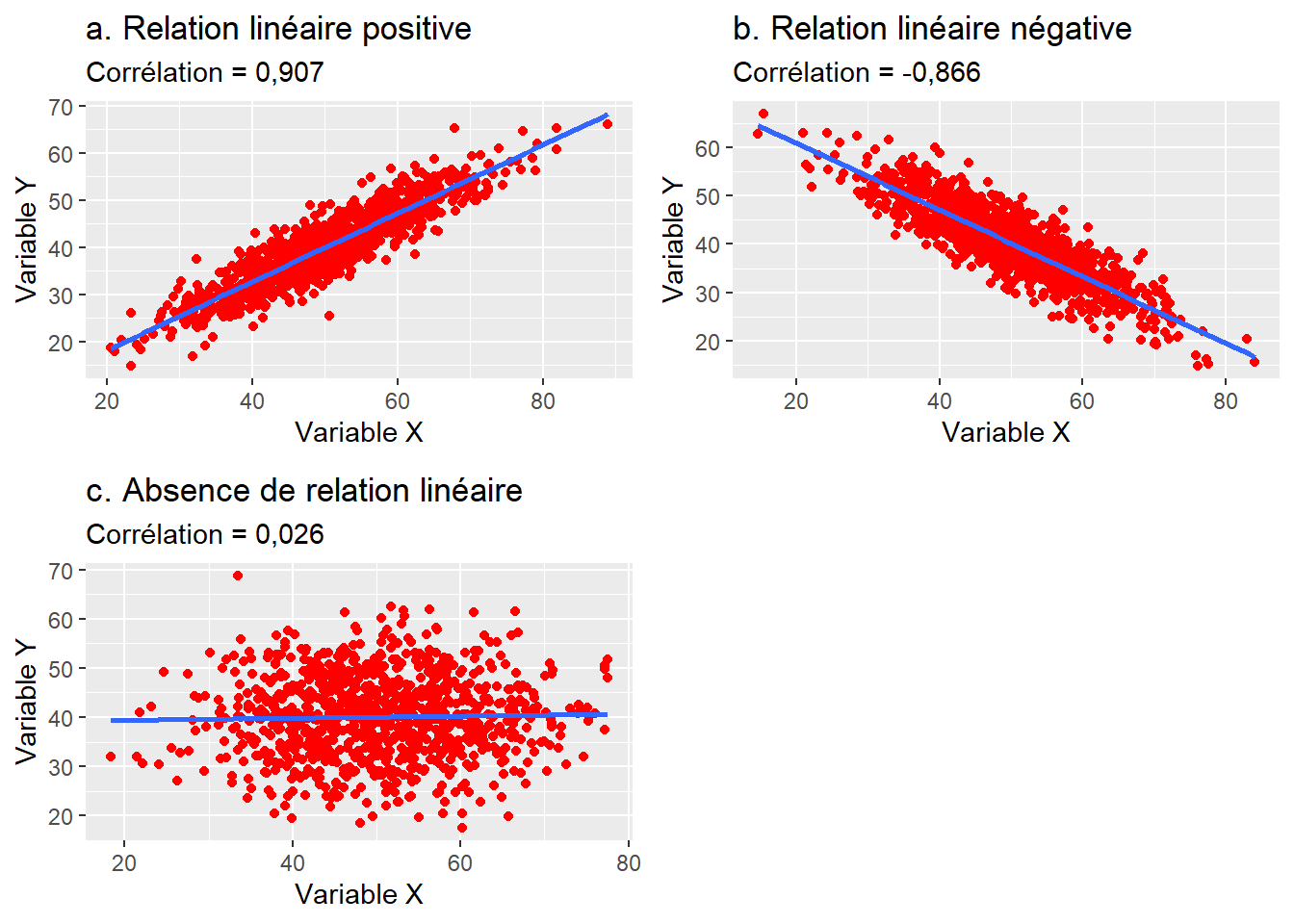
Relations entre deux variables continues et coefficients de corrélation de Pearson

Figure 4.4: Relations entre deux variables continues et coefficients de corrélation de Pearson

Concrètement, le signe du coefficient de corrélation indique si la relation est positive ou négative et la valeur absolue du coefficient indique le degré d’association entre les deux variables. Reste à savoir comment déterminer qu’une valeur de corrélation est faible, moyenne ou forte. En sciences sociales, nous utilisons habituellement les intervalles de valeurs reportés au tableau 4.1. Toutefois, ces seuils sont tout à fait arbitraires. En effet, dépendamment de la discipline de recherche (sciences sociales, sciences de la santé, sciences physiques, etc.) et des variables à l’étude, l’interprétation d’une valeur de corrélation peut varier. Par exemple, en sciences sociales, une valeur de corrélation de 0,2 est considérée comme très faible alors qu’en sciences de la santé, elle pourrait être considérée comme intéressante. À l’opposé, une valeur de 0,9 en sciences physiques pourrait être considérée comme faible. Il convient alors d’utiliser ces intervalles avec précaution.

Tableau 4.1: Intervalles pour l’interprétation du coefficient de corrélation habituellement utilisés en sciences sociales
Corrélation Négative Positive
Faible de −0,3 à 0,0 de 0,0 à 0,3
Moyenne de −0,5 à −0,3 de 0,3 à 0,5
Forte de −1,0 à −0,5 de 0,5 à 1,0

Le coefficient de corrélation mis au carré représente le coefficient de détermination et indique la proportion de la variance de la variable Y expliquée par la variable X et inversement. Par exemple, un coefficient de corrélation de −0,70 signale que 49 % de la variance de la variable de Y est expliquée par X (figure 4.5).

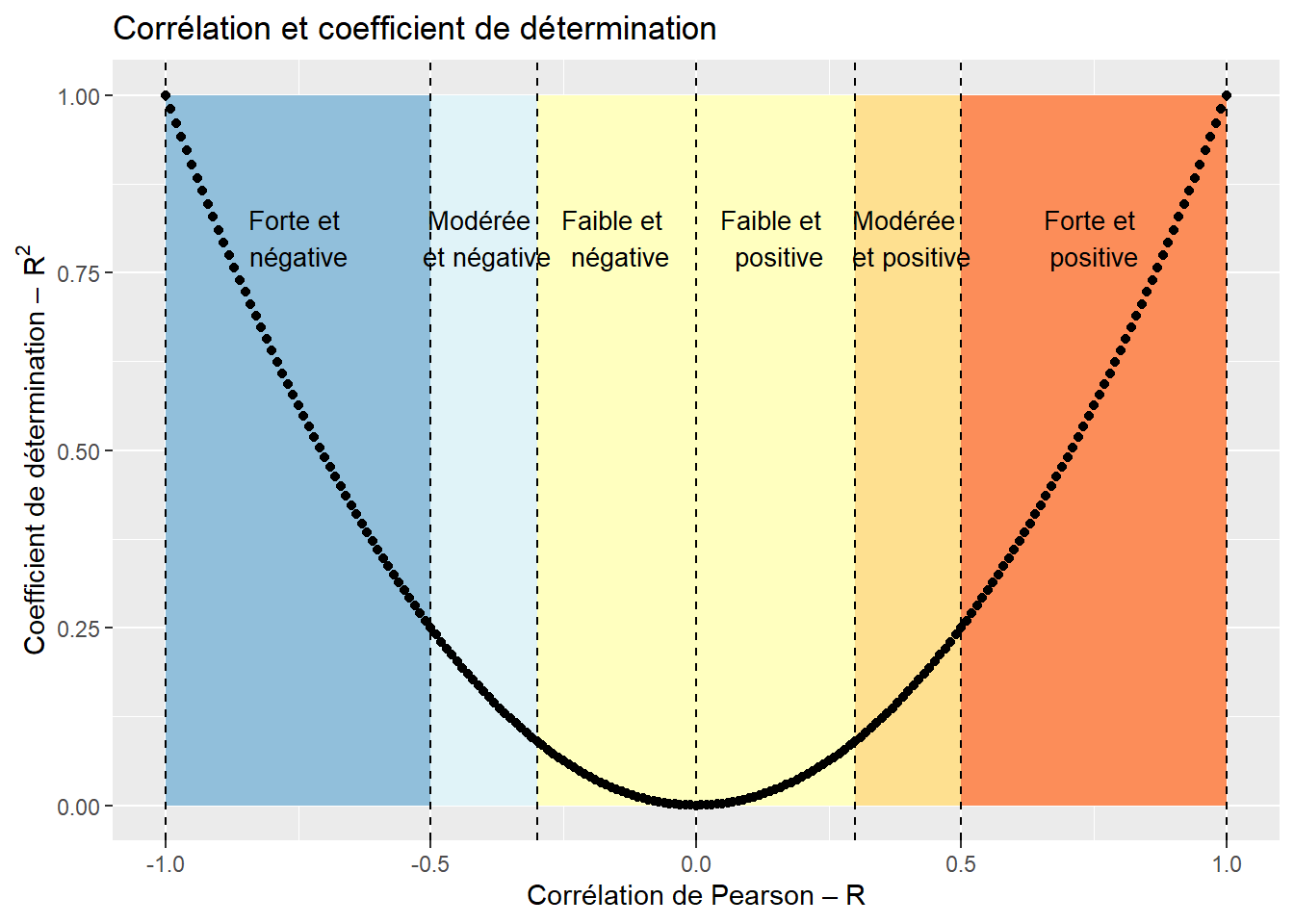
Coefficient de corrélation et proportion de la variance expliquée

Figure 4.5: Coefficient de corrélation et proportion de la variance expliquée

Condition d’application. L’utilisation du coefficient de corrélation de Pearson nécessite que les deux variables continues soient normalement distribuées et qu’elles ne comprennent pas de valeurs aberrantes ou extrêmes. D’ailleurs, plus le nombre d’observations est réduit, plus la présence de valeurs extrêmes a une répercussion importante sur le résultat du coefficient de corrélation de Pearson. En guise d’exemple, dans le nuage de points à gauche de la figure 4.6, il est possible d’identifier des valeurs extrêmes qui se démarquent nettement dans le jeu de données : six observations avec une densité de population supérieure à 20 000 habitants au km2 et deux observations avec un pourcentage de 65 ans et plus supérieur à 55 %. Si l’on supprime ces observations (ce qui est défendable dans ce contexte) – soit moins d’un pour cent des observations du jeu de données initial –, la valeur du coefficient de corrélation passe de −0,158 à −0,194, signalant une augmentation du degré d’association entre les deux variables.

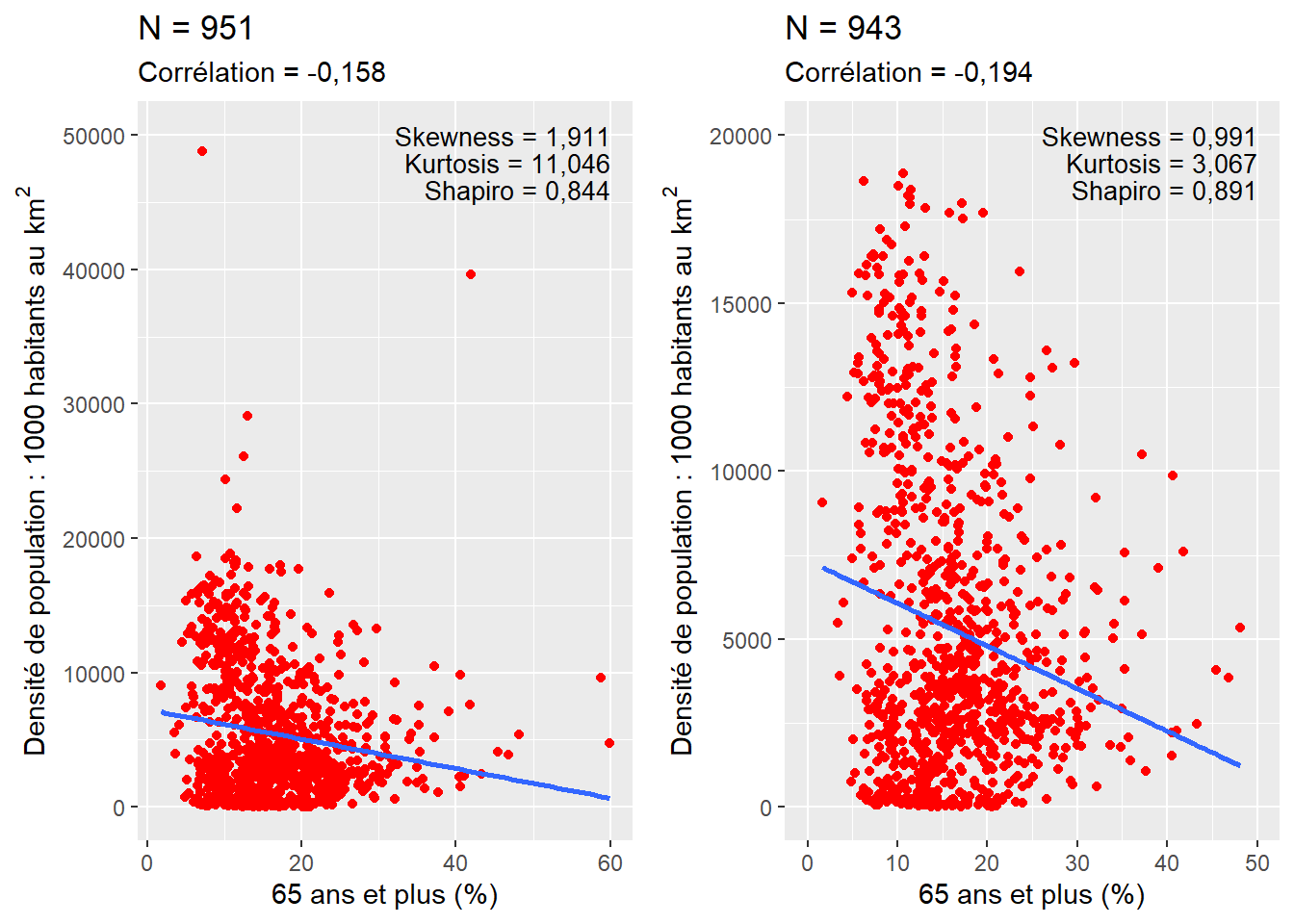
Illustation de l’effet des valeurs extrêmes sur le coefficient de Pearson

Figure 4.6: Illustation de l’effet des valeurs extrêmes sur le coefficient de Pearson

4.3.3 Corrélations pour des variables anormalement distribuées (coefficient de Spearman, tau de Kendall)

Lorsque les variables sont fortement anormalement distribuées, le coefficient de corrélation de Pearson est peu adapté pour analyser leurs relations linéaires. Il est alors conseillé d’utiliser deux statistiques non-paramétriques : principalement, le coefficient de corrélation de Spearman (rho) et secondairement, le tau (\(\tau\)) de Kendall, qui varient aussi tous deux de −1 à 1. Calculé sur les rangs des deux variables, le coefficient de Spearman est le rapport entre la covariance des deux variables de rangs sur les écarts-types des variables de rangs. En d’autres termes, il représente simplement le coefficient de Pearson calculé sur les rangs des deux variables :

\[\begin{equation} r_{xy} = \frac{cov(rg_{x},rg_{y})}{\sigma_{rg_{x}}\sigma_{rg_{y}}} \tag{4.3} \end{equation}\]

La syntaxe ci-dessous démontre clairement que le coefficient de Spearman est bien le coefficient de Pearson calculé sur les rangs (4.3.1).

df <- read.csv("data/bivariee/sr_rmr_mtl_2016.csv")
# Transformation des deux variables en rangs
df$HabKm2_rang <- rank(df$HabKm2)
df$A65plus_rang <- rank(df$A65plus)
# Coefficient de Spearman avec la fonction cor et la méthode spearman
cat("Coefficient de Spearman = ", 
    round(cor(df$HabKm2, df$A65plus, method = "spearman"),5))
## Coefficient de Spearman =  -0.11953
# Coefficient de Pearson sur les variables transformées en rangs
cat("Coefficient de Pearson calculé sur les variables transformées en rangs = ", 
    round(cor(df$HabKm2_rang, df$A65plus_rang, method = "pearson"),5))
## Coefficient de Pearson calculé sur les variables transformées en rangs =  -0.11953
# Vérification avec l'équation
cat("Covariance divisée par le produit des écarts-types sur les rangs :",
    round(cov(df$HabKm2_rang, df$A65plus_rang) / (sd(df$HabKm2_rang)*sd(df$A65plus_rang)),5))
## Covariance divisée par le produit des écarts-types sur les rangs : -0.11953

Le tau de Kendall est une autre mesure non paramétrique calculée comme suit :

\[\begin{equation} \tau = \frac{n_{c}-n_{d}}{\frac{1}{2}n(n-1)} \tag{4.4} \end{equation}\]

avec \(n_{c}\) et \(n_{d}\) qui sont respectivement les nombres de paires d’observations concordantes et discordantes; et le dénominateur étant le nombre total de paires d’observations. Des paires sont dites concordantes quand les valeurs des deux observations vont dans le même sens pour les deux variables (\(x_{i}>x_{j}\) et \(y_{i}>y_{j}\) ou \(x_{i}<x_{j}\) et \(y_{i}<y_{j}\)), et discordantes quand elles vont en sens contraire (\(x_{i}>x_{j}\) et \(y_{i}<y_{j}\) ou \(x_{i}<x_{j}\) et \(y_{i}>y_{j}\)). Contrairement au calcul du coefficient de Spearman, celui du tau Kendall peut être chronophage : plus le nombre d’observations est élevé, plus les temps de calcul et la mémoire utilisée sont importants. En effet, avec n=1000, le nombre de paires d’observations (\({\mbox{0,5}\times n(n-1)}\)) est de 499 500, contre près de 50 millions avec n=10 000 (49 995 000).

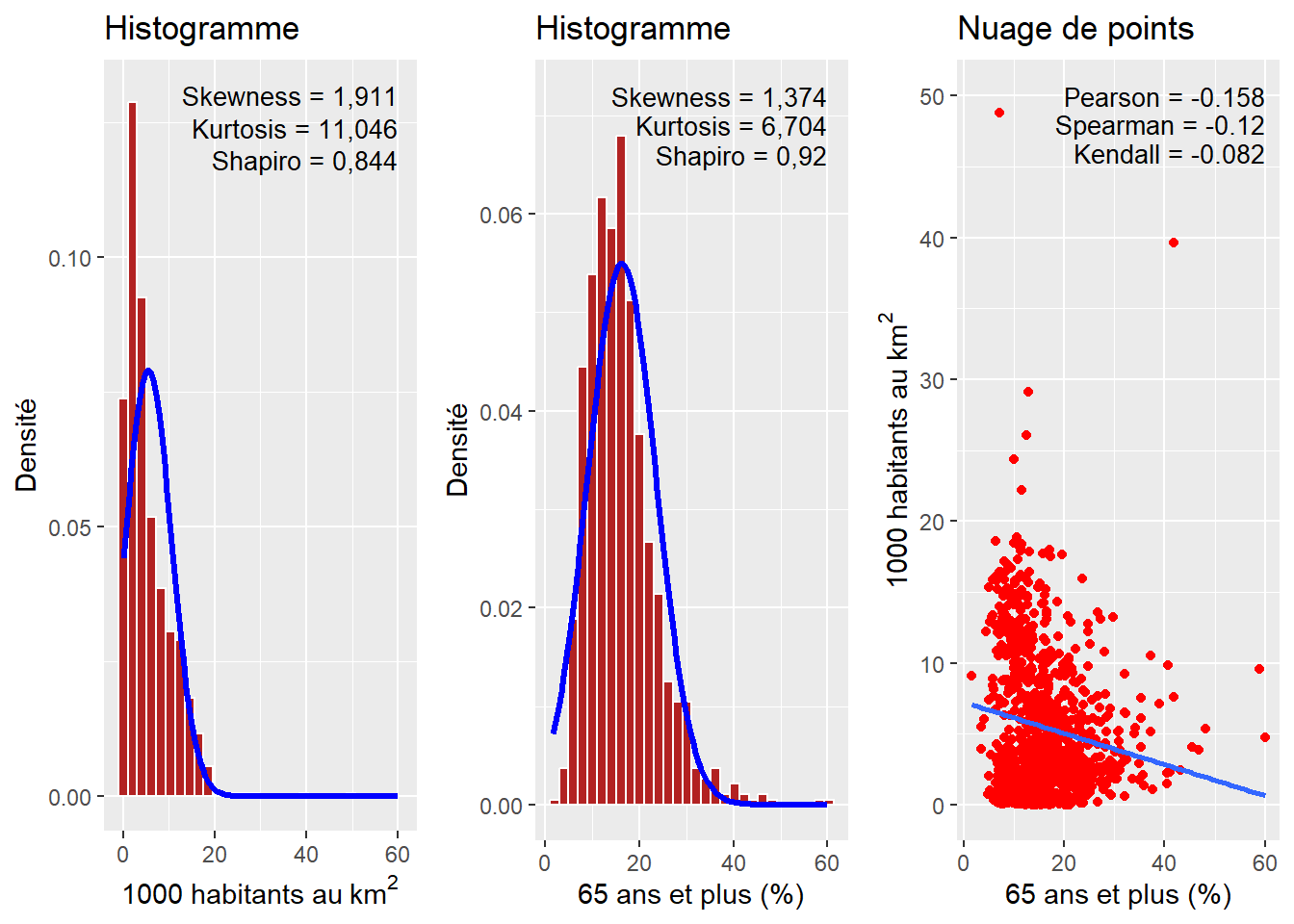
Comparaison des coefficients de Pearson, Spearman et Kendall sur deux variables anormalement distribuées

Figure 4.7: Comparaison des coefficients de Pearson, Spearman et Kendall sur deux variables anormalement distribuées

À la lecture des deux histogrammes à la figure 4.7, il est clair que les variables densité de population et pourcentage de personnes ayant 65 ou plus sont très anormalement distribuées. Dans ce contexte, l’utilisation du coefficient de Pearson peut nous amener à mésestimer la relation existant entre les deux variables. Notez que les coefficients de Spearman et de Kendall sont tous les deux plus faibles.

4.3.4 Corrélations robustes (Biweight midcorrelation, Percentage bend correlation et la corrélation pi de Shepherd)

Dans l’exemple donné à la figure 4.6, nous avions identifié des valeurs extrêmes et les avons retirées du jeu de données. Cette pratique peut tout à fait se justifier quand les données sont erronées (un capteur de pollution renvoyant une valeur négative, un questionnaire rempli par un mauvais plaisantin, etc.), mais parfois les cas extrêmes font partie du phénomène à analyser. Dans ce contexte, les identifier et les retirer peut paraître arbitraire. Une solution plus élégante est d’utiliser des méthodes dites robustes, c’est à dire moins sensibles aux valeurs extrêmes. Pour les corrélations, la Biweight midcorrelation (Wilcox 1994) est au coefficient de Pearson ce que la médiane est à la moyenne. Il est donc pertinent de l’utiliser pour des jeux de données présentant potentiellement des valeurs extrêmes. Elle est calculée comme suit :

\[\begin{equation} \begin{aligned} &u_{i} = \frac{x_{i} - med(x)}{9 \times (med(|x_{i} - med(x)|))} \text{ et } v_{i} = \frac{y_{i} - med(y)}{9 \times (med(|y_{i} - med(y)|))}\\ &w_{i}^{(x)} = (1 - u_{i}^2)^2 I(1 - |u_{i}|) \text{ et } w_{i}^{(y)} = (1 - v_{i}^2)^2 I(1 - |v_{i}|)\\ &I(x) = \begin{cases} 1, \text{si } x = 1\\ 0, \text{sinon} \end{cases}\\ &\tilde{x}_{i} = \frac{(x_{i} - med(x))w_{i}^{(x)}}{\sqrt{(\sum_{j=1}^m)[(x_{j} - med(x))w_{j}^{(x)}]^2}} \text{ et } \tilde{y}_{i} = \frac{(y_{i} - med(y))w_{i}^{(y)}}{\sqrt{(\sum_{j=1}^m)[(y_{j} - med(y))w_{j}^{(y)}]^2}}\\ &bicor(x,y) = \sum_{i=1}^m \tilde{x_i}\tilde{y_i} \end{aligned} \tag{4.5} \end{equation}\]

Comme le souligne l’équation (4.5), la Biweight midcorrelation est basée sur les écarts à la médiane, plutôt que sur les écarts à la moyenne.

Assez proche de la Biweight midcorrelation, la Percentage bend correlation se base également sur la médiane des variables X et Y. Le principe général est de donner un poids plus faible dans le calcul de cette corrélation à un certain pourcentage des observations (20 % sont généralement recommandés) dont la valeur est éloignée de la médiane. Pour une description complète de la méthode, vous pouvez lire l’article de Wilcox (1994).

Enfin, une autre option est l’utilisation de la corrélation \(pi\) de Sherphred (Schwarzkopf, Haas et Rees 2012). Il s’agit simplement d’une méthode en deux étapes. Premièrement, les valeurs extrêmes sont identifiées à l’aide d’une approche par bootstrap utilisant la distance de Mahalanobis (calculant les écarts multivariés entre les observations). Deuxièmement, le coefficient de Spearman est calculé sur les observations restantes.

Appliquons ces corrélations aux données précédentes. Notez que ce simple code d’une dizaine de lignes permet d’explorer rapidement la corrélation entre deux variables selon six mesures de corrélation.

library("correlation")
df1 <- read.csv("data/bivariee/sr_rmr_mtl_2016.csv")
methods <- c("Pearson","Spearman","Biweight","Percentage","Shepherd")
rs <- lapply(methods,function(m){
  test <- correlation::cor_test(data = df1, x="Hab1000Km2",y="A65plus",method = m, ci=0.95)
  return(c(test$r,test$CI_low, test$CI_high))
  })
dfCorr <- data.frame(do.call(rbind,rs))
names(dfCorr) <- c("r","IC_2.5","IC_97.5")
dfCorr$method <- methods

# Impression du tableau avec le package stargazer
library(stargazer)
stargazer(dfCorr, type="text", summary=FALSE, rownames=FALSE, align = FALSE, digits = 3,
          title="Comparaison de différentes corrélations pour les deux variables")
Tableau 4.2: Comparaison de différentes corrélations pour les deux variables
r IC 2,5 % IC 97,5 % Méthode
-0,158 -0,219 -0,095 Pearson
-0,120 -0,184 -0,055 Spearman
-0,137 -0,199 -0,074 Biweight
-0,174 -0,235 -0,111 Percentage
-0,119 -0,185 -0,052 Shepherd

Il est intéressant de mentionner que ces trois corrélations sont rarement utilisées malgré leur pertinence dans de nombreux cas d’application. Nous faisons face ici à un cercle vicieux dans la recherche : les méthodes les plus connues sont les plus utilisées, car elles sont plus facilement acceptées par la communauté scientifique. Des méthodes plus élaborées nécessitent davantage de justification et de discussion, ce qui peut conduire à de multiples sessions de corrections/resoumissions pour qu’un article soit accepté, malgré le fait qu’elles puissent être plus adaptées au jeu de données à l’étude.

4.3.5 Significativité des coefficients de corrélation

Quelle que soit la méthode utilisée, il convient de vérifier si le coefficient de corrélation est ou non statistiquement différent de 0. En effet, nous travaillons la plupart du temps avec des données d’échantillonnage, et très rarement avec des populations complètes. En collectant un nouvel échantillon, aurions-nous obtenu des résultats différents? Le calcul de ce degré de significativité permet de quantifier le niveau de certitude quant à l’existence d’une corrélation entre les deux variables, positive ou négative. Cet objectif est réalisé en calculant la valeur de t et le nombre de degrés de liberté : \(t=\sqrt{\frac{n-2}{1-r^2}}\) et \(dl = n-2\) avec \(r\) et \(n\) étant respectivement le coefficient de corrélation et le nombre d’observations. De manière classique, nous utiliserons la table des valeurs critiques de la distribution de \(t\) : si la valeur de \(t\) est supérieure à la valeur critique (avec p = 0,05 et le nombre de degrés de liberté), alors le coefficient est significatif à 5 %. En d’autres termes, si la vraie corrélation entre les deux variables (calculable uniquement à partir des populations complètes) était 0, alors la probabilité de collecter notre échantillon serait inférieure à 5 %. Dans ce contexte, nous peuvons raisonnablement rejeter l’hypothèse nulle (corrélation de 0).

La courte syntaxe ci-dessous illustre comment calculer la valeur de \(t\), le nombre de degrés de liberté et la valeur de p pour une corrélation donnée.

df <- read.csv("data/bivariee/sr_rmr_mtl_2016.csv")
r <- cor(df$A65plus, df$LogTailInc)     # Corrélation
n <- nrow(df)                           # Nombre d'observations
dl <- nrow(df)-2                        # degrés de liberté
t <-  r*sqrt((n-2)/(1-r^2))             # Valeur de T
p <- 2*(1-pt(abs(t),dl))                # Valeur de p
cat("\nCorrélation =", round(r, 4),       
    "\nValeur de t =", round(t, 4),
    "\nDegrés de liberté =", dl,
    "\np=", round(p, 4))        
## 
## Corrélation = -0.0693 
## Valeur de t = -2.1413 
## Degrés de liberté = 949 
## p= 0.0325

Plus simplement, la fonction cor.test permet d’obtenir en une seule ligne de code le coefficient de corrélation, l’intervalle de confiance à 95 % et les valeurs de t et de p, comme illustré dans la syntaxe ci-dessous. Si l’intervalle de confiance est à cheval sur 0, c’est-à-dire que la borne inférieure est négative et la borne supérieure positive, alors le coefficient de corrélation n’est pas significatif au seuil choisi (95 % habituellement). Dans l’exemple ci-dessous, la relation linéaire entre les deux variables est significativement négative avec une corrélation de Pearson de −0,158 (p = 0,000) et un intervalle de confiance à 95 % de −0,219 à −0,095.

# Intervalle de confiance à 95 %
cor.test(df$HabKm2, df$A65plus, conf.level = .95)
## 
##  Pearson's product-moment correlation
## 
## data:  df$HabKm2 and df$A65plus
## t = -4.9318, df = 949, p-value = 9.616e-07
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  -0.2194457 -0.0954687
## sample estimates:
##        cor 
## -0.1580801
# Vous pouvez accéder à chaque sortie de la fonction cor.test comme suit :
p <- cor.test(df$HabKm2, df$A65plus)
cat("Valeur de corrélation = ", round(p$estimate,3), "\n",
    "Intervalle à 95 % = [", round(p$conf.int[1],3), " ", round(p$conf.int[2],3), "]", "\n",
    "Valeur de t = ", round(p$statistic,3), "\n",
    "Valeur de p = ", round(p$p.value,3),"\n", sep="")
## Valeur de corrélation = -0.158
## Intervalle à 95 % = [-0.219 -0.095]
## Valeur de t = -4.932
## Valeur de p = 0
# Corrélation de Spearman
cor.test(df$HabKm2, df$A65plus, method = "spearman")
## 
##  Spearman's rank correlation rho
## 
## data:  df$HabKm2 and df$A65plus
## S = 160482182, p-value = 0.0002202
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##        rho 
## -0.1195333
# Corrélation de Kendall
cor.test(df$HabKm2, df$A65plus, method="kendall")
## 
##  Kendall's rank correlation tau
## 
## data:  df$HabKm2 and df$A65plus
## z = -3.7655, p-value = 0.0001662
## alternative hypothesis: true tau is not equal to 0
## sample estimates:
##         tau 
## -0.08157061

On pourra aussi modifier l’intervalle de confiance, par exemple à 90 % ou 99 %. L’intervalle de confiance et le seuil de significativité doivent être définis avant l’étude. Leur choix doit s’appuyer sur les standards de la littérature du domaine étudié, du niveau de preuve attendu et de la quantité de données.

# Intervalle à 90 %
cor.test(df$HabKm2, df$A65plus, method ="pearson", conf.level = .90)
## 
##  Pearson's product-moment correlation
## 
## data:  df$HabKm2 and df$A65plus
## t = -4.9318, df = 949, p-value = 9.616e-07
## alternative hypothesis: true correlation is not equal to 0
## 90 percent confidence interval:
##  -0.2096826 -0.1055995
## sample estimates:
##        cor 
## -0.1580801
# Intervalle à 99 %
cor.test(df$HabKm2, df$A65plus, method ="pearson", conf.level = .99)
## 
##  Pearson's product-moment correlation
## 
## data:  df$HabKm2 and df$A65plus
## t = -4.9318, df = 949, p-value = 9.616e-07
## alternative hypothesis: true correlation is not equal to 0
## 99 percent confidence interval:
##  -0.23839910 -0.07561336
## sample estimates:
##        cor 
## -0.1580801

Corrélation et bootstrap. Il est possible d’estimer la corrélation en mobilisant la notion de bootstrap, soit des méthodes d’inférence statistique basées sur des réplications des données initiales par rééchantillonnage. Concrètement, la méthode du bootstrap permet une mesure de la corrélation avec un intervalle de confiance à partir de r réplications, comme illustré à partir de la syntaxe ci-dessous.

library("boot")
df <- read.csv("data/bivariee/sr_rmr_mtl_2016.csv")
# Fonction pour la corrélation
correlation <- function(df, i, X, Y, cor.type="pearson"){
  # Paramètres de la fonction :
  # data : DataFrame
  # X et Y : noms des variables X et Y
  # cor.type : type de corrélation : c("pearson","spearman","kendall")
  # i : indice qui sera utilisé par les réplications (à ne pas modifier)
  cor(df[[X]][i], df[[Y]][i], method=cor.type)
}
# Calcul du Bootstrap avec 5000 réplications
corBootstraped <- boot(data=df, # nom du tableau
                     statistic = correlation, # appel de la fonction à répliquer 
                     R=5000, # nombre de réplications
                     X = "A65plus",
                     Y ="HabKm2", 
                     cor.type="pearson")
# Histogramme pour les valeurs de corrélation issues du Bootstrap
plot(corBootstraped)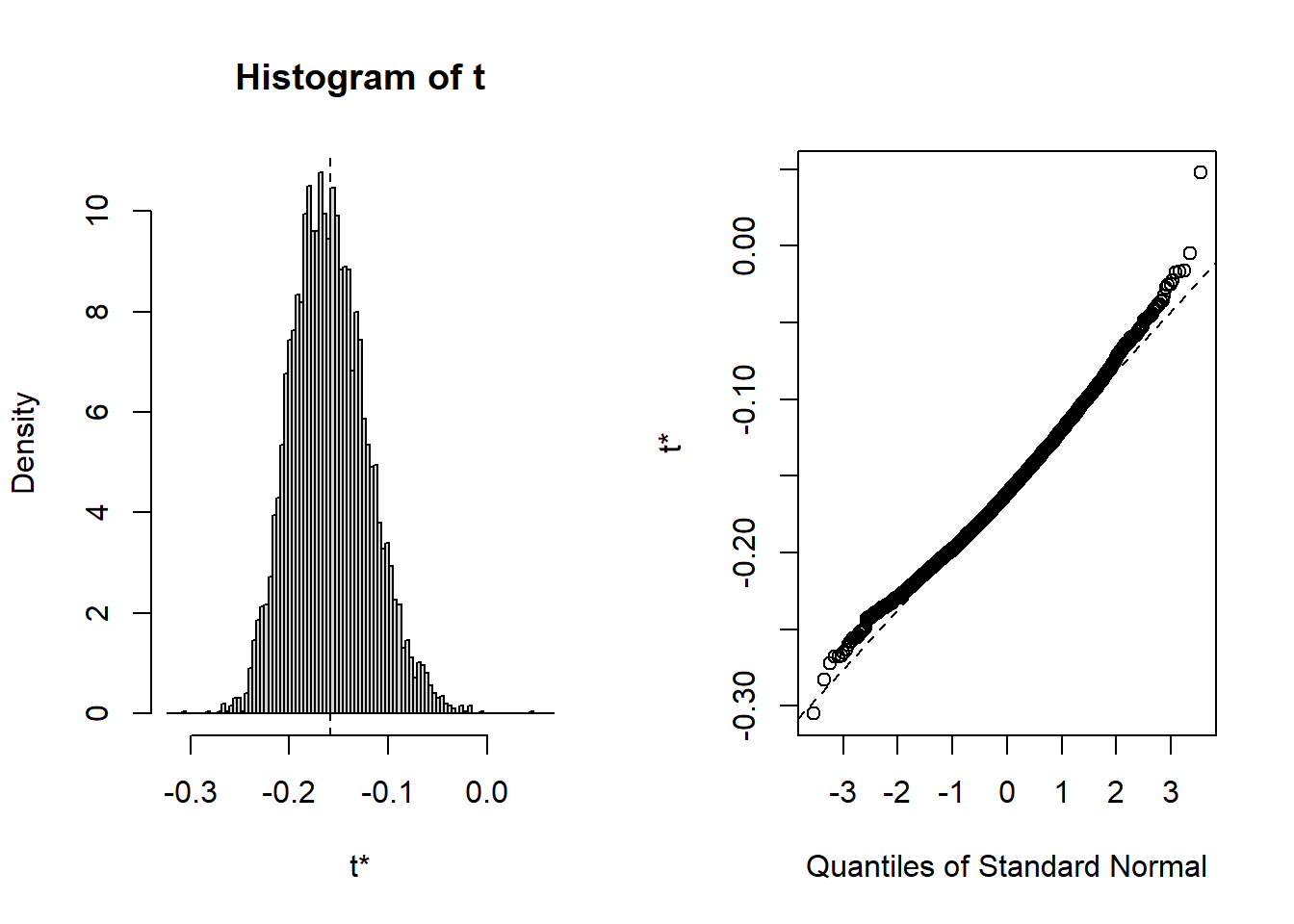
Histogramme pour les valeurs de corrélation issues du Bootstrap

Figure 4.8: Histogramme pour les valeurs de corrélation issues du Bootstrap 

# Corrélation "bootstrapée"
corBootstraped
## 
## ORDINARY NONPARAMETRIC BOOTSTRAP
## 
## 
## Call:
## boot(data = df, statistic = correlation, R = 5000, X = "A65plus", 
##     Y = "HabKm2", cor.type = "pearson")
## 
## 
## Bootstrap Statistics :
##       original       bias    std. error
## t1* -0.1580801 -0.001017975   0.0388877
# Intervalle de confiance du bootstrap à 95 %
boot.ci(boot.out = corBootstraped, conf = 0.95, type = "all")
## BOOTSTRAP CONFIDENCE INTERVAL CALCULATIONS
## Based on 5000 bootstrap replicates
## 
## CALL : 
## boot.ci(boot.out = corBootstraped, conf = 0.95, type = "all")
## 
## Intervals : 
## Level      Normal              Basic         
## 95%   (-0.2333, -0.0808 )   (-0.2403, -0.0882 )  
## 
## Level     Percentile            BCa          
## 95%   (-0.2279, -0.0758 )   (-0.2156, -0.0529 )  
## Calculations and Intervals on Original Scale
# Comparaison de l'intervalle classique basé sur la valeur de T
p <- cor.test(df$HabKm2, df$A65plus)
cat(round(p$estimate,5), " [", round(p$conf.int[1],4), " ",round(p$conf.int[2],4), "]", sep="")
## -0.15808 [-0.2194 -0.0955]

Le bootstrap renvoie un coefficient de corrélation de Pearson de −0,158. Les intervalles de confiance obtenus à partir des différentes méthodes d’estimation (normale, basique, pourcentage et BCa) ne sont pas à cheval sur 0, indiquant que le coefficient est significatif à 5 %.

4.3.6 Corrélation partielle

Quelle est la relation entre deux variables continues une fois prise en compte une autre variable dite de contrôle? En études urbaines, nous pourrions vouloir vérifier si deux variables sont ou non associées après avoir contrôlé la densité de population ou encore la distance au centre-ville.

La corrélation partielle permet d’évaluer la relation linéaire entre deux variables quantitatives continues, après avoir contrôlées une ou plusieurs autres variables quantitatives (dites variables de contrôle).

Le coefficient de corrélation partielle peut être calculé pour plusieurs mesures de corrélation (notamment, Pearson, Spearman et Kendall). Variant aussi de −1 à 1, il est calculé comme suit :

\[\begin{equation} r_{ABC} = \frac{r_{AB}-r_{AC}r_{BC}}{\sqrt{(1-r_{AC}^2)(1-r_{BC}^2)}} \tag{4.6} \end{equation}\]

avec A et B étant les deux variables pour lesquelles nous souhaitons évaluer la relation linéaire, une fois contrôlée la variable C; \(r\) étant le coefficient de corrélation (Pearson, Spearman ou Kendall) entre deux variables.

Dans l’exemple ci-dessous, nous voulons estimer la relation linéaire entre le pourcentage de personnes à faible revenu et la couverture végétale au niveau des îlots de l’île de Montréal, une fois contrôlée la densité de population. En effet, plus cette dernière est forte, plus la couverture végétale est faible (\(r\) de Pearson = −0,563). La valeur du \(r\) de Pearson s’élève à −0,513 entre le pourcentage de personnes à faible revenu dans la population totale de l’îlot et la couverture végétale. Une fois la densité de population contrôlée, elle chute à −0,316. Pour calculer la corrélation partielle, nous pouvons utiliser la fonction pcor.test du package ppcor.

library("foreign")
library("ppcor")
dfveg <- read.dbf("data/bivariee/IlotsVeg2006.dbf")
# Corrélation entre les trois variables
round(cor(dfveg[, c("VegPct", "Pct_FR","LogDens")], method="p"), 3)
##         VegPct Pct_FR LogDens
## VegPct   1.000 -0.513  -0.563
## Pct_FR  -0.513  1.000   0.513
## LogDens -0.563  0.513   1.000
# Corrélation partielle avec la fonction pcor.test entre :
# la couverture végétale de l'îlot (%) et
# le pourcentage de personnes à faible revenu
# une fois contrôlée la densité de population
pcor.test(dfveg$Pct_FR, dfveg$VegPct, dfveg$LogDens, method="p")
##     estimate       p.value statistic     n gp  Method
## 1 -0.3155194 8.093159e-235 -33.59772 10213  1 pearson
# Calcul de la corrélation partielle avec la formule
corAB <- cor(dfveg$VegPct, dfveg$Pct_FR, method = "p")
corAC <- cor(dfveg$VegPct, dfveg$LogDens, method = "p")
corBC <- cor(dfveg$Pct_FR, dfveg$LogDens, method = "p")
CorP  <- (corAB - (corAC*corBC)) / sqrt((1-corAC^2)*(1-corBC^2))
cat("Corr. partielle avec ppcor  = ", 
    round(pcor.test(dfveg$Pct_FR,  dfveg$VegPct, dfveg$LogDens, method="p")$estimate,5),
    "\nCorr. partielle (formule)  = ", round(CorP, 5))
## Corr. partielle avec ppcor  =  -0.31552 
## Corr. partielle (formule)  =  -0.31552

4.3.7 Mise en œuvre dans R

Comme vous l’aurez compris, il est possible d’arriver au même résultat par différents moyens. Pour calculer les corrélations, nous avons utilisé jusqu’à présent les fonctions de base cor et cor.test. Il est aussi possible de recourir à des fonctions d’autres packages, dont notamment :

  • Hmisc, dont la fonction rcorr permet de calculer des corrélations de Pearson et de Spearman (mais non celle de Kendall) avec les valeurs de p.
  • psych, dont la fonction corr.test permet d’obtenir une matrice de corrélation (Pearson, Spearman et Kendall), les intervalles de confiance et les valeurs de p.
  • stargazer pour créer de beaux tableaux d’une matrice de corrélation en HTML, en LaTeX ou en ASCII.
  • apaTables pour créer un tableau avec une matrice de corrélation dans un fichier Word.
  • correlation pour aller plus loin et explorer les corrélations bayésiennes, robustes, non linéaires ou multiniveaux.
df1 <- read.csv("data/bivariee/sr_rmr_mtl_2016.csv")
library("Hmisc")
library("stargazer")
library("apaTables")
library("dplyr")
# Corrélations de Pearson et Spearman et valeurs de p 
# avec la fonction rcorr de Hmisc pour deux variables
Hmisc::rcorr(df1$RevMedMen, df1$Locataire, type="pearson")
##       x     y
## x  1.00 -0.78
## y -0.78  1.00
## 
## n= 951 
## 
## 
## P
##   x  y 
## x     0
## y  0
Hmisc::rcorr(df1$RevMedMen, df1$Locataire, type="spearman")
##       x     y
## x  1.00 -0.91
## y -0.91  1.00
## 
## n= 951 
## 
## 
## P
##   x  y 
## x     0
## y  0
# Matrice de corrélation avec la fonction rcorr de Hmisc pour plus de variables
# Nous créons au préalable un vecteur avec les noms des variables à sélectionner
Vars <- c("RevMedMen","Locataire", "LogTailInc","A65plus","ImgRec", "HabKm2", "FaibleRev")
Hmisc::rcorr(df1[, Vars] %>% as.matrix())
##            RevMedMen Locataire LogTailInc A65plus ImgRec HabKm2 FaibleRev
## RevMedMen       1.00     -0.78      -0.46   -0.07  -0.46  -0.49     -0.74
## Locataire      -0.78      1.00       0.56    0.00   0.64   0.71      0.88
## LogTailInc     -0.46      0.56       1.00   -0.07   0.82   0.48      0.62
## A65plus        -0.07      0.00      -0.07    1.00  -0.06  -0.16     -0.01
## ImgRec         -0.46      0.64       0.82   -0.06   1.00   0.56      0.68
## HabKm2         -0.49      0.71       0.48   -0.16   0.56   1.00      0.64
## FaibleRev      -0.74      0.88       0.62   -0.01   0.68   0.64      1.00
## 
## n= 951 
## 
## 
## P
##            RevMedMen Locataire LogTailInc A65plus ImgRec HabKm2 FaibleRev
## RevMedMen            0.0000    0.0000     0.0441  0.0000 0.0000 0.0000   
## Locataire  0.0000              0.0000     0.9594  0.0000 0.0000 0.0000   
## LogTailInc 0.0000    0.0000               0.0325  0.0000 0.0000 0.0000   
## A65plus    0.0441    0.9594    0.0325             0.0682 0.0000 0.6796   
## ImgRec     0.0000    0.0000    0.0000     0.0682         0.0000 0.0000   
## HabKm2     0.0000    0.0000    0.0000     0.0000  0.0000        0.0000   
## FaibleRev  0.0000    0.0000    0.0000     0.6796  0.0000 0.0000
# # Avec la fonction corr.test du package psych pour avoir la matrice de corrélation
# # (Pearson, Spearman et Kendall), les intervalles de confiance et les valeurs de p
# print(psych::corr.test(df[, Vars], 
#              method = "kendall", 
#              ci=TRUE, alpha = 0.05), short=FALSE) 
# Création d'un tableau pour une matrice de corrélation
# changer le paramètre type pour 'html' or 'latex' si souhaité
p <- cor(df1[, Vars], method="pearson")
stargazer(p, title="Correlation Matrix", type = "text")
## 
## Correlation Matrix
## =========================================================================
##            RevMedMen Locataire LogTailInc A65plus ImgRec HabKm2 FaibleRev
## -------------------------------------------------------------------------
## RevMedMen      1      -0.785     -0.461   -0.065  -0.458 -0.489  -0.743  
## Locataire   -0.785       1       0.562    -0.002  0.645  0.708    0.879  
## LogTailInc  -0.461     0.562       1      -0.069  0.816  0.475    0.622  
## A65plus     -0.065    -0.002     -0.069      1    -0.059 -0.158  -0.013  
## ImgRec      -0.458     0.645     0.816    -0.059    1    0.561    0.678  
## HabKm2      -0.489     0.708     0.475    -0.158  0.561    1      0.642  
## FaibleRev   -0.743     0.879     0.622    -0.013  0.678  0.642      1    
## -------------------------------------------------------------------------
# Créer un tableau avec la matrice de corrélation 
# dans un fichier Word (.doc)
apaTables::apa.cor.table(df1[, c("RevMedMen","Locataire","LogTailInc")], 
                         filename = "data/bivariee/TitiLaMatrice.doc",
                         show.conf.interval = TRUE,
                         landscape = TRUE)
## 
## 
## Means, standard deviations, and correlations with confidence intervals
##  
## 
##   Variable      M        SD       1            2         
##   1. RevMedMen  66065.50 26635.27                        
##                                                          
##   2. Locataire  45.05    26.33    -.78**                 
##                                   [-.81, -.76]           
##                                                          
##   3. LogTailInc 5.54     4.82     -.46**       .56**     
##                                   [-.51, -.41] [.52, .60]
##                                                          
## 
## Note. M and SD are used to represent mean and standard deviation, respectively.
## Values in square brackets indicate the 95% confidence interval.
## The confidence interval is a plausible range of population correlations 
## that could have caused the sample correlation (Cumming, 2014).
##  * indicates p < .05. ** indicates p < .01.
##

Une image vaut mille mots, surtout pour une matrice de corrélation! Le package corrplot vous permet justement de construire de belles figures avec une matrice de corrélation (figures 4.9 et 4.10). L’intérêt de ce type de figure est de repérer rapidement des associations intéressantes lorsque nous calculons les corrélations entre un grand nombre de variables.

library("corrplot")
library("ggpubr")
df1 <- read.csv("data/bivariee/sr_rmr_mtl_2016.csv")
Vars <- c("RevMedMen","Locataire", "LogTailInc","A65plus","ImgRec", "HabKm2", "FaibleRev")
p <- cor(df1[, Vars], method="pearson")
couleurs <- colorRampPalette(c("#053061", "#2166AC","#4393C3", "#92C5DE",
                               "#D1E5F0", "#FFFFFF", "#FDDBC7", "#F4A582",
                               "#D6604D", "#B2182B", "#67001F"))
corrplot::corrplot(p, addrect = 3, method="number",
                   diag=FALSE, col=couleurs(100))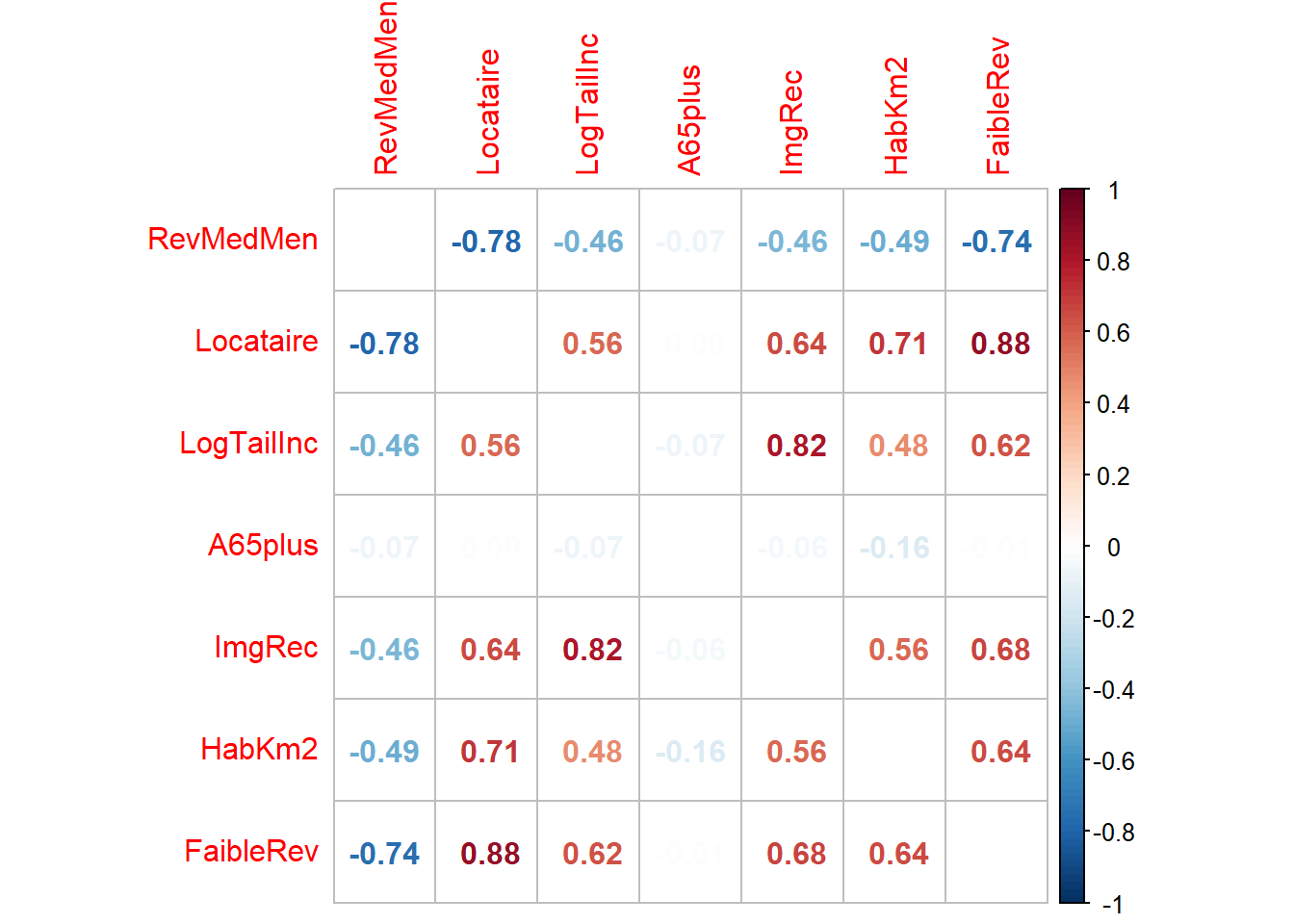
Matrice de corrélation avec corrplot (chiffres)

Figure 4.9: Matrice de corrélation avec corrplot (chiffres) 

fig2 <- corrplot.mixed(p, lower="number", lower.col = "black", 
                      upper = "ellipse", upper.col=couleurs(100))
Matrice de corrélation avec corrplot (chiffres et ellipses)

Figure 4.10: Matrice de corrélation avec corrplot (chiffres et ellipses)

4.3.8 Comment rapporter des valeurs de corrélations?

Bien qu’il n’y ait pas qu’une seule manière de reporter des corrélations, voici quelques lignes directrices pour vous guider :

  • Signaler si la corrélation est faible, modérée ou forte.
  • Indiquer si la corrélation est positive ou négative. Toutefois, ce n’est pas une obligation, car nous pouvons rapidement le constater avec le signe du coefficient.
  • Mettre le r et le p en italique et en minuscules.
  • Deux décimales uniquement pour le \(r\) (sauf si une plus grande précision se justifie dans le domaine d’étude).
  • Trois décimales pour la valeur de p. Si elle est inférieure à 0,001, écrire plutôt p < 0,001.
  • Indiquer éventuellement le nombre de degrés de liberté, soit \(r(dl)=...\)

Voici des exemples :

  • La corrélation entre les variables revenu médian des ménages et pourcentage de locataires est fortement négative (r = −0,78, p < 0,001).
  • La corrélation entre les variables revenu médian des ménages et pourcentage de locataires est forte (r(949) = −0,78, p < 0,001).
  • La corrélation entre les variables densité de population et revenu médian des ménages est modérée (r = −0,49, p < 0,001).
  • La corrélation entre les variables densité de population et pourcentage de 65 ans et plus n’est pas significative (r = −0,08, p = 0,07).

Pour un texte en anglais, référez-vous à : https://www.socscistatistics.com/tutorials/correlation/default.aspx.

Références

Schwarzkopf, Dietrich, Benjamin de Haas et Geraint Rees. 2012. « Better ways to improve standards in brain-behavior correlation analysis. » Frontiers in Human Neuroscience 6: 200. https://www.frontiersin.org/articles/10.3389/fnhum.2012.00200.
Wilcox, Rand R. 1994. « The percentage bend correlation coefficient. » Psychometrika 59 (4): 601‑616. https://doi.org/10.1007/BF02294395.