6.1 Relation entre une variable quantitative et une variable qualitative à deux modalités

Les moyennes de deux groupes de population sont-elles significativement différentes? Nous souhaitons ici comparer deux groupes de population en fonction d’une variable continue. Par exemple, pour deux échantillons respectivement d’hommes et de femmes travaillant dans le même secteur d’activité, nous pourrions souhaiter vérifier si les moyennes des salaires des hommes et des femmes sont différentes et ainsi vérifier la présence ou l’absence d’une iniquité systématique. En études urbaines, dans le cadre d’une étude sur un espace public, nous pourrions vouloir vérifier si la différence des moyennes du sentiment de sécurité des femmes et des hommes est significative (c’est-à-dire différente de 0).

Pour un même groupe, la moyenne de la différence d’un phénomène donné mesuré à deux moments est-elle ou non égale à zéro? Autrement dit, nous cherchons à comparer un même groupe d’individus avant et après une expérimentation ou dans deux contextes différents. Prenons un exemple d’application en études urbaines. Dans le cadre d’une étude sur la perception des risques associés à la pratique du vélo en ville, 50 personnes utilisant habituellement l’automobile pour se rendre au travail sont recrutées. L’expérimentation pourrait consister à leur donner une formation sur la pratique du vélo en ville et à les accompagner quelques jours durant leurs déplacements domicile-travail. Nous évaluerons la différence de leurs perceptions des risques associés à la pratique du vélo sur une échelle de 0 à 100 avant et après l’expérimentation. Nous pourrions supposer que la moyenne des différences est significativement négative, ce qui indiquerait que la perception du risque a diminué après l’expérimentation; autrement dit, la perception du risque serait plus faible en fin de période.

6.1.1 Test t et ses différentes variantes

Le t de Student, appelé aussi test t (t-test en anglais), est un test paramétrique permettant de comparer les moyennes de deux groupes (échantillons), qui peuvent être indépendantes ou non :

• Échantillons indépendants (dits non appariés) : les observations de deux groupes qui n’ont aucun lien entre eux. Par exemple, nous souhaitons vérifier si les moyennes du sentiment de sécurité des hommes et des femmes, ou encore si, les moyennes des loyers entre deux villes sont statistiquement différentes. Ainsi, les tailles des deux échantillons peuvent être différentes (\(n_a \neq n_b\)).

• Échantillons dépendants (dits appariés) : les individus des deux groupes sont les mêmes et sont donc associés par paires. Autrement dit, nous avons deux séries de valeurs de taille identique \(n_a = n_b\) et \(n_{ai}\) est le même individu que \(n_{bi}\). Ce type d’analyse est souvent utilisée en études cliniques : pour \(n\) individus, nous disposons d’une mesure quantitative de leur état de santé pour deux séries (l’une avant le traitement, l’autre une fois le traitement terminé). Cela permet de comparer les mêmes individus avant et après un traitement; nous parlons alors d’étude, d’expérience ou d’analyse pré-post. Concrètement, nous cherchons à savoir si la moyenne des différences des observations avant et après est significativement différente de 0. Si c’est le cas, nous pouvons conclure que l’expérimentation a eu un impact sur le phénomène mesuré (variable continue). Ce type d’analyse pré-post peut aussi être utilisé pour évaluer l’impact du réaménagement d’un espace public (rue commerciale, place publique, parc, etc.). Par exemple, nous pourrions questionner le même échantillon de commerçant(e)s ou personnes l’utilisant avant et après le réaménagement d’une artère commerciale.

Condition d’application. Pour utiliser les tests de Student et de Welch, la variable continue doit être normalement distribuée. Si elle est fortement anormale, nous utiliserons le test non paramétrique de Wilcoxon (section 6.1.2). Il existe trois principaux tests pour comparer les moyennes de deux groupes :

• Test de Student (test t) avec échantillons indépendants et variances similaires (méthode pooled). Les variances de deux groupes sont semblables quand leur ratio varie de 0,5 à 2, soit \(\mbox{0,5}< (S^2_{X_A}/S^2_{X_B})<\mbox{2}\).
• Test de Welch (appelé aussi Satterthwaite) avec échantillons indépendants quand les variances des deux groupes sont dissemblables.
• Test de Student (test t) avec échantillons dépendants.

Il s’agit de vérifier si les moyennes des deux groupes sont statistiquement différentes avec les étapes suivantes :

• Nous posons l’hypothèse nulle (H₀), soit que les moyennes des deux groupes A et B ne sont pas différentes (\(\bar{X}_{A}=\bar{X}_{B}\)) ou, autrement dit, la différence des deux moyennes est nulle (\(\bar{X}_{A}-\bar{X}_{B}=0\)). L’hypothèse alternative (H₁) est donc \(\bar{X}_{A}\ne\bar{X}_{B}\).
• Nous calculons la valeur de t et le nombre de degrés de liberté. La valeur de t est négative quand la moyenne du groupe A est inférieure au groupe B et inversement.
• Nous comparons la valeur absolue de t (\(\mbox{|t|}\)) avec celle issue de la table des valeurs critiques de T (voir section 15) avec le bon nombre de degrés de liberté et en choisissant un degré de signification (habituellement, p = 0,05). Si \(\mbox{|t|}\) est supérieure à la valeur t critique, alors les moyennes sont statistiquement différentes au degré de signification retenu.
• Si les moyennes sont statistiquement différentes, nous pouvons calculer la taille de l’effet.

Cas 1. Test de Student pour des échantillons indépendants avec des variances similaires (méthode pooled). La valeur de t est le ratio entre la différence des moyennes des deux groupes (numérateur) et l’erreur type groupée des deux échantillons (dénominateur) :

\[\begin{equation} t = \frac{\bar{X}_{A}-\bar{X}_{B}}{\sqrt{\frac{S^2_p}{n_A}+\frac{S^2_p}{n_B}}}\mbox{ avec } S^2_p = \frac{(n_A-1)S^2_{X_A}+(n_B-1)S^2_{X_B}}{n_A+n_B-2} \tag{6.1} \end{equation}\]

avec \(n_A\),\(n_B\), \(S^2_{X_A}\) et \(S^2_{X_B}\) étant respectivement les nombres d’observations et les variances pour les groupes A et B, \(S^2_p\) étant la variance groupée des deux échantillons et \(n_A+n_B-2\) étant le nombre de degrés de liberté.

Cas 2. Test de Welch pour des échantillons indépendants (avec variances dissemblables). Le test de Welch est très similaire au test de Student; seul le calcul de la valeur de t est différent, pour tenir compte des variances respectives des groupes :

\[\begin{equation} t = \frac{\bar{X}_{A}-\bar{X}_{B}}{\sqrt{\frac{S^2_{X_A}}{n_A}+\frac{S^2_{X_B}}{n_B}}} \mbox{ et } dl = \frac{ \left( \frac{S^2_{X_A}}{n_A}+\frac{S^2_{X_B}}{n_B} \right)^2} {\frac{S^4_{X_A}}{n^2_A(n_A-1)}+\frac{S^4_{X_B}}{n^2_B(n_B-1)}} \tag{6.2} \end{equation}\]

Dans la syntaxe ci-dessous, nous avons écrit une fonction dénommée test_independants permettant de calculer les deux tests pour des échantillons indépendants. Dans cette fonction, vous pouvez repérer comment sont calculés les moyennes, les nombres d’observations et les variances pour les deux groupes, le nombre de degrés de liberté et les valeurs de t et de p pour les deux tests. Puis, nous avons créé aléatoirement deux jeux de données relativement à la vitesse de déplacement de cyclistes utilisant un vélo personnel ou un vélo en libre-service (généralement plus lourd) :

• Au cas 1, 60 cyclistes utilisant un vélo personnel roulant en moyenne à 18 km/h (écart-type de 1,5) et 50 autres utilisant un système de vélopartage avec une vitesse moyenne de 15 km/h (écart-type de 1,5).

• Au cas 2, 60 cyclistes utilisant un vélo personnel roulant en moyenne à 16 km/h (écart-type de 3) et 50 autres utilisant un système de vélopartage avec une vitesse moyenne de 15 km/h (écart-type de 1,5). Ce faible écart des moyennes, combiné à une plus forte variance réduit la significativité de la différence entre les deux groupes.

D’emblée, l’analyse visuelle des boîtes à moustaches (figure 6.1) signale qu’au cas 1, contrairement au cas 2, les groupes sont plus homogènes (boîtes plus compactes) et les moyennes semblent différentes (les boîtes sont centrées différemment sur l’axe des ordonnées). Cela est confirmé par les résultats des tests.

library("ggplot2")
library("ggpubr")
# fonction ------------------
tstudent_independants <- function(A, B){
    x_a <- mean(A)           # Moyenne du groupe A
    x_b <- mean(B)           # Moyenne du groupe B
    var_a <- var(A)          # Variance du groupe A
    var_b <- var(B)          # Variance du groupe B
    sd_a <- sqrt(var_a)      # Écart-type du groupe A
    sd_b <- sqrt(var_b)      # Écart-type du groupe B
    ratio_v <- var_a / var_b # ratio des variances
    n_a <- length(A)         # nombre d'observation du groupe A
    n_b <- length(B)         # nombre d'observation du groupe B
    
    # T-test (variances égales)
    dl_test <- n_a+n_b-2       # degrés de liberté
    PooledVar <- (((n_a-1)*var_a)+((n_b-1)*var_b))/dl_test
    t_test <- (x_a-x_b) / sqrt(((PooledVar/n_a)+(PooledVar/n_b)))
    p_test <-  2*(1-(pt(abs(t_test), dl_test)))     
    # Test Welch-Sattherwaite (variances inégales)
    t_welch <- (x_a-x_b) / sqrt( (var_a/n_a) + (var_b/n_b))
    dl_num = ((var_a/n_a) + (var_b/n_b))^2
    dl_dem = ((var_a/n_a)^2/(n_a-1))  + ((var_b/n_b)^2/(n_b-1))
    dl_welch = dl_num / dl_dem # degrés de liberté
    p_welch <- 2*(1-(pt(abs(t_welch), dl_welch)))     
    
    cat("\n groupe A (n = ", n_a,"), moy = ", round(x_a,1),", 
           variance = ", round(var_a,1),", écart-type = ", round(sd_a,1),
        "\n groupe B (n = ", n_b,"), moy = ", round(x_b,1),", 
          variance = ", round(var_b,1),", écart-type = ", round(sd_b,1),
        "\n ratio variance = ",round(ratio_v,2),
        "\n t-test (variances égales): t(dl = ", dl_test, ") = ",round(t_test,4),
         ", p = ", round(p_test,6),
         "\n t-Welch (variances inégales): t(dl = ", round(dl_welch,3), ") = ",
        round(t_welch,4), ", p = ", round(p_welch,6),  sep="")    
  
    if (ratio_v > 0.5 && ratio_v < 2)  {
      cat("\n Variances semblables. Utilisez le test de Student!")
      p <- p_test
    } else {
      cat("\n Variances dissemblables. Utilisez le test de Welch-Satterwaithe!")
      p <- p_welch
    }
    
    if (p <=.05){
      cat("\n Les moyennes des deux groupes sont significativement différentes.")
    } else {
      cat("\n Les moyennes des deux groupes ne sont pas significativement différentes.")
    }
}
# CAS 1 : données fictives ------------------
# Création du groupe A : 60 observations avec une vitesse moyenne de 18 et un écart-type de 1,5
Velo1A <- rnorm(60,18,1.5)
# Création du groupe B : 50 observations avec une vitesse moyenne de 15 et un écart-type de 1,5
Velo1B <- rnorm(50,15,1.5)
df1 <- data.frame(
  vitesse = c(Velo1A,Velo1B), 
  type = c(rep("Vélo personnel",length(Velo1A)), rep("Vélopartage",length(Velo1B)))
)
boxplot1 <- ggplot(data=df1, mapping=aes(x=type,y=vitesse, colour=type)) +
  geom_boxplot(width=0.2)+
  ggtitle("Données fictives (cas 1)")+
  xlab("Type de vélo")+
  ylab("Vitesse de déplacement (km/h)")+
  theme(legend.position = "none")
# CAS 2 : données fictives ------------------
# Création du groupe A : 60 observations avec une vitesse moyenne de 18 et un écart-type de 3
Velo2A <- rnorm(60,16,3)
# Création du groupe B : 50 observations avec une vitesse moyenne de 15 et un écart-type de 1,5
Velo2B <- rnorm(50,15,1.5)
df2 <- data.frame(
  vitesse = c(Velo2A,Velo2B), 
  type = c(rep("Vélo personnel",length(Velo2A)), rep("Vélopartage",length(Velo2B)))
)
boxplot2 <- ggplot(data=df2, mapping=aes(x=type,y=vitesse, colour=type)) +
  geom_boxplot(width=0.2)+
  ggtitle("Données fictives (cas 2)")+
  xlab("Type de vélo")+
  ylab("Vitesse de déplacement (km/h)")+
  theme(legend.position = "none")
ggarrange(boxplot1, boxplot2, ncol = 2, nrow = 1)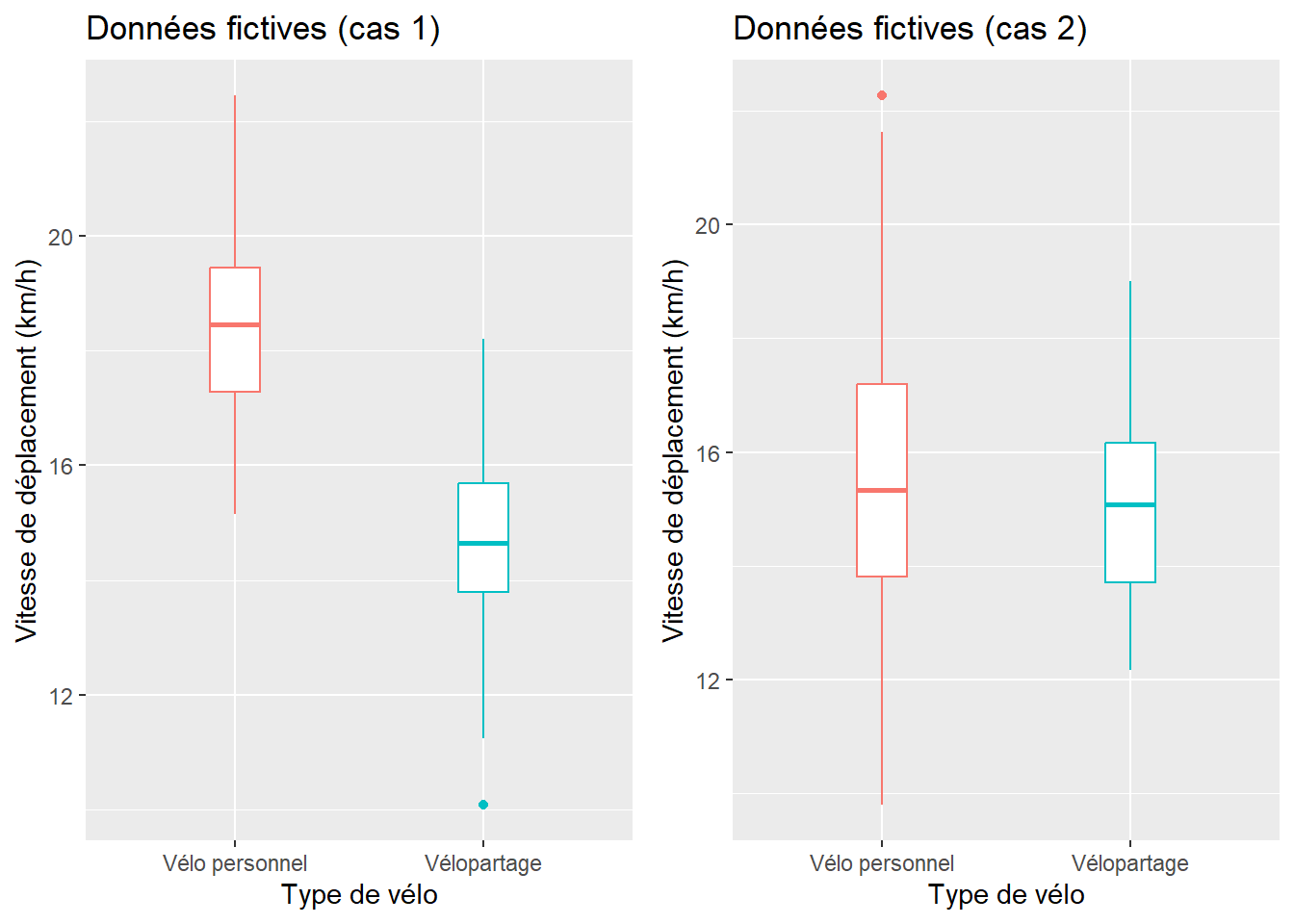

Figure 6.1: Boîtes à moustaches sur des échantillons fictifs non appariés

# Appel de la fonction pour le cas 1
tstudent_independants(Velo1A, Velo1B)

## 
##  groupe A (n = 60), moy = 18.4, 
##            variance = 2.4, écart-type = 1.6
##  groupe B (n = 50), moy = 14.7, 
##           variance = 2.5, écart-type = 1.6
##  ratio variance = 0.95
##  t-test (variances égales): t(dl = 108) = 12.3343, p = 0
##  t-Welch (variances inégales): t(dl = 103.376) = 12.3034, p = 0
##  Variances semblables. Utilisez le test de Student!
##  Les moyennes des deux groupes sont significativement différentes.

# Appel de la fonction pour le cas 2
tstudent_independants(Velo2A, Velo2B)

## 
##  groupe A (n = 60), moy = 15.3, 
##            variance = 7.4, écart-type = 2.7
##  groupe B (n = 50), moy = 15, 
##           variance = 2.5, écart-type = 1.6
##  ratio variance = 2.92
##  t-test (variances égales): t(dl = 108) = 0.7969, p = 0.427233
##  t-Welch (variances inégales): t(dl = 97.605) = 0.8336, p = 0.406549
##  Variances dissemblables. Utilisez le test de Welch-Satterwaithe!
##  Les moyennes des deux groupes ne sont pas significativement différentes.

6.1.1.1 Principe de base et formulation pour des échantillons dépendants (appariés)

Nous disposons de plusieurs personnes pour lesquelles nous avons mesuré un phénomène (variable continue) à deux temps différents : généralement avant et après une expérimentation (analyse pré-post). Il s’agit de vérifier si la moyenne des différences des observations avant et après la période est différente de 0. Pour ce faire, nous réalisons les étapes suivantes :

• Nous posons l’hypothèse nulle (H₀), soit que la moyenne des différences entre les deux séries est égale à 0 (\(\bar{D} = 0\) avec \(d = {x}_{t_1}- {x}_{t_2}\)). L’hypothèse alternative (H₁) est donc \(\bar{D} \ne 0\). Notez que nous pouvons tester une autre valeur que 0.
• Nous calculons la valeur de t et le nombre de degrés de liberté. La valeur de t est négative quand la moyenne des différences entre \({X}_{t_1}\) et \({X}_{t_2}\) est négative et inversement.
• Nous comparons la valeur absolue de t (\(\mbox{|t|}\)) avec celle issue de la table des valeurs critiques de T avec le nombre de degrés de liberté et en choisissant un degré de signification (habituellement, p = 0,05). Si \(\mbox{|t|}\) est supérieure à la valeur t critique, alors les moyennes sont statistiquement différentes au degré de signification retenu.

Pour le test de Student avec des échantillons appariés, la valeur de t se calcule comme suit :

\[\begin{equation} t = \frac{\bar{D}-\mu_0}{\sigma_D / \sqrt{n}} \tag{6.3} \end{equation}\]

avec \(\bar{D}\) étant la moyenne des différences entre les observations appariées de la série A et de la série B, \(\sigma_D\) l’écart des différences, n le nombre d’observations, et finalement \(\mu_0\) la valeur de l’hypothèse nulle que nous voulons tester (habituellement 0). Bien entendu, il est possible de fixer une autre valeur pour \(\mu_0\) : par exemple, avec \(\mu_0 = 10\), nous chercherions ainsi à vérifier si la moyenne des différences est significativement différente de 10. Le nombre de degrés de liberté est égal à \(n-1\).

Dans la syntaxe ci-dessous, nous avons écrit une fonction dénommée tstudent_dependants permettant de réaliser le test de Student pour des échantillons appariés. Dans cette fonction, vous pouvez repérer comment sont calculés la différence entre les observations pairées, la moyenne et l’écart-type de cette différence, puis le nombre de degrés de liberté, les valeurs de t et de p pour les deux tests.

Pour illustrer l’utilisation de la fonction, nous avons créé aléatoirement deux jeux de données. Imaginons que ces données décrivent 50 personnes utilisant habituellement l’automobile pour se rendre au travail. Pour ces personnes, nous avons généré des valeurs du risque perçu de l’utilisation du vélo (de 0 à 100), et ce, avant et après une période de 20 jours ouvrables durant lesquels elles devaient impérativement se rendre au travail à vélo.

• Au cas 1, les valeurs de risque ont une moyenne de 70 avant l’expérimentation et de 50 après l’expérimentation, avec des écarts-types de 5.
• Au cas 2, les valeurs de risque ont une moyenne de 70 avant et de 66 après, avec des écarts-types de 5.

D’emblée, l’analyse visuelle des boîtes à moustaches (figure 6.2) pairées montre que la perception du risque semble avoir nettement diminué après l’expérimentation pour le cas 1, mais pas pour le cas 2. Cela est confirmé par les résultats des tests.

library("ggplot2")
library("ggpubr")
tstudent_dependants <- function(A, B, mu=0){
  d <- A-B           # différences entre les observations pairées
  moy <- mean(d)     # Moyenne des différences
  e_t <- sd(d)       # Écart-type des différences
  n   <- length(A)   # nombre d'observations
  dl  <- n-1         # nombre de degrés de liberté (variances égales)
  
  t <- (moy- mu) / (e_t/sqrt(n)) # valeur de t
  p <-  2*(1-(pt(abs(t), dl)))
  
  cat("\n groupe A : moy = ", round(mean(A),1),", var = ", 
         round(var(A),1),", sd = ", round(sqrt(var(A)),1),
      "\n groupe B : moy = ", round(mean(B),1),", var = ", 
         round(var(B),1),", sd = ", round(sqrt(var(B)),1),
      "\n Moyenne des différences = ", round(mean(moy),1),
      "\n Ecart-type des différences = ", round(mean(e_t),1),
      "\n t(dl = ", dl, ") = ",round(t,2),
      ", p = ", round(p,3),  sep="")
  
  if (p <=.05){
    cat("\n La moyenne des différences entre les échantillons est significative")
  }
  else{
    cat("\n La moyenne des différences entre les échantillons n'est pas significative")
  }
}
# CAS 1 : données fictives ------------------
Avant1 <- rnorm(50,70,5)
Apres1 <- rnorm(50,50,5)
df1 <- data.frame(Avant=Avant1, Apres=Apres1)
boxplot1 <- ggpaired(df1, cond1 = "Avant", cond2 = "Apres", fill = "condition", 
                     palette = "jco", 
                     xlab="", ylab="Sentiment de sécurité", 
                     title = "Données fictives (cas 1)")
# CAS 2 : données fictives ------------------
Avant2 <- rnorm(50,70,5)
Apres2 <- rnorm(50,66,5)
df2 <- data.frame(Avant=Avant2, Apres=Apres2)
boxplot2 <- ggpaired(df2, cond1 = "Avant", cond2 = "Apres", fill = "condition",
                     palette = "jco", 
                     xlab="", ylab="Sentiment de sécurité", 
                     title = "Données fictives (cas 2)")
ggarrange(boxplot1, boxplot2, ncol = 2, nrow = 1)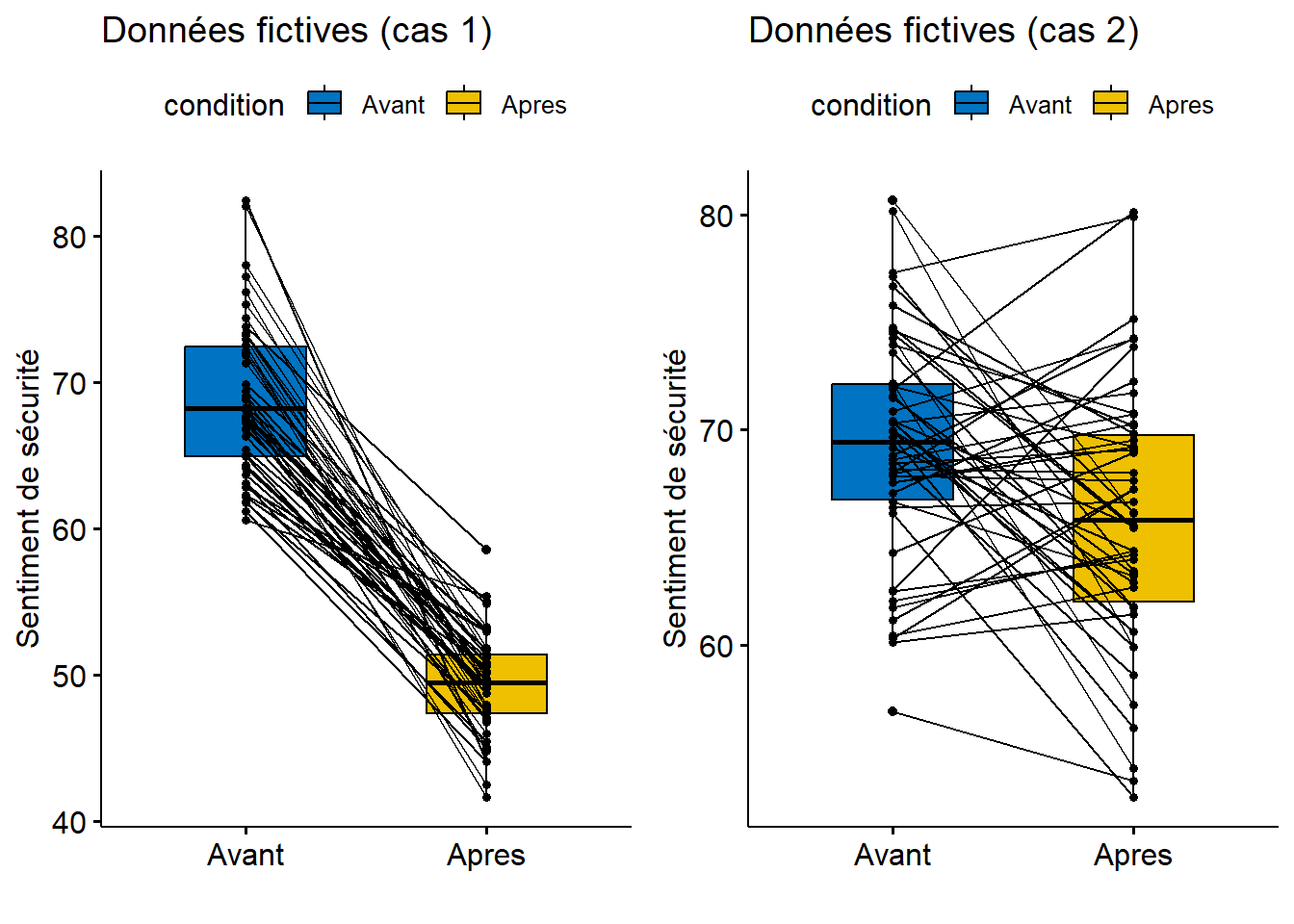

Figure 6.2: Boites à moustaches sur des échantillons fictifs appariés

# Test t : appel de la fonction tstudent_dependants
tstudent_dependants(Avant1, Apres1, mu=0)

## 
##  groupe A : moy = 68.9, var = 27.5, sd = 5.2
##  groupe B : moy = 49.4, var = 11.6, sd = 3.4
##  Moyenne des différences = 19.5
##  Ecart-type des différences = 6.3
##  t(dl = 49) = 21.76, p = 0
##  La moyenne des différences entre les échantillons est significative

tstudent_dependants(Avant2, Apres2, mu=0)

## 
##  groupe A : moy = 69.3, var = 28.5, sd = 5.3
##  groupe B : moy = 65.9, var = 37.6, sd = 6.1
##  Moyenne des différences = 3.3
##  Ecart-type des différences = 7.6
##  t(dl = 49) = 3.1, p = 0.003
##  La moyenne des différences entre les échantillons est significative

6.1.1.2 Mesure de la taille de l’effet

La taille de l’effet permet d’évaluer la magnitude (force) de l’effet d’une variable (ici la variable qualitative à deux modalités) sur une autre (ici la variable continue). Dans le cas d’une comparaison de moyennes (avec des échantillons pairés ou non), pour mesurer la taille de l’effet, nous utilisons habituellement le d de Cohen ou encore le g de Hedges; le second étant un ajustement du premier. Notez que nous analysons la taille de l’effet uniquement si le test de Student ou de Welch s’est révélé significatif (p < 0,05).

Pourquoi utiliser le d de Cohen? Deux propriétés en font une mesure particulièrement intéressante. Premièrement, elle est facile à calculer puisque d est le ratio entre la différence de deux moyennes de groupes (A, B) et l’écart-type combiné des deux groupes. Deuxièmement, d représente ainsi une mesure standardisée de la taille de l’effet; elle permet ainsi l’évaluation de la taille de l’effet indépendamment de l’unité de mesure de la variable continue. Concrètement, cela signifie que, quelle que soit l’unité de mesure de la variable continue X, d est toujours exprimée en unité d’écart-type de X. Cette propriété facilite ainsi grandement les comparaisons entre des valeurs de d calculées sur différentes combinaisons de variables (au même titre que le coefficient de variation ou le coefficient de corrélation, par exemple). Pour des échantillons indépendants de tailles différentes, le d de Cohen s’écrit :

\[\begin{equation} \frac{\bar{X}_{A}-\bar{X}_{B}}{\sqrt{\frac{(n_A-1)S^2_A+(n_B-1)S^2_B}{n_A+n_B-2}}} \tag{6.4} \end{equation}\]

avec \(n_A\), \(n_B\), \(S^2_{X_A}\) et \(S^2_{X_B}\) étant respectivement les nombres d’observations et les variances pour les groupes A et B, \(S^2_p\).

Si les échantillons sont de tailles identiques (\(n_A=n_B\)), alors d s’écrit :

\[\begin{equation} d = \frac{\bar{X}_{A}-\bar{X}_{B}}{\sqrt{(S^2_A+\S^2_B)/2}} = \frac{\bar{X}_{A}-\bar{X}_{B}}{(\sigma_A+\sigma_B)/2} \tag{6.5} \end{equation}\]

avec \(\sigma_A\) et \(\sigma_B\) étant les écarts-types des deux groupes (rappel : l’écart-type est la racine carrée de la variance).

Le g de Hedge est simplement une correction de d, particulièrement importante quand les échantillons sont de taille réduite.

\[\begin{equation} g = d- \left(1- \frac{3}{4(n_A+n_B)-9} \right) \tag{6.6} \end{equation}\]

Moins utilisé en sciences sociales, mais surtout en études cliniques, le delta de Glass est simplement la différence des moyennes des deux groupes indépendants (numérateur) sur l’écart-type du deuxième groupe (démoninateur). Dans une étude clinique, nous avons habituellement un groupe qui subit un traitement (groupe de traitement) et un groupe qui reçoit un placebo (groupe de contrôle ou groupe témoin). L’effet de taille est ainsi évalué par rapport au groupe de contrôle :

\[\begin{equation} \Delta = \frac{\bar{X}_{A}-\bar{X}_{B}}{\sigma_B} \tag{6.7} \end{equation}\]

Finalement, pour des échantillons dépendants (pairés), le delta de Glass s’écrit : \(d = \bar{D}/{\sigma_D}\) avec \(\bar{D}\) et \(\sigma_D\) étant la moyenne et l’écart-type des différences entre les observations.

Comment interpréter le d de Cohen? Un effet est considéré comme faible avec \(\lvert d \rvert\) à 0,2, modéré à 0,50 et fort à 0,80 (Cohen 1992). Notez que ces seuils ne sont que des conventions pour vous guider à interpréter la mesure de Cohen. D’ailleurs, dans son livre intitulé Statistical power analysis for the behavioral sciences, il écrit : « all conventions are arbitrary. One can only demand of them that they not be unreasonable » (Cohen 2013). Plus récemment, Sawilowsky (2009) a ajouté d’autres seuils à ceux proposés par Cohen (tableau 6.1).

Tableau 6.1: Conventions pour l’interprétation du d de Cohen

Sawilowsky	Cohen
0,1 : Très faible
0,2 : Faible	0,2 : Faible
0,5 : Moyen	0,5 : Moyen
0,8 : Fort	0,8 : Fort
1,2 : Très fort
2,0 : Énorme

6.1.1.3 Mise en œuvre dans R

Nous avons écrit précédemment les fonctions tstudent_independants et tstudent_dependants uniquement pour décomposer les différentes étapes de calcul des tests de Student et de Welch. Heureusement, il existe des fonctions de base (t.test et var.test) qui permettent de réaliser l’un ou l’autre de ces deux tests avec une seule ligne de code.

La fonction t.test permet ainsi de calculer les tests de Student et de Welch :

• t.test(x ~ y, data=, mu = 0, paired = FALSE, var.equal = FALSE, conf.level = 0.95) ou t.test(x =, y =, mu = 0, paired = FALSE, var.equal = FALSE, conf.level = 0.95).
• Le paramètre paired est utilisé pour spécifier si les échantillons sont dépendants (paired=TRUE) ou indépendants (paired=FALSE).
• Le paramètre var.equal est utilisé pour spécifier si les variances sont égales pour le test de Student (var.equal=TRUE) ou dissemblables pour le test de Welch (var.equal=FALSE).
• var.test(x, y) ou var.test(x ~ y, data=) pour vérifier au préalable si les variances sont égales ou non et choisir ainsi un t de Student ou un t de Welch.

Les fonctions cohens_d et hedges_g du package effectsize renvoient respectivement les mesures de d de Cohen et du g de Hedge :

• cohens_d(x ~ y, data = DataFrame, paired = FALSE, pooled_sd = TRUE) ou cohens_d(x, y, data = DataFrame, paired = FALSE, pooled_sd = TRUE)

• hedges_g(x ~ y, data = DataFrame, paired = FALSE, pooled_sd = TRUE) ou hedges_g(x, y, data = DataFrame, paired = FALSE, pooled_sd = TRUE)

• glass_delta(x ~ y, data = DataFrame, paired = FALSE, pooled_sd = TRUE) ou glass_delta(x, y, data = DataFrame, paired = FALSE, pooled_sd = TRUE)

Notez que pour toutes ces fonctions, deux écritures sont possibles :

• x ~ y, data= avec un DataFrame dans lequel x est une variable continue et y et un facteur binaire
• x, y qui sont tous deux des vecteurs numériques (variable continue).

Exemple de test pour des échantillons indépendants

La figure 6.3 représente la cartographie du pourcentage de locataires par secteur de recensement (SR) pour la région métropolitaine de recensement de Montréal (RMR) en 2016, soit une variable continue. L’objectif est de vérifier si la moyenne de ce pourcentage des SR de l’agglomération de Montréal est significativement différente de celles de SR hors de l’agglomération.

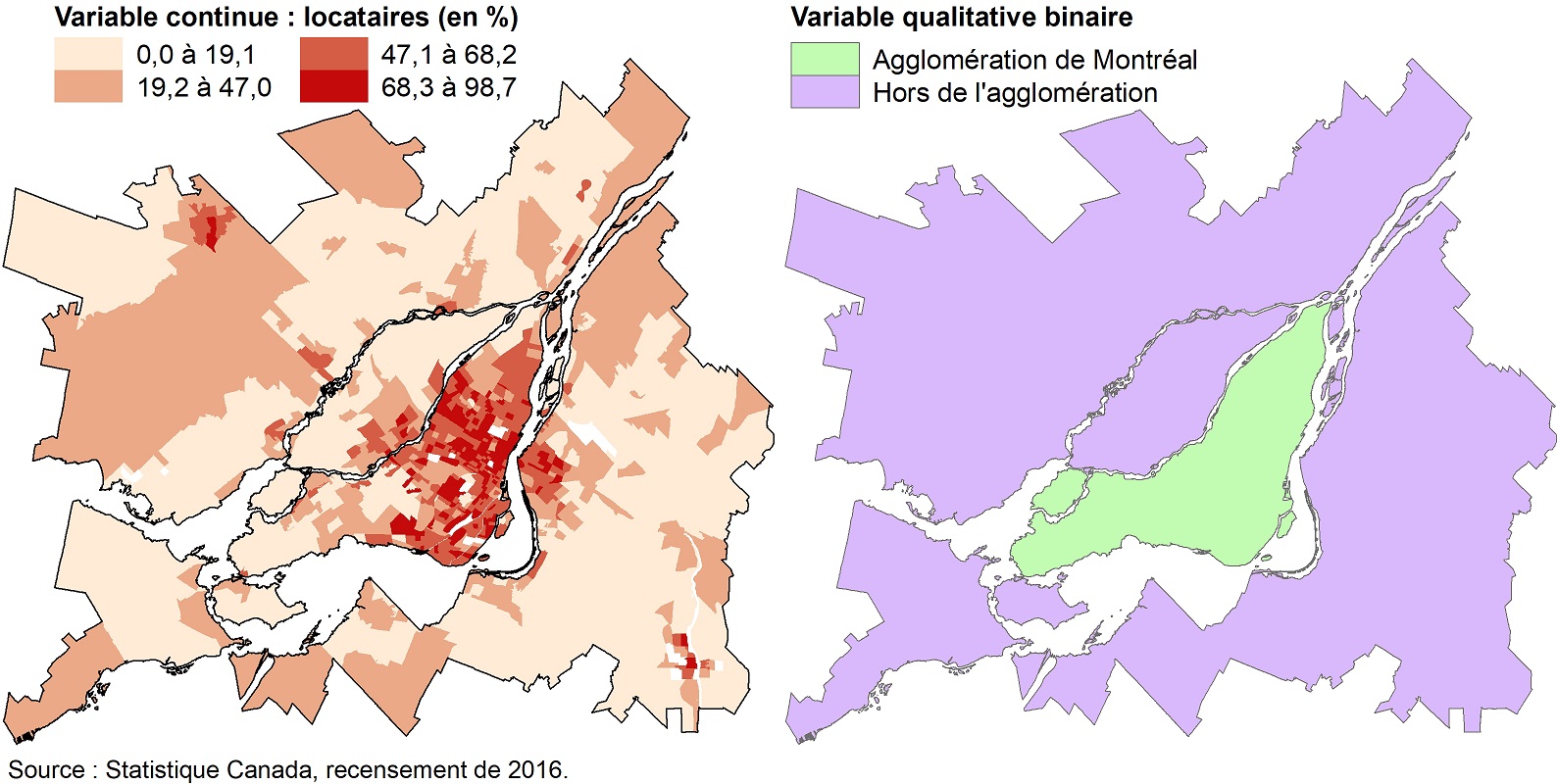
Figure 6.3: Pourcentage de locataires par secteur de recensement, région métropolitaine de recensement de Montréal, 2016

Les résultats de la syntaxe ci-dessous signalent que le pourcentage de locataires par SR est bien supérieur dans l’agglomération (moyenne = 59,7 %; écart-type = 21,4 %) qu’en dehors de l’agglomération de Montréal (moyenne = 27,3 %; écart-type = 20,1 %). Cette différence de 32,5 points de pourcentage est d’ailleurs significative et très forte (t = -23,95; p < 0,001, d de Cohen = 1,54).

library("foreign")
library("effectsize")
library("ggplot2")
library("dplyr")
# Importation du fichier
dfRMR <- read.dbf("data/bivariee/SRRMRMTL2016.dbf")
# Définition d'un facteur binaire                  
dfRMR$Montreal <- factor(dfRMR$Montreal, 
                           levels=  c(0,1), 
                           labels = c("Hors de Montréal","Montréal"))
# Comparaison des moyennes ------------------------
#Boite à moustaches (boxplot)
ggplot(data = dfRMR, mapping=aes(x=Montreal,y=Locataire,colour=Montreal)) +
  geom_boxplot(width=0.2)+
  theme(legend.position="none")+
  xlab("Zone")+ ylab("Pourcentage de locataires")+
  ggtitle("Locataires par secteur de recensement", 
          subtitle="région métropolitaine de recensement de Montréal, 2016")

# nombre d'observations, moyennes et écarts-types pour les deux échantillons
group_by(dfRMR, Montreal) %>%
  summarise(
    n = n(),
    moy = mean(Locataire, na.rm = TRUE),
    ecarttype = sd(Locataire, na.rm = TRUE)
  )

## # A tibble: 2 × 4
##   Montreal             n   moy ecarttype
##   <fct>            <int> <dbl>     <dbl>
## 1 Hors de Montréal   430  27.3      20.1
## 2 Montréal           521  59.7      21.4

# Nous vérifions si les variances sont égales avec la fonction var.test
# quand la valeur de P est inférieure à 0,05 alors les variances diffèrent
v <- var.test(Locataire ~ Montreal, alternative='two.sided', conf.level=.95, data=dfRMR)
print(v)

## 
##  F test to compare two variances
## 
## data:  Locataire by Montreal
## F = 0.88156, num df = 429, denom df = 520, p-value = 0.1739
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.7361821 1.0573195
## sample estimates:
## ratio of variances 
##          0.8815563

Le test indique que nous n’avons aucune raison de rejeter l’hypothèse nulle selon laquelle les variances sont égales. Pour l’île de Montréal, l’écart-type est de 21,4; il est de 20,1 hors de l’île, soit une différence négligeable.

# Calcul du T de Student ou du T de Welch
p <- v$p.value
if(p >= 0.05){
  cat("\n Les variances ne diffèrent pas!",
     "\n Nous utilisons le test de Student avec l'option var.equal=TRUE", sep="")
    t.test(Locataire ~ Montreal,  # variable continue ~ facteur binaire 
           data=dfRMR,            # nom du DataFrame
           conf.level=.95,        # intervalle de confiance pour la valeur de t
           paired = FALSE,        # échantillons non pairés (indépendants)
           var.equal=TRUE)        # variances égales
} else {
  cat("\n Les variances diffèrent!",
      "\n Nous utiliseons le test de Welch avec l'option var.equal=FALSE", sep="")
  t.test(Locataire ~ Montreal,   # variable continue ~ facteur binaire 
         data=dfRMR,             # nom du DataFrame
         conf.level=.95,         # intervalle de confiance pour la valeur de t
         paired = FALSE,         # échantillons non pairés (indépendants)
         var.equal=FALSE)        # variances différentes
}

## 
##  Les variances ne diffèrent pas!
##  Nous utilisons le test de Student avec l'option var.equal=TRUE

## 
##  Two Sample t-test
## 
## data:  Locataire by Montreal
## t = -23.95, df = 949, p-value < 2.2e-16
## alternative hypothesis: true difference in means between group Hors de Montréal and group Montréal is not equal to 0
## 95 percent confidence interval:
##  -35.11182 -29.79341
## sample estimates:
## mean in group Hors de Montréal         mean in group Montréal 
##                       27.27340                       59.72601

# Effet de taille à analyser uniquement si le test est significatif
cohens_d(Locataire ~ Montreal, data = dfRMR, paired = FALSE)

## Cohen's d |         95% CI
## --------------------------
## -1.56     | [-1.71, -1.41]
## 
## - Estimated using pooled SD.

hedges_g(Locataire ~ Montreal, data = dfRMR, paired = FALSE)

## Hedges' g |         95% CI
## --------------------------
## -1.56     | [-1.70, -1.41]
## 
## - Estimated using pooled SD.

Notez que les valeurs du d de Cohen et du g de Hedge sont très semblables; rappelons que le second est une correction du premier pour des échantillons de taille réduite. Avec 951 observations, nous disposons d’un échantillon suffisamment grand pour que cette correction soit négligeable.

Exemple de syntaxe pour un test de Student pour des échantillons dépendants

library("ggpubr")
library("dplyr")
Pre <- c(79,71,81,83,77,74,76,74,79,70,66,85,69,69,82,
         69,81,70,83,68,77,76,77,70,68,80,65,65,75,84)
Post <- c(56,47,40,45,49,51,54,47,44,54,42,56,45,45,48,
          55,59,58,56,41,56,51,45,55,49,49,48,43,60,50)
# Première façon de faire un tableau : avec deux colonnes Avant et Après
df1 <- data.frame(Avant=Pre, Apres=Post)
head(df1)

##   Avant Apres
## 1    79    56
## 2    71    47
## 3    81    40
## 4    83    45
## 5    77    49
## 6    74    51

ggpaired(df1, cond1 = "Avant", cond2 = "Apres", fill = "condition", palette = "jco",
         xlab="", ylab="Variable continue")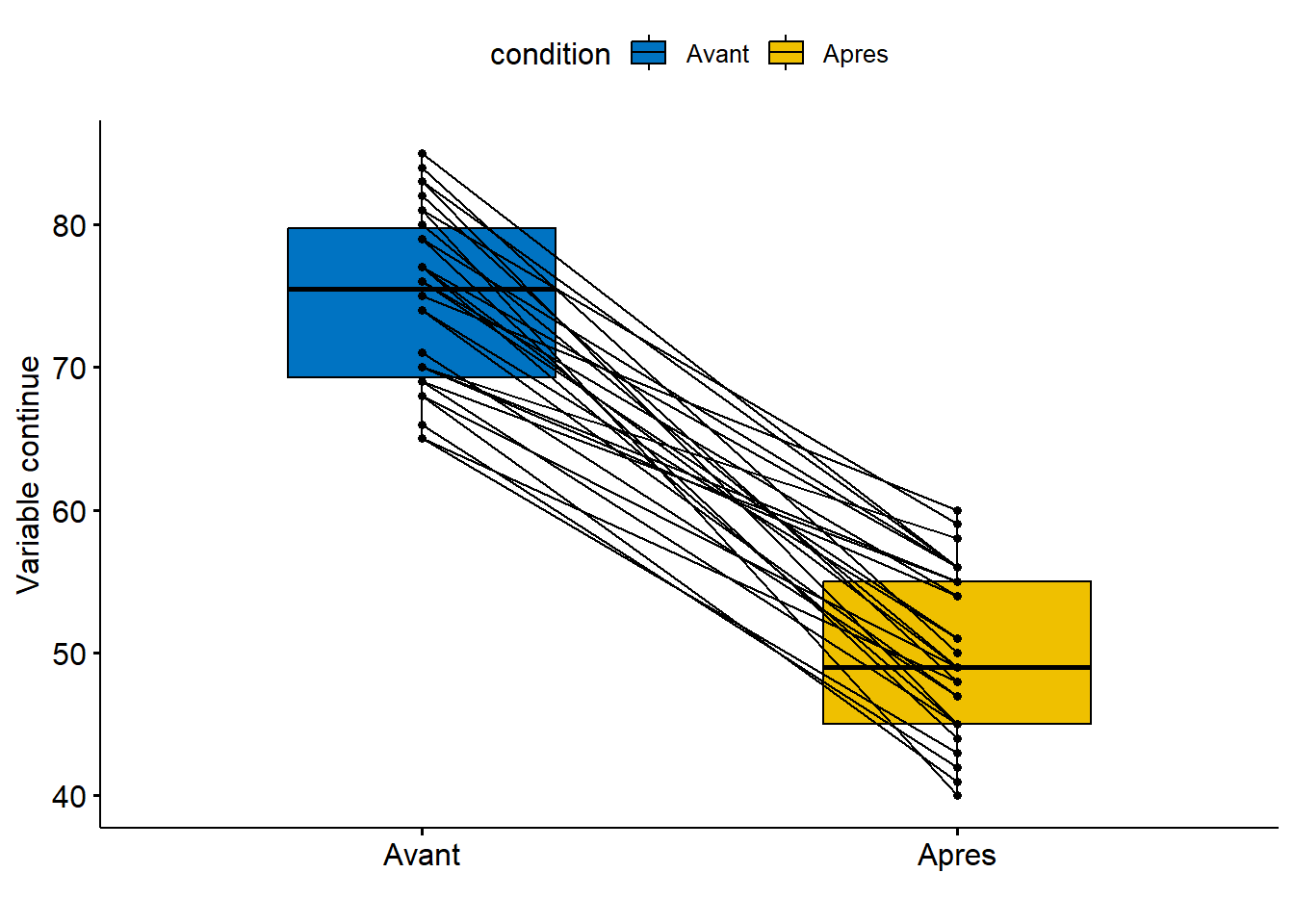

# Nombre d'observations, moyennes et écart-types
cat(nrow(df1), " observations",
    "\nPOST. moy = ", round(mean(df1$Avant),1), ", e.t. = ", round(sd(df1$Avant),1),
    "\nPRE.  moy = ", round(mean(df1$Apres),1), ", e.t. = ", round(sd(df1$Apres),1), sep="")

## 30 observations
## POST. moy = 74.8, e.t. = 6.1
## PRE.  moy = 49.9, e.t. = 5.7

t.test(Pre, Post, paired = TRUE)

## 
##  Paired t-test
## 
## data:  Pre and Post
## t = 18.701, df = 29, p-value < 2.2e-16
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
##  22.11740 27.54926
## sample estimates:
## mean difference 
##        24.83333

# Deuxième façon de faire un tableau : avec une colonne pour la variable continue
# et une autre pour la variable qualitative
n <- length(Pre)*2
df2 <- data.frame(
       id=(1:n),
       participant=(1:length(Pre)),
       risque=c(Pre,Post)
       )
df2$periode <- ifelse(df2$id <= length(Pre), "Pré", "Post")
head(df2)

##   id participant risque periode
## 1  1           1     79     Pré
## 2  2           2     71     Pré
## 3  3           3     81     Pré
## 4  4           4     83     Pré
## 5  5           5     77     Pré
## 6  6           6     74     Pré

# nombre d'observations, moyennes et écarts-types pour les deux échantillons
group_by(df2, periode) %>%
  summarise(
    n = n(),
    moy = mean(risque, na.rm = TRUE),
    et = sd(risque, na.rm = TRUE)
    )

## # A tibble: 2 × 4
##   periode     n   moy    et
##   <chr>   <int> <dbl> <dbl>
## 1 Post       30  49.9  5.67
## 2 Pré        30  74.8  6.10

ggpaired(data=df2, x= "periode", y="risque", fill = "periode",
         xlab="", ylab="Variable continue")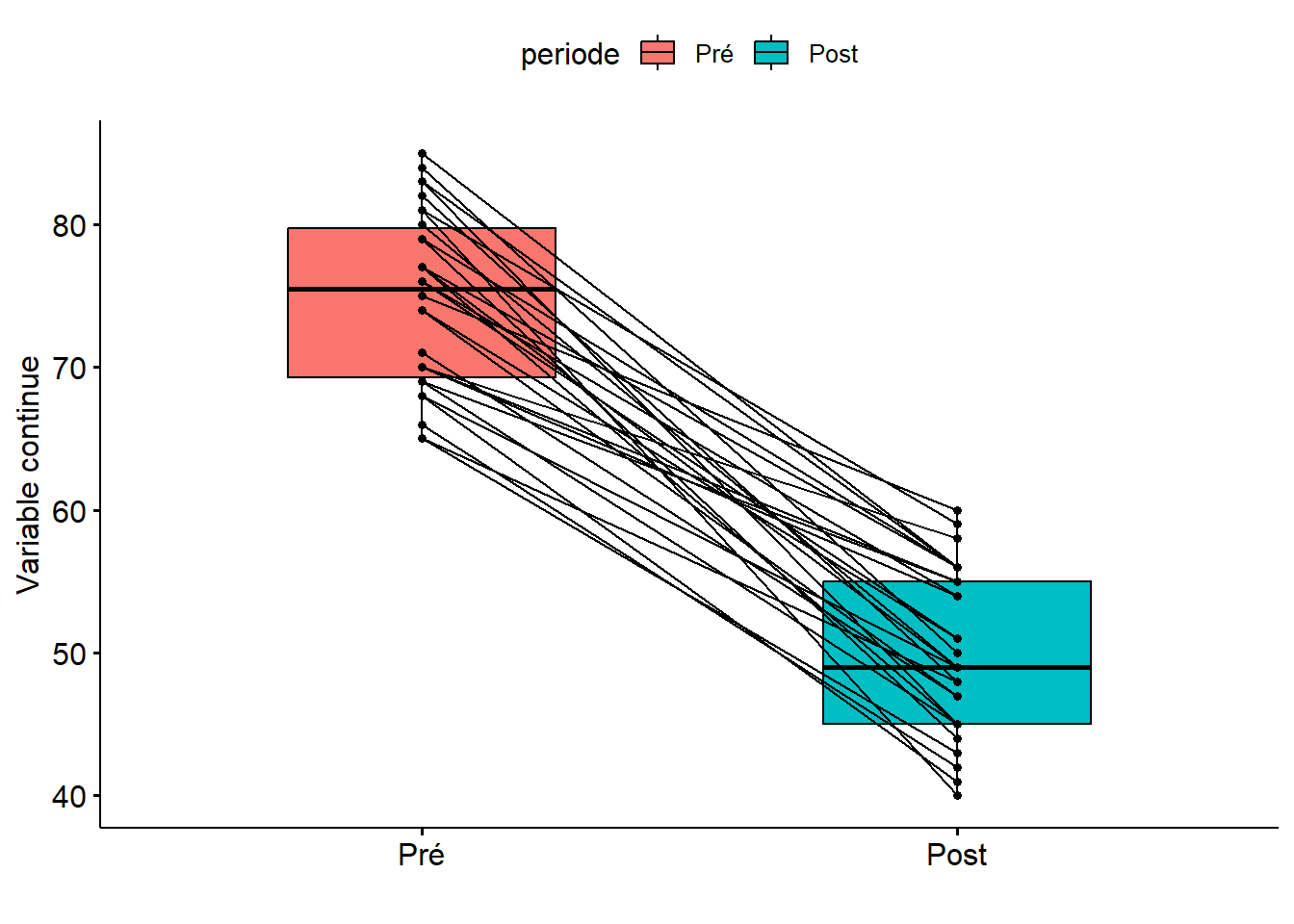

t.test(risque ~ periode, data=df2, paired = TRUE)

## 
##  Paired t-test
## 
## data:  risque by periode
## t = -18.701, df = 29, p-value < 2.2e-16
## alternative hypothesis: true mean difference is not equal to 0
## 95 percent confidence interval:
##  -27.54926 -22.11740
## sample estimates:
## mean difference 
##       -24.83333

6.1.1.4 Comparaison des moyennes pondérées

En études urbaines et en géographie, le recours aux données agrégées (non individuelles) est fréquent, par exemple au niveau des secteurs de recensement (comprenant généralement entre 2500 à 8000 habitants). Dans ce contexte, un secteur de recensement plus peuplé devrait avoir un poids plus important dans l’analyse. Il est possible d’utiliser les versions pondérées des tests présentés précédemment. Prenons deux exemples pour illustrer le tout :

• Pour chaque secteur de recensement des îles de Montréal et de Laval, nous avons calculé la distance au parc le plus proche à travers le réseau de rues avec un système d’information géographique (SIG). Nous souhaitons vérifier si les personnes âgées de moins de 15 ans résidant sur l’île de Montréal bénéficient en moyenne d’une meilleure accessibilité au parc.

• Dans une étude sur la concentration de polluants atmosphériques dans l’environnement autour des écoles primaires montréalaises, Carrier et al. (2014) souhaitaient vérifier si les élèves fréquentant les écoles les plus défavorisées sont plus exposé(e)s au dioxyde d’azote (NO₂) dans leur milieu scolaire. Pour ce faire, ils ont réalisé un test t sur un tableau avec comme observations les écoles primaires et trois variables : la moyenne de NO₂ (variable continue), les quintiles extrêmes d’un indice de défavorisation (premier et dernier quintiles, variable qualitative) et le nombre d’élèves par école (variable pour la pondération).

Pour réaliser un test t pondéré, nous pouvons utiliser la fonction weighted_ttest du package sjstats.

En guise d’exemple appliqué, dans la syntaxe ci-dessous, nous avons refait le même test t que précédemment (Locataire ~ Montreal) en pondérant chaque secteur de recensement par le nombre de logements qu’il comprend.

library("sjstats")
library("dplyr")
# Calcul des statistiques pondérées
group_by(dfRMR, Montreal) %>%
  summarise(
    n = sum(Logement),
    MoyPond = weighted_mean(Locataire, Logement),
    ecarttypePond = weighted_sd(Locataire, Logement)
  )

## # A tibble: 2 × 4
##   Montreal              n MoyPond ecarttypePond
##   <fct>             <int>   <dbl>         <dbl>
## 1 Hors de Montréal 856928    28.4          19.9
## 2 Montréal         870354    60.0          20.8

# Test t non pondéré
t.test(Locataire ~ Montreal, dfRMR, 
               paired = FALSE, var.equal = TRUE, conf.level=.95)

## 
##  Two Sample t-test
## 
## data:  Locataire by Montreal
## t = -23.95, df = 949, p-value < 2.2e-16
## alternative hypothesis: true difference in means between group Hors de Montréal and group Montréal is not equal to 0
## 95 percent confidence interval:
##  -35.11182 -29.79341
## sample estimates:
## mean in group Hors de Montréal         mean in group Montréal 
##                       27.27340                       59.72601

# Test t pondérée
weighted_ttest(Locataire ~ Montreal + Logement, dfRMR, 
               paired = FALSE, ci.lvl=.95)

## 
## Two-Sample t-test (two.sided)
## 
## # comparison of Locataire by Montreal
## # t=-23.91  df=928  p-value=0.000
## 
##   mean in group Hors de Montréal: 28.396
##   mean in group Montréal        : 60.003
##   difference of mean            : -31.608 [-34.202  -29.013]

6.1.1.5 Comment rapporter un test de Student ou de Welch?

Pour les différentes versions du test, il est important de rapporter les valeurs de t et de p, les moyennes et écarts-types des groupes. Voici quelques exemples.

Test de Student ou de Welch pour échantillons indépendants

• Dans la région métropolitaine de Montréal en 2005, le revenu total des femmes (moyenne = 29 117 dollars; écart-type = 258 022) est bien inférieur à celui des hommes (moyenne = 44 463; écart-type = 588 081). La différence entre les moyennes des deux sexes (-15 345) en faveur des hommes est d’ailleurs significative (t = -27,09; p < 0,001).
• Il y un effet significatif selon le sexe (t = -27,09; p < 0,001), le revenu total des hommes (moyenne = 44 463; écart-type = 588 081) étant bien supérieur à celui des femmes (moyenne = 29 117; écart-type = 258 022).
• 50 personnes se rendent au travail à vélo (moyenne = 33,7; écart-type = 8,5) contre 60 en automobile (moyenne = 34; écart-type = 8,7). Il n’y a pas de différence significative entre les moyennes d’âge des deux groupes (t(108) = -0,79; p = 0,427).

Test de Student échantillons dépendants (pairés)

• Nous constatons une diminution significative de la perception du risque après l’activité (moyenne = 49,9; écart-type = 5,7) comparativement à avant (moyenne = 74,8; écart-type = 6,1), avec une différence de -24,8 (t(29) = -18,7; p < 0,001).
• Les résultats du pré-test (moyenne = 49,9; écart-type = 5,7) et du post-test (moyenne = 74,8; écart-type = 6,1) montrent qu’il y une diminution significative de la perception du risque (t(29) = -18,7; p < 0,001).

Pour un texte en anglais, consultez https://www.socscistatistics.com/tutorials/ttest/default.aspx.

6.1.2 Test non paramétrique de Wilcoxon

Si la variable continue est fortement anormalement distribuée, il est déconseillé d’utiliser les tests de Student et de Welch. Nous privilégions le test des rangs signés de Wilcoxon (Wilcoxon rank-sum test en anglais). Attention, il est aussi appelé test U de Mann-Whitney. Ce test permet alors de vérifier si les deux groupes présentent des médianes différentes.

Pour ce faire, nous utilisons la fonction wilcox.test dans laquelle le paramètre paired permet de spécifier si les échantillons sont indépendants ou non (FALSE ou TRUE).

Dans l’exemple suivant, nous analysons le pourcentage de locataires dans les secteurs de recensement de la région métropolitaine de Montréal. Plus spécifiquement, nous comparons ce pourcentage entre les secteurs présents sur l’île et les secteurs hors de l’île. Il s’agit donc d’un test avec des échantillons indépendants.

library("foreign")
library("dplyr")
###############################
# Échantillons indépendants
###############################
dfRMR <- read.dbf("data/bivariee/SRRMRMTL2016.dbf")
# Définition d'un facteur binaire                  
dfRMR$Montreal <- factor(dfRMR$Montreal, 
                           levels=  c(0,1), 
                           labels = c("Hors de Montréal","Montréal"))
# Calcul du nombre d'observations, des moyennes et 
# des écarts-types des rangs pour les deux échantillons
group_by(dfRMR, Montreal) %>%
  summarise(
    n = n(),
    moy_rang = mean(rank(Locataire), na.rm = TRUE),
    med_rang = median(rank(Locataire), na.rm = TRUE),
    ecarttype_rang = sd(rank(Locataire), na.rm = TRUE)
  )

## # A tibble: 2 × 5
##   Montreal             n moy_rang med_rang ecarttype_rang
##   <fct>            <int>    <dbl>    <dbl>          <dbl>
## 1 Hors de Montréal   430     216.     216.           124.
## 2 Montréal           521     261      261            151.

# Test des rangs signés de Wilcoxon sur des échantillons indépendants
wilcox.test(Locataire ~ Montreal, dfRMR, paired = FALSE)

## 
##  Wilcoxon rank sum test with continuity correction
## 
## data:  Locataire by Montreal
## W = 33716, p-value < 2.2e-16
## alternative hypothesis: true location shift is not equal to 0

Nous observons bien ici une différence significative entre le pourcentage de locataires des secteurs de recensement sur l’île (rang médian = 216) et ceux en dehors de l’île (rang médian = 261).

Pour le second exemple, nous générons deux jeux de données au hasard représentant une mesure d’une variable pré-traitement (pre) et post-traitement (post) pour un même échantillon.

###############################
# Échantillons dépendants
###############################
pre <- sample(60:80, 50, replace=T)
post <- sample(30:65, 50, replace=T)
df1 <- data.frame(Avant=pre, Apres=post)
# Nombre d'observations, moyennes et écart-types
cat(nrow(df1), " observations",
    "\nPOST. median = ", round(median(df1$Avant),1), 
             ", moy = ", round(mean(df1$Avant),1),
    "\nPRE.  median = ", round(median(df1$Apres),1), 
             ", moy = ", round(mean(df1$Apres),1), sep="")

## 50 observations
## POST. median = 71, moy = 70.4
## PRE.  median = 49.5, moy = 50

wilcox.test(df1$Avant, df1$Apres, paired = TRUE)

## 
##  Wilcoxon signed rank test with continuity correction
## 
## data:  df1$Avant and df1$Apres
## V = 1265, p-value = 1.411e-09
## alternative hypothesis: true location shift is not equal to 0

À nouveau, nous obtenons une différence significative entre les deux variables.

Comment rapporter un test de Wilcoxon?

Lorsque nous rapportons les résultats d’un test de Wilcoxon, il est important de signaler la valeur du test (W), le degré de signification (valeur de p) et éventuellement la médiane des rangs ou de la variable originale pour les deux groupes. Voici quelques exemples :

• Les résultats du test des rangs signés de Wilcoxon signalent que les rangs de l’île de Montréal sont significativement plus élevés que ceux de l’île de Laval (W = 1223, p < 0,001).
• Les résultats du test de Wilcoxon signalent que les rangs post-tests sont significativement plus faibles que ceux du pré-test (W = 1273,5, p < 0,001).
• Les résultats du test de Wilcoxon signalent que la médiane des rangs pré-tests (médiane = 69) est significativement plus forte que celle du post-test (médiane = 50,5) (W = 1273,5, p < 0,001).

Références

Carrier, Mathieu, Philippe Apparicio, Anne-Marie Séguin et Dan Crouse. 2014. « Ambient air pollution concentration in Montreal and environmental equity: Are children at risk at school? » Case Studies on Transport Policy 2 (2): 61‑69. https://doi.org/10.1016/j.cstp.2014.06.003.

Cohen, Jacob. 1992. « A power primer. » Psychological bulletin 112 (1): 155‑159. https://doi.org/10.1037/0033-2909.112.1.155.

———. 2013. Statistical power analysis for the behavioral sciences. Academic press.

Sawilowsky, Shlomo S. 2009. « New effect size rules of thumb. » Journal of Modern Applied Statistical Methods 8 (2): 467‑474. https://doi.org/10.22237/jmasm/1257035100.