13.3 Classification ascendante hiérarchique

La classification ascendante hiérarchique (CAH) est un algorithme de classification non supervisée dont l’objectif est de créer un arbre de classification des observations. Cet arbre est ensuite utilisé pour déterminer le nombre de groupes à former et à quel groupe appartient chaque observation.

13.3.1 Fonctionnement de l’algorithme

La classification ascendante hiérarchique est un algorithme permettant de regrouper les observations d’un jeu de données de façon itérative. À chaque itération, deux observations similaires sont agrégées en un groupe représenté par le point central entre les deux observations. Le processus est ensuite répété en considérant le nouveau point comme une observation jusqu’à ce que toutes les observations soient fusionnées en un seul groupe.

Ces regroupements successifs créent un arbre de classification appelé dendrogramme. La racine de cet arbre est le groupe unique fusionnant toutes les observations, et ses branches correspondent aux différentes agrégrations effectuées jusqu’aux observations individuelles. Cet arbre peut être vu comme une hiérarchie de classification. Chaque niveau de l’arbre est un regroupement de plus en plus généraliste au fur et à mesure que nous nous approchons de sa racine.

Pour appliquer cette méthode, il est nécessaire de sélectionner une fonction de distance pour mesurer la dissimilarité ou la ressemblance entre deux observations. L’algorithme fonctionne avec n’importe quelle fonction de distance, ce qui permet de l’appliquer aussi bien à des données qualitatives que quantitatives. En effet, l’opération de regroupement des observations se base sur une matrice de distance, soit un tableau de taille n x n indiquant pour chaque paire d’observations leur degré de dissimilarité. La figure 13.11 illustre cette transformation en appliquant la distance du \(\Phi^2\) à un jeu de données comprenant cinq observations et 5 variables qualitatives.

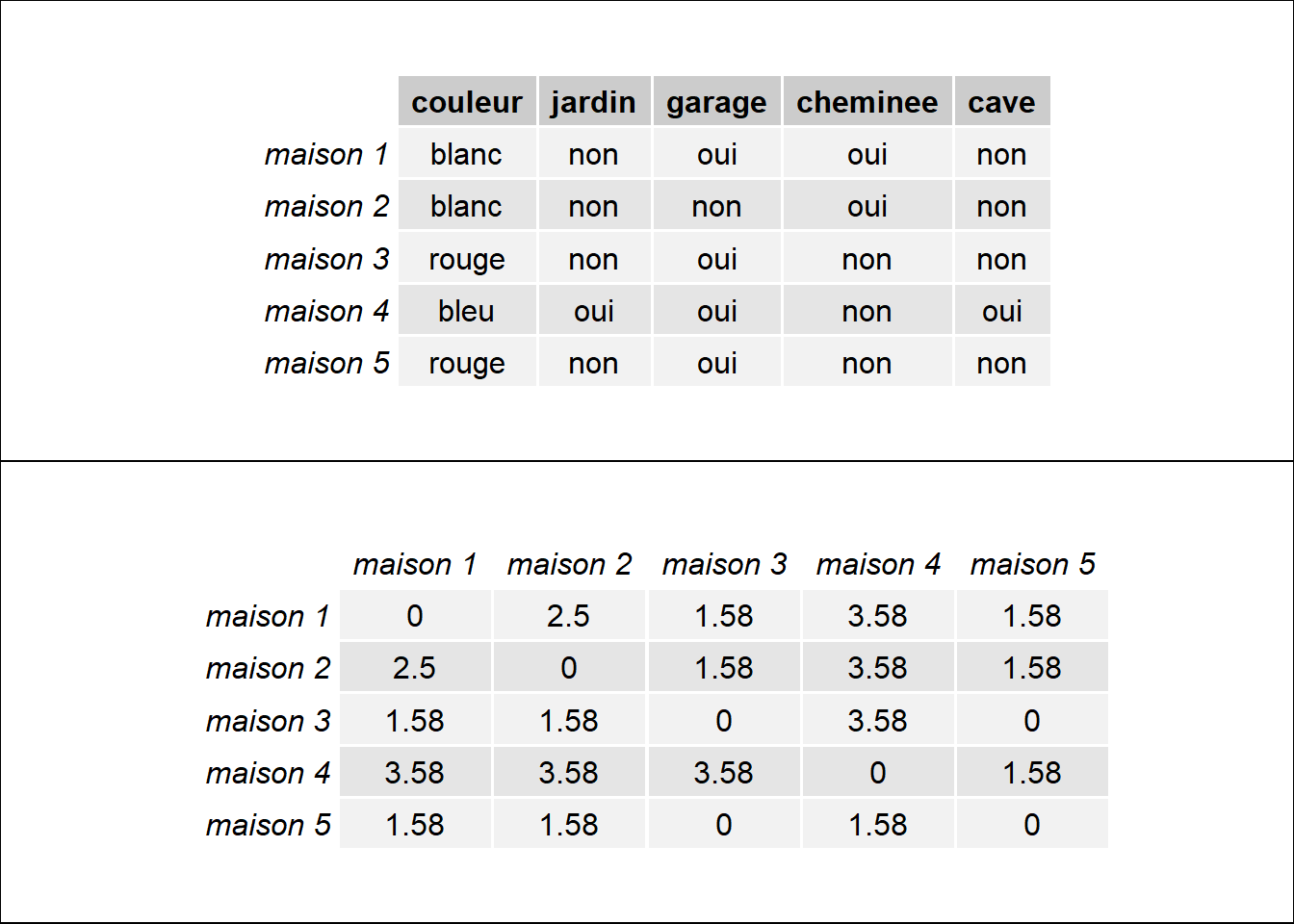
Du tableau de données à la matrice de distance

Figure 13.11: Du tableau de données à la matrice de distance

En plus de la fonction de distance, il est également nécessaire de sélectionner un critère d’agrégation, soit la règle permettant de décider à chaque itération quelles observations doivent être regroupées. Les méthodes les plus courantes sont :

  • Le critère de Ward (1963) : cette méthode consiste à agréger à chaque itération les deux observations permettant de minimiser la variance (ou l’inertie) intra-groupe, ce qui revient à maximiser l’inertie inter-groupe (autrement dit, à rendre les groupes les plus homogènes possible et les plus dissemblables entre eux). Ainsi, l’enjeu est de fusionner les deux observations permettant d’avoir les groupes les plus dissimilaires possible après fusion.
  • Le lien complet : à chaque itération, les deux groupes d’observations associés sont ceux pour lesquels la distance maximale entre les observations les composant est la plus petite parmi tous les groupes.
  • Le lien simple : à chaque itération, les deux groupes d’observations associés sont ceux pour lesquels la distance minimum entre les observations les composant est la plus petite parmi tous les groupes.

La plus utilisée est de loin la méthode de Ward. La méthode du lien complet produit généralement des résultats similaires. En revanche, la méthode du lien simple peut produire des groupes non sphériques (non centrés sur leur moyenne) plus difficle à interpréter.

Prenons un instant pour visualiser cet algorithme (figure 13.12). Cette animation a été réalisée par David Sheehan et est également accessible sur son blog. Elle présente bien le processus d’agglomération de la classification ascendante hiérarchique et la construction progressive du dendrogramme.

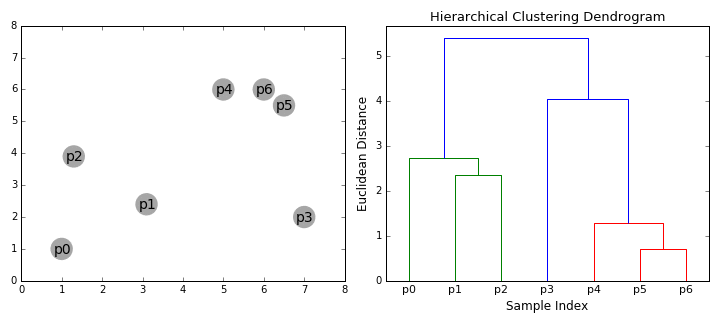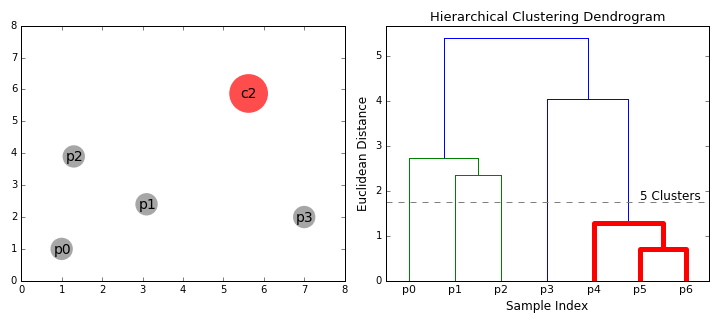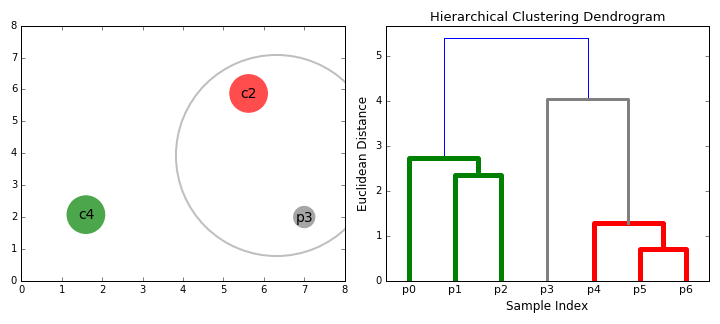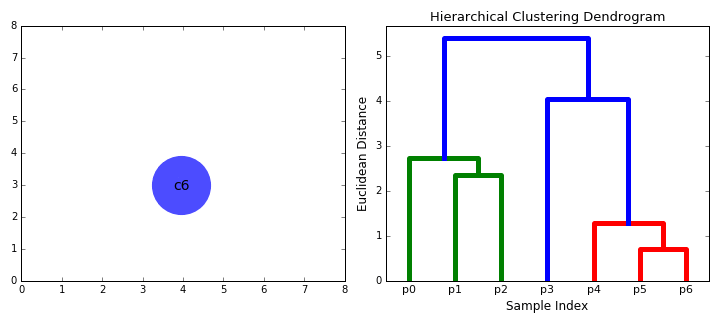
Principe de fonctionnement de la classification ascendante hiérarchique (auteur : David Sheehan)

Figure 13.12: Principe de fonctionnement de la classification ascendante hiérarchique (auteur : David Sheehan)

13.3.2 Choisir le bon nombre de groupes

Une fois que l’algorithme a été appliqué aux données et le dendrogramme obtenu, il faut encore choisir le nombre optimal de groupes pour la classification finale. Chaque embranchement du dendrogramme constitue une classification possible, allant de la plus complexe (chaque observation appartient à un groupe formé d’elle seule) à la plus simple (toutes les observations appartiennent au même groupe). Si le nombre de groupes n’est pas connu à l’avance et qu’aucune forte justification théorique n’existe, il est possible d’utiliser plusieurs techniques pour déterminer un nombre de groupes judicieux à partir des données. Nous en présentons ici trois, mais il convient de ne pas s’en tenir uniquement à ses critères arbitraires. Il est important d’explorer les résultats de la classification obtenue pour plusieurs valeurs de k candidates et de tenir compte de la qualité des informations qu’elles fournissent. Au final, il est pertinent de retenir la classification dont les résultats offrent l’interprétation la plus claire avec un nombre de groupes réduit (principe de parcimonie).

13.3.2.1 Méthode du coude

Cette première approche est la plus simple à mettre en oeuvre. Il s’agit simplement de produire plusieurs classifications à partir du dendrogramme avec différentes valeurs de k (nombre de groupes) et de calculer à chaque fois la part de l’inertie expliquée. Chaque groupe supplémentaire ne peut qu’améliorer l’inertie expliquée, car pour rappel, si \(k=n\), alors nous expliquons 100 % de l’inertie totale. L’objectif est de déterminer à quel moment l’ajout d’un groupe supplémentaire ne contribue que de façon marginale à améliorer l’inertie expliquée. Si nous représentons les valeurs d’inertie expliquée pour les différentes valeurs de k dans un graphique, une rupture (un coude) indiquerait le point au-delà duquel les groupes supplémentaires ne captent finalement que du bruit et non plus de l’information.

Si nous reprenons l’exemple du jeu de données IRIS, nous pouvons créer ce graphique avec k allant de 2 à 8 (figure 13.13). Un premier coude très net est observable pour \(k = 3\) et un second plus faible, mais tout de même marqué pour \(k = 4\).

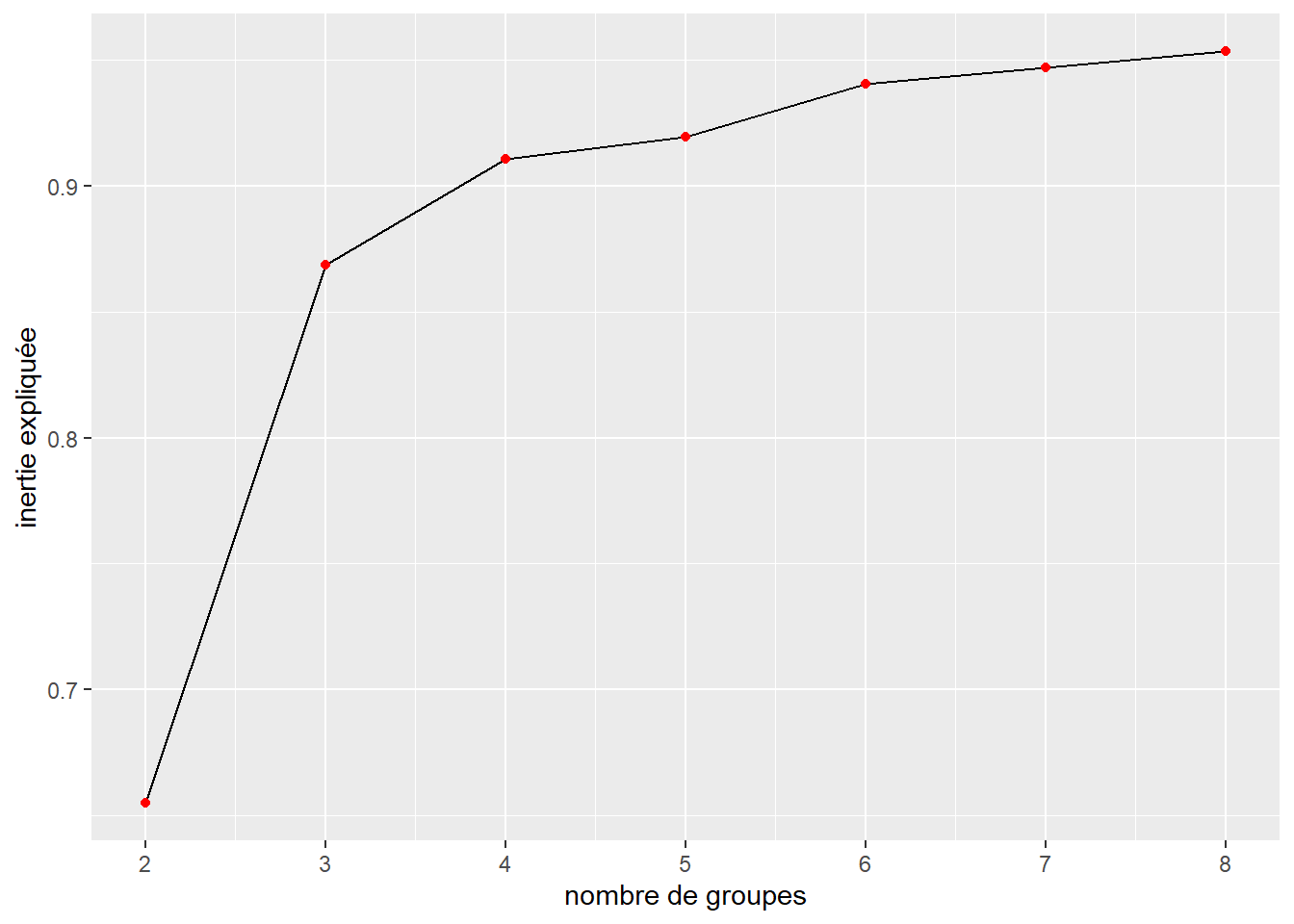
Méthode du coude

Figure 13.13: Méthode du coude

Inertie expliquée et centre de groupe

Pour calculer l’inertie expliquée, il est nécessaire de pouvoir déterminer pour le centre de gravité (ou centroïde) chaque groupe. Lorsque la distance euclidienne est utilisée, il s’agit simplement de calculer pour chaque groupe la valeur moyenne des différentes colonnes des observations. Cependant, lorsque d’autres distances sont utilisées, il peut être plus difficile de déterminer le centre d’un groupe. Avec la distance de Manhattan, il est par exemple recommandé d’utiliser la médiane des colonnes plutôt que la moyenne. Pour la distance de Hamming, la moyenne peut aussi être utilisée, car elle représente pour cette distance la fréquence d’occurrence des différentes modalités des variables qualitatives. Pour d’autres distances plus complexes, il est préférable de définir le centre d’un groupe comme le point de ce groupe minimisant les distances à tous les autres points du groupe. Il s’agit du médoïde du groupe.

13.3.2.2 Indicateur de silhouette

Si un coude net ne s’observe pas pour la méthode précédente, il est possible d’utiliser l’indicateur de silhouette. Il permet de mesurer pour une classification à quel point une observation est similaire à celles dans son propre groupe (cohésion) comparativement aux observations des autres groupes. Elle se calcule de la façon suivante :

\[\begin{equation} \begin{aligned} s(i) &= \frac{b(i)-a(i)}{\max \{a(i), b(i)\}} \\ a(i) &= \frac{1}{|C_i|-1}\sum_{j \in C_i,i \neq j}d(i,j) \\ b(i) &= min_{i \neq j}\frac{1}{|C_j|}\sum_{j \in C_j}d(i,j) \end{aligned} \tag{13.9} \end{equation}\]

avec \(s(i)\) la valeur de l’indice de silhouette pour l’observation i, \(a(i)\) la distance moyenne entre l’observation i et son groupe \(C_i\) et \(b(i)\) la distance minimale entre l’observation i et le centre de chaque autre groupe \(C_j\).

La valeur totale de l’indice est simplement la moyenne des valeurs moyennes des indices de silhouette au sein de chaque groupe. Une valeur plus élevée indique une meilleure classification. Il est nécessaire de déterminer le centre des groupes pour calculer cet indicateur ce qui peut être un exercice difficile quand une distance autre que la distance euclidienne est utilisée. Référez-vous à la note de la section précédente pour plus d’informations. L’indice de silhouette semble indiquer que seulement trois groupes serait un choix optimal, soit la valeur la plus haute (figure 13.14).

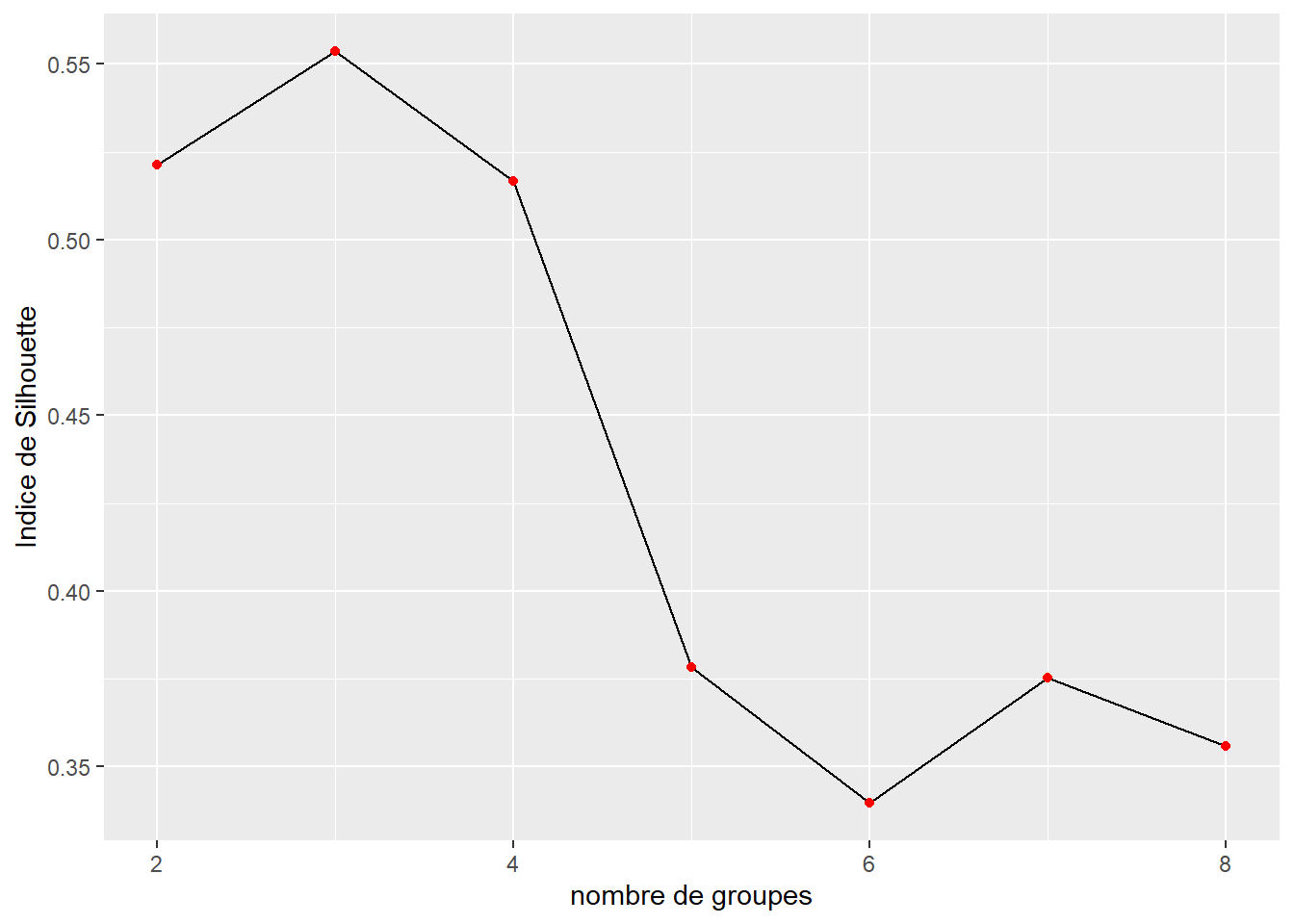
Méthode de l'indice de silhouette

Figure 13.14: Méthode de l’indice de silhouette

13.3.2.3 Méthode GAP

Cette méthode, proposée par Tibshirani, Walther et Hastie (2001), consiste à comparer l’inertie intra-groupe (inexpliquée) avec l’inertie observée pour un jeu de données généré aléatoirement (distribution uniforme des valeurs entre le minimum et le maximum de chaque variable) pour différentes valeurs successives de k. Une fois ces calculs effectués, l’objectif est de trouver la valeur de k telle que la valeur de GAP à k + 1 n’est pas plus grande qu’un écart type pour GAP à k + 1.

La statistique GAP est calculée ainsi :

\[\begin{equation} \begin{aligned} GAP(k) = \frac{1}{\text{nsim}} \sum^{\text{nsim}}_{\text{sim} = 1} log(W_{ksim}) - log(W_k) \end{aligned} \tag{13.10} \end{equation}\]

avec \(W_k\) l’inertie non expliquée (intra-groupe), \(W_{ksim}\) l’inertie non expliquée (intra-groupe) obtenue pour un jeu de données simulé et k le nombre de groupes.

L’idée est qu’une bonne classification doit produire des résultats plus structurés que ce que nous pourrions attendre du hasard. Chaque groupe supplémentaire permet de réduire l’inertie, mais lorsque l’ajout d’un groupe ne permet pas un gain significatif comparativement au hasard, alors l’ajout de ce groupe ne se justifie pas. À nouveau, il est possible de visualiser la situation avec un simple graphique (figure 13.15). Selon cette méthode, il faudrait sélectionner quatre groupes, car il s’agit de la première valeur de k validant le critère de cette méthode. La seconde valeur retenue par cette méthode est 6.

## Clustering k = 1,2,..., K.max (= 8): .. done
## Bootstrapping, b = 1,2,..., B (= 100)  [one "." per sample]:
## .................................................. 50 
## .................................................. 100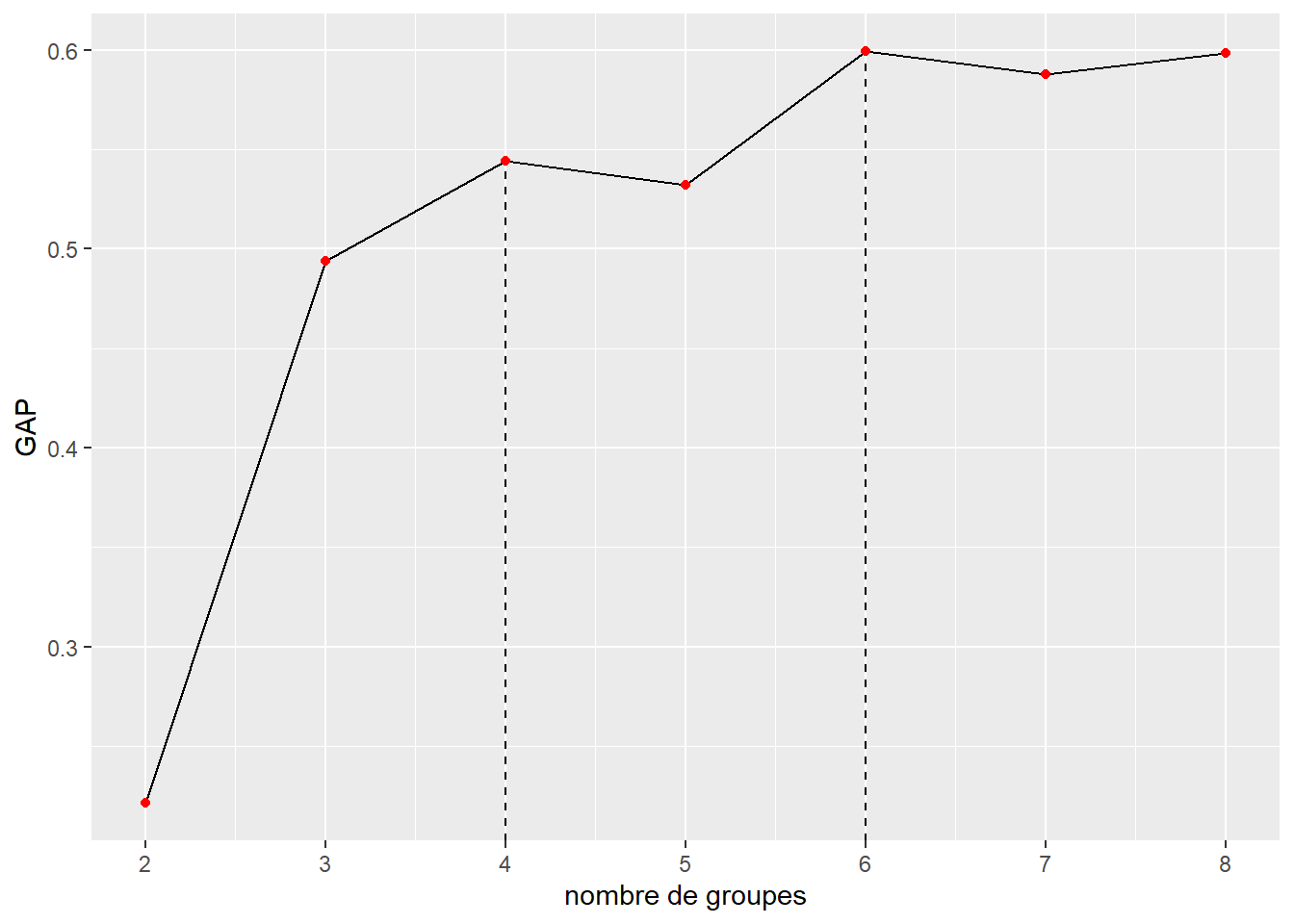
Méthode GAP

Figure 13.15: Méthode GAP

13.3.3 Limites de la classification ascendante hiérarchique

Bien que très flexible (choix de la fonction de distance et du critère d’agrégation), la CAH fait face à un enjeu majeur : la vitesse d’exécution et la consommation de mémoire lorsque des grands jeux de données sont utilisés. En effet, il est nécessaire de calculer à chaque étape une matrice de distance entre les groupes. Si un jeu de données comprend 1000 observations, cette matrice comprend donc 1000 x 1000 cases, soit un million de distances. Même en divisant ce nombre par deux (les éléments de la matrice sont symétriques, donc \(d(ij) = d(ji)\)), ce nombre augmente avec le carré du nombre d’observations. Pour de grands jeux de données, la CAH peut donc échouer à cause des limites de l’ordinateur utilisé. Il existe des versions plus performantes de l’algorithme réduisant cette limite, mais il convient de la garder en mémoire. Quand un très grand jeu de données doit être analysé, les méthodes des nuées dynamiques sont une solution à considérer.

13.3.4 Mise en oeuvre dans R

Nous proposons ici un exemple issu d’un article portant sur les parcs urbains de Montréal (Apparicio et al. 2010), dont l’objectif était notamment de classifier ces parcs en fonction de leur superficie et des équipements qu’ils comprennent, et ce, en utilisant la classification ascendante hiérarchique. Nous proposons ici de reproduire l’étape de classification effectuée dans cet article. La base de données comporte 653 parcs pour lesquels la présence de 18 équipements est codée comme un ensemble de variables binaires (0 signifiant absence et 1 présence). Nous disposons également de la taille de ces parcs, recodée en cinq catégories : moins d’un hectare, de 1 à 5 hectares, de 5 à 10 hectares, de 10 à 20 hectares et 20 hectares et plus. Le tableau 13.4 indique le nombre d’équipements recensés dans les parcs.

Tableau 13.4: Équipements recensés dans les différents parcs de Montréal
Équipements N
Équipements pour les 0 à 4 ans
Aire de jeux 601
Pataugeoire 161
Jeux d’eau 28
Terrains de sport
Baseball 188
Soccer (football) 169
Basketball 144
Tennis 125
Football 36
Volleyball 24
Athlétisme 20
Équipements d’hiver
Patinoire extérieure 241
Glissade 30
Piste de ski de fond 14
Piste de raquette 9
Équipements spécialisés
Parc de planches à roulettes 18
Patins à roues alignées 8
Autres équipements
Piscine intérieure 92
Chemin de randonnée 15

Puisque notre jeu de données ne comporte que des variables qualitatives, nous utilisons la distance du \(\Phi^2\) pour construire notre matrice de distance entre les parcs. Notons que, dans l’article original, la distance euclidienne au carrée avait été utilisée, alors nous n’obtiendrons probablement pas les mêmes résultats, car la distance du \(\Phi^2\) tient compte des fréquences d’occurrence des modalités des variables qualitatives.

13.3.4.1 Calcul de la matrice de distance

La première étape consiste donc à charger notre jeu de données et à calculer la matrice de distance.

# chargement du jeu de données et sélection des colonnes pour l'analyse
parcs <- read.csv("data/classification/Parcs.txt", header = TRUE, stringsAsFactors = FALSE)
X <- parcs[c(5:22, 27)]

Pour calculer la distance du \(\Phi^2\), nous utilisons la fonction dist du package proxy avec le paramètre method = "Phi-squared". Elle requiert que l’ensemble des variables catégorielles soient converties en variables binaires. Pour cela, nous pouvons utiliser la fonction dummy_cols du package fastDummies.

library(fastDummies)
library(proxy)

X <- dummy_cols(X,select_columns = "HaTypo",remove_selected_columns = TRUE)
parc_distances <- dist(as.matrix(X), method = "Phi-squared")

13.3.4.2 Application de l’algorithme de classification ascendante hiérarchique

Une fois la matrice obtenue, il ne reste plus qu’à appliquer la fonction hclust disponible de base dans R pour obtenir le dendrogramme. Comme dans l’article, nous utilisons le critère d’agrégation de Ward pour la création des groupes.

dendogramme_parcs <- hclust(parc_distances, method = "ward.D")

Puisque nous n’utilisons pas la distance euclidienne, nous optons ici pour l’indice de silhouette pour déterminer le nombre adéquat de groupes à former. Nous testons toutes les valeurs comprises entre 2 et 10.

library(cluster)
ks <- 2:10

# Calcul des indices de silhouette pour les différentes valeurs de k
values <- sapply(ks, function(k){
  # découpage du dendrogramme
  groupes <- cutree(dendogramme_parcs, k = k)
  # calcul des valeurs de silhouette
  sil <- silhouette(groupes, dist = parc_distances)
  # extraction de l'indice global (moyenne des moyennes)
  idx <- mean(summary(sil)$clus.avg.widths)
  return(idx)
})

# Création d'un graphique avec les résultats
df <- data.frame(k = ks,  silhouette = values)
ggplot(df) + 
  geom_line(aes(x = k, y = silhouette)) + 
  geom_point(aes(x = k, y = silhouette), color = "red") + 
  labs(x = "nombre de groupes", y="indice global de silhouette")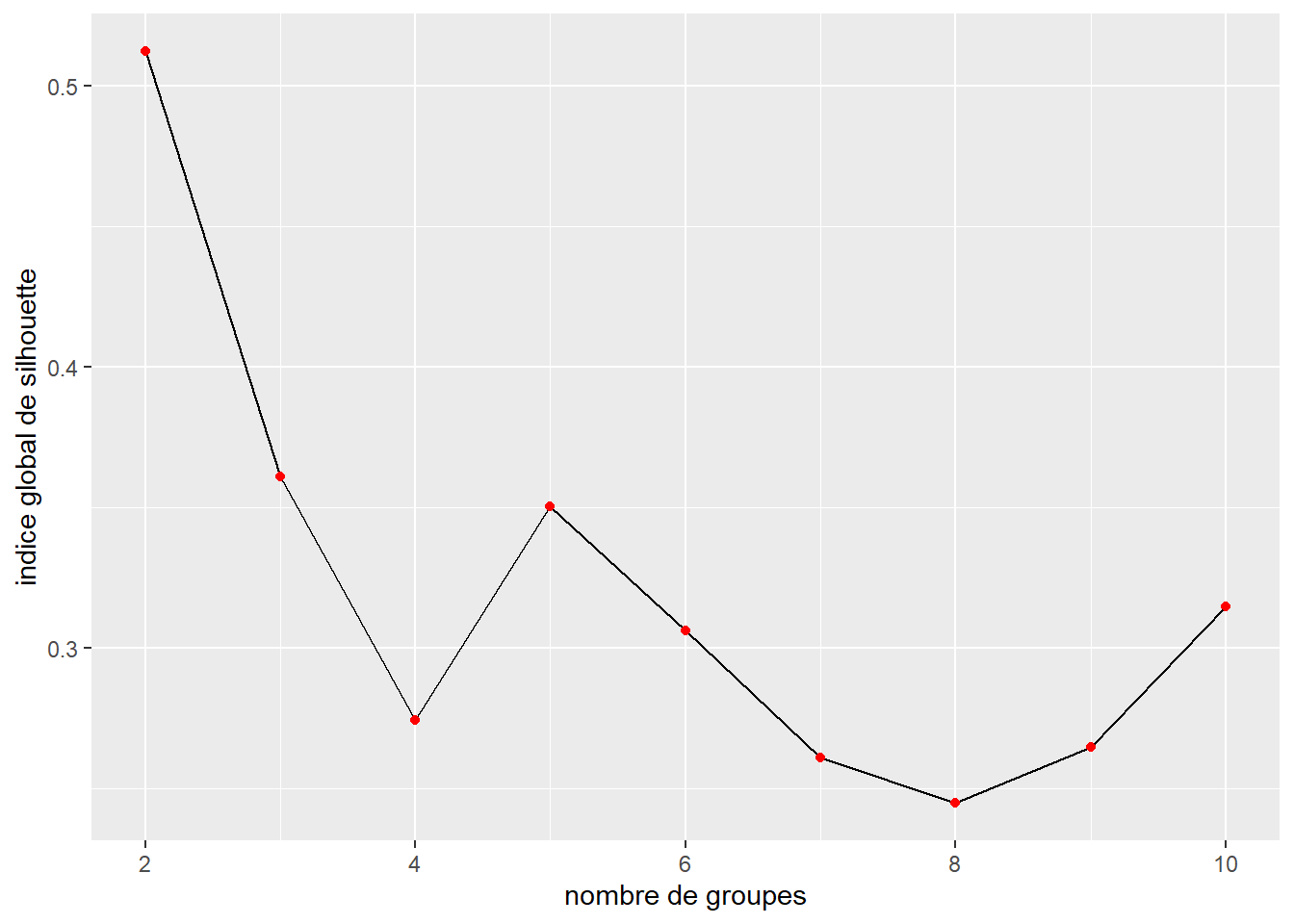
Valeur de l'indice de silhouette pour différents nombres de groupes

Figure 13.16: Valeur de l’indice de silhouette pour différents nombres de groupes

Si nous écartons d’emblée les résultats pour k = 2 et k = 3 (trop peu de groupes pour l’interprétation), nous constatons que la solution optimale selon ce critère est k = 5. Dans l’article original, la solution k = 6 avait été retenue en examinant le dendrogramme. Comparons les résultats pour k = 5 et k = 6.

resk5 <- cutree(dendogramme_parcs, k = 5)
resk6 <- cutree(dendogramme_parcs, k = 6)
sil5 <- silhouette(resk5, dist = parc_distances)
sil6 <- silhouette(resk6, dist = parc_distances)

# résumé pour l'indice de silhouette pour k = 5
summary(sil5)
## Silhouette of 693 units in 5 clusters from silhouette.default(x = resk5, dist = parc_distances) :
##  Cluster sizes and average silhouette widths:
##         116         212         246          84          35 
##  0.07029553  1.00000000 -0.11827930 -0.19969707  1.00000000 
## Individual silhouette widths:
##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
## -0.62041 -0.08502  0.09814  0.30200  1.00000  1.00000
# résumé pour l'indice de silhouette pour k = 6
summary(sil6)
## Silhouette of 693 units in 6 clusters from silhouette.default(x = resk6, dist = parc_distances) :
##  Cluster sizes and average silhouette widths:
##         116         212         197          49          84          35 
##  0.05906553  1.00000000 -0.10289391  0.07935325 -0.19969707  1.00000000 
## Individual silhouette widths:
##     Min.  1st Qu.   Median     Mean  3rd Qu.     Max. 
## -0.62041 -0.06414  0.10998  0.31846  1.00000  1.00000

Nous constatons que le groupe supplémentaire vient séparer le groupe trois comprenant 246 parcs dans la solution avec k = 5. Ce dernier ne comprend plus que 197 parcs pour la solution k = 6 et le nouveau groupe en compte 49. Ce nouveau groupe à un indice de silhouette moyen relativement faible (0,079), et le fait de découper le groupe trois améliore très peu sa propre valeur (passant de -0,12 à -0,10). Nous retenons cependant ici la solution avec k = 6 afin de tenter de reproduire les résultats de l’article.

13.3.4.3 Interprétation des résultats

La dernière étape consiste à identifier les groupes obtenus et leur attribuer un intitulé en fonction de leurs caractéristiques. Dans notre cas, la classification ne comporte que des variables binaires, nous pouvons donc calculer le pourcentage de valeurs à 1 (présence d’un équipement) dans chacun des groupes.

# calcul du nombre de fois où chaque modalité est observée dans un groupe
X$groupe <- resk6
df_groupes <- X %>% 
  group_by(groupe) %>% summarise_all(.funs = sum)

# calcul du nombre d'observations par groupe
nb_gp <- table(resk6)
groupe_ratios <- round(100 * as.matrix(df_groupes)[,2:ncol(df_groupes)] / as.vector(nb_gp),1)
groupe_ratios <- as.data.frame(t(groupe_ratios))
names(groupe_ratios) <- paste0("groupe ", 1:ncol(groupe_ratios))

# calcul du nombre moyen d'équipements par catégorie par parc
equip_class <- list(
  c("AIRE_JEUX", "JEUX_EAU", "PATAUGEOIRE"),
  c("ATHLETISME", "BASEBALL_S", "BASKETBALL", "FOOTBALL", "SOCCER", "TENNIS", "VOLLEY_BALL"),
  c("TOBBOGAN_G", "PATINOIRE_E", "RAQUETTES", "SKI_FOND"),
  c("PATIN_ROUE", "ROULI_ROUL"),
  c("PISC_EXT", "RANDONNEE")
)

class_compte <- data.frame(sapply(equip_class, function(equip){
  rowSums(X[equip])
}))
names(class_compte) <- c("enfants", "terrain_sport", "hiver", "specialise", "autre")
class_compte$groupe <- resk6
df_class_equip <- class_compte %>% 
  group_by(groupe) %>% 
  summarise_all(mean)

df_class_equip <- t(df_class_equip[2:ncol(df_class_equip)])
colnames(df_class_equip) <- paste0("groupe ", 1:ncol(df_class_equip))

# comptage du nombre moyen total d'équipements
df_equip_tot <- data.frame(
  nb = rowSums(X[1:18]),
  groupe = resk6
)
df_equip_tot_mean <- df_equip_tot %>% 
  group_by(groupe) %>% 
  summarize_all(mean)

# mise dans l'ordre de la première partie du tableau
all_types <- do.call(c,equip_class)
idxs <- match(all_types,row.names(groupe_ratios[1:length(all_types),]))
groupe_ratios <- rbind(groupe_ratios[idxs,],
                       groupe_ratios[(length(all_types)+1):nrow(groupe_ratios),])

# combinaison des deux tableaux
groupe_ratios <- rbind(groupe_ratios, df_class_equip, df_equip_tot_mean$nb, as.integer(nb_gp))

Il est ensuite possible d’afficher le tableau obtenu pour l’interpréter. Les résultats sont ici rapportés au tableau 13.5.

Tableau 13.5: Caractéristiques des groupes obtenus lors de la CAH
groupe 1 groupe 2 groupe 3 groupe 4 groupe 5 groupe 6
Équipements pour les 0 à 4 ans (%)
Aire de jeux 69,8 100 83,2 71,4 88,1 100
Jeux d’eau 7,8 0 2,5 18,4 6,0 0
Pataugeoire 36,2 0 47,2 2,0 29,8 0
Terrains de sport (%)
Athlétisme 12,1 0 2,0 2,0 1,2 0
Baseball 62,1 0 50,8 0,0 19,0 0
Basketball 37,9 0 36,0 16,3 21,4 0
Football américain 15,5 0 7,1 8,2 0,0 0
Soccer (football) 52,6 0 29,9 87,8 7,1 0
Tennis 38,8 0 32,5 8,2 14,3 0
Volleyball 7,8 0 4,6 12,2 0,0 0
Équipements d’hiver (%)
Glissade 19,8 0 3,0 2,0 0,0 0
Patinoire 58,6 0 59,4 34,7 46,4 0
Piste de ski de fond 7,8 0 0,0 0,0 0,0 0
Raquettes 12,1 0 0,0 0,0 0,0 0
Équipements spécialisés (%)
Parc de planches à roulettes 6,0 0 0,5 0,0 0,0 0
Patins à roues alignées 8,6 0 4,1 0,0 0,0 0
Autres équipements (%)
Piscine extérieure 27,6 0 27,4 4,1 4,8 0
Chemin de randonnée 12,9 0 0,0 0,0 0,0 0
Superficie (%)
Moins d’un hectare 0,0 100 0,0 0,0 100,0 0
1 à 5 hectares 5,2 0 98,5 100,0 0,0 100
5 à 10 hectares 61,2 0 0,0 0,0 0,0 0
10 à 20 hectares 17,2 0 1,0 0,0 0,0 0
20 hectares et plus 16,4 0 0,5 0,0 0,0 0
Nombre moyen d’équipement du type
Équipements pour les 0 à 4 ans 1,1 1 1,3 0,9 1,2 1
Terrains de sport 2,3 0 1,6 1,3 0,6 0
Équipements d’hiver 1,0 0 0,6 0,4 0,5 0
Équipements spécialisés 0,1 0 0,0 0,0 0,0 0
Autres équipements 0,4 0 0,3 0,0 0,0 0
Tous les équipements 4,9 1 3,9 2,7 2,4 1
Nombre d’observations par groupe
116,0 212 197,0 49,0 84,0 35

  • Le premier groupe correspond à de grands parcs (superficie généralement comprise entre 5 et plus de 20 hectares), il comporte 116 observations. Ces grands parcs sont en moyenne équipés de deux terrains de sport et d’un équipement d’hiver. Il s’agit vraisemblablement des grands parcs identifiés dans l’article original, dans lesquels se retrouvent également les parcs à vocation métropolitaine.

  • Le second groupe (212 parcs) correspond à de très petits parcs (moins d’un hectare) comportant uniquement une aire de jeu.

  • Le troisième groupe (197 parcs) correspond à de petits parcs (entre 1 et 5 hectares), souvent équipés d’une piscine extérieure (27,4 % des cas), et en moyenne de deux terrains de sports (essentiellement des terrains de tennis et de soccer). Ces parcs comprennent en moyenne plus de 4 équipements et doivent donc correspondre à la classe D dans l’article original (Petit parc (1 à 5 ha) avec en moyenne six équipements, dont une patinoire et une piscine).

  • Le quatrième groupe (49 parcs) comprend de petits parcs (entre 1 et 5 hectares) qui ressemblent aux parcs du groupe 2 mais tendent à disposer en plus d’un terrain de sport (baseball ou basketball).

  • Le quatrième groupe (84 parcs) correspond à de petits parcs, il est caractérisé par une présence plus marquée de pataugeoires (39 %).

  • Le cinquième groupe (35 parcs) est très similaire au second groupe (uniquement une aire de jeux), excepté sont les parcs qui s’y trouvent sont de taille supérieure (de 1 à 5 hectares).

Considérant les différences minimes entre certains des groupes que nous avons obtenus, il est clair que retenir seulement trois ou cinq groupes serait préférable. Notez également l’importance du choix de la distance, car nous obtenons des résultats sensiblement différents de ceux de l’article original en ayant opté pour la distance du \(\Phi^2\) plutôt que la distance euclidienne au carré.

13.3.4.4 Utilisation de la matrice de distance eucidienne au carré

Pour obtenir des résultats plus proches de ceux de l’article original, nous pouvons reprendre notre analyse et utiliser cette fois-ci une distance euclidienne au carré.

X$groupe <- NULL
# calcule de la matrice de distance
parc_distances_euc <- dist(as.matrix(X), method = "Euclidean")**2

# Application de la CAH
dendogramme_parcs_euc <- hclust(parc_distances_euc, method = "ward.D")

# calcul de l'indice de silhouette
ks <- 2:10
values <- sapply(ks, function(k){
  # découpage du dendrogramme
  groupes <- cutree(dendogramme_parcs_euc, k = k)
  # calcul des valeurs de silhouette
  sil <- silhouette(groupes, dist = parc_distances_euc)
  # extraction de l'indice global (moyenne des moyennes)
  idx <- mean(summary(sil)$clus.avg.widths)
  return(idx)
})

# création d'un graphique avec les résultats

df <- data.frame(
  k = ks,
  silhouette = values
)

ggplot(df) + 
  geom_line(aes(x = k, y = silhouette)) + 
  geom_point(aes(x = k, y = silhouette), color = "red") + 
  labs(x = "nombre de groupes", y="indice global de silhouette")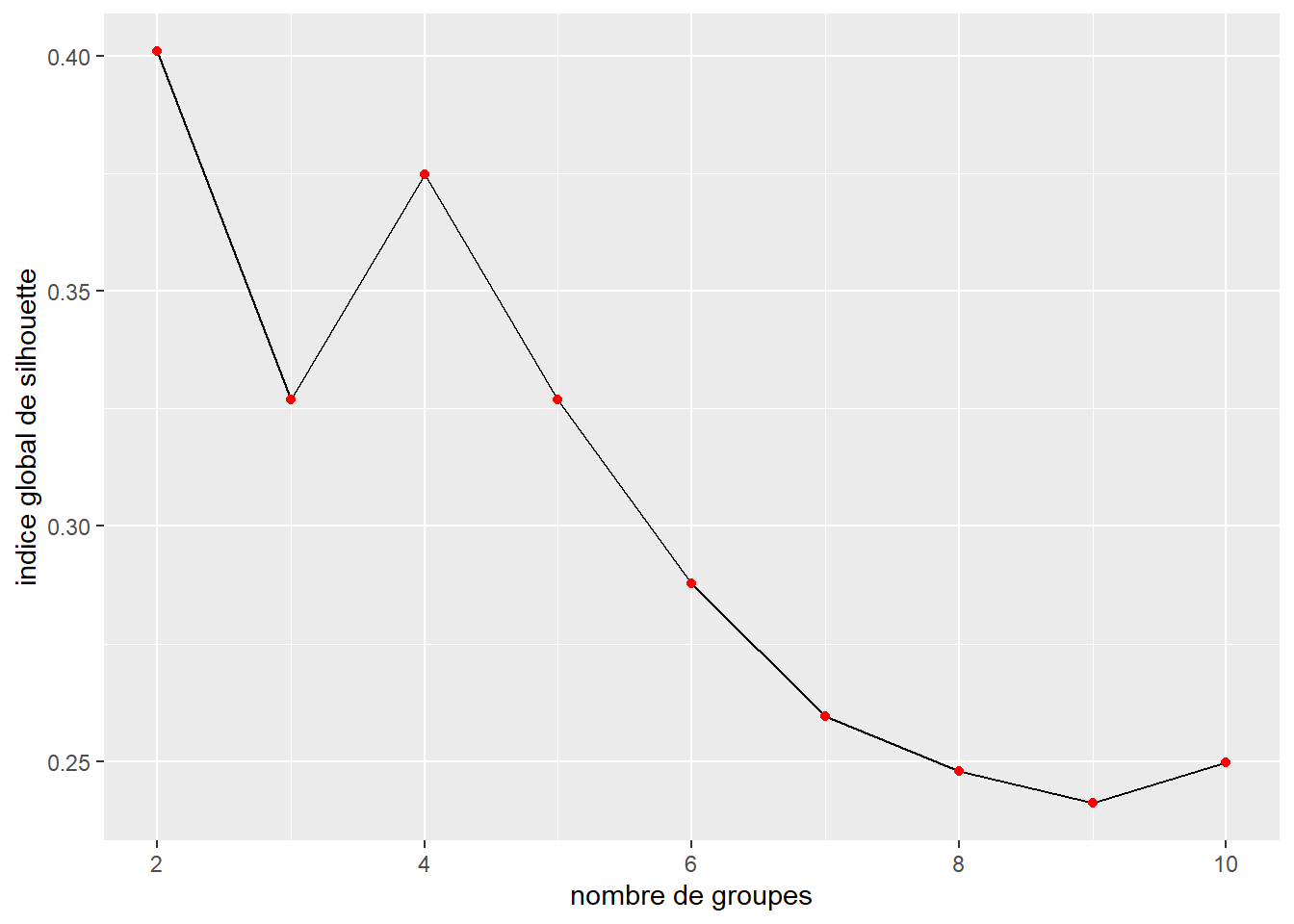
Valeur de l'indice de silhouette pour différents nombres de groupes (distance euclidienne au carré)

Figure 13.17: Valeur de l’indice de silhouette pour différents nombres de groupes (distance euclidienne au carré)

Nous constatons cette fois-ci, que quatre groupes serait probablement le meilleur choix et qu’au-delà de ce nombre, l’indice global de silhouette ne fait que diminuer. Tentons cependant de reproduire les résultats de l’article avec k = 6.

resk6 <- cutree(dendogramme_parcs_euc, k = 6)

# calcul du nombre de fois ou chaque modalité est observée dans un groupe
X$groupe <- resk6
df_groupes <- X %>% 
  group_by(groupe) %>% summarise_all(.funs = sum)

# calcul du nombre d'observations par groupe
nb_gp <- table(resk6)

groupe_ratios <- round(100 * as.matrix(df_groupes)[,2:ncol(df_groupes)] / as.vector(nb_gp),1)
groupe_ratios <- as.data.frame(t(groupe_ratios))
names(groupe_ratios) <- paste0("groupe ", 1:ncol(groupe_ratios))

# calcul du nombre moyen d'équipements par catégorie par parc
equip_class <- list(
  c("AIRE_JEUX", "JEUX_EAU", "PATAUGEOIRE"),
  c("ATHLETISME", "BASEBALL_S", "BASKETBALL", "FOOTBALL", "SOCCER", "TENNIS", "VOLLEY_BALL"),
  c("TOBBOGAN_G", "PATINOIRE_E", "RAQUETTES", "SKI_FOND"),
  c("PATIN_ROUE", "ROULI_ROUL"),
  c("PISC_EXT", "RANDONNEE")
)

class_compte <- data.frame(sapply(equip_class, function(equip){
  rowSums(X[equip])
}))
names(class_compte) <- c("enfants", "terrain_sport", "hiver", "specialise", "autre")
class_compte$groupe <- resk6
df_class_equip <- class_compte %>% 
  group_by(groupe) %>% 
  summarise_all(mean)

df_class_equip <- t(df_class_equip[2:ncol(df_class_equip)])
colnames(df_class_equip) <- paste0("groupe ", 1:ncol(df_class_equip))

# comptage du nombre moyen d'équipements
df_equip_tot <- data.frame(
  nb = rowSums(X[1:18]),
  groupe = resk6
)
df_equip_tot_mean <- df_equip_tot %>% 
  group_by(groupe) %>% 
  summarize_all(mean)

# mise dans l'ordre de la première partie du tableau
all_types <- do.call(c,equip_class)
idxs <- match(all_types,row.names(groupe_ratios[1:length(all_types),]))
groupe_ratios <- rbind(groupe_ratios[idxs,],
                       groupe_ratios[(length(all_types)+1):nrow(groupe_ratios),])

# combinaison des deux tableaux
groupe_ratios <- rbind(groupe_ratios, df_class_equip, df_equip_tot_mean$nb, as.integer(nb_gp))

Recréons le tableau final des résultats au tableau 13.6. Si vous comparez ce tableau avec celui de l’article original, vous verrez que notre groupe 3 correspond exactement à la classe A et que notre groupe 5 correspond exactement à la classe F. Pour les autres groupes, nous pouvons observer de légères variations, ce qui correspond vraisemblablement à des divergences d’implémentation des algorithmes entre le logiciel utilisé pour l’article (SAS) et R.

Tableau 13.6: Caractéristiques des groupes obtenus lors de la CAH (distance euclidienne au carré)
groupe 1 groupe 2 groupe 3 groupe 4 groupe 5 groupe 6
Équipements pour les 0 à 4 ans (%)
Aire de jeux 79,6 74,2 96,6 100,0 20,0 79,3
Jeux d’eau 11,1 3,0 1,7 5,1 0,0 5,9
Pataugeoire 59,3 42,4 8,4 61,0 0,0 19,7
Terrains de sport (%)
Athlétisme 13,0 15,2 0,3 0,0 0,0 1,0
Baseball 88,9 63,6 5,4 89,8 6,7 13,8
Basketball 83,3 30,3 6,1 35,6 0,0 18,2
Football 31,5 12,1 0,0 10,2 0,0 2,5
Soccer (football) 75,9 57,6 2,0 27,1 0,0 33,5
Tennis 90,7 19,7 4,1 35,6 0,0 14,8
Volleyball 20,4 3,0 0,0 1,7 0,0 4,9
Équipements d’hiver (%)
Glissade 14,8 16,7 0,0 1,7 33,3 2,5
Patinoire 87,0 57,6 13,2 86,4 26,7 30,5
Piste de ski de fond 1,9 1,5 0,0 0,0 46,7 0,0
Raquettes 0,0 1,5 0,0 0,0 86,7 0,0
Équipements spécialisés (%)
Parc de planches à roulettes 0,0 0,0 0,0 1,7 46,7 0,0
Patins à roues alignées 16,7 7,6 0,0 5,1 0,0 0,5
Autres équipements (%)
Piscine extérieure 75,9 16,7 1,4 11,9 6,7 13,8
Chemin de andonnée 1,9 0,0 0,0 0,0 93,3 0,0
Superficie (%)
Moins d’un hectare 0,0 0,0 100,0 0,0 0,0 0,0
1 à 5 hectares 42,6 1,5 0,0 98,3 0,0 99,5
5 à 10 hectares 46,3 69,7 0,0 0,0 0,0 0,0
10 à 20 hectares 1,9 27,3 0,0 0,0 13,3 0,5
20 hectares et plus 9,3 1,5 0,0 1,7 86,7 0,0
Nombre moyen d’équipement du type
Équipements pour les 0 à 4 ans 1,5 1,2 1,1 1,7 0,2 1,0
Terrains de sport 4,0 2,0 0,2 2,0 0,1 0,9
Équipements d’hiver 1,0 0,8 0,1 0,9 1,9 0,3
Équipements spécialisés 0,2 0,1 0,0 0,1 0,5 0,0
Autres équipements 0,8 0,2 0,0 0,1 1,0 0,1
Tous les équipements 7,5 4,2 1,4 4,7 3,7 2,4
Nombre d’observations par groupe
54,0 66,0 296,0 59,0 15,0 203,0

Références

Apparicio, Philippe, Marie-Soleil Cloutier, Anne-Marie Séguin et Josefina Ades. 2010. « Accessibilité spatiale aux parcs urbains pour les enfants et injustice environnementale. Exploration du cas montréalais. » Revue internationale de géomatique 20 (3): 363‑389. http://rig.revuesonline.com/article.jsp?articleId=15208.
Tibshirani, Robert, Guenther Walther et Trevor Hastie. 2001. « Estimating the number of clusters in a data set via the gap statistic. » Journal of the Royal Statistical Society: Series B (Statistical Methodology) 63 (2): 411‑423. https://doi.org/10.1111/1467-9868.00293.
Ward, Joe H. 1963. « Hierarchical grouping to optimize an objective function. » Journal of the American statistical association 58 (301): 236‑244. https://doi.org/10.1080/01621459.1963.10500845.