4.4 Régression linéaire simple

Comment expliquer et prédire une variable continue en fonction d’une autre variable? Répondre à cette question relève de la statistique inférentielle. Il s’agit en effet d’établir une équation simple du type \(Y = a + bX\) pour expliquer et prédire les valeurs d’une variable dépendante (Y) à partir d’une variable indépendante (X). L’équation de la régression est construite grâce à un jeu de données (un échantillon). À partir de cette équation, il est possible de prédire la valeur attendue de Y pour n’importe quelle valeur de X. Nous appelons cette équation un modèle, car elle cherche à représenter la réalité de façon simplifiée.

La régression linéaire simple relève ainsi de la statistique inférentielle et se distingue ainsi de la covariance (section 4.2) et de la corrélation (section 4.3) qui relèvent quant à eux de la statistique bivariée descriptive et exploratoire.

Par exemple, la régression linéaire simple pourrait être utilisée pour expliquer les notes d’un groupe d’étudiants et d’étudiantes à un examen (variable dépendante Y) en fonction du nombre d’heures consacrées à la révision des notes de cours (variable indépendante X). Une fois l’équation de régression déterminée et si le modèle est efficace, nous pourrons prédire les notes des personnes inscrites au cours la session suivante en fonction du temps qu’ils ou qu’elles prévoient passer à étudier, et ce, avant l’examen.

Formulons un exemple d’application de la régression linéaire simple en études urbaines. Dans le cadre d’une étude sur les îlots de chaleur urbains, la température de surface (variable dépendante) pourrait être expliquée par la proportion de la superficie de l’îlot couverte par de la végétation (variable indépendante). Nous supposons alors que plus cette proportion est importante, plus la température est faible et inversement, soit une relation linéaire négative. Si le modèle est efficace, nous pourrions prédire la température moyenne des îlots d’une autre municipalité pour laquelle nous ne disposons pas d’une carte de température, et repérer ainsi les îlots de chaleur potentiels. Bien entendu, il est peu probable que nous arrivions à prédire efficacement la température moyenne des îlots avec uniquement la couverture végétale comme variable explicative. En effet, bien d’autres caractéristiques de la forme urbaine peuvent influencer ce phénomène comme la densité du bâti, la couleur des toits, les occupations du sol présentes, l’effet des canyons urbains, etc. Il faudrait alors inclure non pas une, mais plusieurs variables explicatives (indépendantes).

Ainsi, nous distinguons la régression linéaire simple (une seule variable indépendante) de la régression linéaire multiple (plusieurs variables indépendantes); cette dernière est largement abordée au chapitre 7.

Dans cette section, nous décrivons succinctement la régression linéaire simple. Concrètement, nous voyons comment déterminer la droite de régression, interpréter ses différents paramètres du modèle et évaluer la qualité d’ajustement du modèle. Nous n’abordons ni les hypothèses liées au modèle de régression linéaire des moindres carrés ordinaires (MCO) ni les conditions d’application. Ces éléments sont expliqués au chapitre 7, consacré à la régression linéaire multiple.

Corrélation, régression simple et causalité : attention aux raccourcis!

Si une variable X explique et prédit efficacement une variable Y, cela ne veut pas dire pour autant qu’X cause Y. Autrement dit, la corrélation, soit le degré d’association entre deux variables, ne signifie pas qu’il existe un lien de causalité entre elles.

Premièrement, la variable explicative (X, indépendante) doit absolument précéder la variable à expliquer (Y, dépendante). Par exemple, l’âge (X) peut influencer le sentiment de sécurité (Y). Mais, le sentiment de sécurité ne peut en aucun cas influencer l’âge. Par conséquent, l’âge ne peut conceptuellement pas être la variable dépendante dans cette relation.

Deuxièmement, bien qu’une variable puisse expliquer efficacement une autre variable, elle peut être un facteur confondant. Prenons deux exemples bien connus :

Avoir les doigts jaunes est associé au cancer du poumon. Bien entendu, les doigts jaunes ne causent pas le cancer : c’est un facteur confondant puisque fumer augmente les risques du cancer du poumon et jaunit aussi les doigts.
Dans un article intitulé Chocolate Consumption, Cognitive Function, and Nobel Laureates, Messerli (2012) a trouvé une corrélation positive entre la consommation de chocolat par habitant et le nombre de prix Nobel pour dix millions d’habitants pour 23 pays. Ce résultat a d’ailleurs été rapporté par de nombreux médias, sans pour autant que Messerli (2012) et les journalistes concluent à un lien de causalité entre les deux variables :

Les chercheurs et les chercheures savent bien que la consommation de chocolat ne permet pas d’obtenir des résultats intéressants et de les publier dans des revues prestigieuses; c’est plutôt le café ! Plus sérieusement, il est probable que les pays les plus riches investissent davantage dans la recherche et obtiennent ainsi plus de prix Nobel. Dans les pays les plus riches, il est aussi probable que l’on consomme plus de chocolat, considéré comme un produit de luxe dans les pays les plus pauvres.

Pour approfondir le sujet sur la confusion entre corrélation, régression simple et causalité, vous pouvez visionner cette courte vidéo ludique de vulgarisation (https://www.youtube.com/embed/A-_naeATJ6o).

L’association entre deux variables peut aussi être simplement le fruit du hasard. Si nous explorons de très grandes quantités de données (avec un nombre impressionnant d’observations et de variables), soit une démarche relevant du forage ou de la fouille de données (data mining en anglais), le hasard fera que nous risquons d’obtenir des corrélations surprenantes entre certaines variables. Prenons un exemple concret : admettons que nous ayons collecté 100 variables et que nous calculons les corrélations entre chaque paire de variables. Nous obtenons une matrice de corrélation de 100 x 100, à laquelle nous pouvons enlever la diagonale et une moitié de la matrice, ce qui nous laisse un total de 4950 corrélations différentes. Admettons que nous choisissions un seuil de significativité de 5 %, nous devons alors nous attendre à ce que le hasard produise des résultats significatifs dans 5 % des cas. Sur 4950 corrélations, cela signifie qu’environ 247 corrélations seront significatives, et ce, indépendamment de la nature des données. Nous pouvons aisément illustrer ce fait avec la syntaxe suivante :

library("Hmisc")
nbVars <- 100 # nous utilisons 100 variables générées aléatoirement pour l'expérience
nbExperiment <- 1000 # nous reproduirons 1000 fois l'expérience avec les 100 variables
# Le nombre de variables significatives par expérience est enregistré dans Results
Results <- c()
# itérons pour chaque expérimentation (1000 fois)
for(i in 1:nbExperiment){
  Datas <- list()
  # générons 100 variables aléatoires normalement distribuées
  for (j in 1:nbVars){
    Datas[[j]] <- rnorm(150)
  }
  DF <- do.call("cbind",Datas)
  # calculons la matrice de corrélation pour les 100 variables
  cor_mat <- rcorr(DF)
  # comptons combien de fois les corrélations étaient significatives
  Sign <- table(cor_mat$P<0.05)
  NbPairs <- Sign[["TRUE"]]/2
  # ajoutons les résultats dans Results
  Results <- c(Results,NbPairs)
}
# transformons Results en un DataFrame
df <- data.frame(Values = Results)
# affichons le résultat
ggplot(df, aes(x = Values)) + 
  geom_histogram(aes(y =..density..), 
                 colour = "black", 
                 fill = "white") +
  stat_function(fun = dnorm, args = list(mean = mean(df$Values), 
                sd = sd(df$Values)),color="blue")+
  geom_vline(xintercept = mean(df$Values),color="red", size=1.2)+
  annotate("text", x=0, y = 0.028, 
           label = paste("Nombre moyen de corrélations significatives\n
                         sur 1000 réplications : ",
                         round(mean(df$Values),0), sep=""), hjust="left")+
  xlab("Nombre de corrélations significatives")+
  ylab("densité")

Figure 4.11: Corrélations significatives obtenues aléatoirement

4.4.1 Principe de base de la régression linéaire simple

La régression linéaire simple vise à déterminer une droite (une fonction linéaire) qui résume le mieux la relation linéaire entre une variable dépendante (Y) et une variable indépendante (X) : \[\begin{equation} \widehat{y_i} = \beta_{0} + \beta_{1}x_{i} \tag{4.7} \end{equation}\]

avec \(\widehat{y_i}\) et \(x_{i}\) qui sont respectivement la valeur prédite de la variable dépendante et la valeur de la variable indépendante pour l’observation \(i\). \(\beta_{0}\) est la constante (intercept en anglais) et représente la valeur prédite de la variable Y quand X est égale à 0. \(\beta_{1}\) est le coefficient de régression pour la variable X, soit la pente de la droite. Ce coefficient nous informe sur la relation entre les deux variables : s’il est positif, la relation est positive; s’il est négatif, la relation est négative; s’il est proche de 0, la relation est nulle (la droite est alors horizontale). Plus la valeur absolue de \(\beta_{1}\) est élevée, plus la pente est forte et plus la variable Y varie à chaque changement d’une unité de la variable X.

Considérons un exemple fictif de dix municipalités d’une région métropolitaine pour lesquelles nous disposons de deux variables : le pourcentage de personnes occupées se rendant au travail principalement à vélo et la distance entre chaque municipalité et le centre-ville de la région métropolitaine (tableau 4.3).

Tableau 4.3: Données fictives sur l’utilisation du vélo par municipalité

Municipalité	Vélo	KMCV
A	12,5	14,135
B	13,5	10,065
C	15,8	7,762
D	15,9	11,239
E	17,6	7,706

Municipalité	Vélo	KMCV
F	18,5	7,195
G	21,2	7,953
H	23,0	4,293
I	25,3	5,225
J	30,2	2,152

D’emblée, à la lecture du nuage de points (figure 4.12), nous décelons une forte relation linéaire négative entre les deux variables : plus la distance entre la municipalité et le centre-ville de la région métropolitaine augmente, plus le pourcentage de cyclistes est faible, ce qui est confirmé par le coefficient de corrélation (r = −0,90). La droite de régression (en rouge à la figure 4.12) qui résume le mieux la relation entre Vélo (variable dépendante) et KmCV (variable indépendante) s’écrit alors : Vélo = 30,603 − 1,448 x KmCV.

La valeur du coefficient de régression (\(\beta_{1}\)) est de −1,448. Le signe de ce coefficient décrit une relation négative entre les deux variables. Ainsi, à chaque ajout d’une unité de la distance entre la municipalité et le centre-ville (exprimée en kilomètres), le pourcentage de cyclistes diminue de 1,448. Retenez que l’unité de mesure de la variable dépendante est très importante pour bien interpréter le coefficient de régression. En effet, si la distance au centre-ville n’était pas exprimée en kilomètres, mais plutôt en mètres, \(\beta_1\) serait égal à −0,001448. Dans la même optique, l’ajout de 10 km de distance entre une municipalité et le centre-ville fait diminuer le pourcentage de cyclistes de −14,48 points de pourcentage.

Avec, cette équation de régression, il est possible de prédire le pourcentage de cyclistes pour n’importe quelle municipalité de la région métropolitaine. Par exemple, pour des distances de 5, 10 ou 20 kilomètres, les pourcentages de cyclistes seraient de :

\(\widehat{y_i} = \mbox{30,603} + (\mbox{-1,448} \times \mbox{5 km) = 23,363}\)
\(\widehat{y_i} = \mbox{30,603} + (\mbox{-1,448} \times \mbox{10 km) = 8,883}\)
\(\widehat{y_i} = \mbox{30,603} + (\mbox{-1,448} \times \mbox{20 km) = 1,643}\)

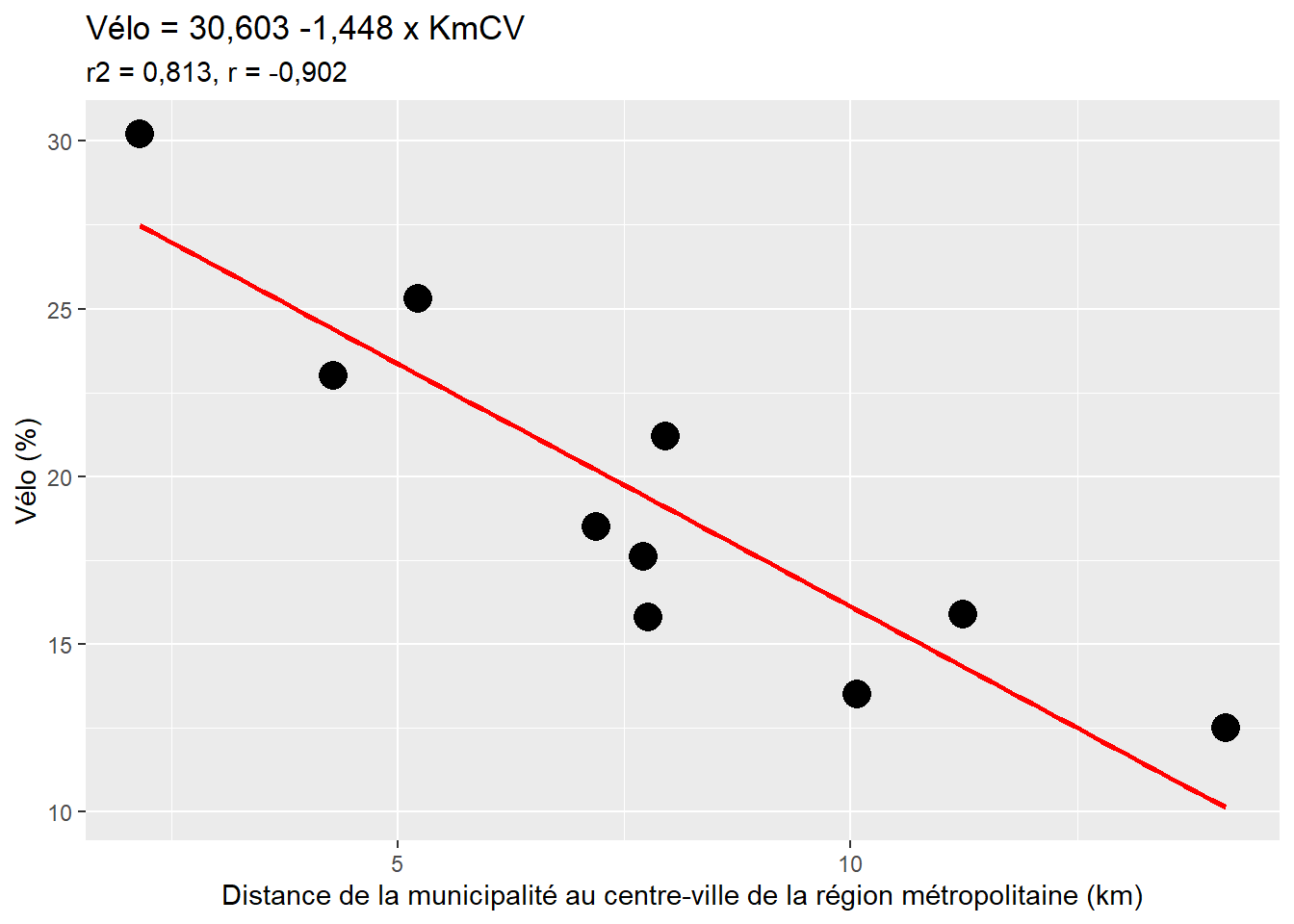
Figure 4.12: Relation linéaire entre l’utilisation du vélo et la distance au centre-ville

4.4.2 Formulation de la droite de régression des moindres carrés ordinaires

Reste à savoir comment sont estimés les différents paramètres de l’équation, soit \(\beta_0\) et \(\beta_1\). À la figure 4.13, les points noirs représentent les valeurs observées (\(y_i\)) et les points bleus, les valeurs prédites (\(\widehat{y_i}\)) par l’équation du modèle. Les traits noirs verticaux représentent, pour chaque observation \(i\), l’écart entre la valeur observée et la valeur prédite, dénommé résidu (\(\epsilon_i\), prononcez epsilon de i ou plus simplement le résidu pour i ou le terme d’erreur de i). Si un point est au-dessus de la droite de régression, la valeur observée est alors supérieure à la valeur prédite (\(y_i > \widehat{y_i}\)) et inversement, si le point est au-dessous de la droite (\(y_i < \widehat{y_i}\)). Plus cet écart (\(\epsilon_i\)) est important, plus l’observation s’éloigne de la prédiction du modèle et, par extension, moins bon est le modèle. Au tableau 4.4, vous constaterez que la somme des résidus est égale à zéro. La méthode des moindres carrés ordinaires (MCO) vise à minimiser les écarts au carré entre les valeurs observées (\(y_i\)) et prédites (\(\beta_0+\beta_1 x_i\), soit \(\widehat{y_i}\)) :

\[\begin{equation} min\sum_{i=1}^n{(y_i-(\beta_0+\beta_1 x_i))^2} \tag{4.8} \end{equation}\]

Pour minimiser ces écarts, le coefficient de régression \(\beta_1\) représente le rapport entre la covariance entre X et Y et la variance de Y (équation (4.9)), tandis que la constante \(\beta_0\) est la moyenne de la variable Y moins le produit de la moyenne de X et de son coefficient de régression (équation (4.10)).

\[\begin{equation} \beta_1 = \frac{\sum_{i=1}^n (x_{i}-\bar{x})(y_{i}-\bar{y})}{\sum_{i=1}^n (x_i-\bar{x})^2} = \frac{cov(X,Y)}{var(X)} \tag{4.9} \end{equation}\]

\[\begin{equation} \beta_0 = \widehat{Y}-\beta_1 \widehat{X} \tag{4.10} \end{equation}\]

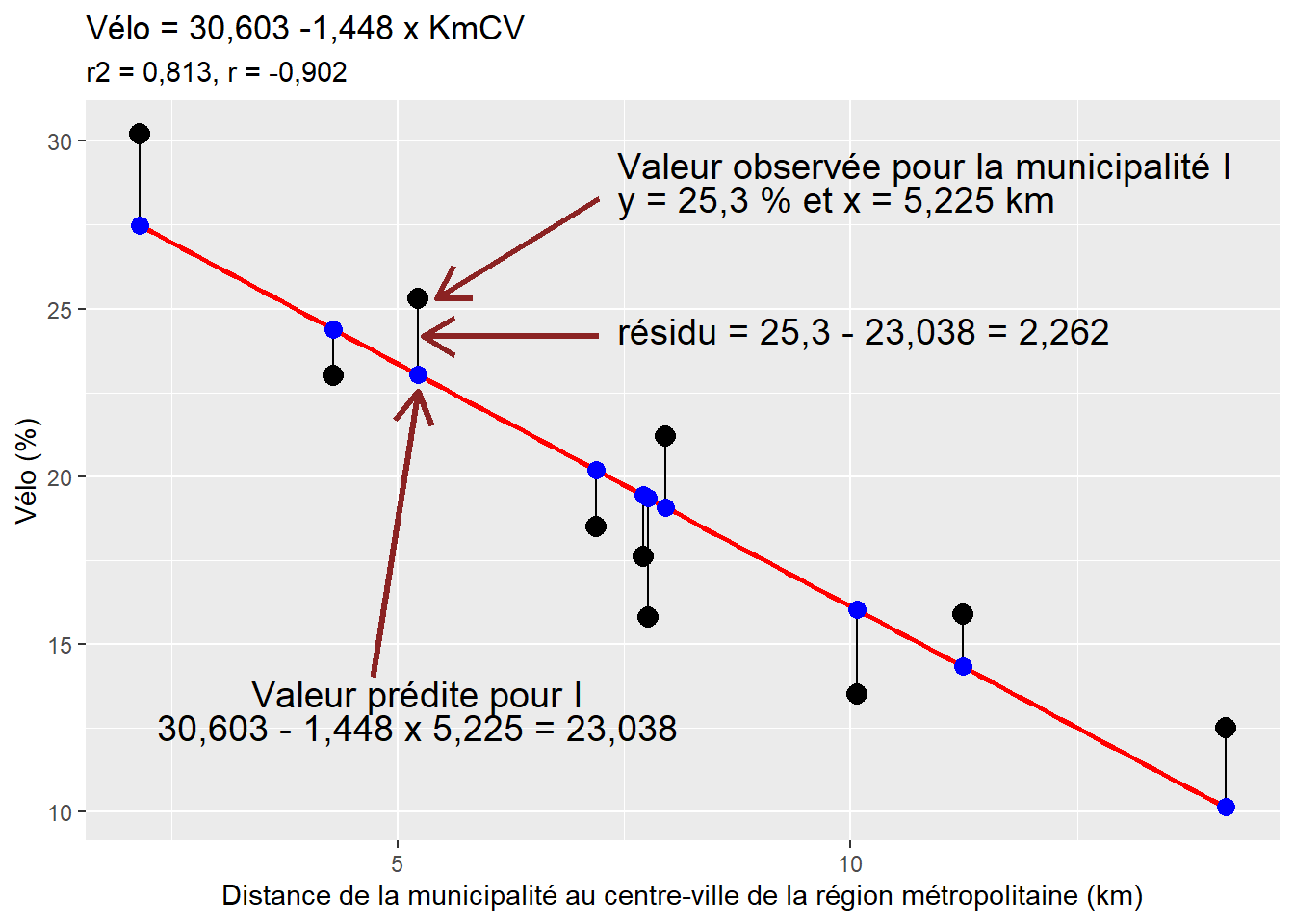
Figure 4.13: Droite de régression, valeurs observées, prédites et résidus

Tableau 4.4: Valeurs observées, prédites et résidus
Municipalité	Vélo	KmCV	Valeur prédite	Résidu	Résidu au carré
A	12,5	14,135	10,138	2,362	5,579
B	13,5	10,065	16,031	-2,531	6,406
C	15,8	7,762	19,365	-3,565	12,709
D	15,9	11,239	14,331	1,569	2,462
E	17,6	7,706	19,446	-1,846	3,408
F	18,5	7,195	20,186	-1,686	2,843
G	21,2	7,953	19,089	2,111	4,456
H	23,0	4,293	24,388	-1,388	1,927
I	25,3	5,225	23,038	2,262	5,117
J	30,2	2,152	27,488	2,712	7,355
Somme				0,000	52,262

4.4.3 Mesure de la qualité d’ajustement du modèle

Les trois mesures les plus courantes pour évaluer la qualité d’ajustement d’un modèle de régression linéaire simple sont l’erreur quadratique moyenne (root-mean-square error en anglais, RMSE), le coefficient de détermination (R²) et la statistique F de Fisher. Pour mieux appréhender le calcul de ces trois mesures, rappelons que l’équation de régression s’écrit :

\[\begin{equation} y_i = \beta_0 + \beta_1 x_1+ \epsilon_i \Rightarrow Y= \beta_0 + \beta_1 X + \epsilon \tag{4.11} \end{equation}\]

Elle comprend ainsi une partie de Y qui est expliquée par le modèle et une autre partie non expliquée, soit \(\epsilon\), appelée habituellement le terme d’erreur. Ce terme d’erreur pourrait représenter d’autres variables explicatives qui n’ont pas été prises en compte pour prédire la variable indépendante ou une forme de variation aléatoire inexplicable présente lors de la mesure.

\[\begin{equation} Y = \underbrace{\beta_0 + \beta_1 X}_{\mbox{partie expliquée par le modèle}}+ \underbrace{\epsilon}_{\mbox{partie non expliquée}} \tag{4.12} \end{equation}\]

Par exemple, pour la municipalité A au tableau 4.4, nous avons : \(y_A = \widehat{y}_A - \epsilon_A \Rightarrow \mbox{12,5} = \mbox{10,138}+\mbox{2,362}\). Souvenez-vous que la variance d’une variable est la somme des écarts à la moyenne, divisée par le nombre d’observations. Par extension, il est alors possible de décomposer la variance de Y comme suit :

\[\begin{equation} \underbrace{\sum_{i=1}^n (y_{i}-\bar{y})^2}_{\mbox{variance de Y}} = \underbrace{\sum_{i=1}^n (\widehat{y}_i-\bar{y})^2}_{\mbox{var. expliquée}} + \underbrace{\sum_{i=1}^n (y_{i}-\widehat{y})^2}_{\mbox{var. non expliquée}} \Rightarrow SCT = SCE + SCR \tag{4.13} \end{equation}\]

avec :

SCT est la somme des écarts au carré des valeurs observées à la moyenne (total sum of squares en anglais)
SCE est la somme des écarts au carré des valeurs prédites à la moyenne (regression sum of squares en anglais)
SCR est la somme des carrés des résidus (sum of squared errors en anglais).

Autrement dit, la variance totale est égale à la variance expliquée plus la variance non expliquée. Au tableau 4.5, vous pouvez repérer les valeurs de SCT, SCE et SCR et constater que 279,30 = 227,04 + 52,26 et 27,93 = 22,70 + 5,23.

Tableau 4.5: Calcul du coefficient de détermination
Municipalité	\(y_i\)	\(\widehat{y}_i\)	\(\epsilon_i\)	\((y_i-\bar{y})^2\)	\((\widehat{y}_i-y_i)^2\)	\(\epsilon_i^2\)
A	12,50	10,14	2,36	46,92	84,86	5,58
B	13,50	16,03	-2,53	34,22	11,02	6,41
C	15,80	19,37	-3,57	12,60	0,00	12,71
D	15,90	14,33	1,57	11,90	25,19	2,46
E	17,60	19,45	-1,85	3,06	0,01	3,41
F	18,50	20,19	-1,69	0,72	0,70	2,84
G	21,20	19,09	2,11	3,42	0,07	4,46
H	23,00	24,39	-1,39	13,32	25,38	1,93
I	25,30	23,04	2,26	35,40	13,60	5,12
J	30,20	27,49	2,71	117,72	66,22	7,36
N	10,00
Somme	193,50		0,00	279,30	227,04	52,26
Moyenne	19,35		0,00	27,93	22,70	5,23

Calcul de l’erreur quadratique moyenne

La somme des résidus au carré (SCR) divisée par le nombre d’observations représente donc le carré moyen des erreurs (en anglais, mean square error - MSE), soit la variance résiduelle du modèle (52,26 / 10 = 5,23). Plus sa valeur est faible, plus le modèle est efficace pour prédire la variable indépendante. L’erreur quadratique moyenne (en anglais, root-mean-square error - RMSE) est simplement la racine carrée de la somme des résidus au carré divisée par le nombre d’observations (\(n\)) :

\[\begin{equation} RMSE = \sqrt{\frac{\sum_{i=1}^n (y_{i}-\widehat{y})^2}{n}} \tag{4.14} \end{equation}\]

Elle représente ainsi une mesure absolue des erreurs qui est exprimée dans l’unité de mesure de la variable dépendante. Dans le cas présent, nous avons : \(\sqrt{5,23}=2,29\). Cela signifie qu’en moyenne, l’écart absolu (ou erreur absolue) entre les valeurs observées et prédites est de 2,29 points de pourcentage. De nouveau, une plus faible valeur de RMSE indique un meilleur ajustement du modèle. Mais surtout, le RMSE permet d’évaluer avec quelle précision le modèle prédit la variable dépendante. Il est donc particulièrement important si l’objectif principal du modèle est de prédire des valeurs sur un échantillon d’observations pour lequel la variable dépendante est inconnue.

Calcul du coefficient de détermination

Nous avons largement démontré que la variance totale est égale à la variance expliquée plus la variance non expliquée. La qualité du modèle peut donc être évaluée avec le coefficient de détermination (R²), soit le rapport entre les variances expliquée et totale :

\[\begin{equation} R^2 = \frac{SCE}{SCT} \mbox{ avec } R^2 \in \left[0,1\right] \tag{4.15} \end{equation}\]

Comparativement au RMSE qui est une mesure absolue, le coefficient de détermination est une mesure relative qui varie de 0 à 1. Il exprime la proportion de la variance de Y qui est expliquée par la variable X; autrement dit, plus sa valeur est élevée, plus X influence/est capable de prédire Y. Dans le cas présent, nous avons : R² = 227,04 / 279,3 = 0,8129, ce qui signale que 81,3 % de la variance du pourcentage de cyclistes est expliquée par la distance entre la municipalité et le centre-ville de la région métropolitaine. Tel que signalé dans la section 4.3.2, la racine carrée du coefficient de détermination (R²) est égale au coefficient de corrélation (\(r\)) entre les deux variables.

Calcul de la statistique F de Fisher

La statistique F de Fisher permet de vérifier la significativité globale du modèle.

\[\begin{equation} F = (n-2)\frac{R^2}{1-R^2} = (n-2)\frac{SCE}{SCR} \tag{4.16} \end{equation}\]

L’hypothèse nulle (H₀ avec \(\beta_1=0\)) est rejetée si la valeur calculée de F est supérieure à la valeur critique de la table F avec 1, n-2 degrés de liberté et un seuil \(\alpha\) (p = 0,05 habituellement) (voir la table des valeurs critiques de F, section 15). Notez que nous utilisons rarement la table F puisqu’avec la fonction pf(f obtenu, 1, n-2, lower.tail = FALSE), nous obtenons obtient directement la valeur de p associée à la valeur de F. Concrètement, si le test F est significatif (avec p < 0,05), plus la valeur de F est élevée, plus le modèle est efficace (et plus le R² sera également élevé).

Notez que la fonction summary renvoie les résultats du modèle, dont notamment le test F de Fisher.

# utiliser la fonction summary
summary(modele)

## 
## Call:
## lm(formula = Velo ~ KmCV, data = data)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.5652 -1.8062  0.0906  2.2241  2.7125 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  30.6032     2.0729  14.763 4.36e-07 ***
## KmCV         -1.4478     0.2456  -5.895 0.000364 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.556 on 8 degrees of freedom
## Multiple R-squared:  0.8129, Adjusted R-squared:  0.7895 
## F-statistic: 34.75 on 1 and 8 DF,  p-value: 0.0003637

Dans le cas présent, \(F = (10 - 2)\frac{\mbox{0,8129}}{\mbox{1-0,8129}} = (10-2)\frac{\mbox{227,04}}{\mbox{52,26}} = \mbox{34,75}\) avec une valeur de \(\mbox{p < 0,001}\). Par conséquent, le modèle est significatif.

4.4.4 Mise en œuvre dans R

Comment calculer une régression linéaire simple dans R. Rien de plus simple avec la fonction lm(formula = y ~ x, data= DataFrame).

df1 <- read.csv("data/bivariee/Reg.csv", stringsAsFactors = F)
## Création d'un objet pour le modèle
monmodele <- lm(Velo ~ KmCV, df1)
## Résultats du modèle avec la fonction summary
summary(monmodele)

## 
## Call:
## lm(formula = Velo ~ KmCV, data = df1)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -3.5652 -1.8062  0.0906  2.2241  2.7125 
## 
## Coefficients:
##             Estimate Std. Error t value Pr(>|t|)    
## (Intercept)  30.6032     2.0729  14.763 4.36e-07 ***
## KmCV         -1.4478     0.2456  -5.895 0.000364 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 2.556 on 8 degrees of freedom
## Multiple R-squared:  0.8129, Adjusted R-squared:  0.7895 
## F-statistic: 34.75 on 1 and 8 DF,  p-value: 0.0003637

## Calcul du MSE et du RMSE
MSE <- mean(monmodele$residuals^2)
RMSE <- sqrt(MSE)
cat("MSE=", round(MSE, 2), "; RMSE=", round(RMSE,2), sep="")

## MSE=5.23; RMSE=2.29

4.4.5 Comment rapporter une régression linéaire simple

Nous avons calculé une régression linéaire simple pour prédire le pourcentage d’actifs occupés utilisant le vélo pour se rendre au travail en fonction de la distance entre la municipalité et le centre-ville de la région métropolitaine (en kilomètres). Le modèle obtient un F de Fisher significatif (F(1,8) = 34,75, p < 0,001) et un R² de 0,813. Le pourcentage de cyclistes peut être prédit par l’équation suivante : 30,603 - 1,448 x (distance au centre-ville en km).

Références

Messerli, Franz H. 2012. « Chocolate consumption, cognitive Function, and Nobel laureates. » The new England Journal of Medicine 367 (16): 1563‑1564. https://doi.org/10.1056/nejmon1211064.