7.6 Diagnostics de la régression
Pour illustrer comment vérifier si le modèle respecte ou non les hypothèses de la régression, nous utilisons le modèle suivant :
modele3 <- lm(VegPct ~ log(HABHA)+poly(AgeMedian,2)+Pct_014+Pct_65P+Pct_MV+Pct_FR, data = DataFinal)
7.6.1 Nombre d’observations
Tous les auteurs ne s’entendent pas sur le nombre d’observations minimal que devrait comprendre une régression linéaire multiple, tant s’en faut! Parallèlement, d’autres auteurs proposent aussi des méthodes de simulation pour estimer les coefficients de régression sur un jeu de données comprenant peu d’observations. Bien qu’aucune règle ne soit bien établie, la question du nombre d’observations mérite d’être posée puisqu’un modèle basé sur trop peu d’observations risque de produire des coefficients de régression peu fiables. Par faible fiabilité des coefficients, nous entendons que la suppression d’une ou de plusieurs observations pourrait drastiquement changer l’effet et/ou la significativité d’une ou de plusieurs variables explicatives.
Dans un ouvrage classique intitulé Using Multivariate Statistics, Barbara Tabachnick et Linda Fidell (2007, 123‑124) proposent deux règles de pouce (à la louche) :
- \(n \geq 50 + 8k\) avec \(n\) et \(k\) étant respectivement les nombres d’observations et de variables indépendantes, pour tester le coefficient de corrélation multiple (R2).
- \(n \geq 104 + k\) pour tester individuellement chaque variable indépendante.
Dans le modèle, nous avons 10 210 observations et variables indépendantes. Les deux conditions sont donc largement respectées.
7.6.2 Normalité des résidus
Pour vérifier si les résidus sont normalement distribués, trois démarches largement décrites dans la section 2.5.4 peuvent être utilisées :
- le calcul des coefficients d’asymétrie et d’aplatissement;
- les tests de normalité, particulièrement celui de Jarque-Bera basé sur un test multiplicateur de Lagrange;
- les graphiques (histogramme avec courbe normale et diagramme quantile-quantile) (figure 7.9).
Les deux premières démarches étant parfois très restrictives, nous accordons habituellement une attention particulière aux graphiques.
Pour notre modèle, les coefficients d’asymétrie (−0,263) et d’aplatissement (1,149) signalent que la distribution est plutôt symétrique, mais leptokurtique, c’est-à-dire que les valeurs des résidus sont bien réparties autour de 0, mais avec une faible dispersion. Puisque la valeur de p associée au test de Jarque-Bera est inférieure à 0,05, nous pouvons en conclure que la distribution des résidus est anormale. La forme pointue de la distribution est d’ailleurs confirmée à la lecture de l’histogramme avec la courbe normale et du diagramme quantile-quantile.
## Skewness Kurtosis
## -0.161 1.193##
## Robust Jarque Bera Test
##
## data: residus
## X-squared = 513.15, df = 2, p-value < 2.2e-16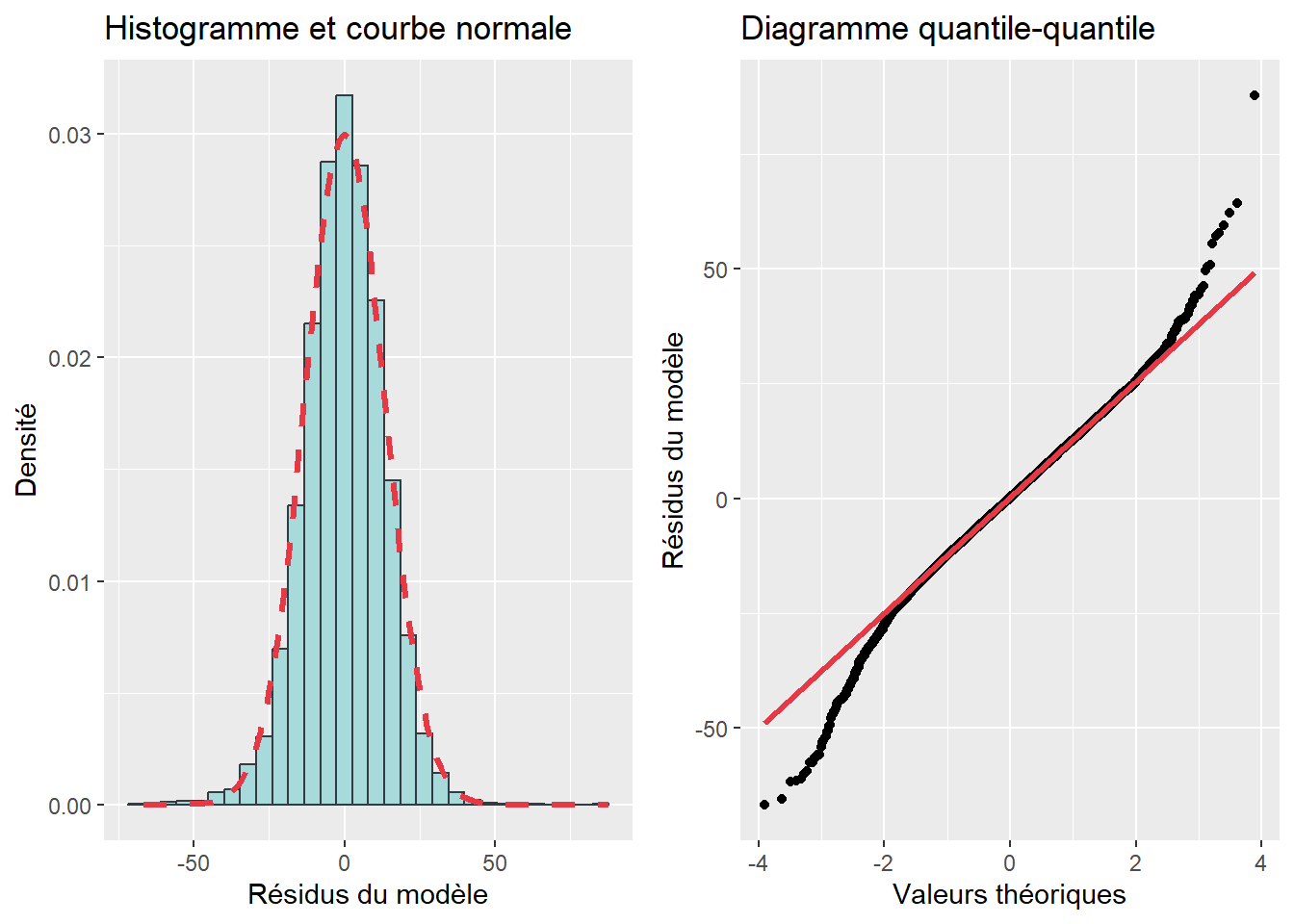
Figure 7.9: Vérification de la normalité des résidus
7.6.3 Linéarité et homoscédasticité des résidus
Un modèle est efficace si la dispersion des résidus est homogène sur tout le spectre des valeurs prédites de la variable dépendante. Dans le cas d’une absence d’homoscédasticité – appelée problème d’hétéroscédasticité –, le nuage de points construit à partir des résidus et des valeurs prédites (figure 7.10) prend la forme d’une trompette ou d’un entonnoir : les résidus sont alors faibles quand les valeurs prédites sont faibles et sont de plus en plus élevés au fur et à mesure que les valeurs prédites augmentent.
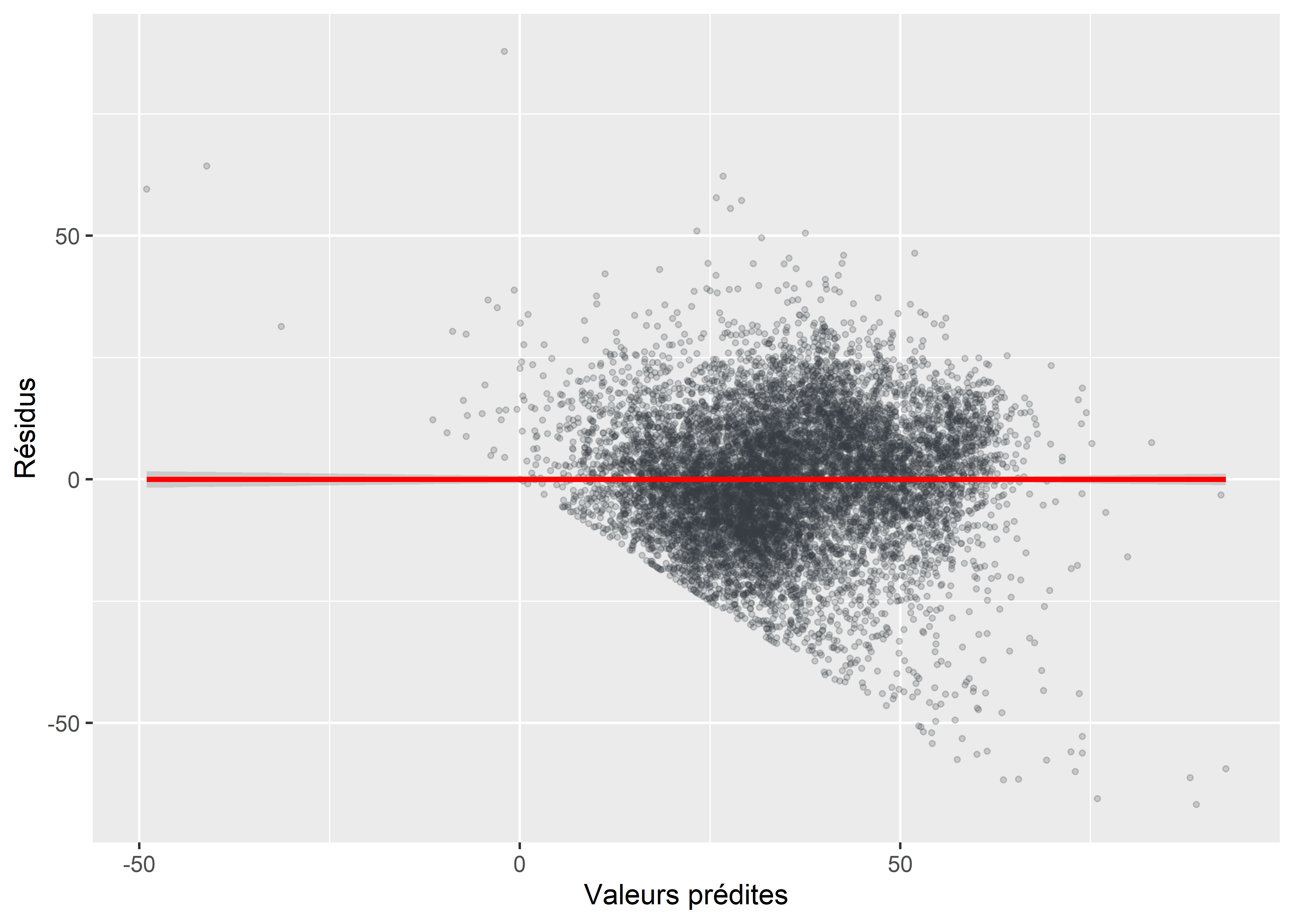
Figure 7.10: Distribution des résidus en fonction des valeurs prédites
Le test de Breusch-Pagan est souvent utilisé pour vérifier l’homoscédasticité des résidus. Il est construit avec les hypothèses suivantes :
- H0 : homoscédasticité, c’est-à-dire que les termes d’erreur ont une variance constante à travers les valeurs prédites.
- H1 : hétéroscédasticité.
Si la valeur de p associée à ce test est inférieure à 0,05, nous réfutons l’hypothèse nulle et nous concluons qu’il y a un problème d’hétéroscédasticité, ce qui est le cas pour notre modèle.
##
## studentized Breusch-Pagan test
##
## data: modele3
## BP = 1722, df = 8, p-value < 2.2e-167.6.4 Absence de multicolinéarité excessive
Un modèle présente un problème de multicolinéarité excessive lorsque deux variables indépendantes ou plus sont très fortement corrélées entre elles. Rappelez-vous qu’un coefficient de régression estime l’effet d’une variable dépendante (\(X_k\)) si toutes les autres VI restent constantes (c’est-à-dire une fois les autres VI contrôlées, toutes choses étant égales par ailleurs…).
Prenons deux variables indépendantes (\(X_1\) et \(X_2\)) fortement corrélées avec un coefficient de Pearson très élevé (0,90 par exemple). Admettons que chacune des deux VI a un effet important et significatif sur votre VD lorsqu’une seule est introduite dans le modèle. Si les deux variables sont introduites dans le même modèle, vous évaluez donc l’effet de \(X_1\) une fois contrôlé \(X_2\) et l’effet de \(X_2\) une fois contrôlé \(X_1\). Par conséquent, l’effet de l’une des deux devient très faible, voire probablement non significatif.
7.6.4.1 Comment évaluer la multicolinéarité?
Pour ce faire, nous utilisons habituellement le facteur d’inflation de la variance (Variance Inflation Factor – VIF en anglais). Le calcul de ce facteur pour chaque VI est basé sur trois étapes.
- Pour chaque VI, nous construisons un modèle de régression multiple où elle est expliquée par toutes les autres variables indépendantes du modèle. Par exemple, pour la première VI (\(X_1\)), l’équation du modèle s’écrit :
\[\begin{equation} X_1 = b_0 + b_2X_2 +\ldots+ b_kX_k + e \tag{7.29} \end{equation}\]
- À partir de cette équation, nous obtenons ainsi un \(R^2\) qui nous indique la proportion de la variance de \(X_1\) expliquée par les autres VI. Par convention, nous calculons la tolérance (équation (7.30)) qui indique la proportion de la variance de \(X_k\) n’étant pas expliquée par les autres VI. En guise d’exemple, une valeur de tolérance égale à 0,1 signale que 90nbsp;% de la variance de \(X_k\) est expliqué par les autres variables, ce qui est un problème de multicolinéarité en soit. Concrètement, plus la valeur de la tolérance est proche de zéro, plus c’est problématique.
\[\begin{equation} \mbox{Tolérance}_k=1-R_k^2=\frac{1}{VIF_k} \tag{7.30} \end{equation}\]
- Puis, nous calculons le facteur d’inflation de la variance (équation (7.31)). Là encore, des règles de pouce (à la louche) sont utilisées. Certains considéreront une valeur de VIF supérieur à 10 (soit une tolérance à 0,1 ou inférieure) comme problématique, d’autres retiendront le seuil de 5 plus conservateur (soit une tolérance à 0,2 ou inférieure).
\[\begin{equation} VIF_k = \frac{1}{1-R_k^2} \tag{7.31} \end{equation}\]
Pour notre modèle, toutes les valeurs de VIF sont inférieures à 2, indiquant, sans l’ombre d’un doute, l’absence de multicolinéarité excessive.
## GVIF Df GVIF^(1/(2*Df))
## VilleMtl 1.319 1 1.149
## log(HABHA) 1.342 1 1.159
## poly(AgeMedian, 2) 1.399 2 1.087
## Pct_014 1.601 1 1.265
## Pct_65P 1.317 1 1.147
## Pct_MV 1.483 1 1.218
## Pct_FR 1.818 1 1.3487.6.4.2 Comment régler un problème de multicolinéarité?
La prudence est de mise! Si une ou plusieurs variables présentent une valeur de VIF supérieure à 5, construisez une matrice de corrélation de Pearson (section 4.3.7) et repérez les valeurs de corrélation supérieures à 0,8 ou inférieures à −0,8. Vous repérerez ainsi les corrélations problématiques entre deux variables indépendantes du modèle.
Refaites ensuite un modèle en ôtant la variable indépendante avec la plus forte valeur de VIF (7 ou 12 par exemple), et revérifiez les valeurs de VIF. Refaites cette étape si le problème de multicolinéarité excessive persiste.
Une multicolinéarité excessive n’est pas forcément inquiétante
Nous avons vu plus haut comment introduire des variables indépendantes particulières comme des variables d’interaction (\(X_1 \times X_2\)) ou des variables sous une forme polynomiale (ordre 2 : \(X_1 + X_1^2\); ordre 3 : \(X_1 + X_1^2 + X_1^3\), etc.). Bien entendu, ces termes composant les variables d’interaction ou d’une forme polynomiale sont habituellement fortement corrélés entre eux. Cela n’est toutefois pas problématique!
Dans l’exemple ci-dessous, nous obtenons deux valeurs de VIF très élevées pour la variable d’interaction Pct_014:DistCBDkm (16,713) et l’un des paramètres à partir duquel elle est calculée, soit DistCBDkm (12,526).
## GVIF Df GVIF^(1/(2*Df))
## log(HABHA) 1.426 1 1.194
## poly(AgeMedian, 2) 1.768 2 1.153
## Pct_014 3.326 1 1.824
## Pct_65P 1.359 1 1.166
## Pct_MV 1.495 1 1.223
## Pct_FR 1.810 1 1.345
## DistCBDkm 12.526 1 3.539
## Pct_014:DistCBDkm 16.713 1 4.0887.6.5 Absence d’observations aberrantes
7.6.5.1 Détection des observations très influentes du modèle
Lors de l’analyse des corrélations (section 4.3), nous avons vu que des valeurs extrêmes peuvent avoir un impact important sur le coefficient de corrélation de Pearson. Le même principe s’applique à la régression multiple, pour laquelle nous nous s’attendrions à ce que chaque observation joue un rôle équivalent dans la détermination de l’équation du modèle.
Autrement dit, il est possible que certaines observations avec des valeurs extrêmes – fortement dissemblables des autres – aient une influence importante, voire démesurée, dans l’estimation du modèle. Concrètement, cela signifie que si elles étaient ôtées, les coefficients de régression et la qualité d’ajustement du modèle pourraient changer drastiquement. Deux mesures sont habituellement utilisées pour évaluer l’influence de chaque observation sur le modèle :
- La statistique de la distance de Cook qui mesure l’influence de chaque observation sur les résultats du modèle. Brièvement, la distance de Cook évalue l’influence de l’observation i en la supprimant du modèle (équation (7.32)). Plus sa valeur est élevée, plus l’observation joue un rôle important dans la détermination de l’équation de régression.
\[\begin{equation} D_i = \frac{\sum_{j=1}^n(\widehat{y}_i-\widehat{y}_{i(j)})^2}{ks^2} \tag{7.32} \end{equation}\]
avec \(\widehat{y}_{i(j)}\) la valeur prédite quand l’observation i est ôté du modèle, k le nombre de variables indépendantes et \(s^2\) l’erreur quadratique moyenne du modèle.
- La statistique de l’effet levier (leverage value en anglais) qui varie de 0 (aucune influence) à 1 (explique tout le modèle). La somme de toutes les valeurs de cette statistique est égale au nombre de VI dans le modèle.
Quel critère retenir pour détecter les observations avec potentiellement une trop grande influence sur le modèle?
Pour les repérer, voire les supprimer, plusieurs auteur(e)s proposent les seuils suivants : \(4/n\) ou \(8/n\) ou \(16/n\). Avec 10210 observations dans le modèle, les seuils seraient les suivants :
## Nombre d'observations = 10210 (100 %)
## 4/n = 0.00039
## 8/n = 0.00078
## 16/n = 0.00157
## Observations avec une valeur supérieure ou égale aux différents seuils
## 4/n = 605 soit 5.93 %
## 8/n = 275 soit 2.69 %
## 16/n = 133 soit 1.3 %Le critère de \(4/n\) étant plutôt sévère, nous privilégions généralement celui de \(8/n\), voire \(16/n\). Il est aussi possible de construire un nuage de points pour les repérer (figure 7.11).
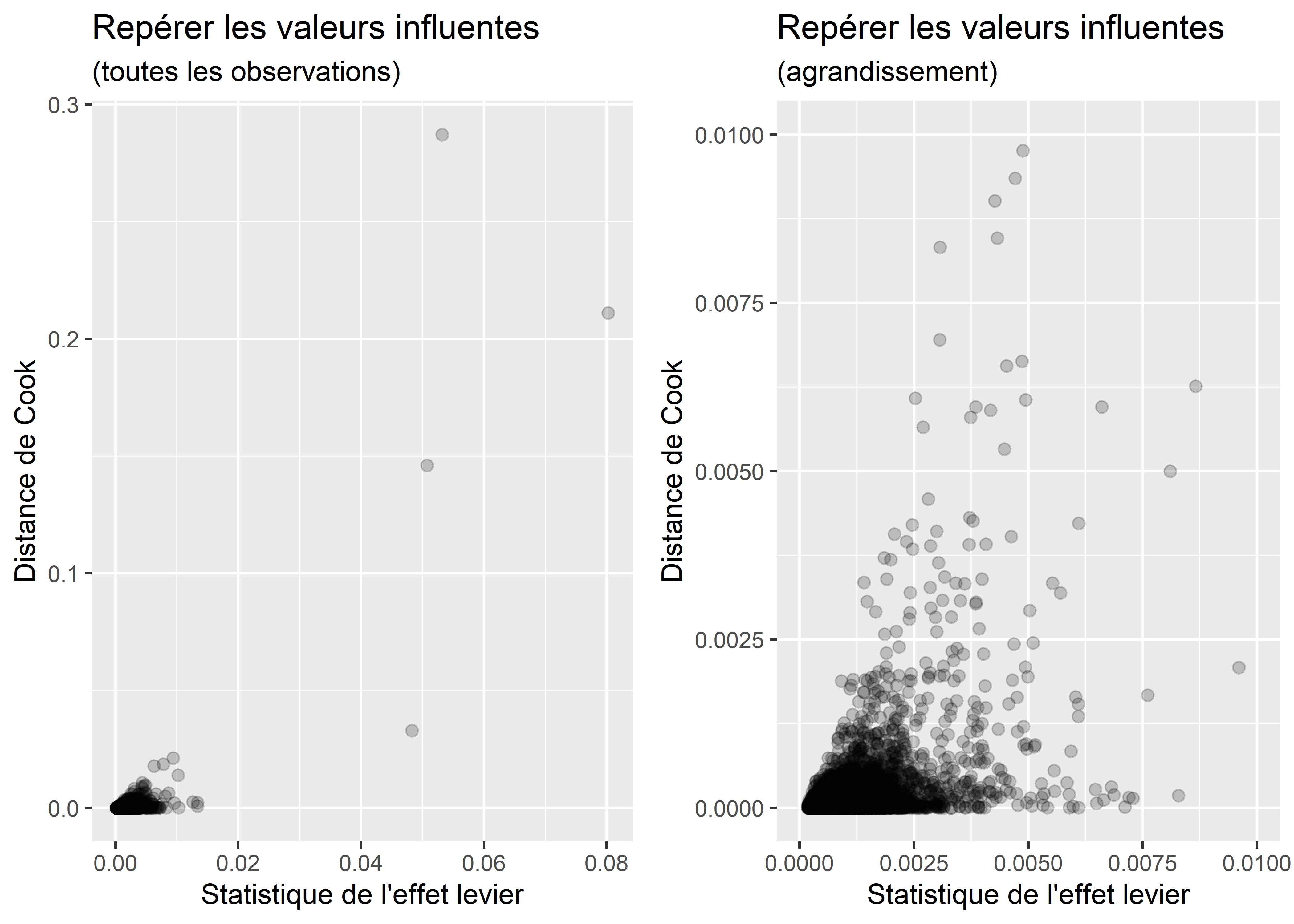
Figure 7.11: Repérage graphique les valeurs influentes du modèle
7.6.5.2 Quoi faire avec les observations très influentes du modèle
Trois approches sont possibles :
Recourir à des régressions boostrap, ce qui permet généralement de supprimer l’effet de ces observations. Brièvement, le principe général est de créer un nombre élevé d’échantillons du jeu de données initial (1000 à 2000 itérations par exemple) et de construire un modèle de régression pour chacun d’eux. On obtiendra ainsi des intervalles de confiance pour les coefficients de régression et les mesures d’ajustement du modèle.
Supprimer les observations trop influentes (avec l’un des critères de \(4/n\), \(8/n\) et \(16/n\) vus plus haut). Une fois supprimées, il convient 1) de recalculer le modèle, 2) de refaire le diagnostic de la régression au complet et finalement, 3) de comparer les modèles avant et après suppression des valeurs trop influentes, notamment la qualité d’ajustement du modèle (R2 ajusté) et les coefficients de régression. Des changements importants indiqueront que le premier modèle est potentiellement biaisé.
Utiliser un modèle linéaire généralisé (GLM) permettant d’utiliser une distribution différente correspondant plus à votre jeu de données (chapitre 8).